2. 国网重庆电力公司 电力科学研究院, 重庆 400021
2. State Grid Chongqing Electric Power Research Institute, Chongqing 400021, P. R. China
世界能源短缺问题日益严重,环境问题日益紧迫,电动汽车作为一种新兴的低碳、无污染的交通工具,在缓解能源危机、促进人类与自然环境和谐友好发展等方面具有传统燃油汽车无法比拟的优势,目前已经成为世界各国政府、汽车制造商以及能源企业关注的焦点,中国更是将电动汽车列入战略性新兴产业的高度[1]。
V2G(vehicle to grid)指电动汽车和电网之间的互动技术,一般通过充电站和充电桩来实现[2]。电动汽车可以通过V2G技术来为电网提供一些辅助服务,比如调峰、调频等,还可以提高电网对间歇性新能源发电的消纳能力,V2G技术在近些年受到了广泛关注和深入研究[3]。
关于电动汽车接入后对原电网的影响,已有相关研究成果发表。参考文献[4]分别建立了电动汽车在时间和空间上的优化模型,并采用整数规划方法进行求解,从而得到时间空间两阶段控制对降低电网负荷峰值的影响。参考文献[5]在分析电动汽车充放电成本和经济效益的基础上,考虑用户起始充放电的泊松分布特性,建立了以电网总负荷波动最小为目标的最优峰谷电价模型。参考文献[6]以电动汽车的充电设施为研究控制对象,采用多目标以及分层分区的有序充电优化控制模型。在此基础上,采用序列二次规划算法和动态规划算法进行求解,通过IEEE34节点算例分析验证了模型和算法的有效性。
文中分别从电网侧和用户侧的角度出发,基于V2G构建了不同的电动汽车有序充放电模型,采用粒子群优化算法进行仿真求解验证。在电网侧主要以减小负荷曲线峰谷差、平抑负荷波动为目标,从而达到削峰填谷的目的;在用户侧主要以使用户参与V2G服务的经济收益最大为目标,从而极大地调动用户参与V2G服务的积极性。通过两方面的算例仿真验证,得到并分析了采用有序充放电策略前后电动汽车对电网负荷曲线的影响。
1 电网侧的电动汽车有序充放电控制策略电网侧的V2G调度策略,是将控制中心管辖区域范围的电动汽车视为一个特殊的分布式电源整体,针对控制中心统计、上传的信息作为制定调度策略的依据。而电动汽车控制中心制定的调度策略则是以整个区域范围内所有加入充放电计划的电动汽车个体实现具体充放电的功率分配为目的[7]。
1.1 V2G参与电网调峰的控制模型电动汽车参与电网侧的V2G控制策略以平抑负荷曲线波动性为优化目标, 其决策变量为每千辆电动汽车在每一时段与电网之间交换功率的大小。采用粒子群优化算法来进行优化求解,设定粒子的维数为n*24, 其中, n是车辆千辆数, 由此可见粒子维数是随着电动汽车数量变化而变化的。粒子I的位置为
| $ {P_{\rm{I}}} = \left[ {{P_{1,1}},{P_{1,2}}, \cdots ,{P_{1,24}},{P_{2,1}}, \cdots ,{P_{2,24}}, \cdots ,{P_{i,j}}, \cdots ,{P_{n,24}}} \right]。$ | (1) |
电动汽车参与电网侧的V2G控制策略以辅助调峰为主要目标, 将1天分为24个时间段, 以每千辆电动汽车在每一时间段的充放电功率为决策变量, 构造目标函数
| $ \min f = \sum\nolimits_{t = 1}^{24} {{{\left( {{P_{Lt}} - {P_{{\rm{av}}}} - \sum\nolimits_{i = 1}^n {{P_{it}}} } \right)}^2}} , $ | (2) |
| $ {P_{{\rm{av}}}} = \sum\nolimits_{t = 1}^{24} {{P_{Lt}}/24} , $ | (3) |
式中:f以电网负荷曲线的平均方差最小为目标函数;n为电动汽车千辆数;PLt为t时段区域的负荷功率;Pav为区域负荷功率的平均值;Pit为第i千辆电动汽车在t时段的充放电功率,kW,正值表示放电,负值表示充电。
1.1.2 约束条件电动汽车参与电网互动受到的约束条件主要为电动汽车可用时间、充放电功率、电池可用容量及用户设置的最低荷电状态(SOC, state of charge)约束4个方面。
1) 可用时间约束
由于车辆最基本的作用还是代步工具, 故电动汽车不可能24 h都处于连网状态, 为了更符合实际情况,根据车辆的出行使用规律考虑了车辆的可用时间约束, 当电动汽车没有连接网络时,其可用功率为零。
2) 功率约束
功率约束主要体现在电动汽车充放电电流的约束, 充电电流最大值为额定电流的一半,放电电流最大值为额定电流2倍。接着考虑线路功率容量约束,充放电功率不超过20 kW。有
| $ {P_{it\max }} = \min \left( {15,{V_{it}} \times 2{I_{iN}}} \right), $ | (4) |
| $ {P_{it\min }} = \max \left( { - 20, - {V_{it}} \times \frac{1}{2}{I_{iN}}} \right), $ | (5) |
式中:Pit为电动汽车i在t时刻的充放电功率;IiN决定于电动汽车电池型号,100 A·h的电池对应此值为100 A;Vit为电动汽车电池实际充电电压值。
3) 可用容量约束
在现阶段电动汽车电池的容量是一定的,电动汽车参与电网侧V2G控制的可用V2G容量是一个有限值。考虑对电池寿命的影响,电池剩余最低容量不能低于电池总容量的20%。
4) 用户设置离开时最低SOC
用户可以设置车辆离开时的最低电池容量, 考虑满足用户的行程需求电量, 电池容量不低于电池容量的30%。约束条件为
| $ {\rm{SO}}{{\rm{C}}_{it}} \ge 0.3, $ | (6) |
式中:SOCit为电动汽车i在t时刻的荷电状态。
1.2 含约束条件的粒子群优化算法1) 粒子群优化算法的基本原理
粒子群优化算法(PSO, particle swarm optimization algorithm)基于种群个体之间通过信息共享和协作搜寻最优解的理念,是一种基于群体迭代优化的随机型启发式搜索算法。PSO在优化求解过程中,每个粒子作为决策变量都有相应的位置和速度以及由目标函数所决定的适应度函数值。其中,粒子的位置代表问题的可行解,粒子的速度决定了粒子移动的方向和距离,粒子的适应函数值由适应度函数决定,其值的大小表示粒子的最优程度[8]。
文中的问题是一高维度、多变量和多约束的优化问题,粒子群算法原理简单,通用性强,适合群体搜索记忆,从而保留局部个体和全局种群的最优信息。文中采用粒子群优化算法来进行模型的求解。
PSO在每次迭代过程中不是完全随机的,而是通过追踪2个极值来进行更新,这2个极值分别为粒子本身所搜寻到的局部最优解和所有粒子在当前时刻搜寻到的全局最优解[9]。粒子i在D维解空间中的位置可表示为矢量xi=[xi1, xi2, xi3, ...xiD],速度为vi=[vi1, vi2, vi3, ...viD]。粒子根据式(7)更新自己的速度和位置。
| $ \mathit{\boldsymbol{v}}_{ij}^{\left( {k + 1} \right)} = \omega \mathit{\boldsymbol{v}}_{ij}^{\left( k \right)} + {c_1}{\rm{ran}}{{\rm{d}}_1}\left( {\mathit{\boldsymbol{p}}_{{\rm{best}},ij}^{\left( k \right)} - \mathit{\boldsymbol{x}}_{ij}^{\left( k \right)}} \right) + {c_2}{\rm{ran}}{{\rm{d}}_2}\left( {\mathit{\boldsymbol{g}}_{{\rm{best}},ij}^{\left( k \right)} - \mathit{\boldsymbol{x}}_{ij}^{\left( k \right)}} \right), $ | (7) |
| $ \mathit{\boldsymbol{x}}_{ij}^{\left( {k + 1} \right)} = \mathit{\boldsymbol{x}}_{ij}^{\left( k \right)} + \mathit{\boldsymbol{v}}_{ij}^{\left( {k + 1} \right)}, $ | (8) |
式中:k代表迭代的次数;vij(k)代表粒子i在第k次迭代中D维向量的速度;pbest,ij(k)为粒子i当前个体最优位置对应的位置向量;gbest,ij(k)为整个群体中对应的最优位置的位置向量。ω称为惯性权重,能使粒子保持运动惯性,是粒子前一次的飞行速度对此次飞行速度的影响因子(较大的值有利于粒子跳出局部最优点,扩大搜索的范围;较小的值有利于算法的收敛);c1和c2称为学习因子,文中取c1=c2=2;rand1和rand2为[0, 1]之间的随机数。惯性权重系数搜索过程为
| $ \omega = {\omega _{\max }} - k\left( {{\omega _{\max }} - {\omega _{\min }}} \right)/{k_{\max }}。$ | (9) |
2) 粒子群算法的参数设置
粒子个数n:粒子个数的多少是根据优化问题的复杂程度来决定的,通常设置为20~50[10]。
最大速度Vmax:粒子的最大速度限制了粒子在一次迭代过程中移动的距离,如果某一维更新后的速度超过了这个速度阈值,则该维速度便被修改为Vmax。研究表明:速度值过大,易导致粒子跳出全局最优解,而过小则会造成搜索解空间不够充分,将粒子的每一维速度都控制在[-VDmax, VDmax]之间。
最大迭代次数kmax:起到终止算法的作用,通常设置为1 000[11]。
3) 带约束条件的PSO算法流程
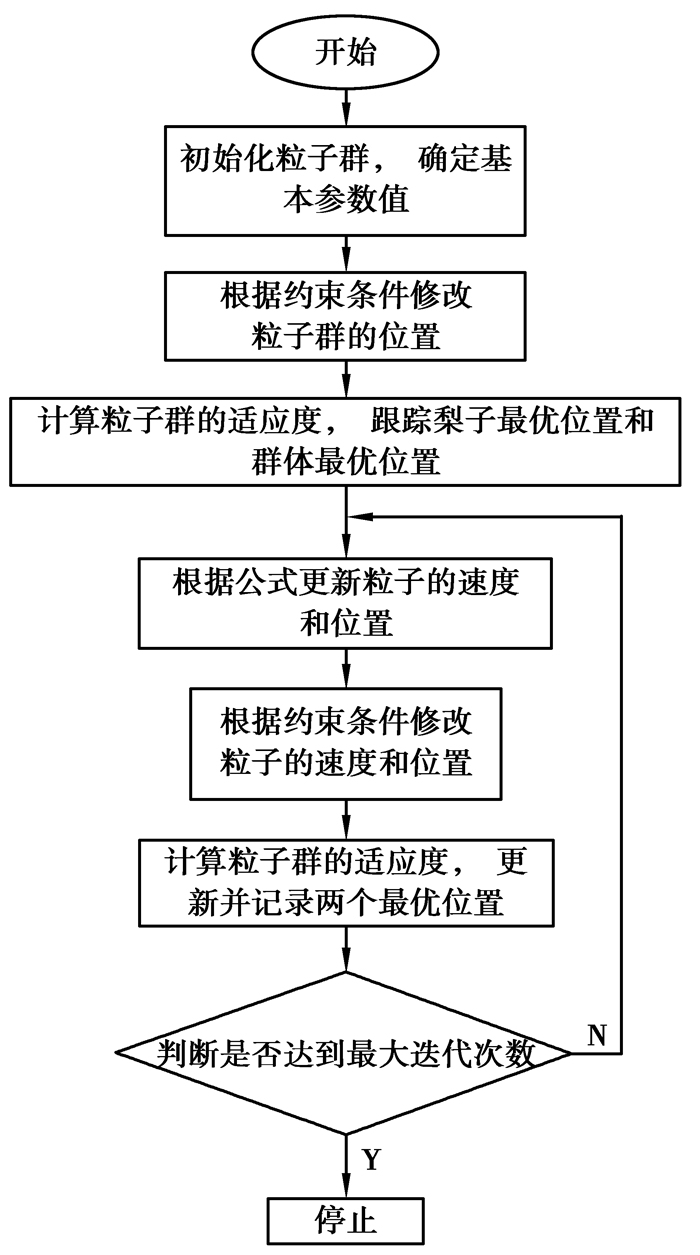
① 初始化粒子群,确定粒子的基本参数值;
② 根据相关约束条件修改粒子群的位置;
③ 计算粒子群的适应度函数值, 跟踪粒子群群体中个体最优位置和群体最优位置;
④ 根据式(7)和式(8)更新粒子的速度和位置;
⑤ 根据约束条件检查粒子速度和位置是否超过限定值, 如果超出限值范围, 将其限制为该限定值, 并重复步骤2;
⑥ 计算粒子群的适应度函数值, 更新并记录粒子群群体中个体最优位置群体最优位置;
⑦ 判断是否达到最大迭代次数,若是,则停止计算;否则,返回步骤4。
带约束的粒子群算法流程图,如图 1所示。
|
图 1 带约束粒子群算法流程 Figure 1 Algorithm flow chart of constrained PSO |
以重庆地区2015年夏季典型日负荷曲线为例, 表 1给出日负荷功率值, 负荷值为小时间隔数据。
| 表 1 重庆地区2015年夏季典型日负荷 Table 1 Typical summer load of Chongqing in 2015 |
根据重庆地区2015年夏季典型日负荷得出特性曲线,如图 2所示, 水平直线为一天负荷的平均值,大小为1 493 MW。观察负荷曲线可以发现:09:00—13:00和18:00—22:00为一天中的2个负荷峰值,01:00—07:00为一天中的负荷谷值。如果可以科学有效地控制电动汽车的充放电来进行“削峰填谷”,将明显减小负荷的峰谷差,同时增大电网侧的负荷率。

|
图 2 重庆地区夏季典型日负荷特性曲线 Figure 2 Typical summer load characteristic curve of Chongqing |
本算例中选择私家电动汽车来参与V2G互动,根据相关文献描述,各类私家电动汽车的电池容量相差不大。以私家电动汽车电池容量为100 A·h为例, 故IiN=100 A,且各电动汽车的初始电池容量SOC0i=0.6(i=1, 2, …)。按照前面分析的功率约束条件, 取电动汽车的最大充放电功率分别为15 kW和20 kW, 该算例中考虑电动汽车可用时间约束和用户对最低SOC的设置约束。表 2列出了V2G站电动汽车参数情况。
| 表 2 电网侧V2G电动汽车参数设置 Table 2 Parameter setting of V2G EVs on power grid side |
粒子群算法中参数设置,如表 3所示,粒子数为N=50, 惯性权重系数ω采用文献中提到的线性递减策略[12], ωmax=0.9, ωmin=0.4;迭代次数Tmax=1 000;粒子速度取经验值vmax=5, vmin=-5。
| 表 3 粒子群算法中参数设置 Table 3 Parameter setting of PSO |
以重庆市2015年夏季的典型日负荷曲线为基本负荷,考虑到基本负荷年增长率为10%,分别计算得到2020年、2025年和2030年重庆市夏季典型日负荷曲线如表 4~表 6所示。
| 表 4 重庆地区2020年夏季典型日负荷 Table 4 Typical summer load of Chongqing in 2020 |
| 表 5 重庆地区2025年夏季典型日负荷 Table 5 Typical summer load of Chongqing in 2025 |
| 表 6 重庆地区2030年夏季典型日负荷 Table 6 Typical summer load of Chongqing in 2030 |
根据前面的分析预测,在2020年重庆地区的私家电动汽车大约为5万辆左右,以5万辆电动汽车的容量来响应日负荷变化曲线。以目标函数f取得最小值为最优解,采用基本PSO算法进行计算。
|
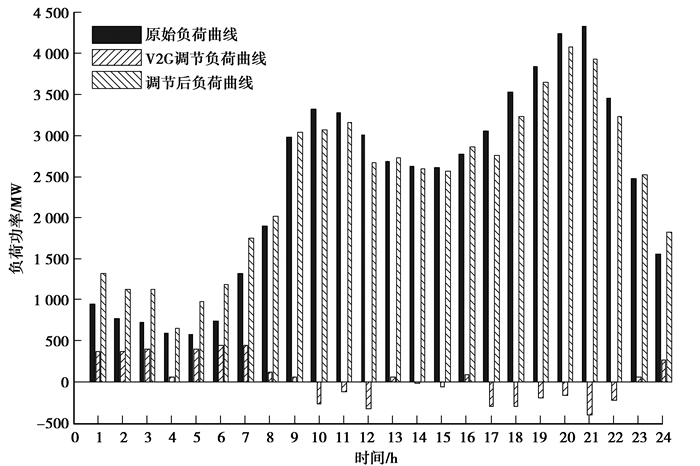
图 3 电动汽车参与电网互动前后负荷曲线(2020年) Figure 3 The load curve before and after the interaction of EVs (2020) |

|
图 4 目标函数值与迭代次数的关系曲线 Figure 4 The relationship curve between the objective function value and the number of iterations |
1) 原始负荷曲线在01:00—07:00期间为负荷低估期, 而在09:00—13:00和18:00—22:00分别出现了2个负荷高峰;
2) 电动汽车的V2G调节负荷基本上实现了在负荷高峰期放电, 在负荷低谷期充电的效果;
3) 经过V2G调节后的电网负荷曲线与原始曲线相比有明显的改善;
4) V2G调节后的负荷曲线最大值为4 053 MW, 平均负荷2 416 MW,负荷率为0.596;原始负荷曲线最大值为4 328 MW,平均负荷2 388 MW,负荷率为0.552。由此可见,电动汽车与电网的互动可以增大电网侧的负荷率;
5) 随着迭代次数的增加,目标函数值逐渐收敛并趋于稳定,在迭代500次之后就逐渐稳定在最终值。
在2025年重庆地区的私家电动汽车大约为15万辆左右,以15万辆电动汽车的充放电容量来响应日负荷变化曲线,电动汽车参与前后的日负荷曲线,如图 5所示。V2G调节后的负荷曲线最大值为6 001 MW, 平均负荷3 841 MW,负荷率为0.640;原始负荷曲线最大值为7 006 MW,平均负荷3 866 MW,负荷率为0.552。

|
图 5 电动汽车参与电网互动前后负荷曲线(2025年) Figure 5 The load curve before and after the interaction of EVs (2025) |
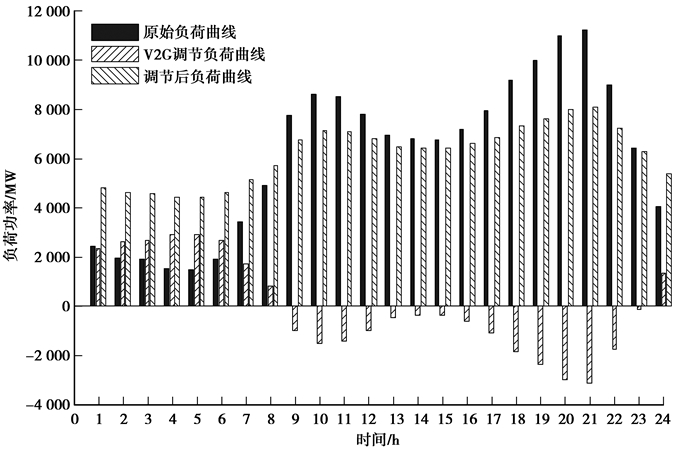
在2030年重庆地区的私家电动汽车大约为75万辆左右,以75万辆电动汽车的充放电容量来响应日负荷变化曲线,电动汽车参与前后的日负荷曲线,如图 6所示。V2G调节后的负荷曲线最大值为8 098 MW, 平均负荷6 197 MW,负荷率为0.765;原始负荷曲线最大值为11 226 MW,平均负荷6 194 MW,负荷率为0.552。
|
图 6 电动汽车参与电网互动前后负荷曲线(2030年) Figure 6 The load curve before and after the interaction of EVs (2030) |
通过仿真算例发现,随着参与车网互动的电动汽车数量增加,V2G调节后的负荷曲线峰谷差大大减小,负荷趋向于平均值,电网侧的负荷率也显著升高,这将极大地有利于电网的高效稳定运行。由于可调节车辆数的增加,电动汽车V2G可用容量也大大增加,目标函数的收敛速度也明显加快。
2 用户侧的电动汽车有序充放电控制策略从用户侧角度考虑,以电动汽车用户参与V2G服务获得经济收益为目的,为参与V2G的电动汽车用户制定充放电控制策略。参与V2G的电动汽车每天集中在一些时段进行充放电,每次只选择充电或放电一种模式,对电动汽车电池的寿命损耗并不是太大,只是将电动汽车充电负荷在时间尺度上进行了一个平移,而对充放电次数没有太大影响。在实行分时电价的基础上,以用户参与V2G获得的经济收益最大化为目标函数,同时考虑电动汽车电池充放电成本、电池充放电约束和可用容量可用时间等约束条件建立数学仿真模型[13]。采用粒子群优化算法对参与V2G的电动汽车一天中充放电时间组合进行最优控制选择[14]。
分时电价(TOU, time of use)是一种有效的需求侧管理手段,是把电价按照一天中24 h负荷的高峰和低谷划分成峰、平、谷3种时段[15],采用国内工业用电分时电价划分方式划分为:峰时段8 h(08:00—12:00,19:00—23:00),电价为0.78元/(kWh);平时段8 h(07:00—08:00,12:00—19:00),电价为0.52元/(kWh);谷时段8 h(23:00—07:00),电价为0.26元/(kWh)[16]。
采用分时电价能够更好地发挥电价经济杠杆的作用,在用电高峰时段采用高电价,在用电低谷时段采用低电价,能够有效减少电网的峰谷差率,降低电网发电成本,提高了整个电力系统的经济效益[17]。考虑到电动汽车充放电功能处于示范阶段,假设放电分时电价与充电分时电价相同[18]。
2.1 V2G响应电价的控制模型在V2G的运行过程中,电池频繁地充放电会对电池的使用寿命产生影响,需要考虑电池的损耗成本。另外,还要计及电动汽车的可用时间、可用容量和实时电价等约束条件[19]。
2.1.1 目标函数在模型中将每天分为24个时段,电动汽车在每个时段都有可能与电网实现功率的交换,将这些交换的能量通过电价这个媒介用货币的形式表现出来。当实现全面智能电网后,在施行实时电价的基础上,每一个时段市场中的电价都是可能有差异的。根据实时变化的电价,电动汽车并网充电和放电行为会给用户带来经济方面的差价收益,以电动汽车参与电网峰谷时段充放电经济收益最大化为目标函数1:
| $ {f_1} = \max \sum\nolimits_{t = 1}^{24} {\left( {\sum\nolimits_{i = 1}^n {\left( {{D_{it}} - {C_{it}} - {l_{it}}} \right)} } \right)} , $ | (10) |
| $ {D_{it}} = {p_t}{p_{it}}/{E_d}, $ | (11) |
| $ {C_{it}} = {p_t}{p_{it}}{E_c}, $ | (12) |
| $ {l_{it}} = C{E_v}, $ | (13) |
式中:pt表示t时刻的市场电价;Cit表示第i辆车在t时刻的充电电价成本;Dit表示第i辆车t时刻的放电获取的电价收益;pit表示第i辆车在t时刻与电网的交换功率,同样设充电功率为负值,放电功率为正值;lit表示电池的损耗成本;C为电池单位能量引起的成本损耗;Ev为电动汽车参与的V2G能量变化量,若某一时刻电动汽车没有参与V2G过程则为0;n表示车辆数;Ec和Ed表示车载电池的充电放电效率,均取0.9。
为体现电动汽车有序充放电在电网削峰填谷方面的作用,以实行峰谷电价政策后的电网日负荷率最大为目标函数2:
| $ {f_2} = \max \left( {{P_{av}}/{P_{\max }}} \right), $ | (14) |
| $ {P_{av}} = \sum\nolimits_{t = 1}^{24} {{P_t}/24} , $ | (15) |
式中:Pav表示实行峰谷分时电价后电网的日负荷平均值;Pmax表示实行峰谷电价后电网的日负荷峰值;Pt表示实行峰谷分时电价后t时刻电网的负荷大小。
在多目标数学模型中,由于各个目标函数的量纲不同,不能直接进行加权[20]。故先对2个目标函数进行归一化处理,使其具有可比性,具体方法为
| $ {{f'}_1} = \frac{{{f_1} - {f_{1\min }}}}{{{f_{1\max }} - {f_{1\min }}}}, $ | (16) |
| $ {{f'}_2} = \frac{{{f_2} - {f_{2\min }}}}{{{f_{2\max }} - {f_{2\min }}}}。$ | (17) |
为了综合考虑目标函数f′1和f′2的影响,运用加权方法处理2个目标函数得到总的目标函数为
| $ F = {\lambda _1}{{f'}_1} + {\lambda _2}{{f'}_2}, $ | (18) |
式中,λ1、λ2为各个目标函数的权重系数,也称偏好系数,反映了不同目标函数f′1和f′2对总的目标函数的影响,且满足λ1+λ2=1,其中λ1、λ2≥0。
2.1.2 约束条件影响电动汽车参与V2G服务的因素主要有:车辆可用时间、电池容量、电池最大充放电功率、电池允许放电深度、电价时段等。因此,约束条件可以归纳为以下几点:
1) 可用时间约束
考虑到电动汽车用户的日常出行需求,电动汽车不可能一天24 h都处于并网状态,当电动汽车处于行驶离网状态时,不参加与电网的互动。在此期间电动汽车未接入到充电桩上,无法参与V2G充放电调度。
2) 可用荷电状态值约束
| $ {S_{\min }} \le {S_{it}} \le {S_{\max }}, $ | (19) |
式中:Sit为t时刻第i辆电动汽车的荷电状态;Smax和Smin分别是保证动力电池安全运行和正常使用寿命的荷电状态上下限。
3) 充放电功率约束
为保证充放电功率在正常范围内,用户放电收益最大化,且考虑到交换功率非任意连续可调,得到充放电功率的范围为
| $ - {P_{d\max }} \le {P_{it}} \le {P_{c\max }}, $ | (21) |
式中:Pcmax为电动汽车最大充电功率;Pdmax为电动汽车最大放电功率。
4) 实时电价上下限约束
考虑代理商的运营成本和用户的承受能为,设定充放电动态电价的上下限为
| $ {p_{t\min }} \le {p_t} \le {p_{t\max }}, $ | (22) |
式中:Ptmin为第t小时充电电价下限值,元/(kWh),其取值应小于居民电价均值;Ptmax为第t小时充电电价上限值,元/(kWh),其取值可根据当地充电服务费允许值设定。
2.2 含约束条件的粒子群优化算法文中是含约束条件的优化问题,所有满足约束条件的变量解空间为可行域,可行域中使目标函数取最优值的解称为最优解。结合所求解问题的特点,对标准PSO算法流程进行修改。含约束条件的PSO算法具体流程如下所示:
1) 初始化粒子群,确定粒子的基本参数值;
2) 根据相关约束条件修改粒子群的位置;
3) 计算粒子群的适应度函数值, 跟踪粒子群群体中个体最优位置和群体最优位置;
4) 根据式(7)和式(8)更新粒子的速度和位置;
5) 根据约束条件检查粒子速度和位置是否超过限定值, 如果超出限值范围,将其设制为该限定值, 并重复步骤2;
6) 计算粒子群的适应度函数值, 更新并记录粒子群群体中个体最优位置和群体最优位置;
7) 判断是否达到最大迭代次数, 是则停止计算否则返回步骤4。
2.3 V2G响应电价算例 2.3.1 电动汽车参数设置本算例中的V2G站电动汽车采用同一种电池型号, 以私家电动汽车电池容量为100 A·h为例,且各电动汽车的初始电池容量取为0.6。按照前面分析的功率约束条件, 取电动汽车的最大充放电功率分别为15 kW和20 kW, 考虑用户对最低SOC的设置约束,电动汽车SOC状态的上下限分别为0.9和0.3。表 3列出V2G站电动汽车参数情况。
| 表 7 用户侧V2G电动汽车参数设置 Table 7 Parameter setting of V2G EVs on user side |
在计算电动汽车充放电费用时,采用重庆市已经实施的电网分时电价的时段划分。文中针对电价时段划分进行研究,各时段充放电电价的比例只要能反应电动汽车在不同时间内充放电的费用不同即可。为引导电动汽车用户在低谷负荷时段充电,在高峰负荷时段适当放电,采取峰、平、谷电价按3:2:1的比例由充电站管理方收取或支付的方法。电网分时电价时段划分和电动汽车充放电电价设置如前所述。
2.3.2 负荷参数设置算例分析时,以重庆市2015年夏季典型日负荷曲线为例,分别计算2020年、2025年和2030年私家电动汽车参与V2G互动的最优充放电控制策略。表 1给出重庆地区2015年夏季典型日负荷功率值, 负荷值为小时间隔数据。以重庆市2015年夏季的典型日负荷曲线为基本负荷,考虑到基本负荷年增长率为10%,分别计算得到2020年、2025年和2030年重庆市夏季典型日负荷曲线,如表 4、表 5、表 6所示。
2.3.3 用户参与度在峰谷分时电价引导下,V2G用户可以选择在谷电价时段充电、峰电价时段放电。此时参与V2G的电动汽车占区域电网内总的电动汽车的比例称为用户参与度[21],其表达式为
| $ \gamma = n/{N_a} \times 100\% , $ | (23) |
式中:n是响应峰谷分时电价的电动汽车数量;Na是区域内电动汽车的总数量。在峰谷分时电价引导下,在不同阶段有不同比例的车主响应峰谷电价而参与V2G,这些车辆根据峰谷电价时段,结合自身充电时长和放电时长,有序地进行充电和放电,但仍会有部分车主不响应峰谷电价政策,该部分车主的充电功率按照无序充电模型进行计算[22]。在文中的仿真中,分别设定用户参与度为20%、50%和80%,由此得到不同用户参与度情况下,电动汽车参与V2G服务对电网负荷的影响[23]。
根据前面的分析预测,在2020年重庆地区的私家电动汽车大约为5万辆左右,以5万辆电动汽车的容量来响应日负荷变化曲线。综合考虑目标函数f1和f2的影响,运用加权方法处理2个目标函数得到总的目标函数F,取权重系数λ1=0.9,λ2=0.1,采用带约束的基本PSO算法进行计算。在仿真中,分别设定用户参与度为20%、50%和80%,由此得到不同用户参与度情况下,电动汽车参与V2G服务对电网负荷曲线的影响。
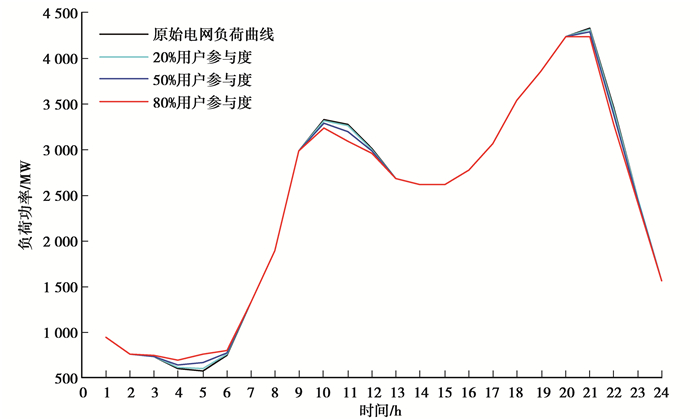
由图 7可得如下结论:
|
图 7 用户不同参与度下电网负荷曲线(2020年) Figure 7 Grid load curve of users with different participation degree (2020) |
1) 原始负荷曲线在02:00—06:00期间为负荷低谷期, 而在09:00—12:00和18:00—22:00分别出现了2个负荷高峰;
2) 电动汽车的V2G调节负荷基本上实现了在负荷高峰期进行放电, 在负荷低谷期进行充电;
3) V2G调节后的负荷曲线(红色曲线)与原始负荷曲线(黑色曲线)相比有明显的改善;
4) V2G调节后的负荷曲线最大值为4 230 MW, 平均负荷2 373 MW,负荷率为0.560;原始负荷曲线最大值为4 328 MW,平均负荷2 388 MW,负荷率为0.552。由此可见,电动汽车与电网的互动可以增大电网侧的负荷率;
5) 随着用户参与度的增加,电动汽车削峰填谷的效果越来越显著,根据仿真结果,参与V2G服务的用户每天的收益大概为15元。
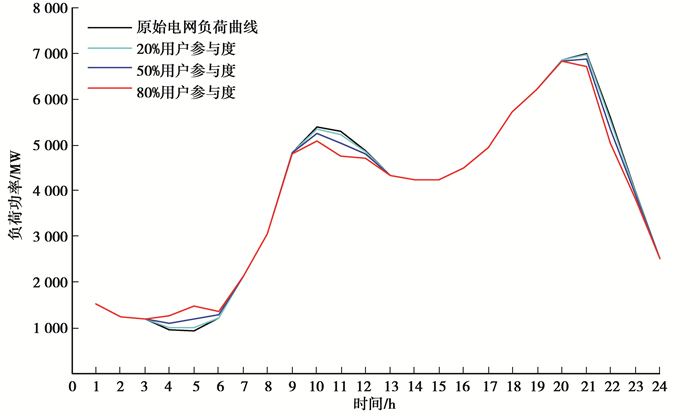
在2025年重庆地区的私家电动汽车大约为15万辆左右,以15万辆电动汽车的V2G充放电容量来响应日负荷变化曲线。在仿真中,分别设定用户参与度为20%、50%和80%,由此得到不同用户参与度情况下,电动汽车参与V2G服务对电网负荷曲线的影响如图 8所示。
|
图 8 用户不同参与度下电网负荷曲线(2025年) Figure 8 Grid load curve of users with different participation degree (2025) |
V2G调节后的负荷曲线最大值为6 632 MW,平均负荷3 822 MW,负荷率为0.576;原始负荷曲线最大值为7 006 MW,平均负荷3 866 MW,负荷率为0.552。
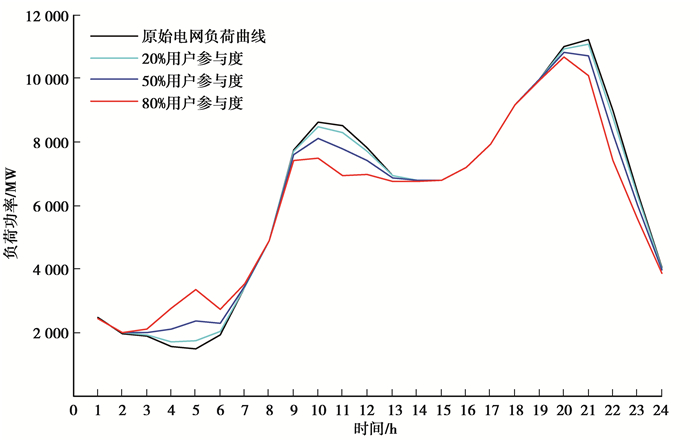
在2030年重庆地区的私家电动汽车大约为75万辆左右,以75万辆电动汽车的V2G充放电容量来响应日负荷变化曲线。在仿真中,分别设定用户参与度为20%、50%和80%,由此得到不同用户参与度情况下,电动汽车参与V2G服务对电网负荷曲线的影响如图 9所示。
|
图 9 用户不同参与度下电网负荷曲线(2030年) Figure 9 Grid load curve of users with different participation degree (2030) |
V2G调节后的负荷曲线最大值为10 250 MW, 平均负荷6 062 MW,负荷率为0.591;原始负荷曲线最大值为11 226 MW,平均负荷6 194 MW,负荷率为0.552。
3 结果分析1) 电网侧的V2G调峰是基于未来电动汽车快速发展并到一定规模后,通过在合适的时段进行充放电从而来达到削峰填谷、平抑负荷波动的目的。建立以电网侧负荷曲线均方差最小为目标函数的数学模型,考虑了电动汽车可用时间约束、充放电功率约束、可用容量约束和用户对车载电池最低容量的设置,采用粒子群优化算法对每辆车的具体充放电时间进行最优求解。
2) 根据电动汽车V2G参与电网调峰的仿真结果,随着参与车网互动电动汽车数量的增加,V2G调节后的负荷曲线峰谷差大大减小,负荷趋向于平均值,电网侧的负荷率也显著升高,有利于电网的高效稳定运行。同时,由于可调节车辆数的增加,电动汽车V2G可用容量也大大增加,目标函数的收敛速度也明显加快。
3) 用户侧的V2G响应是基于未来智能电网技术和电力市场电价机制发展到成熟阶段后,在实行实时电价的基础上,提出用户通过在合适的时段充放电来获得差价收益的思想。建立以用户收益最大化和电网日负荷率最大为目标函数的数学模型,考虑了可用时间约束、可用荷电状态约束、充放电功率约束和对实时电价上下限约束,针对优化问题多维度,多变量的时间组合的特点,提出采用粒子群优化算法对每辆车的具体充放电时间进行最优化安排,使得每位用户能够通过不同时段进行充放电来获取最大的利润。
4) 通过用户侧V2G仿真算例得到,随着参与车网互动电动汽车数量的增加,V2G调节后的负荷曲线峰谷差减小了14%左右,日负荷曲线趋向平稳,电网侧的负荷率也显著升高,这将极大有利于电网的高效稳定运行。同时,参与V2G服务的电动汽车用户每天还能获得一定的经济收益,这将极大地调动用户参与V2G服务的积极性。
4 结论基于电动汽车的V2G功能,分别从电网侧和用户侧的角度考虑,建立了不同侧重的有序充放电模型。考虑了电动汽车可用时间、可用容量约束、充放电功率约束和用户的实际需要等约束条件。以重庆市2015年夏季典型日负荷为基础,分别仿真验证了上述有序充放电模型对重庆市2020、2025和2030年负荷曲线的影响。结果表明:电网侧和用户侧的充放电模型均能起到削峰填谷、平抑电网负荷的作用,同时用户侧的充放电模型还能为参与V2G的用户带来经济收益。
但在建模仿真的过程中也存在一些不足之处。在考虑电网侧的V2G控制策略中,只考虑了车辆的充放电功率限制,没有顾及实际线路的充放电总功率约束,结果可能与实际有些出入。在考虑用户侧的V2G控制策略中,只是对电动汽车在时间维度上的充放电进行了控制,没有考虑实际空间分布对电动汽车用户分布的影响。另外,在仿真中均设定了固定的充放电功率,将来可以进一步研究充放电功率可调时的电动汽车V2G优化控制问题。
| [1] |
孙逢春. 电动汽车发展现状及趋势[J]. 科学中国人, 2006(8): 44-47. SUN Fengchun. The development status and trend of electric vehicles[J]. Scientific Chinese, 2006(8): 44-47. (in Chinese) DOI:10.3969/j.issn.1005-3573.2006.08.010 |
| [2] |
胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4): 1-10. HU Zechun, SONG Yonghua, XU Zhiwei, et al. Inpacts and utilization of electric vehicles integration into power systems[J]. Proceedings of the CSEE, 2012, 32(4): 1-10. (in Chinese) |
| [3] |
王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述[J]. 中国电机工程学报, 2013, 33(1): 1-10. WANG Xifan, SHAO Chengcheng, WANG Xiuli, et al. Survey of electric vehicle charging load and dispatch control strategies[J]. Proceedings of the CSEE, 2013, 33(1): 1-10. (in Chinese) |
| [4] |
葛少云, 黄镠, 刘洪, 等. 电动汽车有序充电的峰谷电价时段优化[J]. 电力系统保护与控制, 2012, 40(10): 1-5. GE Shaoyun, HUANG Liu, LIU Hong, et al. Optimization of peak-valley TOU power price time-period in ordered charging mode of electric vehicle[J]. Power System Protection and Control, 2012, 40(10): 1-5. (in Chinese) |
| [5] |
黄润, 周鑫, 严正, 等. 计及电动汽车不确定性的有序充电调度策略[J]. 现代电力, 2012, 29(3): 57-63. HUANG Run, ZHOU Xin, YAN Zheng, et al. The controlled charging dispatch strategy by considering of the uncertainty of electric vehicles[J]. Modern Electric Power, 2012, 29(3): 57-63. (in Chinese) DOI:10.3969/j.issn.1007-2322.2012.03.012 |
| [6] |
徐智威, 胡泽春, 宋永华, 等. 充电站内电动汽车有序充电策略[J]. 电力系统自动化, 2012, 36(11): 38-43. XU Zhiwei, HU Zechun, SONG Yonghua, et al. Coordinated charging of plug-in electric vehicles in charging stations[J]. Automation of Electric Power Systems, 2012, 36(11): 38-43. (in Chinese) |
| [7] |
Franco J F, Rider M J, Romero R. A mixed-integer linear programming model for the electric vehicle charging coordination problem in unbalanced electrical distribution systems[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2200-2210. DOI:10.1109/TSG.2015.2394489 |
| [8] |
刘晓飞, 张千帆, 崔淑梅. 电动汽车V2G技术综述[J]. 电工技术学报, 2012, 27(2): 121-127. LIU Xiaofei, ZHANG Qianfan, CUI Shumei. Review of V2G technology in electric vehicles[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 121-127. (in Chinese) |
| [9] |
纪震, 廖惠连, 吴青华. 粒子群算法及应用[M]. 北京: 科学出版社, 2009. JI Zhen, LIAO Huilian, WU Qinghua. Particle swarm optimization and its application[M]. Beijing: Science Press, 2009. (in Chinese) |
| [10] |
韩海英, 和敬涵, 王小君, 等. 基于改进粒子群算法的电动车参与负荷平抑策略[J]. 电网技术, 2011, 35(10): 165-169. HAN Haiying, HE Jinghan, WANG Xiaojun, et al. An improved particle swarm optimization-based load response strategy with participation of vehicle to grid[J]. Power System Technology, 2011, 35(10): 165-169. (in Chinese) |
| [11] |
Yao W F, Zhao J H, Wen F S, et al. A hierarchical decomposition approach for coordinated dispatch of plug-in electric vehicles[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2768-2778. DOI:10.1109/TPWRS.2013.2256937 |
| [12] |
Hua L C, Wang J, Zhou C. Adaptive electric vehicle charging coordination on distribution network[J]. IEEE Transactions on Smart Grid, 2014, 5(6): 2666-2675. DOI:10.1109/TSG.2014.2336623 |
| [13] |
张文亮, 武斌, 李武峰, 等. 电动汽车我国纯电动汽车的发展方向及能源供给模式的探讨[J]. 电网技术, 2009, 33(4): 1-5. ZHANG Wenliang, WU Bin, LI Wufeng, et al. Discussion on development trend of battery electric vehicles in China and its energy supply mode[J]. Power System Technology, 2009, 33(4): 1-5. (in Chinese) DOI:10.3969/j.issn.1674-0629.2009.04.001 |
| [14] |
谢俊, 汪震, 杨欢, 等. 对未来电力市场的若干思考[J]. 电力科学与技术学报, 2011, 12, 26(4): 50-56. XIE Jun, WANG Zhen, YANG Huan, et al. Investigation on future electricity market modality[J]. Journal of Electricity Power Science and Technology, 2011, 12, 26(4): 50-56. (in Chinese) DOI:10.3969/j.issn.1673-9140.2011.04.008 |
| [15] |
刘晓飞, 张千帆, 李锦瑭, 等. 停车场电动汽车用户侧最优V2G控制策略研究[J]. 电气工程学报, 2015, 10(10): 44-51. LIU Xiaofei, ZHANG Qianfan, LI Jintang, et al. Research on electric vehicle user-side optimization V2G control strategy in parking lot[J]. Journal of Electrical Engineering, 2015, 10(10): 44-51. (in Chinese) |
| [16] |
孙晓明, 王玮, 苏粟, 等. 基于分时电价的电动汽车有序充电控制策略设计[J]. 电力系统自动化, 2013, 37(1): 191-195. SUN Xiaoming, WANG Wei, SU Su, et al. Coordinated charging strategy for electric vehicles based on time-of-use price[J]. Automation of Electric Power Systems, 2013, 37(1): 191-195. (in Chinese) |
| [17] |
Qian K J, Zhou C K, Allan M, et al. Modeling of load demand due to EV battery charging in distribution systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 802-810. DOI:10.1109/TPWRS.2010.2057456 |
| [18] |
Rolink J, Rehtanz C. Large-scale modeling of grid-connected electric vehicles[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 894-902. DOI:10.1109/TPWRD.2012.2236364 |
| [19] |
Hamid Q R, Barria J A. Congestion avoidance for recharging electric vehicles using smoothed particle hydrodynamics[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1014-1024. DOI:10.1109/TPWRS.2015.2412653 |
| [20] |
Saber A Y, Venayagamoorthy G K. Plug-in vehicles and renewable energy sources for cost and emission reductions[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1229-1238. DOI:10.1109/TIE.2010.2047828 |
| [21] |
Han S, Han S, Sezaki K. Development of an optimal vehicle-to-grid aggregator for frequency regulation[J]. IEEE Transactions on Smart Grid, 2010, 1(1): 65-72. DOI:10.1109/TSG.2010.2045163 |
| [22] |
Cvetkovic I, Thacker T, Dong D, et al. Future home uninterruptible renewable energy system with vehicle-to-grid technology[C]//Energy Conversion Congress and Exposition. IEEE, 2009: 2675-2681. https://ieeexplore.ieee.org/document/5316064
|
| [23] |
Kempton W, Tomi J. Vehicle-to-grid power implementation:from stabilizing the grid to supporting large-scale renewable energy[J]. Journal of Power Sources, 2005, 144(1): 280-294. DOI:10.1016/j.jpowsour.2004.12.022 |
 2019, Vol. 42
2019, Vol. 42


