b. 重庆大学 期刊社, 重庆 400044
b. Journals Department, Chongqing University, Chongqing 400044, P. R. China
推荐系统在当今信息过载的社会中发挥着重要作用,它能帮助用户高效地获取满足自己需求的信息。目前,推荐算法方面的研究也是国内外学者热衷探索的方向,包括基于数据挖掘和信息融合的推荐、基于内容的过滤、协同过滤算法、基于知识的推荐、群组推荐、以及为克服单一算法缺陷而将2种或2种以上传统算法结合起来的混合算法[1-4]。其中,协同过滤算法是推荐效果最好,也在应用场景最为广泛的算法之一。传统的基于邻域的协同过滤算法[5-7]根据用户的历史行为数据,计算用户或项目之间的相似性,然后,将相似性大的用户或项目划分到同一个邻居集合,最后,邻居之间相互进行交叉推荐,该算法能够利用相似用户的反馈信息发现用户潜在的兴趣,但同时也存在着数据冷启动、稀疏性、扩展性,信息过期等问题。为了有效解决这些问题,基于模型的协同过滤算法被提出[8-11],这类算法应用协同过滤的思想,通过各类模型,如聚类、分类、关联规则、贝叶斯网络、矩阵分解等进行建模和推荐。其中,受到广泛关注的矩阵分解模型可以利用降维技术有效缓解数据稀疏性和可扩展性的问题。而对于信息过期问题,前人的研究认为随着时间的流逝,过去的信息对推荐的参考价值也是在逐渐衰减的,所以,提出了通过时间函数来评估历史信息权重的方法。目前, 大多数时间效应方面的研究都用非线性遗忘函数来描述时间权重,利用时间加权信息来区别它们对推荐的影响力,但是根据记忆理论,定期重复可以增加保留的信息量,维持记忆稳定,所以, 受到用户持续关注项目的权重应该比单一时间权重更大,因此, 仅用遗忘函数加权信息的方法不是完全合理的。而且, 现在时间权重的改进方法大多都是针对基于领域的协同过滤算法提出,很难适用于当今具有处理海量信息需求的推荐系统。
研究在已有考虑信息过期问题的协同过滤算法的基础上,以电影推荐模型为例提出新的改进方案。首先, 为了发挥模型算法的优势,将前人改进的结合信息保持期时间权重引入到矩阵分解模型中,提出基于矩阵分解的时间加权协同过滤算法。然后, 利用电影类型特征在用户观看电影中的重复出现,根据出现频率改进时间权重,增加过去相关电影评分的影响力,提出融合时间和类型特征加权的矩阵分解协同过滤算法,进一步提高推荐算法的准确性。最后, 通过实验验证提出的算法,比基于领域的时间加权协同过滤算法具有更高的推荐质量。
1 协同过滤关于时间效应的相关研究近年来,信息过期问题越来越受到国内外学者的广泛关注。1998年,Grabtreel和Soltysialk[12]认为用户近期的信息才是用户现在兴趣所在的体现,而较长时间以前的信息对用户来说已经失去了意义,应该只利用近期信息进行推荐。2000年,Koychev和Schwab[13-14]提出了过去的信息对当前推荐也有一定的参考价值,只是时间距离越近的信息在推荐时更加受重视,在算法中引入了非线性遗忘函数作为时间权重改变信息的价值。2005年,Ding和Li[15]将信息的时间权重应用到用户评分上,让评分随时间衰减,评分越低的项目越是用户不感兴趣的,这种方法削弱了用户过去的兴趣,突出了现在的兴趣。2007年,邢春晓等[16]改进了基于遗忘函数的时间权重,通过引入项目相似度权重,提高了以往与近期信息相似度比较高的信息影响力。2012年,Steffen Rendle[17]将信息按时间进行分段,不同时间段内的信息表现出用户的不同兴趣倾向,从而对推荐产生不同的影响。2017年,赵海燕等[18]将按照时间分段后的信息构成不同的主矩阵,然后,将它们组合成联合矩阵,进行分解和预测,但是联合矩阵分解计算复杂,不太实用。同年,Sun B H和Dong L Y[19]将评分矩阵通过基于遗忘函数的时间权重加权,再采用奇异值方法进行分解和预测未知评分项,利用模型简化了计算的复杂度。兰艳和曹芳芳[20]首次提出信息影响力不是随时间连续衰减的,在较小时间窗口内信息应该具有相同的影响力,但该算法也是基于邻域的协同过滤算法提出的,虽提高了基于遗忘函数时间权重算法的准确性,却不太适应具有大规模数据场景应用的系统。
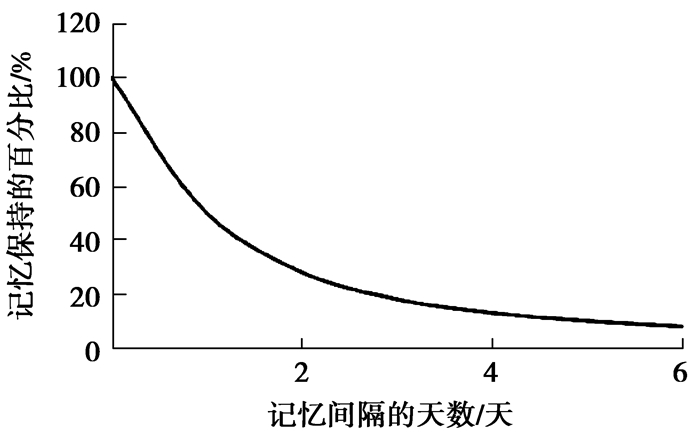
2 改进时间加权的协同过滤算法 2.1 引入改进时间权重的矩阵分解协同过滤算法 2.1.1 结合遗忘曲线的时间权重遗忘曲线描述了人类如何随着时间的推移遗忘信息的规律,它由赫尔曼艾宾浩斯于1885年提出。艾宾浩斯发现,人类在记忆信息后,早期的遗忘速度是非常快速的,并且需要定期回顾信息以保持记忆的稳定,一段时间后,遗忘会达到平稳状态,人们忘记的速度也会变慢。该遗忘规律最后被绘制成了图 1所示的艾宾浩斯遗忘曲线。
|
图 1 艾宾浩斯遗忘曲线 Figure 1 Ebinhaus forgetting curve |
信息过期概念是基于用户的兴趣漂移特性提出的,该特性表述了用户对事物兴趣在时间变化过程中会改变的观点。兴趣信息的价值应该和记忆一样是时间的函数,随时间在衰减。
在遗忘曲线相关应用与时间序列的研究中,用非线性指数函数和信息半衰期[15]来描述遗忘函数,信息半衰期T0是指信息从产生时刻到被遗忘掉一半所经过的时间,定义衰减因子λ=ln(0.5)/T0,最终信息的记忆保持量在当tnow下时刻为
| $ f\left( {{t_{{\rm{now}}}}} \right) = {{\rm{e}}^{\lambda * \left( {{t_{{\rm{now}}}} - {t_0}} \right)}}, $ | (1) |
其数值在(0, 1)之间,可以将它作为电影评分的时间权重。t0是电影被评分的时间,tnow是向用户推荐的时间,(tnow-t0)表示推荐时间和评分时间之间的间隔;T0表示评分对推荐的影响力减少一半所经过的时间。权重f(tnow)随(tnow-t0)的增大而减小,表示评分的时间越久,电影评分对当前推荐贡献的影响力越小。
2.1.2 改进的结合信息保持期的时间权重非线性遗忘函数整体上是一个连续递减的曲线,但是考虑到实际中用户的兴趣漂移不是连续的而是阶段性的,即短时间的几天内兴趣几乎是不改变的,前人由此引出一个信息保持期[20]的概念,补充了艾宾浩斯提出的遗忘规律,更加准确地模拟了信息价值在时间变化中真实衰减的过程。信息保持期理论认为在保持期内的时间权重是相同的,即评分的影响力是相同的,到下一个保持期时,时间权重才发生新的衰减,所以, 将信息保持期引入到非线性遗忘函数定义的时间权重中,提出改进结合信息保持期的时间权重,新的时间权重函数为
| $ f'\left( {{t_{{\rm{now}}}}} \right) = {{\rm{e}}^{\lambda * {T_1}/{\rm{floor}}\left( {\frac{{{t_{{\rm{now}}}} - {t_0}}}{{{T_1}}}} \right)}}。$ | (2) |
改进后的时间函数曲线呈梯度递减趋势,比只考虑遗忘衰减连续递减的时间函数更加符合现实情况。
2.1.3 引入改进时间权重的矩阵分解协同过滤算法现有的算法只是将改进的时间权重应用于基于邻域的协同过滤算法中,而基于领域的协同过滤算法时间复杂度是O(n2),n对于用户的协同过滤来说是用户量,对于项目的协同过滤来说是项目数。但基于矩阵分解的协同过滤在并行计算中的时间复杂度只有O(n),所以将改进的时间权重和矩阵分解结合,不仅可以缓解传统协过滤的数据稀疏性问题,在时间的可扩展性上也大大提高了算法性能。
在矩阵分解协同过滤算法的评分矩阵预处理中,用结合信息保持期的时间权重加权评分矩阵后再进行分解,改进后的时间加权评分计算公式如下
| $ {{\mathit{\boldsymbol{R'}}}_{u,v}} = {\mathit{\boldsymbol{R}}_{u,v}} * \left( {1 + \varepsilon * {{f'}_{u,v}}\left( {{t_{{\rm{now}}}}} \right)} \right), $ | (3) |
式中:Ru, v表示用户u对电影v的原始评分;tnow表示向用户u推荐时的时间;ε表示时间权重的衰减速度,ε越大,衰减速度越慢,ε越小,衰减速度越快;Ru, v′是时间函数fu, v′ (tnow)加权后的评分。
最后,将加权后的评分通过最小最大标准化,映射到电影评分区间[1, 5]
| $ {{\mathit{\boldsymbol{R''}}}_{u,v}} = \frac{{\left( {{\mathit{\boldsymbol{R}}_{\max }} - {\mathit{\boldsymbol{R}}_{\min }}} \right) * \left( {{\mathit{\boldsymbol{R}}_{u,v}} - {\mathit{\boldsymbol{R}}_{\min }}} \right)}}{{\left( {{\mathit{\boldsymbol{R}}_{\max }} - {\mathit{\boldsymbol{R}}_{\min }}} \right) + {\mathit{\boldsymbol{R}}_{\min }}}}, $ | (4) |
Rmax、Rmin分别表示目标区间的最大、最小值,即Rmax=5、Rmin=1,Rmax′、Rmin′分别表示加权评分的最大最小值; Ru, v′表示加权评分;Ru, v″表示标准化后的加权评分。
引入改进时间权重的矩阵分解推荐算法的具体步骤如下
输入:带有评分时间戳的评分矩阵R,目标用户u,信息半衰期T0,信息保持期T1,时间权重衰减速度ε。
输出:向目标用户u推荐的N个项目。
Step1 将目标用户u未评分的电影作为推荐候选集Q (电影v∈Q)。
Step2 利用式(3)计算R中基于改进的时间权重加权后的评分值,并按式(4)进行标准化后,得到新的加权评分矩阵R′。
Step3 矩阵分解,用交替最小二乘法将Step2中的高维加权评分矩阵R′投影到一个隐因子空间,分解为代表用户和项目偏好特征的2个低维矩阵,即用户因子矩阵U′和电影因子矩阵V′。
Step4 预测评分,根据Pi, j= Ui′ Vj′,Ui′为用户u的特征因子向量,Vj′为电影v的特征因子向量,预测目标用户u对电影v的评分。
Step5 对推荐候选集Q中所有的电影重复step4,得到Q的所有预测评分后,向用户u推荐其中评分较高的前N个电影。
2.2 融合时间和类型特征加权的矩阵分解协同过滤算法 2.2.1 改进融合时间和类型特征的时间权重艾宾浩斯发现的遗忘原理不仅通过遗忘曲线说明了遗忘的规律,还发现一个人如果坚持定期回顾记忆信息,他对初始信息的回忆能力会得到很大改善。在电影推荐的场景中,当用户评价过的电影所具有的特征(如电影类型)在接下来的观影中重复出现时,用户对这些电影特征的印象会得到正面或者负面的加强,被加强的特征可以反映出用户近期的兴趣,过去包含这些特征的电影评分,对推荐的影响力自然也应该有所提升。
另外,现有时间权重都仅用电影的一个整体评分来说明对用户的影响价值,忽略了电影特征对用户的独立影响力。例如,电影类型是大多数用户首先考虑也是推荐系统较为看重的因素,如果某用户只是出于对科幻类型的喜爱,给一部喜剧和科幻类型的电影打了高分,却被推荐很多同时包含这2种类型的电影远多于纯科幻类的高质量电影,那这种推荐方式就没有发掘出用户的真实兴趣。
针对以上2点问题,以电影类型作为电影特征的代表,提出融合时间和类型特征的时间权重。从历史信息中收集电影类型被用户关注的频次和评分的高低,从而分析出用户对不同电影类型的偏好程度,再从一个电影评分的影响力是由不同电影类型对用户的影响力共同决定的角度,去修正现有时间权重,使推荐更加准确。
定义一:类型影响力加强周期T′
随着用户对某种电影类型观看次数的增加,导致用户对这种电影类型的印象加深,从而影响力增加,使电影类型的影响力增强1倍所需要的时间就是T′。T′越小,说明用户需要较少的时间就能增加对电影类型的印象,从而加强评分的影响力。
现实中,不同用户的记忆接收和处理能力不一样,T′应该是随用户变化的。根据心理学原理的“曝光效应”,如果某物出现越频繁,人们对其越有好感,熟悉代表了一定程度的安全,而人在情感上有一种寻求安全感的倾向,观看电影越频繁的用户,在相同类型出现时对类型的敏感度更大,相应的印象加深程度就更大。
定义二:类型影响力加强权重wincrease
电影v评分的时间权重随着用户u对电影v包含的电影类型{av1, av2, …, avd}的印象改变而变化的权重。
对于电影v包含的类型avi来说,用户u观看类型avi的频次可以表示为
| $ {\rm{freq}}\left( {{a_{vi}}} \right) = \frac{{{T_{{a_{vi}}{\rm{last}}}} - {T_{{a_{vi}}{\rm{first}}}}}}{{\left( {{t_{{\rm{now}}}} - {T_{{a_{vi}}{\rm{last}}}}} \right)}}, $ | (5) |
式中:Tfirst表示用户u给电影v评分的时间,Tlast表示用户u最近一次观看包含类型avi电影的时间,tnow表示向用户u推荐的时间。
freq(avi)越大,说明用户对类型avi加深了更多次印象。经过印象的积累,avi对用户u增加的影响力权重定义如下
| $ {w_{{\rm{increase}}}} = {\rm{freq}}\left( {{a_{vi}}} \right)T', $ | (6) |
wincrease越大,说明该类型的影响力越大,反之越小。
定义三:类型影响力正向修正权重wpos和负向修正权重wneg
用户u对电影类型avi可以是喜欢也可以是不喜欢, 这是以用户对包含类型avi的电影评分值的高低来决定的。同样,类型avi对用户的影响力也可以是正面影响力或者负面影响力。需要定义一个划分正面评分或负面评分的阈值,使大于等于阈值的评分属于正面评分,小于阈值的评分属于负面评分。
对于每一次电影类型的重复出现,此次电影的评分如果是正面评分,增加的印象对推荐是正向的,应该增大此次电影评分Ru, v,减少其影响力随时间衰减的程度,即减少遗忘函数eln(0.5)的指数权重;如果此次电影评分是负面评分,则应该减小评分Ru, v,增加其影响力衰减的程度,即增加遗忘函数的指数权重。
首先,根据结合信息保持期的遗忘曲线规律,定义遗忘函数eln(0.5)随时间衰减的原始时间权重为
| $ {w_{{\rm{time}}}} = \frac{1}{{{T_0}}} * {T_1} * {\rm{floor}}\left( {\frac{{{t_{{\rm{now}}}} - {t_{\rm{0}}}}}{{{T_1}}}} \right), $ | (7) |
然后,将类型影响力加强权重wincrease和时间权重wtime结合,定义类型avi的正向影响力修正权重为
| $ {w_{{\rm{pos}}}}\left( {{a_{vi}}} \right) = \alpha {w_{{\rm{time}}}} - \beta {w_{{\rm{increase}}}}。$ | (8) |
则类型的负向影响力修正权重为
| $ {w_{{\rm{neg}}}}\left( {{a_{vi}}} \right) = \alpha {w_{{\rm{time}}}} - \beta {w_{{\rm{increase}}}}。$ | (9) |
|wincrease|的大小表示评分的影响力被提升的程度,|wincrease|的正负表示提升的正面影响力还是负面影响力,α和β是权重平衡因子,用来平衡2个权重之间的关系。
定义四:融合时间和类型特征的时间权重Fu, v(tnow)
不同电影类型{av1, av2, …, avd}的影响力修正权重往往不同,电影v的整体影响力应该按照它的类型累加决定。电影v最终被修正后的时间权重定义如下
| $ {F_{u,v}}\left( {{t_{{\rm{now}}}}} \right) = \left\{ \begin{array}{l} \frac{1}{d}\sum\nolimits_{i = 1}^d {{{\rm{e}}^{\ln \left( {0.5} \right) * {w_{{\rm{pos}}}}\left( {{a_{vi}}} \right)}}} ;\\ \frac{1}{d}\sum\nolimits_{i = 1}^d {{{\rm{e}}^{\ln \left( {0.5} \right) * {w_{{\rm{neg}}}}\left( {{a_{vi}}} \right)}}} ; \end{array} \right. $ | (10) |
式中:Fu, v(tnow)表示在tnow时刻向用户u推荐时,电影v修正后的时间权重;d表示电影v包含的电影类型{av1, av2, …, avd}的总数。
2.2.2 结合融合时间和类型特征加权的时间权重矩阵分解协同过滤算法将提出的融合时间和类型特征加权的时间权重用来改进评分,得到通过修正后时间权重加权的评分为
| $ {{\mathit{\boldsymbol{R'}}}_{u,v}} = {\mathit{\boldsymbol{R}}_{u,v}} * \left( {1 + \varepsilon * {F_{u,v}}\left( {{t_{{\rm{now}}}}} \right)} \right), $ | (11) |
式中:Ru, v表示用户u对电影v的原始评分; tnow表示向用户u推荐的时间; ε表示修正后时间权重衰减的速度; Ru, v′反映了原评分在被Fu, v(tnow)加权后的真实影响力。
最后,将加权后的评分同样通过式(4)进行标准化,映射到电影评分区间[1, 5],得到最终融合时间和类型特征加权的评分值。
融合时间和类型特征加权矩阵分解推荐算法的具体步骤如下
输入:带有评分时间戳的评分矩阵R,目标用户u,信息半衰期T0,信息保持期T1,类型影响力加强周期T′,时间权重因子α,类型影响力加强权重因子β,时间权重衰减速度ε,划分正面评分或负面评分的阈值θ。
输出:向目标用户u推荐的N个项目。
Step1 将目标用户u未评分的电影作为推荐候选集Q (电影v∈Q)。
Step2 根据阈值θ划分正面评分和负面评分,再利用式(11)计算R中经过融合时间和类型特征的时间权重加权后的评分值,并按式(4)进行标准化后,得到新的加权评分矩阵R′。
Step3 矩阵分解,用交替最小二乘法将Step2中的高维加权评分矩阵R′投影到一个隐因子空间,分解为代表用户和项目偏好特征的2个低维矩阵,即用户因子矩阵U′和电影因子矩阵V′。
Step4 预测评分,根据Pi, j= Ui′Vj′,Ui′为用户u的特征因子向量,Vj′为电影v的特征因子向量,预测目标用户u对电影v的评分。
Step5 对推荐候选集Q中所有的电影重复Step4,得到Q的所有预测评分后,向用户推荐其中评分较高的前N个电影。
3 实验结果与分析 3.1 数据准备实验采用的数据集是经典电影数据集MovieLens100K,其中包括电影评分的数据集u.data和电影信息的数据集u.item。u.data包含了943个用户在1 682部电影上的100 000条评分信息,每条评分信息都由用户ID、电影ID、评分、评分时间戳组成,其中电影评分数值为1-5分共5个等级,可以把3-5分划分为正面评分,1-2分划分为负面评分。u.item包含了1 682部电影的信息,每条电影信息由电影ID、电影名称、发布时间、上映时间、IMDB地址、和其包含的电影类型组成,一共有19种电影类型。
实验中将评分数据集中每个用户近期的评分数据分离出来作为测试数据,其余数据作为训练数据,按照时间顺序来划分的训练数据集和测试数据集,更加符合实际中真实的推荐场景。
3.2 算法评价指标为了验证推荐质量的高低,需要采用相应的评价指标。目前用于评分预测的准确性评价指标主要有平均绝对误差(MAE, mean absolute error)和均方根误差(RMSE, root mean square error),RMSE加大了对评分预测误差的惩罚,对系统的测评更加苛刻,测量准确性也更加可靠,所以实验选择的评价指标是RMSE。
RMSE是均方误差(MSE, mean squared error)的算术平方根,所以RMSE的计算式是
| $ {\rm{RMSE}} = \sqrt {{\rm{MSE}}} = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^N {{{\left( {{P_i} - {R_i}} \right)}^2}} } , $ | (12) |
式中:Pi表示第i个评分的预测值;Ri表示第i个评分的真实值;N表示测试集中评分个数的总数;RMSE是衡量预测值与真实值之间误差和的均方根,RMSE值越小,说明预测模型的准确性越高。
3.3 实验方案及结果分析 3.3.1 实验方案实验需要分为2个阶段:
1) 由于算法包含的参数:信息半衰期T0,信息保持期T1,类型影响加强周期T′,时间权重因子α,类型影响加强权重因子β,时间权重衰减速度ε,不同的取值会对实验结果产生不同的影响,需要通过调参实验得到使实验结果较优的各个参数值。
2) 将提出的改进算法与传统算法、现有的时间权重算法进行对比实验,比较各个算法的RMSE值。实验中需要实现以下算法:
① 引入改进时间权重的邻域协同过滤算法(NTWCF, neighborhood-based and improved-time weighted collaborative filtering):是前人提出的时间加权协同过滤算法,该算法是在传统基于项目的协同过滤基础上,将遗忘函数和信息保持期结合得到改进的时间权重,再利用改进的时间权重改变相似度度量方法,从而提高了传统协同过滤算法的准确性。
② 基于矩阵分解的协同过滤算法(MFCF, matrix factorization based collaborative filtering):将矩阵分解模型应用到协同过滤算法中,没有引入时间权重,模型技术的优势使其性能优于传统基于邻域的协同过滤算法。
3) 引入改进时间权重的矩阵分解协同过滤算法(MFTWCF, MF-based and improved-time weighted collaborative filtering):将改进的结合信息保持期时间权重应用到矩阵分解模型中,改进的时间权重通过引入时间权重衰减速度加权评分矩阵,解决了矩阵分解协同过滤算法的信息过期问题,也缓解了NTWCF算法存在的数据稀疏性和可扩展性问题。
4) 融合时间和类型特征加权的矩阵分解协同过滤算法(MFTTWCF, MF-based improved-time and type weighted collaborative filtering):进一步改进了上述MFTWCF算法,提出类型影响力加强权重来修正原来的时间权重,得到融合时间和类型特征的时间权重,再将该权重引入矩阵分解模型中,取得更好的推荐效果。
3.3.2 实验结果与分析通过调参实验后,取最优的参数组合T0=60、T1=3、T′=30、α=0.4、β=0.6、ε=0.3、正负面评分阈值θ=3,采用NTWCF算法、MFCF算法、MFTWCF算法、MFTTWCF算法分别对训练数据集进行训练和测试数据集进行评分的预测,每种算法都经过1 000次的实验,得到其结果的平均值,以此来对比各算法的推荐质量。
1) 对比NTWCF算法、MFCF算法和MFTWCF算法预测的准确性。
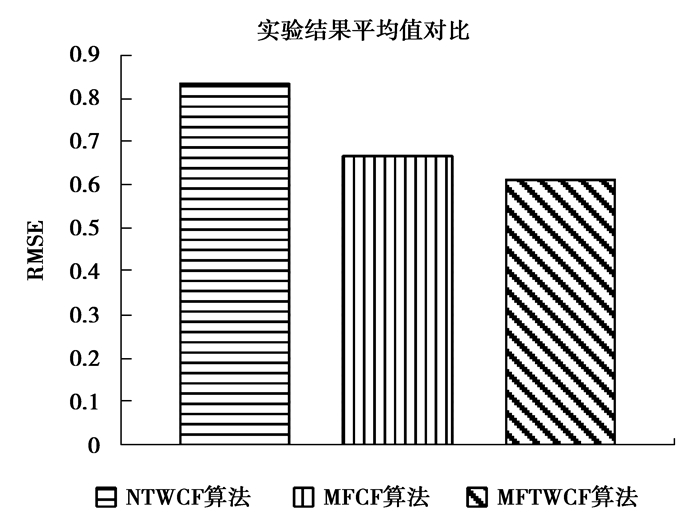
由图 2的实验结果可知,NTWCF算法是传统的基于邻域的协同过滤算法,其平均RMSE最大,为0.835,预测准确性最低。MFCF算法弥补了传统算法的一些缺陷,准确性也有相当大的提升,平均RMSE为0.667,相比NTWCF算法降低了20.11%。MFTWCF算法利用改进的时间权重优化了MFCF算法,其平均RMSE在这3种算法中最小,为0.613,相比NTWCF算法降低了26.58%,取得了更好的推荐准确性,说明MFTWCF算法是有效可行的,能够应用到利用矩阵分解协同过滤算法的推荐系统中。
|
图 2 NTWCF算法、MFCF算法和MFTWCF算法的RMSE值比较 Figure 2 RMSE value comparise of NTWCF algorithm, MFCF algorithm and WFTWCF algorithm |
2) 对比MFTWCF算法、MFTTWCF算法预测的准确性。
由图 3的实验结果可知,MFTTWCF算法的平均RMSE约为0.591,是实现的4种算法中的最小值,因为它继续优化了MFTWCF算法,进一步修正了评分的影响力,让MFTWCF算法的RMSE再次降低了3.58%。实验表明提出的MFTTWCF算法具有最好的预测效果。

|
图 3 MFTWCF算法和MFTTWCF算法的RMSE值比较 Figure 3 RMSE vale comparison between MFTWCH algorithm and MFTWCH algorithm |
经过对MovieLens 1M和10M的数据集的实验,其结果也表示MFTWCF算法和较NTWCF算法准确度均有提高,并且MFTTWCF算法也是4种算法中预测效果最好的算法,说明更大规模的数据集也能体现改进算法的优化效果,得到相同的结论。
4 结语为了解决协同过滤推荐算法信息过期的问题,在矩阵分解协同过滤中,引入遗忘函数和信息保持期的时间权重。提出类型影响力修正权重改进的时间权重,提出融合时间和类型特征加权的矩阵分解协同过滤推荐算法。实验结果表明,研究提出的算法均能提高预测的准确性,为推荐系统提供简单可行的推荐算法模型。后续的研究可以考虑将社会化标签[21]也加入到类型特征中,提高内容匹配准确度,也可以考虑针对不同用户挖掘适合用户自己的类型影响力加强周期,使算法具有更强的个性化推荐能力。
| [1] |
Katarya R, Verma O P. Recent developments in affective recommender systems[J]. Physica A:Statistical Mechanics and its Applications, 2016, 461: 182-190. DOI:10.1016/j.physa.2016.05.046 |
| [2] |
Lu J, Wu D S, Mao M S, et al. Recommender system application developments:a survey[J]. Decision Support Systems, 2015, 74(C): 12-32. |
| [3] |
Chen L, Chen G L, Wang F. Recommender systems based on user reviews:the state of the art[J]. User Modeling and User-Adapted Interaction, 2015, 25(2): 99-154. DOI:10.1007/s11257-015-9155-5 |
| [4] |
Ricci F, Rokach L, Shapira B. Recommender systems handbook[M]. US: Springer, 2015.
|
| [5] |
Wang B L, Huang J H, Ou L B, et al. A collaborative filtering algorithm fusing user-based, item-based and social networks[C]//IEEE International Conference on Big Data, IEEE Big Data 2015. Piscataway, NJ, USA: IEEE, 2015: 2337-2343.
|
| [6] |
Ma X, Wang C, Yu Q, et al. An FPGA-based accelerator for neighborhood-based collaborative filtering recommendation algorithms[C]//IEEE International Conference on Cluster Computing, CLUSTER 2015. Piscataway, NJ, USA: IEEE, 2015: 494-495.
|
| [7] |
郑翠翠, 李林. 协同过滤算法中的相似性度量方法研究[J]. 计算机工程与应用, 2014, 50(8): 147-149. ZHENG Cuicui, LI Lin. Research on method of similarity measurement in collaborative filter algorithm[J]. Computer Engineering and Applications, 2014, 50(8): 147-149. (in Chinese) DOI:10.3778/j.issn.1002-8331.1204-0749 |
| [8] |
Aggarwal C C. Model-Based Collaborative Filtering[C]//Recommender Systems. Cham: Springer International Publishing, 2016: 71-138.
|
| [9] |
孟祥武, 刘树栋, 张玉洁, 等. 社会化推荐系统研究[J]. 软件学报, 2015, 26(6): 1356-1372. MENG Xiangwu, LIU Shudong, ZHANG Yujie, et al. Research on social recommender systems[J]. Journal of Software, 2015, 26(6): 1356-1372. (in Chinese) |
| [10] |
Bokde D, Girase S, Mukhopadhyay D. Matrix factorization model in collaborative filtering algorithms:a survey[J]. Procedia Computer Science, 2015, 49: 136-146. DOI:10.1016/j.procs.2015.04.237 |
| [11] |
Guo H, Tang R, Ye Y M, et al. Deepfm:A factorization-machine based neural network for CTR prediction[J]. International Joint Conferences on Artificial Intelligence, 2017, 1725-1731. |
| [12] |
Barry Crabtree I, Soltysiak S J. Identifying and tracking changing interests[J]. International Journal on Digital Libraries, 1998, 2(1): 38-53. |
| [13] |
Koychev I, Schwab I. Adaptation to drifting user's interests[J]. Proceedings of Ecml Workshop Machine Learning in New Information Age, 2000, 39-46. |
| [14] |
Koychev I. Gradual forgetting for adaptation to concept drift[C]//Proceedings of ECAI 2000 Workshop Current Issues in Spatio-Temporal Reasoning, Berlin: IEEE, 2000: 101-107.
|
| [15] |
Ding Y, Li X. Time weight collaborative filtering[C]//CIKM'05-Proceedings of the 14th ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2005, 1: 485-492.
|
| [16] |
邢春晓, 高凤荣, 战思南, 等. 适应用户兴趣变化的协同过滤推荐算法[J]. 计算机研究与发展, 2007, 44(2): 296-301. XING Chunxiao, GAO Fengrong, ZHAN Sinan, et al. A collaborative filtering recommendation algorithm incorporated with user interest change[J]. Journal of Computer Research and Development, 2007, 44(2): 296-301. (in Chinese) |
| [17] |
Rendle S. Social network and click-through prediction with factorization machines[C]//KDD-Cup Workshop. Beijing, China: IEEE, 2012.
|
| [18] |
赵海燕, 王颖, 陈庆奎, 等. 产品时效性感知的个性化推荐算法[J]. 小型微型计算机系统, 2017, 38(9): 2022-2027. ZHAO Haiyan, WANG Ying, CHEN Qingkui, et al. Timeliness sensitive collective matrix factorization personalized recommendation[J]. Journal of Chinese Computer Systems, 2017, 38(9): 2022-2027. (in Chinese) DOI:10.3969/j.issn.1000-1220.2017.09.020 |
| [19] |
Sun B S, Dong L Y. Dynamic model adaptive to user interest drift based on cluster and nearest neighbors[J]. IEEE Access, 2017, 5: 1682-1691. DOI:10.1109/ACCESS.2017.2669243 |
| [20] |
兰艳, 曹芳芳. 面向电影推荐的时间加权协同过滤算法的研究[J]. 计算机科学, 2017, 44(4): 295-301. LAN Yan, CAO Fangfang. Research of time weighted collaborative filtering algorithm in movie recommendation[J]. Computer Science, 2017, 44(4): 295-301. (in Chinese) |
| [21] |
Wei S X, Zheng X L, Chen D R, et al. A hybrid approach for movie recommendation via tags and ratings[J]. Electronic Commerce Research and Applications, 2016, 18(C): 83-94. |
 2019, Vol. 42
2019, Vol. 42


