近年来,随着无线能量传输技术的迅猛发展,无线可充电传感器网络也吸引了研究人员大量的关注[1]。利用无线充电技术,即电磁感应、磁共振和无线电波技术,可以对无线充电传感器网络(WRSNs, wireless rechargeable sensor networks)中的传感器节点进行能量补充,这大大降低电池消耗,延长网络运行寿命。在大多数场景中,车辆携带的移动式充电器被认为是可以高效为传感器节点补充电量的好方法。
为了进一步提高网络性能,需要解决充电车辆的路径规划和驻停时间分配等问题。就路径规划问题而言,傅凌琨等[2]提出了一种最优的充电器运动策略,该策略将阈值以上所有节点的实时能量充电时间最小化。戴海鹏等[3]也对定向充电下的静态无线充电器器布置优化问题进行了研究。在充电时间优化方面,谢理光等[4]探讨充电器在充电周期中巡检时间占比最大化的问题。石填等[5]进行了无电池网络构造连通支配集规划的研究。舒远超等[6]深入研究了移动充电小车的近最优速率控制。分析发现,尽管人们对无线充电传感器网络有着丰富的研究经验,但在基于定向充电的WRSN这一领域,特别是基于实际的充电模型下的研究还很少。
基于定向充电的路径与时间分配问题是多目标、多约束的组合优化问题,属于NP难题,该问题求解方法可分为精确式算法和启发式算法[7]。鉴于实际应用性的考量,对运算复杂度和时间复杂度进行权衡,提出基于贪婪的启发式算法求出近似解。
基于一对多无线充电的移动充电器在无线充电方向传感器网络(WRDSN, wireless rechargeable directed sensor network)中的运动规划问题得以提出,并从局部和全局的角度加以解决。首先,可调整方向的充电小车(DMC, directional mobile charger)利用局部信息得到节点子集,然后,随机生成初始路径,计算每个子集的有效充电量,通过贪婪原则得到局部信息。最后,DMC从全局的角度利用局部信息来调整逗留点的位置,遍历充电顺序和充电时间。笔者提出了一种考虑实际无线电波极化性的充电模型和移动充电器在WRDSN路径规划问题,同时解决了二维区域充电控制的极化调整问题,并给出了基于一些贪婪原则的启发式算法,最后分析了系统参数如何影响充电网络的性能。这对实际的充电器和配套小车的设计有很好的指导作用。
1 模型描述调用了一种通用的无线充电模型,将其修改为极化无线充电模型。在以下传统充电模式的基础上[8],提出了无线电波充电模型为
| $ \begin{array}{*{20}{c}} {\tau = \frac{{{G_{\rm{s}}}{G_{\rm{r}}}\eta }}{{{L_{\rm{p}}}}}{{\left( {\frac{\lambda }{{4{\rm{ \mathsf{ π} }}}}} \right)}^2}{P_{\rm{o}}},}\\ {{P_{\rm{c}}} = \frac{{{G_{\rm{s}}}{G_{\rm{r}}}\eta }}{{{L_{\rm{p}}}}}{{\left( {\frac{\lambda }{{4{\rm{ \mathsf{ π} }}d + \beta }}} \right)}^2}{P_{\rm{o}}}。} \end{array} $ | (1) |
近似充电功率Pr,j(d)为
| $ {P_{{\rm{r}},j}}\left( d \right) = {\left( {\frac{\tau }{{d + \beta }}} \right)^2},d \le {d_{{\rm{th}}}}, $ | (2) |
式中:d表示传感器节点与充电器之间的距离;Po表示源充电功率;Pc表示实际充电功率;Gs表示源天线增益;Gr表示接收天线增益;Lp是偏振损耗;λ代表波长;η表示整流器的效率;β是调整FRIS自由空间方程的参数;dth代表最大充电距离。由于只考虑移动充电器和传感器是同构的,除了距离d之外,式(1)中的其他参数都是基于环境和设备设置的常数。
为了进一步验证该充电模型并改进其实际适用性,需要对该模型进行修改。POWERSAST公司研制的无线充电器得到了广泛应用,采用其充电功率模型来修改传统模型[10]。对该型无线充电器充电功率测量的结果表明,传感器节点只有在方位角为-30°~30°时才能接收到明显的充电功率。方位角相当于无线充电器的方位与传感器节点连线和无线充电器朝向之间的夹角。然而,实际充电功率是指数衰减的距离,并近似均匀分布,忽略了近似余弦函数的递减。
在文中线充电器是移动的,而无线充电技术要求发射机和接收器共同工作来充电。因此,必须设置发射机是定向的,接收机是全向的。在考虑极化损耗的情况下,先提出了一种充电覆盖范围的确定方法:
| $ p\left( {{s_i},{o_j},{\theta _i}} \right) = 1,\left\| {{s_i},{o_j}} \right\| \le {d_{{\rm{th}}}},{\theta _i} \le {30^ \circ }。$ | (3) |
进一步得到极化充电模型为
| $ {p_{\rm{c}}}\left( {i,j} \right)\left( d \right) = {p_{{\rm{r}},j}}\left( d \right)P\left( {{s_i},{o_j},{\mathit{\boldsymbol{R}}_i},{\mathit{\boldsymbol{D}}_j}} \right), $ | (4) |
式中:P表示无线充电器si是否能向传感器oj充电, 表示充电器si的方向;‖sioj‖表示充电器与传感器节点之间的距离。
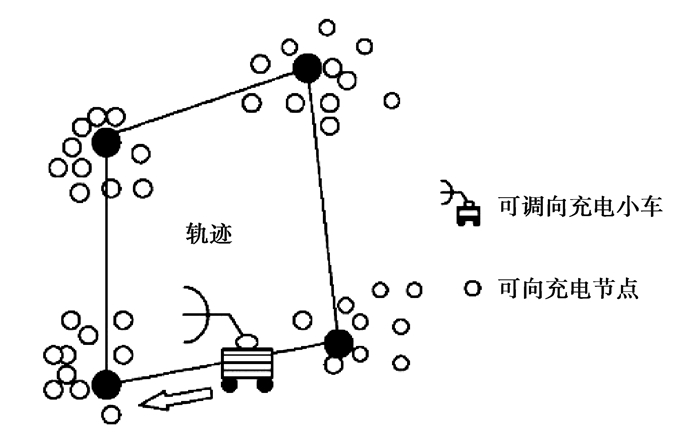
2 问题定义WRDSN包括部署在2D区域的n个已知位置的可充电传感器节点[11],如图 1所示。传感器节点被组织成一些子集。为了保持整个网络的有效运行,笔者采用携带定向充电器TX91501的小车(DMC)周期性巡航,以补充传感器节点的能量。DMC通过每个节点子集,使用旋转调制(RM, rotation modulation)技术旋转充电装置的方向[12]。最后,DMC回到起点,完成整个充电巡航。对于那些充电需求较大的节点,DMC停止为其周围节点充电。假设DMC以恒定的速度移动。为了进一步提高充电效率,采用一对多的方式对传感器节点进行充电。
|
图 1 系统模型示例 Figure 1 An example of system model |
DMC一次旅行的时间被定义为巡逻周期Γ。一些节点可能已经在DMC移动过程中被充电而无需停下来对其充电。鉴于充电极化性,DMC在整个巡航期间不能在不停止移动的情况下完成充电任务,即需要在锚点停止并利用RM的旋转来对周围节点进行充电。假设充电器配备有足够容量的电池在整个行程期间以最大传输功率广播无线电信号,然后使用上述极化电荷模型来计算充电效率。具体而言,DMC根据以下3个因素对每个节点充电:1)传感器节点和充电器之间的距离dj;2)充电器充电的发射功率pc;3)传感器节点相对于充电器方向与充电器朝向之间的夹角θj。事实上,随着DMC的移动,该角度将在子路径之间的交叉点处改变。θj为
| $ {\theta _j} = \left\langle {{\mathit{\boldsymbol{R}}_j},\mathit{\boldsymbol{D}}i} \right\rangle + \left\langle {{\mathit{\boldsymbol{l}}_c},{\mathit{\boldsymbol{l}}_{c + 1}}} \right\rangle , $ | (5) |
式中:Rj表示充电器和节点的地理位置的矢量,即通过从充电器的垂直坐标减去传感器节点的垂直坐标而形成的向量值(x,y);Di表示当前RM上充电器的朝向;lc,lc+1分别表示当前经过某一子集子路径和下一个子路径。各子路径均为直线。研究关注的是移动和充电的能耗,而不是DMC本身的能耗,没有考虑DMC本身的有限的功率容量。在实际情况下,DMC的运行需要消耗大量的能量,而充电也需要大量的能量。因此,假设DMC有足够的能量来移动和充电。
研究的目标是通过控制移动充电器的路径和旋转,在整个巡逻周期Γ最大化网络充电效用,可以表述为
| $ \begin{array}{*{20}{c}} {\max \sum\limits_{j = 1}^n {\left( {\int_0^\mathit{\Gamma } {{P_j}\left( t \right){\rm{d}}t} } \right)} ,}\\ {{\rm{s}}.{\rm{t}}\;\;\;{P_j}\left( t \right) = {P_c}\left( {i,j} \right)\left( {{d_j}\left( t \right)} \right)。} \end{array} $ |
要解决这个问题,需提出一个充电策略,以在一定周期内满足速度限制和极化充电模型的情况下最大可能地延长网络寿命。这包括两个问题:一是如何确定DMC应停止充电的传感器节点;另一个是如何控制DMC的移动速度和旋转速度,以获得最大的充电功率。
3 算法设计为了解决这两个问题,首先,DMC需要根据各节点的地理位置和方向将传感器节点划分成若干连通子集,并获取子集中的中心点。这样将节点集的划分问题转化为磁盘覆盖问题。然后,DMC随机生成初始遍历路径,根据子集中节点的充电需求将磁盘中心视为锚点,再由公式中的极化充电模型调整其在每个锚点的方向,并得到需求参数。最终,通过需求参数生成最小生成树并进行遍历得到整个路径[13]。
当DMC移动到子集中心时,可能会有一个子路径旋转角,〈lc,lc+1〉即当前行进路径lc与下一个行进路径lc+1之间的交角。DMC的旋转角为
| $ \left\langle {{\mathit{\boldsymbol{l}}_c},{\mathit{\boldsymbol{l}}_{c + 1}}} \right\rangle = \left\langle {{X_{cc - 1}} + {X_{cc + 1}} - 2{X_{cc}},{Y_{cc - 1}} + {Y_{cc + 1}} - 2{Y_{cc}}} \right\rangle , $ | (6) |
式中:(Xcc-1,Ycc-1)表示前一个子集中心的位置;(Xcc,Ycc)表示当前子集中心的位置;(Xcc+1,Ycc+1)表示下一个子集中心的位置。
3.1 时间离散化将传感器节点划分成多个子集后,DMC需要对每个子集进行分析,以获得局部信息。在实际应用中,需要识别每个节点与DMC之间的相对距离,并实时获取每个节点的剩余功率。如果时间是连续的,则DMC必须一直计算充电功率,这是不可能的。因此,需要对时间进行离散,并在离散时间的基础上更新位置、速度和功率。与连续位置模型相比,提出了一个离散的位置模型。其中,充电器的位置只能在离散时间(即间隔时间Δt)发生变化。时隙Δt是由相邻2个位置的变化的时间间隔,是最小持续时间。值得注意的是,如果将旅行时间分解得足够小,则总旅行时间总是可以转化为最小持续时间的整数倍。
在第k个时间间隔中2个相邻时间段之间的位置变化受DMC的最大移动速度Vi和时隙Δt的限制,具体为
| $ \sqrt {{{\left( {{X_k} - {X_{k - 1}}} \right)}^2} + {{\left( {{Y_k} - {Y_{k - 1}}} \right)}^2}} \le {V_i}\Delta t。$ | (7) |
基于子集中心的坐标,可以得到节点相对于充电器的实时位置,并由此更新极化角为
| $ \left\langle {{\mathit{\boldsymbol{R}}_i},{\mathit{\boldsymbol{D}}_j}} \right\rangle \left\langle {\frac{{{X_{cj}} - {X_k}}}{{\sqrt {{{\left( {{X_{cj}} - {X_k}} \right)}^2} + {{\left( {{Y_{cj}} - {Y_k}} \right)}^2}} }},\frac{{{Y_{cj}} - {Y_k}}}{{\sqrt {{{\left( {{X_{cj}} - {X_k}} \right)}^2} + {{\left( {{Y_{cj}} - {Y_k}} \right)}^2}} }}} \right\rangle , $ | (8) |
式中,[Xcj, Ycj]是第j个子集中各节点的位置坐标; [Xk, Yk]是DMC该时隙的实际位置。这样就得到了各时隙的实际极化角,并以此来计算实时充电功率。
3.2 空间离散化为了降低运算复杂度,还需要对实际充电功率进行等效近似。首先,需要对充电功率进行离散,即基于二维区域对充电功率进行空间离散。考虑到极化充电模型,使用圆对其进行离散化。
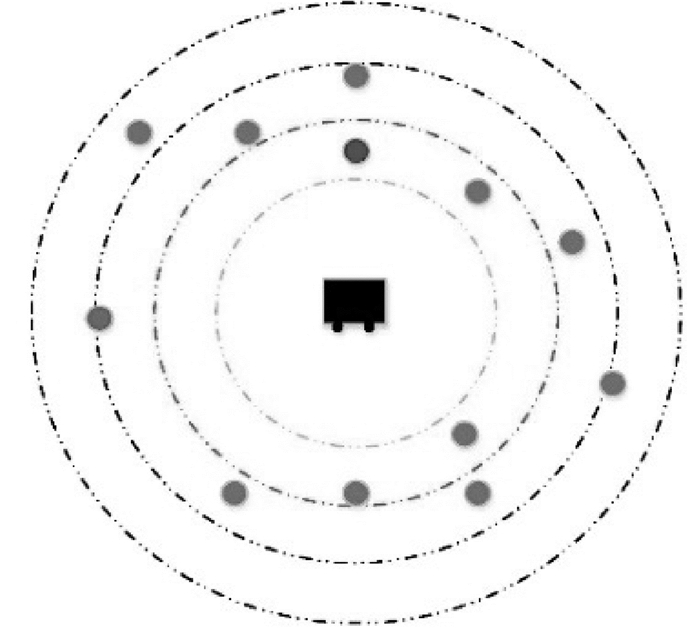
以最大充电距离为半径,充电小车DMC为中心,并将其cq等分画出cq个同心圆,如图 2所示。考虑到在方向可调的情况下,各方向充电功率相等。而各圆环到中心点距离相等,因此,可使用每个圆环的充电功率等效其实际充电功率。图 2的红点位置有一个棕色的内环和一个绿色的外环。在这里,使用外环位置的充电功率来代替该环内节点q的实际功率。对于绿点位置的节点,由于它恰好在环上,直接用它所在的环的充电功率来代替实际的充电功率。通过这种方式,用一组离散的充电权值来逼近每个点的充电功率,为
|
图 2 空间离散化示例 Figure 2 An example of spatial discretization |
| $ {P_g} = \left[ {P_q^1,P_q^2, \cdots ,P_q^{\max }} \right]。$ | (9) |
结合圆环的几何特性,对每个环的电荷功率进行如下处理以进一步简化运算[14]。具体来说,给定一个足够小的离散化因子ε,当划分的同心圆数量足够大时,相邻圈之间的充电功率可以表示为
| $ P_g^q = P_g^q \times {\left( {1 + \varepsilon } \right)^{ - g}},1 \le g \le {c_q}, $ | (10) |
式中:pqmax是充电功率最大的虚圈。仍然以图 2来说明,假设黄色虚圈即是最靠近DMC的虚圈,则根据其半径计算出该圈充电功率即是pqmax。在以某一值ε将其划为4个虚圆环后,可以用pqmax× (1 + ε)-1来代替图中红色位置的节点的充电功率。相应的,绿色位置的节点的充电功率可以用pqmax× (1 +ε)-2来表示。这样将DMC周围的原始不规则2D区域关于节点q的充电功率划分为4段。相邻段(以及圆圈)之间充电功率的差异以阈值(1+ε).为界。在这一区域,结合代数知识,没有计算不同位置的充电功率,而是使用了每个区段充电功率的下界(即在不同圆圈位置上的充电功率)来近似代替以获得较少运算量下好的实际价值。这样,就将复杂的充电功率参数转化为相对简单的参数来计算。
3.3 充电效用基于上述理论,可以将目标函数转换为Pg=[Pq1, Pq2, …, pqmax],最大化各时隙各节点充电功率的总和。模拟退火算法计算过程简单、通用性强、鲁棒性强,便于并行处理,可用于求解复杂的非线性优化问题,尤其是路径规划问题[15]。在获得各条边长度后,首先,采用模拟退火算法分割子集(即计算中心距离,然后按升序排列,最后以一定的概率松弛),得到了各子集中心的最短路径树。在此基础上,针对各路径点进行关于时隙的插值,得到DMC在各个时隙的具体位置。然后,随机设置各节点的初始能量。并利用所提出的充电模型和前面所述的时间离散、空间离散、能量层级近似3种方法结合极化充电模型来获取充电量,并更新各时隙各可获充电节点的能量。当子集内所有节点的剩余能量之和大于该子集所有节点能量容量总和的90%时,判定其为P型子集。反之则为N型子集。
在对子集类型进行细分之后,DMC需要根据不同类型选择合适的充电模式,判断是否停止以对该子集内的节点充电,调整节点遍历顺序。为了更好地调整旋转策略,DMC需要将目标函数与旋转策略相匹配,以获得最佳的旋转策略。同时为了将第1节中提到的局部性和全局性结合起来,提出了新的目标函数:
| $ \max \sum\limits_{c = 1}^j {{N_s}} , $ | (11) |
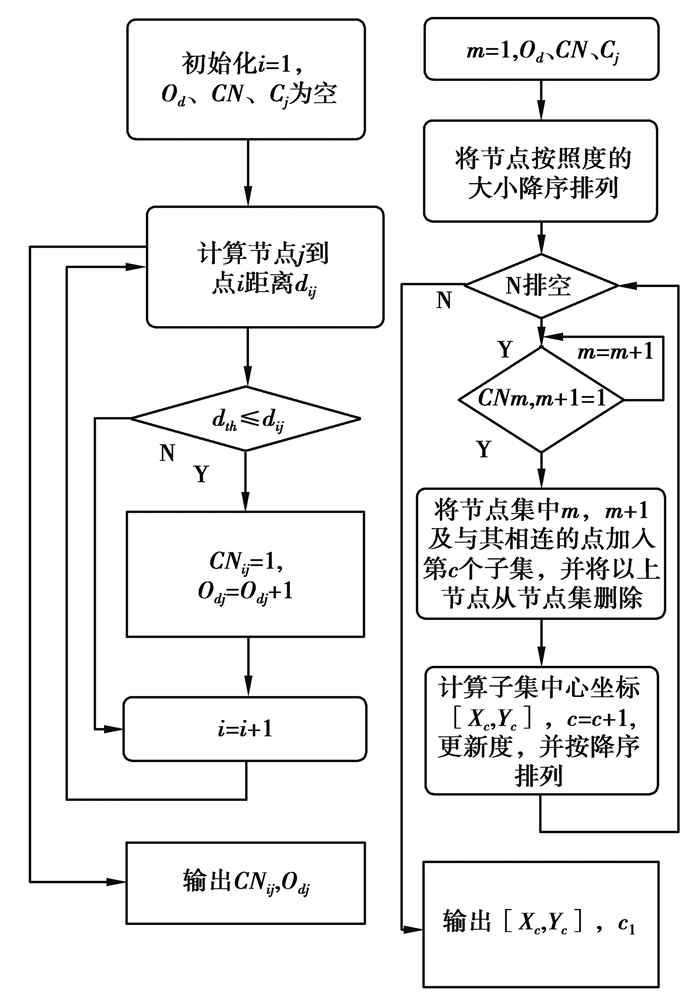
式中,Ns代表了一个子集中充电完成使得实时功率达到能量容量90%以上的节点数,表示充电效用。Ns设置的基准为90%,是考虑到避免能量溢出,充电至90%以上即为节点电量达标,并可以满足整个网络正常运转较长时间。如果以子集的中心为锚点,则DMC将子集类型的值设为1,是P型子集。否则,子集类型的值为0,是N型子集。对于子集类型值为1的节点子集,DMC将其中心视为锚点。对于子集类型值为0的子集,DMC将各节点按剩余能量降序排列,以最后3个能量最少的节点所在位置构成三角形的几个中心位置作为子集的锚点。针对N型子集,DMC制定相应的方向调整策略以获得最大数量的电量达标节点。算法的具体流程图如图 3所示。
|
图 3 局部子集算法流程图 Figure 3 Flow chart of local subset algorithm |
图 3算法流程图给出了节点子集的划分过程。先通过节点坐标计算节点间的距离,判断节点的连通性,得到每个传感器节点的连通度。再将这些传感器节点按角度的大小按降序排列,判断节点集N的节点是否为空。如果是的话,就视为连通,将这2个节点添加到连通子集群Clc中。此外,将连接到这2个节点的所有节点添加到连通子集群Clc中,并从N中删除所有新加入到连通子集的节点。否则,降序检查之后的2个节点是否相连。完成加入和删除的操作后,对N中的传感器节点按其降阶顺序排序,迭代地执行上述步骤。最后,得到了所有的连通子集Clc,即连通子集群Cl, 并计算每个子集中节点位置的平均值作为该子集的中心(Xcc,Ycc)。
图 4给出了全局调整的贪婪算法。首先,通过模拟退火并结合式(6)和式(7)计算出其在各个时隙的具体位置。再根据其位置,结合式(8)和式(9)计算充电量并更新节点能量,以此为依据判定子集类型。最后,统计各子集内部能量未达到能量容量90%的节点数量Nj,利用最小生成树和先序遍历进行全局路径规划。

|
图 4 全局贪婪算法流程图 Figure 4 Flow chart of global greedy algorithm |
雷蒙等[16]针对汽车网络中的车辆交通管理问题,提出了一种随机游走算法,并证实了其良好的性能。仿真使用该算法作为基准算法来评估所提出的基于贪婪的充电规划算法的性能。
仿真结果说明了网络中节点数及其分布、能量消耗率等多个参数对网络性能的影响,对算法进行了分析,并对未来工作进行了展望。在仿真中,400个无线可充电传感器节点随机分布在1 000 m×1 000 m的区域内。有效充电距离dth为200 m。DMC的初始速度为1 m/s,加速度阈值设置为0.1 m/s2。总充电周期为400 s,划分为1 000个时隙。每个节点的总能量容量为100 W。在初始时刻,每一个剩余能量为10~100 W。为了简化运算,将随机步长设置为10 W,设置代表硬件参数的τ值为1。
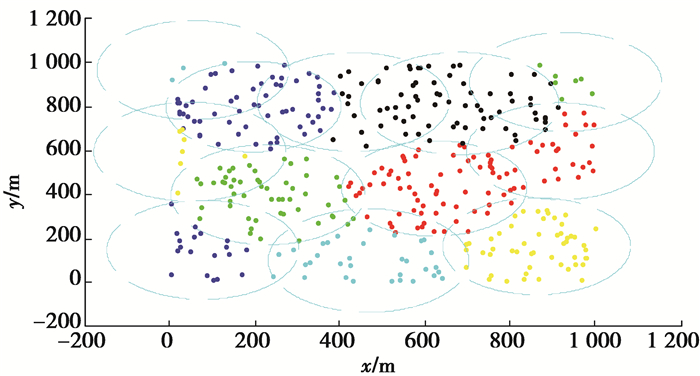
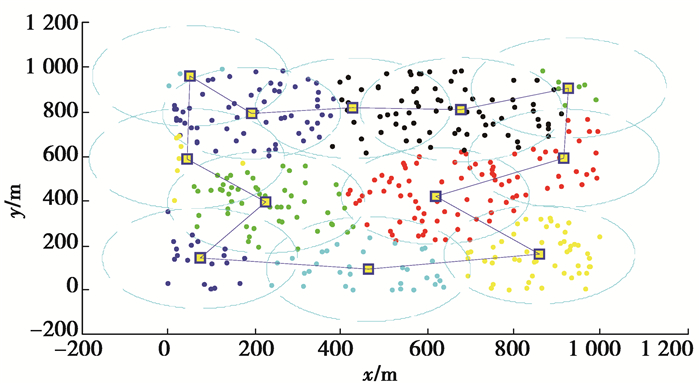
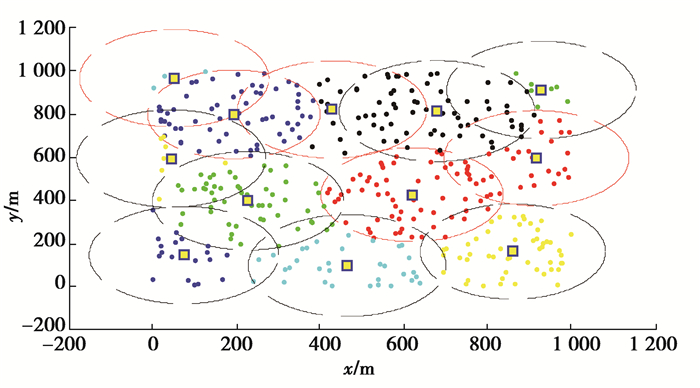
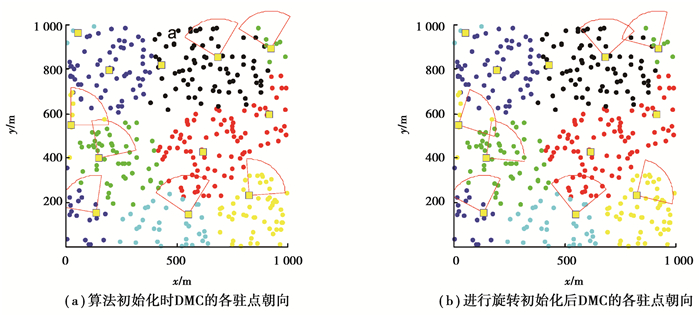
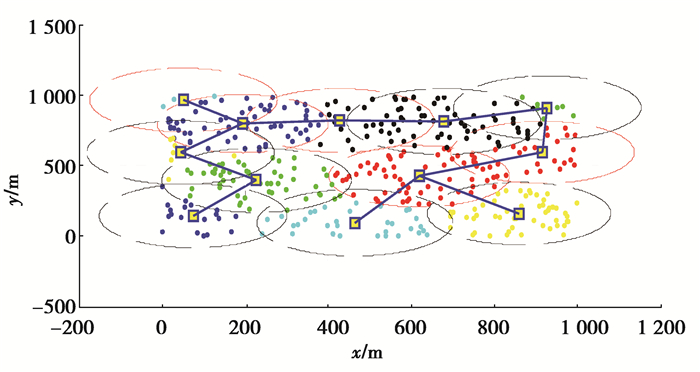
4.1 仿真结果为了解释文中所提算法的执行过程,将各部分执行效果展示出来。首先,DMC调用算法流程图第1、2列获得分割好的子集列表,如图 5所示。然后,DMC调用算法流程图第3列,通过模拟退火算法得到初始路径图,如图 6所示。DMC再用插值和近似计算进行子集类型判别得到子集判别图,如图 7所示。最后,DMC调用算法流程图第4列解决旋转控制问题,如图 8所示。同时, DMC通过各局部信息生成最小生成树并进行前序遍历,完成了整个充电网络的路径规划,如图 9所示。
|
图 5 子集分割 Figure 5 Subset partition |
|
图 6 初始路径 Figure 6 Initial path |
|
图 7 子集划分 Figure 7 Subset partition |
|
图 8 旋转初始化 Figure 8 Rotation initialization |
|
图 9 最终遍历路径 Figure 9 Final traversal path and coordinate unit |
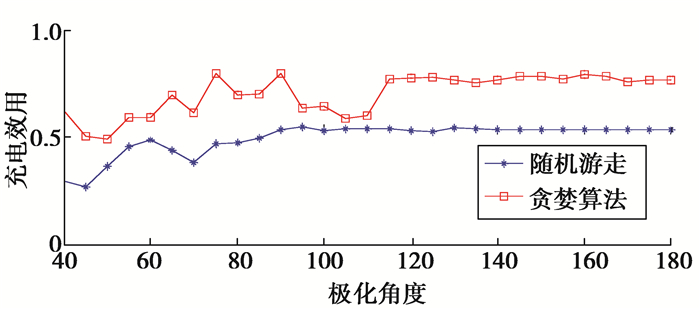
考虑到WRDSN当前的实际模型,尚无成熟的算法。对所提出的贪婪算法与直接使用基于模拟退火的随机游走算法(全程不停止)进行了性能比较,如图 10所示。这里用充电效用(充电后电量达到其总电量90%的节点数占所有节点的比例)来研究网络性能。
|
图 10 2种算法性能对比 Figure 10 Performance comparison of the two algorithms and polarizing unit |
研究了节点数量、节点分布、转速和能量层级对网络性能的影响。鉴于文中主要研究极化性,参考参数集中在极化角上。
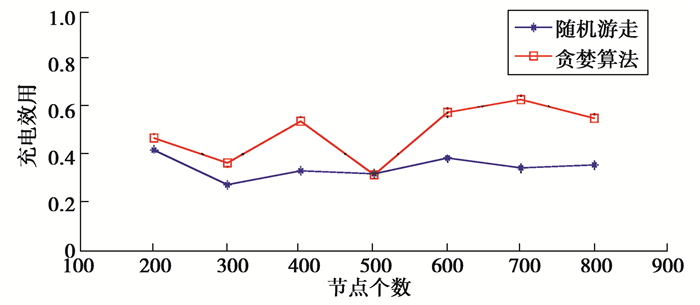
如图 11所示,随着节点数量的增加,网络性能呈现不单调的变化。大约在400~600网络达到最佳性能。同时,所提算法总是优于随机游走算法。只有当节点号为500时,两者性能相似。事实上,随机游走算法具有较高的整体性,更容易得到全局最优解。
|
图 11 节点数量影响 Figure 11 Effect on the number of nodes |
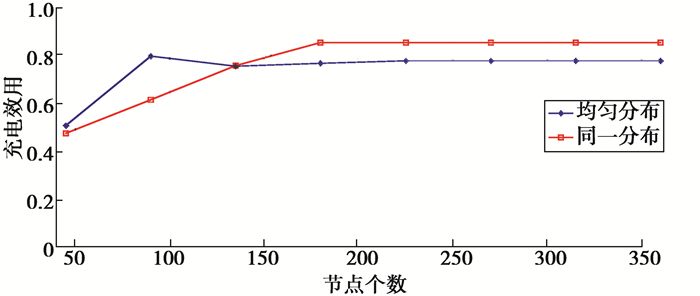
笔者给出了2种情况的节点分布情况(见图 12),并进行了网络性能比较,如图 13所示。当节点数目较小时,对于均匀分布来说,所提算法性能优于正态分布。相反,对于正态分布的性能优于均匀分布。

|
图 12 节点分布 Figure 12 Nodes distribution and coordinate unit |
|
图 13 节点分布影响 Figure 13 Effect of nodes distribution |
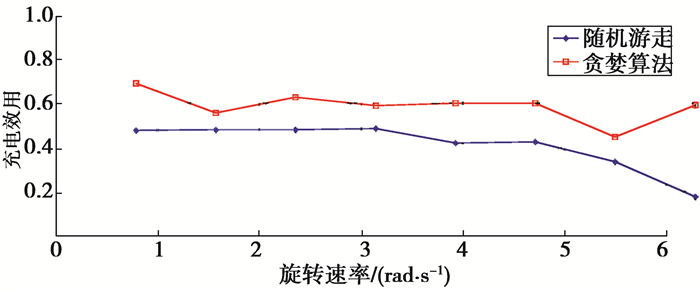
随着转速的增加,充电效率稳定一段时间后逐渐降低(见图 14)。这是由于随着转速的增加,一些节点反而不能稳定地充电,导致一些不必要的重复旋转。因此,充电效率降低。
|
图 14 旋转速率影响 Figure 14 Effect of speed of rotation |
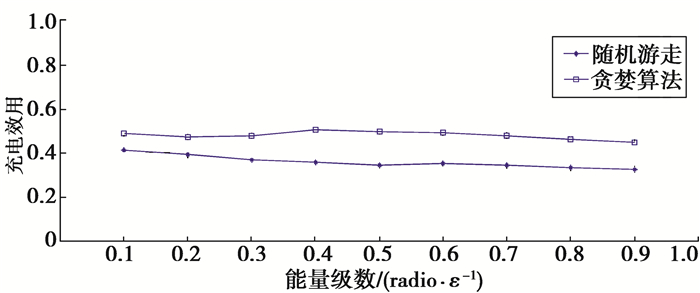
对能量级联对网络性能的影响进行了详细的比较,总体来说贪婪算法始终优于基准算法。两者都呈下降趋势,这是考虑到级数越大运算越复杂,自然贴近实际功率也能带来更好的充电收益。在图 15中,很容易发现网络性能不随能量级数从0.1~0.9单调变化,即能量级数过大或者过小,都会影响充电效率。尤其是,当贪婪算法能量级数为0.4时,网络性能达到最佳。将充电功率进行适中地近似,可以达到最大效率充电。当然,这里用近似的充电效率模拟实际的充电效率。
|
图 15 能量级数影响 Figure 15 Effect of energy levels and coordinate unit |
文章提出了一种无线可充电有向传感网中基于实际极化充电模型的充电路径规划算法。用子集拆分和分类方法将充电路径规划问题转化为旅行商问题。为了得到全局最优解,利用一些贪婪的启发式原理将其进一步转化为动态规划问题进行求解。为了验证算法的性能,使用全局随机游走算法进行仿真,并与所提出的算法进行了比较。实验数据表明,该算法具有良好的性能。将来的工作将进一步研究基于实际模型的多台移动充电器充电规划和基于该模型的移动充电器的能量容量问题。
| [1] |
胡诚, 汪芸, 王辉. 无线可充电传感器网络中充电规划研究进展[J]. 软件学报, 2016, 27(1): 72-95. HU Cheng, WANG Yun, WANG Hui. Research progress of charging planning in wireless rechargeable sensor networks[J]. Journal of Software, 2016, 27(1): 72-95. (in Chinese) |
| [2] |
Fu L, Cheng P, Gu Y, et al. Minimizing charging delay in wireless rechargeable sensor networks[C]//INFOCOM, 2013 Proceedings IEEE. IEEE, 2013: 2922-2930.
|
| [3] |
戴海鹏, 陈贵海, 徐力杰, 等. 一种高效有向无线充电器的布置算法[J]. 软件学报, 2015, 26(7): 1711-1729. DAI Haipeng, CHEN Guihai, XU Lijie, et al. An efficient arrangement algorithm for directed Wireless Chargers[J]. Journal of Software, 2015, 26(7): 1711-1729. (in Chinese) |
| [4] |
Xie L, Shi Y, Hou Y T, et al. On renewable sensor networks with wireless energy transfer: The multi-node case[C]//IEEE INFOCOM. Shanhai, China: IEEE, 2012: 1350-1358.
|
| [5] |
Shi T, Cheng S, Li J, et al. Constructing connected dominating sets in battery-free networks[C]//INFOCOM 2017-IEEE Conference on Computer Communications, IEEE. IEEE, 2017: 1-9.
|
| [6] |
Shu Y, Yousefi H, Cheng P, et al. Near-Optimal velocity control for mobile charging in wireless rechargeable sensor networks[J]. IEEE Transactions on Mobile Computing, 2016, 15(7): 1699-1713. DOI:10.1109/TMC.2015.2473163 |
| [7] |
Thomas H C, Charles E L, Ronald L R, et al.算法导论[M].殷建平, 徐云, 王刚, 等译. 3rd.北京: 机械工业出版社, 2013. Thomas H C, Charles E L, Ronald L R, et al. Introduction to algorithms[M]. YIN Jianping, XU Yun, WANG Gang, et al. 3rd. Beijing: China Machine Press, 2013.(in Chinese) |
| [8] |
Fu L, Cheng P, Gu Y, et al. Optimal charging in wireless rechargeable sensor networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(1): 278-291. DOI:10.1109/TVT.2015.2391119 |
| [9] |
He S, Chen J, Jiang F, et al. Energy provisioning in wireless rechargeable sensor networks[C]//INFOCOM, 2011 Proceedings IEEE. IEEE, 2011: 2006-2014.
|
| [10] |
Crandall A C, Bosarge J W, Hernandez L, et al. An internet search system for retrieving selected results from a previous search[J]. Powercast Media Inc Two Walnut Grove Suite, 2001. |
| [11] |
孟颍辉.无线传感器网络节点定位方法研究[D].沈阳: 东北大学, 2014. MENG Yinhui. Research on node location method in wireless sensor networks[D]. Shenyang: Northeast University, 2014. (in Chinese) |
| [12] |
Zhang R, Hoflinger F, Reind L M. Calibration of an IMU using 3-D rotation platform[J]. IEEE Sensors Journal, 2014, 14(6): 1778-1787. DOI:10.1109/JSEN.2014.2303642 |
| [13] |
王丽.图论在算法设计中的应用[D].西安: 西安电子科技大学, 2010. WANG Li. Application of graph theory in algorithm design[D]. Xi'an: Xi'an University of Electronic Science and Technology, 2010. (in Chinese) |
| [14] |
宫野. 计算多重积分的蒙特卡罗方法与数论网格法[J]. 大连理工大学学报, 2001, 41(1): 20-23. GONG Ye. Monte Carlo method and number theory grid method for calculating multiple integrals[J]. Journal of Dalian University of Technology, 2001, 41(1): 20-23. (in Chinese) DOI:10.3321/j.issn:1000-8608.2001.01.004 |
| [15] |
何庆, 吴意乐, 徐同伟. 改进遗传模拟退火算法在TSP优化中的应用[J]. 控制与决策, 2018, 33(2): 219-225. HE Qing, WU Yile, XU Tongwei. Application of improved genetic simulated annealing algorithm in TSP Optimization[J]. Control and Decision Making, 2018, 33(2): 219-225. (in Chinese) |
| [16] |
Sanchez-Iborra R, Cano M D. On the similarities between urban traffic management and communication networks:application of the random early detection algorithm for self-regulating intersections[J]. IEEE Intelligent Transportation Systems Magazine, 2017, 9(4): 48-61. DOI:10.1109/MITS.2017.2743202 |
 2019, Vol. 42
2019, Vol. 42


