近几年,水下自治机器人技术AUV的发展与应用逐步从近海沿岸延伸到深海水域以及海上作业平台领域[1-2]。自治水下机器人正逐步成为辅助开发海底资源的重要手段。研究主要探讨AUV控制系统当中UKF航迹追踪算法的设计与改进。
AUV控制系统将通过多种水下传感器模块将船体所处水域的环境参数以数字信号的形式传递至Arduino MEGA2560航迹追踪模块进行运算处理,并由算法当前时刻的预测结果产生下一时刻的船体推进器组的控制信号,约束船体沿期望轨迹航行。
AUV航迹追踪UKF算法的设计难点与核心主要体现为:船体所处水域存在多组流体边界条件的约束;AUV船体建模过程复杂;描述船体运动状态的多为非线性方程组,很难得到可靠的线性解[3-5]。
部分学者通过数值优化方法,将AUV船体的非线性运动方程局部线性化求解。例如,王艳艳等提出的基于扩展卡尔曼滤波器算法(EKF, extended kalman filter)的纯方位航迹追踪优化方法[6]。从仿真结果分析,该方法的航迹追踪优化效果较高。然而,EKF方法需要求解AUV模型的状态雅可比矩阵以及测量雅可比矩阵,增大了计算冗余度及误差传递程度, 而且, EKF方法在通过一阶或二阶泰勒展开式进行局部线性化的过程中会不可避免地产生截断误差,进而影响船体状态向量的求解精度。Allotta等提出了基于无迹卡尔曼滤波算法(UKF)[7]的AUV航迹预测方法。该算法的计算复杂度较低,但通过仿真结果可以发现,其导航预测误差依然较大。
由此发现,AUV航迹追踪算法误差精度有很大的提升空间。笔者对标准的UKF算法进行了一些改进,将船体状态转移矩阵中的固定采样时间间隔变换为自适应采样时间间隔以降低UKF航迹追踪算法的累积误差,并通过计算算法当前的状态向量预测值与真实期望值之间的马氏距离,进一步调整自适应采样时间间隔的影响因子,以期改善算法的追踪效率以及抗噪性能。
1 船体建模在该模型中,船体所受的外力与力矩主要由流体静力、流体升力、流体阻力、附加质量力,以及推进器组所受的粘滞阻力等组成,并以矩阵形式分析与表示。AUV建模过程中主要分析船体的3个部分:船壳,推进器组以及龙骨[8-9]。描述AUV的运动方程将保持非线性形式以更好地表征AUV的固有特性。
基于动量定理,船体的非线性运动方程可由式(1)近似表示
| $ \left( {{\mathit{\boldsymbol{M}}_{rb}} + {\mathit{\boldsymbol{M}}_a}} \right) - \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} + \left( {{\mathit{\boldsymbol{C}}_{rb}} + {\mathit{\boldsymbol{C}}_a}} \right)\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{\eta }} \right) = {\mathit{\boldsymbol{\tau }}_G} + {\mathit{\boldsymbol{\tau }}_P} + {\mathit{\boldsymbol{\tau }}_F}, $ | (1) |
其中:Mrb表示由刚体特性产生的质量矩阵;Ma表示由附加质量力产生的质量矩阵;v表示广义速度向量;D表示船体的阻力矩阵,其中包括船体所受的粘滞阻力,非对称阻力,滚转阻力以及偏航阻力等;Crb表示由刚体特性产生的科里奥利矩阵;Ca表示由附加质量力产生的科里奥利矩阵;g(η)表示由船体的滚转运动所产生的恢复力向量;η表示广义位移向量;τG表示由船体质量与浮力所产生的外力向量;τP表示由推进器组所产生的外力向量;τF表示由船体龙骨所产生的外力向量。
由于在测试过程中,AUV会出现相对于固定笛卡尔惯性坐标系的船首航向变化现象,因此,必须在AUV状态模型中添加运动学方程如下
| $ \mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\eta }} \right)\mathit{\boldsymbol{v}} + {\omega _\mathit{\boldsymbol{\eta }}}, $ | (2) |
式中:J(η)为参考坐标系转换矩阵;ωη为体坐标系与定坐标系变量转换时所产生的过程噪声。
结合式(1)与式(2),可获得船体的状态模型方程组如下
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\eta }}\\ \mathit{\boldsymbol{v}} \end{array}} \right] = f\left( {x,u} \right) + \omega =\\\; \left( \begin{array}{l} \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{\eta }} \right)\mathit{\boldsymbol{v}}\\ \left( {{\mathit{\boldsymbol{M}}_{rb}} + {\mathit{\boldsymbol{M}}_a}} \right) - \left( {{\mathit{\boldsymbol{\tau }}_G} + {\mathit{\boldsymbol{\tau }}_P} + {\mathit{\boldsymbol{\tau }}_F}} \right) + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} - \left( {{\mathit{\boldsymbol{C}}_{rb}} + {\mathit{\boldsymbol{C}}_a}} \right)\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{\eta }} \right) \end{array} \right) + \omega , $ | (3) |
式中,ω为预测算法的过程噪声。由式(3)当中的状态方程组求得船体在o-NED平面的状态向量,并通过式(4)对状态向量进行离散化处理
| $ {\mathit{\boldsymbol{X}}_{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{F}}_{\left( k \right)}}\left( {{\mathit{\boldsymbol{X}}_{\left( k \right)}}} \right) + {\omega _{\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} {1,0,t,0,0,0}\\ {0,1,0,t,0,0}\\ {0,0,1,0,t,0}\\ {0,0,0,1,0,t}\\ {0,0,0,0,1,0}\\ {0,0,0,0,0,1} \end{array}} \right] * {\mathit{\boldsymbol{X}}_{\left( k \right)}} + {\omega _{\left( k \right)}}, $ | (4) |
式中:F为基于标准UKF算法的六样本点状态转移矩阵;t为算法采样时间间隔;X为算法当前一步(第k步)的状态向量,其具体表达式为
| $ \mathit{\boldsymbol{X}} = \left[ {x,y,\dot x,\dot y,\dot u,\dot v} \right]T, $ | (5) |
式中:x为船体当前的横向位移;y为其纵向位移;ẋ为其沿x轴的线速率分解量;ẏ为其沿y轴的线速率分解量;
实际测试过程中,AUV将由基站船初始位置下水,并由基站船的GPS收发设备确定AUV在测试水域自由表面的具体位置。AUV追踪轨迹将由基于测试水域的固定笛卡尔惯性坐标系确定。因此,在仿真研究过程中,可以通过目标AUV与基站船体之间的实时距离r(k)以及2者间的方向角φ(k)建立AUV船体的离散化观测模型。不妨设基站船的初始位置在(0.2,2),则目标AUV的观测模型可由如下方程组表示
| $ {Z_{\left( k \right)}} = {H_{\left( k \right)}}\left( {{\mathit{\boldsymbol{X}}_{\left( k \right)}}} \right) + {\mathit{\boldsymbol{v}}_{\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} {{r_{\left( k \right)}} + {\mathit{\boldsymbol{v}}_{r\left( k \right)}}}\\ {{\varphi _{\left( k \right)}} + {v_{\varphi \left( k \right)}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sqrt {\left( {{x_{e\left( k \right)}} - 0.2} \right)2 + \left( {{y_{e\left( k \right)}} - 2} \right)} + {\mathit{\boldsymbol{v}}_{r\left( k \right)}}}\\ {\arctan \left( {\frac{{{y_{e\left( k \right)}} - 2}}{{{x_{e\left( k \right)}} - 0.2}}} \right) + {v_{\varphi \left( k \right)}}} \end{array}} \right], $ | (6) |
式中:vr(k)为距离观测仪的传感器误差;vφ(k)为惯性坐标系下方向角观测陀螺仪的传感器误差;xe(k)为算法当前时刻对AUV状态向量中船体的横向位移预测值;ye(k)为算法当前时刻对AUV状态向量中船体的纵向位移的预测值。观测模型中的距离方程与方向角方程共同反映了AUV船体在固定惯性坐标系当中对应算法当前一步的位置。
在标准的UKF算法过程中,每一时刻都会更新一组离散化AUV状态向量及相对应的协方差矩阵,经过sigma采样矩阵计算,均值、协方差权值计算,一步状态预测,一步协方差预测,卡尔曼增益计算,状态更新及协方差更新等步骤可完成标准UKF算法的一个运算周期。与传统的EKF、PF等数值航迹追踪方法相比,标准的UKF方法也可达到二阶运算精度,从部分UKF学者的研究成果分析,算法的效率以及航迹追踪效果比较理想[10-11]。
2 优化UKF算法 2.1 采样时间间隔无迹卡尔曼滤波算法的采样时间间隔t反映了该算法对于AUV船体状态方程组的离散化程度,同时也反映了AUV内置的IMU等数字传感器的真实采样率,是衡量算法抗噪性、预测追踪效率以及误差精度高低的重要参数。
在Introduction in ship hydromechanics中[5],作者在构造船体Nomoto状态模型时,考虑了采样间隔对于模型设计所产生的影响,并将状态模型划分为采样间隔关联项与采样间隔独立项2部分。通过舵角、修正舵角输入控制量和船体回转实验数据等系统输出量为基础,确定了状态模型公式的主要待定系数。文献也给出了基于该模型的仿真实验对比结果,反映出方法具备较高的船体位移预测能力。由此,可以考虑将自适应采样间隔构造为与算法上一步采样间隔相关联项和与算法上一步采样间隔非关联项2部分,并通过仿真调试加以验证。同时,为了能提升优化后的UKF算法效率,也需对采样间隔表达式适当添加约束项。在高机动条件下组合导航自适应滤波算法研究及改进中[12],作者依据极大似然原则,在卡尔曼滤波算法一步状态预测阶段,对系统导航KF算法添加了调节因子。该调节因子由速度矢量范数和速度经验最优值确定,文献给出了算法仿真结果,且算法效率较高。
由此,参考船体Nomoto状态模型的构造方法,通过设置采样间隔关联项与采样间隔非关联项的方式构造自适应UKF算法的采样间隔表达式,并参考高机动条件下组合导航自适应滤波算法研究及改进一文,尝试添加递归影响因子、尺度参数、航迹约束项及极值采样间隔项进一步约束自适应UKF算法的采样间隔。
依据采样间隔表达式构造思路,在自适应UKF算法当前一步(第k步)会对采样间隔表达式添加航迹约束项M(k)。用于表示船体在算法当前一步中真实期望位移及预测位移之间偏差程度的航迹约束项表达式
| $ {M_{\left( k \right)}} = \frac{{d_t^2}}{{d_e^2}} = \frac{{{{\left( {{x_{t\left( k \right)}} - {x_{t\left( {k - 1} \right)}}} \right)}^2} + {{\left( {{y_{t\left( k \right)}} - {y_{t\left( {k - 1} \right)}}} \right)}^2}}}{{{{\left( {{x_{e\left( k \right)}} - {x_{e\left( {k - 1} \right)}}} \right)}^2} + {{\left( {{y_{e\left( k \right)}} - {y_{e\left( {k - 1} \right)}}} \right)}^2} + {\gamma _1}}}, $ | (7) |
式中:de为AUV当前时刻的通过算法追踪的航行轨迹;dt为AUV当前时刻真实期望的航行轨迹;xe(k)为算法当前时刻对AUV状态向量中船体的横向位移的预测值;xe(k-1)为算法上一时刻(第k-1步)对船体横向位移的预测值;xt(k)为船体在算法当前时刻的真实期望横向位移;xt(k-1)为船体在算法上一时刻的真实期望横向位移。关于纵向位移项的含义由此类推,γ1为约束值,用于尽量保证M(k)<1,同时防止式(7)分母接近0而产生的算法奇异现象。
当AUV航行至当前时刻预期航迹终点时,若船体预测航行轨迹与真实期望航迹偏差过大时,M(k)→0。而船体当前一步预测航迹最大距离接近对应真实期望航迹总距离时,则M(k)≈0.9。因此,算法的轨迹约束项的值,默认处于区间0<M(k)<0.9。
假设T(k)为自适应UKF算法过程中当前时刻的采样间隔。由于受香浓定理的约束,算法采样间隔T(k)可被设置为Tmin≤T(k)≤Tmax区间上的自适应变量。结合采样间隔极值的约束,标准UKF算法以及文献[5, 12]的设计思路,自适应UKF算法控制过程中当前时刻的采样时间间隔T(k)的表达式可由上一时刻的采样间隔T(k-1)与极值采样间隔的加权和表示,即
| $ {T_{\left( k \right)}} = \left( {1 - {\tau _{\left( k \right)}}} \right) \times \varphi \times {T_{\left( {k - 1} \right)}} + {\tau _{\left( k \right)}} \times {M_{\left( k \right)}} \times {T_{{\rm{maxc}}}}, $ | (8) |
式中:φ为尺度参数,用于收敛采样间隔的具体数值,默认为0.1;Tmaxc为极值采样间隔,用于约束算法采样时间间隔的范围,一般情况下Tmaxc的取值较大;τ为当前时刻的采样间隔影响因子,用以控制采样时间间隔的数值,τ∈(0,1)。
该自适应采样间隔将被添加至AUV船体的系统状态模型当中,以期达到改善UKF算法效率,降低算法预测误差,以及提升算法抗噪能力的目的。
2.2 马氏距离影响因子影响自适应UKF算法性能优劣的关键在于采样间隔影响因子τ的构造与选取。在UKF算法的每一时刻k,采样间隔影响因子τ(k)将会由影响程度最大的算法因素决定。将通过计算当前一步(第k步)的航迹预测状态向量与当前一步的总体样本之间的综合马氏距离d(k),以确定算法下一步的采样间隔影响因子τ(k+1)的值,并进一步确定算法下一步的自适应采样时间间隔T(k+1)。与标准的马氏距离的计算过程相类似,不妨设算法当前一步的航迹预测状态向量为X(k)、当前一步的真实期望向量为T(k)、上一步的航迹预测状态向量为X(k-1)以及上一步的真实期望向量为T(k-1),并由此4项构成总体样本,每个样本点中只取船体的横纵位移x,y,可以获得一组2维4样本点的总体样本[13]
| $ {\mathit{\boldsymbol{X}}}{({\mathit{k}})_2},{\mathit{\boldsymbol{T}}}{({\mathit{k}})_2},{\mathit{\boldsymbol{X}}}{({\mathit{k}}{\rm{ - 1}})_2},{\mathit{\boldsymbol{T}}}{({\mathit{k}}{\rm{ - 1}})_2}\} 。$ |
其中:X(k)2=[xe(k), ye(k)]T;
| $ \begin{array}{l} \left\{ {\mathit{\boldsymbol{X}}{{\left( k \right)}_2},\mathit{\boldsymbol{T}}{{\left( k \right)}_2},\mathit{\boldsymbol{X}}{{\left( {k - 1} \right)}_2},\mathit{\boldsymbol{T}}{{\left( {k - 1} \right)}_2}} \right\}。\\ 其中:\mathit{\boldsymbol{X}}{\left( k \right)_2} = {\left[ {{\mathit{\boldsymbol{x}}_{e\left( k \right)}},{y_{e\left( k \right)}}} \right]^{\rm{T}}};\\ \mathit{\boldsymbol{T}}{\left( k \right)_2} = {\left[ {{\mathit{\boldsymbol{x}}_{t\left( k \right)}},{y_{t\left( k \right)}}} \right]^{\rm{T}}};\\ \mathit{\boldsymbol{X}}{\left( {k - 1} \right)_2} = {\left[ {{\mathit{\boldsymbol{x}}_{e\left( {k - 1} \right)}},{y_{e\left( {k - 1} \right)}}} \right]^{\rm{T}}};\\ \mathit{\boldsymbol{T}}{\left( {k - 1} \right)_2} = {\left[ {{\mathit{\boldsymbol{x}}_{t\left( {k - 1} \right)}},{y_{t\left( {k - 1} \right)}}} \right]^{\rm{T}}}。\end{array} $ | (9) |
计算航迹预测状态向量与总体样本之间的综合马氏距离d(k),并由此决定算法仿真下一步的采样间隔影响因子τ(k+1)。此方法需要考虑算法当前一步总体样本的均值向量μ(k)与协方差矩阵Σ(k)[14],其求解方法为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\mu }}_{\left( k \right)}} = \frac{{\mathit{\boldsymbol{X}}{{\left( k \right)}_2} + \mathit{\boldsymbol{T}}{{\left( k \right)}_2} + \mathit{\boldsymbol{X}}{{\left( {k - 1} \right)}_2} + \mathit{\boldsymbol{T}}{{\left( {k - 1} \right)}_2}}}{4}}\\ {{\mathit{\Sigma }_{\left( k \right)}} = {\mathop{\rm cov}} \left( {x,y} \right)。} \end{array} $ | (10) |
根据算法当前一步总体样本的均值向量μ(k)、协方差矩阵Σ(k)以及自适应UKF算法当前一步的航迹预测状态向量,可获得算法当前一步的综合马氏距离d(k) [15]:
| $ {d_{\left( k \right)}} = \sqrt {{{\left( {\mathit{\boldsymbol{X}}{{\left( k \right)}_2} - {\mathit{\boldsymbol{\mu }}_{\left( k \right)}}} \right)}^\prime }{\mathit{\Sigma }_{\left( k \right)\left( k \right)}} - \left( {\mathit{\boldsymbol{X}}{{\left( k \right)}_2} - {\mathit{\boldsymbol{\mu }}_{\left( k \right)}}} \right)} , $ | (11) |
式中的综合马氏距离包涵了算法当前一步船体横纵位移的预测-真实偏差信息,表征了航迹预测状态向量与总体样本之间的偏移程度。若算法下一步的采样间隔影响因子τ(k+1),由影响程度最大的当前一步的综合马氏距离d(k)决定,则应有
| $ {\mathit{\boldsymbol{\tau }}_{\left( {k + 1} \right)}} = \frac{\varepsilon }{{{{\left( {{d_{\left( k \right)}}} \right)}_2} + {\mathit{\boldsymbol{\gamma }}_2}}}, $ | (12) |
式中,ε为尺度参数,用于约束影响因子的取值范围。γ2为约束项,使采样间隔影响因子τ(k+1)尽量收敛,同时防止式(12)分母接近0而产生的算法奇异现象。
3 仿真结果与分析通过Labocean的AUV SLAM模型分别对标准的UKF追踪算法以及自适应UKF追踪算法进行了仿真实验,并对所获得的航迹预测结果、采样间隔曲线、仿真效果曲线以及2种算法在不同加性噪声下的单侧误差值进行了对比分析。AUV将在测试区域追踪真实期望航迹方向前行。仿真过程中的具体参数设置,如表 1所示。
| 表 1 仿真实验参数设置列表 Table 1 Simulation experiment parameter setting list |
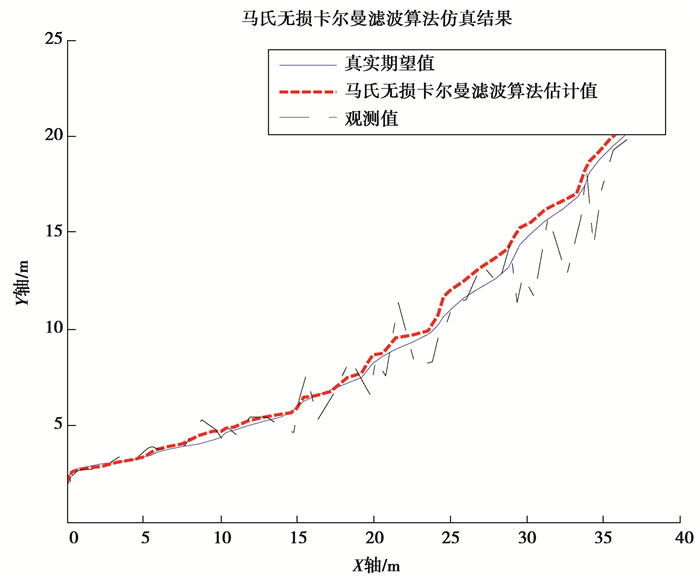
在o-NED参考坐标系中,应用标准UKF算法以及自适应UKF算法后,会获得2幅AUV航迹追踪曲线的结果对比图。其中,第1幅图为标准UKF算法的航迹追踪结果;第2幅图为自适应UKF算法的航迹追踪结果。2种算法当中,均添加了服从(0,1)均匀分布的白噪声。2张图中红色虚线为通过算法所获得的预测航迹;蓝色曲线为真实期望航迹;黑色点画线为观测航迹。

|
图 1 标准UKF算法的航迹追踪结果 Figure 1 Trajectory tracking results of standard UKF algorithm |
|
图 2 马氏UKF算法的航迹追踪结果 Figure 2 Trajectory tracking results of Mahalanobis UKF algorithm |
通过上述结果可以发现:标准的UKF预测曲线后半段的偏差较大,追踪效果一般,且预测曲线有逐渐发散的趋势,这与算法误差累计和算法自身的自适应性有一定关系;而自适应UKF算法的追踪效果相对有一些改善;AUKF算法曲线的总体追踪效果较稳定,曲线前半段方差较低,预测航迹曲线后半段偏差较大;AUKF算法的总体平均追踪误差略低于标准UKF算法,其路径契合度也比较理想。根据航迹追踪的仿真结果对比,可以发现自适应UKF算法可以比较准确地追踪AUV真实预期航迹,相对于标准UKF算法,AUKF追踪曲线更加稳定平滑,自适应能力更强,与之前的理论预期相符合,预测误差也一直保持在可接受的范围。
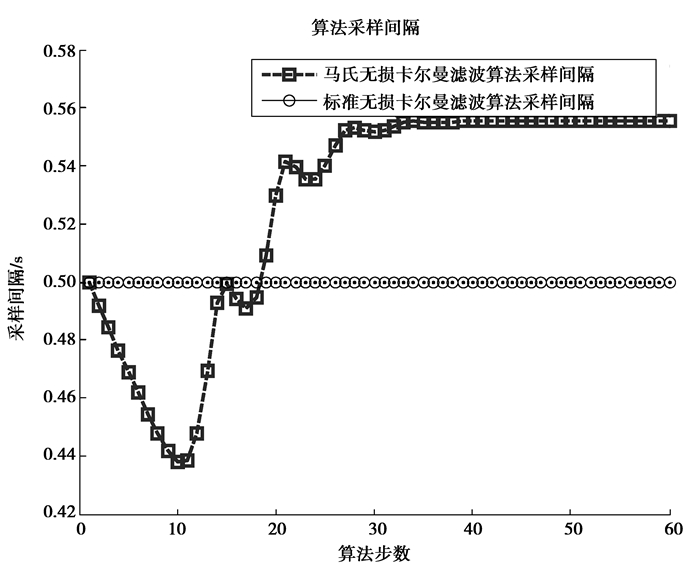
3.2 采样间隔曲线图 3为在60个算法周期内,2种UKF航迹追踪算法的采样间隔对比。图中,蓝色点画虚线为自适应UKF算法的采样间隔;黑色点画线为标准UKF算法的采样间隔;曲线的横轴表示仿真步数。由对比图能够发现:自适应UKF算法的采样间隔在仿真初始阶段略低于标准的UKF算法,之后逐渐高于标准UKF算法并趋近于定值,AUKF算法总体的采样间隔普遍高于标准UKF算法的采样间隔。这表明AUKF算法的采样间隔需要一定时间收敛于某一定值,由于算法每一步都存在反馈补偿机制,其总体累积误差将低于标准UKF算法。当算法预测值与真实期望值之间的差值较大时,AUV相关传感器的采样间隔就将随之减小,航迹追踪的精度就会随之提升。反之,采样间隔将适当提升,以减小能耗及算法冗余。
|
图 3 采样时间间隔对比图 Figure 3 sampling interval comparison chart |
所提出的自适应UKF算法当中,式(8)确定了算法当前一步的采样间隔。其中,采样间隔影响因子τ对于决定算法当前一步的采样间隔起了关键作用。τ由AUV船体在算法当前一步及上一步的横纵位移预测真实值之间的马氏距离所决定。而采样间隔影响因子τ的初值为预设值,其取值范围为(0,1)。为了对比分析τ的初值选取对于AUKF算法收敛性能以及算法效率的影响,对于选取不同初值τ的自适应UKF算法进行对比仿真,以期寻找初值τ的最佳预设范围。分别选取了4组不同初值τ的AUKF算法仿真航迹曲线,其结果如下(如图 4~图 7所示)
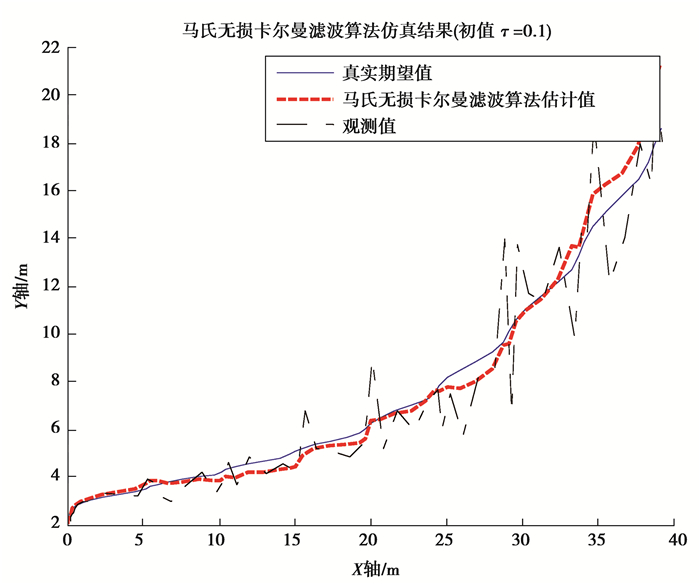
当初值τ=0.1时,
|
图 4 初值τ=0.1时, 自适应UKF算法仿真结果 Figure 4 Trajectory tracking results of AUKF algorithm with τ=0.1 |
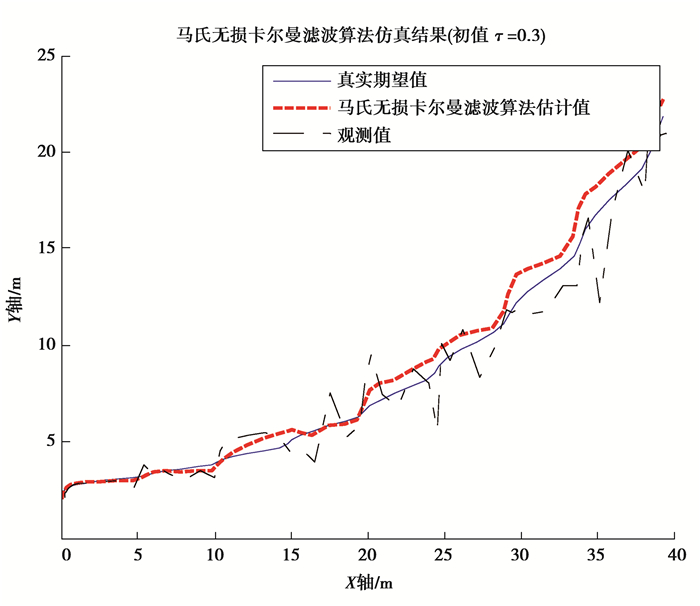
当初值τ=0.3时,
|
图 5 初值τ=0.3时, 自适应UKF算法仿真结果 Figure 5 Trajectory tracking results of AUKF algorithm with τ=0.3 |
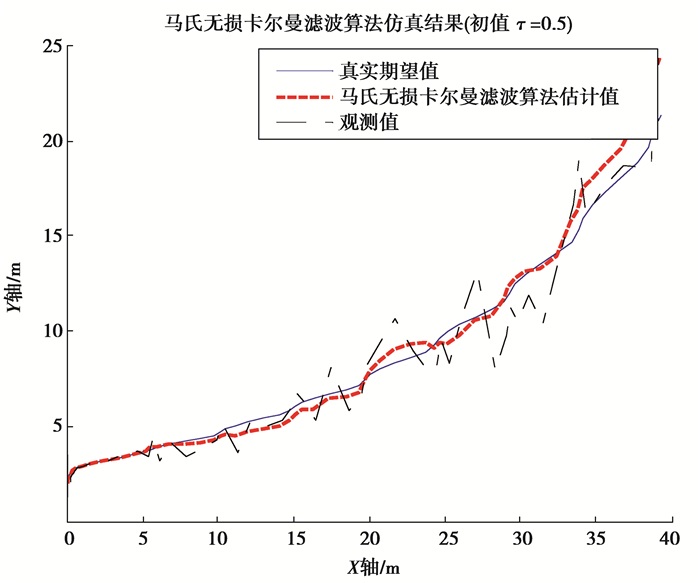
当初值τ=0.5时,
|
图 6 初值τ=0.5时, 自适应UKF算法仿真结果 Figure 6 Trajectory tracking results of AUKF algorithm with τ=0.5 |
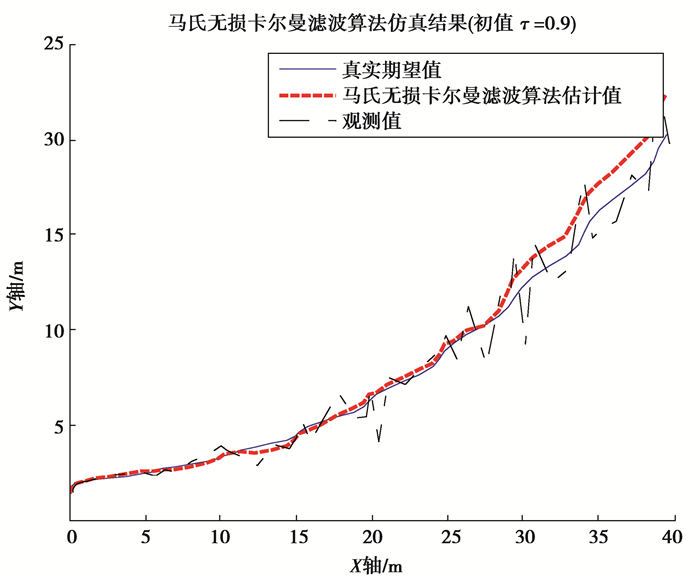
当初值τ=0.9时,
|
图 7 初值τ=0.9时, 自适应UKF算法仿真结果 Figure 7 Trajectory tracking results of AUKF algorithm with τ=0.9 |
由以上4组仿真结果可以发现,当初值τ取值接近边界值0或1时,真实期望轨迹和观测航迹的横纵位移会出现一定程度的偏移。这与AUV状态模型的设计和采样间隔的实时变化有关。当初值τ取值在0.3到0.5之间时,真实期望轨迹和观测航迹比较接近标准UKF算法的仿真轨迹,其横纵位移不会出现较大偏移。而对比初值τ取值为0.3和0.5的仿真结果可以发现,当初值τ取值在0.5附近时,AUKF算法预测误差较小,算法效率更高。当面对算法预测精度要求较高的问题时,可以将算法采样间隔影响因子τ的初值预设在0.3~0.5附近,并依据实际预测效果进行调整。
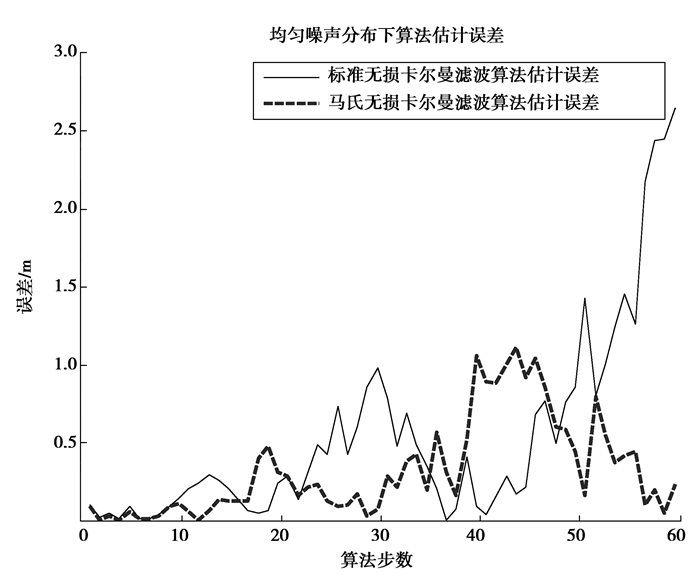
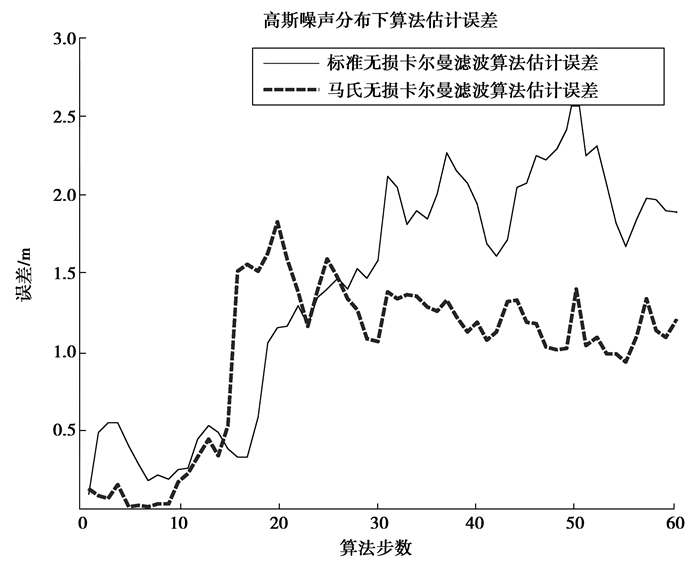
3.4 预测误差精度对比自适应UKF算法的目的是为了降低AUV航迹追踪过程中的累积误差对追踪结果的影响。因此,为了验证算法对误差精度的改善效果以及抗噪性能,分别对2种UKF算法添加了3种不同分布的加性白噪声,以便比较2种算法的降噪水平及自适应性。图中,蓝色虚线为AUKF算法的预测误差结果;黑色曲线为标准UKF算法的预测误差结果;曲线的横轴表示仿真步数;介于篇幅所限,笔者仅列出了2种UKF算法关于o-NED参考坐标系中X轴方向的预测航迹误差曲线(如图 8~图 10所示)。
|
图 8 均匀分布噪声下的航迹误差曲线 Figure 8 track error curve under uniform noise distribution |
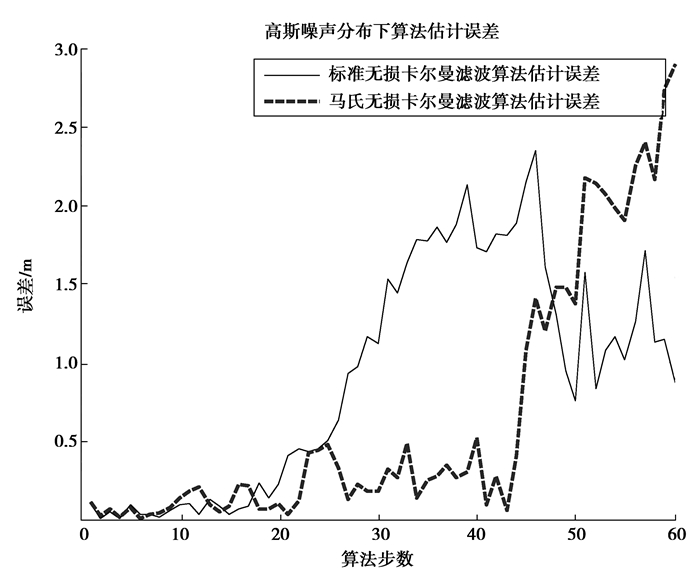
|
图 9 高斯白噪声下的航迹误差曲线 Figure 9 Gaussian white noise trajectory error curve |
|
图 10 对数分布噪声下的航迹误差曲线 Figure 10 track error curve under logarithmic distribution |
由3组误差曲线,可以发现自适应UKF算法的误差曲线的预测误差普便低于标准UKF算法。这验证了AUKF算法具备较高的抗噪性以及航迹预测自适应性。在作业精度需求较高的环境下,可尝试采用AUKF算法来追踪AUV的航行轨迹。
4 结论提出了基于AUV航迹追踪技术的自适应UKF控制方法。通过AUKF算法航迹追踪实验,可以发现在选取合适的系统模型和自适应采样间隔影响因子的初值后,AUV航迹追踪曲线更加平滑契合,这说明AUKF算法具有更加理想的航迹追踪契合度以及信号采样自适应性。同时,在添加了3种不同的加性白噪声的环境下,AUKF算法仍然具有较低的累积误差,算法的误差精度及抗噪性较高,基本达到了预期的要求。在之后的研究中,可以考虑将AUV的系统模型扩展至5自由度或6自由度,并添加更多的边界条件,以验证自适应UKF算法的效率与兼容性。
| [1] |
Allotta B, Caiti A, Chisci L, et al. Development of a navigation algorithm for autonomous underwater vehicles[J]. IFAC-Papers OnLine, 2015, 48(2): 64-69. DOI:10.1016/j.ifacol.2015.06.011 |
| [2] |
Rasmussen C E, Williams C K I. Gaussian processes for machine learning[M]. London: MIT Press, 2006: 207-220.
|
| [3] |
姚绪梁, 杨光仪, 彭宇. 水下自主航行器垂直面运动的预测控制[J]. 哈尔滨工业大学学报, 2017, 46(9): 166-173. YAO Xuliang, YANG Guangyi, PENG Yu. Predictive control for diving of an autonomous underwater vehicle[J]. Journal of Harbin Institute of Technology, 2017, 46(9): 166-173. (in Chinese) |
| [4] |
Kundu P K, Cohen I M. Fluid mechanics[M]. Burlington, USA: Elsevier Press, 2008.
|
| [5] |
Journée J M J, Jakob P. Introduction in ship hydromechanics[M]. Mekelweg, Netherlands: Delft University of Technology Press, 2002.
|
| [6] |
王艳艳, 刘开周, 封锡盛. AUV纯方位目标跟踪轨迹优化方法[J]. 机器人, 2014, 36(2): 179-184. WANG Yanyan, LIU Kaizhou, FENG Xisheng. Optimal AUV trajectories for bearings-only tracking[J]. Robot, 2014, 36(2): 179-184. (in Chinese) |
| [7] |
Allotta B, Caiti A, Costanzi R, et al. Development and online validation of an UKF-based navigation algorithm for AUVs[J]. IFAC-Papers OnLine, 2016, 49(15): 69-74. DOI:10.1016/j.ifacol.2016.07.711 |
| [8] |
Xiao L, Jouffroy J. Modeling and nonlinear heading control of sailing yachts[J]. IEEE Journal of Oceanic Engineering, 2014, 39(2): 256-268. DOI:10.1109/JOE.2013.2247276 |
| [9] |
Inzartsev A V. Underwater vehicles[M]. Vienna, Austria: Intech Press, 2009: 539-556.
|
| [10] |
Miyabayashi K, Tonomura O, Kano M, et al. Comparative study of state estimation of tubular microreactors using UKF and EKF[J]. IFAC Proceedings Volumes, 2012, 45(15): 513-518. DOI:10.3182/20120710-4-SG-2026.00174 |
| [11] |
刘斌, 马晓川, 侯朝焕. 针对高速自治水下航行器的UKF主动目标跟踪算法[J]. 系统仿真学报, 2008, 20(4): 947-950. LIU Bin, MA Xiaochuan, HOU Chaohuan. A UKF-based active target tracking algorithm for high-speed autonomous underwater vehicles[J]. Journal of System Simulation, 2008, 20(4): 947-950. (in Chinese) |
| [12] |
李小龙, 段凤阳, 许金凯, 等. 高机动条件下组合导航自适应滤波算法研究及改进[J]. 长春理工大学学报(自然科学版), 2010, 33(3): 48-51. LI Xiaolong, DUAN Fengyang, XU Jinkai, et al. Study and improvement on adaptive filter of integrated navigation system in highly dynamic environment[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2010, 33(3): 48-51. (in Chinese) DOI:10.3969/j.issn.1672-9870.2010.03.014 |
| [13] |
梅江元.基于马氏距离的度量学习算法研究及应用[D].哈尔滨: 哈尔滨工业大学, 2016. MEI Jiangyuan. Research on mahalanobis distance based metric learning algorithm and its applications[D]. Haerbin: Harbin Institute of Technology, 2016.(in Chinese) |
| [14] |
吴香华, 牛生杰, 吴诚鸥, 等. 马氏距离聚类分析中协方差矩阵估算的改进[J]. 数理统计与管理, 2011, 30(2): 240-245. WU Xianghua, NIU Shengjie, WU Chengou, et al. An improvement on estimating covariance matrix during cluster analysis using mahalanobis distance[J]. Application of Statistics and Management, 2011, 30(2): 240-245. (in Chinese) |
| [15] |
韩涵, 王厚军, 龙兵, 等. 基于改进马氏距离的模拟电路故障诊断方法[J]. 控制与决策, 2013, 28(11): 1713-1717. HAN Han, WANG Houjun, LONG Bing, et al. Method for analog circuit fault diagnosis based on improved mahalanobis distance[J]. Control and Decision, 2013, 28(11): 1713-1717. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42


