极化是除幅度、频率和相位以外,电磁波的又一基本参量,极化信息的利用可显著提高雷达在目标检测、抗干扰、反隐身等方面的性能。当前,作为雷达家族中的重要一员,极化雷达在防空反导、战场侦察、精确制导、地理遥感等方面发挥着重要作用,成为信息感知领域内的中坚力量之一[1-3]。
发射波形的选择对雷达系统的整体性能有着显著的影响,高速数字处理器技术与微波固态功率放大器技术的发展使得现代雷达系统能够采用更加灵活的波形设计,发射适应不同目标和环境的“匹配”波形。如图 1描述了自适应波形设计流程框图,雷达利用场景先验信息设计初始发射波形,根据接收回波获取目标和杂波/噪声的信息,设计下一次发射波形,实现对目标的匹配照射。相较于传统雷达发射固定波形,上述波形优化设计可显著提高雷达在目标检测、跟踪、参数估计以及杂波抑制等方面的性能。当前,在认知雷达、多输入多输出(MIMO, multiple-input multiple-output)雷达方面,发射波形优化设计是其重要的研究方向[4-11]。

|
图 1 自适应波形设计流程框图 Figure 1 The flow chart of adaptive waveform design |
在一定意义上,全极化雷达可看作为一个2×2的集中式MIMO雷达(即具备2个发射通道和2个接收通道的MIMO雷达),但是不同于MIMO雷达的是,在极化雷达范畴内,目标和杂波的极化散射矩阵以及二阶协方差矩阵有着明确的物理意义,因此,有必要开展极化雷达波形设计的专门研究。在这方面,以最大化滤波器输出信杂噪比(SCNR,signal clutter-plus-noise ratio)为准则,文献[10]提出了一种发射波形功率约束条件下,色噪声和发射信号相关杂波背景中的目标波形接收滤波器联合优化设计方法。以最大化滤波器组输出最小SCNR为准则,文献[11]研究了发射波形功率约束和与给定波形具有一定相似度约束(使优化设计后的波形保持在峰值旁瓣比、带宽等方面的良好性质)同时作用下,发射波形和接收滤波器组的联合优化方法。文献[10]的研究表明,在仅有噪声存在的条件下,最优发射波形为目标自相关矩阵和噪声自相关矩阵之和的主本征矢量的正交矢量,最优接收滤波器为该最优发射波形条件下的匹配滤波器;而在信号相关杂波和噪声同时存在的条件下,前述自相关矩阵依赖于全极化发射波形的功率谱,为此文献[10]提出了一种迭代优化方法求解最优发射波形。然而,需要指出的是,该迭代优化方法不能保证迭代结果的单调性和收敛性。
针对现有研究中存在的问题和不足,笔者立足于提高极化雷达的目标检测性能,以最大化SCNR为准则,提出一种新的发射波形和接收滤波器迭代优化算法。与文献[10]不同的是,新算法将确保目标函数随迭代步骤的单调递增和收敛性。实验环节证实了方法的有效性,以及相对Pillai方法的优势。
1 问题模型首先,全极化雷达发射波形s在快时间域的N个采样可表示为如下2N维复矢量的形式,
| $ s \buildrel \Delta \over = {\left[ {\left( {{s_H},0,{s_V},0} \right) \cdots \left( {{s_H},N - 1,{s_V},N - 1} \right)} \right]^{\rm{T}}} \in {\mathit{\boldsymbol{C}}^{2N}}, $ | (1) |
其中,符号
其次,已知在给定视线角θ和距离单元n的条件下,目标的全极化散射矩阵为[12]
| $ {\mathit{\boldsymbol{T}}_n}\left( \theta \right) \buildrel \Delta \over = \left[ \begin{array}{l} {\mathit{\boldsymbol{T}}_{{\rm{HH}},n}}\left( \theta \right){\mathit{\boldsymbol{T}}_{{\rm{HV}},n}}\left( \theta \right)\\ {\mathit{\boldsymbol{T}}_{{\rm{VH}},n}}\left( \theta \right){\mathit{\boldsymbol{T}}_{{\rm{VV}},n}}\left( \theta \right) \end{array} \right],\theta \in \left[ {0,2{\rm{ \mathsf{ π} }}} \right), $ | (2) |
其中,TXY, n(θ)表示雷达视线角为θ、发射极化为“X”极化、接收极化为“Y”极化(X, Y∈{H, V})条件下目标的第n个距离单元的散射系数。另外,杂波的第n个距离单元极化散射矩阵为
| $ {\mathit{\boldsymbol{C}}_n}\left( \theta \right) \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{{\rm{HH}},n}}}&{{\mathit{\boldsymbol{C}}_{{\rm{HV}},n}}}\\ {{\mathit{\boldsymbol{C}}_{{\rm{VH}},n}}}&{{\mathit{\boldsymbol{C}}_{{\rm{VV}},n}}} \end{array}} \right]。$ | (3) |
又已知目标极化散射特性的时域离散形式为其脉冲响应矩阵(TIRM, target impulse response matrix)。假定TIRM的支撑区间大小为Q(Q的值由雷达视线方向上目标径向长度和雷达的距离分辨率决定),回波观测样本个数为M。令M=Q+N-1,以使得目标的回波信息在一次数字采样中被雷达完全接收。那么,目标的脉冲响应矩阵TIRM和杂波的脉冲响应矩阵CIRM分别为
| $ {\mathit{\boldsymbol{T}}_n}\left( \theta \right) \buildrel \Delta \over = \sum\limits_{n = 0}^{Q - 1} {{\mathit{\boldsymbol{J}}_n} \otimes {\mathit{\boldsymbol{T}}_n}\left( \theta \right)} , $ | (4) |
| $ \mathit{\boldsymbol{C}} \buildrel \Delta \over = \sum\limits_{n = - N + 1}^{M - 1} {{\mathit{\boldsymbol{J}}_n} \otimes {\mathit{\boldsymbol{C}}_n}} , $ | (5) |
其中,符号“⊗”表示Kronecker乘积,Jn为M×N维转移矩阵,即
| $ {\mathit{\boldsymbol{J}}_n}\left( {{l_1},{l_1}} \right) \buildrel \Delta \over = \left\{ {\begin{array}{*{20}{c}} 1&{{\rm{if}}}&{{l_1} - {l_1} = n}\\ 0&{{\rm{if}}}&{{l_1} - {l_1} \ne n} \end{array}} \right.,{l_1} \in \left\{ {1, \cdots ,M} \right\},{l_2} \in \left\{ {1, \cdots ,N} \right\}。$ | (6) |
根据式(4)和(5)写出TIRM和CIRM的显性形式分别为
| $ \mathit{\boldsymbol{T}}\left( \theta \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_0}\left( \theta \right)}&0& \cdots &0\\ {{\mathit{\boldsymbol{T}}_1}\left( \theta \right)}&{{\mathit{\boldsymbol{T}}_0}\left( \theta \right)}& \cdots &0\\ \vdots&\vdots&\ddots&\vdots \\ {{\mathit{\boldsymbol{T}}_{N - 1}}\left( \theta \right)}&{{\mathit{\boldsymbol{T}}_{N - 2}}\left( \theta \right)}& \cdots &{{\mathit{\boldsymbol{T}}_0}\left( \theta \right)}\\ \vdots&\vdots&\ddots&\vdots \\ {{\mathit{\boldsymbol{T}}_{Q - 1}}\left( \theta \right)}&{{\mathit{\boldsymbol{T}}_{Q - 2}}\left( \theta \right)}& \cdots &{{\mathit{\boldsymbol{T}}_{Q - N + 1}}\left( \theta \right)}\\ \vdots&\vdots&\ddots&\vdots \\ 0&0& \cdots &{{\mathit{\boldsymbol{T}}_{Q - 1}}\left( \theta \right)} \end{array}} \right], $ | (7) |
| $ \mathit{\boldsymbol{C}}\left( \theta \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_0}}&{{\mathit{\boldsymbol{C}}_{ - 1}}}& \cdots &{{\mathit{\boldsymbol{C}}_{ - N + 1}}}\\ {{\mathit{\boldsymbol{C}}_1}}&{{\mathit{\boldsymbol{C}}_0}}& \cdots &{{\mathit{\boldsymbol{C}}_{ - N + 2}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{\mathit{\boldsymbol{C}}_{N - 1}}}&{{\mathit{\boldsymbol{C}}_{N - 2}}}& \cdots &{{\mathit{\boldsymbol{C}}_0}}\\ {{\mathit{\boldsymbol{C}}_N}}&{{\mathit{\boldsymbol{C}}_{N - 1}}}& \cdots &{{\mathit{\boldsymbol{C}}_1}}\\ \vdots&\vdots&\ddots&\vdots \\ {{\mathit{\boldsymbol{C}}_{M - 1}}}&{{\mathit{\boldsymbol{C}}_{M - 2}}}& \cdots &{{\mathit{\boldsymbol{C}}_{M - N}}} \end{array}} \right]。$ | (8) |
将接收回波样本放入如下2M维矢量,即
| $ r \buildrel \Delta \over = {\left[ {\left( {{r_{H,0}},{r_{V,0}}} \right), \cdots ,\left( {{r_{H,M - 1}},{r_{V,M - 1}}} \right)} \right]^{\rm{T}}} \in {\mathit{\boldsymbol{C}}^{{\rm{2M}}}}, $ | (9) |
则全极化雷达回波信号具有如下数学形式,即
| $ \mathit{\boldsymbol{r}} = {\alpha _T}\mathit{\boldsymbol{T}}\left( \theta \right)s + \mathit{\boldsymbol{c}} + \mathit{\boldsymbol{v}} = {\alpha _T}\mathit{\boldsymbol{T}}\left( \theta \right)s + \mathit{\boldsymbol{C}}s + \mathit{\boldsymbol{v}}, $ |
其中:αT为雷达方程、传播因子等决定的复系数;c为发射信号相关杂波矢量;v为如下形式的2M维加性噪声矢量,即
| $ \mathit{\boldsymbol{v}} \buildrel \Delta \over = {\left[ {\left( {{\mathit{\boldsymbol{v}}_{H,0}},{\mathit{\boldsymbol{v}}_{V,0}}} \right), \cdots \left( {{\mathit{\boldsymbol{v}}_{H,M - 1}},{\mathit{\boldsymbol{v}}_{V,M - 1}}} \right)} \right]^{\rm{T}}} \in {\mathit{\boldsymbol{C}}^{{\rm{2}}M}}。$ | (11) |
统计特性方面,假定杂波和噪声之间不相关。复噪声矢量v是均值为零(E[v]=0)、协方差矩阵为Σv=σv2I的圆对称矢量,其中,σv2为单个极化通道噪声分量的方差。杂波的统计特性方面,对于单基地雷达,根据互易性定理有CHV, n=CVH, n, n∈{-N+1, …, M-1}。此外,对c的多分量统计特性不作任何严格假定,但对于单个距离单元n,假定杂波的均值为零(即E[Cn]=0),于是有E[C]=0。为表示杂波在极化域和距离域2个维度的相关性,定义下式
| $ {r_{jk}}\left( {n,n'} \right) \buildrel \Delta \over = \frac{{\mathit{\boldsymbol{IE}}\left[ {{\mathit{\boldsymbol{C}}_{j,n}}\mathit{\boldsymbol{C}}_{k,n'}^ * } \right]}}{{\sqrt {\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{j,n}}} \right|}^2}} \right]} \sqrt {\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{k,n'}}} \right|}^2}} \right]} }},j,k \in \left\{ {HH,HV,VV} \right\}, $ | (12) |
作为第n个距离单元“j”极化通道杂波和第n′个距离单元“k”极化通道杂波的归一化散射系数。又杂波冲击响应矩阵C可表示成如下形式,即
| $ \begin{array}{l} \mathit{\boldsymbol{C}} = \sum\limits_{n = - N + 1}^{M - 1} {{\mathit{\boldsymbol{J}}_n} \otimes {\mathit{\boldsymbol{C}}_n}} \\ \;\;\; = \sum\limits_{n = - N + 1}^{M - 1} {\left[ {{\mathit{\boldsymbol{C}}_{HH}},{}_n{\mathit{\boldsymbol{J}}_n}{\mathit{\boldsymbol{A}}_1} + {\mathit{\boldsymbol{C}}_{HV}},{}_n{\mathit{\boldsymbol{J}}_n} \otimes {\mathit{\boldsymbol{A}}_2} + {\mathit{\boldsymbol{C}}_{VV}},{}_n{\mathit{\boldsymbol{J}}_n} \otimes {\mathit{\boldsymbol{A}}_3}} \right]} \end{array} $ |
其中,
| $ \begin{array}{*{20}{c}} {\bar \Sigma \mathit{\boldsymbol{C}}\left( w \right) = \mathit{\boldsymbol{IE}}\left[ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^\mathit{\dagger }}} \right] = \mathit{\boldsymbol{IE}}\left[ {\mathit{\boldsymbol{Cs}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }}{\mathit{\boldsymbol{C}}^\mathit{\dagger }}} \right] = \sum\limits_{n = - N + 1}^{M - 1} {\sum\limits_{n' = - n + 1}^{M - 1} {\left[ {\sqrt {{\sigma _n}} \sqrt {{\sigma _{n'}}} \mathit{\boldsymbol{r}}_{11}^ * \left( {n,n'} \right)\left( {\mathit{\boldsymbol{J}}_n^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_1}} \right);} \right.} } }\\ {\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }}\left( {\mathit{\boldsymbol{J}}_{n'}^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_1}} \right) + \sqrt {{e_n}{\sigma _n}} \sqrt {{e_{n'}}{\sigma _{n'}}} \mathit{\boldsymbol{r}}_{22}^ * \left( {n,n'} \right)\left( {{\mathit{\boldsymbol{J}}^n} \otimes {\mathit{\boldsymbol{A}}_2}} \right);}\\ {\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }}\left( {\mathit{\boldsymbol{J}}_{n'}^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_2}} \right) + \sqrt {{\sigma _n}} \sqrt {{\sigma _{n'}}{x_{n'}}} {\mathit{\boldsymbol{r}}^{13}}\left( {n,n'} \right)\left( {{\mathit{\boldsymbol{J}}^n} \otimes {\mathit{\boldsymbol{A}}_1}} \right)\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }};}\\ {\left( {\mathit{\boldsymbol{J}}_{n'}^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_3}} \right) + \sqrt {{\sigma _n}{x_n}} \sqrt {{\sigma _{n'}}} \mathit{\boldsymbol{r}}_{13}^ * \left( {n,n'} \right)\left( {{\mathit{\boldsymbol{J}}^n} \otimes {\mathit{\boldsymbol{A}}_3}} \right)\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }};}\\ {\left( {\mathit{\boldsymbol{J}}_{n'}^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_1}} \right) + \sqrt {{\sigma _n}{x_n}} \sqrt {{\sigma _{n'}}{x_{n'}}} {\mathit{\boldsymbol{r}}^{33}}\left( {n,n'} \right)\left( {{\mathit{\boldsymbol{J}}^n} \otimes {\mathit{\boldsymbol{A}}_3}} \right)\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }};}\\ {\left. {\left( {\mathit{\boldsymbol{J}}_{n'}^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_3}} \right)} \right],} \end{array} $ |
这里σ、ε和χ为引入的文献[9]中的参数,有
| $ {\sigma _n} \buildrel \Delta \over = \mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{HH,n}}} \right|}^2}} \right],{e_n} \buildrel \Delta \over = \frac{{\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{VV,n}}} \right|}^2}} \right]}}{{\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{HH,n}}} \right|}^2}} \right]}},{X_n} \buildrel \Delta \over = \frac{{\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{HV,n}}} \right|}^2}} \right]}}{{\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{C}}_{HH,n}}} \right|}^2}} \right]}}。$ | (15) |
研究设计的目的在于,给定目标特性矩阵T(θ)、杂波参数{(ri, j(n, n′), σn, εn, χn), {i, j}∈{1, 2, 3}, n=-N+1, …, M-1}和系统噪声v的条件下,以最大化滤波器输出SCNR为目标函数,优化设计全极化发射波形和接收滤波器。首先,2M维接收矢量r包括以下几项:目标回波αTT(θ)s、系统噪声v和信号相关杂波Cs,即有
| $ \mathit{\boldsymbol{r}} = {\alpha _T}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{C}}_s} + \mathit{\boldsymbol{v}}。$ | (16) |
然后,雷达接收到的回波矢量r经过滤波器w[w(0), …, w(2M-1)]T∈C2M处理,有滤波器输出为
| $ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{r = }}{\alpha _T}{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{Cs}} + {\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{v}}。$ | (17) |
相应的输出SCNR为
| $ {\rm{SCN}}{{\rm{R}}_\theta }\left( {\mathit{\boldsymbol{s}},\mathit{\boldsymbol{w}}} \right) \buildrel \Delta \over = \left( {\frac{{{{\left| {\alpha \mathit{\boldsymbol{T}}} \right|}^2}{{\left| {{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2}}}{{\mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{Cs}}} \right|}^2}} \right] + \mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{v}}} \right|}^2}} \right]}}} \right)。$ | (18) |
发射波形方面,要求其满足功率约束,不失一般性,令‖s‖2,其中‖·‖为Frobenius范数。在上述发射波形功率约束条件下,以最大化滤波器输出SCNR为目标的全极化雷达发射波形和接收滤波器联合优化问题为
| $ \bar P\left\{ \begin{array}{l} \mathop {\max }\limits_{s,w} \frac{{{{\left| {{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\sum\nolimits_c {\left( \mathit{\boldsymbol{s}} \right)\mathit{\boldsymbol{w}}} + \mathit{\boldsymbol{\sigma }}_v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}}}\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;{\left\| \mathit{\boldsymbol{s}} \right\|^2} = 1 \end{array} \right., $ | (19) |
上式省去了式(18)中的常数项|αT|2,因为它并不影响待处理问题的解。至此,得到待求解问题的数学形式。不难看出,问题P是一个非凸优化问题,因为其目标函数非凸,且定义域是一个半径为1的圆,为非凸集。
可以证明,问题P的分母部分具有如下等价形式,即
| $ {\mathit{\boldsymbol{w}}^\mathit{\dagger }}\sum\nolimits_c {\left( \mathit{\boldsymbol{s}} \right)\mathit{\boldsymbol{w}}} + \mathit{\boldsymbol{\sigma }}_v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{s}}^\mathit{\dagger }}\left( {\sum\nolimits_c {\left( \mathit{\boldsymbol{w}} \right)} \mp \mathit{\boldsymbol{\sigma }}_v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{wI}}} \right)\mathit{\boldsymbol{s}}, $ | (20) |
其中,
| $ \begin{array}{l} \bar \Sigma \mathit{\boldsymbol{C}}\left( w \right) = \mathit{\boldsymbol{IE}}\left[ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^\mathit{\dagger }}} \right] = \mathit{\boldsymbol{IE}}\left[ {{\mathit{\boldsymbol{C}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{C}}} \right]\\ = \sum\limits_{n = - N + 1}^{M - 1} {\sum\limits_{n' = - n + 1}^{M - 1} {\left[ {\sqrt {{\sigma _n}} \sqrt {{\sigma _{n'}}} \mathit{\boldsymbol{r}}_{11}^ * \left( {n,n'} \right)\left( {\mathit{\boldsymbol{J}}_n^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_1}} \right) \times } \right.} } \\ \mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {{\mathit{\boldsymbol{J}}_{n'}} \otimes {\mathit{\boldsymbol{A}}_1}} \right) + \sqrt {{e_n}{\sigma _n}} \sqrt {{e_n}{\sigma _{n'}}} \mathit{\boldsymbol{r}}_{22}^ * \left( {n,n'} \right)\left( {\mathit{\boldsymbol{J}}_n^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_2}} \right) \times \\ \mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {{\mathit{\boldsymbol{J}}_{n'}} \otimes {\mathit{\boldsymbol{A}}_2}} \right) + \sqrt {{\sigma _n}} \sqrt {{\sigma _{n'}}{x_{n'}}} \mathit{\boldsymbol{r}}_{13}^ * \left( {n,n'} \right)\left( {\mathit{\boldsymbol{J}}_n^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_1}} \right) \times \\ \mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {{\mathit{\boldsymbol{J}}_{n'}} \otimes {\mathit{\boldsymbol{A}}_3}} \right) + \sqrt {{\sigma _n}{x_n}} \sqrt {{\sigma _{n'}}} {\mathit{\boldsymbol{r}}_{13}}\left( {n,n'} \right)\left( {\mathit{\boldsymbol{J}}_n^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_3}} \right) \times \\ \mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {{\mathit{\boldsymbol{J}}_{n'}} \otimes {\mathit{\boldsymbol{A}}_1}} \right) + \sqrt {{\sigma _n}{x_n}} \sqrt {{\sigma _{n'}}{x_{n'}}} \mathit{\boldsymbol{r}}_{33}^ * \left( {n,n'} \right)\left( {\mathit{\boldsymbol{J}}_n^{\rm{T}} \otimes {\mathit{\boldsymbol{A}}_3}} \right) \times \\ \left. {\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {{\mathit{\boldsymbol{J}}_{n'}} \otimes {\mathit{\boldsymbol{A}}_3}} \right)} \right]。\end{array} $ | (21) |
证明:已知对于P,有‖s‖2=1成立,于是有
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {\sum\nolimits_c {\left( \mathit{\boldsymbol{s}} \right)} + \sigma _v^2I} \right)\mathit{\boldsymbol{w}} = \mathit{\boldsymbol{IE}}\left[ {{{\left| {{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{Cs}}} \right|}^2}} \right] + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}{\left\| \mathit{\boldsymbol{s}} \right\|^2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\mathit{\boldsymbol{s}}^\mathit{\dagger }}\mathit{\boldsymbol{IE}}\left[ {{\mathit{\boldsymbol{C}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{C}}} \right]\mathit{\boldsymbol{s}} + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}{s^\mathit{\dagger }}\mathit{\boldsymbol{s}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \buildrel \Delta \over = {\mathit{\boldsymbol{s}}^\mathit{\dagger }}\left( {\sum\nolimits_c {\left( \mathit{\boldsymbol{w}} \right)} \mp \sigma _v^2{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{s}}。\end{array} $ | (22) |
得证。
进一步地,可以证明,优化问题P等价于如下问题P,即
| $ P\left\{ \begin{array}{l} \mathop {\max }\limits_{s,w} \frac{{{{\left| {{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\sum {\mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{s}} \right)} + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}}},\\ {\rm{s}}.{\rm{t}}.\;{\left\| \mathit{\boldsymbol{s}} \right\|^2} \le 1, \end{array} \right. $ | (23) |
证明:首先,对比P和P,发射波形约束条件由‖s‖2=1放宽为‖s‖2≤1,于是P的可行解包含在P的可行解中,有v(P)≤v(P);另一方面,对于P,结合式,给定可行解
根据P的表达式可知,虽然它依然是一个非凸优化问题(目标函数非凸),但是其约束条件更为宽松(由半径为1的圆变为半径为1的圆面)。对这一优化问题,文献[10]提出了一种迭代优化方法,通过不断优化发射波形s使之满足给定终止条件,但这种方法并不能确保目标函数的收敛性,而且随着迭代过程的进行,终止条件参数也并非单调递减,故而终止条件并不一定得以满足。
3 Pillai方法求解问题P现在回顾一下文献[10]提出的求解问题P的Pillai方法。首先,给定发射波形s,优化问题可以写为
| $ {p_\omega }\left\{ {\mathop {\max }\limits_\omega \frac{{{{\left| {{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2}}}{{{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\sum\nolimits_C {\left( \mathit{\boldsymbol{s}} \right)\mathit{\boldsymbol{\omega }}} + \sigma _v^2{\mathit{\boldsymbol{\omega }}^\mathit{\dagger }}\mathit{\boldsymbol{\omega }}}},} \right. $ | (24) |
上式又等价于
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_w {\mathit{\boldsymbol{w}}^\mathit{\dagger }}\left( {\sum\nolimits_c {\left( \mathit{\boldsymbol{s}} \right)} + \sigma _v^2\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{w}},}\\ {{\rm{s}}.{\rm{t}}.\;\;{{\left| {{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2} = 1。} \end{array} $ | (25) |
对于上式描述的优化问题,它事实上是信号处理领域熟知的最小方差非畸变响应(MVDR,minimum variance distortionless response)问题,这里直接给出其解[13-15]为
| $ \mathit{\boldsymbol{\omega }} = {\mathit{\boldsymbol{\alpha }}_\omega }\left( {\sum\nolimits_C {\left( \mathit{\boldsymbol{s}} \right)} + \sigma _v^2\mathit{\boldsymbol{I}}} \right) - \mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}, $ | (26) |
其中,αw为尺度系数,不难看出,αw的值不影响问题P的目标函数值,因此,不妨取w的归一化值作为接收滤波器的最优解,即有
| $ \mathit{\boldsymbol{\omega }} = \frac{{{{\left( {\sum {\mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{s}} \right)} + \delta _v^2\mathit{\boldsymbol{I}}} \right)}^{ - 1}}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}}}{{\left\| {{{\left. {\sum {\mathit{\boldsymbol{c}}\left( \mathit{\boldsymbol{s}} \right)} + \delta _v^2\mathit{\boldsymbol{I}}} \right)}^{ - 1}}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right\|}}, $ | (27) |
将式(27)所得w代回p,目标函数变为发射波形s的函数
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_s {\mathit{\boldsymbol{s}}^\mathit{\dagger }}{\mathit{\boldsymbol{T}}^\mathit{\dagger }}\left( \theta \right)\left( {\sum\nolimits_c {\left( \mathit{\boldsymbol{s}} \right)} + \sigma _v^2\mathit{\boldsymbol{I}}} \right) - \mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}},}\\ {{\rm{s}}.{\rm{t}}.\;{{\left\| \mathit{\boldsymbol{s}} \right\|}^2} \le 1} \end{array} $ | (28) |
此时,如果
第一步:令k=0,给定初始发射波形s0(‖ s0‖2=1),取s(k)= s0;
第二步:根据式Ω(k)=
第三步:计算矩阵Ω(k)的最大本征值λ(k)及其对应的归一化本征矢量v1(k);
第四步:计算误差因子
第五步:更新发射波形为:
第六步:重复第二到第五步,直至εk≤ζ;
第七步:输出s*=s(k+1),w+=
上述迭代过程提供了发射波形相关杂波条件下的最优发射波形和接收滤波器求解方法。需要指出的是,上述迭代过程不能保证目标函数随迭代次数的单调收敛特性。事实上,在实际的执行过程中,参数ε并非单调递减,这使得上述算法常常无法跳出迭代循环过程。
4 本文迭代方法求解问题P研究提出一种新的迭代算法求解问题P。具体为,首先固定发射波形s,优化接收滤波器w,然后固定接收滤波器w,优化发射波形s,如此迭代前进。已经证明[6-7, 11],这种循环迭代方法可保证目标函数的单调不减特性,即迭代过程进行的每一步输出SCNR的值均不小于上一步的值。此外,这种迭代方法求解所得最优解不仅仅是局部最优的,而且是全局最优解[14]。下面,根据上述迭代优化思路,首先分别求解s固定条件下w的最优解和w固定条件下s的最优解,接着给出完整的迭代优化流程。
首先,由式(26)已经得到了s已知条件下w的解。然后,对于w已知条件下的最优s求解问题,有
| $ {P_s}\left\{ \begin{array}{l} \mathop {\max }\limits_s \frac{{{{\left| {{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\sum\nolimits_c {\left( \mathit{\boldsymbol{s}} \right)\mathit{\boldsymbol{w}}} + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}}}\\ {\rm{s}}.{\rm{t}}.\;{\left\| \mathit{\boldsymbol{s}} \right\|^2} \le 1, \end{array} \right. $ | (29) |
对上述优化问题,有如下推论存在,即
推论一:如果s*是优化问题
| $ \mathop {\max }\limits_s \frac{{{{\left| {{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2}}}{{{\mathit{\boldsymbol{s}}^\mathit{\dagger }}{{\bar \Sigma }_c}\left( \mathit{\boldsymbol{w}} \right)\mathit{\boldsymbol{s}} + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{s}}^\mathit{\dagger }}\mathit{\boldsymbol{s}}}}, $ | (30) |
的解,那么
证明:对问题Ps,结合式(20),有其目标函数形式等价于
推论一使得可以去掉优化问题Ps中的约束条件限制,转而解决没有条件约束的式(30)。而式(31)可进一步等价转换为又一MVDR问题,即
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_s {\mathit{\boldsymbol{s}}^\mathit{\dagger }}\left( {{{\bar \Sigma }_c}\left( \mathit{\boldsymbol{w}} \right) + \sigma _v^2\mathit{\boldsymbol{I}}{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}} \right)\mathit{\boldsymbol{s}},}\\ {{\rm{s}}.{\rm{t}}.\;{{\left| {{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{T}}\left( \theta \right)\mathit{\boldsymbol{s}}} \right|}^2} = 1,} \end{array} $ | (31) |
采用与最优接收波形相同的求解方法,得式(32)的解为
| $ \mathit{\boldsymbol{s}} = {\alpha _s}\left( {{{\bar \Sigma }_c}\left( \mathit{\boldsymbol{w}} \right) + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{wI}}} \right) - \mathit{\boldsymbol{T}}{\left( \theta \right)^\mathit{\dagger }}\mathit{\boldsymbol{w}}, $ | (32) |
其中αs为满足功率约束条件的系数。进一步地,为满足初始条件‖‖=1的要求,则最优发射波形为
| $ \mathit{\boldsymbol{s}} = \frac{{\left( {{{\bar \Sigma }_c}\left( \mathit{\boldsymbol{w}} \right) + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{wI}}} \right) - \mathit{\boldsymbol{T}}{{\left( \theta \right)}^\mathit{\dagger }}\mathit{\boldsymbol{w}}}}{{\left\| {\left( {{{\bar \Sigma }_c}\left( \mathit{\boldsymbol{w}} \right) + \sigma _v^2{\mathit{\boldsymbol{w}}^\mathit{\dagger }}\mathit{\boldsymbol{wI}}} \right) - \mathit{\boldsymbol{T}}{{\left( \theta \right)}^\mathit{\dagger }}\mathit{\boldsymbol{w}}} \right\|}}。$ | (33) |
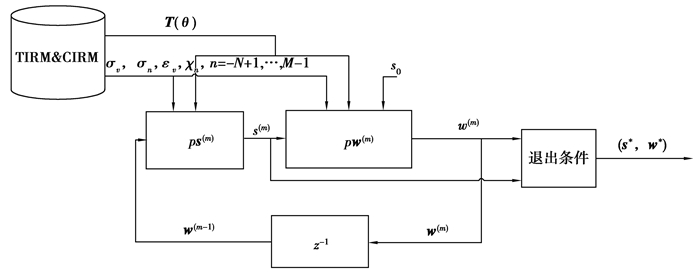
至此,分别求解了发射波形s固定条件下的最优接收滤波器w和w固定条件下的最优s。而通过迭代求解s和w,将使得目标函数(也即输出SCNR)单调不减,从而求得满足要求的最优SCNR。需要指出的是,上述迭代优化方法需要一个退出条件,常用的方法包括:能够允许的最大迭代次数、连续2次迭代所得目标函数值之间的差值。本方法选取后者,即给定门限ζ,当第κ=1次迭代所得目标函数SCNRk+1与第k次迭代所得目标函数SCNR(k)满足|SCNRk+1-SCNR(k)|<ζ,迭代过程结束,结束点所得SCNR为最优SCNR,相应的s和w分别为解得的最优发射波形和最优接收滤波器。上述优化算法的完整流程,如表 1所示,对应的流程框图,如图 2所示。
| 表 1 优化算法的完整流程 Table 1 Complete flow of optimization algorithm |
|
图 2 提出的迭代算法的流程框图 Figure 2 The flow chart of the proposed iteration method |
下面对算法的性能进行验证。采用佐治亚理工学院(georgia institute of technology)公开的T-72坦克全极化雷达实测数据作为目标特性数据,图 3描述了目标与测量雷达间的位置关系。

|
图 3 转台目标与测量雷达间的位置关系 Figure 3 The scenario of the relative position between the turntable target and measuring radar |
由表 2中参数可知,雷达的距离分辨率0.304 8 m。另外,在仿真中,取俯仰角为30.42°,根据T-72坦克的长度信息和雷达的距离分辨率,选定TIRM支撑范围为Q,对于目标特性回波,采用下式对其进行归一化处理
| 表 2 目标数据基本信息 Table 2 The basic information of the target data |
| $ {\mathit{\boldsymbol{T}}_n}\left( \theta \right) = \frac{{{{\mathit{\boldsymbol{\bar T}}}_n}\left( \theta \right)}}{{\sqrt {\sum\nolimits_{n = 0}^{Q - 1} {{{\left\| {{{\mathit{\boldsymbol{\bar T}}}_n}\left( \theta \right)} \right\|}^2}} } }}, $ | (34) |
其中,Tn和Tn(θ)分别表示非归一化和归一化目标散射矩阵。
在整个仿真过程中,取|αT|2=1。发射波形长度取2N=60,初始发射波形s0的水平极化和垂直极化分量均取如下线性调频信号
| $ {\mathit{\boldsymbol{s}}_{{H_0}}}\left( n \right) = {\mathit{\boldsymbol{s}}_{{V_0}}}\left( n \right) = \frac{1}{{\sqrt {2N} }}{{\rm{e}}^{j{\rm{ \mathsf{ π} }}\frac{{{n^2}}}{{2N}}}},n = 0, \cdots ,N - 1, $ | (35) |
另外,算法1的退出条件门限取ζ=10-3。
杂波参数方面,采用文献[9]报道的草地杂波参数,即εn=ε=0.19, χn=χ=1.03和ρn=ρ=0.52和。杂波和噪声功率σn、σv2分别根据信噪比TNR和杂噪比CNR确定,其定义分别为
| $ {\rm{TNR}} \buildrel \Delta \over = \frac{{\sum\nolimits_{n = 0}^{Q - 1} {{{\left\| {{\mathit{\boldsymbol{T}}_n}\left( \theta \right)} \right\|}^2}} }}{{2 \times M \times \sigma _v^2}}, $ | (36) |
| $ {\rm{CNR}} \buildrel \Delta \over = \frac{{\sigma _v^2 \times \left( {\sum\nolimits_{n = 0}^{Q - 1} {\left[ {\mathit{\boldsymbol{IE}}\left[ {{\mathit{\boldsymbol{C}}_n}\mathit{\boldsymbol{C}}_n^\mathit{\dagger }} \right]} \right]{\sigma _n}} = 1} \right)}}{{2 \times M \times \sigma _v^2}}, $ | (37) |
其中,tr[E[CnCn†]]σn=1表示期望在αn条件下得到。在整个仿真过程中,取TNR=5 dB,CNR=10 dB。另外,假定不同距离单元杂波间相互独立。
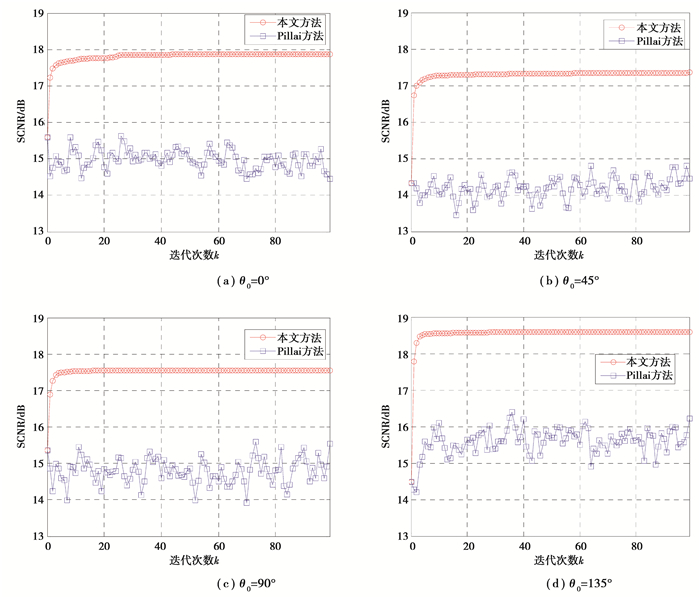
5.1 研究方法的单调不减性能随机取目标相对雷达视线角①θ0=0, 45°, 90°和135°,如图 4(a)~图 4(d)给出了这4种目标视线角取值条件下,滤波器输出最小SCNR随迭代次数的变化曲线,其中每个子图包括对应于Pillai方法和研究方法的2条曲线。
|
图 4 滤波器输出SCNR随迭代次数的变化曲线 Figure 4 The change of SCNR curves at the output of the filter with iteration number |
① 可取θ=∈[0°, 360°]的任一值。
根据图 4(a)-图 4(d)可以看出,随着迭代步骤的增加,方法单调增加滤波器输出SCNR,而Pillai方法所得迭代结果不具有单调收敛特性。此外,上述实验结果也验证了方法的有效性,即相对于传统的发射/接收设计(对应于k=0的情形),优化方法显著提高接收SCNR。
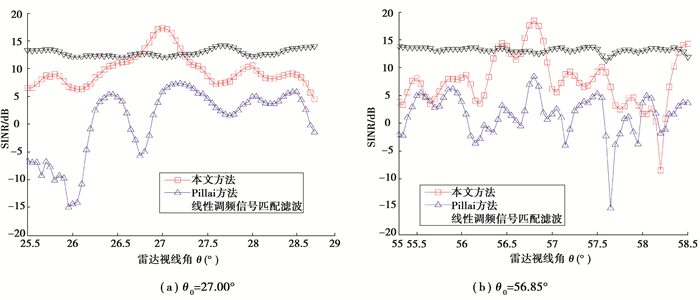
5.2 方法和Pillai方法的性能对比已经证实Pillai方法不能确保目标函数随迭代进程的单调收敛性能。这将带来2方面的问题:一是算法的计算量不确定,二是优化的结果不能保证其质量,尤其是第二点,严重制约算法的优化性能。为验证这一点,随机取θ0=27.00°和θ0=56.85°,如图 5(a)-图 5(b)所示,分别给出了上述2种雷达视线角取值条件下,方法、Pillai方法所得最优发射波形/滤波器的输出SCNR(θ)和传统的固定波形/匹配滤波器设计(这里的固定波形取双极化线性调频信号s0)所得输出SCNRML(θ)随θ的变化曲线。可以看出,在实际雷达视线角θ与名义雷达视线角θ0吻合的位置,优化设计获得了较大的SCNR得益。另外,由于Pillai方法不能保证获得有效的最优发射波形/接收滤波器,方法所得输出SCNR显著高于Pillai方法。
|
图 5 方法、Pillai方法和固定发射波形匹配滤波器输出SCNR随θ的变化曲线 Figure 5 The SCNR curves at the output of the filter w.r.t. θ of the proposed method, Pillai one and the method with fixed transmit waveform. |
但值得一提的是,根据图 5不难看出,虽然方法在θ=θ0处(实际雷达视线角与名义雷达视线角吻合)条件下具有显著的SCNR得益,但在其它位置(即先验信息与实际信息失配),SCNR不及发射波形固定的匹配滤波器输出SCNR。而在实际条件下,假定目标先验信息已知常常过于理想,所以,下一步将重点研究如何提高优化方法对目标视线角的鲁棒性。
6 结论为提高极化雷达的输出SCNR,研究了其发射波形和接收滤波器的联合优化问题。以最大化输出SCNR为目标函数,对发射波形施加能量约束条件限制,构建优化问题,该问题为一非凸优化问题。为解决这一非凸优化问题,首先回顾了Pillai方法,在指出该优化方法的缺陷的基础上,提出了一种准最优的发射波形接收滤波器迭代优化方法,随着迭代步数的增加,目标函数单调收敛于其上确界,从而确保解出最优发射波形和接收滤波器的必然性。在实验验证环节,采用了美国佐治亚理工学院实测T-72坦克目标特性数据,验证了本文算法的有效性以及相对Pillai方法的优势,展现了波形优化设计的潜力。
| [1] |
庄钊文. 雷达极化信息处理及其应用[M]. 北京: 国防工业出版社, 1999. ZHUANG Zhaowen. Radar polarization information processing and application[M]. Beijing: National Defense Industry Press, 1999. (in Chinese) |
| [2] |
Touzi R. Target scattering decomposition in terms of roll-invariant target parameters[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(1): 73-84. DOI:10.1109/TGRS.2006.886176 |
| [3] |
杨建宇. 雷达技术发展规律和宏观趋势分析[J]. 雷达学报, 2012, 01(1): 19-27. YANG Jianyu. Development laws and macro trends analysis of radar technology[J]. Journal of Radars, 2012, 01(1): 19-27. (in Chinese) |
| [4] |
Gini F, De Maio A, Patton L. Waveform design and diversity for advanced radar systems[M]. London, UK: Institution of Engineering and Technology, 2012.
|
| [5] |
De Maio A, De Nicola S, Huang Y W, et al. Code design to optimize radar detection performance under accuracy and similarity constraints[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5618-5629. DOI:10.1109/TSP.2008.929657 |
| [6] |
Stoica P, He H, Li J. Optimization of the receive filter and transmit sequence for active sensing[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1730-1740. DOI:10.1109/TSP.2011.2179652 |
| [7] |
Aubry A, Demaio A, Farina A, et al. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 93-117. DOI:10.1109/TAES.2013.6404093 |
| [8] |
Kay S. Waveform design for multistatic radar detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1153-1166. DOI:10.1109/TAES.2009.5259190 |
| [9] |
Novak L M, Sechtin M B, Cardullo M J. Studies of target detection algorithms that use polarimetric radar data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 150-165. DOI:10.1109/7.18677 |
| [10] |
Garren D A, Odom A C, Osborn M K, et al. Full-polarization matched-illumination for target detection and identification[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 824-837. DOI:10.1109/TAES.2002.1039402 |
| [11] |
Cheng X, Aubry A, Ciuonzo D, et al. Robust waveform and filter bank design of polarimetricradar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 370-384. DOI:10.1109/TAES.2017.2650619 |
| [12] |
Melvin W L, Scheer J A. Principles of modern radar:advanced techniques[M]. Raleigh, NC: Scitech Publishing, 2013.
|
| [13] |
Horn R A, Johnson C R. Matrix analysis[M]. Cambridge, U.K: Cambridge University Press, 1990.
|
| [14] |
Tkacenko A, Vaidyanathan P P. Iterative greedy algorithm for solving the FIR paraunitary approximation problem[J]. IEEE Transactions on Signal Processing, 2006, 54(1): 146-160. DOI:10.1109/TSP.2005.861054 |
| [15] |
Li J, Stoica P, Wang Z S. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715. DOI:10.1109/TSP.2003.812831 |
 2019, Vol. 42
2019, Vol. 42

