金属带回流无级变速传动系统具有低速增扭、传动效率高与无级调速速比范围宽等特点[1-2]。搭载了回流无级变速传动系统的混合动力汽车(以下简称“回流式混合动力汽车”)具有如下优点:
1) 在功能方面,因为传统的金属带CVT(continuously variable transmission)速比范围很窄,通过回流模式与无级模式的组合,传动范围可以拓宽一倍,在保证车辆最佳经济性的同时,大大提高汽车动力性。
2) 采用电动CVT省去了液力变矩器和液压控制机构,成本比传统金属带无级变速系统更低。增加了行星排和齿轮传动机构,通过回流的方式实现ECVT(electric continuously variable transmission)的效果,整体来讲回流式混合动力系统的效率更高。
回流式混合动力汽车在模式切换控制方面存在两种形式:驱动模式切换控制和调速模式切换控制。在模式切换中因为动力源的切换以及系统功率流的转变会引起系统输出扭矩突变,影响整车平顺性,因此需要对回流无级变速传动的混合动力汽车运行模式转换进行控制。
对于驱动模式转换控制的研究,国内外已经有很多成熟的想法。文献[3]指出了并联式混合动力系统动态协调控制问题,提出了“发动机转矩开环+发动机动态转矩估计+电动机转矩补偿”的控制算法,并对其进行了试验研究,证明该控制方法能有效地减少转矩波动。文献[4]针对P12构型的并联式混合动力汽车提出了模型预测控制(MPC, model predictive control),并对控制策略的鲁棒性进行了验证。文献[5-6]对插电式混合动力汽车行进间启动发动机过程进行了研究,发现发动机点火时刻选择不当及离合器接合过程控制不当是造成整车冲击的原因,从而提出了发动机目标转速点火、电动机和离合器协调控制相结合的纯电动行进间启动发动机的控制策略。以上文献针对并联式混合动力汽车驱动模式切换做了大量研究,但是因为金属带回流无级传动系统的特殊性,在驱动模式切换控制时需要考虑回流功率的影响,这也是笔者研究的重点。
对于调速模式转换控制的研究,主要是回流无级变速传动系统中常见的回流传动模式与无级传动模式之间的切换,文献[7]针对超轻度混合动力汽车回流式无级变速器,提出了状态连续转换的控制策略,但是该控制策略只将回流无级变速系统作为一个变速器黑箱来控制,并没有考虑到与其他切换模式的协调控制。
鉴于搭载金属带回流式无级变速传动系统的混合动力汽车的两种运行模式切换控制存在的问题,笔者提出了一种协调发动机、电机和离合器的动态控制策略,并通过SIMULINK仿真验证其有效性。
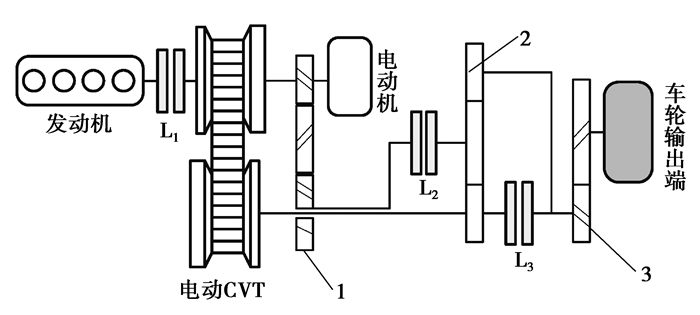
1 系统结构与主要工作模式搭载回流式无级变速传动系统的插电混合动力汽车,其动力耦合系统结构组成如图 1所示,主要由发动机、电动机、电动CVT、定速比齿轮、行星排以及3个湿式离合器L1,L2,L3组成。发动机与电机同轴并联均可输出动力,输出的动力经过CVT、定速比齿轮和行星排组成的动力传动耦合系统输出到主减速器,最终流入车轮。
|
1.定速比齿轮组;2.行星排;3.主减速器 图 1 回流式插电混合动力系统结构简图 Fig. 1 Structural sketch of the HEV with RPCVT |
通过控制发动机、电机以及湿式离合器的工作状态,可以实现多种工作模式,如表 1所示。其中将通过电机与发动机工作状态切换实现的模式切换称之为驱动模式切换;将通过湿式离合器实现的回流状态与纯无级状态的切换称之为调速模式切换。
| 表 1 混合动力系统工作模式及各部件工作状态 Table 1 Relationship between the working mode and component state |
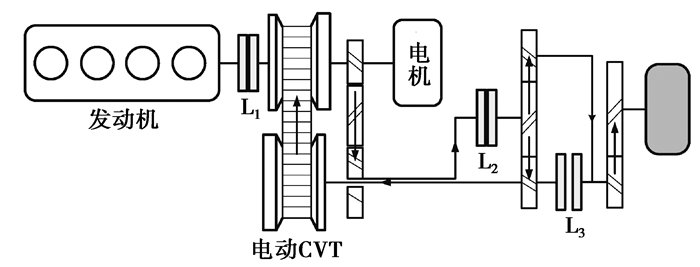
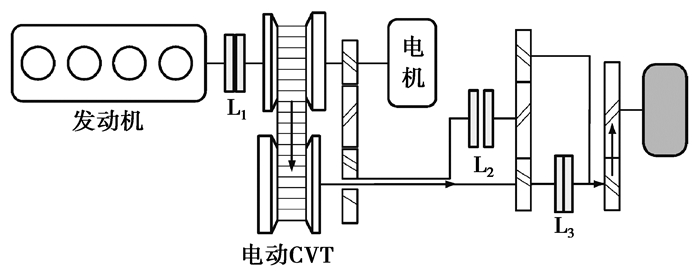
根据系统速比的需求,在速比较大时采用回流模式输出,如图 2所示,L2闭合、L3断开,此时动力源发出功率经定速比齿轮传递到行星齿轮传动结构的行星架上,通过行星排的功率分流,一部分功率通过齿圈用于驱动汽车行驶,另一部分功率通过太阳轮回流,经过CVT调速,与动力源一起共同驱动汽车行驶。在需求速比较小时采用CVT无级调速状态,如图 3所示,L2断开,L3闭合,系统动力源直接通过CVT输出动力,因为在车辆高速运行时对扭矩需求较小,可以最大化地利用CVT特性提高系统效率[7]。此时行星排齿圈与太阳轮接合,行星架空转,不传递扭矩。
|
图 2 回流状态下功率流走向 Fig. 2 Power flow in RPCVT mode |
|
图 3 纯无级状态下功率流走向 Fig. 3 Power flow in the pure CVT mode |
在回流式插电混合动力构型中,离合器L1主要用于模式切换时电动机与发动机动力源的切换。离合器L2,L3主要用于回流与纯无级之间的状态变换。在实际切换过程中,两个过程不能同时进行,因此将分别对两个切换过程进行动力学分析,并制定相应的协调控制方案。
2.1 驱动模式转换动力学分析相对于快速响应的电机,发动机的响应速度过慢是造成插电式混合动力汽车扭矩输出波动的重要原因。因此,在驱动模式切换中电机启动发动机的工况最为复杂,笔者以此为例对构型进行动力学分析。
根据离合器L1的接合状态可以将切换过程划分为两个阶段。
1) L1完全接合前。整车控制器发出信号,离合器液压单元控制L1接合,此时电机输出的转矩一部分用于驱动车辆行驶,另一部分扭矩通过离合器传递拖动发动机转动。该阶段动力耦合系统输入转矩为
| $ {T_{{\rm{in}}}} = {T_{\rm{m}}} + {T_{\rm{h}}} - {T_{{\rm{cl}}}}, $ | (1) |
式中:Tm为电机扭矩;Tc1为离合器L1传递扭矩;Th为系统回流扭矩,如果系统处于纯无级工作状态,则Th=0。在电机拖动状态中,发动机的动力学模型为
| $ {J_{\rm{e}}}\frac{{{\rm{d}}{\omega _{\rm{e}}}}}{{{\rm{d}}t}} = {T_{{\rm{cl}}}} + {T_{\rm{e}}}, $ | (2) |
式中:Je为发动机的转动惯量,kg·m2;ωe为发动机角速度,rad/s;Te为发动机转矩,N·m,在发动机未点火时,Te为负,用于表征发动机的反拖转矩,当发动机点火后,Te为正。
2) L1完全接合后。对于离合器L1,当发动机与电机转速和扭矩相同时,离合器接合,在接合的前后其传递扭矩Tc1会发生突变:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_{{\rm{cl}}\left( {接合前} \right)}} = {J_{\rm{e}}}\frac{{{\rm{d}}{\omega _{\rm{e}}}}}{{{\rm{d}}t}} - {T_{\rm{e}}};}\\ {{T_{{\rm{cl}}\left( {接合后} \right)}} = {T_{\rm{e}}}。} \end{array}} \right. $ | (3) |
与此同时,在离合器同步前后,动力耦合传动系统的输出扭矩也会发生突变,同步前如式(1)所示,同步后如式(4)所示:
| $ {T_{{\rm{in}}}} = {T_{\rm{m}}} + {T_{\rm{h}}} + {T_{\rm{e}}}。$ | (4) |
由式(1)~(4)的扭矩变化可知,在转速同步前后的扭矩突变是产生整车冲击度的主因,如式(5)所示:
| $ {T_{\rm{m}}} + {T_{\rm{h}}} - {T_{\rm{c}}} \to {T_{\rm{m}}} + {T_{\rm{h}}} + {T_{\rm{e}}}。$ | (5) |
因此在实际控制中,需要通过控制各部件扭矩的变换从而减少输出扭矩的突变。
在纯电动切换发动机工作的动态过程中,无论系统采用回流或者无级工作状态,输入到动力耦合传动装置的扭矩Tin是不会随着调速模式切换而改变的。但是动力耦合传动装置内部的动力学模型会随无级和回流两个状态的改变而发生变化,需要分情况讨论。
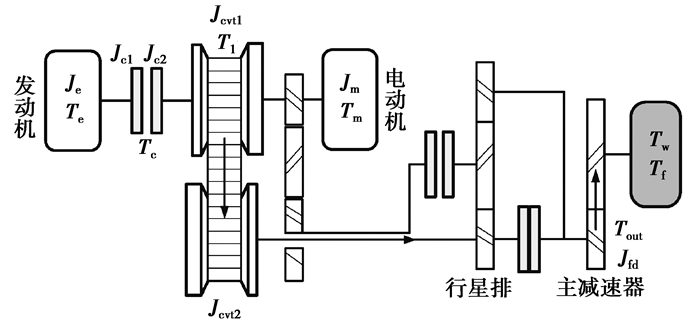
2.1.1 纯无级状态动力学分析在纯无级状态中,因为整个传动系统只有CVT参与工作,在整个动态过程中的动力学模型如图 4所示。
|
图 4 纯无级模式动力学模型 Fig. 4 Dynamic model of the pure CVT mode |
在图 4中,Je为发动机转动惯量,Jc1,Jc2为离合器前后端转动惯量,Jm为电机转动惯量,Jcvt1为CVT输入端转动惯量,Jcvt2为CVT输出端转动惯量,Jfd为主减速器转动惯量,Jω为车轮转动惯量。
根据图 4可以将该系统的转动惯量分为两部分,将CVT输入轴以及同轴各部分转动惯量等效为输入转动惯量J1:
| $ {J_1} = \left\{ {\begin{array}{*{20}{l}} {{J_{\rm{m}}} + {J_{{\rm{c}}2}} + {J_{{\rm{cvt}}1}},离合器\;{{\rm{L}}_1}\;分离;}\\ {{J_{\rm{e}}} + {J_{{\rm{cl}}}} + {J_{{\rm{c}}2}} + {J_{\rm{m}}} + {J_{{\rm{cvt}}1}},离合器\;{{\rm{L}}_1}\;接合。} \end{array}} \right. $ |
将CVT输出轴与主减速器输出部分转动惯量等效为J2:
| $ {J_2} = {J_{{\rm{cvt}}2}} + {J_{{\rm{fd}}}}。$ | (6) |
如果将系统所有转动惯量整合到车轮,可得整车等效转动惯量为
| $ J = {J_1}i_{{\rm{cvt}}}^2i_0^2 + {J_2}i_0^2 + {J_\omega } + m{r^2}, $ | (7) |
式中:icvt为电控CVT速比;i0为主减速器速比;m为汽车整备质量,kg;r为车半径,m。定义汽车阻力为
| $ {F_{\rm{r}}} = mgf\cos \alpha + mg\sin \alpha + \frac{{{C_{\rm{D}}}A}}{{21.15}}{u^2}。$ | (8) |
对于纯无级状态下的动力学模型为
| $ J\frac{{{\rm{d}}u}}{{{\rm{d}}t}} \cdot \frac{1}{r} = {T_{{\rm{in}}}}{i_{{\rm{cvt}}}}{i_0}{\eta _{{\rm{cvt}}}} - {F_{\rm{r}}}r。$ | (9) |
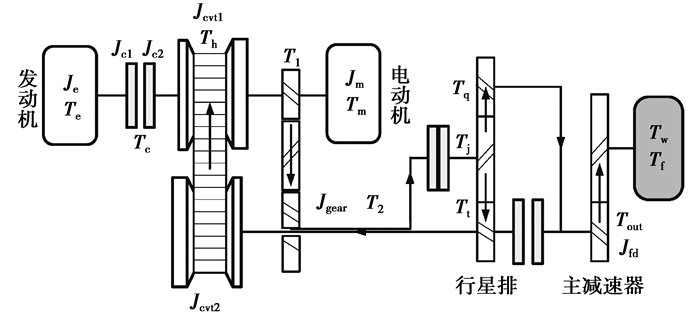
回流状态动力学仿真模型如图 5所示。回流状态与纯无级状态主要是通过改变离合器L2,L3的接合分离实现功率流的改变。
|
图 5 回流状态动力学模型 Fig. 5 Dynamic model of RPCVT mode |
在离合器L1接合的过程中,按照功率流的方向,对混合动力系统各部件进行动力学分析,并建立了数学模型,具体分析计算模型如式(10)所示。
| $ {\left\{ {\begin{array}{*{20}{l}} {{T_{{\rm{in}}}} - {T_1} = \left( {{J_{\rm{m}}} + {J_{{\rm{cvt}}1}}} \right){{\dot \omega }_{\rm{m}}},}\\ {{T_1}{i_{\rm{f}}} - {T_2} = {J_{{\rm{gear}}}}{{\dot \omega }_{\rm{m}}}/{i_{\rm{f}}},}\\ {{T_2} = {T_{\rm{j}}} = {T_{\rm{h}}}{i_{{\rm{cvt}}}},}\\ {{T_t}:{T_{\rm{q}}}:{T_{\rm{j}}} = 1:\alpha : - \left( {1 + \alpha } \right),}\\ {{T_2}/{i_{{\rm{cvt}}}} - {T_{\rm{h}}} = {J_{{\rm{cvt2}}}}{{\dot \omega }_{\rm{m}}}/{i_{{\rm{cvt}}}},}\\ {{T_{\rm{q}}} - {T_{{\rm{out}}}} = {J_{{\rm{fd}}}}{{\dot \omega }_{\rm{v}}}{i_0},}\\ {{T_{{\rm{out}}}}{i_0} - {T_{\rm{f}}} = \left( {{J_{\rm{ \mathsf{ ω} }}} + m{r^2}} \right){{\dot \omega }_{\rm{v}}},}\\ {{T_{\rm{h}}} = \frac{{{\eta _{{\rm{cvt}}}}{i_{\rm{f}}}}}{{{i_{{\rm{cvt}}}}\left( {1 + \alpha } \right)}}\left( {{T_{\rm{m}}} + {T_{\rm{c}}} - {T_{\rm{c}}}} \right)。} \end{array}} \right.} $ | (10) |
式中:
在回流状态中,离合器L2接合,离合器L3断开,可以将L3右侧的转动惯量等效到车轮,记为
| $ {J_3} = {J_{\rm{ \mathsf{ ω} }}} + m{r^2} + {J_{{\rm{fd}}}}i_0^2。$ | (11) |
根据式(10)(11)可以得到整车等效转动惯量为
| $ J = {J_1}\frac{\alpha }{{1 + \alpha }}{i_0}{i_{\rm{f}}}{i_{{\rm{sys}}}} + {J_{{\rm{gear}}}}\frac{\alpha }{{1 + \alpha }}\frac{{{i_0}}}{{{i_{\rm{f}}}}}{i_{{\rm{sys}}}} + {J_3}。$ | (12) |
在回流状态下的整车动力学模型为
| $ J\frac{{{\rm{d}}u}}{{{\rm{d}}t}} \cdot \frac{1}{r} = {T_{{\rm{in}}}}\frac{\alpha }{{1 + \alpha }}{i_{\rm{f}}}{i_0} - {F_{\rm{r}}}r。$ | (13) |
根据驱动模式切换的动力学建模可以看出,因为冲击度即为车辆纵向加速度的导数,如果Fr不变,可以发现冲击度其实只和Tin的变化率有关。在电机拖动阶段,冲击度的大小主要取决于电机和离合器传递的转矩差的变化率, 在离合器转速同步后,冲击度的大小主要取决于电机和发动机扭矩变化率, 即
| $ j = \frac{{{i_{{\rm{cvt }}}}{i_0}{\eta _{\rm{t}}}}}{J}\frac{{{\rm{d}}{T_{{\rm{in }}}}}}{{{\rm{d}}t}}。$ | (14) |
在控制策略中,通过控制电机扭矩变化率与离合器的油压变化率即可以达到控制车辆冲击度的效果。
2.2 调速模式转换动力学分析在调速模式转换过程中,离合器L1并不发挥作用,仍需对L2,L3的切换过程进行动力学分析。因此以纯无级状态向回流状态切换的调速模式转换过程为例搭建L2,L3动力学模型。
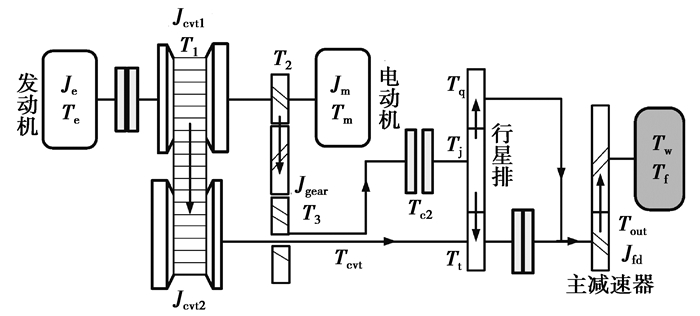
如图 6所示,在纯无级状态情况下离合器L2处于分离状态,L3处于接合状态,此时系统功率从CVT流向L3。当系统接到调速模式转换的命令时,L2开始先进入接合状态,此时离合器开始传递扭矩Tc2为
| $ {T_{{\rm{c}}2}} = {\rm{sign}}\left( {{n_{\rm{m}}} - {n_{\rm{e}}}} \right)\mu ZS{R_{\rm{c}}}\left( {P - {P_0}} \right), $ | (15) |
|
图 6 L2动力学模型 Fig. 6 Dynamic model of L2 Engagement |
式中:μ为离合器动态摩擦系数;Z为离合器摩擦面数;S为离合器活塞作用面积,m2,Rc为离合器等效摩擦半径,m;P,P0为离合器油压及初始油压,Pa。
随着离合器L2开始传递扭矩,一部分功率通过L2进入行星架中,通过行星架的分流作用驱动汽车运行,整个过程动力学模型如式(16)所示。
| $ \left\{ \begin{array}{l} {T_{{\rm{in}}}} - {T_1} - {T_2} = {J_1}{{\dot \omega }_{\rm{m}}}{i_{\rm{s}}},\\ {T_1}{i_{{\rm{cvt}}}} - {\eta _{{\rm{cvt}}}} = {T_{{\rm{cvt}}}},\\ {T_{{\rm{cvt}}}} + {T_{\rm{t}}} + {T_{\rm{q}}} - {T_{{\rm{out}}}} = \left( {{J_{{\rm{fd}}}} + {J_{{\rm{cv}}2}}} \right){{\dot \omega }_{\rm{v}}}{i_0},\\ {T_{{\rm{out }}}}{i_0} - {T_{\rm{f}}} = \left( {{J_\omega } + m{r^2}} \right){{\dot \omega }_{\rm{v}}},\\ {T_{{\rm{c}}2}} = {T_{\rm{j}}},\\ {T_2}{i_{\rm{f}}} - {T_3} = {J_{{\rm{gear}}}}{{\dot \omega }_{\rm{m}}}/{i_{\rm{f}}},\\ {T_3} = {T_{{\rm{c2}}}} = {T_{\rm{j}}},\\ {T_{\rm{t}}}:{T_{\rm{q}}}:{T_{\rm{j}}} = 1:\alpha : - \left( {1 + \alpha } \right)。\end{array} \right. $ | (16) |
通过式(16)可以得出在L2接合过程中系统动力学模型为
| $ J\frac{{{\rm{d}}u}}{{{\rm{d}}t}} \cdot \frac{1}{r} = {T_{{\rm{in}}}}{i_{{\rm{cvt}}}}{i_0}{\eta _{{\rm{cvt}}}} - \left( {1 - {\eta _{{\rm{cvt}}}}} \right){T_{{\rm{c}}2}}{i_0} - {F_{\rm{r}}}r。$ | (17) |
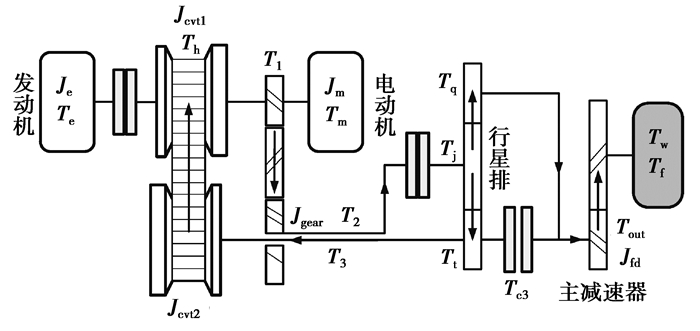
当离合器L2完全接合后功率不再通过CVT传输,完全通过定速比齿轮进入到L2,通过行星排的分流作用,一部分通过太阳轮流入L3,另一部分功率通过齿圈分流,与太阳轮的功率汇流,共同驱动汽车行驶。之后系统发出指令控制L3分离,如图 7所示,随着L3的分离,离合器L3传递的扭矩越来越小,此时系统会开始产生回流扭矩,当L3不再传递扭矩时,系统进入如图 2所示的回流状态。
|
图 7 L3动力学模型 Fig. 7 Dynamic model of L3 Engagement |
在L3分离过程中,输出转矩为
| $ {T_{{\rm{out}}}} = {T_{\rm{q}}} + {T_{{\rm{c}}3}} - {J_{{\rm{fd}}}}{{\dot \omega }_{\rm{v}}}{i_0}。$ | (18) |
通过离合器L3传递的一部分扭矩随着L3的分离流入CVT,变为回流扭矩重新驱动汽车运行,整个过程的动力学计算公式为
| $ \left\{ \begin{array}{l} {T_{{\rm{in}}}} - {T_1} = {J_1}{{\dot \omega }_{\rm{m}}}{i_{{\rm{sys}}}},\\ {T_{\rm{h}}}{i_{{\rm{cvt}}}} = {T_3}{\eta _{{\rm{cvt}}}},\\ {T_1}{i_{\rm{f}}} - {T_2} = {J_{{\rm{gear}}}}{{\dot \omega }_{\rm{m}}}/{i_{\rm{f}}},\\ {T_2} = {T_{\rm{j}}},\\ {T_{\rm{t}}}:{T_{\rm{q}}}:{T_{\rm{j}}} = 1:\alpha : - (1 + \alpha ),\\ {T_{{\rm{out }}}} = {T_{\rm{q}}} + {T_{{\rm{c}}3}} - {J_{{\rm{fd}}}}{{\dot \omega }_{\rm{v}}}{i_0},\\ {T_{{\rm{out}}}}{i_0} - {T_{\rm{f}}} = \left( {{J_\omega } + m{r^2}} \right){{\dot \omega }_{\rm{v}}},\\ {T_{\rm{h}}} = \frac{{{\eta _{{\rm{cvt}}}}{i_{\rm{f}}}}}{{{i_{{\rm{cvt}}}}\left( {1 + \alpha } \right)}}\left( {{T_{{\rm{in}}}} - {T_1}} \right)。\end{array} \right. $ | (19) |
根据计算可以得到在L3分离过程中的动力学计算公式为
| $ J\frac{{{\rm{d}}u}}{{{\rm{d}}t}} \cdot \frac{1}{r} = {T_{{\rm{in}}}}\frac{\alpha }{{1 + \alpha }}{i_{\rm{f}}}{i_0} + {T_{{\rm{c}}3}}{i_0} - {F_{\rm{r}}}r。$ | (20) |
由式(17)(20)可以看出,在Tin与Fr保持恒定的情况下,影响调速模式转换冲击度的只有离合器L2和L3的扭矩变化率dTc/dt。调速模式切换主要需对湿式离合器的油压实施控制,保证整车平顺性。
3 模式切换动力协调控制对于回流插电式混合动力汽车存在不同性质的动态过程,很难用统一的时间尺度和控制方法去控制,因此引入了混合动态系统理论(hybrid dynamical system)[11]对回流式插电混合动力汽车实行分层控制。将驾驶员行为输入控制层进行模式切换判断,并通过执行层控制电机、发动机以及离合器协调工作。
3.1 执行层控制方法 3.1.1 发动机控制对于有发动机参与的模式切换过程,对发动机的控制尤为重要。因为发动机的转矩动态响应受多种因素的影响,笔者采用发动机曲轴角加速度来表征发动机动态转矩与稳态转矩之间的差值,具体计算方法如式(21)(22)所示。
| $ {{\hat T}_{\rm{e}}} = {T_{{\rm{e\_stable}}}} + \Delta {{\hat T}_{\rm{e}}}\left( {\frac{{{\rm{d}}n}}{{{\rm{d}}t}}} \right), $ | (21) |
| $ \Delta {T_{\rm{e}}}\left( {\frac{{{\rm{d}}n}}{{{\rm{d}}t}}} \right) = {k_1}\frac{{{\rm{d}}n}}{{{\rm{d}}t}}\left( {1 - {e^{ - \frac{{n - {n_0}}}{{k2}}}}} \right) + {k_3}。$ | (22) |
式中:
发动机的扭矩主要通过节气门开度控制,这里采用增量PID方法控制发动机节气门开度如式(23)所示。
| $ \Delta \alpha = {k_{\rm{p}}} \cdot e + {k_i}\int {e \cdot {\rm{d}}t} + {k_{\rm{d}}} \cdot \dot e。$ | (23) |
对湿式离合器来说,其传递扭矩如式(15)所示,对离合器扭矩变化率的控制即为离合器油压控制。笔者以离合器主从动盘转速差Δω以及驾驶员加速踏板唯一变化率
| 表 2 离合器滑磨状态压力变化率模糊控制规则 Table 2 Fuzzy control rule table of the clutch slipping phase pressure change rate |
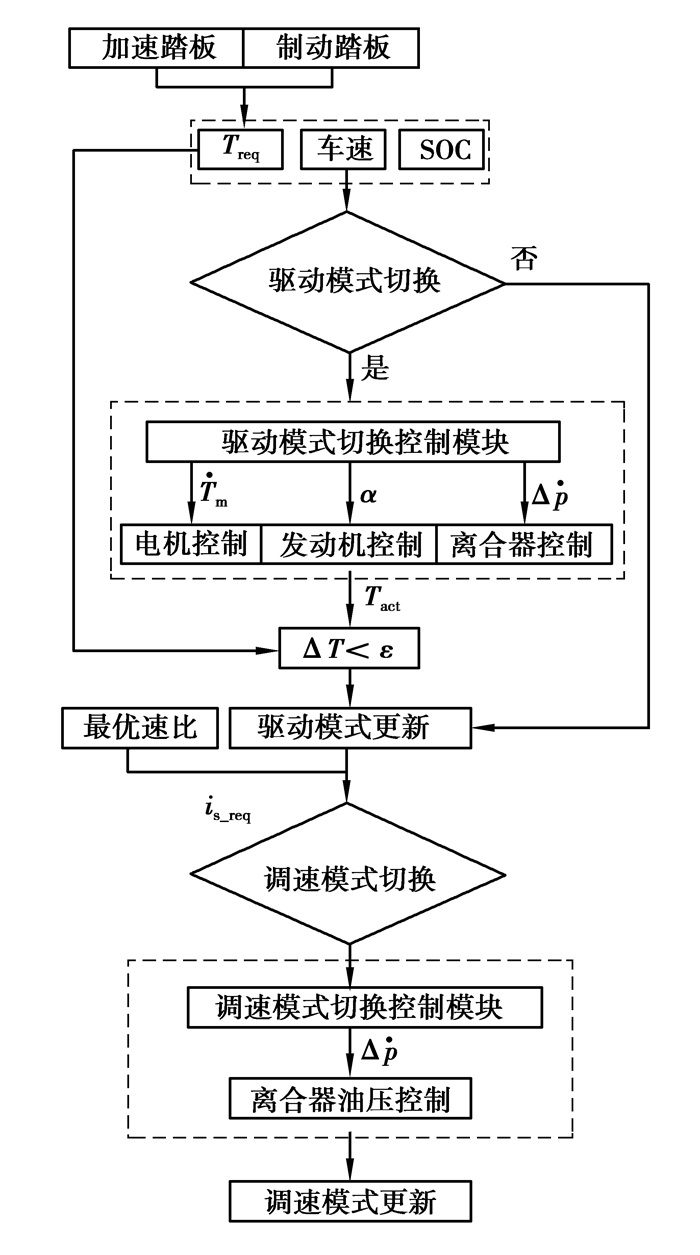
因为驱动模式切换和调速模式切换牵扯部件较多,不能同时进行,所以制定了不同类型的模式切换扭矩协调控制策略,图 8所示为整个模式切换过程总体思路。
|
图 8 模式转换控制策略流程 Fig. 8 Control flow of mode switching |
因为回流式混合动力汽车驱动模式切换分为多种,其中最为复杂的就是启动发动机的控制,需要电机、发动机以及离合器的协调配合,据此提出了离合器二次分离的控制方法,具体控制思路如图 9所示。
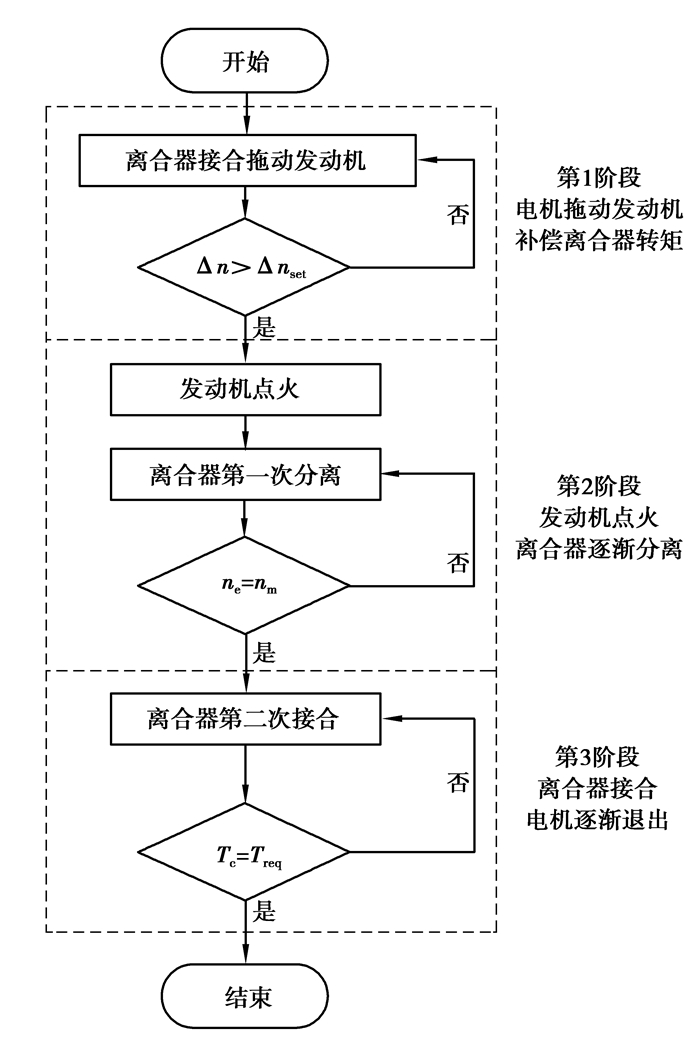
|
图 9 驱动模式切换模块控制流程 Fig. 9 Control flow of driving mode switching |
1) 在电机拖动发动机阶段,当系统发出启动发动机的指令,湿式离合器开始接合并拖动发动机转动,此时电机扭矩随离合器扭矩改变用以补偿离合器扭矩,保证输出扭矩不变。当电机扭矩达到电机最大限值,保持离合器油压不变,进入保压状态。此时发动机转速继续上升直至达到点火条件(nset=800 r/min),发动机点火, 进入第2阶段。
2) 在发动机点火后,发动机扭矩与离合器传递扭矩Tc一起带动发动机转动。此时控制离合器油压下降,使离合器缓缓分离,由发动机单独驱动飞轮转速上升。当发动机转速ne与电机转速nm相同时,进入第3阶段。
3) 第3阶段为离合器二次接合阶段,此时发动机转速处于超调状态,离合器对发动机做负功,用于提供发动机负载并减少转速。对于电机来说,此时离合器转矩为正,与电机一起共同驱动汽车行驶。
| $ {T_{{\rm{in}}}} = {T_{\rm{m}}} + {T_{\rm{c}}} + {T_{\rm{h}}}。$ | (24) |
因此,为保证输出扭矩不变,需要控制电机转矩相应减少,用于补偿离合器传递的扭矩。当离合器完全接合时,发动机转矩等于需求扭矩,此时电机转矩为0。通过二次离合器的分离和接合动作,可以将驱动模式转换过程中的扭矩突变,转换为离合器的扭矩变化,并通过电机扭矩补偿,与其他的控制策略相比,控制效果更为精确,并且减少了扭矩突变的产生。
具体的控制过程反映到发动机的转速变化中如图 10所示。
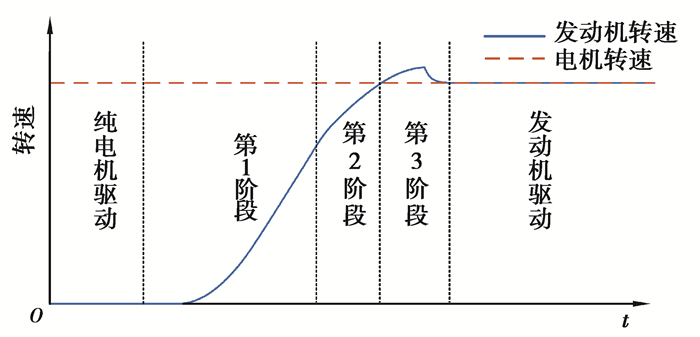
|
图 10 驱动模式转换控制与转速关系 Fig. 10 Relationship between speed and driving mode switching |
在驱动模式切换控制完成时,每个驱动模式下均存在最优速比,通过CVT的调速作用使发动机及电机工作在最优工作区间内,但是系统速比的变化会引发调速模式切换,因此为保证整车平顺性,也需要对调速模式切换进行控制。
对于回流式插电混合动力汽车来说,其系统速比与CVT速比满足特性如式(25)所示。
| $ {i_{\rm{s}}} = \frac{{\alpha \cdot {i_{\rm{f}}} \cdot {i_{{\rm{cvt}}}}}}{{(1 + \alpha ) \cdot {i_{{\rm{cvt}}}} - {i_{\rm{f}}}}}。$ | (25) |
如图 11所示,在速比is=2.47时需要进行无级模式与回流模式之间的切换,为避免频繁换挡,设置了一个过渡区间2.40~2.55;当速比is<2.40时,开始实施回流向无级的转换;当速比is>2.55时,开始实施无级向回流的转换,系统速比在过渡区间内时,保持系统速比is=2.47,不实施转换。具体判断过程如图 12所示。
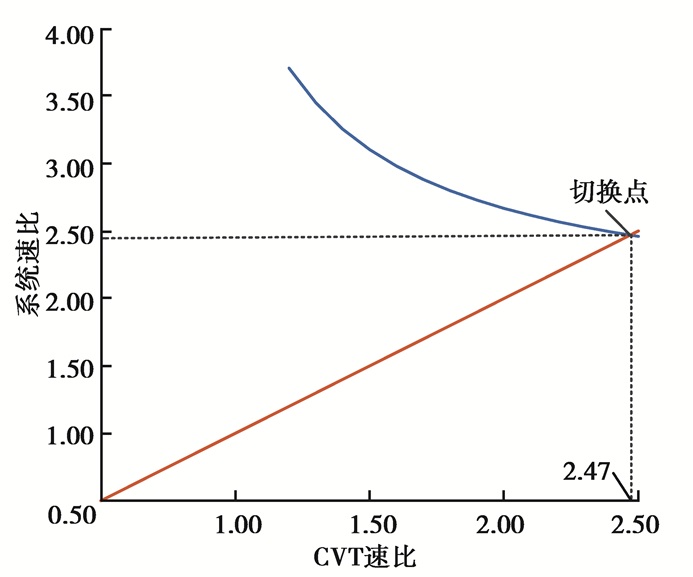
|
图 11 回流式插电混合动力速比关系图 Fig. 11 Relationship between CVT speed ratio and system speed ratio |
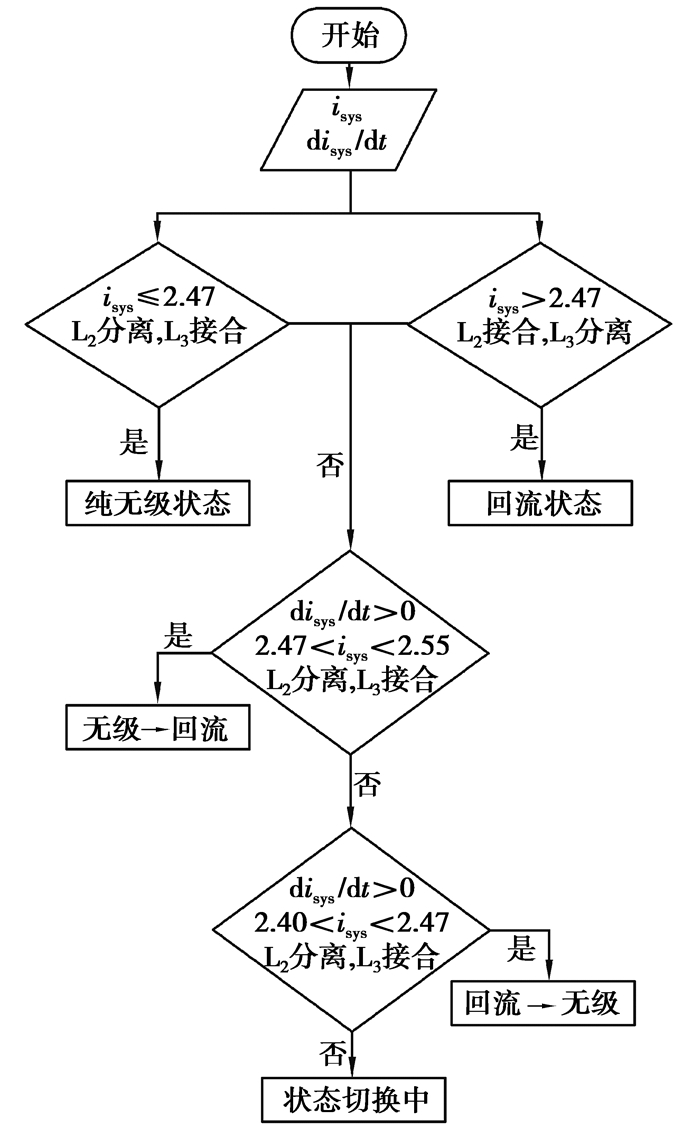
|
图 12 调速模式转换控制策略 Fig. 12 Control flow of speed control mode switching |
在具体的切换过程中,对于回流-无级的切换,因为回流状态如图 2所示L2处于接合状态,L3处于分离状态,因此应当保证系统速比为2.47不变,先接合L3。此时系统随着L3的接合慢慢地由回流变为分流,在L3接合完毕后,L2开始分离,最终进入纯无级工况。
对于无级-回流的模式切换,总体思路与回流-无级的切换类似,首先L2接合,一部分系统功率开始流入定速比齿轮组,通过行星架分流,最终输出到车轮。当L2传递的扭矩达到行星架处最大值Tinif时,L2接合完成,开始分离L3,待L3完全分离后系统进入回流模式。
4 仿真分析笔者以回流式混合动力汽车为研究对象,根据系统动力学分析以及模式切换控制策略,建立了MATLAB/SIMULINK前向仿真模型。模型主要包括:驾驶员模型、电机、发动机、离合器模型、扭矩分配模型、模式切换控制模型以及整车动力学模型[12]。在此基础上,模拟回流式插电混合动力汽车的模式切换过程。
当汽车在匀速状态下,系统速比为2.8时,在0.5 s发出电机切换发动机驱动的驱动模式转换命令,最终仿真结果如图 13所示。
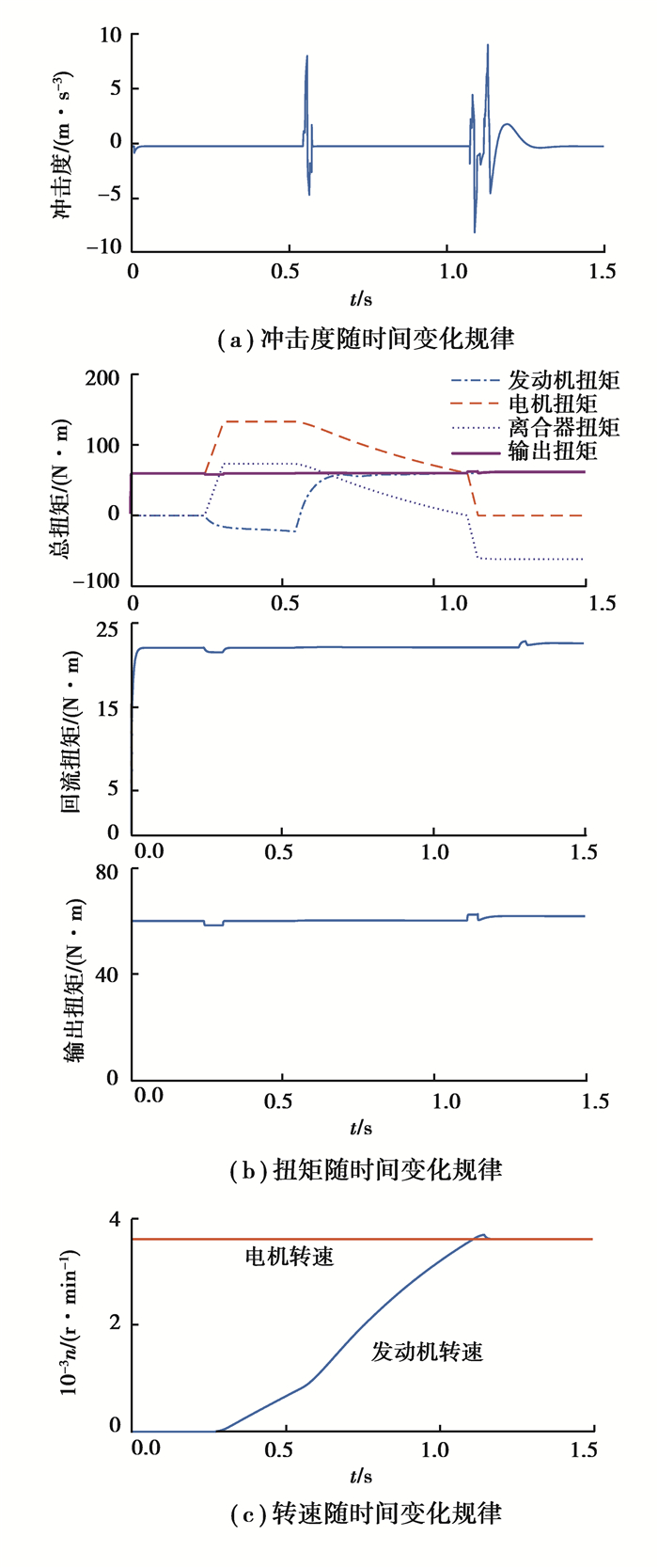
|
图 13 回流模式下驱动模式转换仿真结果 Fig. 13 Simulation results of the driving mode switching in the RPCVT mode |
根据仿真发现,回流模式下整个驱动模式切换过程中会产生2次扭矩突变。如图 13(a),在0.5 s左右,发动机点火瞬间会产生第1次扭矩波动。发动机启动后转速逐渐上升,在1.1 s左右发动机转速达到电机转速,此时离合器开始接合,当离合器接合的一瞬间扭矩发生突变,产生了第2次扭矩突变。因为采用了2次分离的控制方法,在第1次扭矩波动时因为离合器尚未完全接合,发动机的点火冲击不会完全传递到动力耦合系统。第2次扭矩波动主要取决于离合器扭矩变化率,通过离合器油压控制可以提高整车平顺性。
汽车在匀速状态下,当系统速比为0.9处于纯无级模式时进行定工况仿真,最终的仿真结果如图 14所示。
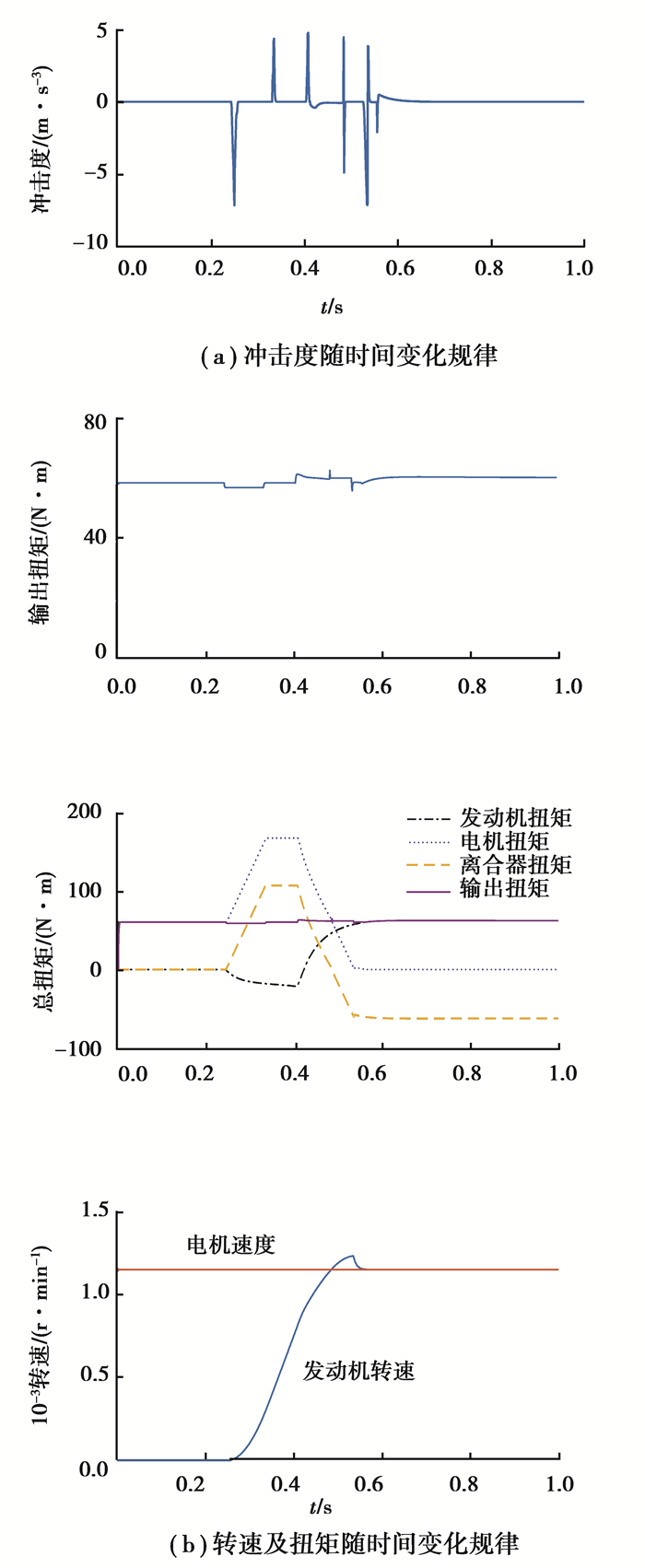
|
图 14 纯无级模式下驱动模式转换仿真结果 Fig. 14 Simulated driving mode switching results in the pure CVT mode |
根据仿真纯无级模式下因为不存在回流扭矩,扭矩控制较为简单,在0.2 s左右发出驱动模式转换命令后,发动机点火,并且转速很快接近电机转速,完成离合器接合工作。整个切换过程时间很短,并且控制冲击度不超过7 m/s3,符合整车平顺性的要求。
对于调速模式切换和驱动模式切换的联合控制也可以通过仿真平台进行仿真,仿真结果如图 15所示。
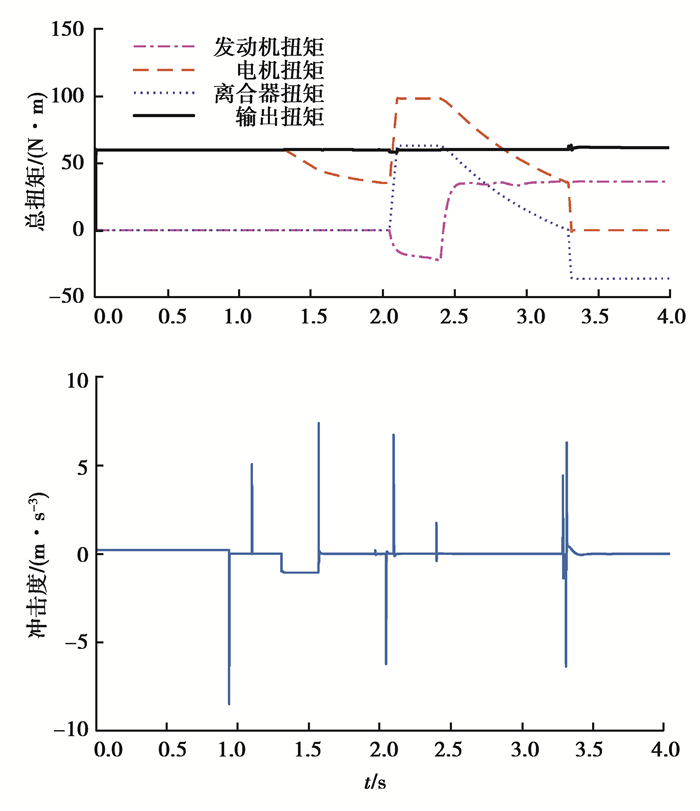
|
图 15 回流式混合动力模式转换仿真结果 Fig. 15 Simulation results of the switching control strategy of the HEV with RPCVT |
根据调速模式与驱动模式切换的联合仿真可以发现,调速模式转换过程冲击度主要产生于离合器接合瞬间,可以通过离合器油压控制冲击度的大小。在调速模式完成后,因为实际速比与理论速比存在差距,也会导致一定的扭矩突变但是冲击度变化不大,可以忽略不计。在驱动模式转换过程的冲击度产生原因与上文的分析结果相同。通过仿真可以发现,使用动态协调的控制策略可以减少回流式插电混合动力汽车在模式切换过程中的冲击度。
5 结论1) 对回流式插电混合动力汽车进行了参数匹配并建模,针对其典型动力切换过程:驱动模式切换中的纯电动切换至发动机状态以及调速模式切换中回流状态与纯无级状态之间切换进行了动力学分析,发现影响整车平顺性的原因主要为输出扭矩在切换瞬间的突变及输出扭矩在切换过程中的扭矩变化率。
2) 针对回流式混合动力汽车模式切换遇到的整车平顺性问题,笔者以冲击度为控制目标,对驱动模式切换提出了离合器2次分离的电机、发动机以及离合器协调控制的控制方法,对调速模式切换提出了离合器油压控制方法。
3) 建立了回流式混合动力汽车整车仿真模型,对典型的模式切换过程进行了仿真分析,结果表明,所提出的控制策略能够有效减少模式切换中的扭矩波动,减少整车冲击。
| [1] |
Vahabzadeh H, Linzell S M. Modeling, simulation, and control implementation for a split-torque, geared neutral, infinitely variable transmission[C]//SAE Technical Paper Series, 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 1991.
|
| [2] |
Kimura A, Abe T, Sasaki S. Drive force control of a parallel-series hybrid system[J]. JSAE Review, 1999, 20(3): 337-341. DOI:10.1016/S0389-4304(99)00017-X |
| [3] |
童毅.并联式混合动力系统动态协调控制问题的研究[D].北京: 清华大学, 2004. TONG Yi. Study on the coordinated control issue in parallel hybrid electric system[D]. Beijing: Tsinghua Univesity, 2004. (in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10003-2005036031.htm |
| [4] |
Beck R, Richert F, Bollig A, et al. Model predictive control of a parallel hybrid vehicle drivetrain[C]//Proceedings of the 44th IEEE Conference on Decision and Control, 15-15 Dec, 2005, Seville, Spain. New York, USA: IEEE, 2005: 2670-2675. https://ieeexplore.ieee.org/document/1582566/
|
| [5] |
Hu M H, Jiang G C, Fu C Y, et al. Torque coordinated control in engine starting process for a single-motor hybrid electric vehicle[J]. Advances in Mechanical Engineering, 2017, 9(7): 168781401770596. DOI:10.1177/1687814017705965 |
| [6] |
秦大同, 尚阳, 杨官龙. 插电式混合动力汽车纯电动行进间启动发动机的平顺性控制[J]. 重庆大学学报, 2015, 38(4): 1-9. QIN Datong, SHANG Yang, YANG Guanlong. The ride comfort control of PHEV during engine starting in-motion process[J]. Journal of Chongqing University, 2015, 38(4): 1-9. (in Chinese) |
| [7] |
孙冬野, 尹燕莉, 郝允志, 等. 回流式无级变速器动力连续转换的控制策略仿真研究[J]. 中国机械工程, 2012, 23(1): 89-93. SUN Dongye, Yin Yanli, Hao Yunzhi, et al. Continuous power shift control strategy of continuously variable transmission system with reflux power[J]. China Mechanical Engineering, 2012, 23(1): 89-93. (in Chinese) DOI:10.3969/j.issn.1004-132X.2012.01.019 |
| [8] |
叶明, 谢佳佳, 李鑫. 搭载机电控制无级变速器混合动力汽车模式切换仿真分析[J]. 重庆大学学报, 2015, 38(6): 58-67. YE Ming, XLE Jiajia, LI Xin. Mode-switch simulation analysis of hybrid electric vehicle equipped with electrical-mechanical continuously variable transmission[J]. Journal of Chongqing University, 2015, 38(6): 58-67. (in Chinese) |
| [9] |
Song M, Oh J, Choi S, et al. Motor control of a parallel hybrid electric vehicle during mode change without an integrated starter generator[J]. Journal of Electrical Engineeringand Technology, 2013, 8(4): 930-937. DOI:10.5370/JEET.2013.8.4.930 |
| [10] |
张青, 罗求顺, 张力, 等. CVT刚性联接发动机曲轴轴系结构的扭振分析[J]. 重庆大学学报, 2017, 40(1): 20-29. ZHANG Qing, LUO Qiushun, ZHANG Li, et al. Torsional vibration analysis of the crankshaft with rigidly coupling CVT[J]. Journal of Chongqing University, 2017, 40(1): 20-29. (in Chinese) |
| [11] |
Zhang R J, Chen Y B. Control of hybrid dynamical systems for electric vehicles[C]//Proceedings of the 2001 American Control Conference. (Cat. No.01CH37148), June 25-27, 2001, Arlington, VA, USA. New York, USA: IEEE, 2001. Control of hybrid dynamical systems for electric vehicles
|
| [12] |
王宇翔, 林富, 胡明辉. 高原环境下AMT汽车动力性换挡规律分析[J]. 重庆大学学报, 2018, 41(2): 10-20. WANG Yuxiang, LIN Fu, HU Minghui. Analysis on the dynamic gear shift schedule of AMT vehicles in plateau environment[J]. Journal of Chongqing University, 2018, 41(2): 10-20. (in Chinese) |
| [13] |
van Berkel K, Veldpaus F, Hofman T, et al. Fast and smooth clutch engagement control for a mechanical hybrid powertrain[J]. IEEE Transactions on Control Systems Technology, 2014, 22(4): 1241-1254. DOI:10.1109/TCST.2013.2279935 |
 2019, Vol. 42
2019, Vol. 42

