b. 能源科学与工程学院, 河南 焦作 454000
b. School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454000, Henan, P. R. China
运输问题是企业或社会运营中常见的决策问题。运输问题的寻优具有高度复杂性,因此高效的运输问题寻优方法成为一个重要的研究课题。自20世纪40年代运输问题提出之日起[1],学者对运输问题的寻优方法进行了大量的研究,取得了较为丰富的研究成果。
从计算原理看,运输问题的寻优方法主要有线性规划法、表上作业法、图上作业法、网络解法[2]。运输问题是线性规划问题的特例,理论上可采用线性规划法寻优[3]。然而,由于运输问题决策变量和约束条件多[4],线性规划法的计算量大、计算效率低。表上作业法先利用最小元素法、伏格尔法[5]、西北角法[6]等方法获取初始基可行解,再利用位势法获取非基变量的检验数,进而利用闭合回路调整法进行基可行解的调整直到所有非基变量的检验数非负[4]。相对于线性规划法,表上作业法的计算量小得多,不过仍然需要多次反复计算。图上作业法是一种基于图论的寻优方法,该方法需先在图上构造边、权、边线,再在图上进行求解。然而,随着产地数、销地数的增多,导致边、权、边线相应增多,容易混淆,难以保证结果的准确性。网络解法将运输问题视作网络问题,采用图与网络技术寻优。该方法虽然可以更直观、快速地获取初始解,然而随着产地数、销地数的增多,网络图的绘制较麻烦、效率低。
从计算方式看,运输问题的寻优有手工求解和计算机求解2种方式。手工求解方式的计算效率低、准确性难以保证。图上作业法、网络解法难以实现计算机求解,通常采用手工方式求解。要提高运输问题的应用面,计算机寻优方式必然成为首选。围绕运输问题的计算机寻优,近年来学者进行相应的研究。文献[7]利用Excel的规划求解工具求解运输问题,在一定程度上提高了计算效率,但仅能求解小规模运输问题。文献[8]给出了Matlab求解运输问题的计算机算法。利用文献[7]、[8]的方法获得的最优解无法区分出基变量和非基变量,因而无法通过再调整得到多个最优解。文献[9]基于表上作业原理,提出了一种计算机算法,但文中未给出详细求解步骤。文献[10]、[11]提出了一种神经网络法,虽有一定的创新性,却将问题复杂化导致难以推广应用。近年来,部分学者还提出了计算机启发式算法,如遗传算法[12-13]、蚁群算法[14]等。然而,这些算法具有两个缺陷,一是普适性差,主要用于求解复杂、特殊的运输问题;二是无法保证解的最优性[15]。
表上作业法是求解运输问题的经典方法,相对于线性规划法其计算量小得多,相对于图上作业法、网络解法其更易于实现计算机求解,相对于神经网络法其更简单更易掌握,相对于遗传算法、蚁群算法其不仅可以保证获得最优解还有可能得到多个最优解。然而,在表上作业过程中,闭合回路的选取是影响计算机求解效率的关键环节[16]。若依靠人工进行闭合回路的选取,则属于人机半自动计算机求解方式,其计算效率取决于闭合回路的人工选取效率。虽然理论上讲,从任意一个非正的检测数出发一定能找到唯一的闭合回路[17],但随着产地数、销地数的增多,人工往往难以在短时间内找到该闭合回路。反之,若能借助计算机算法自动寻找到闭合回路,则能实现表上作业过程的全自动化,这将使计算效率得到大幅度提升。
基于此,笔者以Excel VBA为平台,基于表上作业原理,提出了一种基于“递归过程”的闭合回路寻找方法,在此基础上研究提出一种系统、高效的运输问题计算机寻优算法。
2 数学模型及问题描述设某种物品有m个产地Ai, i=1, 2, …, m,各产地的供应量为ai, i=1, 2, …, m,有n个销地Bj, j=1, 2, …, n,各销地的需求量为bj, j=1, 2, …, n。产地Ai向销地Bj供应物品的单位成本为cij、供应量为xij。对于产销平衡的运输问题有如下标准的数学模型。
| $ \begin{array}{*{20}{l}} {\min }&{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{c_{ij}}} } {x_{ij}}, }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}}&{\quad \sum\limits_{j = 1}^n {{x_{ij}}} = {a_i}, i = 1, 2, \cdots , m, }\\ {}&{\sum\limits_{i = 1}^m {{x_{ij}}} = {b_i}, j = 1, 2, \cdots , n, }\\ {}&{{x_{ij}} \ge 0, i = 1, 2, \cdots , m, j = 1, 2, \cdots , n。} \end{array} $ |
该模型中cij除了为单位供应成本以外,还可为其他类型的参数,如时间、距离等。对于产销不平衡的运输问题可通过增加虚拟产地或虚拟销地的方式将其转化为上述产销平衡的运输问题。因此,只需研究提出产销平衡运输问题的寻优算法。为便于后续内容的描述,现给出示例1。
示例1 某厂按合同规定须于当年每个季度末分别提供10、15、25、20台同规格的柴油机。已知该厂各季度的生产能力及柴油机的单位生产成本如表 1所示。如果生产出来的柴油机当季不交货,每台每积压一个季度需储存、维护费用0.15万元。要求在完成合同的情况下,制定使该厂全年总成本(包括生产、储存、维护费用)最少的生产方案[4]。
| 表 1 生产能力及单位生产成本 Table 1 Production capacity and production cost per unit |
虽然上述问题是一个生产计划问题,但可将其转化为运输问题进行寻优。根据题意可得,单位供应成本、供应量、需求量如表 2所示。本文中所有表中空白处均表示不能供应或单位供应成本为无穷大。
| 表 2 单位供应成本、供应量、需求量 Table 2 Supply cost per unit, quantity supplied and quantity needed |
根据算法需要,定义如表 3所示的计算机变量及数组。其中,g为相对于单位供应成本大得多的正数;P为(m+2)×(n+2)的数组,用于存储单位供应成本、供应量、需求量,前m×n个元素为单位供应成本,第m+1行为各销地需求量,第m+2行与m+1行元素值相等,第n+1列为各产地供应量,第n+2列与n+1列元素值相等;X、Y均为m×n的数组;BH为3行的数组,用于存储形成闭合回路的各点行号(第1行)、列号(第2行)和试探方向(第3行),其列数随着闭合回路中点数的变化而变化;TB为3×(m+n-1)的数组,用于存储Y中空检验数所在行号(第1行)、列号(第2行)及试探标志(第3行),试探标志初值为“”(空)表示未试探过,当试探标志置为1时表示已试探过该空检验数;LD为2行的数组,用于存储While循环退出时0检验数所在行号(第1行)、列号(第2行),其列数不确定,取决于0检验数的个数;U为m×1的数组;V为1×n的数组。
| 表 3 变量及数组定义 Table 3 Definition of variables and arrays |
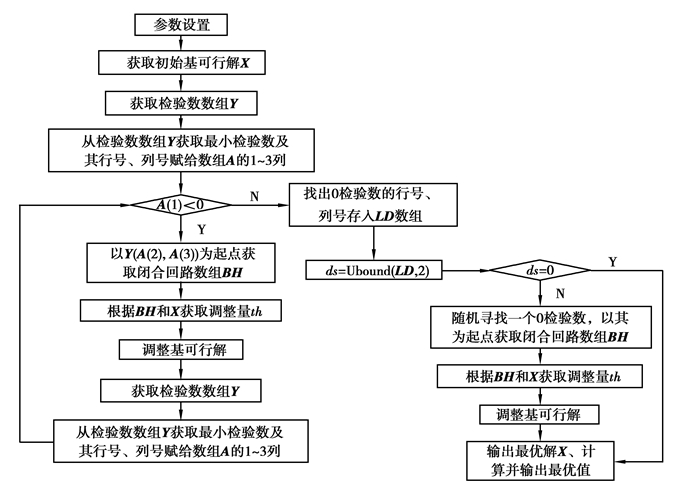
算法流程如图 1所示。具体如下:1)采用“最小元素法”获取初始基可行解X;2)运用“位势法”获取检验数数组Y;3)根据检验数数组Y找出最小检验数;4)若最小检验数小于0,则转5),否则转10);5)利用“递归过程”寻找闭合回路数组BH;6)根据基可行解X和闭合回路数组BH获取调整量;7)在闭合回路上对基可行解进行调整;8)运用“位势法”获取检验数数组Y;9)根据检验数数组Y找出最小检验数,转4);10)找出所有0检验数将其行号、列号存入LD数组;11)若0检验数的个数为0,则输出最优解X、最优值;若0检验数的个数不为0,则随机寻找一个0检验数,以此0检验数为起点获取闭合回路数组BH,进而获取调整量并进行调整得到并输出最优解X、最优值。
|
图 1 计算流程 Fig. 1 Calculation flow |
从图 1可见,采用该算法不仅能将运输问题的表上作业过程全部计算机程序化,而且当循环结束时,若存在0检验数,则多次计算可能得到不同的随机最优解。
3.3 参数设置设计“参数”工作表,用于向算法传递必要的输入参数。对于示例1,其参数如表 4所示。由于示例1的供应量比需求量多30台,故需增加一个虚拟销地(表 4最右一栏),其需求量设为30台、单位供应成本设为0,从而将产销不平衡问题转变为产销平衡问题,产地数为4,销地数为5,g取1 000 000。算法从“参数”工作表读入参数后,m=5,n=5,g=1 000 000,P如式(1)所示。
| $ \mathit{\boldsymbol{P}}=\left[\begin{array}{cccccc}{10.80} & {10.95} & {11.10} & {11.25} & {0} & {25} & {25} \\ {1000000} & {11.10} & {11.25} & {11.40} & {0} & {35} & {35} \\ {1000000} & {1000000} & {11.00} & {11.15} & {0} & {30} & {30} \\ {1000000} & {1000000} & {1000000} & {11.30} & {0} & {10} & {10} \\ {10} & {15} & {25} & {20} & {30} \\ {10} & {15} & {25} & {20} & {30}\end{array}\right]。$ | (1) |
| 表 4 参数 Table 4 Parameters |
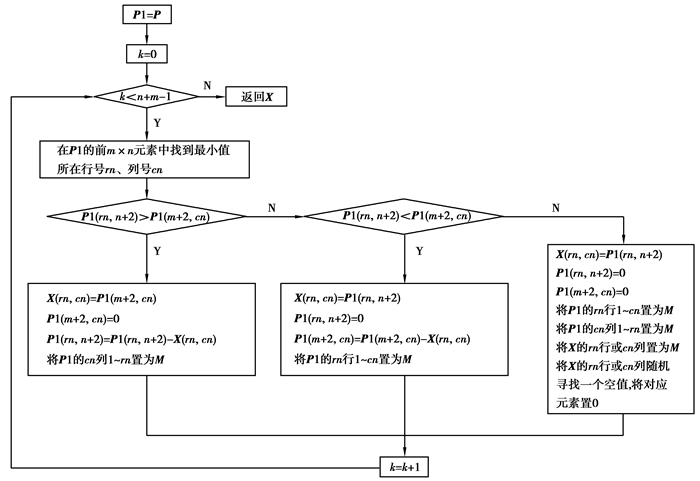
采用“最小元素法”获取初始基可行解X,计算流程如图 2所示。其中,P1的第n+2列为各产地的供应余量,它随着供应量的分配而变化;第m+2行为各销地的需求余量,也随着供应量的分配而变化;在寻找初始基可行解的过程中,在P1中划去某行或某列采用的方法如下:将对应行或列的单位供应成本全部置为g。示例1得到的初始基可行解如式2)所示,对应成本为1 000 668万元。
| $ \boldsymbol{X}=\left[\begin{array}{ccc}{} & {} & {}& {} &{25} \\ {} & {15} & {15} & {} & {5}\\ {} & {} & {10} & {20}& {} \\ {10} & {} & {}&& {} {0}& {}\end{array}\right]。$ | (2) |
|
图 2 获取初始基可行解的流程 Fig. 2 Flow of getting initial basic feasible solution |
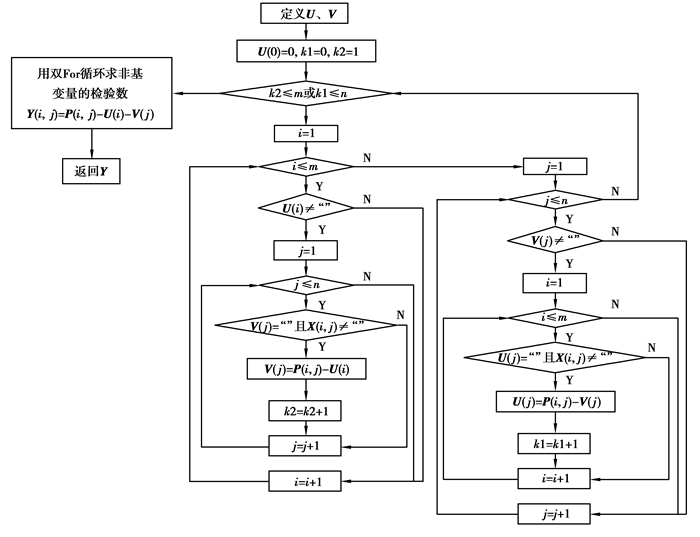
采用“位势法”获取检验数数组Y,计算流程如图 3所示。分两步进行:第一步,用While循环求得位势向量U、V;第二步,用双重For循环求得非基变量的检验数(基变量的检验数为“”即空值)得到检验数数组Y。其中,第一步是关键,基本思路如下:由已知U(i)求得未知V(j),再由已知V(j)求得未知U(i),每计算一个U(i)让计数器k2增加1,每计算一个V(j)让计数器k1增加1,如此循环,直到k2=m+1且k1=n+1时退出While循环。对于示例1,根据式(2)所示的初始基可行解计算得到的U如式(3)所示、V如式(4)所示、Y如式(5)所示。
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{l}} 0&0&{ - 0.25}&{ - 0.1} \end{array}} \right], $ | (3) |
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1\;000}&{000.1}&{11.1}&{11.25} \end{array}}&{11.4}&0 \end{array}} \right], $ | (4) |
| $ \boldsymbol{Y}=\left[\begin{array}{cccc}{-999989.3} & {-0.15} & {-0.15} & {-0.15} & {}\\ {-0.1} & {} & {} & {0} \\ {0.15} & {999989.2} & {} & {} & {0.25} \\ {}& {999989} & {999988.9} & {} & {0.1}\end{array}\right]。$ | (5) |
|
图 3 获取检验数数组的流程 Fig. 3 Flow of getting the array of check numbers |
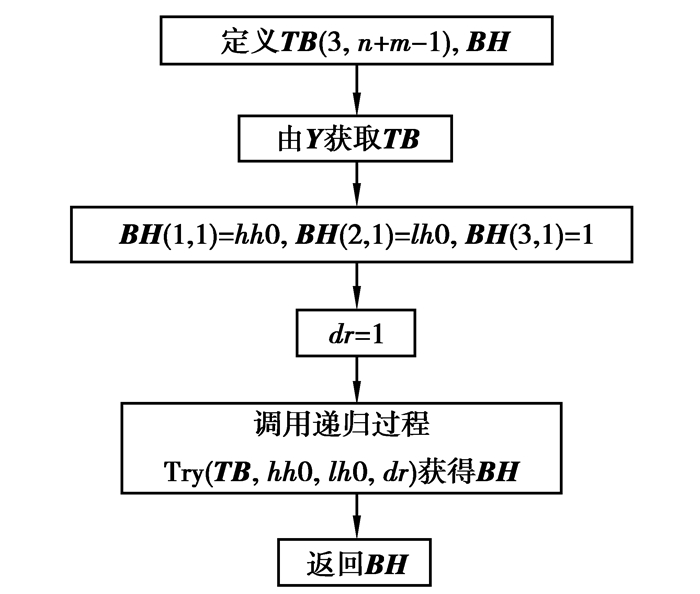
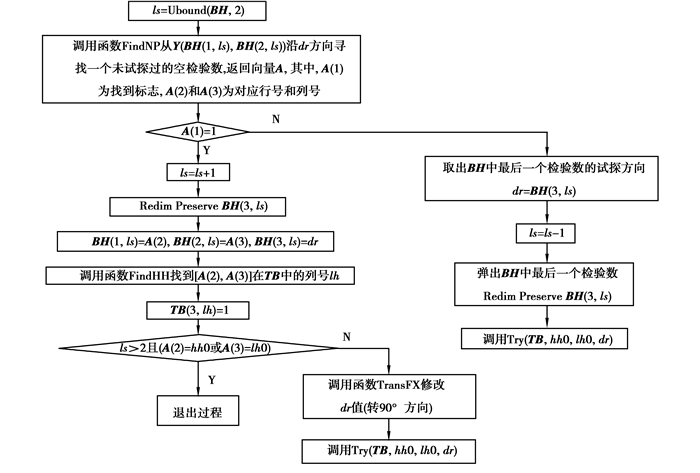
设初始检验数(闭合回路的起始点,通常选最小检验数为起始点,其值小于或等于0)在检验数数组Y中对应的行号为hh0、列号为lh0。此步的目的是从Y(hh0, lh0)为起始点,沿dr方向(设dr=1表示横向、dr=2表示纵向)出发寻找闭合回路,最终回到Y(hh0, lh0),将得到的可行检验数(对应X中的基变量)在检验数数组Y中对应的行号、列号、试探方向依次记录在闭合回路数组BH中。由于空检验数的个数往往比最终闭合回路数组BH中的空检验数个数多,沿某个方向找到空检验数时可转90°方向也可不转90°方向,并且,转方向时可顺时针转也可逆时针转,因此利用算法自动寻找闭合回路需采用“试探”方法进行。本文算法获取闭合回路数组BH的计算流程如图 4所示。TB为局部数组,用于存储Y中所有空检验数所在的行号(第1行)、列号(第2行)及试探标志(第3行);BH为全局数组;Try为“递归过程”,通过该过程对空检验数不断进行试探直到找到闭合回路为止,试探过程中,若空检验数可行,则将其在Y中对应的行号、列号、试探方向加入BH的末尾,不论可行与不可行,都在TB中对应位置的试探标志置为1。递归过程Try的计算流程如图 5所示,受篇幅所限,自定义函数FindNP、FindHH、TransFX不作详述。对于示例1,根据式(5)所示的检验数数组可知最小检验数为-16.5,对应的行号、列号为4、3,得到的闭合回路数组如式(6)所示。
|
图 4 获取闭合回路数组的流程 Fig. 4 Flow of getting the closed loop array |
|
图 5 递归过程Try的流程 Fig. 5 Flow of the recursive process Try |
用For循环依次取出闭合回路数组BH中偶数列的前2行值(行号、列号),在基可行解X找出对应基变量的值,再取其最小值得到调整量th。获取调整量th后即可对基可行解X进行调整,方法如下:用For循环依次取出闭合回路数组BH中前2行值(行号、列号),对基可行解X中对应元素值进行如下调整:第奇数个元素减去th,第偶数个元素加上th。若减去th后值为0的元素只有1个,则将该元素置为“”(空值),若减去th后值为0的元素不只1个,则从这些元素中任选1个元素将其置为“”(空值)。对于示例1,根据式(2)和式(6)得X(1, 5)=25、X(2, 3)=15、X(3, 4)=20、X(4, 1)=10,故调整量th=10。对(2)进行调整后得到的基可行解如式(7)所示,对应成本降为775万元。
| $ \mathit{\boldsymbol{B H}}=\left[\begin{array}{llllllll}{1} & {1} & {2} & {2} & {3} & {3} & {4} & {4} \\ {1} & {5} & {5} & {3} & {3} & {4} & {4} & {1} \\ {1} & {1} & {2} & {1} & {2} & {1} & {2} & {1}\end{array}\right], $ | (6) |
| $ \boldsymbol{X}=\left[\begin{array}{cccc}{10} & {} & {}& {} & {15} \\ {} & {15} & {5} & {} & {15}\\ {} & {} & {20} & {10}& {} \\ {} & {} & {} & {10}& {}\end{array}\right]。$ | (7) |
示例1 利用本文算法对示例1进行多次独立求解,可以得到多个最优解,表 5、6为其中2个,最低成本为773万元,计算时间为1 s左右。
| 表 5 最优解1 Table 5 Optimal solution 1 |
| 表 6 最优解1 Table 6 Optimal solution 1 |
若采用Matlab程序和规划求解工具求解,最低成本也为773万元,得到的最优解如表 7所示。
| 表 7 用Matlab程序或规划求解工具得到的最优解 Table 7 Optimal solution got by Matlab program or planning solution tool |
将本文算法与Matlab程序、规划求解工具进行对比分析,结果如表 8所示。从表 8可见,相对于Matlab程序或规划求解工具来说,本文算法具有计算速度快、扩展性好、平台简单、可获得多个随机最优解的综合优越性。
| 表 8 对比分析 Table 8 Comparative analysis |
示例2 某汽车厂2018年1—6月预计的某轿车市场需求量分别是3 000、3 600、5 200、6 000、5 000、4 400辆,1月份期初库存量为0。该厂在3种不同生产方案下的生产能力和相应的单位制造成本数据如表 9所示,单位产品每月存储成本为1 000元。试确定该厂2018年1—6月总成本最低的产出计划[18]。
| 表 9 生产能力及单位成本 Table 9 Production capacity and cost |
与示例1相似,示例2也是一个生产计划问题,由题意可将其转化为一个运输问题。由于需求量为27 200辆,供应量为(4 000+600+1 000)×6=33 600辆,供应量比需求量多6 400辆,因此需增加一个虚拟销地(表 10最右一栏),其需求量设为6 400辆、单位供应成本设为0,从而构造一个产销平衡的运输问题,产地数为18,销地数为7, g取1 000 000,具体参数如表 10所示。表 10中,从上往下,每3个产地对应1个月的3种不同的生产方式。
| 表 10 参数 Table 10 Parameters |
利用本文算法对上述产销平衡的运输问题进行多次独立求解,也可以得到多个最优解,表 11为其中一个,最低成本为55 000万元,计算时间为3 s左右。
| 表 11 最优解 Table 11 Optimal solution |
示例3 有一份中文说明书,要翻译成英、日、德、俄4种文字,分别记作E、J、G、R,现有甲、乙、丙、丁4人,他们将中文说明书翻译成不同语种的所明书所需时间如表 12所示,每人分担1份说明书的翻译任务,试求总时间最少的指派方案[4]。
| 表 12 翻译时间 Table 12 Translation time |
示例3是一个任务数和人员数相等、一项任务唯一指派给一人完成、每人唯一被指派一项任务的狭义指派问题。由题意,可构造一个产销平衡的运输问题,产地数为4,销地数为4,g取1 000 000,具体参数如表 13所示。
| 表 13 参数 Table 13 Parameters |
利用本文算法对上述产销平衡的运输问题进行求解,得到的最优解如表 14所示,最少总时间为28 d,计算时间为1 s左右。
| 表 14 最优解 Table 14 Optimal solution |
示例4 有一份中文说明书,要翻译成英、日、德、俄、法、意、韩7种文字,分别记作E、J、G、R、F、I、K,现有甲、乙、丙、丁4人,他们将中文说明书翻译成不同语种的所明书所需时间如表 15所示,甲、乙、丁分别分担2项任务、丙分担1项任务,试求总时间最少的指派方案。
| 表 15 翻译时间 Table 15 Translating time |
示例4是一个任务数和人员数不相等、一项任务唯一指派给一人完成、一人完成的任务数不一定唯一但事先已确定[19]的一类广义指派问题。由题意,可构造一个产销平衡的运输问题,产地数为7,销地数为4,g取1 000 000, 具体参数如表 16所示。
| 表 16 参数 Table 16 Parameters |
利用算法对上述产销平衡问题寻优,得到的最优解如表 17所示,最少总时间为31 d,计算时间为1 s左右。
| 表 17 最优解 Table 17 Optimal solution |
研究提出高效的运输问题计算机寻优算法对于提高运输问题的应用面具有重要意义。本文提出的计算机寻优算法基于表上作业原理,将初始基可行解的获取、检验数的获取、闭合回路的寻找、调整量的获取、基可行解的调整工作全部由计算机程序完成,从而实现了运输问题计算机寻优过程的全自动化。与Matlab程序、规划求解工具等其他算法相比,本文算法具有计算速度快、扩展性好、平台简单、可获得多个随机最优解的综合优越性。从理论上讲,只要能转化为产销平衡运输问题,就能利用本文寻优算法加以快速求解,如生产计划问题、指派问题、物流问题等。
| [1] |
Hitchcock F L. The distribution of a product from several sources to numerous localities[J]. Journal of Mathematics and Physics, 1941, 20(1/2/3/4): 224-230. |
| [2] |
王有鸿, 费威. 运输问题国内外研究评述[J]. 商业时代, 2010(24): 31-32. WANG Youhong, FEI Wei. International and domestic review on transportation problems[J]. Commercial Times, 2010(24): 31-32. (in Chinese) |
| [3] |
彭程, 薛伟宁, 黄轶. 露天矿运输问题的模拟退火优化[J]. 中国矿业, 2018, 27(4): 138-141. PENG Cheng, XUE Weining, HUANG Yi. Simulated annealing algorithm for the open-pit mine transportation problem[J]. China Mining Magazine, 2018, 27(4): 138-141. (in Chinese) |
| [4] |
甘应爱, 田丰. 运筹学[M]. 修订版. 北京: 清华大学出版社, 2005. GAN Yingai, TIAN Feng. Operations research[M]. Revised ed. Beijing: Tsinghua University Press, 2005. (in Chinese) |
| [5] |
Zhang L F, Zhao X D. Research on non-standard assignment problem based on the vogel method[J]. Applied Mechanics and Materials, 2012, 256/257/258/259: 3028-3032. |
| [6] |
Klinz B, Woeginger G J. The Northwest corner rule revisited[J]. Discrete Applied Mathematics, 2011, 159(12): 1284-1289. DOI:10.1016/j.dam.2011.04.007 |
| [7] |
Sanchez L C, Herrera J. Solution to the multiple products transportation problem: linear programming optimization with Excel Solver[J]. IEEE Latin America Transactions, 2016, 14(2): 1018-1023. DOI:10.1109/TLA.2016.7437253 |
| [8] |
司守奎. 数学建模算法与应用[M]. 北京: 国防工业出版社, 2017. SI Shoukui. Mathematical modeling algorithms and applications[M]. Beijing: National Defense Industry Press, 2017. (in Chinese) |
| [9] |
司南, 任佳莉. 运输问题的一种计算机算法[J]. 计算机应用与软件, 2004, 21(7): 120-121. SI Nan, REN Jiali. A computer algorithm for transportation problem[J]. Computer Applications and Software, 2004, 21(7): 120-121. (in Chinese) DOI:10.3969/j.issn.1000-386X.2004.07.050 |
| [10] |
程国忠. 运输问题的神经网络解法[J]. 计算机应用研究, 2001, 18(11): 16-18. CHENG Guozhong. A neural network method for solving transportation problem(TRP)[J]. Application Research of Computers, 2001, 18(11): 16-18. (in Chinese) DOI:10.3969/j.issn.1001-3695.2001.11.005 |
| [11] |
毛云英, 亢京力, 杨正方. 运输问题的人工神经网络方法[J]. 天津商学院学报, 2001(6): 15-16, 23. MAO Yunying, KANG Jingli, YANG Zhengfang. Artificial neural network method of transportation problem[J]. Journal of Tianjin University of Commerce, 2001(6): 15-16, 23. (in Chinese) DOI:10.3969/j.issn.1674-2362.2001.06.005 |
| [12] |
刘云飞, 赵磊, 朱道立. 出口汽车零部件集货运输问题的双层遗传算法[J]. 计算机集成制造系统, 2016, 22(9): 2227-2234. LIU Yunfei, ZHAO Lei, ZHU Daoli. Two-level genetic algorithm for consolidated transportation problem of exporting auto-parts[J]. Computer Integrated Manufacturing Systems, 2016, 22(9): 2227-2234. (in Chinese) |
| [13] |
Ghassemi Tari F, Hashemi Z. A priority based genetic algorithm for nonlinear transportation costs problems[J]. Computers & Industrial Engineering, 2016, 96: 86-95. |
| [14] |
Abdulkader M M S, Gajpal Y, ElMekkawy T Y. Hybridized ant colony algorithm for the multi compartment vehicle routing problem[J]. Applied Soft Computing, 2015, 37: 196-203. DOI:10.1016/j.asoc.2015.08.020 |
| [15] |
Bulut H. Multiloop transportation simplex algorithm[J]. Optimization Methods and Software, 2017, 32(6): 1206-1217. DOI:10.1080/10556788.2016.1260568 |
| [16] |
沈爱凤. 基于区间数/贝叶斯的不确定性改进表上作业法与运用[J]. 统计与决策, 2015(10): 76-78. SHEN Aifeng. An improved tableau working method and application based on interval number/Bayesian uncertainty[J]. Statistics and Decision, 2015(10): 76-78. (in Chinese) |
| [17] |
盛秀艳, 窦志伟. 农业运输问题的表上作业法与图上作业法的比较[J]. 安徽农业科学, 2010, 38(14): 7202-7203. SHENG Xiuyan, DOU Zhiwei. Comparison of tableau working method and graphic operation method for agricultural transportation problems[J]. Journal of Anhui Agricultural Sciences, 2010, 38(14): 7202-7203. (in Chinese) DOI:10.3969/j.issn.0517-6611.2010.14.004 |
| [18] |
李怀祖. 生产计划与控制[M]. 北京: 中国科学技术出版社, 2005. LI Huaizu. Production planning and control[M]. Beijing: Science and Technology of China Press, 2005. (in Chinese) |
| [19] |
Munapo E, Lesaoana 'M, Nyamugure P, et al. A transportation branch and bound algorithm for solving the generalized assignment problem[J]. International Journal of System Assurance Engineering and Management, 2015, 6(3): 217-223. DOI:10.1007/s13198-015-0343-9 |
 2019, Vol. 42
2019, Vol. 42


