b. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045
b. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University, Chongqing 400045, P. R. China
近30年来,工程结构的健康监测和安全检测备受关注。结构的损伤会改变材料的物理参数和力学特性,特别是刚度特性会发生下降等变化,进一步改变结构的振动特性和动力响应。因此,有必要利用结构的振动特性或动力响应变化进行损伤识别研究[1]。结构的动力响应数据是可以直接测量的数据,包含加速度、速度以及位移等响应数据,其中,加速度的测量精度较高,更适合于作为损伤检测的动力响应数据。时间序列模型可以直接利用加速度等响应数据进行损伤信息的特征提取,并具有建模简单以及对条件变量敏感等优点,广泛地应用于结构的健康监测和损伤识别等领域[2-3]。时间序列模型可以划分为两大类,一类是线性模型,一类是非线性模型。线性模型主要有自回归(AR, autoregressive)、有源自回归(ARX, autoregressive exogenous)、自回归滑动平均(ARMA, Autoregressive moving average)等模型[4]。Zheng等[5]基于ARMA模型的距离函数构建了损伤指标,对损伤的位置和程度进行了分析。Xing等[6]利用了损伤前后的低阶AR模型及其相应的倒谱距离进行了损伤位置的检测。Liu等[7]则基于AR模型系数矩阵提出了一种非概率损伤诊断方法,利用损伤前后的马氏距离判断损伤位置。非线性模型包含自回归条件异方差(ARCH, autoregressive conditional heteroskedasticity)、广义自回归条件异方差(GARCH, generalized autoregressive conditional heteroskedasticity)等模型[8]。由于常见的裂纹等损伤在振动时会出现张开和闭合效应,该效应使结构在振动时呈现为变刚度特性,进一步使结构的时域响应具有非线性特征,故有必要对裂纹等非线性损伤进行识别研究。Chen等[9]基于时域ARMA/GARCH模型对非线性损伤进行了识别研究。Cheng等[10]则进一步采用了AR/ARCH模型分析了非线性损伤问题,但均缺乏对非线性损伤不确定问题的有效处理策略。与传统的ARMA/GARCH模型相比,AR/GARCH模型采用了AR模型来过滤线性特征信息,这样的优势是模型的建立更为简单便捷,可以保留更为丰富的非线性特征信息。文中拟采用加速度响应数据构造AR/GARCH模型,并与概率理论相结合提出一种概率损伤指标,以解决损伤的非线性和不确定性问题。
1 AR/GARCH模型 1.1 AR/GARCH模型AR/GARCH模型是由AR模型和GARCH模型组合而成的一种混合模型,包含有AR模型和GARCH模型。对于条件均值可以建立如下AR(p)模型:
| $ {{y}_{t}}=c+\sum\limits_{i=1}^{p}{{{\phi }_{i}}{{y}_{t-i}}+{{\varepsilon }_{t}}, } $ | (1) |
式中:yt是加速度响应等时间序列数据;c是自回归常数;p是自回归阶数;ϕii是自回归参数;εt是残差。通常而言,残差项被假定为均值为0,方差为常数的时间序列数据。但是,对于许多实际工况下的时域动力响应数据,残差序列并不满足恒定方差的同方差假定,会产生条件异方差问题。残差序列的条件方差σt2为
| $ {{\sigma }_{t}}^{2}=\text{Va}{{\text{r}}_{t-1}}({{\varepsilon }_{t}})={{E}_{t-1}}({{\varepsilon }_{t}}^{2})。$ | (2) |
对于残差序列的条件方差可建立GARCH (r, h)模型如下:
| $ {{\sigma }_{t}}^{2}=s+\sum\limits_{i=1}^{r}{{{B}_{i}}{{\sigma }_{t-i}}^{2}+}\sum\limits_{j=1}^{h}{\text{ }{{A}_{j}}{{\varepsilon }_{t-j}}^{2}, } $ | (3) |
式中,s是GARCH模型常量;Bi和Aj均为GARCH模型参数;r和h是GARCH模型的阶数。这些参数需满足如下约束条件:
| $ s>0, {{B}_{i}}\ge 0\left( i=1, \ldots , r \right), {{A}_{j}}\ge 0\left( j=1, \ldots , h \right), $ | (4) |
| $ \sum\limits_{i=1}^{r}{{{B}_{i}}+\sum\limits_{j=1}^{h}{{{A}_{j}}<1}}。$ | (5) |
约束条件(4)保证了条件方差的正值性,约束条件(5)保证了条件方差的稳定性。这样,AR/GARCH模型总结如下:
| $ \left\{ \begin{align} & {{y}_{t}}=c+\sum\limits_{i=1}^{p}{{{\phi }_{i}}{{y}_{t-i}}+{{\varepsilon }_{t}}, {{\varepsilon }_{t}}\sim N(0, {{\sigma }_{t}}^{2}), } \\ & \ \ \ \ {{\sigma }_{t}}^{2}=s+\sum\limits_{i=1}^{r}{{{B}_{i}}{{\sigma }_{t-i}}^{2}+\sum\limits_{j=1}^{h}{{{A}_{j}}{{\varepsilon }_{t-j}}^{2}, }} \\ & \text{ }\ \ \ \ \ \ \ \ \ \ \ \ \ {{\varepsilon }_{t}}={{\sigma }_{t}}{{z}_{t}}, {{z}_{t}}\sim N\left( 0, 1 \right), \\ \end{align} \right. $ | (6) |
式中,zt是均值为0,标准差为1的随机白噪声序列。
1.2 参数估计和定阶 1.2.1 AR模型参数估计可采用矩估计中的Yule-Walker法进行p阶AR模型的参数估计,Yule-Walker法主要是利用自相关函数和自回归参数之间的关系,建立方程如下:
| $ \left[ \begin{array}{*{35}{l}} \ \ {{\rho }_{0}} & \ \ {{\rho }_{1}} & \cdots & {{\rho }_{p-1}} \\ \ \ {{\rho }_{1}} & \ \ {{\rho }_{2}} & \cdots & {{\rho }_{p-2}} \\ \ \ \ \vdots & \ \ \ \vdots & \ddots & \ \ \ \vdots \\ ~{{\rho }_{p-1}} & {{\rho }_{p-2}} & \cdots & \ \ {{\rho }_{0}} \\ \end{array} \right]\left[ \begin{array}{*{35}{l}} {{\phi }_{p1}} \\ {{\phi }_{p2}} \\ \ \ \vdots \\ {{\phi }_{pp}} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} {{\rho }_{1}} \\ {{\rho }_{2}} \\ \ \ \vdots \\ {{\rho }_{p}} \\ \end{array} \right], $ | (7) |
式中,ρ0,ρ1,...,ρp为自相关系数,可利用自相关函数的样本估计值
GARCH模型常用2种简化形式,即GARCH(1, 1)模型和GARCH(0, h)模型。而GARCH(1, 1)模型阶数已确定,故主要分析GARCH(0, h)形式的参数估计。文中采用极大似然估计法进行参数估计,即建立其对数条件似然函数为
| $ \text{ln}L\left( \theta \right)=\sum\limits_{t=h+1}^{N}{\left( -\frac{1}{2}~\text{ln}(2\text{ }\!\!\pi\!\!\text{ })-\frac{1}{2}~\text{ln}({{\sigma }_{t}}^{2})-\frac{\varepsilon _{t}^{2}}{2{{\sigma }_{t}}^{2}} \right), } $ | (8) |
式中,θ是未知估计参数。采用极大似然估计法时,可忽略不含参数的第一项,则式(8)为
| $ \text{ln}L\left( \theta \right)=\sum\limits_{t=h+1}^{N}{\left( -\frac{1}{2}\text{ }\!\!~\!\!\text{ ln}({{\sigma }_{t}}^{2})-\frac{\varepsilon _{t}^{2}}{~2{{\sigma }_{t}}^{2}} \right)}。$ | (9) |
这样,可利用对数条件似然函数进行参数估计。
1.2.3 定阶时间序列模型需要进行定阶分析并确定合适的模型阶数。BIC和AIC准则是常用的2种时域模型定阶方法,可采用如下AIC准则进行模型定阶:
| $ \text{AIC}=-2\text{ln}L+2m, $ | (10) |
式中,lnL和m分别是对数最大似然函数和估计参数数量。AIC准则主要利用最优模型阶数可以生成较小AIC值原理进行阶数确定,在实际应用中尽量选取较小的阶数以简化计算。
2 概率理论和损伤指标 2.1 非线性损伤特征提取由于裂纹的不断张开和闭合效应造成了刚度的不断往复性突变,使测量响应数据具有往复性的时域非线性特征,该类非线性特征可以利用方差变异性进行识别。AR/GARCH模型可用来提取时程响应数据中的非线性特征。其中,AR部分可用来描述加速度响应序列的条件均值,GARCH部分可用来描述AR模型提取的加速度响应残差序列的条件异方差。在非线性损伤提取过程中,考虑了2种状态,即未损伤状态和损伤状态。具体损伤特征因子提取过程如下:
首先,获取损伤前后的加速度响应时间序列数据,并构建损伤前后的AR模型,得到损伤前后的残差序列{εtU}和{εtD}。
然后,测试残差序列的异方差效应,利用残差序列构建GARCH模型并计算出损伤前后残差序列的条件方差序列{σt2U}和{σt2D}。
最后,计算出损伤前后条件方差序列的方差v{σt2U}and v{σt2D},并采用下式提取非线性特征因子:
| $ \eta =v\left\{ \sigma _{t}^{{{2}^{D}}} \right\}-v\left\{ \sigma _{t}^{{{2}^{U}}} \right\}~。$ | (11) |
但是,该损伤特征因子难于直接处理测量误差等造成的不确定问题,故需要利用概率理论来构建概率损伤指标。
2.2 概率理论和基本损伤指标考虑到噪声等因素产生的测量信号的不确定性,假设非线性特征因子概率分布函数f(η)服从均值为μ(η),标准差为σ(η)的正态分布,损伤检测是基于损伤前后的加速度响应,并利用非线性特征因子与未损状态下结构性能的显著性区别来识别非线性损伤。非线性特征因子η在显著性水平α下的假设检验为
| $ \begin{align} & {{H}_{0}}:\mu =0\text{ }(\text{Undamaged}), \\ & {{H}_{1}}:\mu \ne 0\text{ }(\text{Damaged})。\\ \end{align} $ | (12) |
损伤识别的不确定性影响主要体现在损伤概率中,需要依赖公式(12)假设检验的显著性水平选取。损伤存在概率可以通过计算物体系统实际状态接受假设H1并拒绝H0的概率来获取[11]。具体可通过损伤状态下的因子ηd和未损伤状态下的因子ηu的概率分布来获取。假定ηu服从均值为μ(ηu)标准差为σ(ηu)的正态分布,ηd服从均值为μ(ηd)标准差为σ(ηd)的正态分布,并经过了Kolmorogov-Smirnov(K-S)检验,就可以得到f(ηu)和f(ηd)的相应概率密度函数。采用Lu表示状态因子ηu的下限。当显著性水平为α时,利用Xu等[11]的方法可得Lu计算公式:
| $ {{L}_{u}}=\mu ({{\eta }_{u}})-\phi \left( 1-\alpha \right)\sigma ({{\eta }_{u}}), ~ $ | (13) |
式中,ϕ(1-α)是具有α置信水平单侧置信区间下标准正态分布的(1-α)分位数,意味着未损状态因子ηu有1个α概率落入了区间范围[Lu, ∞)。借鉴文献[11]可得损伤存在概率计算公式为
| $ P=\int_{0}^{{{L}_{u}}}{f({{\eta }_{d}})\text{d}{{\eta }_{d}}}。$ | (14) |
对于一个n层剪切结构,每层均有加速度响应信号,可利用损伤前后的加速度响应提取损伤存在概率值Pj(j=1, …, n)。但是结构的损伤往往发生在层间柱上,表现为层间刚度的损伤形式,需要将基于自由度的损伤形式转化为基于层间刚度的损伤形式。基于转换前后概率等效原则首先构建了基本概率损伤指标为
| $ {{d}_{j}}=\frac{({{P}_{j-1}}+{{P}_{j}})/2}{2\sum\limits_{j=1}^{n}{({{P}_{j-1}}+{{P}_{j}})/2}}\cdot \sum\limits_{j=1}^{n}{{{P}_{j}}, } $ | (15) |
其中,当j=1时,令Pj-1=P0=0,可采用该基本概率指标进行层间刚度的损伤识别。
2.3 改进的概率指标由于基本概率损伤指标只是简单利用了相邻自由度的损伤数据,其识别效果仍有待提高。因此,研究基于加权机制和概率等效原则提出了一种损伤识别的改进概率指标,以提高非线性损伤识别的可靠性和精度。由于1个自由度数据往往对应2个刚度层,故需要消减相邻不相关因素对损伤识别的干扰,基于加权机制和概率等效原则对非线性损伤识别指标进行了改进,改进后的损伤指标为
| $ {{c}_{j}}=\frac{{{T}_{j}}}{2\sum\limits_{j=1}^{n}{{{T}_{j}}}}\cdot \sum\limits_{j=1}^{n}{{{P}_{j}}, } $ | (16) |
| $ \text{ }{{T}_{j}}=\text{max}[0, ({{P}_{j-1}}+{{P}_{j}})/2-\zeta \cdot \text{ }\left| {{P}_{j}}-{{P}_{j-1}} \right|], $ | (17) |
式中,ζ是加权参数,满足了转换前后概率等效原则,并利用权化技术削弱了相邻不相关因素的影响。
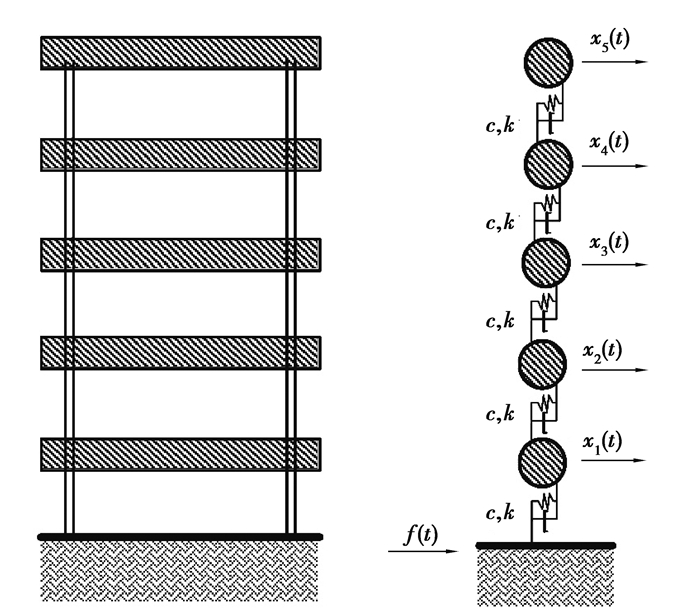
3 数值计算采用1个五层的层间剪切结构,如图 1所示,其结构参数为:每层质量是100 kg,层间刚度是1 MN/m。该五层剪切结构的阻尼采用瑞利阻尼,并根据阻尼比0.03和结构的频率计算出瑞利阻尼参数,其阻尼参数α为1.460 7和β为0.000 3。利用白噪声数据作为输入激励,并采用Newmark-β方法计算每层的加速度响应,测量的不确定性模拟主要是通过在输出的加速度响应上附加10%的随机噪声序列。由于噪声的随机性和不确定性,可通过模拟形成多组不同的加速度响应时间序列数据,从而计算损伤特征因子正态分布的均值和标准差。非线性损伤则采用双线性刚度法[12]进行模拟,该方法可以模拟呼吸裂缝形式的非线性损伤特征,双线性刚度定义为
| $ {{k}_{i}}[{{x}_{i}}\left( t \right)]=\left\{ \begin{align} & \ \ \ {{k}_{i}}\ \ \ \ \ \ \ \ ~if\text{ }{{x}_{i}}\left( t \right)-{{x}_{i-1}}\left( t \right)\le 0, {{x}_{i}}\left( t \right)\le 0, \\ & \left( 1-c \right){{k}_{i}}~\ \ if\text{ }{{x}_{i}}\left( t \right)-{{x}_{i-1}}\left( t \right)>0, {{x}_{i}}\left( t \right)>0, \\ \end{align} \right.\text{ }(i=1, \ldots n;{{x}_{0}}\left( t \right)=0), $ | (18) |
|
图 1 五层层间剪切结构 Fig. 1 Five-storey shear structure |
式中,xi(t)和xi-1(t)是第i层和第(i-1)层的振动位移;ki[xi(t)]是第i层的层间刚度;c是损伤系数。其中,x0(t)=0表示基础位移固定。该双线性刚度法可用来进行呼吸裂缝的仿真。
考虑6种损伤工况,具体如表 1所示。在计算加速度响应数据时,均加入了10%的随机测量噪声。进行Kolmorogov-Smirnov检验可验证损伤特征因子的分布与正态分布相一致;再利用AIC准则和自相关性函数确定了AR模型和GARCH模型的阶数,AR模型的阶数为28,GARCH模型的阶数为0和7,而加权参数为0.4。
| 表 1 五层剪切结构损伤工况 Table 1 Damaged states of five-story shear structure |
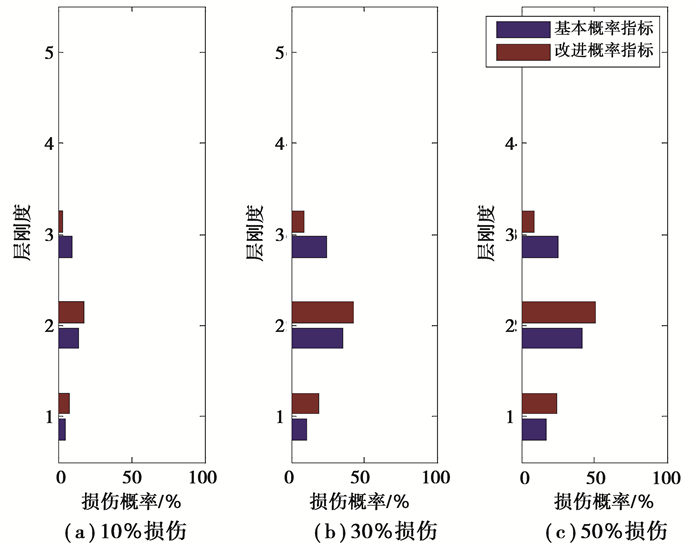
首先,考虑第2层依次发生10%、30%和50%的非线性损伤(即工况1~3),该3个工况的识别结果如图 2所示。由图 2可以发现,基本概率指标和改进概率指标均可以较好地识别出第2层的非线性损伤,其第2层的损伤概率值均高于其他层,随着损伤程度的增加,从10%增加到50%时,2种指标的损伤概率指标也依次增高,说明概率指标也具有一定的损伤程度判定能力。另外,通过2种概率指标的对比分析可知,改进概率指标的识别结果明显好于基本概率指标。例如,对于损伤的第二层,改进概率指标的计算值要高于基本概率指标的计算值;而对于无损伤的其它层,改进概率指标的计算值要明显低于基本概率指标的计算值。故改进概率指标显著地降低了误识别概率,可以更有效和更直观地识别出损伤位置。
|
图 2 第2层在10%、30%、50%损伤下的识别结果 Fig. 2 Damage identification results of the 2nd-storey with damage degrees 10%, 30% and 50% |
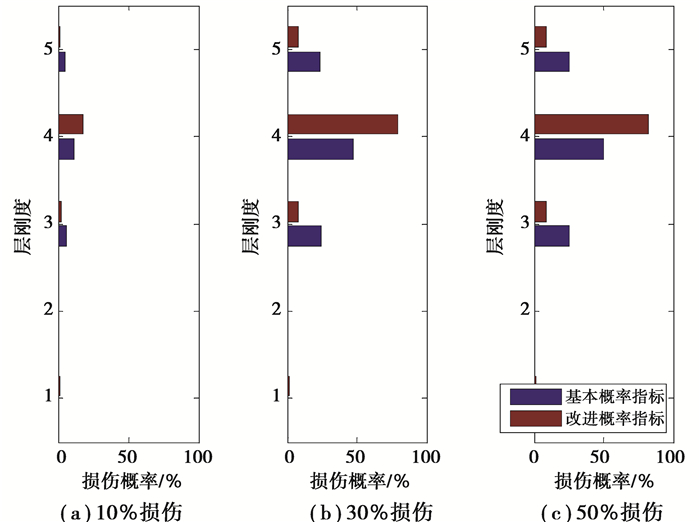
然后,考虑第4层依次发生10%、30%和50%的非线性损伤(工况4~6),该3种工况的识别结果如图 3所示。由图 3可以观察到,2种损伤概率指标依然可以较好地识别出非线性损伤,其第4层的损伤概率值均高于其他层,而且随着损伤程度的增加,2种概率指标相应的损伤概率指标也依次增高,说明概率指标也具有一定的损伤程度判定能力。由2种指标的识别结果对比分析可知,改进概率指标的识别结果明显好于基本概率指标。对于损伤的第4层,改进概率指标的计算值要高于基本概率指标的计算值;而对于其它层,改进概率指标的计算值则低于基本指标值,故改进概率指标计算具有更好的非线性识别能力。另外,由6个工况计算结果可知,随着损伤程度的增加,改进概率指标的计算值具有随之增大的趋势,可以认为该指标具有一定的损伤程度识别能力。当然,损伤程度和非线性损伤指标的具体量化关系还需进一步研究。
|
图 3 第4层在10%、30%、50%损伤下的识别结果 Fig. 3 Damage identification results of the 4th-storey with damage degrees 10%, 30% and 50% |
一个三层框架实验装置如图 4(a)所示,该三层实验结构由铝柱通过螺栓连接而成。层间的铝柱尺寸为17.7 cm×2.5 cm×0.6 cm,构建为1个三层框架结构。在第3层层间设置了悬臂柱和缓冲器所构成的机械装置以模拟非线性损伤源,详见图 4(b),两者随着结构的振动会产生接触引起变刚度效应,类似于“呼吸裂纹”引起的非线性损伤[13]。通过调节缓冲器和悬臂柱的间隙距离可以模拟不同程度的非线性损伤情况。该非线性损伤具有“呼吸裂纹”所具有的双线性刚度特点。

|
图 4 三层框架实验 Fig. 4 Three-story frame experiment |
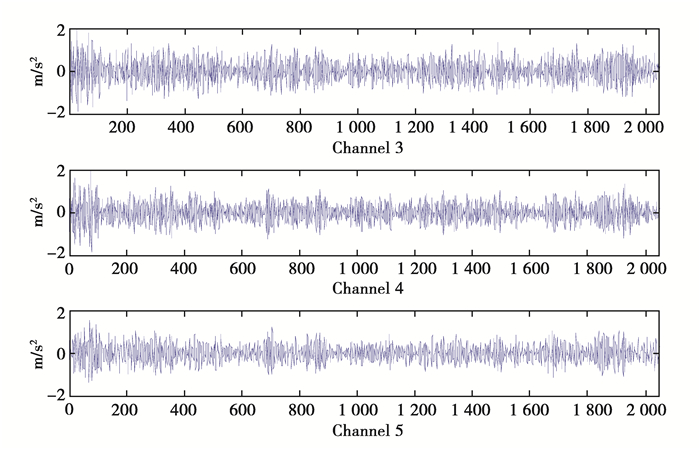
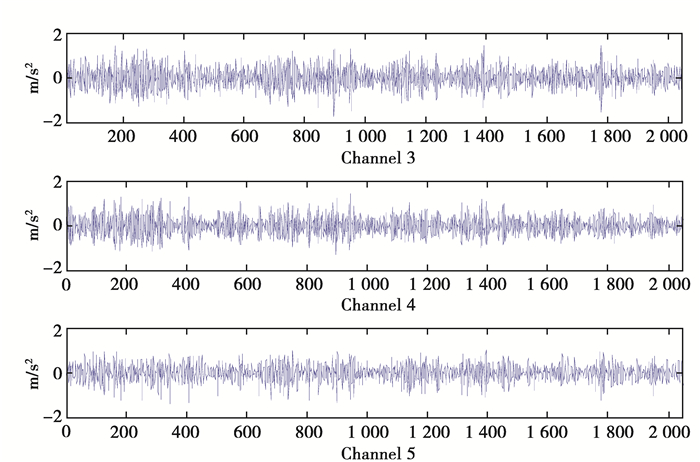
传感器参数如表 2所示,三层结构的自由度1~3层对应着传感器通道3~5。损伤工况如表 3所示。由2种工况可知,随着缓冲器和悬臂柱间隙的增大,其非线性程度将降低,当间隙足够大时,缓冲器和悬臂柱将脱离接触,从而不具有变刚度引起的时域非线性特性。因此,工况1~工况2的非线性程度是依次降低的,对于工况2的0.20 mm间隙距离,缓冲器和悬臂柱在振动时碰触较少,相应因变刚度产生的非线性效应较低,将工况2标记为弱非线性。每工况均利用50组测量数据处理测量噪声引起的不确定问题。首先,利用K-S检验验证了损伤特征因子的正态分布特性,并通过模型定阶和检验分析,得到AR模型的阶数为6,GARCH模型的阶数为0和7,并估计出相关模型参数。未损伤和损伤工况1下的一次加速度响应测量数据如图 5、图 6所示,由两图的曲线轮廓对比可发现两者差异较大。
| 表 2 传感器参数 Table 2 The parameters of sensors |
| 表 3 3层框架结构的非线性损伤工况 Table 3 The damaged state setting of the three-story frame structure |
|
图 5 无损状态下的加速度响应曲线 Fig. 5 Acceleration response time curve in undamaged State |
|
图 6 损伤工况1的加速度响应曲线 Fig. 6 Acceleration response time curve in damaged State 1 |
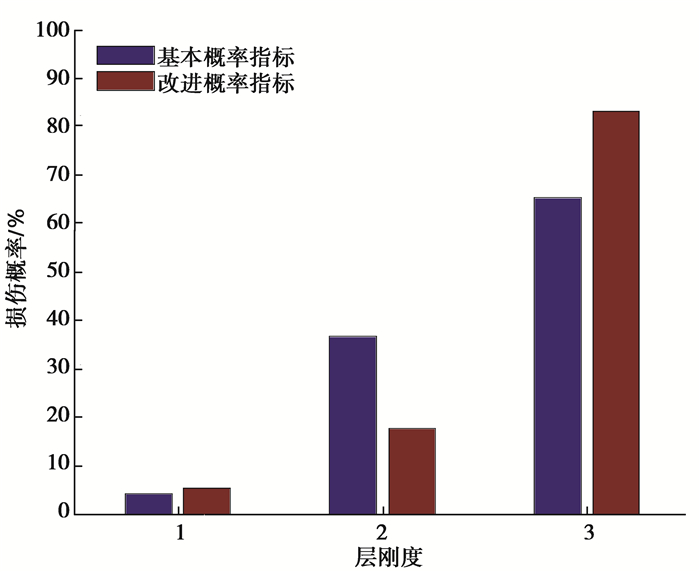
由于缓冲器和悬臂柱的间隙距离较小时,非线性程度较强,故损伤工况1具有较强的非线性程度。其损伤识别结果如图 7所示,可观察到,在较强非线性情况下,基本概率指标和改进概率指标均有较好的非线性识别能力和较高的识别概率。另外,改进概率指标的识别结果明显好于基本概率指标。对于发生损伤的层刚度第3层,改进概率指标的计算值要高于基本概率指标的计算值,而对于第1层和第2层,改进概率指标的计算值要明显低于基本概率指标的计算值。改进概率指标有效地提高了识别精度,降低了误识别概率,可以更有效和更直观地识别出损伤位置。
|
图 7 损伤工况1的识别结果 Fig. 7 Detection results for damaged State 1 |
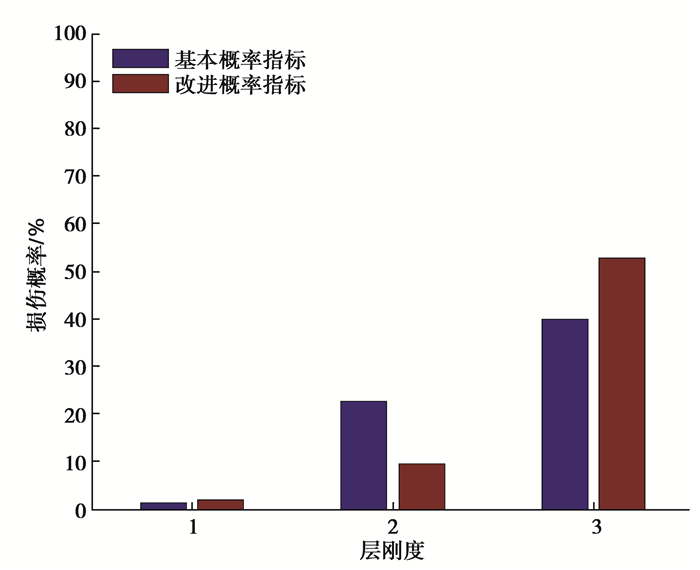
当缓冲器和悬臂柱的间隙距离增大时,非线性损伤程度将减弱,故损伤工况2的损伤程度较弱。其损伤识别结果如图 8所示,可以看到,在弱非线性情况下,基本概率指标和改进概率指标依然具有一定的非线性识别能力,但是其识别概率相对于工况1的强非线性相对较低。另外,改进概率指标的识别依然明显好于基本概率指标,例如,对于损伤的层刚度第3层,改进概率指标的计算值要高于基本概率指标的计算值,而对于无损的第1层和第2层,改进概率指标的计算值要明显低于基本概率指标。故改进概率指标具有更好的非线性损伤识别能力。
|
图 8 损伤工况2的识别结果 Fig. 8 Detection results for damaged State 2 |
由数值仿真和实验研究可知,对于测量噪声引起的不确定问题,采用基于概率理论和AR/GARCH模型相结合的方法可以较好地识别出损伤位置,并且在一定程度上可以有效地反映非线性损伤程度的强弱。而文中所建议的改进概率指标明显优于基本概率指标,其对损伤位置的识别更为精确,并在一定程度上降低了误识别概率,更适合解决具有不确定性的非线性损伤识别问题。
5 结论文中提出了基于概率理论和AR/GARCH模型相结合的损伤检测方法。首先,利用损伤前后结构的加速度时程响应分析和构建相应的AR/GARCH模型,进行模型的参数估计和定阶计算;然后,利用该混合模型提取非线性特征因子,结合概率理论建立了基本损伤概率指标,在此基础上利用加权机制进行了相应改进研究,最终建立了非线性损伤识别的改进概率指标。通过数值计算和实验研究,得出结论如下:1)基于概率理论和AR/GARCH模型的损伤识别方法可以较好地处理测量误差等引起的不确定问题,所建立的基本概率指标具有一定的非线性损伤识别能力。2)文中建立的改进概率指标对于非线性损伤具有更好的损伤识别能力,明显优于基本概率指标,并且对非线性损伤程度也具有一定的反映能力。由于实际工程结构更为复杂,往往缺乏健康状态下的时程响应记录,采用基于统计理论和时域模型的损伤识别技术仍需进一步探索和完善。
| [1] |
Zhou J, Li Z, Chen J L. Damage identification method based on continuous wavelet transform and mode shapes for composite laminates with cutouts[J]. Composite Structures, 2018, 191(1): 12-23. |
| [2] |
Abdeljaber O, Avci O, Kiranyaz S, et al. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks[J]. Journal of Sound and Vibration, 2017, 388(3): 154-170. |
| [3] |
Musafere F, Sadhu A, Liu K. Towards damage detection using blind source separation integrated with time-varying auto-regressive modeling[J]. Smart Materials and Structures, 2016, 25(1): 1-19. |
| [4] |
Sun J, Xu X S, Liu Y T, et al. FOG random drift signal denoising based on the improved AR model and modified sage-husa adaptive kalman filter[J]. Sensors, 2016, 16(7): 1073. DOI:10.3390/s16071073 |
| [5] |
Zheng H T, Mita A. Damage indicator defined as the distance between ARMA models for structural health monitoring[J]. Structural Control and Health Monitoring, 2008, 15(7): 992-1005. DOI:10.1002/stc.235 |
| [6] |
Xing Z H, Mita A. Locating the damaged storey of a building using distance measures of low-order AR models[J]. Smart Structures and Systems, 2010, 6(9): 991-1005. DOI:10.12989/sss.2010.6.9.991 |
| [7] |
Liu G, Mao Z, Luo J. Damage detection with interval analysis for uncertainties quantification[C]//International Conference on Performance-based and Life-cycle Structural Engineering, 10 January 2015, Queensland, Australia, 2015: 272-281.
|
| [8] |
Zhang Y J, Zhang Y X, Deng Z M, et al. Sea surface target detection based on complex ARMA-GARCH processes[J]. Digital Signal Processing, 2017, 70: 1-13. DOI:10.1016/j.dsp.2017.07.017 |
| [9] |
Chen L J, Yu L. Structural nonlinear damage identification algorithm based on time series ARMA/GARCH model[J]. Advances in Structural Engineering, 2013, 16(9): 1597-1609. DOI:10.1260/1369-4332.16.9.1597 |
| [10] |
Cheng J J, Guo H Y, Wang Y S. Structural nonlinear damage detection method using AR/ARCH model[J]. International Journal of Structural Stability and Dynamics, 2017, 17(8): 1-27. |
| [11] |
Xu Y L, Qian Y, Chen J J, et al. Probability-based damage detection using model updating with efficient uncertainty propagation[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 958-970. DOI:10.1016/j.ymssp.2014.11.008 |
| [12] |
Rébillat M, Hajrya R, Mechbal N. Nonlinear structural damage detection based on cascade of Hammerstein models[J]. Mechanical Systems and Signal Processing, 2014, 48(1/2): 247-259. |
| [13] |
Figueiredo E, Park G, Figueiras J, et al. Structural health monitoring algorithm comparisons using standard data sets[C]//Proceedings of the 7th International Workshop on Structural Health Monitoring, 9-11 September 2009, United States, 2009(2): 1320-1327.
|
 2019, Vol. 42
2019, Vol. 42

