b. 天津大学 滨海土木工程结构与安全教育部重点实验室, 天津 300072;
c. 天津大学 水利工程仿真与安全国家重点实验室, 天津 300072
b. Key Laboratory of Coast Civil Structure Safety, Ministry of Education, Tianjin University, Tianjin 300072, P. R. China;
c. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China
边坡稳定是岩土工程三大稳定问题之一,评估边坡稳定性的方法主要有极限平衡法、极限分析法和数值方法等。条分法相对成熟,Fredlund等[1]对6种经典条分法,如Bishop法等,做了对比和评述。部分学者将条分思想运用到三维边坡稳定分析,如Hungr[2]建立了适用于三维模型的简化Bishop法,Zhang[3]和陈祖煜[4]将Spencer法推广应用到三维。Duncan[5]对前人研究进行了总结,详细论述了极限平衡法解决三维边坡问题的方法特点和局限性。随着计算机技术发展,数值分析方法愈发普遍,比如,Griffiths等[6]研究了三维边坡稳定性问题中边界情况和几何条件的影响,Won等[7]基于有限差分法对抗滑桩加固边坡的稳定性进行了分析。
极限平衡法需要理想化假定,得到的边坡稳定结果并非上限或者下限解;数值分析法针对实际工况需要进行复杂的建模,工程应用不便。为此,许多学者采用极限分析方法,具有严格的假设,能够提供精确的上限解或下限解。对均质边坡问题,基于旋转破坏机制,Chen[8]进行了二维分析,Michalowski[9]、Gao等[10]进行三维研究,Ausilio[11]、何思明等[12]基于转动破坏机构对二维抗滑桩加固边坡进行了稳定性分析。
上述研究主要针对均质边坡。实际工程中常见具有软弱夹层的边坡,这种软弱土层的强度较低,对边坡的稳定性影响显著。Huang等[13]等通过离心机试验和上限法[14]提出一种转动-平动-转动破坏机制,对含有软弱层无加固的边坡进行了静力稳定性分析,并得出了有益结论。然而,该类边坡在地震条件下的稳定特性以及破坏形式尚缺乏深入研究。
在Huang等[14]的研究基础上,笔者提出一种平动剪切破坏机制,分析了含软弱层边坡的静、动力稳定特性,研究了抗滑桩对于边坡稳定性的影响。通过与之前学者在静力作用下的计算结果进行对比,证明了平动破坏机制的有效性。采用此机制,对静、动力作用下单排抗滑桩加固软弱边坡进行了稳定分析,并探究了各个参数对安全系数和破坏面的影响。
1 含有软弱夹层边坡上限分析 1.1 上限定理极限分析法基于塑性理论的假定,具体涵盖了上限理论和下限理论,常被运用于求解边坡稳定和地基承载力等土力学问题。极限分析上限法对岩土问题中的材料给出如下假定:1)材料的本构为理想塑性;2)材料的屈服方程形状为应力空间内外凸;3)材料遵循相关联流动法则。假定系统具备一种机动许可的机构,此时系统的内能耗散率总是大于或等于外力功率,即
| $ \int\limits_V {{\sigma _{ij}}\dot \varepsilon {\rm{d}}V} \ge \int\limits_\mathit{\Gamma } {{T_i}{v_i}{\rm{d}}\mathit{\Gamma }} + \int\limits_V {{X_i}{v_i}{\rm{d}}V} , $ | (1) |
式中:σij为遵循相关联流动法则的应力场;
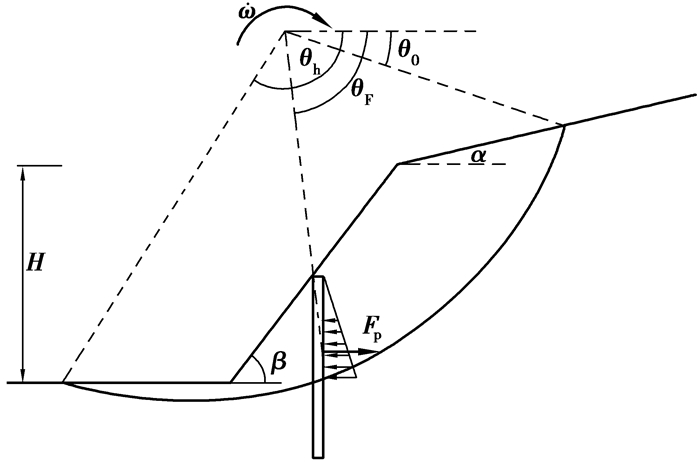
对于二维边坡的稳定问题,当土层为遵循Mohr-Coulomb准则的均质土层,或者含有埋置深度较深的软弱层、不影响边坡整体稳定时,对单排抗滑桩加固情况的研究常基于转动破坏机制,如图 1所示。此时破坏面为对数螺旋线r=r0eθ tan φ,其稳定性分析在文献[12]中有详细论述。
|
图 1 均质边坡破坏模式 Fig. 1 Homogeneous slope failure mechanism |
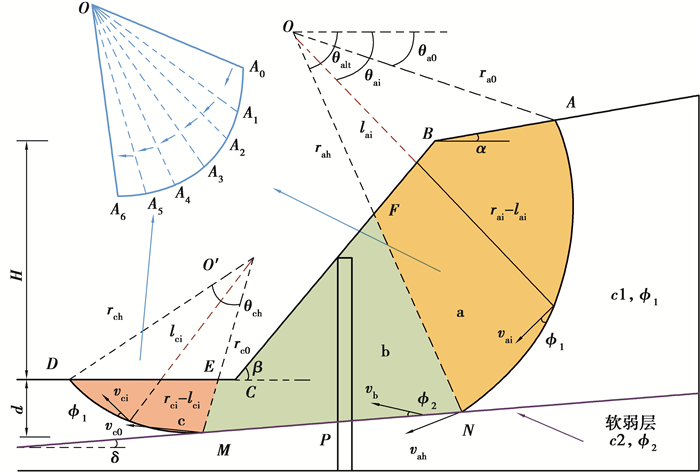
对于无加固的二维边坡,如果含有埋置深度较浅并且强度较弱的软弱层,此时边坡的破坏面会呈现沿软弱层滑动的趋势,而不再具有整体转动破坏机制[14];黄茂松等[15]基于极限分析上限解提出了一种刚性旋转-平动-旋转破坏机制进行计算分析,为满足刚性旋转与刚性平动面上的速度相容,其速度间断面为曲线,需引入相应的数值手段求解该曲线。Zhou等[16]提出一种满足速度相容条件的平动破坏机制,如图 2所示。图中OAB和O’MD为连续变形的对数螺旋线受剪破坏面,包含一系列的三角形刚性体,三角形之间产生速度间断面,满足速度相容条件;MECFN为沿软弱层平动的刚性体。研究局限于地震后边坡累积位移的影响,未对各类影响因素进行深入分析。图 2定义了相关的几何参数,其中,软弱层与水平面的夹角为δ,坡脚与软弱层的高度差为d。
|
图 2 含软弱层边坡破坏模式 Fig. 2 Slope with weak layer failure mechanism |
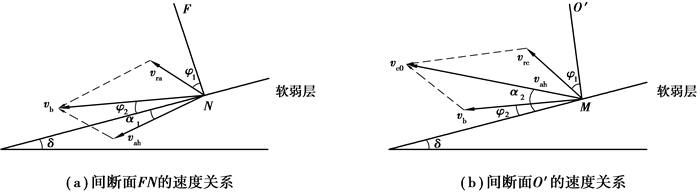
根据相关联流动法则,假定刚性体和外界土体之间的3个间断面分别为AN、NM、MD,刚性体之间的速度间断面分别为FN和O’M。其速度关系如图 3所示。
|
图 3 相容速度场 Fig. 3 Velocity hodo-graph |
图 3显示了速度矢量图线,其中,vb是刚性块b的速度;vah是对数螺旋线剪切区域a在终点N处的速度,vc0是对数螺旋线剪切区域c起始点M的速度;块体速度方向与断裂线之间的夹角ψ=φ。对数螺旋线区域是由速度图确定的,这些速度构成了一个相容速度场。
假定vb为刚性体2的速度,根据此速度推导出了相容关系,刚性体ABFN的对数螺旋线在N点处速度分量vah=vb(cos(φ1+φ2+α1)/cos φ1),可得到刚性体旋转体ABFN的旋转角速度ω1=vah/rah。刚性体c在M点速度vc0=vb(cos(φ1+φ2-α2/cos φ1)),从而可得到旋转刚性体O’MD的角速度ω2=vc0/rc0。
1.4 上限法公式推导根据极限分析理论,对于任何运动许可的破坏机构,当外力和土体自重的功率超过内能的耗散,那么边坡就会坍塌。在这一转化机制中,由于土体自重而产生的外功率是不同部分的总和。
| $ {W^\gamma } = {W_{\rm{a}}} + {W_{\rm{b}}} + {W_{\rm{c}}}。$ | (2) |
对数螺旋线剪切带a和c的自重而产生的外功率为
| $ \begin{array}{*{20}{c}} {{W_{\rm{a}}} = \int_{{\theta _{{\rm{a}}0}}}^{{\theta _{{\rm{ah}}}}} {{m_{\rm{a}}}} \cdot g \cdot {v_{\rm{a}}} \cdot \cos \theta {\rm{d}}\theta = }\\ {\int_{{\theta _{{\rm{a}}0}}}^{{\theta _{{\rm{ah}}}}} {\frac{1}{2}} \left( {r_{\rm{a}}^2 - l_{\rm{a}}^2} \right)\cos \theta \cdot {v_{{\rm{a}}0}}\exp \left( {\left( {\theta - {\theta _{{\rm{ao}}}}} \right) \cdot \tan {\varphi _1}} \right){\rm{d}}\theta ,} \end{array} $ | (3) |
| $ \begin{array}{*{20}{c}} {{W_{\rm{c}}} = \int_{{\theta _{{\rm{c}}0}}}^{{\theta _{{\rm{ch}}}}} {{m_{\rm{c}}}} \cdot g \cdot {v_{\rm{c}}} \cdot \cos \theta {\rm{d}}\theta = }\\ {\int_{{\theta _{{\rm{c}}0}}}^{{\theta _{{\rm{ch}}}}} {\frac{1}{2}} \left( {r_{\rm{c}}^2 - l_{\rm{c}}^2} \right)\cos \theta \cdot {v_{{\rm{c}}0}}\exp \left( {\left( {\theta - {\theta _{{\rm{co}}}}} \right) \cdot \tan {\varphi _1}} \right){\rm{d}}\theta 。} \end{array} $ | (4) |
对数螺旋线剪切带b的自重量而产生的外功率为
| $ {W_{\rm{b}}} = {m_{\rm{b}}}g\sin \left( {\delta - {\varphi _2}} \right){v_{\rm{b}}} = \gamma {S_{\rm{b}}}\sin \left( {\delta - {\varphi _2}} \right){v_{\rm{b}}}, $ | (5) |
式中:ra和rc分别是对数螺旋线对应角度为θa0,θc0时的半径;γ是土的重度;φ1、φ2是土的内摩擦角;la和lc如图 2所示;Sb是区域b的面积。
当含软弱夹层的边坡承受水平加速度时,能量平衡方程需要考虑惯性力的影响。分析中假定破坏机构为初始破坏机构,且不影响震动方式。通过将水平荷载施加在潜在滑块的重心上以反映震动荷载的影响,其通过地震系数k以及潜在滑块的质量确定。由惯性力产生的外功率为下列部分的总和
| $ {W^s} = W_{\rm{a}}^s + W_{\rm{b}}^s + W_{\rm{c}}^s, $ | (6) |
惯性力在对数螺旋剪切区域a、c所做的外功率可表示为
| $ W_{\rm{a}}^s = k\int_{{\theta _{\rm{a}}}0}^{{\theta _{\rm{a}}}{\rm{h}}} {{m_{\rm{a}}}} \cdot g \cdot {v_{\rm{a}}} \cdot \sin \theta {\rm{d}}\theta = k\int_{{\theta _{\rm{a}}}0}^{{\theta _{\rm{a}}}{\rm{h}}} {\frac{1}{2}} \gamma \left( {r_{\rm{a}}^2 - l_{\rm{a}}^2} \right)\sin \theta \cdot {v_{{\rm{ao}}}}\exp \left( {\theta - {\theta _{{\rm{a}}0}} \cdot \tan {\varphi _1}} \right){\rm{d}}\theta 。$ | (7) |
| $ W_{\rm{c}}^s = k\int_{{\theta _{\rm{c}}}0}^{{\theta _{\rm{c}}}{\rm{h}}} {{m_{\rm{c}}}} \cdot g \cdot {v_{\rm{c}}} \cdot \sin \theta {\rm{d}}\theta = k\int_{{\theta _{\rm{c}}}0}^{{\theta _{\rm{c}}}{\rm{h}}} {\frac{1}{2}} \gamma \left( {r_{\rm{c}}^2 - l_{\rm{c}}^2} \right)\sin \theta \cdot {v_{{\rm{co}}}}\exp \left( {\theta - {\theta _{{\rm{a}}0}} \cdot \tan {\varphi _1}} \right){\rm{d}}\theta 。$ | (8) |
块体b惯性力外功率为
| $ W_{\rm{b}}^s = k{m_{\rm{b}}}g\cos \left( {\delta - {\varphi _2}} \right){v_{\rm{b}}} = k\gamma {S_{\rm{b}}}\cos \left( {\delta - {\varphi _2}} \right){v_{\rm{b}}}。$ | (9) |
抗滑桩加固含软弱夹层边坡的总能量耗散为Dc和Dp之和。
| $ D = {D^p} + {D^c}, $ | (10) |
式中:Dp为桩体引起的能量耗散;Dc为土体粘聚力引起的能量耗散。为计算桩体的作用,假定一个水平力施加于潜在破坏面上,由此得到的能量耗散为
| $ {D^p} = {F_{\rm{p}}}{v_{\rm{i}}}\cos \left( {\delta - {\varphi _2}} \right), $ | (11) |
式中:Fp为桩体为单位宽度土体提供的水平抗力;vi为滑动土体的速度。
采用了Ito和Matsui[17]提出的计算桩体水平抗力Fp,单位宽度土体施加于桩体上的水平力Fp的计算公式为
| $ \begin{array}{*{20}{c}} {{F_{\rm{p}}} = AcH\left( {\frac{1}{{{N_\varphi }\tan \varphi }}\left\{ {\exp \left[ {\frac{{{D_1} - {D_2}}}{{{D_2}}}{N_\varphi }\tan \varphi \tan \left( {\frac{{\rm{ \mathsf{ π} }}}{8} + \frac{\varphi }{4}} \right)} \right] - 2N_\varphi ^{1/2}\tan \varphi - 1} \right\} + \frac{{2\tan \varphi + 2N_\varphi ^{1/2} + N_\varphi ^{ - 1/2}}}{{N_\varphi ^{1/2}{\rm{tan}}\varphi + {N_\varphi } - 1}}} \right) - }\\ {cH\left( {{D_1}\frac{{2\tan \varphi + 2N_\varphi ^{1/2} + N_\varphi ^{ - 1/2}}}{{N_\varphi ^{1/2}\tan \varphi + {N_\varphi } - 1}} - 2{D_2}N_\varphi ^{ - 1/2}} \right) + }\\ {\frac{{\gamma {H^2}}}{{2{N_\varphi }}}\left\{ {A\exp \left[ {\frac{{{D_1} - {D_2}}}{{{D_2}}}{N_\varphi }\tan \varphi \tan \left( {\frac{{\rm{ \mathsf{ π} }}}{8} + \frac{{\rm{ \mathsf{ π} }}}{4}} \right)} \right] - {D_2}} \right\},} \end{array} $ | (12) |
式中:D1为相邻桩体间的桩间距;D2为相邻桩体间的净距;H为滑动土体由顶面至破坏面的高度;Nφ =tan2(π/4+φ/2);A=D1(D1/D2)(Nφ1/2tan φ+ Nφ-1)。由公式可知,水平力随D2/D1的减小而增大。Li等[12]研究表明,当D2/D1小于0.5~0.6时,桩体的行为类似于连续墙,桩间土不可能进入塑性状态。因此,仅考虑了D2/D1大于0.5的情况。
对于破坏机制,内能耗散中的土体粘聚力部分可通过下式计算:
| $ {D^c} = {D_a} + {D_{{\rm{FN}}}} + {D_{\rm{b}}} + {D_{{\rm{EM}}}} + {D_{\rm{c}}}, $ | (13) |
其中:
| $ {D_{\rm{b}}} = {l_{{\rm{MN}}}}{c_2}{v_{\rm{b}}}\cos {\varphi _2}, $ | (14) |
| $ {D_{{\rm{FN}}}} = {c_1}{l_{{\rm{FN}}}}\sin 2{\varphi _2}{v_{\rm{b}}}, $ | (15) |
| $ {D_{{\rm{EM}}}} = {c_1}{l_{{\rm{EM}}}}\sin \left( {{\varphi _1} - {\varphi _2}} \right){v_{\rm{b}}}。$ | (16) |
剪切区a、c的能量耗散为不连续面之间的能量耗散以及对数螺旋线破坏面上的能量耗散的总和。如图 2所示,剪切区a、c包含n个刚性块体,由于所有刚性三角形沿着与不连续面呈φ1角度的方向运动,沿着射线OA0, OA1, OA2等发生能量耗散;同时,沿着滑动面A0 A1 A2 A3 A4 A5 A6也存在能量耗散。不连续面间的能量耗散为粘聚力乘以相对速度以及土体中不连续面的长度:
| $ {D_a} = {c_1}\int_{{\theta _{{\rm{a}}0}}}^{{\theta _{{\rm{ah}}}}} {\left( {2{r_{{\rm{a}}0}} - {l_{\rm{a}}}} \right)} \cdot {v_{{\rm{a}}0}}\exp \left( {2\left( {\theta - {\theta _{{\rm{a}}0}}} \right) \cdot \tan {\varphi _1}} \right){\rm{d}}\theta , $ | (17) |
| $ {D_c} = {c_1}\int_{{\theta _{{\rm{c0}}}}}^{{\theta _{{\rm{ch}}}}} {\left( {2{r_{{\rm{c}}0}} - {l_{\rm{c}}}} \right)} \cdot {v_{{\rm{c0}}}}\exp \left( {2\left( {\theta - {\theta _{{\rm{c}}0}}} \right) \cdot \tan {\varphi _1}} \right){\rm{d}}\theta . $ | (18) |
通过计算内能耗散与外功率相等的情况,确定使边坡处于临界状态的临界水平地震加速度kc,此时有
| $ {W^\gamma } + {W^s} = {D^p} + {D^C}。$ | (19) |
为了求解边坡安全系数,将公式(19)改变为公式(20)的形式:
| $ \mathit{\Gamma } = \frac{{{D^p} + {D^c}}}{{{W^\gamma } + {W^s}}}。$ | (20) |
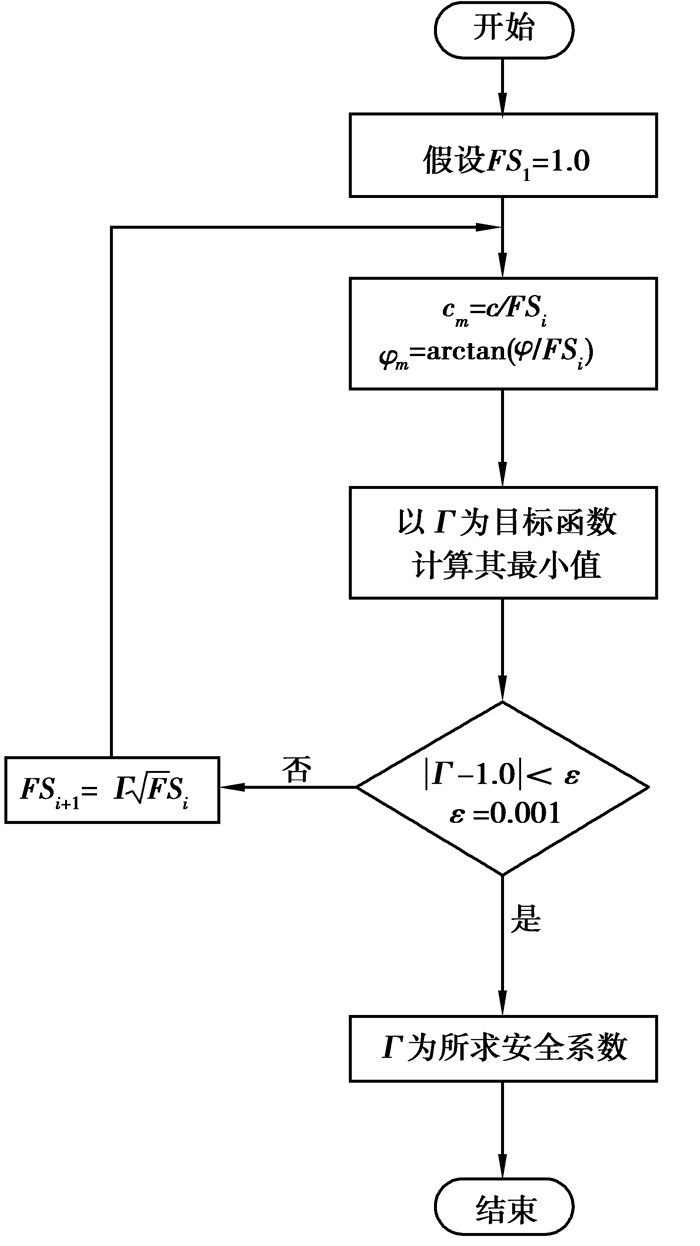
边坡的安全系数通常采用折减土的强度参数的方式[18],定义为FS=c/cm=tan φ/tan φm。对式(20)中的土体参数由安全系数进行强度折减,以Γ为目标函数,通过FSi+1=
|
图 4 安全系数计算 Fig. 4 Determination of the factor of safety |
为了对文中破坏模式的正确性进行验证,首先选取已有文献中的含软弱层无加固边坡的经典算例对安全系数进行比较分析,然后求解地震荷载作用下抗滑桩加固边坡的安全系数和破坏面。
2.1 对比验证1) 工况1
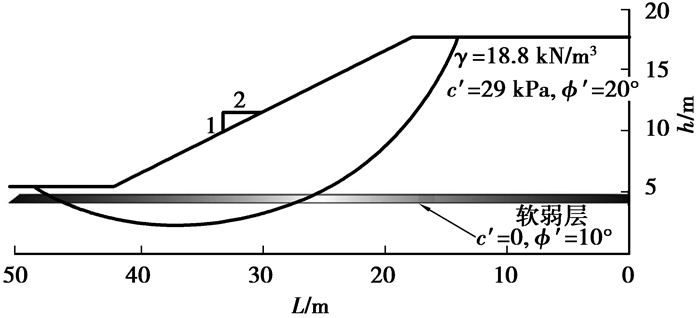
Fredlund[1]通过经典的6种二维边坡分析方法(如,简单Bishop法,Janbu法等),Zhang[3]、Lam等[19]通过三维极限平衡法,以及Griffiths等[6]通过强度折减有限元法对工况1的边坡进行了稳定性分析,如图 5所示。
|
图 5 工况1 Fig. 5 Case1 |
计算结果如表 1所示。对于二维边坡的稳定性问题,忽略了滑体两侧的抗滑力,因此安全系数要小于三维情况的结果。此外,文中的计算结果较Janbu法[1]计算结果保守,与简化Bishop法[1]的解答较为接近。
| 表 1 各种方法计算结果 Table 1 The results calculated by different methods |
2) 工况2
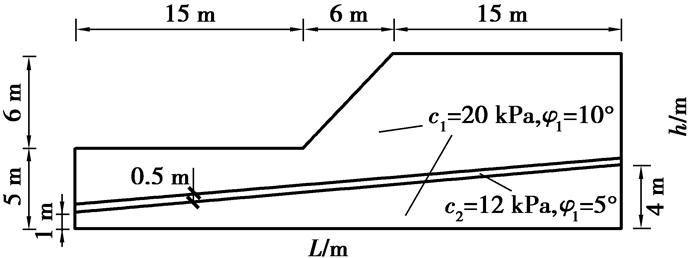
Huang等[14]分别采用上限法和强度折减有限元法对无加固边坡的安全系数进行研究,如图 6所示。
|
图 6 工况2 Fig. 6 Case2 |
计算结果如表 2所示。文中的结果与Huang等的上限解及有限单元法的差异约为2.8%。可见,所采用的破坏机制与前人在计算边坡的静力稳定时具有较好的一致性,适合进一步的抗震分析。
| 表 2 各种方法计算结果 Table 2 The results calculated by different methods |
根据平动机制,分别以2种典型工况的边坡稳定安全系数与文献进行了对比,结果表明,平动机制的计算结果与文献的数值解以及极限平衡解较为接近,证明了文中所采用破坏模式的有效性。
2.2 静动力加固边坡安全系数和破坏面以工况1为例,分别对无加固二维边坡和有加固二维边坡进行静、动力荷载作用时的稳定性分析。根据对边坡安全系数和破裂面的影响,主要考虑的因素包括:地震加速度k,桩体距离坡脚位置Px以及桩间距系数λ。
|
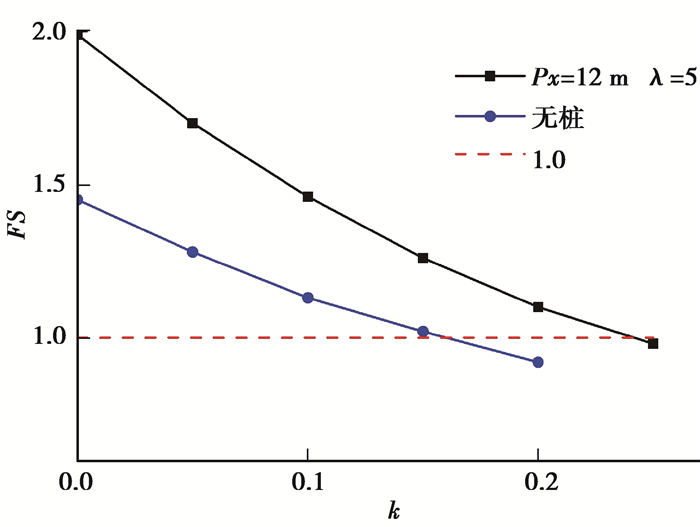
图 7 地震加速度与安全系数的关系(k为地震水平加速度与重力加速度之比;FS为安全系数) Fig. 7 Relationship between eismic accelerationt and safe coefficient |
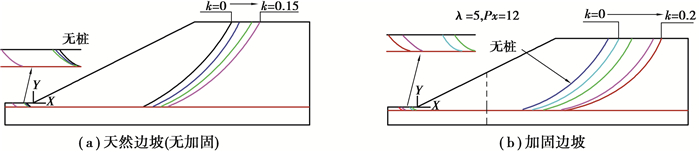
抗滑桩加固边的最有效位置坡位于边坡中部靠上[19],因此,采用的几何条件为桩体位置Px=12 m、桩间距系数λ=5。分别研究加固边坡和无加固边坡安全系数与地震加速度的关系,如图 7所示。容易看出,边坡安全系数随着地震加速度的增大急剧减小。对于无加固边坡,安全系数在k=0.2g时,降低为0.96,这意味着边坡已经失稳。而对于有加固的边坡,安全系数直到k=0.25g时,才降低为0.98,加固作用可显著提高边坡动力稳定性。并且可以看出,安全系数的增幅在地震加速度较小时更为显著。图 8为地震加速度对破裂面的影响,桩体位置如虚线所示。结果表明,桩体右侧的破裂面会随着地震加速度的增加急剧增大。而对于坡脚处的破裂面,随着地震加速度的增加,一开始变化不大;当地震加速度增大到一定程度时,破裂面会急剧增大,此时,坡体破裂面在软弱层有较大的滑移,坡体发生整体失稳。
|
图 8 地震加速度与破裂面的关系 Fig. 8 Relationship between eismic acceleration and sliding surface |
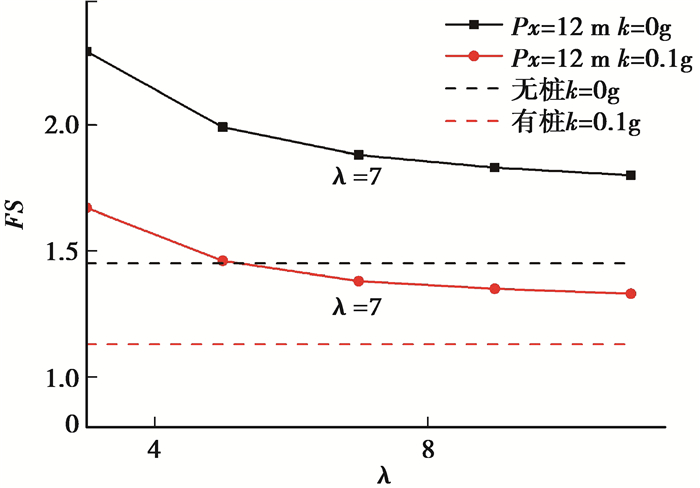
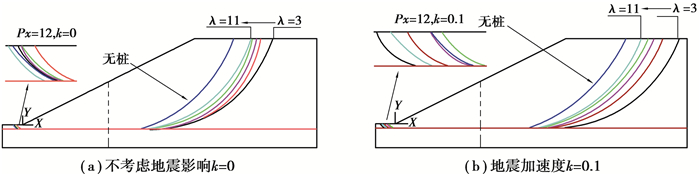
类似的,采用桩体位置Px=12 m、地震加速度k=0.1g,分别对有地震和无地震条件下的边坡进行稳定性分析,进而研究安全系数与桩间距系数关系,如图 9所示。结果表明,边坡安全系数随着桩间距系数的增大而持续减小,但这个减小的趋势在桩间距系数达到7时逐渐变得平缓。这意味着对于一定的工况,改变桩间距系数的做法对安全系数的影响不大。图 10描绘出桩间距系数与破裂面的关系,结果表明,桩体上方的破裂面会随着桩间距系数的增大而减小;坡脚位置处的破裂面对桩间距系数不敏感。
|
图 9 桩间距系数与安全系数的关系(FS为安全系数;λ为桩间距与桩径之比) Fig. 9 Relationship between pile spacing and safe coefficient |
|
图 10 桩间距系数与破裂面的关系 Fig. 10 Relationship between pile spacing and sliding surface |
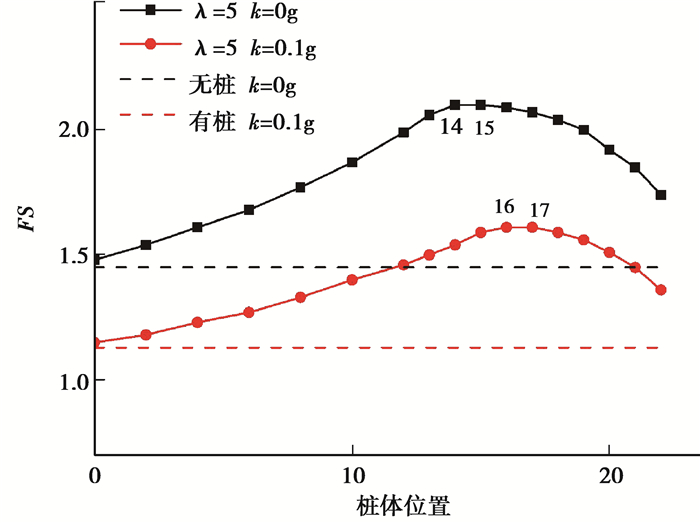
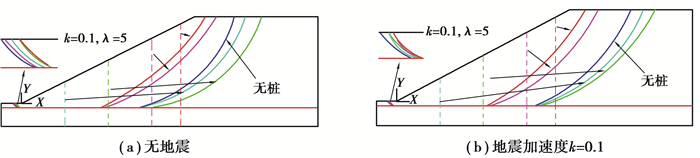
采用桩间距系数λ=5,分别对静力条件下和地震加速度k=0.1g时,不同桩体位置加强边坡的效果进行分析,研究安全系数和桩体位置的关系,如图 11所示。结果表明,边坡安全系数随着桩体位置的向右移动呈现先增大后减小的趋势。对于静力条件,安全系数在桩体位于14~15 m(坡长24 m)时达到峰值2.1;对于地震加速度k=0.1g时,安全系数在桩体位于16~17 m时达到峰值1.61。定义桩体加固最有效位置为安全系数达到峰值时所对应的桩体位置。根据Ausilio[11]基于转动破坏机构对二维抗滑桩加固边坡的稳定性分析结果,对于均质边坡,抗滑桩体的最有效位置应在靠近坡体中部。而对于含有软弱层的边坡,抗滑桩体的最有效位置则变得更为复杂,与软弱层的强度指标、埋深和倾角等因素均有关。图 11表明,对于含有软弱层的边坡桩体最有效位置位于坡体中间靠上。对于动力情况,桩体最有效位置随着地震加速度的增大而逐渐向坡顶方向移动。图 12表明,当桩体从坡脚向坡体中间移动时,边坡破裂面不断扩大;当桩体位置超过坡体中间向上时,边坡破裂面急剧缩小。桩体有效长度Hp与桩体位置明显相关,当边坡含有软弱层,可以得出,桩体有效长度最大值并不在坡体中部位置时取得,而在坡体中部偏上的位置取得。由于桩体对坡体加固的抗力与其有效长度Hp直接相关,因此,在坡体中间偏上的位置时含软弱层边坡加固桩体的最有效位置。
|
图 11 桩体位置与安全系数的关系(FS为安全系数;桩体位置为以坡脚为原点的水平坐标) Fig. 11 Relationship between pile location and safe coefficient |
|
图 12 桩体位置与破裂面的关系 Fig. 12 Relationship between pile location and sliding surface |
文中基于极限分析上限法,提出一种平动破坏机制,对静、动力作用下抗滑桩加固的含有软弱层边坡进行研究,分析了抗滑桩对坡体稳定的贡献,探讨了地震加速度、桩间距以及桩体位置对安全系数和破裂面的影响,得出以下主要结论:
1) 对于含软弱层的天然边坡,通过与文献计算结果的对比,证明了文中提出的平动剪切破坏机制适用于含软弱夹层的稳定性分析。
2) 抗滑桩可以提高边坡的安全系数,这是由于抗滑桩对土体的阻拦作用。随着桩间距系数λ的增加,安全系数不断减小,但是在桩间距系数达到7之后变得平稳,说明在安全系数满足要求时,适当选取较大的桩体间距对边坡稳定影响很小。
3) 在地震荷载的影响下,边坡坡顶破裂面由坡中心向外延伸。边坡安全系数随着地震加速度的增加而不断下降,破裂面呈现沿软弱层延展的趋势,坡体从而丧失稳定性。
4) 对于含有软弱层的边坡,抗滑桩的最有效位置为边坡坡体中间靠上。当存在地震作用时,抗滑桩的位置应适当上移。边坡安全系数随着地震加速度和桩间距的增加而减小,破裂面呈现沿软弱层延展的趋势。
| [1] |
Fredlund D G, Krahn J. Comparison of slope stability methods of analysis[J]. Canadian Geotechnical Journal, 1977, 14(3): 429-439. DOI:10.1139/t77-045 |
| [2] |
Hungr O. An extension of Bishop's simplified method of slope stability analysis to three dimensions[J]. Géotechnique, 1987, 37(1): 113-117. DOI:10.1680/geot.1987.37.1.113 |
| [3] |
Xing Z. Three-dimensional stability analysis of concave slopes in plan view[J]. Journal of Geotechnical Engineering, 1988, 114(6): 658-671. DOI:10.1061/(ASCE)0733-9410(1988)114:6(658) |
| [4] |
陈祖煜, 弥宏亮, 王小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525-529. CHEN Zuyu, MI Hongliang, WANG Xiaogang. A three-dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525-529. (in Chinese) |
| [5] |
Duncan J M. State of the art: limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering, 1996, 122(7): 577-596. DOI:10.1061/(ASCE)0733-9410(1996)122:7(577) |
| [6] |
Griffiths D V, Marquez R M. Three-dimensional slope stability analysis by elasto-plastic finite elements[J]. Géotechnique, 2007, 57(6): 537-546. DOI:10.1680/geot.2007.57.6.537 |
| [7] |
Won J, You K, Jeong S, et al. Coupled effects in stability analysis of pile-slope systems[J]. Computers and Geotechnics, 2005, 32(4): 304-315. DOI:10.1016/j.compgeo.2005.02.006 |
| [8] |
Mccook D K. Limit Analysis and Soil Plasticity[M]. Elsevier Scientific Pub, 1975.
|
| [9] |
Michalowski R L, Drescher A. Three-dimensional stability of slopes and excavations[J]. Géotechnique, 2009, 59(10): 839-850. DOI:10.1680/geot.8.P.136 |
| [10] |
Gao Y F, Zhang F, Lei G H, et al. An extended limit analysis of three-dimensional slope stability[J]. Géotechnique, 2013, 63(6): 518-524. DOI:10.1680/geot.12.T.004 |
| [11] |
Ausilio E, Conte E, Dente G. Stability analysis of slopes reinforced with piles[J]. Computers and Geotechnics, 2001, 28(8): 591-611. DOI:10.1016/S0266-352X(01)00013-1 |
| [12] |
Li X P, He S M, Wu Y. Seismic displacement of slopes reinforced with piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(6): 880-884. DOI:10.1061/(ASCE)GT.1943-5606.0000296 |
| [13] |
刘怡林, 黄茂松, 袁伟, 等. 斜坡含软夹层地基路堤离心模型试验与数值模拟[J]. 岩土力学, 2013, 34(S2): 22-26, 34. LIU Yilin, HUANG Maosong, YUAN Wei, et al. Centrifugal model test and numerical simulation of embankments on sloping ground with weak interlayer[J]. Rock and Soil Mechanics, 2013, 34(S2): 22-26, 34. (in Chinese) |
| [14] |
Huang M S, Wang H R, Sheng D C, et al. Rotational-translational mechanism for the upper bound stability analysis of slopes with weak interlayer[J]. Computers and Geotechnics, 2013, 53: 133-141. DOI:10.1016/j.compgeo.2013.05.007 |
| [15] |
王浩然, 黄茂松, 刘怡林. 含软弱夹层边坡的三维稳定性极限分析[J]. 岩土力学, 2013, 34(S2): 156-160. WANG Haoran, HUANG Maosong, LIU Yilin. Three-dimensional stability analysis of slope with weak interlayer[J]. Rock and Soil Mechanics, 2013, 34(S2): 156-160. (in Chinese) |
| [16] |
Zhou H Z, Zheng G, Yang X Y, et al. Displacement of pile-reinforced slopes with a weak layer subjected to seismic loads[J]. Mathematical Problems in Engineering, 2016, 1-10. |
| [17] |
Ito T, Matsui T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43-59. DOI:10.3208/sandf1972.15.4_43 |
| [18] |
Taylor D W. Fundamentals of soil mechanics[J]. Soil Science, 1948, 66(2): 161. |
| [19] |
Wei W B, Cheng Y M. Strength reduction analysis for slope reinforced with one row of piles[J]. Computers and Geotechnics, 2009, 36(7): 1176-1185. DOI:10.1016/j.compgeo.2009.05.004 |
| [20] |
Lam L, Fredlund D G. A general limit equilibrium model for three-dimensional slope stability analysis[J]. Canadian Geotechnical Journal, 1993, 30(6): 905-919. DOI:10.1139/t93-089 |
 2019, Vol. 42
2019, Vol. 42

