b. 湖南大学 工程结构损伤诊断湖南省重点实验室,长沙 410012
b. Hunan Provincial Key Lab on Diagnosis for Engineering Structures,Hunan University,Changsha 410012,P. R. China
收缩徐变是混凝土固有的特性,它会使混凝土的变形随着时间的增长而不断变化,进而改变结构的内力分布。早期国内外学者主要针对素混凝土试件进行了大量收缩徐变试验[1-3],而忽略了钢筋对混凝土收缩徐变的影响,实际情况下钢筋与混凝土之间存在着相互作用,混凝土的收缩徐变会受到钢筋的影响。因此国内外学者和专家开始对钢筋混凝土构件进行收缩徐变分析,以此研究钢筋和混凝土之间相互作用的机理。Morano等[4]提出了一种新的计算方法来计算钢筋混凝土梁的收缩徐变,并研究分析了Ⅰ字型梁的性能。Dilger[5]提出了“徐变换算截面法”,简化了考虑钢筋影响的配筋构件徐变计算方法。Dezi等[6]等采用逐步积分法计算钢筋混凝土梁的徐变。国内也对钢筋混凝土构件收缩徐变进行了大量的研究,曹国辉等[7]对素混凝土及钢筋混凝土柱进行了收缩徐变试验,并采用国内外多种收缩徐变预测模型对实测数据进行拟合回归分析,对比分析了不同预测模型之间的差异。潘钻峰等[8]开展了不同配筋率下混凝土试件收缩徐变研究,得出了配筋率对收缩徐变的影响规律。张克波等[9]在混凝土柱受压徐变试验的基础上,提出了较精确的混凝土徐变系数预测模型,并对比了素混凝土试件的徐变应变,提出规范中存在着对钢筋混凝土构件徐变估计不足的问题。张望喜等[10]分析了收缩徐变对配筋柱和单层单跨结构的内力重分布的影响。
以上研究中虽然分析了钢筋对混凝土收缩徐变的影响,但针对多种影响因素下考虑钢筋影响的混凝土收缩徐变分析以及钢筋影响下混凝土收缩徐变简化计算方法,用于分析高层以及超高层结构中收缩徐变效应还有待研究。
为此,笔者采用ABAQUS软件二次开发收缩徐变计算子程序,计算不同影响因素下素混凝土和钢筋混凝土柱、框架梁构件的竖向变形,并定义考虑钢筋影响的变形折减系数,分析不同因素与折减系数之间存在的规律性关系,同时拟合不同因素与折减系数的曲线,提出了考虑钢筋影响的混凝土柱收缩徐变计算方法。
1 徐变系数的拟合当混凝土龄期不同时,收缩徐变效应存在着差异,为了能够准确考虑这种差异,采用有限元法时常用级数方程来表示徐变系数。由于混凝土徐变变化规律能通过指数函数ekix很好地表示出来,因此将1-ekix作为基函数来拟合徐变系数。当ki<0时,不同的ki所对应的基函数在区间[0,+∞]上线性无关,得到最常用来表示徐变系数的Dirichlet级数形式为
| $ \varphi \left( {t,\tau } \right) = \sum\limits_{j - 1}^m {{\phi _j}} (\tau )[1 - {e^{ - {\lambda _j}(t - \tau )}}], $ | (1) |
式中:φ(t,τ)为τ时刻加载、t时刻的徐变系数;φj(τ)为取决于试验的函数,λj为拟合的参数。
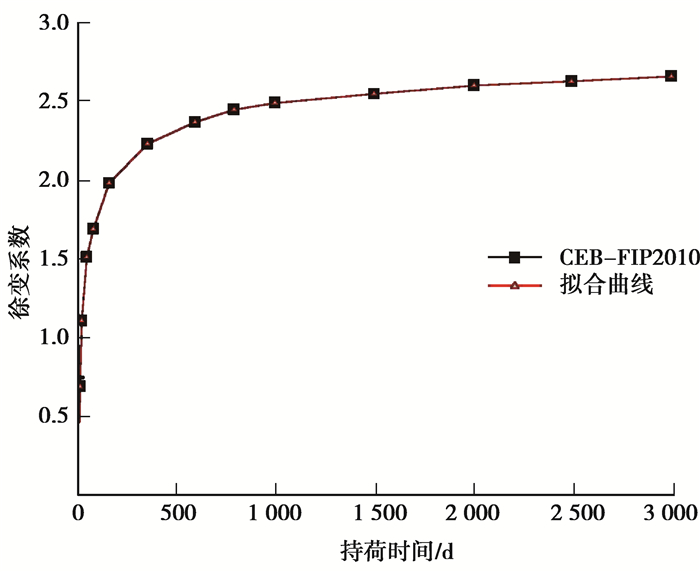
采用Matlab中自带的非线性拟合函数LSQCUR-VEFIT来拟合徐变系数,在用公式(1)拟合徐变系数时,取m=4,此时徐变系数函数中有4个参数,并赋予初值λ1=1,λ2=0.1,λ3=0.001,λ4=0.001。通过不断改变λj的值,使
|
图 1 徐变系数的拟合曲线 Fig. 1 Fitting curve of creep coefficient |
USDFLD子程序主要用来定义随场变量变化的复杂材料特性,通过USDFLD子程序来定义随龄期变化的混凝土弹性模量。通过调用子程序GETVRM,可以使子程序USDFLD进入数据库提取相应的轴向应力与应变来准备计算后续膨胀应变,同时还定义了状态变量,供其他子程序来使用。
2.2 UEXPAN子程序UEXPAN子程序可以计算状态变量引起的膨胀应变,将计算出的膨胀应变来模拟徐变收缩对轴向应变的影响。
文中材料的收缩徐变计算是通过结合子程序USDFLD和UEXPAN来进行的,为保证计算结果的准确性,采取计算时间间隔为7 d。UEXPAN子程序是根据按龄期调整的有效模量法(AEMM法)[12]的计算模型进行编制,同时为了避免对于应力历史的考虑而采用递推的方法计算膨胀应变。
子程序中对材料收缩徐变的计算是基于CEB-FIP(2010)模型,计算原理参考文献[11],将计算收缩徐变的方法写入UEXPAN子程序中。其中收缩应变εsh(t,ts)的计算公式为
| $ {{\rm{ \mathsf{ ε} }}_{{\rm{sh}}}}(t,{t_{\rm{s}}}) = {{\rm{ \mathsf{ ε} }}_{{\rm{sh0}}}}{\beta _{\rm{s}}}(t - {t_{\rm{s}}}), $ | (2) |
| $ {{\rm{ \mathsf{ ε} }}_{{\rm{sh0}}}} = {\beta _{{\rm{RH}}}}\left[ {160 + {\beta _{{\rm{sc}}}}(90 - {f_{\rm{c}}}) \times {{10}^{ - 6}}} \right], $ | (3) |
式中:εsh(t,ts)为从ts时刻开始发生收缩至t时刻时混凝土收缩应变;εsh0为名义收缩系数,即极限收缩变形;βsc为取决于水泥种类的系数;βs、βRH分别为随环境湿度及时间变化的系数;fc为圆柱体抗压强度。
基于刘忠[13]提出的混凝土收缩徐变递推AEMM法,在Boltzman原理和线性徐变的假定情况下由收缩徐变产生的总应变为
| $ {\rm{ \mathsf{ ε} }}\left( t \right) = \sigma ({\tau _0})J(t,{\tau _0}) + \smallint _{_{{\tau _0}}}^{^t}J\left( {t,\tau } \right)d\sigma (\tau ) + {{\rm{ \mathsf{ ε} }}_{{\rm{sh}}}}\left( t \right), $ | (4) |
| $ J(t,{\tau _0}) = \frac{1}{{E({\tau _0})}}[1 + \varphi (t,{\tau _0})]。$ | (5) |
式(4)为徐变定律的积分形式,其中σ(τ0)、σ(τ)为加载应力;J(t,t0)为在混凝土加载龄期为τ0时,单位常应力加载t时间后产生的弹性和徐变应变之和;ε(t)为t时刻的总应变;φ(t,τ0)为徐变系数;E(t0)为弹性模量;εsh(t)是收缩应变。
tn-1~tn时间段的变形为
| $ \Delta {{\rm{ \mathsf{ ε} }}_n} = {{\rm{ \mathsf{ ε} }}_{{\rm{sh}}}}({t_n}) - {{\rm{ \mathsf{ ε} }}_{{\rm{sh}}}}({t_{n - 1}}) + \sum\limits_{j - 1}^m {{\Phi _{j,n}}} (1 - {e^{ - {\lambda _j}\Delta {t_n}}}), $ | (6) |
式中
| $ {\Phi _{j,n}} = {\Phi _{j,n - 1}}{e^{ - {\lambda _j}\Delta {t_{n - 1}}}} + {\sigma _{n - 1}}{\phi _j}({t_{n - 1}}) + \sigma _{_{n - 1}}^{^*}\chi ({t_n},{t_{n - 1}}){\phi _j}({t_{n - 1}}), $ | (7) |
| $ {\sigma ^*}({t_n}) = {E_\varphi }({t_n},{t_{n - 1}})({{\rm{ \mathsf{ ε} }}_n} - \Delta {{\rm{ \mathsf{ ε} }}_n})。$ | (8) |
χ(tn,tn-1)为tn-1加载到tn时的与时间有关的效应系数,参考文献[13]取值为0.82;Eφ(tn,tn-1)为按龄期调整的有效弹性模量;σn-1*、σ*(tn)为徐变应力增量,Δεn为tn-1~tn时间段的变形,εn为总变形,Δtn、Δtn-1为时间间隔。
2.3 UEXTERNALDB子程序UEXTERNALDB子程序起到提取外部数据的作用,文中将徐变系数拟合值存入数组,供UEXPAN子程序调用。
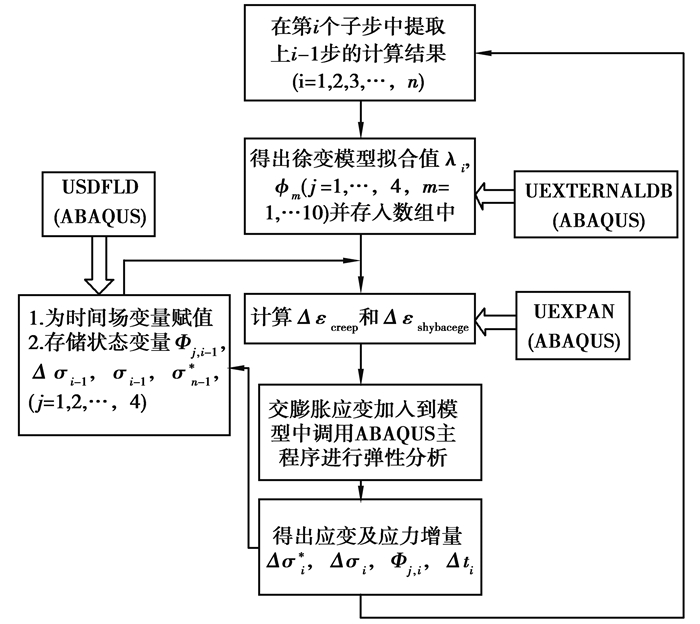
2.4 子程序的调用在混凝土本构定义中加入用户自定义场变量(user defined field)、状态变量(depvar)、自定义膨胀(expansion)选项。同时在文件creep.in中,将拟合好的徐变系数写入文件中来供子程序调用。文中通过USDFLD定义场变量和状态变量来计算随时间变化的弹性模量。在ABAQUS中提交分析任务进行计算时,应将子程序的路径从General选项中添加进去,来供ABAQUS调用,流程图如图 2所示。
|
图 2 计算程序流程图 Fig. 2 The flow chart of calculation process |
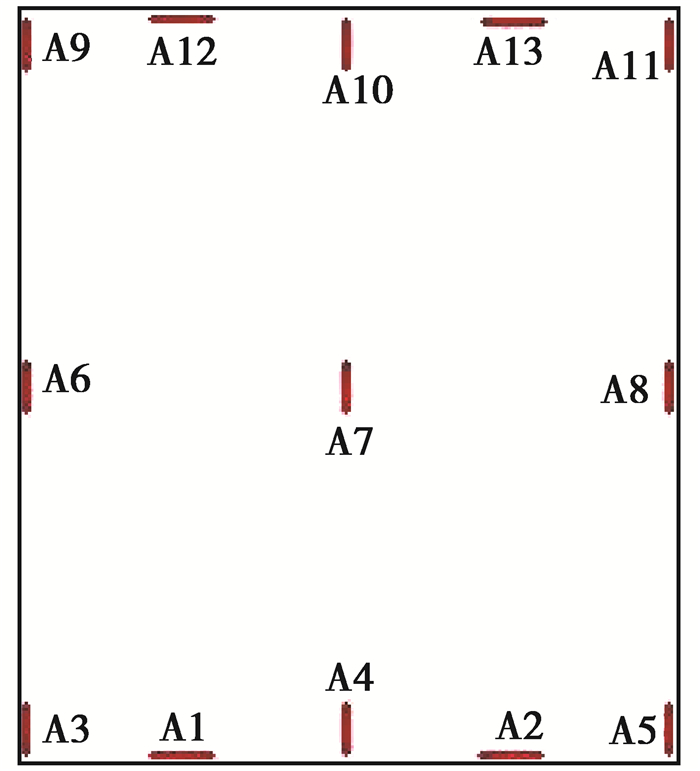
选取文献[14]中的试验剪力墙开展有限元分析,试验剪力墙缩尺模型比例为1:2,缩尺后剪力墙长为1.5 m,高为1.8 m,墙厚为120 mm。剪力墙配筋为:分布筋为双排双向布置,采用直径8 mm、间距为125 mm的HPB235型钢筋,拉结筋采用直径为6 mm、间距为200 mm的HPB235型钢筋,根据规范确定剪力墙的边缘构件长度为300 mm,配筋采用6根直径为10 mm的HPB235钢筋。在剪力墙顶部放置型钢,然后用千斤顶对型钢施加荷载,使剪力墙受力形式为轴心受压。试验时对剪力墙施加荷载800 kN,控制轴压比在0.3左右,持荷时间为1 a,通过千斤顶下压力传感器来监测施加的轴压力,确保在持荷过程中轴力变化范围不超过2.5%。通过在剪力墙多点布置应变计来分析加载过程中剪力墙的变形特性,试验加载装置图如图 3所示,混凝土应变计的布置示意图如图 4所示。

|
图 3 试验加载装置图 Fig. 3 Test loading device diagram |
|
图 4 混凝土应变计布置示意图 Fig. 4 Arrangement diagram of strain gauge for shear wall |
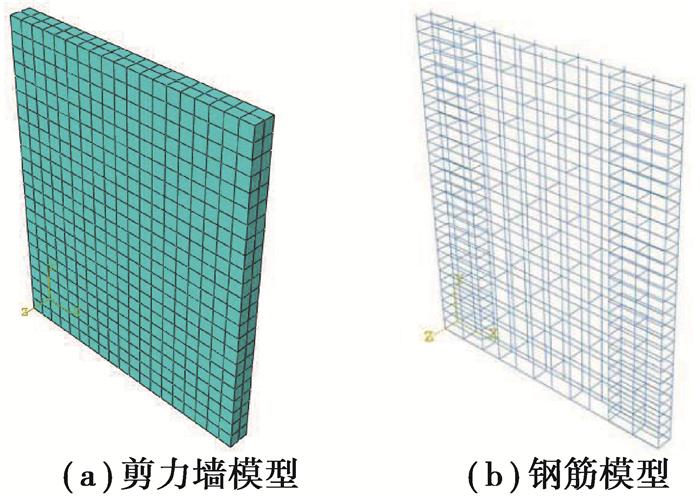
采用三维实体单元C3D8R模拟混凝土,三维桁架线性单元T3D2来模拟钢筋,通过有限元软件ABAQUS建立如图 5所示的有限元模型,提取模型中对应A10应变计位置的混凝土应变与试验结果进行对比分析,如图 6所示。
|
图 5 钢筋混凝土剪力墙模型 Fig. 5 Model of reinforced concrete shear wall |
|
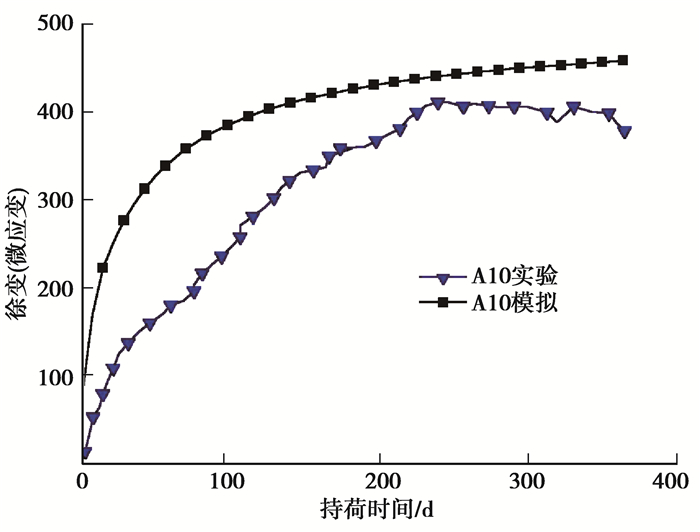
图 6 徐变应变随时间变化曲线 Fig. 6 Creep strain curves with time variation |
由图 6曲线可以看出,试验测得最大应变值为411 με,对应同一持荷时间模拟计算得到的应变为440 με,两者相差在10%以内,误差在工程容许范围内,有限元计算结果偏大,偏于保守。试验加载前期曲线相差较大,分析原因是计算早期龄期混凝土收缩徐变时,采用叠加原理进行计算会有误差,同时环境和混凝土级配对混凝土收缩徐变影响很大,应变片A10在试验后期应变出现了下降,说明试验测量本身也存在着误差。总体来看,通过ABAQUS编制子程序能较好地模拟混凝土的收缩徐变,计算模拟方法是可行的。
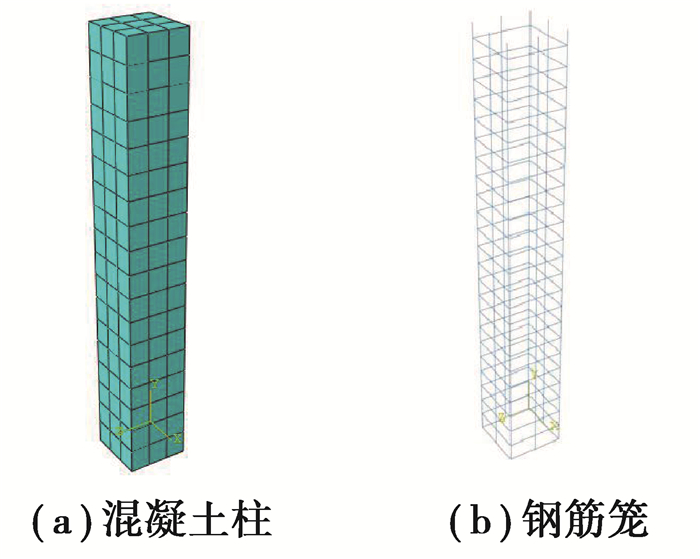
4 混凝土柱收缩徐变分析 4.1 模型参数采用ABAQUS软件分别建立不同参数下素混凝土柱以及钢筋混凝土柱有限元模型,并通过收缩徐变计算程序得到混凝土柱竖向变形。有限元模型中柱边界条件为:上端自由,下端固结,采用实体分离式方式建模,在ABAQUS中采用三维实体单元C3D8R模拟混凝土,三维桁架线性单元T3D2模拟钢筋,通过EMBEDDED命令将钢筋和混凝土绑定在一起,使混凝土与钢筋之间存在可靠的粘结,所建立的混凝土柱有限元模型见图 7所示。
|
图 7 钢筋混凝土柱模型图 Fig. 7 Model of reinforced concrete column |
定义折减系数为考虑钢筋和不考虑钢筋时构件竖向变形的比值,并通过分析柱不同参数与折减系数之间的变化规律,来研究钢筋对混凝土柱收缩徐变的影响。本章研究的相关参数有柱截面尺寸、混凝土强度,轴压比、湿度以及配筋率。考虑到收缩徐变主要发生在前两年,在软件中设置计算时长为805 d。
4.2.1 柱截面尺寸对折减系数的影响混凝土柱截面尺寸分别为400 mm×400 mm、500 mm×500 mm、600 mm×600 mm、700 mm×700 mm、800 mm×800 mm,柱高3 600 mm,混凝土强度为C30,柱轴压比为0.4,纵筋采用8 
采用有限元方法计算得到了不同柱截面尺寸下考虑徐变、收缩及收缩徐变时素混凝土以及钢筋混凝土柱竖向变形,并根据素混凝土以及配筋混凝土柱竖向变形比值求出折减系数,如表 1所示,表中数据按徐变、收缩及收缩徐变排列,后面表格与此相同,不再赘述。
| 表 1 不同截面柱的竖向变形及折减系数 Table 1 Vertical deformation and reduction coefficient of columns with different section size |
由表 1分析可知,不考虑钢筋作用时,在单独考虑徐变影响下,柱竖向变形随尺寸增大而增大,但增幅很小,表明柱尺寸对混凝土的徐变影响较小;而单独考虑收缩影响下,柱竖向变形随尺寸增大而减小,表明体表比的增大会减小收缩引起的变形;综合考虑收缩徐变时,混凝土柱竖向变形随尺寸增大而减小,表明由收缩引起的竖向变形比徐变大。3种情况下,折减系数随尺寸的增大而增大,表明钢筋对混凝土变形的约束作用随着尺寸增大而减弱。
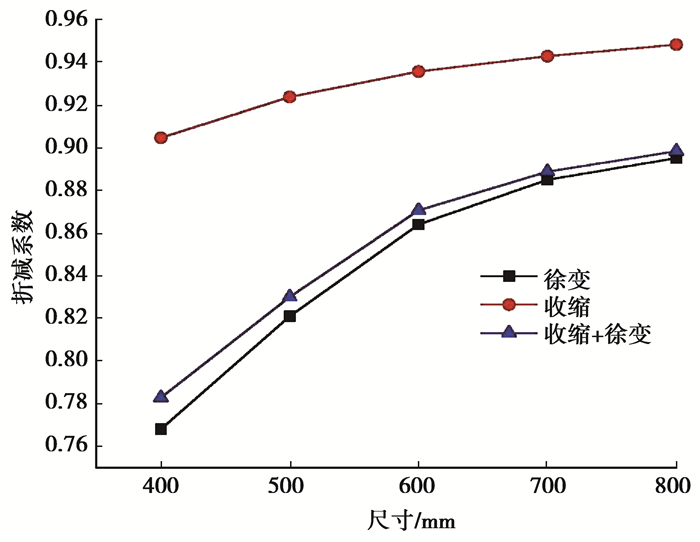
由图 8曲线可知,3种情况下,折减系数与尺寸曲线近似于抛物线,考虑徐变以及收缩徐变时折减系数曲线相隔很近,形状相似;而考虑收缩时,折减系数曲线曲率较小,曲线平缓,表明徐变对折减系数影响更大。
|
图 8 不同截面尺寸柱的折减系数变化曲线 Fig. 8 Reduction factor variation curves of columns with different section size |
混凝土柱截面为500 mm×500 mm,柱轴压比取为0.4,环境湿度取为60%,纵筋采用8 
从表 2分析可知,不考虑钢筋作用时,随着混凝土强度的提高,混凝土柱的竖向变形减小,相比于单独考虑收缩时柱的竖向变形,单独考虑徐变时,柱竖向变形减小幅度更大,表明混凝土强度对徐变影响更大,同时折减系数随着混凝土强度的提高而增大,表明提高混凝土强度能减弱钢筋对混凝土的约束作用。
| 表 2 不同混凝土强度柱的竖向变形及折减系数 Table 2 Vertical deformation and reduction coefficient of columns with different concrete strength |
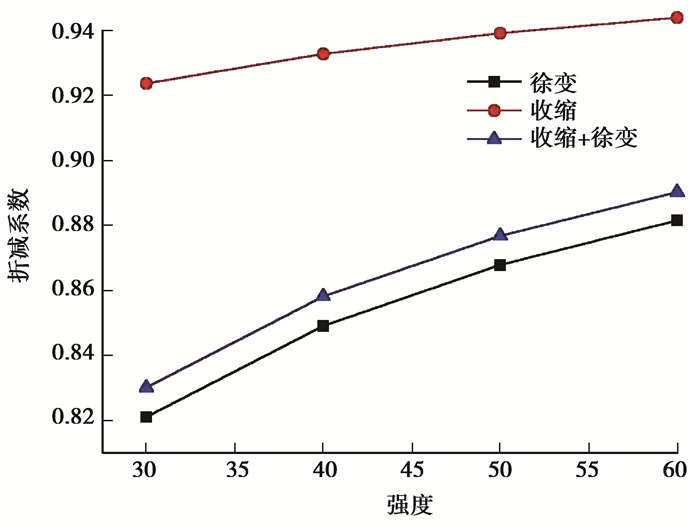
由图 9曲线可知,3种情况下的折减系数与强度曲线近似于抛物线,考虑徐变和收缩徐变的曲线接近,折减系数相差很小。而考虑收缩的曲线折减系数较大,在0.92以上,变化幅度较小。
|
图 9 不同混凝土强度柱的折减系数变化曲线 Fig. 9 Reduction factor variation curves of columns with different concrete strength |
混凝土柱截面为500 mm×500 mm,混凝土强度为C30,环境湿度取为60%,纵筋采用8C20,箍筋采用φ8@150,柱轴压比分别为0.2、0.3、0.4、0.5,对应的轴力设计值为715、1 072.5、1 430、1 787.5 kN。
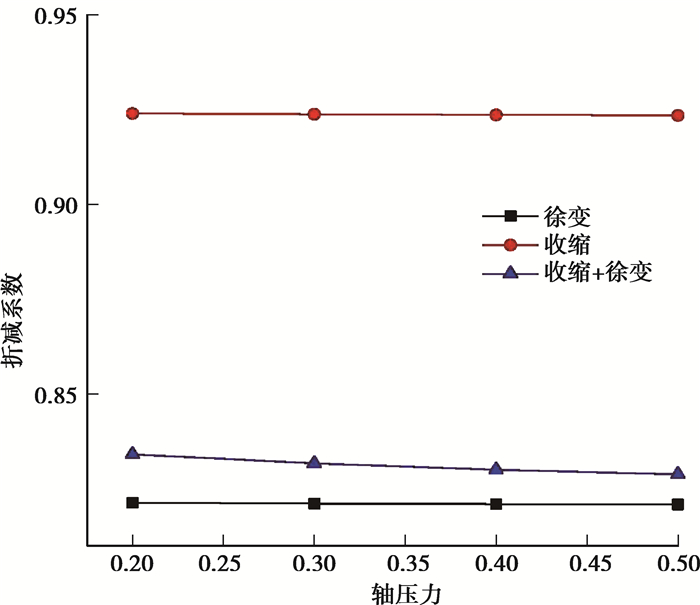
从表 3分析可知,不考虑钢筋作用时,混凝土柱的竖向变形随轴压比增大而增大,当轴压比从0.2增大至0.5、分别考虑徐变以及收缩时,柱竖向变形增大幅度分别为1.753 7 mm和0.484 3 mm,表明轴压比对徐变影响更大。折减系数随着轴压比的增大基本没有变化,表明提高轴压比对钢筋与混凝土的约束影响不大,在不同轴压比下,单独考虑徐变、收缩和收缩徐变时,折减系数可分别取值为0.82、0.92和0.83。
| 表 3 不同轴压比柱的竖向变形及折减系数 Table 3 Vertical deformation and reduction coefficient of columns with different compressive ratio |
由图 10曲线可以看出,3种情况下折减系数与轴压比之间为线性关系,并且随着轴压比的增大,折减系数变化很小,折减系数曲线近似为平行直线。
|
图 10 不同轴压比下柱的折减系数变化曲线 Fig. 10 Reduction coefficient variation curves of columns with different compressive ratio |
混凝土柱截面尺寸为500 mm×500 mm,混凝土强度为C30,柱轴压比取为0.4,纵筋采用8C20,箍筋采用φ8@150,环境湿度分别为50%、60%、70%、80%。
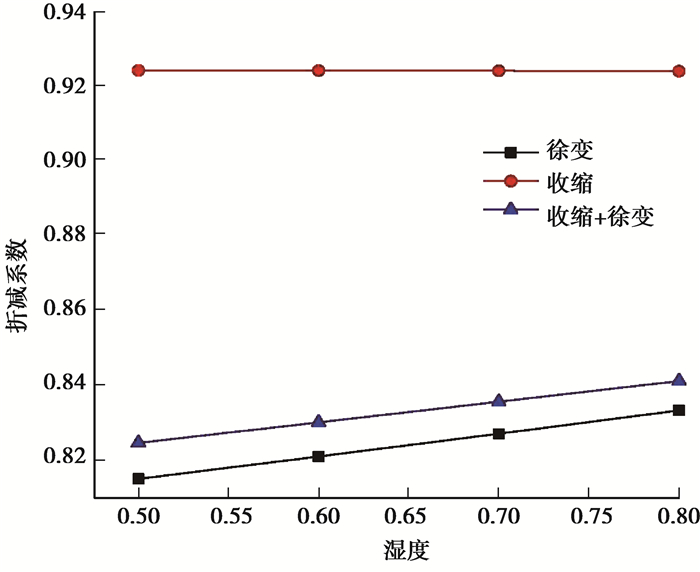
由表 4分析可知,随着环境湿度增加,混凝土柱竖向变形减小,并且单独考虑收缩时混凝土柱竖向变形减小幅度大于单独考虑徐变时柱竖向变形减小幅度,表明湿度对收缩影响更大;考虑徐变以及收缩徐变时,折减系数随着湿度的增大而增大,表明随着湿度增加,钢筋对混凝土的约束减弱;而考虑收缩时,湿度对折减系数影响较小,此时折减系数可取一定值,为0.923。
| 表 4 不同湿度下柱的竖向变形及折减系数 Table 4 Vertical deformation and reduction coefficient of columns under different moister |
由图 11曲线可知,折减系数曲线都近似于直线,考虑徐变和收缩徐变的折减系数随着湿度的增大而增大;而单独考虑收缩,随着湿度增大,折减系数变化很小,折减曲线近似为平行直线。
|
图 11 不同湿度下柱的折减系数变化曲线 Fig. 11 Reduction coefficient variation curves of columns under different moister |
混凝土柱截面尺寸为500 mm×500 mm,混凝土强度为C30,环境湿度为60%,柱轴压比取0.4,柱截面配筋分别为4 






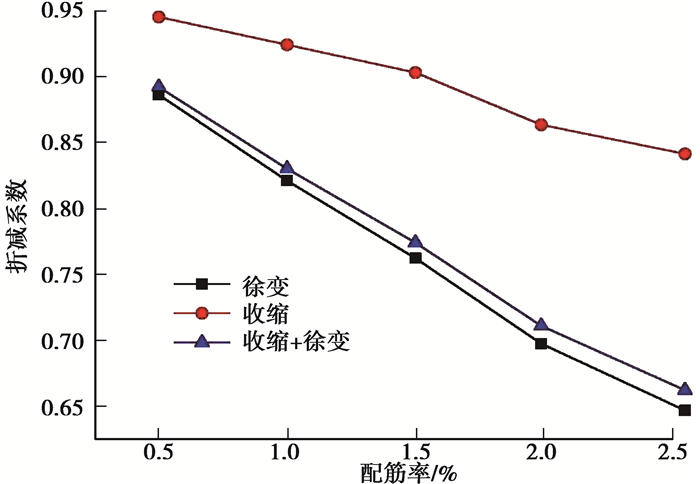
由表 5分析可知,随着配筋率的提高,混凝土柱的竖向变形减小,单独考虑徐变时,柱竖向变形减小幅度大于单独考虑收缩时柱竖向变减小幅度,表明配筋率对徐变影响更大。折减系数随着配筋率的提高而减小,钢筋对混凝土约束作用随着配筋率提高而显著增强,因此在对混凝土结构进行收缩徐变分析时,考虑钢筋的影响是非常有必要的。
| 表 5 不同配筋率柱的竖向变形及折减系数 Table 5 Vertical deformation and reduction coefficient of columns with different reinforcement ratio |
从图 12曲线可知,折减系数与配筋率之间近似为线性关系,随着配筋率的增大,折减系数下降幅度大。
|
图 12 不同配筋率柱的折减系数变化曲线 Fig. 12 Reduction coefficient variation curves of columns with different reinforcement ratio |
将文献[15]中不同配筋率下的混凝土柱竖向变形与本节结果进行对比分析,如表 6所示。文献中混凝土柱只考虑了徐变的影响,因此只取本节考虑徐变的计算结果。同时文献中混凝土柱轴压比为0.7,由前面分析可知,在单独考虑徐变时,折减系数与柱轴压比之间为线性关系。将文献中柱竖向变形结果进行换算,可知结果相差最大为0.5 mm,由于文献中未考虑环境湿度的影响,因此存在着误差,所以文中的计算结果是合理可信的。
| 表 6 文中计算结果与文献结果的对比 Table 6 Comparison between calculation results and reference's |
采用ABAQUS软件分别建立单层三跨素混凝土以及钢筋混凝土框架有限元模型,并根据收缩徐变计算程序得到框架梁跨中竖向变形。有限元模型中柱底端边界条件为固支,采用实体分离式方式建模,在ABAQUS中使用C3D8R单元模拟混凝土,采用三维桁架线性单元T3D2模拟钢筋,采用EMBEDDED命令将钢筋与混凝土绑定在一起,使两者之间有可靠的粘结,在梁上施加线荷载来模拟实际结构中梁的受力,设计了一个三跨的单层框架,取其中跨来分析,框架有限元模型见图 13所示。

|
图 13 框架模型图 Fig. 13 Model of frame structure |
对不同的相关参数进行定量分析,考虑的相关参数有梁高、混凝土的强度、竖向荷载、环境湿度以及梁配筋率,在软件中设置收缩徐变的计算时长为805 d,计算得到中跨梁跨中以及两端竖向位移,将跨中位移减去梁两端竖向位移平均值得到中跨的竖向变形,定义框架梁折减系数为考虑钢筋与不考虑钢筋影响时梁跨中竖向变形的比值。
5.2.1 梁高对折减系数的影响框架梁截面宽度为250 mm,梁截面高度分别为500、550、600、650、700 mm,混凝土强度采用C30,梁上线荷载为20 kN/m,环境湿度为60%,梁截面配筋为:梁底纵筋6 


从表 7分析可知,随着梁高的增大,框架梁竖向变形减小,考虑徐变时,梁竖向变形减小幅度大于考虑收缩时梁竖向变形减小幅度,表明梁高对徐变影响更大。折减系数随着梁高的增大而增大,表明梁高的增加会减弱混凝土与钢筋之间的约束。
| 表 7 不同梁高下框架梁的竖向变形及折减系数 Table 7 Vertical deformation and reduction coefficient of frame beams with different beam height |
从图 14曲线可知,3种情况下,折减系数曲线形状近似于二次曲线,其中考虑收缩时,折减系数曲线平缓,变化较小,考虑徐变以及收缩徐变的曲线相隔较近。

|
图 14 不同梁高下框架梁的折减系数变化曲线 |
混凝土梁截面尺寸为250 mm×700 mm,梁上作用线荷载为20 kN/m,混凝土强度分别为C30、C40、C50、C60,环境湿度取为60%,梁配筋为:梁底纵筋6 


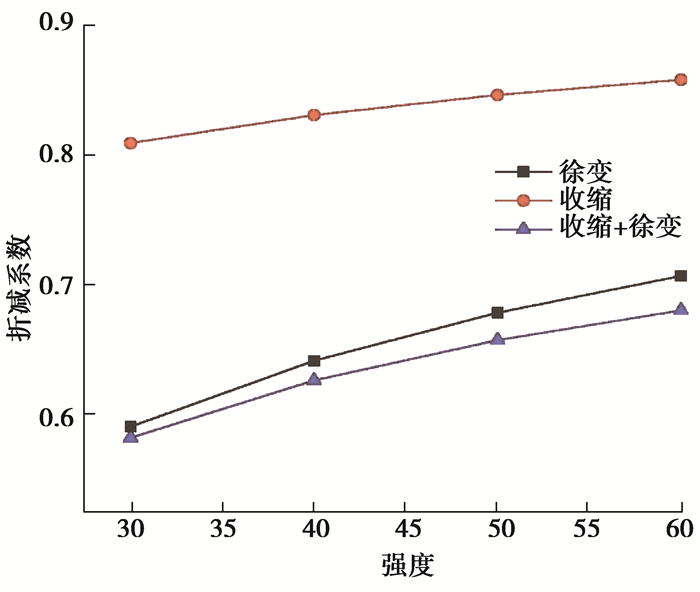
由表 8分析可知,随着混凝土强度的提高,中跨竖向位移减小,单独考虑徐变时,柱竖向变形减幅大于单独考虑收缩时柱竖向变形减小幅度,混凝土强度对徐变影响更大。折减系数随着混凝土强度的提高而增大,混凝土强度的提高会减弱钢筋对混凝土的约束作用。
| 表 8 不同混凝土强度下框架梁的竖向变形及折减系数 Table 8 Vertical deformation and reduction coefficient of frame beams with different concrete strength |
从图 15曲线可知,3种情况下,折减系数曲线形状类似于抛物线。
|
图 15 不同混凝土强度框架梁的折减系数变化曲线 Fig. 15 Reduction coefficient variation curves of frame beams with different concrete strength |
混凝土梁尺寸为250 mm×700 mm,混凝土强度为C30,环境湿度取为60%,梁上作用线荷载6、8、10、12 kN/m,梁截面配筋为:梁底纵筋6 


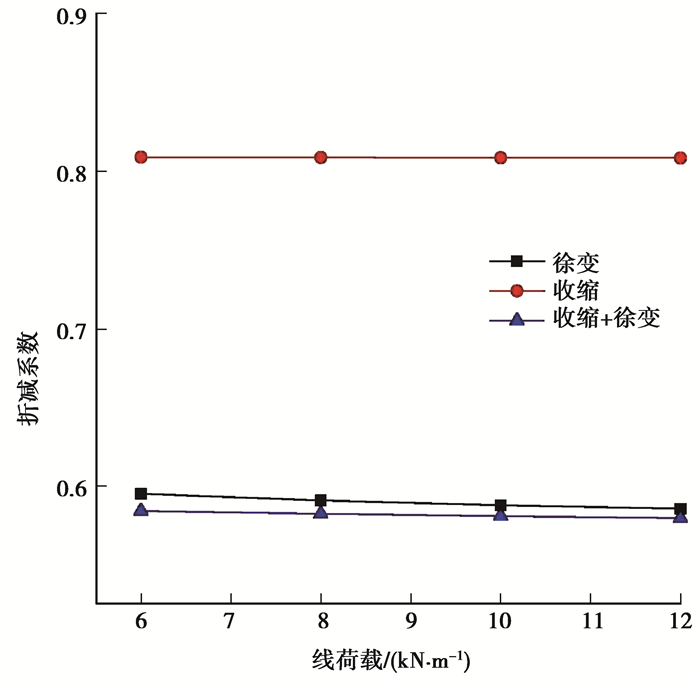
由表 9分析可知,随着梁上线荷载的增大,中跨的跨中竖向变形增大,单独考虑徐变时,梁跨中竖向变形增大幅度大于单独考虑收缩时竖向变形增大幅度,表明竖向荷载对徐变影响更大。折减系数随着竖向荷载的增大而变化很小,表明竖向荷载的增大对混凝土与钢筋之间的约束影响较小,折减系数在考虑徐变、收缩以及收缩徐变时可取值为0.59、0.809和0.582。
| 表 9 不同竖向荷载下框架梁的竖向变形及折减系数 Table 9 Vertical deformation and reduction coefficient of frame beams with different vertical load |
从图 16曲线可知,3种情况下,折减系数曲线形状近似于直线。
|
图 16 不同竖向荷载下框架梁的折减系数变化曲线 Fig. 16 Reduction factor variation curves of frame beams with different vertical load |
混凝土梁尺寸为250 mm×700 mm,混凝土强度为C30,梁上作用线荷载20 kN/m,环境湿度取为50%、60%、70%、80%,梁截面配筋为:梁底纵筋6 


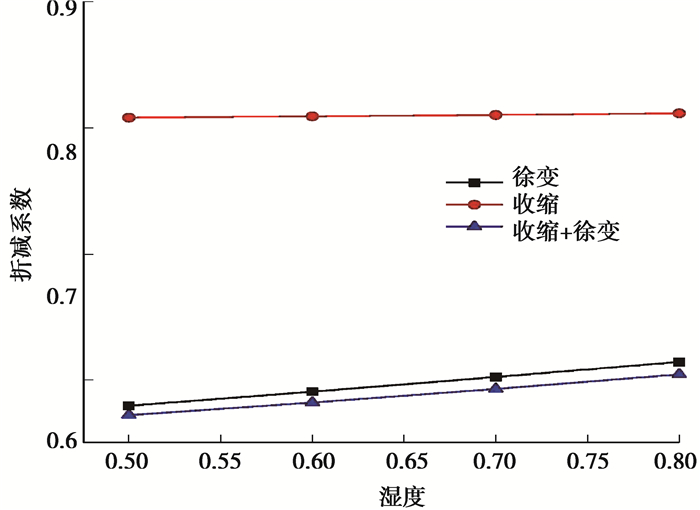
从表 10分析可知,随着湿度增加,框架梁竖向变形减小,考虑收缩时,框架梁竖向变形减幅较大,湿度对框架梁的收缩有明显的影响; 考虑徐变和收缩徐变时,折减系数随着湿度的增加而增大,考虑收缩时; 湿度对折减系数影响较小,折减系数可取值为0.81。
| 表 10 不同湿度下框架梁的竖向变形及折减系数 Table 10 Vertical deformation and reduction coefficient of frame beams under different moisture |
由图 17曲线可知,3种情况下的折减系数曲线都近似于直线,其中单独考虑收缩时,可认为折减系数变化较小,可取值为0.81。
|
图 17 不同湿度下框架梁的折减系数变化曲线 Fig. 17 Reduction coefficient variation curves of frame beams with different moisture |
混凝土梁截面尺寸为250 mm×700 mm,混凝土强度为C30,梁上作用线荷载20 kN/m,环境湿度取为60%,梁底部纵筋4 







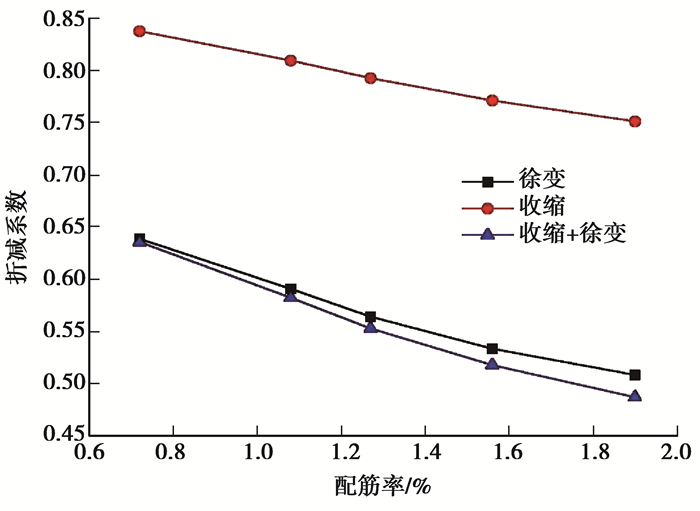
由表 11分析可知,随着配筋率的提高,中跨的跨中竖向变形减小,配筋率对框架梁徐变影响更大,随着配筋率的提高,折减系数减小,混凝土与钢筋之间约束增强。
| 表 11 不同配筋率下框架梁的竖向变形及折减系数 Table 11 Vertical deformation and reduction coefficient of frame beams with different reinforcement ratio |
由图 18曲线可知,3种情况下,折减系数曲线形状类似于抛物线。
|
图 18 不同配筋率框架梁的折减系数变化曲线 Fig. 18 Reduction coefficient variation curves of frame beams with different reinforcement ratio |
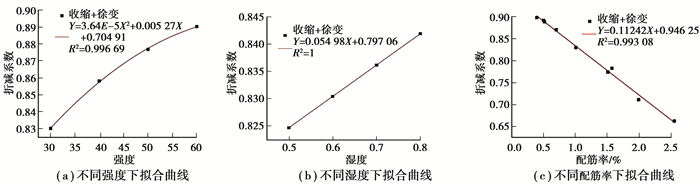
文中第4节和第5节得到了柱和框架梁折减系数与不同影响因素之间的变化曲线,并发现两者之间存在着规律性关系。为此本节通过Origin软件对考虑收缩徐变时不同影响因素下折减系数曲线进行公式上的拟合,以期提出一种可计算配筋混凝土构件收缩徐变计算方法。不同轴压比下,考虑收缩徐变时柱折减系数为一定值取为0.83,不同柱截面尺寸下,柱配筋率发生改变,此时分别计算不同截面尺寸对应的配筋率,得到尺寸与配筋率换算表,如表 12所示,将表中数据点加入到不同配筋率折减系数曲线中进行拟合,得到了不同影响因素下柱折减系数拟合曲线如图 19所示。从图 19中可以看出,不同强度、湿度以及不同配筋率下拟合相关系数均在0.99以上,表示拟合良好。
| 表 12 尺寸与配筋率对应表 Table 12 Correspondence table of size and reinforcement ratio |
|
图 19 不同影响因素下折减系数拟合曲线 Fig. 19 Fitting curve of reduction coefficient under different influencing factors |
根据混凝土强度、湿度以及配筋率与折减系数的拟合公式,假定各参数之间互不影响,将各参数的拟合公式相加并添加一个常数项,得到了考虑收缩徐变时柱折减系数公式:
| $ y = 3.641 \times {10^{ - 5}}x_1^2 + 0.005{\rm{ }}27{x_1} + 0.054{\rm{ }}98{x_2} - 0.112{\rm{ }}42{x_3} + 0.784{\rm{ }}72, $ | (9) |
式中:x1为混凝土强度;x2为湿度;x3指配筋率;y为折减系数。
用公式(9)计算第4节配筋混凝土柱考虑收缩徐变时折减系数值,与第4节有限元计算结果对比,误差最大为2.43%,因此所得公式能很好地反映折减系数与参数之间的关系。
6.2 公式验证混凝土柱尺寸分别为400 mm×400 mm,长度为3 600 mm,混凝土强度C30,环境湿度为80%,配筋采用8 
| 表 13 柱折减系数对比 Table 13 Comparisons of column reduction coefficient |
1) 相比较而言,在各影响因素中,柱截面尺寸、湿度对柱收缩影响更大,柱混凝土强度、湿度以及配筋率对徐变影响更大。梁高、混凝土强度、竖向荷载以及配筋率对梁徐变影响更大,而湿度对梁收缩影响更大。
2) 柱竖向变形折减系数与柱截面尺寸、混凝土强度之间为二次曲线关系,环境湿度以及柱配筋率与折减系数之间的关系为线性关系,轴压比对折减系数影响不大,考虑徐变、收缩以及收缩徐变时,折减系数可取0.82、0.92和0.83。在湿度增大的情况下,折减系数在考虑徐变和收缩徐变时增大,考虑收缩时折减系数变化较小,可取值为0.923,折减系数随着配筋率的提高而大幅减小,因此在对混凝土构件进行收缩徐变分析时,考虑钢筋的影响是非常有必要的。
3) 梁的截面高度、混凝土强度、配筋率与折减系数为二次曲线关系,湿度、梁上线荷载与折减系数呈线性关系。梁折减系数随着强度的提高而增大,随着配筋率的增大而减小,不同湿度下考虑收缩时,折减系数可取值为0.81。梁上线荷载大小对折减系数影响不大,考虑徐变、收缩以及收缩徐变时折减系数可取0.59、0.809和0.582。
4) 对徐变、收缩、收缩徐变情况下的混凝土柱、框架梁中跨的折减系数进行比较可知,混凝土柱在单独考虑徐变时的折减系数最小,而框架梁在单独考虑收缩徐变时最小。混凝土柱和框架梁考虑收缩时的折减系数最大,考虑收缩徐变和单独考虑徐变时折减系数相差不大。
5) 提出了考虑钢筋影响时混凝土构件收缩徐变计算方法,通过实例验证了计算方法的可行性,可为钢筋混凝土构件收缩徐变计算和工程应用提供有益的参考和借鉴。
| [1] |
刘枫, 刘军进. 混凝土收缩徐变对天津津塔施工模拟及预变形的影响分析[J]. 建筑结构, 2012, 42(9): 142-145. LIU Feng, LIU Junjin. Effect of creep and shrinkage on construction simulation and pre-deformation analysis for Jin Tower in Tianjin[J]. Building Structure, 2012, 42(9): 142-145. (in Chinese) |
| [2] |
Vandewalle L. Concrete creep and shrinkage at cyclic ambient conditions[J]. Cement and Concrete Composites, 2000, 22(3): 201-208. DOI:10.1016/S0958-9465(00)00004-4 |
| [3] |
Bazant Z P, Murphy W P. Creep and shrinkage prediction model for analysis and design of concrete structures-mod B3[J]. Matériaux et constructions, 1995(28): 357-365. |
| [4] |
Morano S G, Mannini C. Preflex beams:A method of calculation of creep and shrinkage effects[J]. Journal of Bridge Engineering, 2006, 11(1): 48-58. DOI:10.1061/(ASCE)1084-0702(2006)11:1(48) |
| [5] |
Dilger W H. Creep analysis of prestressed concrete structures using creep-transformed section properties[J]. PCI Journal, 1982, 27(1): 98-119. DOI:10.15554/pcij.01011982.98.119 |
| [6] |
Dezi L, Leoni G, Tarantino M. Creep and shrinkage analysis of composite beams[J]. Progress in Structural Engineering and Materials, 1998, 1(2): 170-177. |
| [7] |
曹国辉, 胡佳星, 张锴. 配筋对混凝土圆柱体长期徐变的影响[J]. 建筑结构, 2015, 45(8): 54-58. CAO Guohui, HU Jiaxing, ZHANG Kai. Influence of reinforcement on long-term creep of concrete circular column[J]. Building Structure, 2015, 45(8): 54-58. (in Chinese) |
| [8] |
潘钻峰, 吕志涛, 孟少平. 配筋对高强混凝土收缩徐变影响的试验研究[J]. 土木工程学报, 2009, 42(2): 11-23. PAN Zuanfeng, LV Zhitao, MENG Shaoping. Experimental study on the influence of steel on high-strength concrete creep and shrinkage[J]. China Civil Engineering Journal:Natural Science, 2009, 42(2): 11-23. (in Chinese) DOI:10.3321/j.issn:1000-131X.2009.02.002 |
| [9] |
张克波, 许康, 吕毅刚, 等. 配筋混凝土柱徐变试验[J]. 长沙理工大学学报:自然科学版, 2011, 8(2): 17-20,27. ZHANG Kebo, XU Kang, LYU Yigang, et al. Experimental research on creep of reinforced concrete pillars[J]. Journal of Changsha University of Science and Technology(Natural Science), 2011, 8(2): 17-20,27. (in Chinese) DOI:10.3969/j.issn.1672-9331.2011.02.004 |
| [10] |
张望喜, 谭泽腾, 薛凯, 等. 基于ABAQUS的钢筋混凝土收缩徐变分析[J]. 西安建筑科技大学学报(自然科学版), 2015, 47(3): 347-353. ZHANG Wangxi, TAN Zeteng, XUE Kai, et al. Analysis of shrinkage and creep of reinforced concrete based on ABAQUS[J]. Journal of Xi'an University of Architecture & Technology, 2015, 47(3): 347-353. (in Chinese) |
| [11] |
Du Beton C E I. CEB-FIP model code 1990[J]. Design Code, 1991, 54-58. |
| [12] |
孙宝俊. 混凝土徐变理论的有效模量法[J]. 土木工程学报, 1993, 26(3): 66-68. SUN Baojun. Effective modulus method of concrete creep[J]. China Civil Engineering Journal, 1993, 26(3): 66-68. (in Chinese) |
| [13] |
刘忠. 混凝土徐变收缩的递推AEMM法[J]. 重庆交通学院学报, 1994, 13(5): 31-34. LIU Zhong. AEMM method with recurrence realtions in analysis of creep and shrinkage of concrete[J]. Journal of Chongqing Jiaotong University, 1994, 13(5): 31-34. (in Chinese) |
| [14] |
郭磊磊.湿度和配筋对混凝土收缩、徐变性能影响研究[D].哈尔滨: 哈尔滨工业大学,2012. GUO Leilei. Effect of humidity and bar arrangement on creep and shrinkage of concrete[D]. Harbin: Harbin Institute of Technology,2012.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10213-1013038385.htm |
| [15] |
刘明洲.高层建筑施工过程中的混凝土徐变分析[D].大连: 大连理工大学,2014. LIU Mingzhou. Concrete creep analysis of high-rise building in construction process[D]. Dalian: Dalian University of Technology,2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10141-1015570774.htm |
 2019, Vol. 42
2019, Vol. 42

