2. 中国科学院力学研究所 流固耦合系统力学重点实验室, 北京 100190;
3. 中国科学院大学 工程科学学院, 北京 100049
2. Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, P. R. China;
3. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, P. R. China
高压富水地区岩溶隧道修建过程中,出于保护地下水资源和环境的需要, 常采取“以堵为主, 限量排放”的原则, 导致衬砌结构承受了较大的外水压力, 高外水压可能对隧道结构安全带来不利影响,科学合理地评估衬砌在高外水压时的承压能力对于隧道的安全运行非常重要。由于岩溶隧道工程的复杂性和地质条件的多变性,且缺乏系统的理论指导,目前常用的基于经验类比法隧道结构设计,在某些条件下过于保守,造成浪费,而在另外一些条件下又过于薄弱,给隧道工程的建设和后期的运营带来安全隐患。因此,深入研究衬砌结构的力学特性、承载能力,不仅对隧道工程的合理设计、施工十分重要,而且对已建隧道加固维修方案的制定具有重要的指导意义,可以有效延长隧道的使用寿命。
近年来,众多学者针对衬砌的抗水压能力和衬砌强度安全性展开了深入的研究。李忠[1]采用有限元计算分析隧道衬砌环向裂缝机理,其中裂缝的实现,通过在不同材料组之间的分界面采用接触对单元来实现;王志杰[2]基于双线铁路隧道设计标准,利用有限元软件计算和分析了双线铁路隧道衬砌在不同水压作用下隧道衬砌安全系数的变化规律,确定了该隧道衬砌的高水压分界值。陈耀华[3]基于现场试验和有限元数值模拟相结合的方法,研究隧道衬砌外水压力变化规律,并提出二次衬砌厚度优化方案。王秀英[4]通过理论分析、模型试验和现场实测数据,计算了高水压隧道衬砌的抗水压上限及衬砌设防合理尺寸。万飞等[5]采用现场试验和数值模拟手段,研究局部水压作用下隧道衬砌的受力特征和安全性。在以往的研究中,主要采用不考虑破裂的连续介质模型计算,或只考虑不同的材料组界面破裂的非连续模型,未计算材料内部的破坏。混凝土衬砌结构受力后会开裂,衬砌受力的有效截面积降低,衬砌结构应力重新分布,进而加速裂缝生成,随着大量裂缝产生甚至贯通,最终导致衬砌结构失稳。上述过程中,裂纹既存在于不同结构间的接触面,也存在于单一结构内部。连续介质方法不能很好地处理裂纹生成以及演化过程,而预设特定区域发生破裂的方法也不能客观地刻画衬砌结构内部的变形破坏。故基于连续介质模型或仅考虑材料界面破裂的连续介质模型分析衬砌的破坏过程存在一定的局限性。
为实现衬砌结构从连续到非连续的完整破坏过程演化,文中采用有限元与离散元耦合的连续-非连续方法(CDEM)[6-10],建立某岩溶发育地区铁路隧道钢筋混凝土衬砌的三维模型,计算衬砌结构在不同水压条件下的位移、应力应变、破裂因子、破裂率等特征,研究钢筋混凝土衬砌变形、开裂和破坏过程。最后,分析衬砌结构失效和界面破裂率之间的相关性,基于界面破裂率提出衬砌结构抗水压能力的评估方法,对优化隧道防水衬砌的设计参数具有重要的实际应用价值。
1 数值方法及本构模型文中采用连续-非连续单元方法(CDEM),分析西南高压富水地区某岩溶铁路隧道钢筋混凝土衬砌结构在不同水压条件下的变形和破坏过程。CDEM (continuous discontinuous element method)是一种有限元与离散元耦合的显式数值分析方法。CDEM中的数值模型由块体及界面两部分构成。块体由一个或多个有限元单元组成,用于表征材料的弹性、塑性、损伤等连续特征;两个块体间的公共边界即为界面,用于表征材料的断裂、滑移、碰撞等非连续特征。CDEM中的界面包含真实界面及虚拟界面两个概念。真实界面用于表征材料的交界面、断层、节理等真实的不连续面,其强度参数与真实界面的参数一致。虚拟界面主要有两个作用,一是连接两个块体,用于传递力学信息;二是为显式裂纹的扩展提供潜在的通道(即裂纹可沿着任意一个虚拟界面进行扩展);因此,虚拟界面的强度参数与块体的强度参数一致。
隧道钢筋混凝土衬砌计算模型中,钢筋为梁单元,混凝土为块体单元,混凝土内部单元间为虚拟界面;衬砌不同结构间,如初支、预留缝、二衬、三衬、盖板、底板间为真实界面。
1.1 有限元显式求解过程有限元的显式求解主要包含节点合力计算及节点运动计算两个部分。节点合力计算为
| $ \mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{F}}^E} + {\mathit{\boldsymbol{F}}^d} + {\mathit{\boldsymbol{F}}^c}, $ | (1) |
其中,F为节点合力; FE为节点外力; Fd为节点变形力(由单元应力贡献);Fc为节点阻尼力。
节点运动计算为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{a}} = \mathit{\boldsymbol{F}}/m, v = \sum\limits_{t = 0}^{{T_{{\rm{now }}}}} a \Delta t;}\\ {\Delta \mathit{\boldsymbol{u}} = v\Delta t, u = \sum\limits_{t = 0}^{{T_{{\rm{now }}}}} \Delta u;} \end{array}} \right. $ | (2) |
其中:a为节点加速度;v为节点速度;Δu为节点位移增量;u为节点位移全量;m为节点质量;Δt为计算时步。基于式(1)、式(2)的交替计算,即可实现有限元的显式求解过程。
采用增量法进行单元应力及节点变形力的计算
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta {\mathit{\boldsymbol{\varepsilon }}_i} = {{\mathit{\boldsymbol{B}}}_i}\Delta {\mathit{\boldsymbol{u}}_e}, }\\ {\Delta {\sigma _i} = D\Delta {\mathit{\boldsymbol{\varepsilon }}_i}, }\\ {{\bf{ \pmb{\mathsf{ σ}} }}_i^n = {\bf{ \pmb{\mathsf{ σ}} }}_i^o + \Delta {{\bf{ \pmb{\mathsf{ σ}} }}_i}, }\\ {{\mathit{\boldsymbol{F}}_e} = \sum\limits_{i = 1}^N {{\bf{B}}_i^{\rm{T}}} {\bf{ \pmb{\mathsf{ σ}} }}_i^n{w_i}{J_i};} \end{array}} \right. $ | (3) |
其中:Bi、Δεi、Δσi、wi、Ji分别为高斯点i的应变矩阵、增量应变向量、增量应力向量、积分系数及雅克比行列式;σin及σio为高斯点i当前时刻及上一时刻的应力向量;D、Δue、Fe分别表示单元的弹性矩阵、节点增量位移向量及节点力向量;N表示高斯点个数。
1.2 拉剪复合的弹塑性模型为了模拟钢筋混凝土材料在水压条件下的塑性破坏过程,采用拉剪复合的理想弹塑性本构对式(3)计算的试探应力σij进行修正。首先,根据应力张量σij计算当前时步的主应力σ1、σ2及σ3,然后根据式(4)判断该应力状态是否已经达到或超过了Mohr-Coulomb准则或最大拉应力准则,为
| $ \left\{ {\begin{array}{*{20}{l}} {{f^s} = {\sigma _1} - {\sigma _3}{N_\varphi } + 2C\sqrt {{N_\varphi }} , }\\ {{f^t} = {\sigma _3} - T, }\\ {h = {f^t} + {\alpha ^P}\left( {{\sigma _1} - {\sigma ^p}} \right);} \end{array}} \right. $ | (4) |
式中:C,φ,T为粘聚力、内摩擦角及抗拉强度; Nφ,αp,σp为常数。如果fs≥0, 且h≤0,则发生剪切破坏;如果ft≥0,且h>0,则发生拉伸破坏。
| $ {\left\{ {\begin{array}{*{20}{l}} {{N_\varphi } = \frac{{1 + \sin (\varphi )}}{{1 - \sin (\varphi )}}, }\\ {{\alpha ^p} = \sqrt {1 + N_\varphi ^2} + {N_\varphi }, }\\ {{\sigma ^p} = T(t){N_\varphi } - 2C(t)\sqrt {{N_\varphi }}。} \end{array}} \right.} $ | (5) |
当单元发生剪切破坏时,采用式(6)进行主应力的修正:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{1 - {\rm{new }}}} = {\sigma _1} - {\lambda ^s}\left( {{\alpha _1} - {\alpha _2}{N_\psi }} \right), }\\ {{\sigma _{2 - {\rm{new }}}} = {\sigma _2} - {\lambda ^s}{\alpha _2}\left( {1 - {N_\phi }} \right), }\\ {{\sigma _{3 - {\rm{new }}}} = {\sigma _3} - {\lambda ^s}\left( { - {\alpha _1}{N_\psi } + {\alpha _2}} \right);} \end{array}} \right. $ | (6) |
式中,λs,NΨ,α1和α2为常数,其表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda ^s} = \frac{{{f^s}\left( {{\sigma _1}, {\sigma _3}} \right)}}{{\left( {{\alpha _1} - {\alpha _2}{N_\psi }} \right) - \left( { - {\alpha _1}{N_\phi } + {\alpha _2}} \right){N_\phi }}}, }\\ {{\alpha _1} = K + \frac{4}{3}G, }\\ {{\alpha _2} = K - \frac{2}{3}G, }\\ {{N_\psi } = \frac{{1 + \sin (\psi )}}{{1 - \sin (\psi )}};} \end{array}} \right. $ | (7) |
式中,Ψ,K和G分别表示剪胀角、体积模量及剪切模量。
当单元发生拉伸破坏时,采用式(8)修正主应力为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{1 - {\rm{new}}}} = {\sigma _1} - \left[ {{\sigma _3} - T(t)} \right]\frac{{{\alpha _2}}}{{{\alpha _1}}}, }\\ {{\sigma _{2 - {\rm{new}}}} = {\sigma _2} - \left[ {{\sigma _3} - T(t)} \right]\frac{{{\alpha _2}}}{{{\alpha _1}}}, }\\ {{\sigma _{3 - {\rm{new}}}} = T{{(t)}_0}。} \end{array}} \right. $ | (8) |
将经过Mohr-Coulomb准则及最大拉应力准则修正后的主应力转换至整体坐标系,根据有限元法计算由单元应力贡献出的节点变形力(即式(1)中的Fd)。
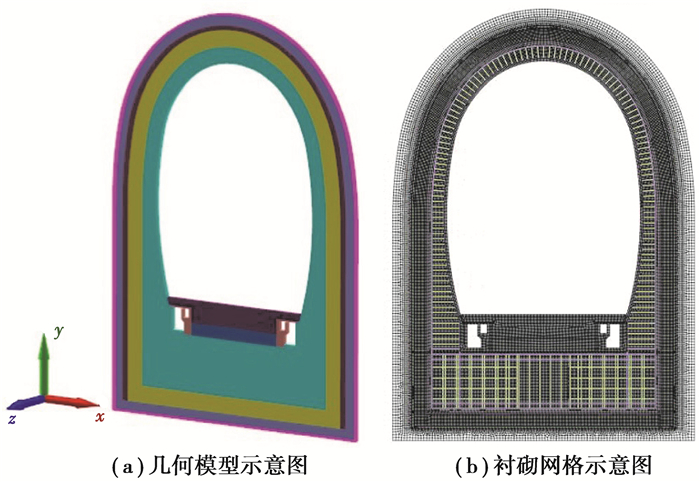
2 钢筋混凝土三层衬砌变形破坏数值模拟西南高压富水地区某铁路隧道钢筋混凝土衬砌为三层结构,包括初支、二衬和三衬。由于水压条件下衬砌的变形和破坏主要发生在衬砌环向上,衬砌纵向变形较小,因此,建立模型时不考虑衬砌纵向钢筋分布。文中以环向钢筋分布间距12.5 cm作为模型纵向长度,以某一环向钢筋分布的横断面为中间平面,前后各取6.25 cm,建立该衬砌结构的三维数值计算模型如图 1所示。
|
图 1 衬砌计算模型 Fig. 1 The calculation model of lining |
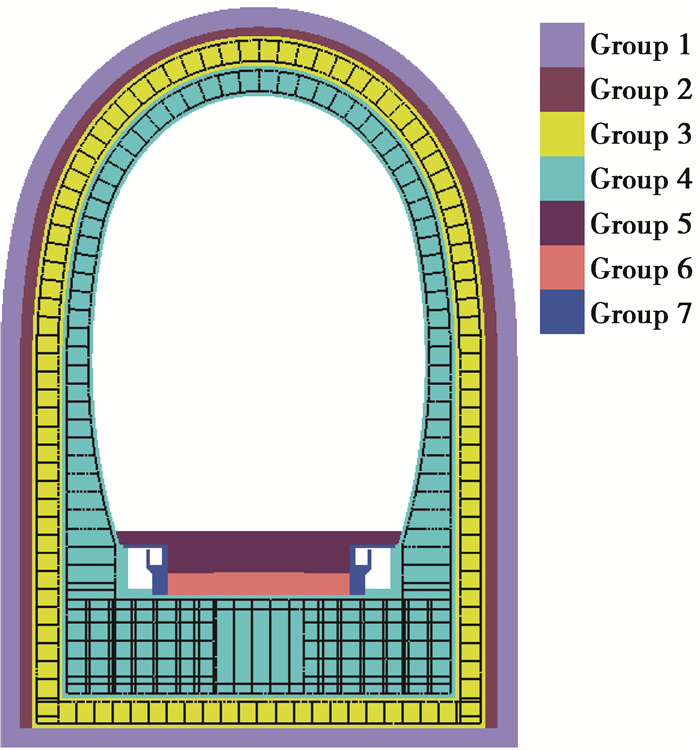
该隧道钢筋混凝土衬砌结构如图 2所示,其中,初支、预留缝、盖板、底板、水沟、电缆槽为C25素混凝土。二衬和三衬为C35钢筋混凝土,厚度均为50 cm。环向钢筋和径向钢筋为HBR400螺纹钢,直径分别为28 mm和12 mm。
|
图 2 衬砌结构示意图 Fig. 2 The schematic diagram of lining structure |
钢筋计算采用各向同性的理想弹塑性模型,弹性模量为200 GPa,泊松比为0.3,钢筋抗拉强度和抗压强度取360 MPa。混凝土计算采用Mohr-Coulomb模型及最大拉应力准则,基于《铁路隧道设计规范》(TB 10003—2016)提供的混凝土单轴抗压强度和抗拉强度的标准值,换算得到不同标号混凝土的内摩擦角φ和黏聚力c,如表 1所示。此外,由文献[11]的分析结果可知,混凝土抗拉强度满足双参数Weibull分布,其分布函数参数为:m=55.544,β=1.086。双参数Weibull分布的分布函数和密度函数为
| $ {F(x) = 1 - \exp \left[ { - {{\left( {\frac{x}{\beta }} \right)}^m}} \right], } $ | (9) |
| $ {f(x) = \frac{{{\rm{d}}F(x)}}{{{\rm{d}}x}} = \frac{m}{\beta }{{\left( {\frac{x}{\beta }} \right)}^{m - 1}}\exp \left[ { - {{\left( {\frac{x}{\beta }} \right)}^m}} \right], } $ | (10) |
式中:β代表尺度参数;m代表形状参数。
| 表 1 数值计算参数 Table 1 Numerical calculation parameters |
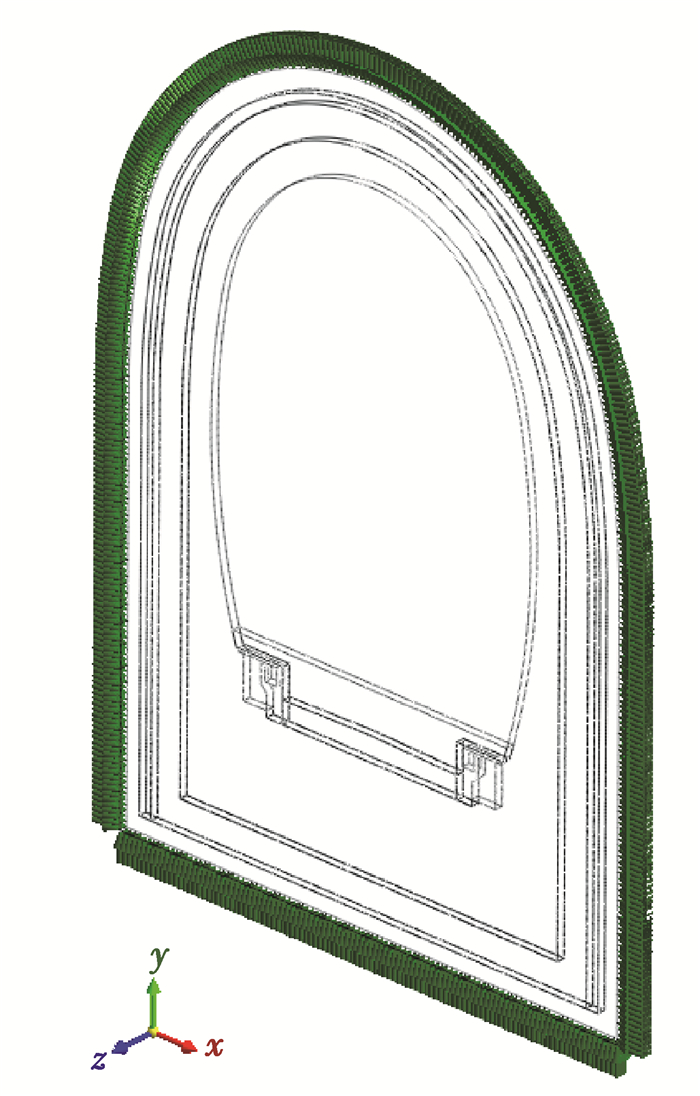
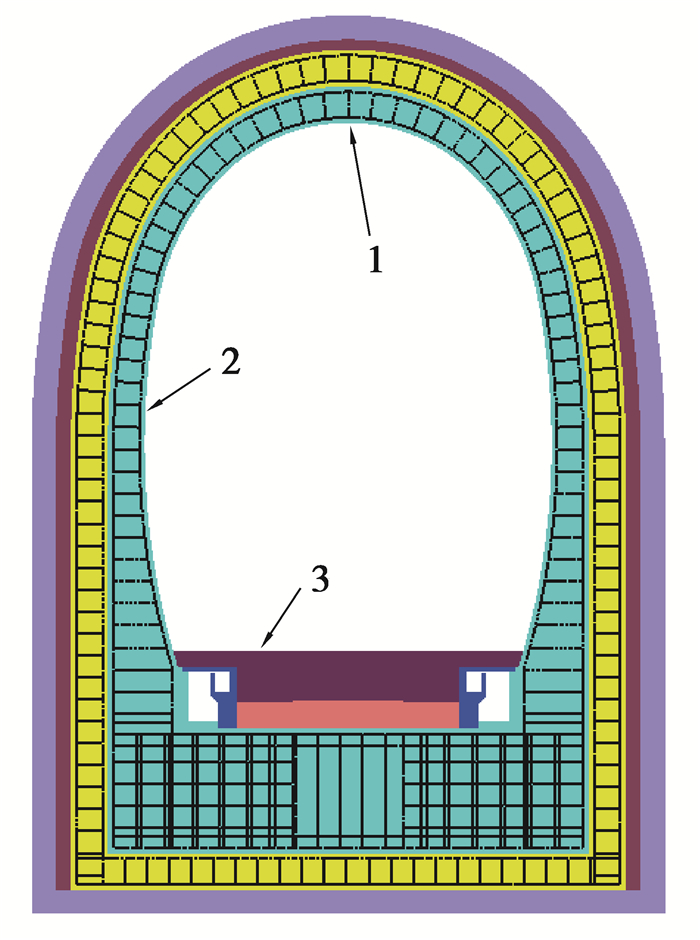
由于该隧道围岩稳定性较好,忽略围岩压力荷载,同时地下水压力较大,地下水压力沿衬砌高度方向变化忽略不计。仅考虑地下水静水压力载荷时,可在模型外侧自由面节点上施加法向水压力载荷,如图 3所示。水压载荷从0.1 MPa~10 MPa线性增加,同时约束模型纵向位移(Uz=0)。选取衬砌内侧拱顶、拱腰和盖板3个监测点,监测加载过程中结构的位移变化,如图 4所示。
|
图 3 水压力加载示意图 Fig. 3 The schematic diagram of water pressure |
|
图 4 监测点位置示意图 Fig. 4 The schematic diagram of monitoring points |
基于数值模拟结果,分析衬砌结构的位移、应力应变、界面破裂率等参数变化,研究衬砌结构随水压增加的渐进破坏过程。限于篇幅,仅给出10 MPa水压作用下钢筋混凝土衬砌的位移、应力、第一主应力等计算结果。
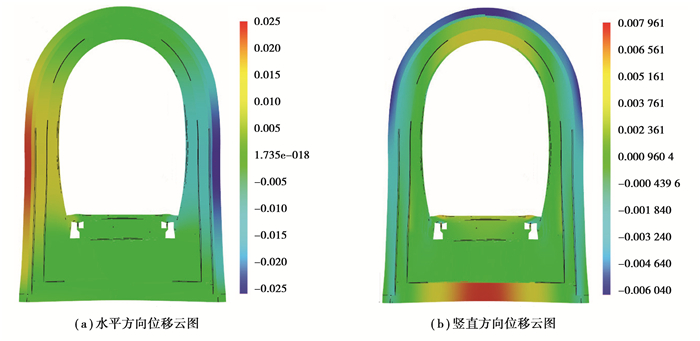
衬砌结构位移云图显示放大100倍后的云图,如图 5所示。最大水平位移位于衬砌中部,外侧为2.5 cm,内侧为1.2 cm。竖直位移较大处位于衬砌外侧顶部和底部,分别为0.8 cm和0.6 cm。衬砌内盖板向上隆起0.2~0.8 cm,盖板变形直接影响到铁轨抬升,对铁路安全运行有很大影响。初支变形大于二衬和三衬,3种结构间存在真实结构面且结构的物理力学参数不同,因此3种结构变形不连续。衬砌顶部初支向内变形,但二衬、三衬向外变形;衬砌中部初支、二衬、三衬均向内变形;衬砌底部初支向内变形,二衬、三衬变形较小。同时,初支、预留缝、二衬、三衬、底板、盖板相互界面间有明显裂缝,三衬内侧临空面和电缆槽侧壁也有大量裂纹。
|
图 5 衬砌结构位移云图 Fig. 5 The displacement of lining structure |
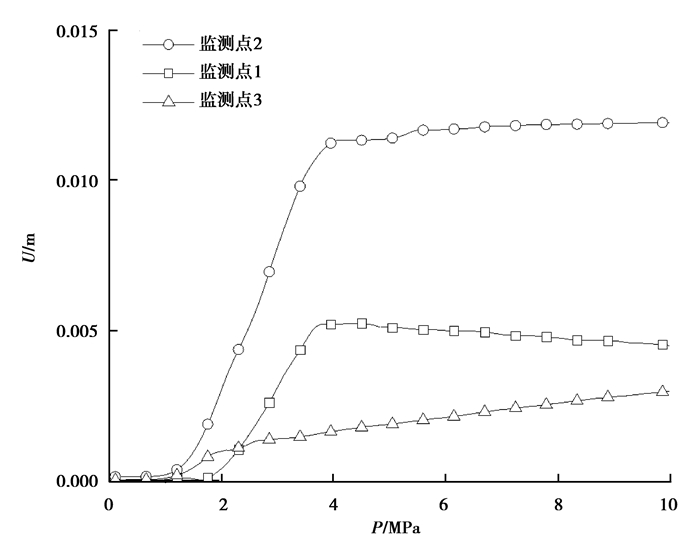
监测点的荷载-位移关系曲线如图 6所示,监测点1位于衬砌拱顶位置,监测点2位于衬砌拱腰位置,监测点3位于衬砌内部盖板表面。可以看出,隧道衬砌结构变形首先从衬砌拱腰位置开始,然后盖板变形,最后拱顶变形。各监测点位移量随水压增大而增加,水压从1.19 MPa到3.96 MPa,不同位置监测点变形量都迅速增加。水压大于3.96 MPa后,由于拱腰位置开裂,变形趋于稳定;因衬砌结构破裂,应力重新分布,拱顶变形方向发生改变;盖板变形持续增加,与水压近似线性关系。
|
图 6 监测点载荷位移曲线 Fig. 6 The curve of load-displacement on monitoring points |
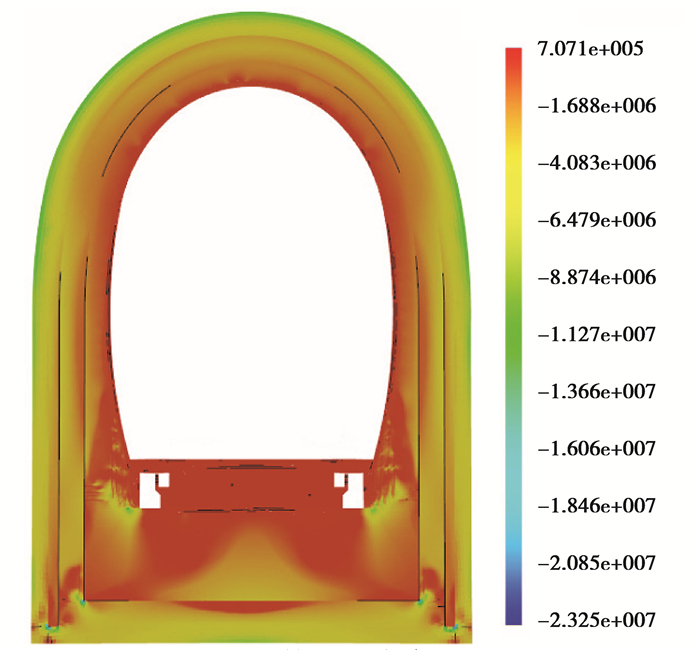
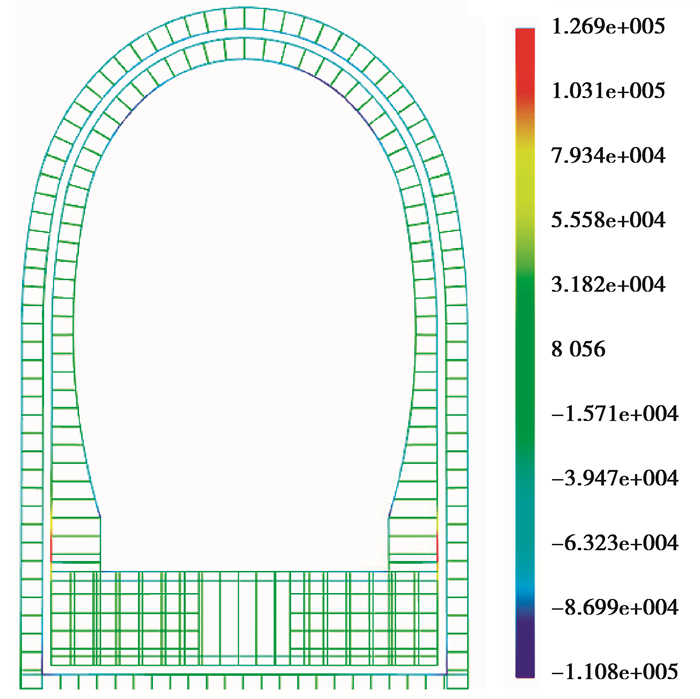
衬砌结构第一主应力云图,如图 7所示,第一主应力由外至内逐渐减小,三衬内部第一主应力为拉应力,最大为0.7 MPa,衬砌外侧表面第一主应力为压应力,最大为14 MPa。由于衬砌结构采用了直角边墙,排水沟、三衬以及二衬底角有明显的应力集中,最大值为23 MPa。钢筋轴力图,如图 8所示,环向钢筋轴向拉力最大值为127 kN,轴向拉应力为206 MPa,位于三衬直角边墙的外侧;轴向压力最大值为111 kN,轴向压应力为180 MPa,位于三衬内侧拱肩位置。径向钢筋轴向拉力和轴向压力最大值接近,轴向拉应力和压应力最大为137 MPa,位于三衬直角边墙内部。综合以上分析,环向钢筋和纵向钢筋均未达到屈服。
|
图 7 第一主应力云图 Fig. 7 The first principal stress of structure |
|
图 8 钢筋轴力图 Fig. 8 The Axial force of steel bar |
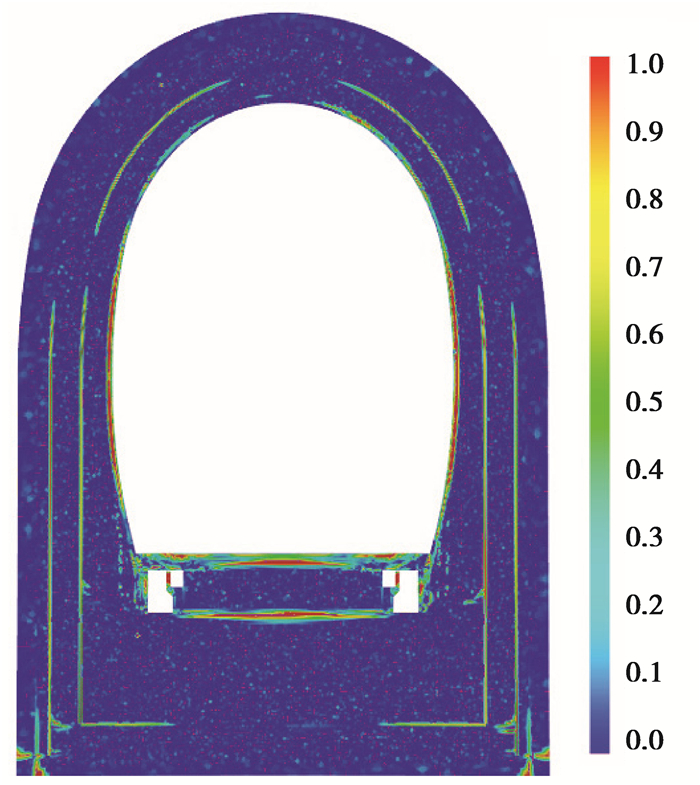
界面破裂包含衬砌中多层结构间的真实界面破裂,也包括块体间的虚拟界面破裂。界面破裂因子从0~1变化,达到1时界面完全破裂。衬砌结构界面破裂因子云图,如图 9所示。首先,初支、预留缝、二衬、三衬、盖板、底板相互接触的真实界面发生破裂,随后,三衬混凝土临空面和盖板混凝土的虚拟界面发生破裂。三衬部分界面破裂后,衬砌受力的有效截面积降低,衬砌结构有失稳风险。
|
图 9 界面破裂因子云图 Fig. 9 The interface crack ratio of structure |
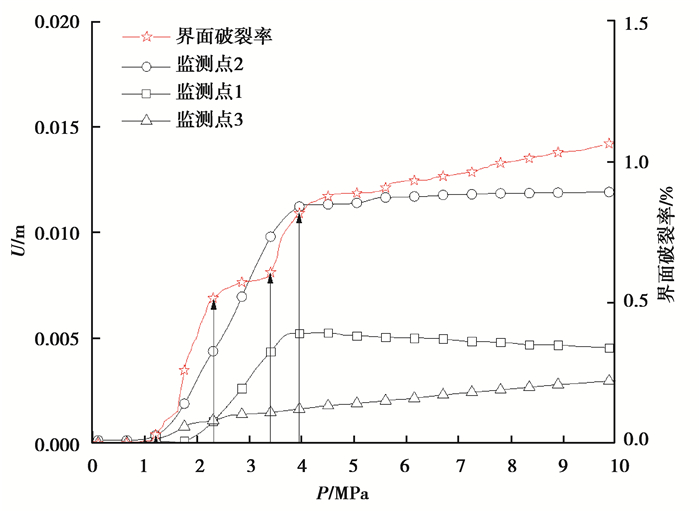
界面破裂率是衡量固体材料内部界面破坏程度的物理量,包含真实界面和虚拟界面。界面破裂率定义为界面破裂因子达到1的区域在模型中的占比,适合描述岩土体、混凝土等脆性材料的破坏程度,衬砌载荷-位移-界面破裂率关系曲线,如图 10所示。当载荷小于1.19 MPa时,衬砌内各监测点位移均无明显变化。当载荷在1.19~2.30 MPa时,由于初支、预留缝、二衬、三衬、盖板以及底板间界面破裂,界面破裂率迅速增加,各监测点位移也均迅速增加,变形先从拱腰和盖板开始。当载荷在2.30~3.41 MPa时,由于之前大量裂缝产生,衬砌结构应力重新分布,各监测点位移不断增加,结构变形仍在继续,但界面破裂率增加缓慢。当载荷在3.41~3.96 MPa时,由于三衬中部临空面混凝土、盖板混凝土、底板混凝土开裂,界面破裂率迅速增加。当载荷大于3.96 MPa时,由于三衬中部临空面混凝土已经破裂,拱腰监测点位移逐渐稳定,同时三衬承压有效截面积减小,应力重新分布,拱顶变形方向发生改变,开始向隧道内变形,盖板变形持续增大,此时界面破裂率持续增加,衬砌结构面临失稳。
|
图 10 载荷位移界面破裂率关系曲线 Fig. 10 The curve of load-displacement-interface crack ratio |
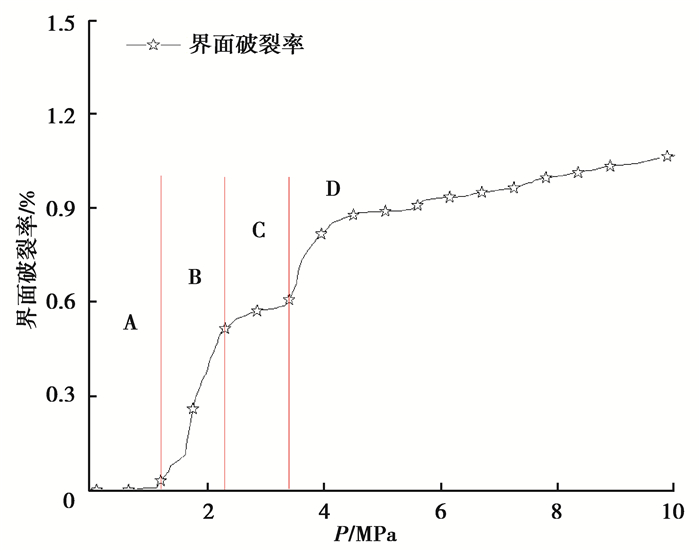
衬砌载荷-界面破裂率关系曲线,如图 11所示,分析得知衬砌结构失稳是一个渐变过程,该变化过程与界面破裂率变化有很强的相关性。界面破裂率随载荷变化可以分为A、B、C、D4个阶段。A阶段内,界面破裂率小于0.03%,随载荷增加没有明显改变,衬砌结构处于安全状态;B阶段内,界面破裂率从0.03%迅速增加至0.5%,随载荷增加衬砌内不同结构间真实界面破裂,界面破裂率迅速增加,此时衬砌内混凝土并未破裂,但结构安全性已经降低;C阶段内,界面破裂率从0.5%逐渐增加至0.6%,由于真实界面破裂后,应力重新分布,界面破裂率增加缓慢,混凝土结构内部发生局部破坏;D阶段,界面破裂率随载荷增加由0.6%迅速增加至0.8%,衬砌结构中混凝土开始破裂,衬砌承压有效截面积减小;当界面破裂率大于0.8%后,界面破裂率随载荷线性增加,衬砌结构逐步失稳。
|
图 11 载荷界面破裂率曲线 Fig. 11 The curve of load-interface crack ratio |
衬砌结构界面破坏从真实界面破坏逐步发展为块体内部虚拟界面破坏,最后结构失稳。因此,可以通过界面破裂率变化与衬砌结构渐变失稳之间的关系,来评估衬砌结构的当前状态以及承压能力。A阶段时,界面破裂率小于0.03%,可以认为衬砌结构处于安全状态;B阶段时,界面破裂率从0.03%迅速增加至0.5%,衬砌结构安全性降低,但仍处于安全状态,即相对安全状态;C阶段时,界面破裂率从0.5%逐渐增加至0.6%,衬砌结构处于临界失稳状态;D阶段时,界面破裂率大于0.6%,衬砌结构发生破坏,逐步失稳。在这4个阶段中,安全阶段载荷最大值可视为安全承压上限值,临界失稳阶段载荷最大值可视为极限承压值。文中三层钢筋混凝土衬砌,其安全承压最大值为1.19 MPa,临界承压值为3.41 MPa。
4 结论1) 基于有限元与离散元耦合的连续-非连续方法(CDEM),在块体和界面上采用拉剪复合的Mohr-Coulomb模型,引入拉伸破坏准则,可以较为准确地模拟材料的内部拉伸破坏、剪切破坏等问题,实现了钢筋混凝土衬砌在水压条件下渐变破坏过程的真实模拟。
2) 通过位移、第一主应力、界面破裂因子以及界面破裂率等参数变化规律可知,文中三层钢筋混凝土衬砌破坏以拉剪破坏为主。破坏首先发生在初支、二衬、三衬、底板、盖板等结构间的真实界面上,随着载荷不断增加,三衬内部、底板、盖板混凝土开裂破坏。当三衬内部开裂破坏,衬砌结构有效承载面积降低,逐渐失稳。
3) 通过界面破裂率变化与衬砌结构渐变失稳之间的关系,得到了评估衬砌结构当前状态以及承压能力的方法。衬砌结构界面破坏从真实界面破坏逐步发展为块体内部虚拟界面破坏,最后结构失稳。根据界面破裂率变化规律,衬砌承压可以分为4个阶段,即安全阶段(界面破裂率小于0.03%)、相对安全阶段(界面破裂率0.03%~0.5%)、临界失稳阶段(界面破裂率0.5%~0.6%)和失稳阶段(界面破裂率大于0.6%)。在这4个阶段中,安全阶段载荷最大值视为安全承压上限值,临界失稳阶段载荷最大值视为极限承压值。例如,文中三层钢筋混凝土结构的安全承压最大值为1.19 MPa,极限承压值为3.41 MPa。该方法可以优化衬砌结构设计和衬砌结构风险评估。
| [1] |
李忠.寒区公路隧道二次衬砌环向裂缝机理研究[D].长春: 吉林大学, 2011. LI Zhong. Mechanism study on circumferential cracks of secondary lining of road tunnel in cold regions[D]. Changchun: Jilin University, 2011. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-1011101521.htm |
| [2] |
王志杰, 赵启超, 刘若愚, 等. 深埋双线铁路隧道衬砌高水压分界值研究[J]. 铁道标准设计, 2017(2): 78-84. WANG Zhijie, ZHAO Qichao, LIU Ruoyu, et al. Research on boundary value of high hydraulic pressure on lining in deep-lying double-track railway tunnel[J]. Railway Standard Design, 2017(2): 78-84. (in Chinese) |
| [3] |
陈耀华. 铁路隧道抗水压衬砌结构稳定性研究[J]. 铁道建筑, 2016(5): 100-103. CHEN Yaohua. Study on stability of anti-hydraulic pressure lining of railway tunnel[J]. Railway Engineering, 2016(5): 100-103. (in Chinese) DOI:10.3969/j.issn.1003-1995.2016.05.22 |
| [4] |
王秀英, 王北华, 谭忠盛, 等. 高水压单线铁路隧道二次衬砌水压设计限值研究[J]. 现代隧道技术, 2018, 55(3): 37-45. WANG Xiuying, WANG Beihua, TAN Zhongsheng, et al. Study on designed water pressure limit on secondary lining for single-track railway tunnels with high water pressure[J]. Modern Tunnelling Technology, 2018, 55(3): 37-45. (in Chinese) |
| [5] |
万飞, 王华牢, 谭忠盛. 局部水压作用下单线铁路隧道衬砌设计参数研究[J]. 现代隧道技术, 2017, 54(3): 8-16, 25. WAN Fei, WANG Hualao, TAN Zhongsheng. Research on the design parameters of a single-track railway tunnel lining under local water pressure[J]. Modern Tunnelling Technology, 2017, 54(3): 8-16, 25. (in Chinese) |
| [6] |
Li S H, Wang J G, Liu B S, et al. Analysis of critical excavation depth for a jointed rock slope using a face-to-face discrete element method[J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 331-348. DOI:10.1007/s00603-006-0084-9 |
| [7] |
冯春, 李世海, 刘晓宇. 半弹簧接触模型及其在边坡破坏计算中的应用[J]. 力学学报, 2011, 43(1): 184-192. FENG Chun, LI Shihai, LIU Xiaoyu. Semi-spring contact model and its application to failure simulation of slope[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 184-192. (in Chinese) |
| [8] |
Feng C, Li S H, Liu X Y, et al. A semi-spring and semi-edge combined contact model in CDEM and its application to analysis of Jiweishan landslide[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(1): 26-35. DOI:10.1016/j.jrmge.2013.12.001 |
| [9] |
Li S H, Wang J G, Liu B S, et al. Analysis of critical excavation depth for a jointed rock slope using a face-to-face discrete element method[J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 331-348. DOI:10.1007/s00603-006-0084-9 |
| [10] |
Wang Y N, Zhao M H, Li S H, et al. Stochastic structural model of rock and soil aggregates by continuum-based discrete element method[J]. Science in China Series e Engineering & Materials Science, 2005, 48(1): 95-106. |
| [11] |
金浏, 韩亚强, 杜修力. 混凝土单轴动态拉伸强度随机性的统计特性分析[J]. 振动与冲击, 2016, 35(24): 6-13, 26. JIN Liu, HAN Yaqiang, DU Xiuli. Statistical investigationon the randomness of uniaxial dynamic tensile strengths of concrete[J]. Journal of Vibration and Shock, 2016, 35(24): 6-13, 26. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

