2. 西安公路研究院, 西安 710064
2. Xi'an Highway Research Institute, Xi'an 710064, P. R. China
多梁式桥梁具有受力性能良好、施工简单快捷等优点, 已被广泛应用于城市道路、高速公路的中小跨径桥梁, 相关研究表明[1], 多梁式结构的横向联系保证着全桥整体受力, 一旦横向联系受损, 导致主梁单梁受力, 其整体性能将严重下降, 威胁行车安全。
结构强度的损伤必然导致结构动力参数的改变, 利用这些参数的变化进行工程结构健康检测是近年来研究的热点问题, 其中基于结构振动模态的损伤识别方法由于其良好的适用性得到了广泛的关注。Pandey等[2]于1991年提出曲率模态损伤识别的概念, 该方法由于损伤灵敏度高而受到了大量应用[3-4]。文献[5]通过单梁理论分析和算例证明了曲率模态差相较于曲率模态损伤识别效果更好, 但后续研究发现曲率模态差[6-7]无法识别出梁结构振动模态节点处的损伤, 陈翔[8]、Rucevskis[9]在对板这类二维结构进行损伤识别时指出, 由于模态节线的存在, 在运用多阶曲率模态差综合判别效果会更好。徐飞鸿等[10-12]在得到单梁的曲率模态后, 利用拟合的方法构造了新的损伤识别指标, 弱化了节点节线的干扰。参考文献[13-15]运用单梁弯曲理论推得了T型多梁结构的曲率表达式, 并利用高斯曲率模态差进行了主梁损伤位置定位, 识别效果较好, 但因为损伤因子不是指标的单一变量, 无法对损伤程度进行判别。
综上, 目前大部分桥梁损伤识别都仅针对单梁结构, 对于多梁结构横向联系的损伤识别尚研究较少, 且其曲率模态指标也仅针对单梁单阶弯曲振动, 运用多阶曲率模态综合判别也较少。文中对在役多梁式桥梁结构横向损伤识别进行研究, 利用G-M法的思想将多梁式结构转化为一块正交异性板, 基于梁弯曲理论, 引入该结构横纵两向曲率的计算表达式, 定性得到了刚度折减对两向曲率影响, 之后考虑曲率模态差损伤识别的不足, 提出利用结构多阶叠加曲率模态差变化率进行单位置、多位置的损伤工况识别, 识别结果表明:利用桥梁纵向叠加曲率模态差变化率损伤点识别精度更高, 未损伤位置处的指标数据变动更小。
1 叠加曲率模态差变化率的提出 1.1 理论基础不同于单箱截面形式的连续刚构桥梁、连续梁桥振动位移为一条振型线函数, 多梁式结构的振动位移类似于薄板结构在空间上表现为一个曲面, 即一个二维平面上的振型面函数, 而且根据相关算例表明, 对于多梁式桥梁结构无论宽窄, 都可将其转化为正交异性板计算横向分布系数, 即其结构的受力接近一块薄板受力, 在韩西[15]的研究中也发现多梁式结构的低阶振型也更接近薄板的振动形态, 而非单梁的振动形式, 因此考虑利用G-M法中相关理论, 将多梁式结构转化为正交异性板考虑其振动形态。应用薄板振动理论中的相关定义, 可以将此种结构的振动位移函数设为
| $ \omega = \sum\limits_{m = 1}^\infty {{\omega _m}} = \sum\limits_{m = 1}^\infty {{q_m}} (t){\varphi _m}(x, y), $ | (1) |
式中:φm(x, y)为第m阶振型, 可以将其分解为x向振型φ(x)和y向振型φ(y); qm(t)为时间坐标函数。
正交异性板结构在发生振动弯曲变形时, 主截面和其正交的横截面都将发生偏转, 设主截面绕横向偏转角度为θx, 横截面绕纵向偏转角度为θy, 在小挠度理论振动的前提下, 偏转角θx和θy可以用振动位移函数ω(x, y, t)对主向x和横向y的变化率来表示, 即:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _x} = \frac{{\partial \omega }}{{\partial x}}, }\\ {{\theta _y} = \frac{{\partial \omega }}{{\partial y}}。} \end{array}} \right. $ | (2) |
根据式(2), 类似于梁弯曲理论中关于曲率的定义, 假设振型面函数在x向和y向曲率变化函数分别为ρ(x)和ρ(y), 则有
| $ \left\{ {\begin{array}{*{20}{l}} {\rho (x) = \frac{{{\partial ^2}\omega }}{{\partial {x^2}}} = \sum\limits_{m = 1}^\infty {{q_m}} (t)\varphi _{mx}^{\prime \prime }(x, y), }\\ {\rho (y) = \frac{{{\partial ^2}\omega }}{{\partial {y^2}}} = \sum\limits_{m = 1}^\infty {{q_m}} (t)\varphi _{my}^{\prime \prime }(x, y)。} \end{array}} \right. $ | (3) |
根据弹性力学可知, 对于正交异性板结构的x向和y向弯矩计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{M_x}}}{{{D_x}}} = \frac{{{\partial ^2}\omega }}{{\partial {x^2}}} + \mu \frac{{{\partial ^2}\omega }}{{\partial {y^2}}}, }\\ {\frac{{{M_y}}}{{{D_y}}} = \frac{{{\partial ^2}\omega }}{{\partial {y^2}}} + \mu \frac{{{\partial ^2}\omega }}{{\partial {x^2}}}, } \end{array}} \right. $ | (4) |
式中:Mx为纵向截面单位长度作用的绕横向y的弯矩; My为横向截面单位长度作用的绕纵向x的弯矩; Dx, Dy为在弹性主向上的弯曲刚度; μ为材料泊松比。
根据式(3)及式(4)可以得到:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{M_x}}}{{{D_x}}} = \rho (x) + {\mu _2}\rho (y), }\\ {\frac{{{M_y}}}{{{D_y}}} = \rho (y) + {\mu _1}\rho (x)。} \end{array}} \right. $ | (5) |
假定结构局部发生损伤后, 对整体受力和振型模态分布都影响非常小, 即弯矩M保持不变, 正交异性板某点某一方向刚度折减也对应着多梁式结构桥梁某点某方向上的刚度折减, 则由式(5)可知, 多梁式结构在某方向截面刚度的改变将导致处于该点2个方向上曲率之和增大, 在无刚度折减处2个方向的曲率之和不会发生明显改变, 因此, 结构在2个方向上曲率模态的差值必定发生了改变, 致使两正交方向的曲率模态之和发生突变, 振型面不再为光滑的曲面, 故可以将曲面上某一点曲率模态差的突变数值化, 作为多梁式结构损伤识别的重要依据; 对于多梁式结构桥梁, 类似于薄板结构, 其振型面上一点具有2个正交方向的曲率模态, 但尚未可知这2个方向上的曲率模态受纵向或者横向刚度折减影响的程度, 因而需要分别求解2个方向上的曲率模态差, 综合2个方向上的曲率模态差的改变确定损伤位置。
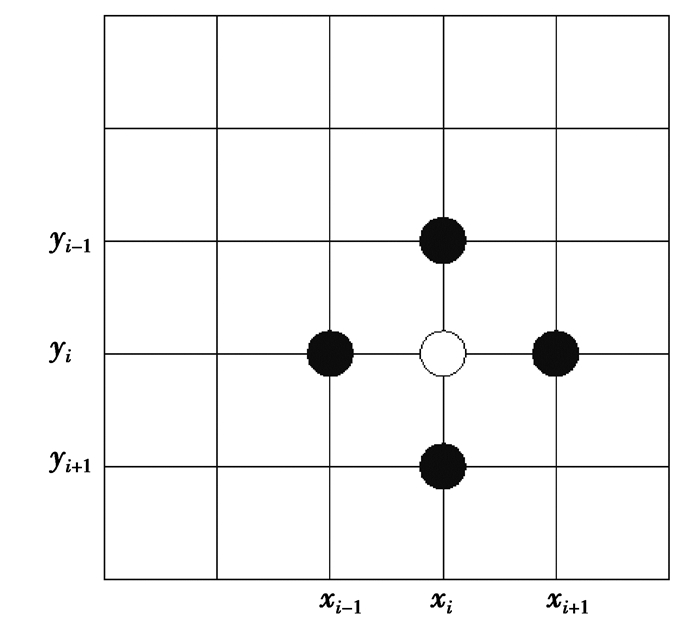
1.2 曲率模态差变化率理论及及其缺点国内外尚未有能够直接测量结构曲率的传感器, 在相关试验中通常是等间距均匀布置并测取多个点的位移模态值, 再通过差分的算法得到某一点的曲率模态, 计算图示如图 1所示。
|
图 1 差分法计算示意图 Fig. 1 Schematic chart of differential method |
利用差分公式求取的任意点曲面两正交方向的曲率公式为
| $ \left\{ {\begin{array}{*{20}{l}} {\varphi _{xx}^{\prime \prime }\left( {{x_i}, {y_i}} \right) = \frac{{\varphi \left( {{x_{i + 1}}, {y_i}} \right) - 2\varphi \left( {{x_i}, {y_i}} \right) + \varphi \left( {{x_{i - 1}}, {y_i}} \right)}}{{h_x^2}}, }\\ {\varphi _{yy}^{\prime \prime }\left( {{x_i}, {y_i}} \right) = \frac{{\varphi \left( {{x_i}, {y_{i + 1}}} \right) - 2\varphi \left( {{x_i}, {y_i}} \right) + \varphi \left( {{x_i}, {y_{i - 1}}} \right)}}{{h_y^2}}, } \end{array}} \right. $ | (6) |
式中:φ(xi, yi)为第m阶振型中点(xi, yi)处的振型值; hx和hy分别表示在x向和y向的间距值。
计算结构损伤前后某点在x向或y向上的曲率模态, 并基于此得到曲率模态差值为
| $ \Delta {\varphi ^{\prime \prime }} = {\varphi ^{\prime \prime }} - {\varphi ^{\prime \prime }}_D, $ | (7) |
式中:φ″和φ″D分别表示利用差分法算得的x向或y向损伤前后曲率模态。
根据以往的研究表明, 应用曲率模态差值可以达到初步识别损伤的效果, 但是曲率模态差值会在无损伤位置处或临近损伤位置处均出现差值较大的情况, 因此, 仅以曲率模态差值为损伤识别的指标会引起误判。为了减少误判并明确损伤位置, 提出曲率模态差变化率, 以x向为例, 为
| $ k\left( {{x_i}, {y_i}} \right) = \frac{{\Delta {\varphi ^{\prime \prime }}\left( {{x_{i + 1}}, {y_i}} \right) - \Delta {\varphi ^{\prime \prime }}\left( {{x_i}, {y_i}} \right)}}{{{h_x}}}, $ | (8) |
式中:k(xi, yi)表示(xi, yi)处曲率模态差变化率; Δφ″(xi+1, yi)和Δφ″(xi, yi)分别表示(xi+1, yi)和(xi, yi)点曲率模态差; hx为(xi+1, yi)和(xi, yi)点之间的距离。
由式(7)和式(8)可知, 若在曲率模态差为零值处, 即损伤点处于曲率模态差的节点、节线位置或者前后插值处振型面值差距较小处, 例如薄板一阶对称竖弯跨中处, 会导致此点的数值变化幅度不明显, 无法判断出是否发生了损伤, 有可能存在此处发生了严重的损伤却无法判别, 这是使用单阶曲率模态差进行损伤识别的不足之处。
1.3 叠加曲率模态差变化率前文分析每阶模态都存在节点, 且众多文献中也说明采用高阶振型对于损伤进行判别比低阶振型效果更为明显, 因此考虑将多阶振型进行叠加, 以避免使用单阶模态在其节点或节线处无法判别损伤, 继续以x向为例, 叠加曲率模态差变化率为
| $ K\left( {{x_i}, {y_i}} \right) = \frac{{\sum\limits_{m - 1}^N \Delta \varphi _m^{\prime \prime }\left( {{x_{i + 1}}, {y_i}} \right) - \sum\limits_{m - 1}^N \Delta \varphi _m^{\prime \prime }\left( {{x_i}, {y_i}} \right)}}{{N{h_x}}}。$ | (9) |
K(xi, yi)为结构的前N阶叠加曲率模态差变化率。理论上叠加曲率模态差变化率可以避免使用单阶模态导致在节点或节线上损伤误判, 提高对结构损伤位置的识别准确率, 弥补曲率模态差变化率指标的不足。叠加曲率模态差变化率的计算步骤为:第一步, 根据式(6)和式(7)计算2个方向的多阶曲率模态差; 第二步, 根据式(8)计算2个方向上多阶曲率模态差变化率; 第三步, 由式(9)计算x向或y向叠加曲率模态差变化率, 综合2个方向上识别结果得到最终损伤位置。
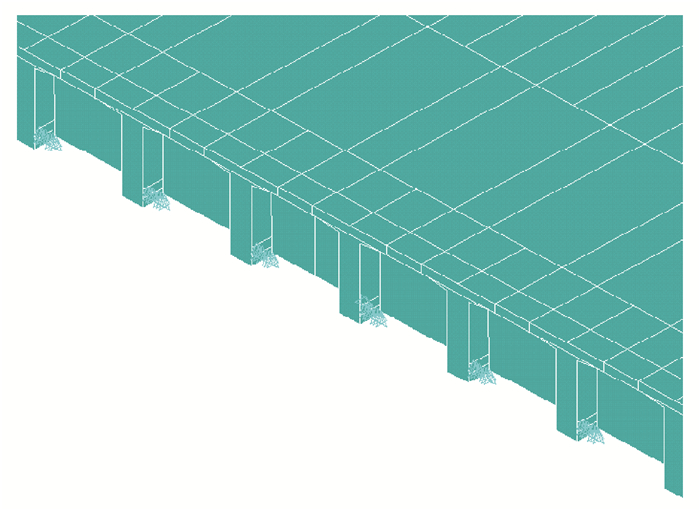
2 算例分析 2.1 有限元模型利用Ansys有限元软件, 建立跨径为30 m的简支T梁桥为研究对象, 横桥向为7片T梁, 5片横隔梁从端部起均匀布置于桥跨径方向, 考虑到实体切分法建模比较麻烦, 因此本模型采用节点耦合法建立, 分别建立混凝土单元和钢筋单元, 即利用耦合节点自由度的方式将力筋单元与混凝土单元联系起来, 采用初应变法施加预应力。混凝土采用solid65实体单元模拟, 预应力钢筋采用link8单元建立, 其力学参数分别为:混凝土弹性模量取3.45×104 MPa, 预应力钢筋弹性模量取1.95×105 MPa, 具体模型见图 2所示。
|
图 2 有限元模型 Fig. 2 Finite element model |
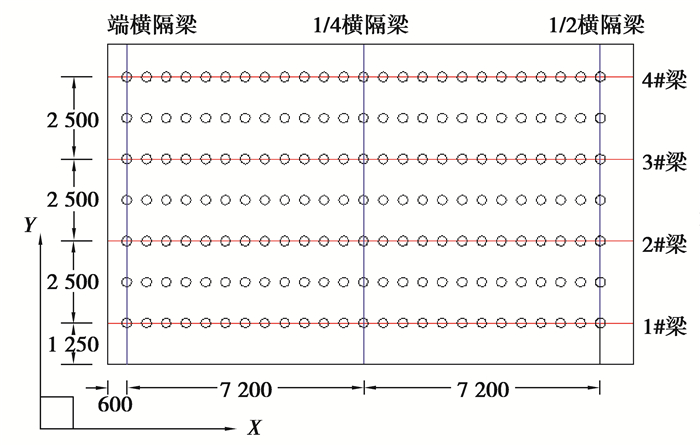
考虑到在实际工程中, 位移模态差的测取一般为均匀布置传感器得到各个点的位移模态值, 再根据差分算法近似求得, 为与实际工程情况保持相同, 在求得有限元模型各阶振型之后, 将桥面划分成横纵向等间距的网格, 横纵向网格线的交点作为拾取点, 利用拾取点的振型位移作为损伤识别的基本数据。图 3为桥梁左下角1/4范围内拾取点布置情况图。
|
图 3 桥梁左下1/4范围内振型拾取点布置情况示意图 Fig. 3 Schematic diagram of vibration pick-up point arrangement in the left lower 1/4 range of bridge |
得到未损伤结构的曲率模态参数后, 采用结构刚度折减的方式来模拟多梁式桥梁结构的损伤, 定义结构刚度系数为D, 其意义为损伤后单元刚度与损伤前的比值, 因为所选结构的对称性, 故模拟的损伤位置均选取在桥梁左下角1/4范围内, 为充分验证本方法的适用性, 文中所模拟的损伤工况, 包含了主梁损伤、湿接缝损伤及横隔梁损伤在内的单位置、多位置不同损伤程度共计6种工况, 损伤节段平面为一长宽为600~800 mm的矩形, 节段中心点详细位置(单位:mm):①主梁(13 500, 7 500), ②横隔梁(7 800, 3 750), ③湿接缝(11 400, 1 250), 各损伤工况的损伤单元组合及其结构刚度系数见表 1所示。
| 表 1 损伤工况 Table 1 Damage condition |
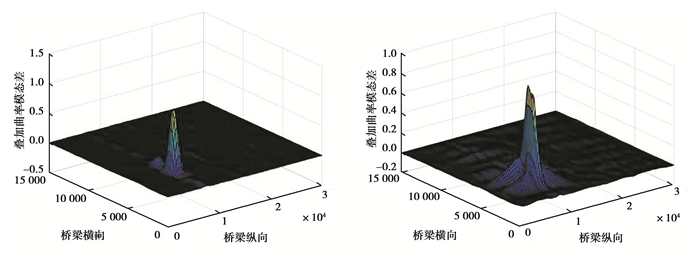
针对中小跨径多梁式结构桥梁, 在实际工程中小跨径桥梁高阶振型较难获取, 且根据有限元模型计算结果显示文中依托桥梁的第4阶振型为主梁对称横弯, 已无法识别竖向的损伤, 因此决定选择基于前3阶振型计算x向和y向叠加曲率模态差变化率, 将叠加指标计算结果归一化后, 利用Matlab编制程序进行绘图, 限于篇幅原因仅列出工况1、2、5绘图结果, 见图 4~图 6。详细损伤识别结果坐标见表 2。损伤突变点数值变化见表 3所示。
|
图 4 工况1 x向和y向叠加曲率模态差变化率 Fig. 4 Condition 1 x-scale and y-scale change rate of superposition curvature mode difference |
|
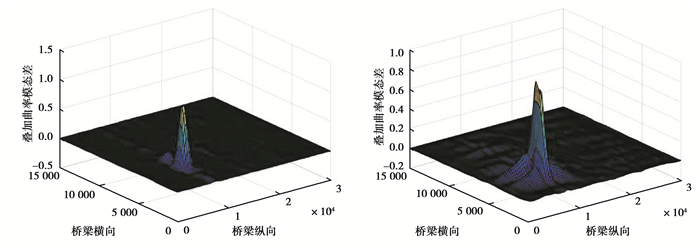
图 5 工况2 x向和y向叠加曲率模态差变化率 Fig. 5 Condition 2 x-scale and y-scale change rate of superposition curvature mode difference |
|
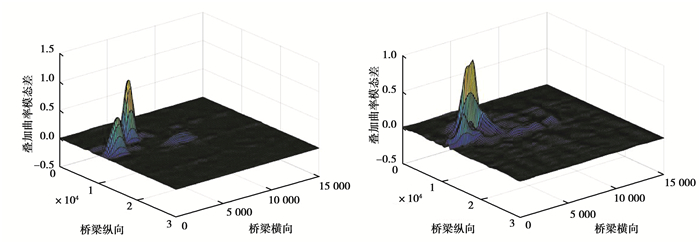
图 6 工况5 x向和y向叠加曲率模态差变化率 Fig. 6 Condition 5 x-scale and y-scale change rate of superposition curvature mode difference |
| 表 2 损伤识别坐标结果表 Table 2 Damage identification coordinate results table |
| 表 3 叠加曲率模态差变化率突变点数值表 Table 3 Number table of sudden change points of superposition curvature mode difference rate |
由图 3~图 5可以看出, 多梁式桥梁结构在损伤点2个方向上的曲率模态差均发生了突变, 导致该点叠加曲率模态差变化率发生了变化, 2个方向上的叠加指标都可识别横向联系损伤; 对比各工况计算结果发现, 纵向叠加曲率模态差改变率要比横向更加精确, 引起其他无损伤位置的指标值变化幅度更小, 误判识别率更低, 在利用横向指标进行主梁损伤判别时, 出现了多处未损伤位置数值突变; 应用文中提出的叠加曲率模态差变化率判别时, 无损伤位置处的指标数值基本为零或变动很小, 损伤处指标数值变化幅值大, 损伤识别效果良好。
由表 2可以看出, 利用文中方法进行单位置、多位置损伤识别中, 损伤识别坐标与实际损伤坐标位置十分接近, 考虑到文中有限元模型中设置的损伤单元平面尺寸实为一长宽在600~800 mm的矩形, 故损伤识别结果基本都在损伤单元平面范围内, 根据各损伤工况识别结果可以看出, 多位置的损伤位置识别并未受到多处损伤影响。
由表 3可以看出, 工况1~3的单位置的叠加曲率模态差变化率与工况5的数值基本相同, 故可以认为多位置损伤引起的单位置上叠加曲率模态差变化率改变值可以忽略不计, 即可忽略多位置损伤之间的耦合效应, 利用单点位置上文中损伤指标数值的变化即可定量的判断损伤程度。
3 结论1) 利用G-M法中的思想将多梁式结构比拟成一块正交异性板, 利用梁的弯曲理论, 引入多梁式结构的纵向和横向曲率表达式, 并利用该表达式得到了此结构横纵向刚度与2个方向上曲率模态关系, 基于以上推导, 针对单阶曲率模态差变化率识别损伤的不足, 提出了叠加曲率模态差变化率并进行了多个损伤工况的识别, 算例表明该指标能够较为准确识别结构损伤点位置。
2) 从识别结果中亦可看出, 文中提出的叠加曲率模态差对于单位置及多位置的损伤点损伤指标数值变化幅度明显, 未损伤点其值基本为零, 识别效果明显, 且单损伤点指标数值几乎不受其他位置影响, 具有很强的独立性, 可利用单损伤点指标的变化定量的判别损伤程度。总之, 叠加曲率模态差变化率能够较为准确全面地提供损伤信息, 可以为后续桥梁检测提供有效损伤识别参数。
| [1] |
杜晶.在役T型梁桥横向联系损伤的动静力参数分析[D].北京: 北京交通大学, 2018. DU Jing. Dynamic and static parameter analysis on transverse connection damage of in-service T girder bridges[D]. Beijing: Beijing Jiaotong University, 2018. (in Chinese) |
| [2] |
Pandey A K, Biswas M, Samman M M. Damage detection from changes in curvature mode shapes[J]. Journal of Sound and Vibration, 1991, 145(2): 321-332. DOI:10.1016/0022-460X(91)90595-B |
| [3] |
Abdel Wahab M M, de Roeck G. Damage detection in bridges using modal curvatures:application to a real damage scenario[J]. Journal of Sound and Vibration, 1999, 226(2): 217-235. DOI:10.1006/jsvi.1999.2295 |
| [4] |
邓焱, 严普强. 梁及桥梁应变模态与损伤测量的新方法[J]. 清华大学学报(自然科学版), 2000, 40(11): 123-127. DENG Yan, YAN Puchiang. New approach for strain modal measurement and damage detection of bridges[J]. Journal of Tsinghua University(Science and Technology), 2000, 40(11): 123-127. (in Chinese) |
| [5] |
Li F C, Li C, Zhang A F. Curvature modal analysis and numerical simulation in diverse structural damage identification[J]. Journal of Ship Mechanics, 2006, 10(6): 115-121. |
| [6] |
Qin Y. Study on damage identification of simple beam bridge based on the first-order curvature mode ratio[J]. Applied Mechanics and Materials, 2014, 578/579: 1032-1036. DOI:10.4028/www.scientific.net/AMM.578-579.1032 |
| [7] |
Frans R, Arfiadi Y, Parung H. Comparative study of mode shapes curvature and damage locating vector methods for damage detection of structures[J]. Procedia Engineering, 2017, 171: 1263-1271. DOI:10.1016/j.proeng.2017.01.420 |
| [8] |
陈翔, 彭华, 张宏宇, 等. 板结构损伤识别的叠加曲率法研究[J]. 武汉大学学报(工学版), 2015, 48(4): 538-541. CHEN Xiang, PENG Hua, ZHANG Hongyu, et al. Research on curvature modal superposition method for plate structure damage identification[J]. Engineering Journal of Wuhan University, 2015, 48(4): 538-541. (in Chinese) |
| [9] |
Rucevskis S, Akishin P, Chate A. Numerical and experimental study on the application of mode shape curvature for damage detection in plate-like structures[J]. Solid State Phenomena, 2015, 220/221(264): 270. |
| [10] |
徐飞鸿, 朱检, 张婷婷. 基于曲率模态曲线的结构损伤识别方法[J]. 世界地震工程, 2015, 31(4): 36-42. XU Feihong, ZHU Jian, ZHANG Tingting. A method for structural damage identification based on curvature-mode curve[J]. World Earthquake Engineering, 2015, 31(4): 36-42. (in Chinese) |
| [11] |
徐宏文, 李宁, 谢永健. 基于模态曲率曲线拟合的板结构损伤识别研究[J]. 工程抗震与加固改造, 2018, 40(4): 16-20. XU Hongwen, LI Ning, XIE Yongjian. Research on damage identification of the plate-type structures based on curve fitting of themodal curvature[J]. Earthquake Resistant Engineering and Retrofitting, 2018, 40(4): 16-20. (in Chinese) |
| [12] |
周奎, 徐宏文, 方早, 等. 基于柔度曲率曲线拟合的薄板结构损伤识别研究[J]. 上海理工大学学报, 2018, 40(3): 296-301. ZHOU Kui, XU Hongwen, FANG Zao, et al. Damage identification of thin plate-type structures based on the flexibility curvature curve fitting[J]. Journal of University of Shanghai for Science and Technology, 2018, 40(3): 296-301. (in Chinese) |
| [13] |
张波, 王宗元, 王赟, 等. 利用模态曲率差法进行弹性薄板的损伤检测[J]. 地下空间与工程学报, 2011, 7(1): 144-149. ZHANG Bo, WANG Zongyuan, WANG Bin, et al. Damage detection for elastic thin late with modal curatured difference method[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(1): 144-149. (in Chinese) |
| [14] |
何钦象, 杨智春, 姜峰, 等. 薄板损伤检测的高斯曲率模态差方法[J]. 振动与冲击, 2010, 29(7): 112-115. HE Qinxiang, YANG Zhichun, JIANG Feng, et al. Damage detection for an elastic thin plate based on Gauss curvature modal difference[J]. Journal of Vibration And Shock, 2010, 29(7): 112-115. (in Chinese) |
| [15] |
韩西, 李庆达, 钟厉, 等. 基于高斯曲率模态差的T梁结构二维损伤识别研究[J]. 重庆交通大学学报(自然科学版), 2012, 31(4): 747-750. HAN Xi, LI Qingda, ZHONG Li, et al. Study on two-dimensional damage identification of T-beam based on gaussian curvature mode difference[J]. Journal of Chongqing Jiaotong University(Natural Science), 2012, 31(4): 747-750. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

