b. 重庆大学 机械传动国家重点实验室, 重庆 400044
b. State Key Laboratory of Mechanical Transmission, Chongqing 400044, P. R. China
近场声全息(nearfield acoustic holography, NAH)[1]是识别声源和可视化声场的有效工具。该方法利用麦克风阵列捕获声源辐射中的倏逝波成分,使其重建结果不受瑞利判据的限制,从而提高声场重建分辨率。NAH技术有多种实现方法,如基于空间傅里叶变换[2-3],平面或球面波展开[4],逆问题数值方法等[5-6]。波叠加法(wave superposition method, WSM)[7-8],也称为等效源法(equivalent source method, ESM),是一种性能优越的方法。根据ESM理论[9],任意形状的声源所辐射的声场可以被虚拟表面上的一系列虚拟等效源替代。等效源的强度可以通过匹配源或全息图表面上的边界条件来确定。这种方法因其较强的适应性以及在数值计算上的优势,近年来已得到广泛应用[10-11]。
在大多数声学研究中麦克风的数量是有限的,因此,等效源法和其他全息变换方法一样,在求解的过程中也会存在不适定性问题。为了解决这个问题,通常采用l2范数正则化方法[12]来稳定求解过程。然而,该方法受Nyquist采样定理限制,当声源频率大于麦克风平均间距所对应的半波长频率时,该方法的重建精度便会迅速降低。
近年来,基于稀疏正则化的压缩感知(compressed sensing, CS)技术在信号/图像处理领域受到越来越多的关注[13-14]。CS的基本思想是:利用信号的稀疏性或可压缩性,通过某种观测方法得到少量非相关的测量值,进而通过优化算法来实现高维信号的精确或近似精确的重构。目前,CS已逐步应用于NAH领域以减少空间采样点数量并扩大声源识别的频率范围。Chardon等[15]首先将CS的概念引入NAH并构建了NAH的稀疏框架。Fernandezg-Grande等[16]将CS理论应用于基于球形麦克风阵列测量的平面波展开方法中。Hald [17]提出了快速宽带声全息法(fast wideband holography, WBH),构造了平方残差方程并利用包含动态滤波过程的最速下降法求取等效源幅值的稀疏解。Fernandezg-Grande[18]对压缩等效源法(compressive equivalent source method, CESM)进行了详细的研究,讨论了获取具有较低列相干性的感知矩阵的重要性。Bi等[19]提出了一种压缩模态等效点源法(a compressed modal equivalent point source method, CMESM), 通过对辐射阻抗矩阵进行特征值分解,得到源强的一系列模态,在l1范数约束下,对板结构声源辐射声场进行重构。
为进一步提升空间连续型声源声场重建与声源识别性能,笔者结合等效源法和压缩感知理论,提出了一种压缩奇异值分解等效源法。该方法首先采用等效源法和奇异值分解法得到一系列正交基,然后在l1范数约束下,利用CVX凸优化工具箱对声场进行重构。最后结合高阶矩阵函数波束形成理论对所提方法的输出结果进行修正,通过提高阶次值,不断缩小识别到的声学中心覆盖范围,提高声源识别定位精度。数值仿真分析和实验应用均验证了该方法的有效性和实用性。
1 等效源法基本原理ESM的基本思想是:将声源体的辐射声场用一系列等效源产生的声场叠加替代,然后通过全息面测得声压反求出一系列等效源的强度,进而实现整个声场重建与预测。该方法不涉及波数域中的傅里叶变换,因此可以从根本上避免“有限截断误差”和“卷绕误差”。ESM原理如图 1所示。其中M表示全息面(测量面),E表示等效源面,R表示重建面。

|
图 1 ESM原理示意图 Fig. 1 The diagram of ESM |
假设在等效源面上分布有N个虚拟等效源,在测量面上有M个麦克风,则第m个测量点的声压可以表示为
| $ \mathit{\boldsymbol{p}}\left( m \right) = \sum\limits_{n = 1}^N {g\left( {{\mathit{\boldsymbol{r}}_m}\left| {{\mathit{\boldsymbol{r}}_n}} \right.} \right){\mathit{\boldsymbol{q}}_n}} , $ | (1) |
其中,g(rm|rn)表示第n个等效源与第m个测点之间的声压传递函数,它可以表示为
| $ g\left( {{\mathit{\boldsymbol{r}}_m}\left| {{\mathit{\boldsymbol{r}}_n}} \right.} \right) = \frac{{\exp \left( { - ik\left\| {{\mathit{\boldsymbol{r}}_{mn}}} \right\|} \right)}}{{4{\rm{ \mathsf{ π} }}\left\| {{\mathit{\boldsymbol{r}}_{mn}}} \right\|}}, $ | (2) |
式中:k=ω/c表示波数,ω为角频率,c为声速;‖rmn‖为第m个测点与第n个等效源之间的矢量距离。全息面测量声压可以写成
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{Aq}}, $ | (3) |
式中:p(M×1)为全息面测量声压列向量;q(N×1)为等效源强构成的列向量;A(M×N)为等效源面与全息面之间的传递矩阵,具体表示为
| $ \mathit{\boldsymbol{A}} = i\rho ckg\left( {{\mathit{\boldsymbol{r}}_m}\left| {{\mathit{\boldsymbol{r}}_n}} \right.} \right), $ | (4) |
式中ρ为空气密度。考虑到实际应用中的测量条件和成本,测量点的数量一般远远小于等效源的数量,即M≪N。因此,式(3)一般是欠定的,在反向求解等效源强的过程中往往具有不适定性。为了解决这个问题,一般采取正则化的方法来提高重建精度。Tikhonov正则化是应用最为广泛的正则化方法之一,其基本思想是利用l2范数对解向量进行约束,通过选取合适的正则化参数解决不适定问题。在l2范数约束下,式(3)可以转化为下列最小化问题:
| $ {\rm{argmin}}{\left\| {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{Aq}}} \right\|_2} + \lambda {\left\| \mathit{\boldsymbol{q}} \right\|_2}, $ | (5) |
其中λ为正则化参数,‖·‖2表示l2范数。利用式(5)求解出最佳等效源强度后,声场中任意重建面的声压可以通过式(6)求得
| $ {\mathit{\boldsymbol{P}}_R} = \mathit{\boldsymbol{Gq}}, $ | (6) |
式中G表示任意重建面与等效源面之间的声压传递矩阵。
2 压缩奇异值分解等效源法当等效源分布是稀疏或者近似稀疏时,CS理论可以直接被引入。对于这种稀疏信号,式(5)中解的l2范数可以替换成l1范数,即
| $ {\rm{argmin}}\left\| {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{Aq}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{q}} \right\|_1}, $ | (7) |
其中‖·‖1表示l1范数。当等效源分布非稀疏时,需要构建适当的基对其进行稀疏分解,从而使得其满足CS理论所要求的稀疏条件。基于这种思想,笔者提出一种压缩奇异值分解等效源法(CSVDESM)。首先,对等效源面与重建面之间的声压传递矩阵G进行奇异值分解并代入式(6)可得
| $ {\mathit{\boldsymbol{P}}_R} = \mathit{\boldsymbol{Gq}} = \mathit{\boldsymbol{US}}{\mathit{\boldsymbol{V}}^{\rm{H}}}\mathit{\boldsymbol{q}} = \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{u}}_i}{\mathit{\boldsymbol{\lambda }}_i}} < \mathit{\boldsymbol{v}}_i^{\rm{H}}{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{q}} > = \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{u}}_i}{\mathit{\boldsymbol{\alpha }}_i}} = \mathit{\boldsymbol{U\alpha }}, $ | (8) |
式中:U和V均为酉矩阵;ui和vi分别是U和V的列向量;上标H表示共轭转置;S是一个包含实正奇异值λi的对角矩阵;α表示基的加权系数向量。文献[20]对U的稀疏性进行了详细的阐述,即声信号可通过U中少许的列向量实现重构,这些列向量对应着较大的奇异值。
根据式(3)和(6),可以得到
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{Aq}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{G}}^ + }{\mathit{\boldsymbol{P}}_R}, $ | (9) |
将式(8)代入式(9),可得
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{Aq}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{G}}^ + }{\mathit{\boldsymbol{P}}_R} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{G}}^ + }\mathit{\boldsymbol{U\alpha }} = \mathit{\boldsymbol{D\alpha }}, $ | (10) |
其中D=AG+U,上标“+”表示广义逆。
使用l1范数正则化求解式(10),可以将其转化为
| $ {\rm{argmin}}\left\| {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{D\alpha }}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1}, $ | (11) |
式(11)可以等效为l1范数最小化问题
| $ \min {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1}{\rm{subject}}\;{\rm{to}}\left\| {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{D\alpha }}} \right\|_2^2 \le \varepsilon , $ | (12) |
其中ε表示所允许的误差上限。参考文献[18]的设置,可以将式(12)中的约束调整之后使用CVX工具箱进行求解。
| $ \min {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1}{\rm{subject to}}\left\| {{\mathit{\boldsymbol{D}}^{\rm{H}}}\left( {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{D\alpha }}} \right)} \right\|_2^2 \le \delta 。$ | (13) |
根据经验,式(13)中参数δ定义如下:
| $ \delta = \sigma {\left\| {\nabla \left( {{\mathit{\boldsymbol{D}}^{\rm{H}}}\left( {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{D\alpha }}} \right)} \right)} \right\|_2} = \sigma {\left\| {{\mathit{\boldsymbol{D}}^{\rm{H}}}\mathit{\boldsymbol{p}}} \right\|_2}, $ | (14) |
其中σ为取值很小的数,从而保证CVX工具箱求出相对最优解。
求解出α后,将其代入到式(8)中即可求得重建面声压值。对声压传递矩阵G进行奇异值分解得到的U可以看作声模态,因为声模态在空间上是连续的并且覆盖整个研究区域,因此CSVDESM适用于空间连续型声源。
对于空间连续型声源,如结构板件,在实际的工程测量中,不仅关心其声压分布,而且更关注声压分布的最大区域。因此,借鉴高阶矩阵函数波束形成基本思想[21-22]构造系数矩阵对CSVDESM的输出结果进行修正。首先,计算向量α的互谱矩阵:
| $ \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{\alpha }}^{\rm{H}}}, $ | (15) |
由于C是非负的Hermitian矩阵,因此其谱分解可以写成
| $ \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{V}}{\rm{diag}}\left( {{\gamma _1},{\gamma _2}, \cdots ,{\gamma _N}} \right){\mathit{\boldsymbol{V}}^{\rm{H}}}, $ | (16) |
其中C为特征向量,γ1, γ2, …, γN是C的特征值。C的指数矩阵函数定义为
| $ {\mathit{\boldsymbol{C}}^{\frac{1}{v}}} = \mathit{\boldsymbol{V}}{\rm{diag}}\left( {{\gamma _1}^{\frac{1}{v}},{\gamma _2}^{\frac{1}{v}}, \cdots ,{\gamma _N}^{\frac{1}{v}}} \right){\mathit{\boldsymbol{V}}^{\rm{H}}}, $ | (17) |
式中v为一固定正整数,表示阶数。基于高阶矩阵波束形成计算得到的第i个重建面网格节点的声压可以表示为
| $ {\mathit{\boldsymbol{Z}}_i} = {\left( {\frac{{{\mathit{\boldsymbol{u}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{u}}_i}} \right\|}_2}}}{\mathit{\boldsymbol{C}}^{\frac{1}{v}}}{{\left( {\frac{{{\mathit{\boldsymbol{u}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{u}}_i}} \right\|}_2}}}} \right)}^{\rm{H}}}} \right)^v}, $ | (18) |
式中ui是U的列向量。
为了保证最大声压幅值的真实估计,可以将式(8)和(18)联合起来进行修正。最终,CSVDESM的输出结果为
| $ {\mathit{\boldsymbol{P}}_{{\rm{out }}}} = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_R},}&{v = 0;}\\ {{\mathit{\boldsymbol{Z}}_i}\frac{{\max \left( {\left| {{\mathit{\boldsymbol{P}}_R}} \right|} \right)}}{{\max \left( {\left| {{\mathit{\boldsymbol{Z}}_i}} \right|} \right)}},}&{v = 1,2,3, \cdots 。} \end{array}} \right. $ | (19) |
如果想确保声场真实重建,取阶数v=0;如果想确定具有高精度和宽动态范围的源位置,则可以应用v=1, 2, 3, …的输出结果。
3 仿真分析为验证所提算法的声源识别定位性能,利用MATLAB软件对传统的最小二乘等效源法(TRESM),CESM[18],CMESM[19]和CSVDESM4种方法进行对比仿真分析。其中,TRESM使用Tikhonov正则化进行约束,正则化参数通过L-curve法选取。仿真采用简支钢板,结构尺寸为0.5 m×0.5 m,钢板的厚度为3 mm,材料密度为7 800 kg/m3,泊松比为0.23,弹性模量为2.1×105MPa,阻尼比为0.02。该板件由振幅为1 N的简谐点力驱动,激励点位于板件中心,辐射声场由瑞利第一积分公式计算。测量面与重建面尺寸均为0.5 m×0.5 m,划分的网格间距为2.5 cm。两个平面分别位于板上方5 cm(测量面)和2 cm(重建面)处。等效源分布在钢板上方0.001 m的平面上。测量面上的传声器阵列如图 2所示,利用测量面中随机分布的64个传声器来重构重建面上441个点的声压分布。在仿真过程中添加20 dB的高斯白噪声模拟干扰噪声信号。
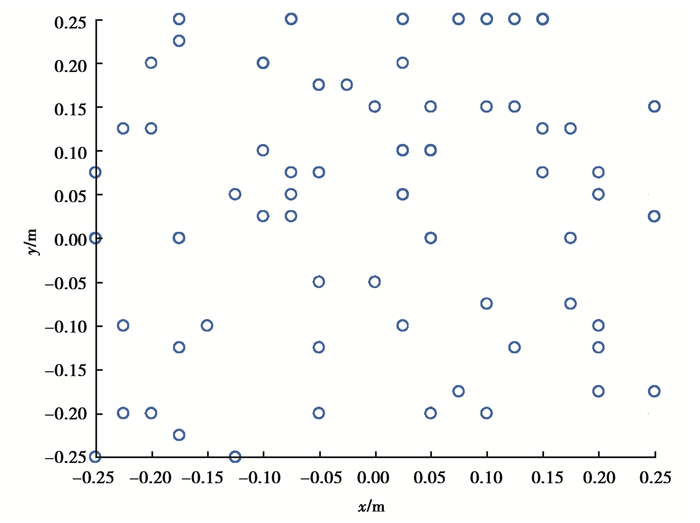
|
图 2 具有64个随机分布的麦克风的测量阵列 Fig. 2 The array with 64 randomly distributed microphones |
为了量化所提方法的重建精度,定义重建误差为
| $ \xi = \frac{{{{\left\| {{P_{\rm{r}}} - {P_{\rm{t}}}} \right\|}_2}}}{{{{\left\| {{P_{\rm{t}}}} \right\|}_2}}} \times 100\% , $ | (20) |
其中Pt和Pr分别代表重建面上理论声压值和重建声压值。
根据式(20),在图 3中显示了50~3 000 Hz频率范围内4种方法的重建误差。每个频率的误差结果计算10次以产生平均误差。从图 3可以看出,在较宽的频率范围内,相比于其他3种重建方法,CSVDESM的重建精度较高且稳定。CESM的重建效果不佳主要是因为CESM的基函数稀疏分解不适用于连续型声源。如果想提高CESM的重建精度,则需布置更多的测量点。
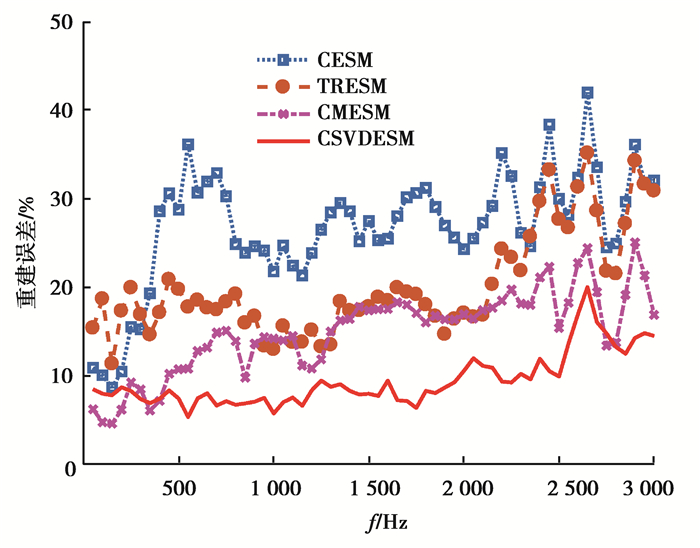
|
图 3 重建误差曲线(频率间隔为50 Hz) Fig. 3 Reconstructed error curve (Frequency interval is 50 Hz) |
图 4展示了在500和2 000 Hz时采用不同重建方法得到的结构板件上的声压分布成像图。在500和2 000 Hz时,CESM的重建效果均不理想(重建误差分别为30.46%和22.36%)。主要原因在于结构板件的辐射声场比较复杂,空间稀疏性较差,CESM采用的稀疏基适用性降低。当测量点的数量增加时,CESM的声场重建效果能得到改善。与CMESM(重建误差分别为17.17%和16.33%)相比,CSVDESM(重建误差分别为6.40%和8.21%)在2个频率下均能取得更优越的重建效果。主要原因在于CMESM是通过对辐射矩阵进行特征值分解,从而获取源强一系列模态,该方法构建的辐射矩阵为实对称矩阵;而CSVDESM是通过对等效源面与重建面之间的传递矩阵进行奇异值分解来获取声场一系列正交基(也可称之为声模态),该方法所获取的正交基构成的是复矩阵,包含更多的相位信息。因此在采样点数相同的情况下,CSVDESM的声场重构误差更低,这与图 3显示的结果是一致的。
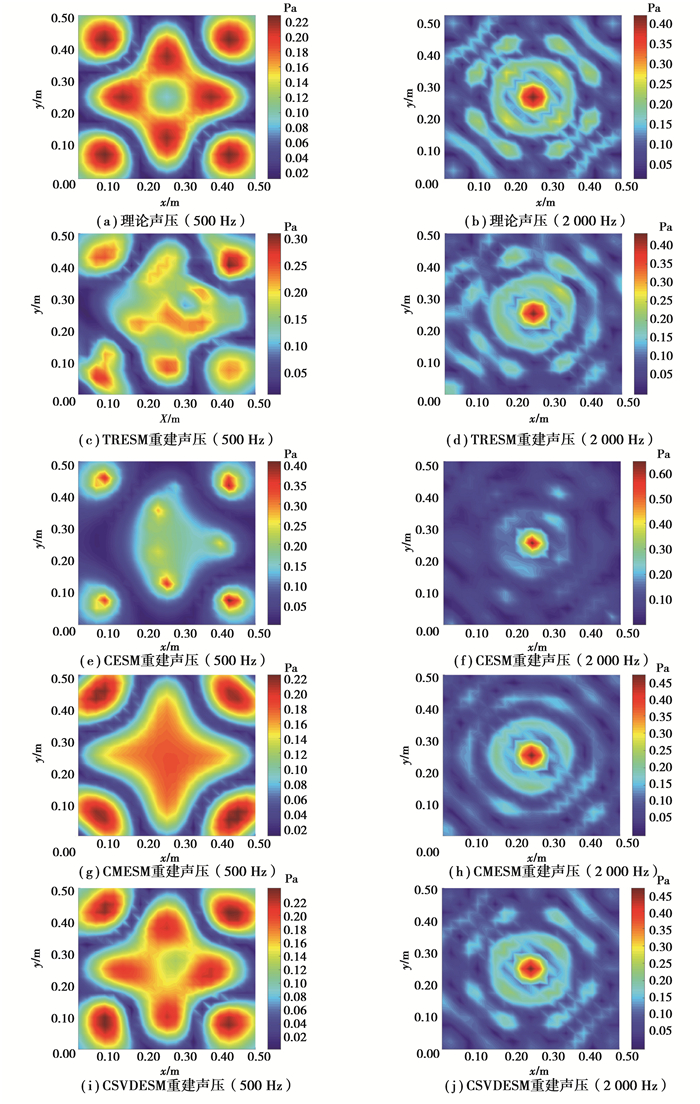
|
图 4 结构板件上声压分布成像图 Fig. 4 The source imaging map for the plate source |
图 5为钢板在500 Hz激励下,运用高阶矩阵函数波束形成思想对CSVDESM输出结果进行修正后的结构板件上声压分布成像图。可以看出,当v=1,识别到的声压分布与理论值(图 4(a))近似,随着阶数的提高,识别到的声学中心的覆盖范围逐步减小。因此可通过提高阶次值,不断缩小识别到的声学中心覆盖范围,定位出结构板件声压分布的最大区域,从而为结构板件的优化改进提供方向。值得注意的是,当阶次过高时,可能会丢失某些重要的声压信息(如当v=5(图 5(d))时,部分声学信息出现丢失),因此,在结构板件声源识别时,建议采用较小的阶次值。
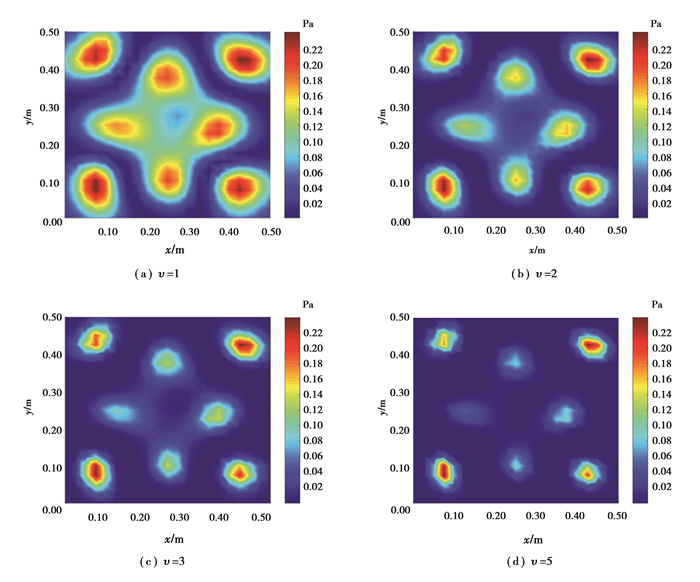
|
图 5 受激励力激励的板结构声源在500 Hz时声学成像图 Fig. 5 Acoustic imaging map for plate source excited by excitation at 500 Hz |
为进一步验证所提方法的可行性与实用性,将该方法应用在钢制板声源识别实验中。实验在一普通房间进行,采用厚度为0.002 m的钢板,结构尺寸为0.35 m×0.30 m。钢板结构通过4个G型夹具将其四角固定,然后利用激振器在板件(0.1, 0.1) m处施加简谐激振力。激振器采用型号为WY1603信号发生器进行信号驱动,采用LMS公司的16通道SCR02型采集器进行信号采集与控制。由3个间隔为5 cm的传声器组成的扫描阵列进行测量,一个传声器作为声场参考传声器进行固定。实验布置如图 6所示:图中板件左下方有一圆形螺栓,为激励点所处方位,在该位置激振器通过螺栓和垫片固定在钢板上。测量面位于板上方0.05 m,分布有7×6个间隔为5 cm的数据测量点;重建面与等效源面分别位于板上方0.020 m和0.001 m处,网格间距均为0.010 m。在实验中,还需测量重建面的声压作为重建面声压理论值(或者称之为重建面声压参考值)。

|
图 6 受激励力激励的板结构测试现场图 Fig. 6 Measurement system of vibration plate excited by an electrodynamic shaker |
利用TRESM, CESM, CMESM, CSVDESM4种方法对该板件进行声压重建。为更好分析重建效果,对输出根据最大声压进行归一化处理。
图 7展示的是板结构受到激振器单位激励力作用下500和2 000 Hz时得到的重建面声压分布图像。可以看出,在500 Hz时,除TRESM(图 7(c))和CESM(图 7(e))外,其他2种方法均能识别到两个声压较大的区域。TRESM受采样点数量以及测量噪声影响较大,因此重建结果与理论值出现较大偏差;CESM识别失效主要原因在于其稀疏基不再适用于连续型声源。相比于CMESM(图 7(g)),CSVDESM(图 7(i))在声压分布上与理论值(图 7(a))更接近。
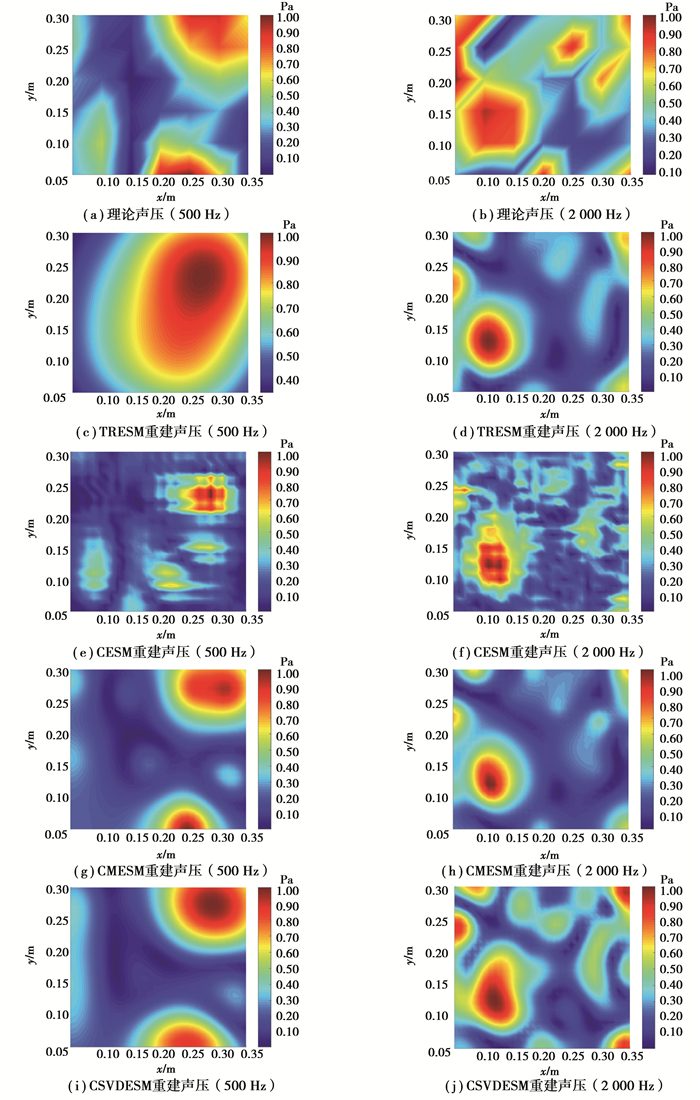
|
图 7 实验条件下重建面声压分布成像图 Fig. 7 Comparison of pressure distributions under experimental conditions |
在2 000 Hz时,3种方法的重建效果均不佳。主要原因在于当板的厚度较低时,具有高空间频率的倏逝波更容易被激起,从而削弱声场的稀疏性;另一个原因是CS的本质是基于信号压缩理论,倏逝分量具有较低的权重,因此当采样不够时,倏逝分量将被丢弃。然而,这并不影响对辐射声压最强区域的识别与定位。相比于其他3种方法,CSVDESM(图 7(j))所重建的辐射声压最强区域与理论区域(图 7(b))最接近。
图 8为钢板在500 Hz激励下,运用高阶矩阵函数波束形成思想对CSVDESM输出结果进行修正后的结构板件上声压分布成像图。从图中可以看出,在能准确重构声压分布的基础上,随着阶数的提高,识别到的声学中心覆盖范围逐步减小,辐射声压最强区域变得愈发明显,主要噪声源的识别定位更加准确。将仿真与实验的应用相结合,可以看出所提方法(CSVDESM)在重构板结构声源辐射声场的有效性与实用性。

|
图 8 受激励力激励的板结构声源在500 Hz时声学成像图 Fig. 8 The pressure distributions of plate sound source at 500 Hz |
基于等效源法和压缩感知理论,提出了压缩奇异值分解等效源法(CSVDESM)。通过对等效源面与重建面之间的传递矩阵进行奇异值分解,将要重构的声场分解成一系列“声学模态”。因此CSVDESM特别适用于空间连续型声源。
将CSVDESM与高阶矩阵函数波束形成理论结合,通过提高阶次值,不断缩小识别到的声学中心覆盖范围,定位出结构板件声压分布的最大区域,从而可为结构板件的优化改进提供方向。
进行数值仿真和实验应用来比较CESM, TRESM,CMESM以及CSVDESM的重建效果,结果验证了CSVDESM方法在较宽频率范围内的优越性,同时,通过引入高阶矩阵函数能有效提高CSVDESM声源成像的动态显示范围,提高声源识别定位精度。但是,当阶数过高时可能会丢失某些重要的声学信息。如何快速准确地为结构板件声源识别选取一个合适的阶数需要进一步的研究。
| [1] |
Maynard J D, Williams E G, Lee Y. Nearfield acoustic holography:I. Theory of generalized holography and the development of NAH[J]. The Journal of the Acoustical Society of America, 1985, 78(4): 1395-1413. DOI:10.1121/1.392911 |
| [2] |
Pasqual A M. A patch near-field acoustical holography procedure based on a generalized discrete Fourier series[J]. Mechanical Systems and Signal Processing, 2017, 90: 285-297. DOI:10.1016/j.ymssp.2016.12.035 |
| [3] |
Li X L, Wang N, Gao D Z, et al. A sound field separation and reconstruction technique based on reciprocity theorem and fourier transform[J]. Chinese Physics Letters, 2018, 35(11): 114301. DOI:10.1088/0256-307X/35/11/114301 |
| [4] |
Wall A T, Gee K L, Neilsen T B. Multisource statistically optimized near-field acoustical holography[J]. The Journal of the Acoustical Society of America, 2015, 137(2): 963-975. DOI:10.1121/1.4906585 |
| [5] |
Pereira A, Antoni J, Leclère Q. Empirical Bayesian regularization of the inverse acoustic problem[J]. Applied Acoustics, 2015, 97: 11-29. DOI:10.1016/j.apacoust.2015.03.008 |
| [6] |
Le Magueresse T, Thomas J H, Antoni J, et al. Bayesian regularization applied to real-time near-field acoustic holography[J]. The Journal of the Acoustical Society of America, 2014, 136(4): 2171. |
| [7] |
Koopmann G H, Song L, Fahnline J B. A method for computing acoustic fields based on the principle of wave superposition[J]. Journal of the Acoustical Society of America, 1989, 86(6): 2433-2438. DOI:10.1121/1.398450 |
| [8] |
Geng L, Zhang X Z, Bi C X. Reconstruction of transient vibration and sound radiation of an impacted plate using time domain plane wave superposition method[J]. Journal of Sound and Vibration, 2015, 344: 114-125. DOI:10.1016/j.jsv.2015.01.046 |
| [9] |
Lee S. Review:The Use of Equivalent Source Method in Computational Acoustics[J]. Journal of Computational Acoustics, 2017, 25(1): 1630001. DOI:10.1142/S0218396X16300012 |
| [10] |
Xu Z M, Wang Q H, He Y S, et al. A monotonic two-step iterative shrinkage/thresholding algorithm for sound source identification based on equivalent source method[J]. Applied Acoustics, 2018, 129: 386-396. DOI:10.1016/j.apacoust.2017.07.012 |
| [11] |
Ping G L, Chu Z G, Xu Z M, et al. A refined wideband acoustical holography based on equivalent source method[J]. Scientific Reports, 2017, 7: 43458. DOI:10.1038/srep43458 |
| [12] |
张磊, 曹跃云, 杨自春. 迭代总体最小二乘正则化的近场声全息方法研究[J]. 振动与冲击, 2016, 35(21): 96-101. ZHANG Lei, CAO Yueyun, YANG Zichun. Near field acoustic holography based on Newton iteration total least square regularization[J]. Journal of Vibration and Shock, 2016, 35(21): 96-101. (in Chinese) |
| [13] |
宋忠友, 仲元红, 陈涛, 等. 基于交替迭代的压缩感知多目标定位算法[J]. 重庆大学学报, 2018, 41(3): 42-50. SONG Zhongyou, ZHONG Yuanhong, CHEN Tao, et al. Multiple target localization algorithm based on alternate iteration using compressive sensing[J]. Journal of Chongqing University, 2018, 41(3): 42-50. (in Chinese) |
| [14] |
葛永新, 林梦然, 洪明坚. 联合局部和全局稀疏表示的磁共振图像重建方法[J]. 重庆大学学报, 2017, 40(1): 93-102. GE Yongxin, LIN Mengran, HONG Mingjian. MR image reconstruction by combining local and global sparse representations[J]. Journal of Chongqing University, 2017, 40(1): 93-102. (in Chinese) |
| [15] |
Chardon G, Daudet L, Peillot A, et al. Near-field acoustic holography using sparse regularization and compressive sampling principles[J]. The Journal of the Acoustical Society of America, 2012, 132(3): 1521-1534. DOI:10.1121/1.4740476 |
| [16] |
Fernandez-Grande E, Xenaki A. Compressive sensing with a spherical microphone array[J]. The Journal of the Acoustical Society of America, 2016, 139(2): EL45-EL49. DOI:10.1121/1.4942546 |
| [17] |
Hald J. Fast wideband acoustical holography[J]. The Journal of the Acoustical Society of America, 2016, 139(4): 1508-1517. DOI:10.1121/1.4944757 |
| [18] |
Fernandez-Grande E, Xenaki A, Gerstoft P. A sparse equivalent source method for near-field acoustic holography[J]. The Journal of the Acoustical Society of America, 2017, 141(1): 532-542. DOI:10.1121/1.4974047 |
| [19] |
Bi C X, Liu Y, Xu L, et al. Sound field reconstruction using compressed modal equivalent point source method[J]. The Journal of the Acoustical Society of America, 2017, 141(1): 73-79. DOI:10.1121/1.4973567 |
| [20] |
Photiadis D M. The relationship of singular value decomposition to wave-vector filtering in sound radiation problems[J]. The Journal of the Acoustical Society of America, 1990, 88(2): 1152-1159. DOI:10.1121/1.399811 |
| [21] |
Li S, Xu Z M, He Y S, et al. Functional generalized inverse beamforming based on the double-layer microphone array applied to separate the sound sources[J]. Journal of Vibration and Acoustics, 2016, 138(2): 021013. DOI:10.1115/1.4032305 |
| [22] |
褚志刚, 段云炀, 沈林邦, 等. 函数波束形成声源识别性能分析及应用[J]. 机械工程学报, 2017, 53(4): 67-76. CHU Zhigang, DUAN Yunyang, SHEN Linbang, et al. Performance analysis and application of functional beamforming sound source identification[J]. Journal of Mechanical Engineering, 2017, 53(4): 67-76. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

