2. 河北省矿井灾害防治重点实验室 河北 廊坊 065201;
3. 辽宁 工程技术大学 矿山热动力灾害与防治教育部重点实验室, 辽宁 阜新 123000;
4. 中国矿业大学 煤炭资源与安全 开采国家重点实验室, 江苏 徐州 221116;
5. 越南煤炭集团工业及煤矿投资咨询股份公司 越南 北江 21000
2. Hebei Provincial Key Lab of Mine Disaster Prevention and Control, Langfang 065201, Hebei, P. R. China;
3. Key Laboratory of Mine Thermo-motive Disaster and Prevention, Ministry of Education, Liaoning Technical University, Fuxin 123000, Liaoning, P. R. China;
4. State Key Laboratory of Coal Resources & Mine Safety, China University of Mining & Technology, Xuzhou 211116, Jiangsu, P. R. China;
5. Vietnam Coal-Mineral Industries Group and Coal Mining Investment Consulting Co. Ltd., Bac Giang 21000, Vietnam
随着中国煤矿开采技术和开采机械设备不断完善,大型矿井综合机械化放顶煤开采已变得非常普遍,而且中国的综放开采技术在国际上也处于领先地位。掌握综放开采超前支承压力显现和巷道围岩变形特征,对深入研究综放开采的矿压显现、巷道支护和设备选型具有重要的意义。
在钱鸣高院士和侯朝炯教授等老一辈采矿工作者的带领下,目前对工作面超前支承压力和巷道围岩变形研究取得了许多建设性成果[1-2]。许家林等[3]和Xie等[4]深入研究了关键层对综放工作面矿压显现特征的影响;王家臣等[5]和Meng等[6]对综放工作面采放比对矿压显现特征的影响研究取得了丰硕成果;张宏伟等[7]、杨小礼等[8]和赵健等[9]对综放工作面不同地域不同矿井的矿压显现特征研究已经掌握了一些关键的规律;马念杰等[10]和Li等[11]对开采过程中巷道应力分布和巷道破坏特征进行了深入的理论研究和实验研究;康红普等[12]和张国华等[13]对巷道变形破坏和控制技术的研究已经非常成熟,并在业界得到了普遍的认可;勾攀峰等[14]和谢福星等[15]对巷道破坏的力学过程进行了深入的研究;姜福兴等[16]和Zhang等[17]研究了工作面推进过程中圆形巷道冲击地压发生的机理,并检验和推广了应力监测技术在现场实践中的应用。但对综放开采超前支承压力对巷道变形的影响以及二者之间的联系很少有研究报道。笔者主要研究超前支承压力对巷道围岩变形的影响,进而建立二者之间的关系。
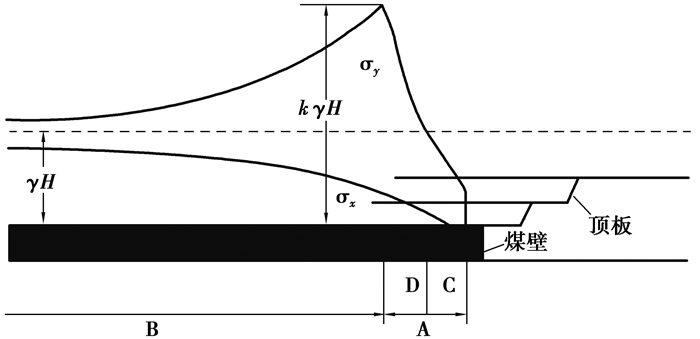
1 变形阶段分析由于在工作面推进过程中有梁结构存在,显然在工作面前方会形成一个应力增高区,如图 1所示。当工作面不断推进, 在梁结构破坏前超前支承压力会不断增大,巷道围岩的移近量和移进速度也不断增大[1-2, 15, 18]。由于超前支承压力的影响,工作面开采后会在工作面前方形成两个区域,塑性区(A区)和弹性区(B区)[19-20]。
|
图 1 超前支承压力示意图 Fig. 1 Sketch map of advanced support pressure |
在塑性区内任意位置水平方向和垂直方向上的应力平衡方程为:
| $ m{\sigma _x} + 2f{\sigma _y}{d_x} - m\left( {{\sigma _x} + d{\sigma _y}} \right) = 0。$ | (1) |
式中:m为工作面采厚;f为摩擦系数;σx为单元的水平方向应力;σy为单元的垂直方向应力;dx为水平方向的位移;dσy为垂直方向的单位应力。
采用摩尔库伦准则对式(1)进行整理,得到
| $ {\sigma _y} = 2C\sqrt {\frac{{1 + \sin \psi }}{{1 - \sin \psi }}} + \frac{{1 + \sin \psi }}{{1 - \sin \psi }}{\sigma _x}, $ | (2) |
式中:C为煤体内聚力;ψ为煤体的内摩擦角。
令:
| $ {\sigma _y} = {N_0}{{\rm{e}}^{\frac{{2xfR\psi }}{m}}}, {N_0} \le {\sigma _y} \le k\gamma H, $ | (3) |
式中:N0为煤壁处的支承能力;k为超前应力集中系数。
在σy=kγH时达到超前支承压力的峰值,此时的峰值位置与煤壁间的距离为x0(单位,m),表示为
| $ {x_0} = \frac{m}{{2f}}\frac{{1 - \sin \psi }}{{1 + \sin \psi }}\ln \left( {\frac{{k\gamma H}}{{(C + \sigma \tan \psi )\cot \psi }}\frac{{1 - \sin \psi }}{{1 + \sin \psi }}} \right)。$ | (4) |
式中σ为支架对煤帮的阻力。
工作面前方超前支承压力的峰值出现在x0处,以超前支承压力峰值位置为边界,在工作面前方x0以外的范围为弹性变形区(B区),在0~x0为塑性变形区,在塑性区内以超前支承压力曲线与原岩应力线交叉处为分界,又分为破坏区(C区)和极限平衡区(D区)。
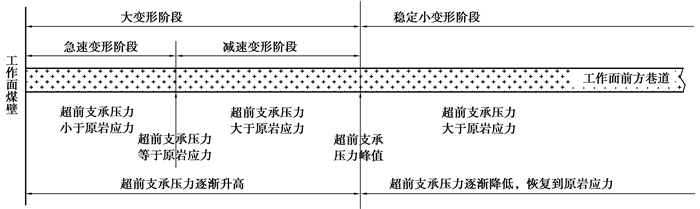
在破坏区内煤岩层已经失去了完整性,承载能力很差,承载的压力一般都小于原岩应力,所以会造成巷道围岩变形量非常大,而且变形速度快,将此阶段称为巷道围岩急速变形阶段。在极限平衡区内煤岩层虽然发生了塑性变形,但还是一个非连续排列的整体,完整性和承载能力明显优于破坏区,承载的压力逐渐变大,且承载的压力一般都大于原岩应力,此区域的巷道变形量逐渐减小,变形速度放缓,将此阶段称为巷道围岩减速变形阶段。破坏区和极限平衡区统称为塑性区,塑性区的巷道变形量大,称为大变形阶段。在弹性变形区内煤岩层状态完好,岩层具有很好的承载能力,由于该阶段巷道受到的力大于原岩应力,巷道变形必然大于原岩应力状态下的巷道变形,但巷道变形量小,将此阶段称为稳定小变形阶段。可以得到超前支承压力与巷道围岩变形的位置关系,如图 2所示。
|
图 2 超前支承压力与巷道围岩变形的位置关系 Fig. 2 The location relationship between advancing abutment pressure and surrounding rock deformation of roadway |
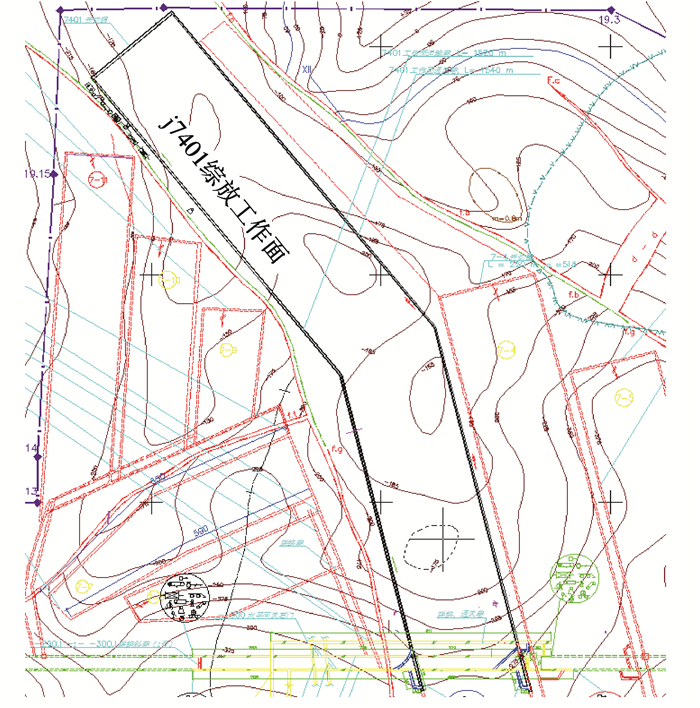
河林煤矿j7401工作面为7(4)煤层的首采工作面,工作面布置如图 3所示。该工作面所处位置的地表标高为+255.0~+310.0 m,工作面水平标高-150.0~-270.0 m,工作面的长度为240.0 m,推进方向长度为1 520.0 m,工作面倾角变化范围较大,但工作面的平均倾角大约为6°。工作面煤层厚度范围是7.80~13.60 m,煤层平均厚度大约为11.40 m,煤层硬度相对较小,且稳定性较低,顶煤冒放性较好,采用后退式全部垮落综合机械化放顶煤的采煤方法,采高3.40 m,放高为8.00 m。工作面上覆岩层构造比较简单,顶底板以泥岩和砂岩为主,直接底为炭质泥岩,黑灰色,薄层状,致密较硬,平均厚度为6.70 m。老底也为炭质泥岩黑褐灰色,块状层理,含粉砂岩,致密坚硬,平均厚度为8.65 m。
|
图 3 j7401综放工作面布置图 Fig. 3 Layout of j7401 fully mechanized caving face |
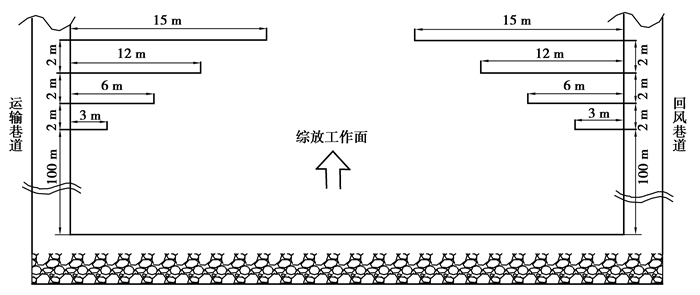
J7401工作面推进100.0 m后初次来压已经结束,而且在此段煤层趋于近水平煤层,煤层厚度稳定,地质构造简单。故超前j7401综放工作面100.0 m开始布置4组观测站,每组布置2个钻孔,2个钻孔分别在运输巷道和回风巷道。为使监测得到的数据具有代表性,得到不同深度的应力显现特征,4组观测站的钻孔深度各不相同:第1组钻孔的孔深为3.0 m;第2组6.0 m;第3组12.0 m;第4组15.0 m。每个钻孔内布置1台钻孔应力计,钻孔高度距回采巷道底板1.5 m。应力计和钻孔在工作面内的布置参数如图 4所示。现场可根据j7401综放工作面的推进情况安排观测工作。在距离综放工作面50.0 m以外的测点,每隔2天观测1次,50.0~30.0 m需每天观测1次,30.0 m以内每天早班和中班分别观测1次,并将观测数据作记录。
|
图 4 应力钻孔测点布置示意图 Fig. 4 Measuring point arrangement sketch map of stress drilling |
随着j7401综放工作面不断向前推进,现场观测并记录工作面推进过程中各个钻孔内应力计的读数,对4组观测站8个钻孔观测到的数据进行整理,结果见图 5。
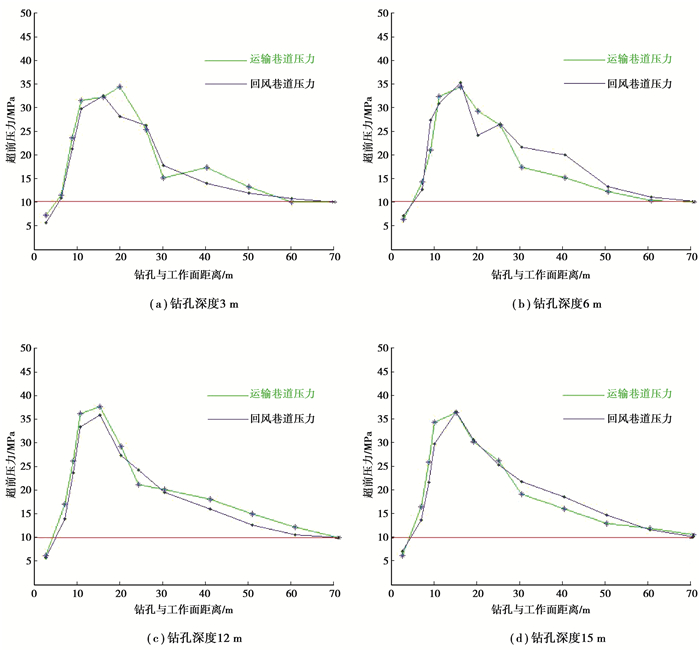
|
图 5 各深度钻孔超前压力变化 Fig. 5 Advanced abutment pressure with diggerent drilling depth |
图 5中的红色直线为原岩应力线,绿色和蓝色分别为运输巷道压力和回风巷道压力,可以看出:1)当综放工作面与钻孔的距离大约为70.0 m时,钻孔应力计的读数开始大于原岩应力,由此可以说明j7401综放工作面的超前支承压力影响范围约为70.0 m;2)超前压力的峰值出现在工作面前方15.0~22.0 m之间,超前压力的峰值范围大约为33.0~39.0 MPa,超前支承压力峰值大约为原岩应力的3.2~3.8倍。
2.3 观测数据分析为得出综放工作面前方不同位置超前支承压力的变化曲线,采用最小二乘拟合的数学方法对图 5中的96组数据点(xi, yi),(i=1, 2, ..., 96)进行分析,此处不再单独区分考虑运输巷道和回风巷道的超前支承压力,求96组数据的近似函数y=S(x)。该方法的原理是将拟合值与实际值之间的偏差平方和最小化[21-22],在向量函数空间Φ=span{φ0(x), φ1(x), …, φn(x)}中寻找f(x)的逼近函数(其中φi(x)为关于x的i次向量函数),即求ak,(k=0, 1, …, n),使Φ空间中的
将图 5中的测点到工作面的距离作为自变量,超前支承压力为因变量,拟合出的函数曲线如图 6所示。
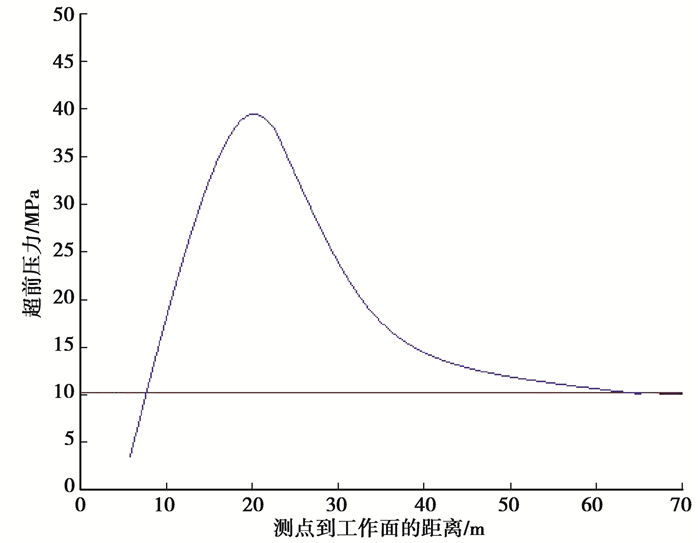
|
图 6 超前支承压力拟合曲线 Fig. 6 Fitting curve of advance supporting pressure |
从图 6中可以看出:1)工作面前方0.0~19.8 m支承压力逐渐增加,在8.1 m处超前支承压力等于原岩应力;2)超前支承压力的峰值出现在工作面前方的19.8 m处,峰值为39.4 MPa;3)工作面前方19.8~65.0 m的范围内超前支承压力逐渐减小,大约在65.0 m之后恢复到原岩应力。
可确定巷道围岩的变形阶段:0.0~8.1 m为急速变形阶段;8.1~19.8 m为减速变形阶段;19.8~65.0 m为稳定小变形阶段;大变形阶段的范围是0.0~19.8 m。
3 精度检验 3.1 巷道围岩变形观测为了掌握j7401综放面运输巷道和回风巷道受采动影响的围岩变形特征,研究分析综放工作面采动对回采巷道围岩变形的影响,需要进行回采巷道变形观测。根据巷道围岩变形观测的内容,确定在两条回采巷道内各布置一条观测线,每个观测线分别布置3个测站,测站间距为30.0 m,并采用“十”字交叉布点法对回采巷道的表面移近量进行观测,巷道内测站的布置参数如图 7所示。
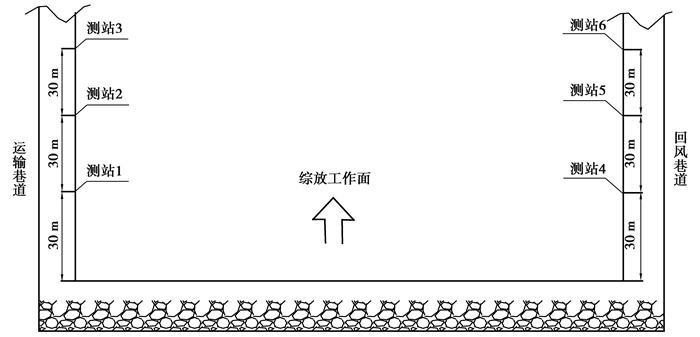
|
图 7 巷道测站布置图 Fig. 7 Layout of station in mining roadway |
通过在j7401综放工作面回采巷道布置“十”字交叉测站,对回采巷道围岩变形量进行连续观测,对观测数据进行整理和分析,绘制出j7401综放工作面运输巷道和回风巷道各测站的巷道围岩日移近量的变化过程,如图 8所示。
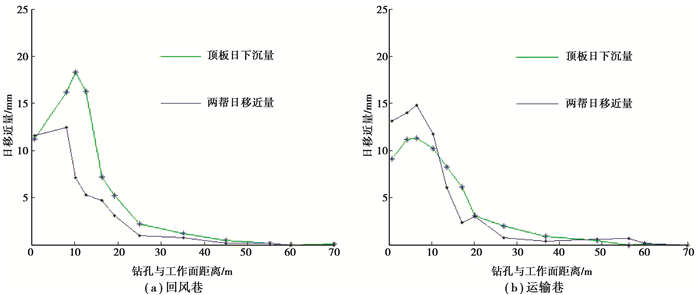
|
图 8 工作面前方巷道围岩移近的速度变化 Fig. 8 Moving speed of the surrounding rock in the roadway in front of the working face |
通过对图 8分析可以得出:1)综放工作面前方大约0.0~20.0 m范围内顶板活动剧烈,顶板日下沉量最大速度大约在工作面前方5.0~11.0 m范围内,顶板日下沉量的最大值达到了18.0 mm。工作面前方大约20.0 m以外的日移近量较小,回风巷顶板日下沉量小于5.0 mm,运输巷顶板日下沉量小于3.0 mm,工作面前方60.0 m以外的日移近量接近于0;2)综放工作面前方0.0~20.0 m范围内两帮的移近量很大,两帮日移近量的最大速度大约在工作面前方6.0~9.0 m范围内,两帮日移近量的最大值达到了14.9 mm。工作面前方大约20.0~60.0 m范围的日移近量都小于3.0 mm,工作面前方60.0 m以外的日移近量接近于0。
上述分析说明工作面前方0.0~20.0 m范围内围岩变形活动程度非常强,20.0~60.0 m以外的围岩变形活动减弱,60.0 m以外围岩基本不受采动影响。
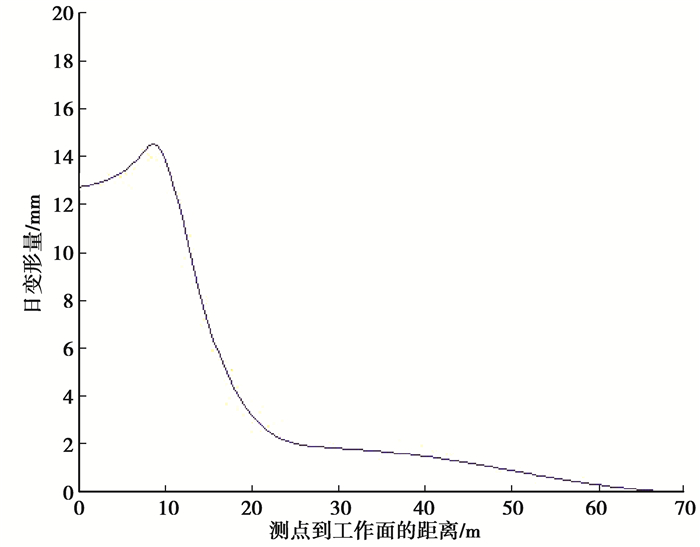
3.3 观测数据分析同样采用最小二乘拟合的方法对图 8中的数据进行分析,分析过程中不区分两帮移近量和顶板下沉量,将两者统一视为巷道日变形量。将测点到工作面的距离作为自变量,工作面前方巷道日变形量为因变量,拟合出的函数曲线如图 9所示。
|
图 9 工作面前方巷道日变形量拟合曲线 Fig. 9 Fitting curve of daily deformation of roadway in front of the working face |
从图 9中可以看出:1)日变形量最大值出现在工作面前方的8.9 m处,0.0~8.9 m范围内日变形量都大于12.0 mm,此阶段为急速变形阶段;2)工作面前方8.9~20.1 m,巷道的日变形量由14.5 mm减小到大约3.0 mm,此阶段为减速变形阶段;3)工作面前方20.1 m之后巷道的日变形量非常小,工作面前方65.0 m处巷道变形量变为了0,在20.1~65.0 m的范围内巷道日变形量由3.0 mm缓慢减小到0.0 mm,此阶段为稳定小变形阶段。
对比图 6和图 9的分析结果,超前支承压力曲线与原岩应力曲线的交点位于工作面前方8.1 m,巷道急速变形阶段和减速变形阶段的分界为工作面前方8.9 m,二者相距0.8 m;超前支承压力的峰值位置为工作面前方19.8 m,巷道减速变形阶段和稳定小变形阶段的分界为工作面前方20.1 m,二者相距0.3 m。可见在工程实践中采用监测应力数据确定巷道围岩变形阶段的方法精度较高,可以在现场实践中应用。
4 结论采用理论分析和现场实测方法,对综放工作面的超前支承压力和巷道围岩变形二者的关系进行了分析,得出以下主要结论:
1) 提出了工作面前方巷道的围岩变形阶段划分方法,将巷道围岩变形阶段划分为急速变形、减速变形和稳定小变形3个阶段,急速变形阶段和减速变形阶段统称为大变形阶段。急速变形阶段和减速变形阶段的分界为超前支承压力与原岩应力的交点,减速变形阶段与稳定变形阶段的分界为超前支承压力的峰值位置。
2) 对现场观测得到的超前支承压力和巷道围岩变形数据采用最小二乘拟合的方法进行分析,分析结果显示:根据超前支承压力曲线划分的巷道急速变形阶段和减速变形阶段的分界点与巷道围岩变形观测数据得到的二者分界点误差为0.8 m;根据超前支承压力曲线划分的巷道减速变形阶段和稳定变形阶段的分界点与巷道围岩变形观测数据得到的分界点的误差为0.3 m。可见根据超前支承压力划分工作面前方巷道围岩变形阶段的方法可行,精度较高。
3) 揭示了煤壁前方区域巷道围岩变形阶段与超前支承压力之间的联系:破坏区(急速变形阶段)和极限平衡区(减速变形阶段)的分界为超前支承压力曲线与原岩应力曲线的交点;塑性区(大变形阶段)和弹性区(稳定小变形阶段)的分界为超前支承压力峰值位置。
| [1] |
钱鸣高, 石平五. 矿山压力与岩层控制[M]. 江苏徐州: 中国矿业大学出版社, 2003. QIAN Minggao, SHI Pingwu. Mining pressure and strata control[M]. Xuzhou, Jiangsu: China University of Mining and Technology Press, 2003. (in Chinese) |
| [2] |
侯朝炯团队.巷道围岩控制[M].江苏徐州: 中国矿业大学出版社, 2013. Research Team of HOU Zhaojiong. Ground control of roadways[M]. Xuzhou, Jiangsu: China University of Mining and Technology Press, 2013. (in Chinese) |
| [3] |
许家林, 鞠金峰. 特大采高综采面关键层结构形态及其对矿压显现的影响[J]. 岩石力学与工程学报, 2011, 30(8): 1547-1556. XU Jialin, JU Jinfeng. Structural morphology of key stratum and its influence on strata behaviors in fully-mechanized face with super-large mining height[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(8): 1547-1556. (in Chinese) |
| [4] |
Xie J L, Xu J L. Effect of key stratum on the mining abutment pressure of a coal seam[J]. Geosciences Journal, 2017, 21(2): 267-276. DOI:10.1007/s12303-016-0044-7 |
| [5] |
王家臣, 杨胜利, 杨宝贵, 等. 长壁矸石充填开采上覆岩层移动特征模拟实验[J]. 煤炭学报, 2012, 37(8): 1256-1262. WANG Jiachen, YANG Shengli, YANG Baogui, et al. Simulation experiment of overlying strata movement features of longwall with gangue backfill mining[J]. Journal of China Coal Society, 2012, 37(8): 1256-1262. (in Chinese) |
| [6] |
Meng X R, Peng R, Zhao G M, et al. Roadway engineering mechanical properties and roadway structural instability mechanisms in deep wells[J]. KSCE Journal of Civil Engineering, 2018, 22(5): 1954-1966. DOI:10.1007/s12205-017-1298-y |
| [7] |
张宏伟, 荣海, 陈建强, 等. 基于地质动力区划的近直立特厚煤层冲击地压危险性评价[J]. 煤炭学报, 2015, 40(12): 2755-2762. ZHANG Hongwei, RONG Hai, CHEN Jianqiang, et al. Risk assessment of rockburst based on geo-dynamic division method in suberect and extremely thick coal seam[J]. Journal of China Coal Society, 2015, 40(12): 2755-2762. (in Chinese) |
| [8] |
杨小礼, 王作伟. 非线性破坏准则下浅埋隧道围岩压力的极限分析[J]. 中南大学学报(自然科学版), 2010, 41(1): 299-302. YANG Xiaoli, WANG Zuowei. Limit analysis of earth pressure on shallow tunnel using nonlinear failure criterion[J]. Journal of Central South University(Science and Technology), 2010, 41(1): 299-302. (in Chinese) |
| [9] |
赵健, 肖明, 杨阳, 等. 基于逼近阶跃函数和拉格朗日插值的改进DDA方法[J]. 岩土力学, 2017, 38(7): 2103-2112. ZHAO Jian, XIAO ming, YANG Yang, et al. Improved DDA method based on approximated step function and lagrange interpolation[J]. Rock and Soil Mechanics, 2017, 38(7): 2103-2112. (in Chinese) |
| [10] |
马念杰, 李季, 赵志强, 等. 圆形巷道围岩偏应力场及塑性区分布规律研究[J]. 中国矿业大学学报, 2015, 44(2): 206-213. MA Nianjie, LI Ji, ZHAO Zhiqiang, et al. Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock[J]. Journal of China University of Mining & Technology, 2015, 44(2): 206-213. (in Chinese) |
| [11] |
Li J P, He F L, Yan H, et al. The caving and sliding control of surrounding rocks on large coal roadways affected by abutment pressure[J]. Safety Science, 2012, 50(4): 773-777. DOI:10.1016/j.ssci.2011.08.036 |
| [12] |
康红普. 深部煤矿应力分布特征及巷道围岩控制技术[J]. 煤炭科学技术, 2013, 41(9): 12-17. KANG Hongpu. Stress distribution characteristics and strata control technology for roadways in deep coal mines[J]. Coal Science and Technology, 2013, 41(9): 12-17. (in Chinese) |
| [13] |
张国华, 梁冰, 张宏伟, 等. 回采巷道顶板离层分析与锚杆组合支护技术参数确定[J]. 重庆大学学报, 2010, 33(7): 135-140. ZHANG Guohua, LIANG Bing, ZHANG Hongwei, et al. Analysis of the roof separation in mining roadway and technical parameters determination of bolt combined supporting[J]. Journal of Chongqing University, 2010, 33(7): 135-140. (in Chinese) |
| [14] |
勾攀峰, 辛亚军. 深井巷道围岩锚固体流变控制力学解析[J]. 煤炭学报, 2013, 38(12): 2119-2125. GOU Panfeng, XIN Yajun. Rheological control mechanical analyticity of surrounding rock anchorage body in deep roadway[J]. Journal of China Coal Society, 2013, 38(12): 2119-2125. (in Chinese) |
| [15] |
谢福星, 张召千, 崔凯. 大采高采场超前支承压力分布规律及应力峰值位置研究[J]. 煤矿开采, 2013, 18(1): 80-83. XIE Fuxing, ZHANG Zhaoqian, CUI Kai. Advanced abutment pressure distribution rule and stress summit location in mining field with large mining-height[J]. Coal Mining Technology, 2013, 18(1): 80-83. (in Chinese) |
| [16] |
郭延华, 姜福兴, 张常光. 高地应力下圆形巷道临界冲击地压解析解[J]. 工程力学, 2011, 28(2): 118-122. GUO Yanhua, JIANG Fuxing, ZHANG Changguang. Analytical solution for critical rockburst of a circular chamber subjected to high in-situ stress[J]. Engineering Mechanics, 2011, 28(2): 118-122. (in Chinese) |
| [17] |
Zhang N, Zhang N C, Han C L, et al. Borehole stress monitoring analysis on advanced abutment pressure induced by longwall mining[J]. Arabian Journal of Geosciences, 2014, 7(2): 457-463. DOI:10.1007/s12517-013-0831-7 |
| [18] |
吴顺川, 潘旦光, 高永涛. 深埋圆形巷道围岩和衬砌相互作用解析解[J]. 工程力学, 2011, 28(3): 136-142. WU Shunchuan, PAN Danguang, GAO Yongtao. Analytic solution for rock-liner interaction of deep circular tunnel[J]. Engineering Mechanics, 2011, 28(3): 136-142. (in Chinese) |
| [19] |
高召宁, 孟祥瑞, 付志亮. 考虑渗流、应变软化和扩容的巷道围岩弹塑性分析[J]. 重庆大学学报, 2014, 37(1): 96-101. GAO Zhaoning, MENG Xiangrui, FU Zhiliang. Elasto-plastic analysis on surrounding rock of roadways based on seepage, strain softening and dilatancy[J]. Journal of Chongqing University, 2014, 37(1): 96-101. (in Chinese) |
| [20] |
赵瑜, 张春文, 刘新荣, 等. 高应力岩石局部化变形与隧道围岩灾变破坏过程[J]. 重庆大学学报, 2011, 34(4): 100-106. ZHAO Yu, ZHANG Chunwen, LIU Xinrong, et al. Study on strain localization and progressive failure of surrounding rock under high pressure environment[J]. Journal of Chongqing University, 2011, 34(4): 100-106. (in Chinese) |
| [21] |
李喆, 丁振良, 袁峰. 基于分层插值和最小二乘拟合的亚像素细分算法[J]. 南京理工大学学报(自然科学版), 2008, 32(5): 615-618. LI Zhe, DING Zhenliang, YUAN Feng. Subpixel algorithm based on level interpolation and least squares fitting[J]. Journal of Nanjing University of Science and Technology(Nature Science), 2008, 32(5): 615-618. (in Chinese) DOI:10.3969/j.issn.1005-9830.2008.05.018 |
| [22] |
陈跃宁, 徐征, 赵谡玲, 等. 最小二乘拟合计算有机薄膜晶体管迁移率的研究[J]. 物理学报, 2010, 59(11): 8113-8117. CHEN Yuening, XU Zheng, ZHAO Suling, et al. Research on least-squares fitting calculation of the field-effect mobility[J]. Acta Physica Sinica, 2010, 59(11): 8113-8117. (in Chinese) DOI:10.7498/aps.59.8113 |
 2019, Vol. 42
2019, Vol. 42


