电网可靠性评估过程包括系统状态抽取、系统状态分析与可靠性指标累计3个基本环节^[1-2]，其中系统状态分析是核心环节，包括对抽取的系统状态进行潮流计算，并对违背运行约束的故障系统状态进行优化校正。优化校正涉及最优化问题的求解，其计算复杂性随网络规模增大而急剧增加，成为可靠性评估的主要耗时环节，而为满足精度要求，又需要对大量故障系统状态进行优化校正分析^[3-5]，因此研究高效、计算复杂度与系统规模解耦的优化校正模型对提高可靠性评估效率有重要意义。

为缓解系统规模增大导致电网可靠性评估耗时严重的难题，可以采用等值方法简化外部网络，将其对研究网络的影响等值到研究网络边界，然后对等值后的研究网络进行可靠性评估^[6]。该思路通过降低评估系统的规模减小计算复杂度，有效提高了可靠性评估效率。现有文献中，基于上述思路的研究主要集中在如何构建有效、精确的等值模型上。文献[7]和[8]提出基于充裕性等值的电网可靠性状态分析求解模型；文献[9]~[11]提出基于Ward等值的电网可靠性评估模型；文献[12]提出基于REI等值的输电网可靠性评估模型。上述文献中用于研究网络的系统状态分析方法大致相同，仍然采取对研究网络进行整体优化校正，当研究网络规模很大时，可靠性评估依然面临高计算复杂性。

本研究中我们在研究网络内部构建动态校正域，将大规模全局优化校正问题转变成为一系列在动态校正域上的小规模逐次优化校正问题，从而大大缩短计算时间，在此基础上我们提出基于动态校正域和Ward等值的最优负荷削减模型。我们推导了反映节点有功调节能力的交叉权重解析计算表达式，给出了动态校正域的获取方法，提出计及等效平衡节点的静态Ward等值方法，实现了对动态校正域的外部网络灵活等值，并构建了基于动态校正域的线性规划最优削减模型。该模型有效降低了优化校正的计算规模，提高了系统状态分析的计算效率。

1 故障状态动态校正域计算

电网设备随机故障并导致线路过载时，校正过载线路的有效调节区域往往局限在过载线路邻近区域。通过改变校正区域内控制节点的注入有功功率，可有效缓解或消除线路过载。我们将过载线路校正调节区域定义为动态校正域，给出动态校正域的求解思路如下。

1.1 控制节点交叉权重推导

控制节点的选取是确定动态校正域的关键，节点选取应考虑如下两方面因素。

1) 针对过载线路：所选控制节点具有较强有功调节能力，即通过改变节点注入有功功率能够较大程度缓解或消除线路过载。

2) 针对正常线路：所选控制节点考虑有功调节对正常线路有功潮流的影响，以避免调节引起正常线路潮流过载的拉锯现象。

基于线路有功潮流——节点注入有功的潮流灵敏度可以有效揭示节点有功调整对线路有功潮流的影响，选取的控制节点能够保证对过载线路有较强的调节能力。设除平衡节点的电网节点总数为N_B；线路总数为N_L；线路l有功潮流向量为P_l；节点注入有功向量为P_s；根据直流潮流方程，潮流灵敏度S为：

$ \mathit{\boldsymbol{S}} = \partial {\mathit{\boldsymbol{P}}_l}/\partial {\mathit{\boldsymbol{P}}_s} = \mathit{\boldsymbol{X}}_{{N_{\rm{L}}} \times {N_{\rm{L}}}}^{ - 1}\mathit{\boldsymbol{A}}_{{N_{\rm{B}}} \times {N_{\rm{L}}}}^{\rm{T}}\mathit{\boldsymbol{B}}_{{N_{\rm{B}}} \times {N_{\rm{B}}}}^{ - 1}。$

(1)

式中：X_NL×NL为线路电抗组成的对角矩阵；A_NB×NL为节点—线路关联矩阵；B_NB×NB为节点电纳矩阵。

其中：

$ {B_{ij}} = - 1/{x_{ij}},{B_{ii}} = \sum\limits_{j \ne i} {1/{x_{ij}}} , $

(2)

式中x_ij为线路(i, j)的电抗。

仅仅根据潮流灵敏度选取控制节点会忽略节点有功调整对正常线路有功潮流的影响，导致调节过程中正常线路潮流频繁出现过载。文献[13]提出交叉权重因子概念，基于潮流灵敏度，通过权衡节点有功调整对所有线路的综合潮流影响计算节点交叉权重，以此优化控制节点的选取。该方法计及节点有功调整对正常线路潮流的影响，但容易造成数据淹没，即正常线路存在较大有功裕度情况下，当节点注入有功对正常线路的潮流灵敏度较小时，不论该节点对过载线路的潮流灵敏度大小如何，该节点都很可能被错选为控制节点，因此我们提出节点交叉权重的修正公式。

设过载线路和正常线路编号分别l和m，过载线路l与正常线路m有功潮流对节点j注入有功的潮流灵敏度为(S_lj，S_mj)，正常线路m的有功传输极限与实际有功潮流为(p_m^max, p_m)。当(S_lj＞0, S_mj＞0)或(S_lj＜0, S_mj＜0)时，减少或增加节点j注入有功可同时降低过载线路l和正常线路m的有功潮流；当(S_lj＞0, S_mj＜0)或(S_lj＜0, S_mj＞0)时，减少或者增加节点j注入有功可降低过载线路l有功潮流，但正常线路m的有功潮流反而会增加并可能过载，故不引起正常线路m过载的节点j允许有功调节上限为(p_m^max-p_m)/|S_mj |。

根据上述分析，为反映节点j在不引起正常线路过载条件下对过载线路的有功调节能力，设正常线路的集合为ψ′，定义节点j交叉权重为I_{l, j}，对上述两种情况作如下分析。

情况一：若集合ψ′中所有正常线路的潮流灵敏度S_mj与S_lj符号均相同，I_l,j表达式如下：

$ {I_{l,j}} = \left| {{S_{lj}}} \right|。$

(3)

由式(3)可知若S_lj绝对值较大，则节点j在调整线路l过载时有较强调节能力，同时由于灵敏度S_mj与S_lj符号相同，该调节也不易造成正常线路过载。

情况二：若集合ψ′中存在若干条正常线路的潮流灵敏度S_mj与S_lj符号相反，设这些线路组成的集合ψ″(ψ″⊂ψ′)，I表_{l, j}达式如下：

$ {I_{l,j}} = \left| {{S_{lj}}} \right| \times \mathop {\min }\limits_{m \in \psi '',m \ne l} \left\{ {\left( {p_m^{\max } - {p_m}} \right)/\left| {{S_{mj}}} \right|} \right\}。$

(4)

由式(4)可知S_lj绝对值较大，则节点j有较强过载调节能力；同时，若min_{m∈ψ″,m≠l}{(p)_m^max-p_m)/S_mj}也较大，说明需要很大的调节量才可能引起正常线路过载。因此I_l,j越大也说明节点j越适合作为控制节点。

从式(3)和(4)可以看出，I_l,j的求解难度主要在于潮流灵敏度S的计算。由于电网可靠性评估含大量故障系统状态分析，直接采用式(2)求S涉及大规模矩阵求逆计算，求解耗时。因此我们根据Wood Bury矩阵求逆引理，基于基态潮流灵敏度，给出故障状态S的解析计算式如下^[14]。

$ \mathit{\boldsymbol{S}} = {\mathit{\boldsymbol{L}}_{\left( {{N_{\rm{L}}} - {F_{\rm{L}}}} \right) \times {N_{\rm{L}}}}}{\mathit{\boldsymbol{S}}^{\left( 0 \right)}}\left( {{\mathit{\boldsymbol{E}}_{{N_{\rm{B}}} \times {N_{\rm{B}}}}} - {\mathit{\boldsymbol{F}}_{{N_{\rm{B}}} \times {N_{\rm{B}}}}}\mathit{\boldsymbol{B}}{{_{{N_{\rm{B}}} \times {N_{\rm{B}}}}^{\left( 0 \right)}}^{ - 1}}} \right); $

(5)

$ {\mathit{\boldsymbol{S}}^{\left( 0 \right)}} = \mathit{\boldsymbol{X}}{_{{N_{\rm{L}}} \times {N_{\rm{L}}}}^{\left( 0 \right)}}^{ - 1}\mathit{\boldsymbol{A}}{_{{N_{\rm{B}}} \times {N_{\rm{L}}}}^{\left( 0 \right)}}^{\rm{T}}\mathit{\boldsymbol{B}}{_{{N_{\rm{B}}} \times {N_{\rm{B}}}}^{\left( 0 \right)}}^{ - 1}; $

(6)

$ {\mathit{\boldsymbol{F}}_{{N_{\rm{B}}} \times {N_{\rm{B}}}}} = {\mathit{\boldsymbol{M}}_{{N_{\rm{B}}} \times {F_{\rm{L}}}}}{\mathit{\boldsymbol{K}}_{{F_{\rm{L}}} \times {F_{\rm{L}}}}}\mathit{\boldsymbol{M}}_{{N_{\rm{B}}} \times {N_{\rm{L}}}}^{\rm{T}}; $

(7)

$ {\mathit{\boldsymbol{K}}_{{F_{\rm{L}}} \times {F_{\rm{L}}}}} = {\left( {{\mathit{\boldsymbol{W}}_{{F_{\rm{L}}} \times {F_{\rm{L}}}}} + \mathit{\boldsymbol{M}}_{{N_{\rm{B}}} \times {N_{\rm{L}}}}^{\rm{T}}\mathit{\boldsymbol{B}}{{_{{N_{\rm{B}}} \times {N_{\rm{B}}}}^{\left( 0 \right)}}^{ - 1}}{\mathit{\boldsymbol{M}}_{{N_{\rm{B}}} \times {F_{\rm{L}}}}}} \right)^{ - 1}}; $

(8)

$ {\mathit{\boldsymbol{W}}_{{F_{\rm{L}}} \times {F_{\rm{L}}}}} = {\mathit{\boldsymbol{L}}_{{F_{\rm{L}}} \times {N_{\rm{L}}}}}\mathit{\boldsymbol{X}}_{{N_{\rm{L}}} \times {N_{\rm{L}}}}^{\left( 0 \right)}\mathit{\boldsymbol{L}}_{{F_{\rm{L}}} \times {N_{\rm{L}}}}^{\rm{T}}; $

(9)

$ {\mathit{\boldsymbol{M}}_{{N_{\rm{B}}} \times {F_{\rm{L}}}}} = \mathit{\boldsymbol{A}}_{{N_{\rm{B}}} \times {N_{\rm{L}}}}^{\left( 0 \right)}\mathit{\boldsymbol{L}}_{{F_{\rm{L}}} \times {N_{\rm{L}}}}^{\rm{T}}。$

(10)

式中：F_L为故障线路总数目；N_L-F_L为正常线路总数目；B_NB×NB⁽⁰⁾, X_NL×NL⁽⁰⁾, A_NB×NL⁽⁰⁾为基态节点电纳矩阵、线路电纳矩阵和节点-线路关联矩阵；S⁽⁰⁾为基态潮流灵敏度矩阵；E_NL×NL为N_L阶单位对角阵；L_FL×NL为E_NL×NL中对应故障线路编号的行向量组成的块矩阵；L_{(NL－FL)×NL}为E_NL×NL中对应正常线路编号的行向量组成的块矩阵。

输电线路或变压器线路故障概率通常很小，而多条线路同时故障的概率则更小，即F_L一般较小，这意味着W_FL×FL、K_FL×FL与M_NB×FL的阶数不大。由于基态S⁽⁰⁾和B_NB×NB^(0)－1为已知量，因此求取S涉及到的主要计算量在于F_L阶矩阵求逆。而若采用式(2)计算S，则涉及N_L阶矩阵求逆。可见式(5)使求取S所需计算量大幅降低。

1.2 动态校正域的搜索与影响因素

根据电网设备故障影响及对应校正措施的局部性特点，参考各节点交叉权重选择合适的阈值，动态校正域控制节点的集合D_CAl(dynamic correction area, D_CA)为：

$ {D_{{\rm{CA}}l}} = \left\{ {j\left| {{I_{l,j}} \ge B} \right.} \right\},j \in W。$

(11)

式中：B为节点交叉权重阈值，这里取所有节点交叉权重的平均值；W为电网节点的集合。

动态校正域的计算流程如下：

1) 利用式(5)~(10)计算当前故障系统状态下潮流灵敏度的数值；

2) 确定过载线路集合，对每一条过载线路，从线路首端节点沿潮流方向逆向搜索电源节点，从线路末端节点沿潮流方向顺向搜索负荷节点；

3) 对上一步中搜索到的所有节点，用式(3)和(4)计算交叉权重，根据式(11)判断该节点是否为控制节点，若是，则标记该节点；

4) 所有已标记的控制节点及其彼此之间的输电线路形成动态校正域。

通过改变交叉权重阈值，可有效调节动态校正域规模。B越大，动态校正域包含的控制节点数越少，动态校正域规模越小；反之，动态校正域规模越大，特别当B取0，动态校正域规模将等于整个研究网络。

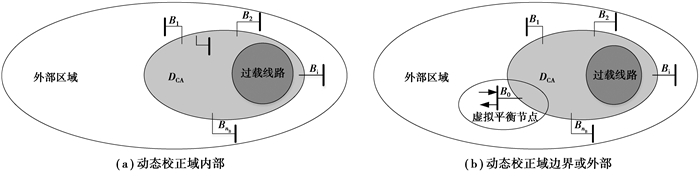
2 动态校正域的外部网络等值

为计及动态校正域节点功率调整过程中外部网络的影响，需将动态校正域外部网络等值到动态调节域边界。Ward等值可以实现对外部网络有效等值，应用比较广泛。但现有等值方法均假设平衡节点在研究网络内部，这意味现有Ward等值方法仅能处理平衡节点在动态校正域内部的情况，当平衡节点在动态校正域外部时，则无法处理。因此我们提出一种计及等效平衡节点的改进Ward等值方法，以实现对动态校正域外部网络的灵活等值。

设动态校正域内部、边界和外部节点的总数目分别为n_I、n_B和n_E，由此形成的集合分别为ϕ_I、ϕ_B和ϕ_E，其中(ϕ_I, ϕ_B∈D_CAl)，设平衡节点为s。根据直流潮流方程可得：

$ \left( {\begin{array}{*{20}{c}} {{b_s}}&{{\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}}&{{\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{I}}}}}}\\ {{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times 1}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}}&{{{\bf{0}}_{{n_{\rm{E}}} \times {n_{\rm{I}}}}}}\\ {{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times 1}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{I}}}}}}\\ {{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times 1}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{E}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{I}}}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{E}}} \times 1}}}\\ {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}}}\\ {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{I}}} \times 1}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{p_s}}\\ {{\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}}\\ {{\mathit{\boldsymbol{P}}_{{n_{\rm{B}}} \times 1}}}\\ {{\mathit{\boldsymbol{P}}_{{n_{\rm{I}}} \times 1}}} \end{array}} \right)。$

(12)

式中：θ_nE×1、${\mathit{\boldsymbol{\theta }}_{n_{\rm{B}} \times \mathit{\boldsymbol{1}}}} $和$ {\mathit{\boldsymbol{\theta }}_{n_{\rm{I}} \times \mathit{\boldsymbol{1}}}}$为ϕ_E、ϕ_B和ϕ_I中的节点电压相角列向量；${\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}$、$ {\mathit{\boldsymbol{P}}_{{n_{\rm{B}}} \times 1}}$和$ {\mathit{\boldsymbol{P}}_{{n_{\rm{I}}} \times 1}}$为ϕ_E、ϕ_B和ϕ_I中的节点有功注入列向量；b_s为平衡节点自电纳；$ {\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}}$、$ {\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{B}}}}}$和$ {\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{I}}}}}$为ϕ_E、ϕ_B和ϕ_I的自电纳矩阵；$ {\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}$，$ {\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}$为ϕ_E与ϕ_B之间的互电纳矩阵；$ {\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{I}}}}}$和$ {\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{B}}}}}$是ϕ_B与ϕ_I之间的互电纳矩阵；$ {\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times 1}}$、$ {\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times 1}}$、$ {\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times 1}}$、$ {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}$、$ {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}}$和$ {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{I}}}}}$是平衡节点s与ϕ_E、ϕ_B和ϕ_I之间的互电纳矩阵。

保留平衡节点，对式(12)进行高斯-赛德尔变换，消去动态校正域外部节点得：

$ \left( {\begin{array}{*{20}{c}} 0&{{\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{I}}}}}}\\ {{{\bf{0}}_{{n_{\rm{B}}} \times 1}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{B}}}}} - {\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{I}}}}}}\\ {{{\bf{0}}_{{n_{\rm{I}}} \times 1}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{I}}}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}}}\\ {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{I}}} \times 1}}} \end{array}} \right) = \\ \left( {\begin{array}{*{20}{c}} {{p_s} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}}\\ {{\mathit{\boldsymbol{P}}_{{n_{\rm{B}}} \times 1}} - {\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}}\\ {{\mathit{\boldsymbol{P}}_{{n_{\rm{I}}} \times 1}}} \end{array}} \right)。$

(13)

由式(13)可知，动态校正域外部网络对校正过程的影响通过边界节点有功注入和边界线路电纳反映，平衡节点的位置并不影响校正域边界参数，但影响平衡节点等效出力。平衡节点等效出力为：

$ {{\bar p}_s} = {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}} + {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{I}}}}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{I}}} \times 1}} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}} = \left( {{p_s} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}} \right)。$

(14)

当平衡节点在动态校正域的内部时，$ {\mathit{\boldsymbol{B}}_{{n_{\text{E}}} \times 1}} = 0, {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}} = 0$，此时$ {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}={\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}}$，$ {p_s} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{P}}_{{n_{\text{E}}} \times \mathit{\boldsymbol{1}}}} = {p_s}$，式(14)可表示为：

$ {{\bar p}_s} = {p_s} = {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{B}}}}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}} + {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{I}}}}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{I}}} \times 1}}。$

(15)

由式(15)可知，当平衡节点在动态校正域内部时，p_s等于动态校正域所有节点的功率不平衡量，该结论与文献[9]相同，证明了本文等值思路的有效性。

对比式(14)和(15)可见，当平衡节点在动态校正域的外部或边界时，式(14)还可表示为：

$ {{\bar p}_s} = {p_s} - {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}}。$

(16)

为统一分析，定义分配矩阵$ {\mathit{\boldsymbol{D}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}} = {\mathit{\boldsymbol{B}}_{{n_{\text{B}}} \times {n_{\rm{E}}}}}\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{E}}}}^{ - 1}$，式(13)可写为如下形式：

$ \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{B}}}}} + {\mathit{\boldsymbol{D}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}{\mathit{\boldsymbol{B}}_{{n_{\rm{E}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{B}}} \times {n_{\rm{I}}}}}}\\ {{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{B}}}}}}&{{\mathit{\boldsymbol{B}}_{{n_{\rm{I}}} \times {n_{\rm{I}}}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}}}\\ {{\mathit{\boldsymbol{\theta }}_{{n_{\rm{I}}} \times 1}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{{n_{\rm{B}}} \times 1}} + {\mathit{\boldsymbol{D}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}{\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}}\\ {{\mathit{\boldsymbol{P}}_{{n_{\rm{I}}} \times 1}}} \end{array}} \right)。$

(17)

图 1给出了平衡节点不同位置对应的等值网络。式(15)和(16)可统一表达为：

$ {{\bar p}_s} = {p_s} + \mu {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{D}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}^{ - 1}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}} $

式中：μ为特征参数。当平衡节点在动态校正域内部时，μ=0；当平衡节点在动态校正域的外部或边界时，μ=－1，此时μ可看作平衡节点等效至动态校正域边界的传递参数。通过μ，外部网络的平衡节点被等效至动态校正域边界上。

3 基于动态校正域的改进负荷削减模型

电网可靠性评估中，常规校正分析采用基于直流潮流的最优负荷削减模型^[3]，算式如下：

$ \min \sum\limits_{i \in {N_{\rm{D}}}} {{\mathit{\boldsymbol{C}}_i}} ; $

(18)

$ {\mathit{\boldsymbol{P}}_{\rm{L}}} = \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{P}}_{\rm{G}}} - {\mathit{\boldsymbol{P}}_{\rm{D}}} + \mathit{\boldsymbol{C}}} \right); $

(19)

$ \sum\limits_{i \in {N_{\rm{G}}}} {{\mathit{\boldsymbol{P}}_{{{\rm{G}}_i}}}} + \sum\limits_{i \in {N_{\rm{D}}}} {{\mathit{\boldsymbol{C}}_i}} - \sum\limits_{i \in {N_{\rm{D}}}} {{\mathit{\boldsymbol{P}}_{{\rm{D}}i}}} = 0; $

(20)

$ \mathit{\boldsymbol{P}}_{\rm{G}}^{\min } \le {\mathit{\boldsymbol{P}}_{\rm{G}}} \le \mathit{\boldsymbol{P}}_{\rm{G}}^{\max }; $

(21)

$ 0 \le \mathit{\boldsymbol{C}} \le {\mathit{\boldsymbol{P}}_{\rm{D}}}; $

(22)

$ \left| {{\mathit{\boldsymbol{P}}_{\rm{L}}}} \right| \le \mathit{\boldsymbol{P}}_{\rm{L}}^{\max }。$

(23)

式中：C为全网所有节点组成的削负荷向量；P_L为全网线路潮流组成的行向量；S为线路有功潮流与节点注入有功之间的潮流灵敏度矩阵；P_G和P_D分别为全网机组出力与负荷功率的行向量；P_Gi、P_Di和C_i分别为P_G、P_D和C的第i个元素；P_G^max和P_G^min分别为P_G中上、下限约束组成的行向量；P_L^min为线路有功传输极限组成的行向量；N_G和N_D分别为机组节点和负荷节点组成的集合。

从式(17)和(22)可见，常规最优负荷削减模型从全网优化角度求取负荷削减量，模型计算复杂度与校正规模密切相关，校正规模越大，计算复杂性越大。考虑到大规模电网中设备随机故障的影响往往呈现局部性特点，对应的校正措施实际常在就近局部区域进行优化调整。针对这一特点，本文结合过载调整的动态校正域，提出校正域内部进行局部优化校正的最优负荷削减模型，算式如下：

$ \min \sum {{\mathit{\boldsymbol{C}}_{\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}} ; $

(24)

$ {\mathit{\boldsymbol{P}}_{{n_{\rm{K}}} \times 1}} = {\mathit{\boldsymbol{S}}_{{n_{\rm{K}}} \times \left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right)}}\left( {{\mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}} - {\mathit{\boldsymbol{P}}_{{\rm{D}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}} + {\mathit{\boldsymbol{C}}_{\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}} \right) + {\mathit{\boldsymbol{S}}_{{n_{\rm{K}}} \times {n_{\rm{B}}}}}{\mathit{\boldsymbol{D}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}}{\mathit{\boldsymbol{P}}_{{n_{\rm{E}}} \times 1}}; $

(25)

$ \sum {\left( {{\mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}} + {\mathit{\boldsymbol{C}}_{\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}} - {\mathit{\boldsymbol{P}}_{{\rm{D}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}} \right)} + {p_s} + \mu {\mathit{\boldsymbol{B}}_{1 \times {n_{\rm{E}}}}}\mathit{\boldsymbol{D}}_{{n_{\rm{B}}} \times {n_{\rm{E}}}}^{\rm{T}}{\mathit{\boldsymbol{\theta }}_{{n_{\rm{B}}} \times 1}} = 0; $

(26)

$ \mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}^{\min } \le {\mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}} \le \mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}^{\max }; $

(27)

$ 0 \le {\mathit{\boldsymbol{C}}_{\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}} \le {\mathit{\boldsymbol{P}}_{{\rm{D}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}; $

(28)

$ p_s^{\min } \le {p_s} \le p_s^{\max }; $

(29)

$ \left| {{\mathit{\boldsymbol{P}}_{{n_{\rm{K}}} \times 1}}} \right| \le \mathit{\boldsymbol{P}}_{{n_{\rm{K}}} \times 1}^{\max }。$

(30)

式中：n_K为动态校正域线路总数；$ {\mathit{\boldsymbol{P}}_{{n_{\rm{K}}} \times 1}}$为动态校正域的线路有功潮流；$ {\mathit{\boldsymbol{S}}_{{n_{\rm{K}}} \times \left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right)}}$为动态校正域中线路有功潮流对所有节点注入有功的潮流灵敏度；$ {\mathit{\boldsymbol{S}}_{{n_{\rm{K}}} \times {n_{\rm{B}}}}}$为$ {\mathit{\boldsymbol{S}}_{{n_{\rm{K}}} \times \left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right)}}$的子块，表示动态校正域中线路有功潮流对边界节点的潮流灵敏度；$ {\mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}, {\mathit{\boldsymbol{P}}_{{\rm{D}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}$为动态校正域中所有节点的机组注入有功和负荷有功向量；$ {\mathit{\boldsymbol{C}}_{\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}}$为动态校正域中所有节点的负荷削减向量；p_slack为平衡节点的有功；$ \mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}^{\min }$和$ \mathit{\boldsymbol{P}}_{{\rm{G}}\left( {{n_{\rm{I}}} + {n_{\rm{B}}}} \right) \times 1}^{\max }$分别为动态校正域中所有节点的机组上、下限约束向量；p_s^min和p_s^max为平衡节点的有功上、下限约束；$ \mathit{\boldsymbol{P}}_{{n_{\rm{K}}} \times 1}^{\max }$为动态校正域中线路有功传输极限的约束向量。

对比常规模型与本文模型可知，常规负荷削减模型始终从全网整体角度进行优化校正，而我们的模型则是在动态校正域内部进行优化校正。从计算效率上讲，我们的模型处理的网络规模更小，节省了大量计算时间。从计算精度上讲，本文模型覆盖了校正过载线路最有效的控制节点，模型精度与全网优化相差很小；此外模型的计算精度与计算效率还可通过改变动态校正域的规模灵活调节。

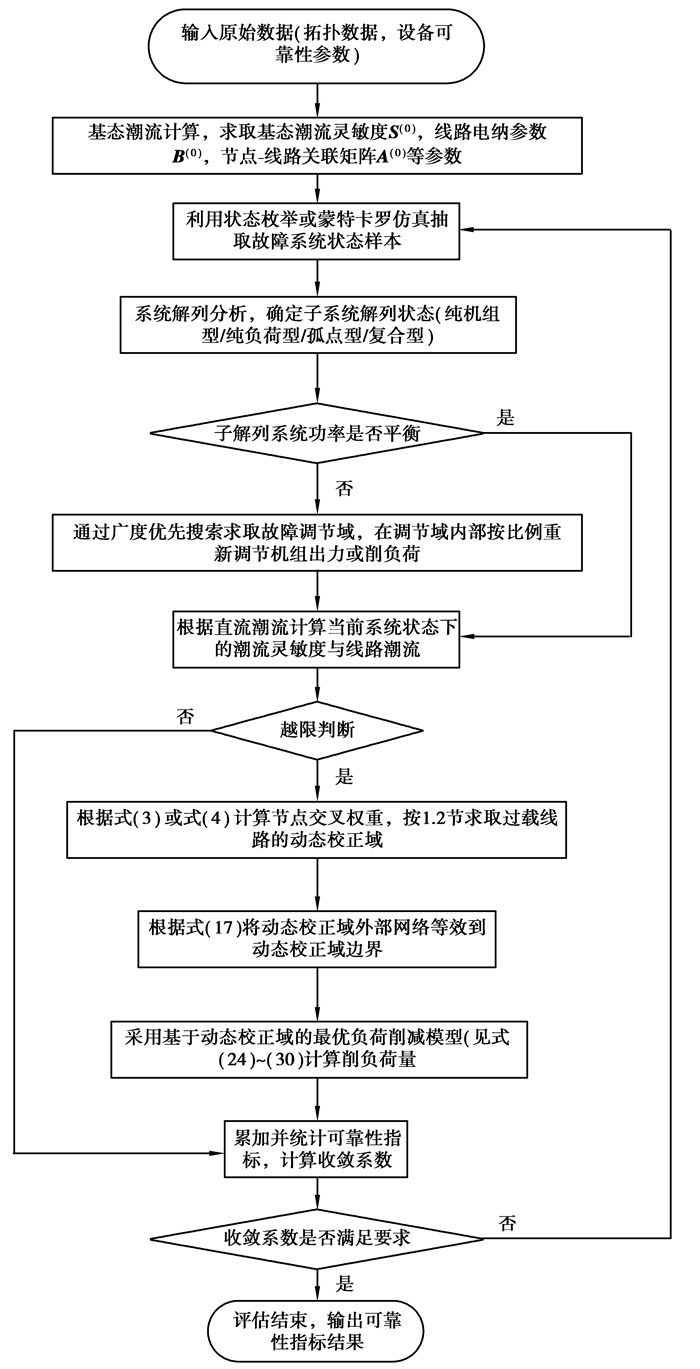
4 算法流程

采用基于动态校正域与Ward等值的线性规划最优负荷削减模型进行电网可靠性评估，算法流程如图 2所示。

其中的系统分析流程如下：

1) 计算基态下的潮流分布P_l⁽⁰⁾与线路有功潮流对节点注入有功的潮流灵敏度S⁽⁰⁾；

2) 基于基态潮流灵敏度S⁽⁰⁾，对抽取到的故障系统状态用式(5)计算潮流灵敏度矩阵S，根据直流方程求取线路有功潮流；

3) 线路越限判断，确定是否有线路过载，若是，转步骤4)；否则，转步骤7)；

4) 用式(5)计算节点交叉权重，根据式(11)挑选控制节点，按1.2节所述方法求取动态校正域；

5) 用式(17)将动态校正域外部网络等值到动态校正域边界上；

6) 用式(17)~(23)求取削负荷量，记录机组节点与负荷节点的调节功率和削负荷量，转入下一条过载线路的校正调节；

7) 若所有过载线路均已校正，计算总的切负荷量，进行系统可靠性指标统计。

5 算例分析 5.1 可靠性评估精度验证

采用非序贯蒙特卡罗仿真对RBTS^[15]、IEEE-RTS79^[16]与IEEE-RTS96^[17]进行可靠性评估。对每个可靠性测试系统，分别采用常规最优负荷削减模型^[3]和本文改进负荷削减模型进行计算分析：

1) 采用线性规划方法，通过全网重新调节机组有功出力和切负荷使故障系统恢复至安全水平。模型算式见式(19)~(24)；

2) 改进负荷削减模型：根据节点交叉权重求取动态校正域；利用式(17)将动态校正域外部网络等效至动态校正域边界，并在动态校正域内部进行最优负荷削减计算。模型算式见式(24)~(30)；

两种模型的可靠性评估结果如表 1所示。表中I_LOLP为失负荷概率指标；I_EENS为缺失电量指标，指标计算公式见文献[3]。

结果表明：

1) 本文模型所得各项可靠性指标与常规最优负荷削减模型相近，这说明本文模型应用于电网可靠性评估时，计算精度能够满足要求。

2) 与常规模型相比，本文模型所得可靠性指标偏大，这是因为常规模型基于全网机组出力优化和负荷削减，属于全网优化校正，而本文模型采用局部调整思路，在规模相对较小的动态校正域中优化机组出力和削减负荷。本文模型将全网优化校正转变为在动态校正域的连续局部优化校正，与常规全网优化模型相比，本文模型涉及的优化控制变量较少，从而校正结果偏大。以常规模型为参照，表 2给出了本文模型所得各项可靠性指标的相对偏差，两种模型下失负荷概率LOLP和缺供电量EENS指标的相对偏差都小于6%，验证了本文方法同样具有较好准确性。

5.2 可靠性评估速度验证

表 3给出了常规模型与本文模型评估电网可靠性的计算时间结果。

与常规模型相比，本文模型优势明显。原因在于常规模型计算复杂度与系统规模密切相关，系统规模越大，计算过程越复杂，评估越耗时。而本文模型校正范围仅在动态校正域内部，动态校正域大小和系统规模关联不大，故本文模型计算效率受系统规模影响不大，计算速度更快。

5.3 动态校正域规模对可靠性评估的影响分析

动态校正域规模是影响本文模型计算精度与计算速度的关键因素，同时也是本文模型区别于常规模型的关键。为深入分析动态校正域规模对可靠性评估结果的影响，逐次降低节点交叉权重阈值，在此基础上利用本文模型进行可靠性评估。表 4给出了不同阈值下本文模型的可靠性评估结果。其中K₁=(1/N_B)$ \sum\limits_{j = {D_{{\rm{CA}}l}}} {{I_j}, {K_2} = \left( {1/2{N_{\rm{B}}}} \right)\sum\limits_{j \in {D_{{\rm{CA}}l}}} {{I_j}} } $，K₃=0。可见，随动态校正域规模增加，本文模型的可靠性评估结果的相对偏差降低。当交叉权重阈值为K₁时，LOLP的相对偏差依次为1.58%、2.78%与4.18%，EENS的相对偏差依次为5.26%、5.23%与2.78%；当交叉权重阈值取K₂时，LOLP的相对偏差依次为1.36%、2.45%与2.17%，EENS指标相对偏差依次为3.31%、5.19%与2.53%；当交叉权重阈值取K₃，即动态校正域范围始终相当于全网规模时，LOLP相对偏差依次为0.07%，0.03%与0.11%，EENS相对偏差依次为0.01%、0.08%与0.79%。因此改变节点交叉权重阈值，可有效改变动态校正域计算规模，进而改变可靠性评估精度。

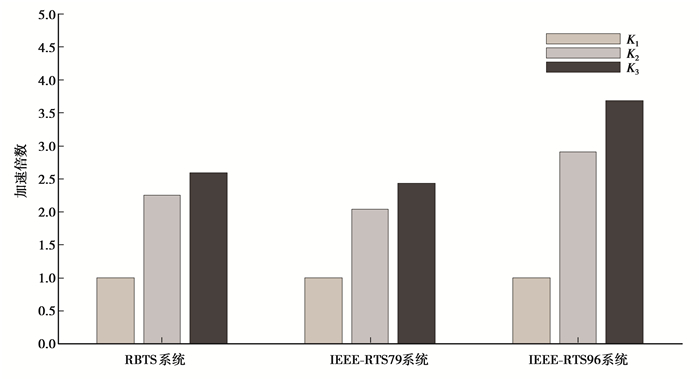
图 3给出了以K₁情况下计算时间为基准,交叉权重阈值取K₂与K₃时的计算时间对比。可见,随动态校正域规模增加本文模型计算时间将增加,原因在于动态校正域计算规模增加时,进行节点有功优化调整的控制节点数目相应增加,优化计算更耗时,但校正优化效果也越接近全网整体优化。

为进一步揭示优化校正过程中动态校正域的计算规模与可靠性评估时间的关系，以IEEE-RTS96系统(全网节点总数N_B=73)为例，根据非参数核密度估计，图 4给出了利用本文模型进行电网可靠性评估时，故障状态分析中动态校正域的概率密度分布曲线。动态校正域所包含的控制节点总数目在[0, 25]和[60, 73]区间分布较为密集，在[25, 60]区间分布较为稀疏。由此可见采用本文模型在对IEEE-RTS96系统进行电网可靠性评估时，动态校正域的计算规模始终小于全网规模，这验证了本文模型能有效减少进行优化校正的网络规模。

6 结论

电网设备随机故障的影响往往呈现局部性，通过局部调整即可快速消除故障影响。我们提出一种基于动态校正域与Ward等值的改进负荷削减模型。该模型将常规最优负荷削减由全网优化转变为一系列在动态校正域的逐次优化过程，通过降低优化校正的计算规模，提高了计算速度，并具有较好精度，在大规模电网可靠性评估问题中有一定优越性。