2. 山东大学 a. 青岛校区公共(创新)实验教学中心, b. 信息科学与工程学院, 山东 青岛 266237
2. a. Public(Innovation) Experimental Teaching Center, Qingdao Campus; b. School of Information Science and Engineering Shandong University, Qingdao 266237,Shandong Province, P. R. China
传统智能诊断以数据为驱动,主要通过机器学习方法对由信号处理得到的故障特征进行分类识别,诊断效果取决于故障特征的提取能否准确地反映故障类型的本质区别[1]。经典的诊断算法主要有:支持向量机(support vector machine,SVM)、核方法(KMs)、流形学习(ML)等。常用的分类故障特征有时、频域统计特征和小波、EMD(empirical mode decompostion)能量域特征,或将不同分析域内参数组合多变量特征。李嫄源等[2]提出一种基于SVM与粒子群优化(particle swarm optimization,PSO)相结合的电机轴承故障诊断方法, 该方法结合振动信号的时域与小波包能量特征,使表征振动信号的特征具有较好的可靠性和敏感性,提高了故障的诊断准确率;Shen等[3]组合裕度因子、波形因子、均方根频率等29个特征,通过SVM分类识别齿轮故障。基于机器学习的智能诊断取得了重要的成果,但依赖于信号处理技术和诊断经验来实现故障特征的提取,孤立地对待特征提取与分类识别两个环节[4]。深度学习模型可通过模型的自适应学习将特征抽取与分类识别融为一体,实现由数据到诊断结果的“端-端”过程,不仅降低了对信号处理与诊断经验的依赖,更适应工业大数据背景下海量监测数据的分析需求[5]。传统的基于机器学习的诊断过程与深度学习分析过程比较如图 1所示, 其中DL代表深度学习(deep learning),kNN表示k最近邻(k-nearest neighbor),RBF是径向基函数网络(radial basis function),BP是反向传播(back propagation)。

|
图 1 诊断过程比较 Figure 1 Comparison of the diagnostic processes |
本文使用深度学习的经典架构——卷积神经网络(CNN),针对不同故障类型的样本不平衡问题,引入深度学习的模型优化技术,提出适于轴承故障诊断的深度卷积神经网络模型,模型直接作用于原始实测轴承振动信号,自适应地从原始数据中逐层学习故障特征,模型顶层分类器实现不同故障的准确识别。我们引入批量归一化、dropout、L2正则项等模型优化技术配合改进型的weighted-softmax-loss加权损失函数[6],使模型能够在不平衡数据集上保持较高准确率并且拥有较快的收敛速度与泛化能力。
1 CNN卷积神经网络算法原理卷积神经网络是包括滤波特征提取和目标分类的多级前馈式神经网络,基于感受野的层间连接设计,基本结构包括卷积层、池化层和全连接层与分类器。
1.1 卷积层与池化层卷积层中一定大小的卷积核遍历输入特征图,卷积核与输入特征图的局部区域作卷积运算,计算方式见公式(1)。卷积核权值共享降低了网络的连接数量,同时可以提取丰富的结构化特征,卷积层一般组合多个不同的卷积核以提取不同的特征。卷积后再经过激活函数的非线性转化,将线性不可分的多维特征映射到线性可分性强的空间。为避免反向传播过程中的梯度弥散问题和ReLu激活函数导致的某些神经元梯度为零即参数不再更新的“神经元坏死”现象,本文拟采用如公式(2)所示的PReLU激活函数[7]。
池化层又称下采样层,对卷积得到的特征图做进一步压缩和二次特征提取,以均值池化和最大值池化最为常见,池化层的计算见公式(3),本文拟采用均值池化的方式进行下采样操作。
| $ a_j^l = f\left( {{z^l}} \right) = f\left( {\sum\nolimits_{i \in Mi} {a_i^{l - 1}K_j^l} + b_j^l} \right); $ | (1) |
| $ {\rm{PReLU}}\left( {{x_i}} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {x_i}\\ {a_i}{x_i} \end{array}&\begin{array}{l} {\rm{if}}\;{x_i} > 0,\\ {\rm{if}}\;{x_i} \le 0; \end{array} \end{array}} \right. $ | (2) |
| $ a_j^l = f\left( {{\rm{down}}\left( {a_j^{l - 1}} \right) + b_j^l} \right)。$ | (3) |
式中:ajl表示第l层第j个卷积核输出的特征图,Mi表示第l-1层输出特征图集合;ajl-1表示第l-1层输出的第j个特征图;Kjl表示第l层第j个卷积;bjl为对应偏置项;f(·)为激活函数;xi表示进入激活函数的值;f(down())为池化函数。基于一维振动信号的卷积池化均在如图 2所示的一维向量上进行计算。

|
图 2 振动信号的卷积、池化示意图 Figure 2 The convolution process and pooling process of vibration signal |
全连接层将卷积池化后提取到的特征进行分类,首先需将卷积后的特征图光栅化为一维向量,使得局部特征在更高维度上进行全局信息整合。在最后一层全连接层上使用softmax分类器对不同故障类型的振动信号进行分类识别。
1.3 模型训练与优化算法在监督学习中,使用目标函数(loss函数Ls)来评价输入样本经模型判别后的输出值与真实值的一致性程度,常用的损失函数有平方误差函数(squared loss function)、交叉熵损失函数(cross-entropy loss function)和softmax损失函数(softmax loss function)。本文拟采用softmax-loss损失函数,考虑到在故障诊断的实际应用中故障状态的样本比健康状态样本更难以收集,会出现极不平衡的数据集,因此引入权重损失函数Ws见公式(4),对数量较多的类型给予较小的权值,数量较少的类型给予较大的权值,同时加入的L2正则化惩罚项见公式(5),以此改善样本不均衡问题带来的模型泛化能力差的问题。将正则项与交叉熵函数合并的权重损失函数见公式(6)。
| $ {W_{\rm{s}}} = - \frac{1}{Q}\sum\nolimits_{q = 1}^Q {\sum\nolimits_{c = 1}^C {{v_c}l\left\{ {{y^q} = c} \right\}\log \left( {P_c^{\left( q \right)}} \right)} } ; $ | (4) |
| $ {v_c} = \frac{{\max \left\{ {{n_c}} \right\}_{c = 1}^C}}{{{n_c}}}; $ | (5) |
| $ {n_c} = \sum\nolimits_{q = 1}^Q {l\left\{ {{y^q} = c} \right\}} ; $ | (6) |
| $ P_c^{\left( q \right)} = \frac{{\exp \left( {{{\left( {\mathit{\boldsymbol{w}}_c^{K,l}} \right)}^{\rm{T}}}{x^{\left( q \right),L - 1}}} \right)}}{{\sum\limits_{c = 1}^C {\exp \left( {{{\left( {\mathit{\boldsymbol{w}}_c^{K,l}} \right)}^{\rm{T}}}{x^{\left( q \right),L - 1}}} \right)} }}; $ | (7) |
| $ \mathit{\boldsymbol{R}}\left( W \right) = \sum\nolimits_K {\sum\nolimits_l {\mathit{\boldsymbol{W}}_{K,l}^2} } ; $ | (8) |
| $ {L_{\rm{s}}} = {W_{\rm{s}}} + \lambda \mathit{\boldsymbol{R}}\left( W \right)。$ | (9) |
式中:nc表示第c类样本的个数;vc表示第c类样本相对于其他类样本的不平衡程度;C与Q分别表示总的类别数与样本总数;Pc(q)表示输入样本经过softmax函数的输出值;wcK,l表示连接权值;yq是指样本y在第q类下的类标;L是深度网络层数;λ表示正则项的惩罚系数;R(W)表示偏差项权值矩阵;Wk, l2是不卷积层之间传递的权值矩阵。
Adam优化算法:Adam是一种学习率自适应的优化算法,利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率,在反向传播阶段,更新权值求得全局最优解,使loss函数达到最小值[8]。
1.4 模型的优化提升在引入加权损失函数和L2正则项来提升不平衡样本的识别能力的基础上,为加快模型收敛速度和提升泛化能力,本研究在搭建轴承故障诊断深度卷积神经网络模型时在全连接层引入dropout处理,并尝试在卷积层使用批量归一化处理。Dropout[9]将隐层神经元按一定比例随机置零,使部分神经元不参与训练过程,从而降低模型过拟合的风险,提升模型的泛化能力,批量归一化[10]旨在减少内部协变量的转移。
2 滚动轴承故障诊断数据集 2.1 实验数据集的处理为对比算法的优劣,采用CWRU(美国凯斯西储大学)的滚动轴承标准故障数据集,此数据集故障轴承通过电火花加工单点损伤,故障位置有内圈、外圈、滚动体,故障大小有0.18、0.36、0.54 mm 3种。实验在1、2、3 hp(1 hp=746 W)3种负荷下,由12 kHz加速度传感器测得振动加速度,将3种工况下的数据分别分为A、B、C 3个数据集。考虑在实际应用中,一方面,同一种故障类型可能出现在不同的工况、不同轴承位置中,数据集要尽可能全面地呈现轴承状态,另一方面,故障态样本数量可能远低于健康状态样本,尤其是重度损坏的轴承样本更加难以获取,从而造成数据集各故障类型样本量的极不平衡。为更接近实际应用,制作包含3种工况的不平衡数据集D。传感器采样频率12 kHz,轴承转速1 730~1 797 r/min,轴承旋转一圈采集约430个数据,单个样本长度应保证可以准确反映此状态下轴承振动信号的数据分布情况,故以1 024个数据点为一个样本长度,实验数据集如表 1所示。
| 表 1 实验数据集 Table 1 Experimental data sets |
随机挑选表 1中的数据样本,10种不同状态的轴承振动信号时域波形如图 3所示。
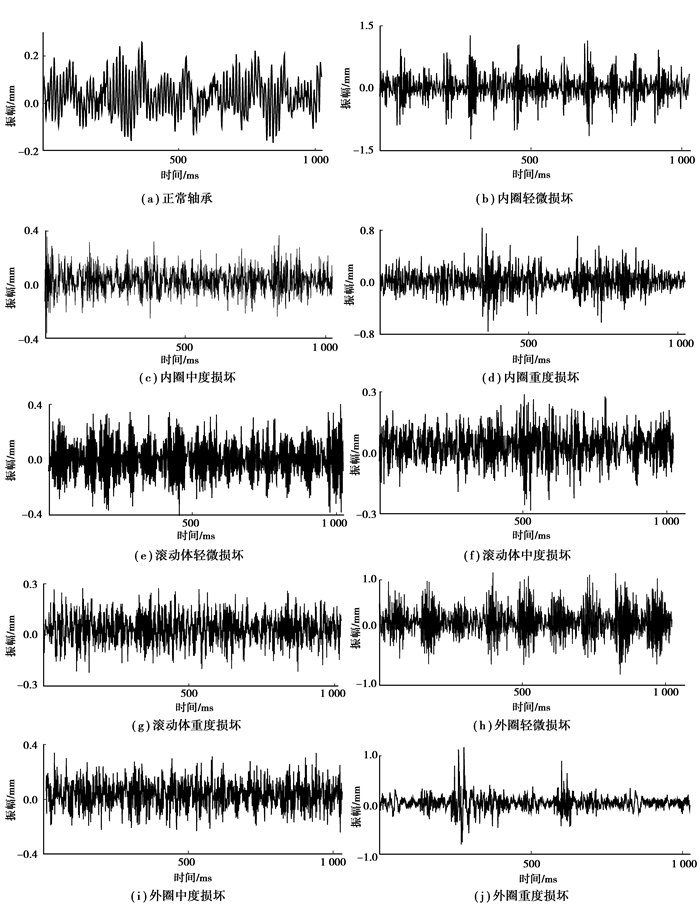
|
图 3 不同状态的轴承振动信号时域波形 Figure 3 Time-domain waveforms of bearing vibration signals in different states |
从图 3可看出,不同故障类型的轴承振动信号有较为显著的差异,而同种故障的不同损伤程度则差异微小,难以区分。为了实现早期微弱故障的诊断和不同故障程度的准确识别,研究基于深度学习模型的自适应特征提取和目标分类方法有较大的意义。
3 卷积神经网络模型设计与实验验证 3.1 卷积网络架构设计卷积网络模型为图 4所示的“卷积-池化-卷积-池化-卷积-池化-卷积-池化-卷积-池化-全连接-softmax分类器”结构,五层的卷积池化结构从1 024维的原始时域信号提取特征,全连接层实现信息整合和目标分类。基于感受野理论的卷积核设计[11],卷积核大小和数量须合适,在尽可能完整地提取有效特征的情况下尽量避免冗余的参数,模型具体参数见表 2。图 4中BN是批量标准化(batch normalization),它可以有效缓解训练中的梯度消失/爆炸现象,加快模型的训练速度。
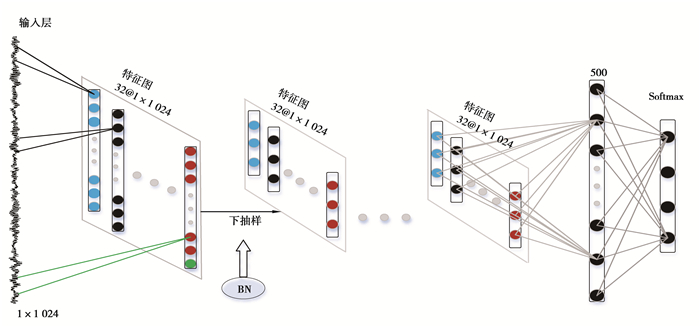
|
图 4 模型结构图 Figure 4 Model structure diagram |
| 表 2 模型参数表 Table 2 Model parameters |
基于python-tensorflow搭建模型,A、B、C、D 4个数据集均按照6:4划分为训练集和测试集。模型参数使用表 2给出的参数,其中最优超参数选择为经验值,设置如下:学习率0.002 5,dropout为0.70, 正则项系数λ为1.25,预设训练次数epoch为5 000。卷积神经网络模型的另一个非常重要的超参数批次(mini_batch)是影响模型收敛速度和分类准确率的重要参数,关于批次大小的设置尚无定论,需要根据特定的数据集和模型结构不断调整以期最佳。因此,本文以mini_batch取值20、40、60、80、100、120、140、160、180、200、220、240、260、280下数据集D的训练集准确率来确定最佳批次,结果如图 5所示,最终确定最佳mini_batch为200。
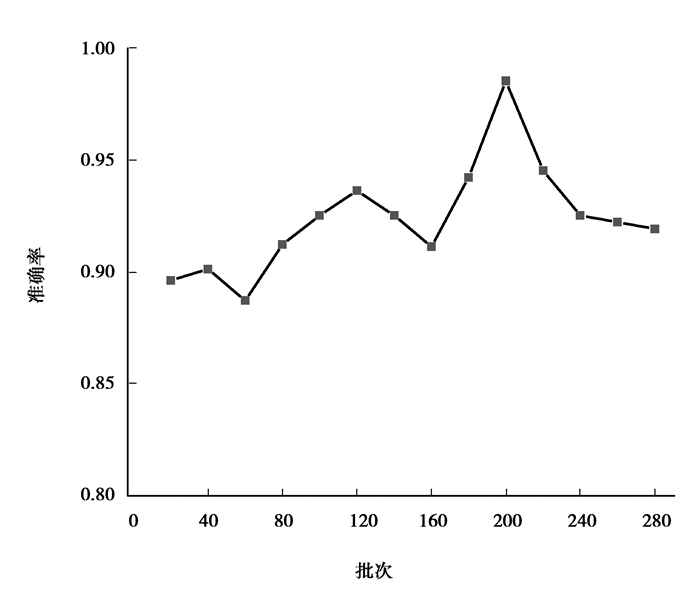
|
图 5 训练集准确率随批次大小变化曲线图 Figure 5 Curve of accuracy of training set changing with mini_batch |
为了加快模型收敛,提升模型的识别准确率和泛化能力,在每个卷积层中添加批量归一化处理。由于篇幅有限,仅展示数据集D前3 000次的训练过程中训练集与测试集的准确率和loss函数值变化曲线。如图 6所示,在训练至1 200次左右时,模型已经收敛,训练集准确率达到98%,测试集上的准确率达到了95%,随着训练次数的增加损失函数也降至1.46、1.50。A、B、C、D四个数据集的整体准确率如图 7所示,可以看到,A、B、C、D的训练集、测试集都有较高的识别准确率。
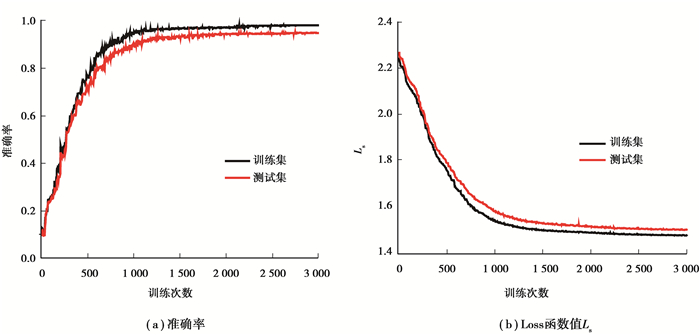
|
图 6 训练过程中的准确率和Loss值变化曲线 Figure 6 Accuracy and loss function value curves during training |

|
图 7 各数据集的识别准确率 Figure 7 The accuracy of identification of each data set |
上述准确率是分类正确的样本个数与样本总数的比值,是对模型分类能力和泛化能力的最基本的判断。考虑到实际应用中,故障态样本比健康样本更难收集,不同故障程度的样本也有较大差异,从而导致各个类型样本数量的严重不均衡,此时若单一考量总体的准确率来评估模型,会得到较高的总体准确率,而在一些数据量少的类型上产生严重误差。为客观地评估模型的性能,引入精确率P(Precision)、召回率Re(Recall)、F1(F-measure)值3个分类模型综合评价指标,针对二分类问题的混淆矩阵(表 3)可得到计算公式(10)~(12)。
| 表 3 二分类混淆矩阵 Table 3 Two-classification confusion matrix |
| $ P = \frac{{{p_{\rm{t}}}}}{{{p_{\rm{t}}} + {p_{\rm{f}}}}}; $ | (10) |
| $ {R_{\rm{e}}} = \frac{{{p_{\rm{t}}}}}{{{p_{\rm{t}}} + {p_{\rm{f}}}}}; $ | (11) |
| $ {F_1} = \frac{{2{p_{\rm{t}}}}}{{2{p_{\rm{t}}} + {p_{\rm{f}}} + {n_f}}}。$ | (12) |
针对本研究中的多分类问题,在计算某一类的评价指标时可将其余类均视为反例,由此得到测试集-D的评价指标值(表 4)和精确率(P)混淆矩阵(图 8)。可以看到,即使在不平衡训练集-D的模型训练下,测试集-D的精确率和召回率都较高,对IF3、RF3、OF3这3类数据量较小的样本也可得到较高的精确率、召回率以及F1值,说明卷积神经网络模型不仅对均衡样本有着很好的分类识别性能,对不均衡样本也能得到较为理想的分类效果,也验证了引入weighted-softmax-loss和正则项对模型泛化性能的提升效果,从而客观地评估了模型的性能。
| 表 4 测试集-D模型评价指标 Table 4 Test Set-D model evaluation indexes |

|
图 8 测试集-D混淆矩阵图 Figure 8 Testing set-D confusion matrix |
为进一步验证本文搭建模型的轴承诊断效果,将其与如下几种基于传统机器学习分类的轴承诊断方法进行对比:1)文献[12]提出的采用EEMD(ensemble EMD)分解提取本征模态排列熵作故障特征,使用SVM进行分类识别;2)文献[3]提出的组合波形因子、裕度因子等8种时频域特征构造8维特征向量,使用SVM进行分类识别;3)文献[13]提出的使用小波分解提取相对小波能量作为特征向量,使用BP神经网络进行分类识别。以上述方法搭建模型,得到各测试集的准确率如表 5所示,可以看到,在平衡数据集A、B、C上几种方法均可取得较高的准确率,而在不平衡的混合测试集D上本文提出的改进型的卷积神经网络有着明显的优势。如果直接使用卷积神经网络模型对数据集进行训练与检测,不做任何算法模型的改进,其识别准确率相当低。主要是因为传统的卷积网络对振动信号适应力不强,无法准确地进行故障分类。因此,本节只对本文改进的算法与传统的几种成熟技术进行对比。
| 表 5 不同方法对测试数据集A、B、C、D的识别准确率 Table 5 Recognition accuracy by different methods |
本文基于深度学习的理论基础,提出适于滚动轴承故障诊断的卷积神经网络模型,并引入统计学原理的评价指标更加客观准确地对模型进行评估与验证。卷积神经网络模型配合改进的加权loss函数、正则化以及批量归一化和dropout处理,可以有效地进行滚动轴承的故障诊断,实现早期故障和不同程度故障的准确识别,并且在高度不平衡数据集上也可取得较好的识别效果。通过与传统智能诊断经典方法的对比,证明了深度学习模型不仅降低了对信号处理技术的依赖,而且有优越的不平衡样本识别能力,更适应于今后海量监测数据的分析需求。
| [1] |
谷东伟, 张学文, 王志琼, 等. Petri网逆网在主轴故障诊断中的应用[J]. 重庆大学学报, 2016, 39(6): 111-117. GU Dongwei, ZHANG Xuewen, WANG Zhiqiong, et al. Inverse Petri net and its application to spindle fault diagnosis[J]. Journal of Chongqing University, 2016, 39(6): 111-117. (in Chinese) |
| [2] |
李嫄源, 袁梅, 王瑶, 等. SVM与PSO相结合的电机轴承故障诊断[J]. 重庆大学学报, 2018, 41(1): 99-107. LI Yuanyuan, YUAN Mei, WANG Yao, et al. Fault diagnosis of motor bearings based on SVM and PSO[J]. Journal of Chongqing University, 2018, 41(1): 99-107. (in Chinese) |
| [3] |
Shen Z J, Chen X F, Zhang X L, et al. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM[J]. Measurement, 2012, 45(1): 30-40. DOI:10.1016/j.measurement.2011.10.008 |
| [4] |
雷亚国, 何正嘉. 混合智能故障诊断与预示技术的应用进展[J]. 振动与冲击, 2011, 30(9): 129-135. LEI Yaguo, HE Zhengjia. Advances in applications of hybrid intelligent fault diagnosis and prognosis technique[J]. Journal of Vibration and Shock, 2011, 30(9): 129-135. (in Chinese) DOI:10.3969/j.issn.1000-3835.2011.09.028 |
| [5] |
雷亚国, 贾峰, 周昕, 等. 基于深度学习理论的机械装备大数据健康监测方法[J]. 机械工程学报, 2015, 51(21): 49-56. LEI Yaguo, JIA Feng, ZHOU Xin, et al. A deep learning-based method for machinery health monitoring with big data[J]. Journal of Mechanical Engineering, 2015, 51(21): 49-56. (in Chinese) |
| [6] |
Jia F, Lei Y G, Lu N, et al. Deep normalized convolutional neural network for imbalanced fault classification of machinery and its understanding via visualization[J]. Mechanical Systems and Signal Processing, 2018, 110: 349-367. DOI:10.1016/j.ymssp.2018.03.025 |
| [7] |
Shao H D, Jiang H K, Lin Y, et al. A novel method for intelligent fault diagnosis of rolling bearings using ensemble deep auto-encoders[J]. Mechanical Systems and Signal Processing, 2018, 102: 278-297. DOI:10.1016/j.ymssp.2017.09.026 |
| [8] |
Kingma D, Ba J. Adam: a method for stochastic optimization[EB/OL]. (2017-01-30)[2018-09-25] https://arxiv.org/pdf/1412.6980v9.pdf.
|
| [9] |
Szegedy C, Ioffe S, Vanhoucke V, et al. Inception-v4, inception-resnet and the impact of residual connections on learning[C]//Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17). Association for the Advancement of Artificial Intelligence, 2017: 4278-4284.
|
| [10] |
Hinton G E, Srivastava N, Krizhevsky A, et al. Improving neural networks by preventing co-adaptation of feature detectors[EB/OL].(2012-07-03)[2018-09-25]. https://arxiv.org/pdf/1207.0580.pdf.
|
| [11] |
Bengio Y, Lamblin P, Popovici D, et al. Greedy layer-wise training of deep networks[J]. Advances in Neural Information Processing Systems, 2007, 19: 153-160. |
| [12] |
姚德臣, 杨建伟, 程晓卿, 等. 基于多尺度本征模态排列熵和SA-SVM的轴承故障诊断研究[J]. 机械工程学报, 2018, 54(9): 168-176. YAO Dechen, YANG Jianwei, CHENG Xiaoqing, et al. Railway rolling bearing fault diagnosis based on muti-scale IMF permutation entropy and SA-SVM classifier[J]. Journal of Mechanical Engineering, 2018, 54(9): 168-176. (in Chinese) |
| [13] |
赵志宏, 杨绍普. 基于相对小波能量的滚动轴承故障诊断[J]. 电子测量与仪器报, 2011, 25(1): 44-49. ZHAO Zhihong, YANG Shaopu. Fault diagnosis of roller bearing based on relative wavelet energy[J]. Journal of Electronic Measurement and Instrument, 2011, 25(1): 44-49. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

