2. 北京汽车研究总院有限公司, 北京 101300
2. Beijing Automotive Technology Center, Beijing 101300, P. R. China
编织复合材料由于具有比强度高、比模量大、可设计性好、抗冲击、耐疲劳、整体结构性能好、无脱层等优点,已经广泛的应用于航天、医疗、汽车等多个领域。
目前,编织复合材料力学性能研究主要集中于弹性性能分析和强度预测。Potluri等[1]提出了简易透镜几何模型,并预测了非正交结构的玻璃纤维编织复合材料的刚度、强度及剪切性能。Aggarwal等[2]在考虑了纺线波动和纺线间隙的情况下提出了一种预测二维棱形碳纤维编织复合材料面内弹性参数的解析模型,对比了多种编织物的材料弹性性能,并对材料进行了渐进损伤分析。Master等[3]通过有限元方法预测了二维三轴碳纤维编织复合材料的力学性能。Byun等[4]基于单胞模型讨论了编织参数间的相互关系,并对材料的弹性常数进行预测,预测结果与试验结果吻合。Quek等[5]从微观角度出发分析了二维三轴编织材料的代表性单元,并且预测了材料的宏观弹性性能,并讨论了编织角和纤维束弯曲对材料性能的影响。Kier等[6]通过对比Quek模型理论解和实验结果验证了Quek模型在预测二维三轴编织复合材料的宏观力学性能上的准确性和可行性。Shokrieh等[7]通过简易层合板模型,分析并预测了二维三轴编织材料的力学性能。国内的严雪等[8]建立了编织复合材料有限元模型,并且通过体积平均法预测了材料的弹性性能。张芳芳等[9]基于Murakami损伤理论预测了复合材料的细观损伤过程,预测结果与实验结果吻合较好。张超等[10]和张平等[11]也对编织复合材料的力学性能进行了理论研究。
上述研究中,研究对象为单一纤维,以碳纤维居多,而实际工程中一般会综合考虑性能和价格因素,将昂贵的碳纤维与其他造价便宜的纤维混编到一起使用,因此需要展开更加深入的研究。统观力学性能和价格因素,笔者设计了一种碳纤维/玻璃纤维混编二维三轴编织复合材料,建立了该编织复合材料的刚度和强度预测模型,并且针对其三点弯力学性能进行了仿真分析。
1 细观几何模型碳纤维/玻璃纤维混编二维三轴编织复合材料细观结构如图 1所示。其中0°方向为碳纤维,45°和-45°方向为玻璃纤维,纤维之间的空隙由基体材料填充。图 1中黑框部分为代表性单胞胞元。该胞元由四部分构成,如图 2所示,其中三部分为三个方向含有基体的同轴圆柱体纤维束,第四部分是基体。

|
图 1 二维三轴编织复合材料示意图 Figure 1 Schematic diagram of 2DTBC |

|
图 2 代表单元的组分 Figure 2 Components of a representative unit cell |
碳纤维/玻璃纤维混编二维三轴编织复合材料的总体弹性刚度由三部分纤维束刚度和基体刚度按体积分数加权求和得到。
2.1 轴向碳纤维束刚度传统的同心圆柱体模型(CCM)使用了5个弹性系数来描述二维三轴编织复合材料的局部刚度,分别为横向体积弹性模量k23,纵向杨氏模量E11,纵向泊松比ν12,纵向剪切模量G12和横向剪切模量G23。前4个参数可以由式(1)~(4)得到:
| $ {k_{23}} = {k_{\rm{m}}} + \frac{{{V_{\rm{f}}}}}{{1/\left( {{k_{23{\rm{f}}}} - {k_{\rm{m}}}} \right) + {V_{\rm{m}}}/\left( {{k_{\rm{m}}} + {G_{\rm{m}}}} \right)}}, $ | (1) |
| $ {E_{11}} = {E_{11{\rm{f}}}}{V_{\rm{f}}} + {E_{\rm{m}}}{V_{\rm{m}}} + \frac{{4{V_{\rm{f}}}{V_{\rm{m}}}{{\left( {{\nu _{12{\rm{f}}}} - {\nu _{\rm{m}}}} \right)}^2}}}{{{V_{\rm{f}}}/{k_{\rm{m}}} + {V_{\rm{m}}}/{k_{{\rm{23f}}}} + 1/{G_{\rm{m}}}}}, $ | (2) |
| $ {\nu _{12}} = \frac{{{V_{\rm{f}}}{V_{\rm{m}}}\left( {{\nu _{12{\rm{f}}}} - {\nu _{\rm{m}}}} \right)\left( {1/{k_{\rm{m}}} - 1/{k_{{\rm{23f}}}}} \right)}}{{{V_{\rm{f}}}/{k_{\rm{m}}} + {V_{\rm{m}}}/{k_{{\rm{23f}}}} + 1/{G_{\rm{m}}}}} + {v_{{\rm{12f}}}}{V_{\rm{f}}} + {v_{\rm{m}}}{V_{\rm{m}}}, $ | (3) |
| $ {G_{12}} = {G_{\rm{m}}}\frac{{{G_{{\rm{12f}}}}\left( {1 + {V_{\rm{f}}}} \right) + {G_{\rm{m}}}{V_{\rm{m}}}}}{{{G_{\rm{m}}}\left( {1 + {V_{\rm{f}}}} \right) + {G_{{\rm{12f}}}}{V_{\rm{m}}}}}。$ | (4) |
式中:V是体积百分比(Vf+Vm=1);k是横向体积弹性模量;E是杨氏模量;ν是泊松比;G是剪切模量;下标m和f分别代表了基体和纤维。
三相CCM模型在此基础上提出横向剪切模量G23,满足方程(5):
| $ A{\left( {\frac{{{G_{23}}}}{{{G_{\rm{m}}}}}} \right)^2} + B\left( {\frac{{{G_{23}}}}{{{G_{\rm{m}}}}}} \right) + D = 0, $ | (5) |
式中A、B、D三个系数可以由以下方程得到:
| $ D = 3{V_{\rm{f}}}V_{\rm{m}}^2\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right)\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} + {\zeta _{\rm{f}}}} \right) + \left[ {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} +\\ \left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right){V_{\rm{f}}} + 1} \right] \times \left[ {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} + {\zeta _{\rm{f}}} + \left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} - {\zeta _{\rm{f}}}} \right)V_{\rm{f}}^3} \right], $ | (6) |
| $ \begin{array}{*{20}{c}} {B = - 6{V_{\rm{f}}}V_{\rm{m}}^2\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right)\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} + {\zeta _{\rm{f}}}} \right) +\\ \left[ {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} + \left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right){V_{\rm{f}}} + 1} \right] \times \left[ {\left( {{\zeta _{\rm{m}}} - 1} \right)\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} + {\zeta _{\rm{f}}}} \right) - } \right.}\\ {\left. {2V_{\rm{f}}^3\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} - {\zeta _{\rm{f}}}} \right)} \right] + {V_{\rm{f}}}\left( {{\zeta _{\rm{m}}} + 1} \right)\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right) \times \\ \left[ {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} + {\zeta _{\rm{f}}} + V_{\rm{f}}^3\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} - {\zeta _{\rm{f}}}} \right)} \right],} \end{array} $ | (7) |
| $ \begin{array}{l} A = 3{V_{\rm{f}}}V_{\rm{m}}^2\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right)\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} + {\zeta _{\rm{f}}}} \right) + \left[ {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} + {\zeta _{\rm{f}}}{\zeta _{\rm{m}}} - \left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} - {\zeta _{\rm{f}}}} \right)V_{\rm{f}}^3} \right] \times \\ \;\;\;\;\;\;\left[ {{\zeta _{\rm{m}}}{V_{\rm{f}}}\left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}} - 1} \right) - \left( {\frac{{{G_{23{\rm{f}}}}}}{{{G_{\rm{m}}}}}{\zeta _{\rm{m}}} + 1} \right)} \right]。\end{array} $ | (8) |
其中:
| $ {\zeta _{\rm{m}}} = 3 - 4{\nu _{\rm{m}}}, $ | (9) |
| $ {\zeta _{\rm{f}}} = 3 - 4{\nu _{{\rm{23f}}}}。$ | (10) |
模型使用了横向体积弹性模量k23来描述材料的局部刚度。k23与E22之间满足如下关系:
| $ \psi = 1 + \frac{{4{k_{23}}\nu _{12}^2}}{{{E_{11}}}}, $ | (11) |
| $ {\nu _{23}} = \frac{{{k_{23}} - \psi {G_{23}}}}{{{k_{23}} + \psi {G_{23}}}}, $ | (12) |
| $ {E_{22}} = 2{G_{23}}\left( {1 + {\nu _{23}}} \right)。$ | (13) |
在CMM模型的基础上,Quek等[5]提出了一种新的修正模型。该模型直接使用E22来描述材料的局部刚度,并满足如下关系:
| $ \frac{1}{{{E_{22}}}} = \frac{{{\eta _{\rm{f}}}{V_{\rm{f}}}}}{{{E_{{\rm{22f}}}}}} + \frac{{{\eta _{\rm{m}}}{V_{\rm{m}}}}}{{{E_{\rm{m}}}}}。$ | (14) |
其中:
| $ {\eta _{\rm{f}}} = \frac{{{E_{{\rm{11f}}}}{V_{\rm{f}}} + \left( {{E_{\rm{m}}}\left( {1 - {\nu _{{\rm{12f}}}}{\nu _{{\rm{21f}}}}} \right) + {E_{{\rm{11f}}}}{\nu _{\rm{m}}}{\nu _{{\rm{21f}}}}} \right){V_{\rm{m}}}}}{{{E_{{\rm{11f}}}}{V_{\rm{f}}} + {E_{\rm{m}}}{V_{\rm{m}}}}}, $ | (15) |
| $ {\eta _{\rm{m}}} = \frac{{{E_{\rm{m}}}{V_{\rm{m}}} + \left( {{E_{{\rm{11f}}}}\left( {1 - \nu _{\rm{m}}^2} \right) + {E_{\rm{m}}}\left( {1 - {\nu _{\rm{m}}}{\nu _{{\rm{12f}}}}} \right)} \right){V_{\rm{f}}}}}{{{E_{{\rm{11f}}}}{V_{\rm{f}}} + {E_{\rm{m}}}{V_{\rm{m}}}}}。$ | (16) |
除E22外,Quek模型需要的其他4个参数E11、ν12、G12、G23满足方程(1)~(4),与CMM模型完全相同。
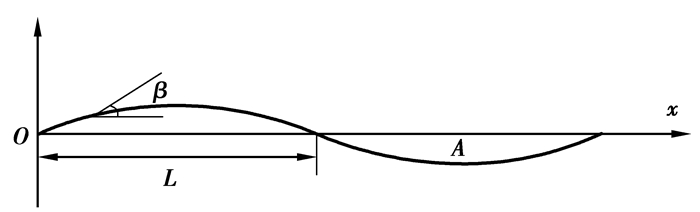
2.2 斜向玻璃纤维束刚度为了计算编织纤维束的弯曲角,这里对其做了简化,认为它(如图 3所示)近似满足如式(17)所示的正弦关系。
| $ z = A\sin \left( {\frac{{{\rm{ \mathsf{ π} }}x}}{L}} \right)。$ | (17) |
|
图 3 编织纤维束走向曲线 Figure 3 Undulating curve of braid tows |
将式(17)进行微分后即可得到弯曲角:
| $ \tan \left( \beta \right) = \frac{{{\rm{ \mathsf{ π} }}A}}{L}\cos \left( {\frac{{{\rm{ \mathsf{ π} }}x}}{L}} \right)。$ | (18) |
将局部刚度沿着波长积分即可得到丝束的等效刚度:
| $ \left[ \mathit{\boldsymbol{C}} \right] = \frac{1}{{2L}}\int_{2L} {{{\left[ {{{\mathit{\boldsymbol{\hat T}}}_1}} \right]}^{ - 1}}\left[ {{C_0}} \right]\left[ {{{\mathit{\boldsymbol{\hat T}}}_2}} \right]{\rm{d}}x} , $ | (19) |
式中C0代表由CCM模型确立的纤维束的刚度,而转换矩阵满足下列方程:
| $ \left[ {{{\mathit{\boldsymbol{\hat T}}}_1}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\hat m}^2}}&0&{{{\hat n}^2}}&0&{2\hat m\hat n}&0\\ 0&1&0&0&0&0\\ {{{\hat n}^2}}&0&{{{\hat m}^2}}&0&{ - 2\hat m\hat n}&0\\ 0&0&0&{\hat m}&0&{ - \hat n}\\ { - \hat m\hat n}&0&{\hat m\hat n}&0&{{{\hat m}^2} - {{\hat n}^2}}&0\\ 0&0&0&{\hat n}&0&{\hat m} \end{array}} \right], $ | (20) |
| $ \left[ {{{\mathit{\boldsymbol{\hat T}}}_2}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\hat m}^2}}&0&{{{\hat n}^2}}&0&{\hat m\hat n}&0\\ 0&1&0&0&0&0\\ {{{\hat n}^2}}&0&{{{\hat m}^2}}&0&{ - \hat m\hat n}&0\\ 0&0&0&{\hat m}&0&{ - \hat n}\\ { - 2\hat m\hat n}&0&{2\hat m\hat n}&0&{{{\hat m}^2} - {{\hat n}^2}}&0\\ 0&0&0&{\hat n}&0&{\hat m} \end{array}} \right], $ | (21) |
式中:
| $ \hat m = \cos \left( \beta \right),\hat n = \sin \left( \beta \right)。$ | (22) |
在获得等效刚度矩阵之后,再根据编织角进行旋转即可得到全局坐标系下的刚度矩阵:
| $ \left[ {{\mathit{\boldsymbol{C}}_\alpha }} \right] = {\left[ {{\mathit{\boldsymbol{T}}_1}} \right]^{ - 1}}\left[ \mathit{\boldsymbol{C}} \right]\left[ {{\mathit{\boldsymbol{T}}_2}} \right]。$ | (23) |
式(23)中C代表了沿特定方向编织的丝束在局部坐标系中的等效刚度,而等式中的转换矩阵可以通过计算下式得到:
| $ \left[ {{\mathit{\boldsymbol{T}}_1}} \right] = \left[ {\begin{array}{*{20}{c}} {{m^2}}&{{n^2}}&0&0&0&{ - mn}\\ {{n^2}}&{{m^2}}&0&0&0&{ - 2mn}\\ 0&0&1&0&0&0\\ 0&0&0&m&{ - n}&0\\ 0&0&0&n&m&0\\ { - mn}&{mn}&0&0&0&{{m^2} - {n^2}} \end{array}} \right], $ | (24) |
| $ \left[ {{\mathit{\boldsymbol{T}}_2}} \right] = \left[ {\begin{array}{*{20}{c}} {{m^2}}&{{n^2}}&0&0&0&{mn}\\ {{n^2}}&{{m^2}}&0&0&0&{ - mn}\\ 0&0&1&0&0&0\\ 0&0&0&m&{ - n}&0\\ 0&0&0&n&m&0\\ { - 2mn}&{2mn}&0&0&0&{{m^2} - {n^2}} \end{array}} \right], $ | (25) |
式中:
| $ m = \cos \left( \alpha \right),n = \sin \left( \alpha \right)。$ | (26) |
碳纤维/玻璃纤维混编二维三轴编织复合材料在全局坐标系中的宏观刚度可以由三部分纤维束和基体按体积分数加权求和得到:
| $ \left[ {{C_{{\rm{global}}}}} \right] = {V_0}\left[ {{C_{\rm{0}}}} \right] + {V_{ + \alpha }}\left[ {{C_{ + \alpha }}} \right] + {V_{ - \alpha }}\left[ {{C_{ - \alpha }}} \right] + {V_{{\mathop{\rm matrix}\nolimits} }}\left[ {{C_{{\mathop{\rm matrix}\nolimits} }}} \right], $ | (27) |
式中:V0, V-α, V+α, Vmatrix分别代表了0度编织角、-α度编织角、α度编织角和基体的体积分数,并且满足V0+V-α+V+α+Vmatrix=1。
注意到V0, V-α, V+α, Vmatrix并没有与Vf, Vm的直接关系,这是因为在实际加工中,编织用的纤维束中会夹杂少量基体材料,致使两者之间不能简单的相互换算。然而V0, V-α, V+α, Vmatrix可以通过CAD工具计算几何关系或是实验得到。
3 强度准则判断碳纤维/玻璃纤维混编二维三轴编织复合材料是否发生了破坏采用的是Tsai-Wu准则[12],其强度准则表示为:
| $ \begin{array}{l} {F_{11}}\sigma _1^2 + {F_{22}}\sigma _2^2 + {F_{33}}\sigma _3^2 + {F_{44}}\sigma _{23}^2 + {F_{55}}\sigma _{13}^2 + {F_{66}}\sigma _{12}^2 + 2{F_{12}}{\sigma _1}{\sigma _2} + 2{F_{13}}{\sigma _1}{\sigma _3} + \\ 2{F_{23}}{\sigma _2}{\sigma _3} + {F_1}{\sigma _1} + {F_2}{\sigma _2} + {F_3}{\sigma _3} \ge 1, \end{array} $ | (28) |
式中共有12个强度张量系数,这些系数均可通过单轴拉伸(压缩)和纯剪切实验得到,对应的关系如下:
| $ \begin{array}{l} {F_{11}} = \frac{1}{{{X_{\rm{T}}}{X_{\rm{C}}}}},{F_{22}} = {F_{33}} = \frac{1}{{{Y_{\rm{T}}}{Y_{\rm{C}}}}},{F_{44}} = \frac{1}{{S_{23}^2}},\\ {F_{55}} = \frac{1}{{S_{13}^2}},{F_{66}} = \frac{1}{{S_{12}^2}},{F_{23}} = - \frac{1}{2}\sqrt {{F_{22}}{F_{33}}} ,\\ {F_{12}} = {F_{13}} = - \frac{1}{2}\sqrt {{F_{11}}{F_{22}}} ,\\ {F_1} = \frac{1}{{{X_{\rm{T}}}}} - \frac{1}{{{X_{\rm{C}}}}},{F_2} = {F_3} = \frac{1}{{{Y_{\rm{T}}}}} - \frac{1}{{{Y_{\rm{C}}}}}, \end{array} $ | (29) |
式中下标数字代表局部坐标轴,T和C分别代表受拉和压的情形;XT、XC分别为材料在纤维轴向方向的拉伸、压缩强度;YT、YC分别为纤维横向方向的拉伸、压缩强度;S为剪切强度。强度系数由纤维和基体强度共同决定,可根据经验公式(30)求得:
| $ \begin{array}{l} {X_{\rm{T}}} = {X_{{\rm{ft}}}}{V_{\rm{f}}} + {X_{{\rm{mt}}}}{V_{\rm{m}}},{X_{\rm{C}}} = {X_{{\rm{fc}}}}\left( {{V_{\rm{f}}} + {E_{\rm{m}}}{V_{\rm{m}}}/{E_{{\rm{fl}}}}} \right),\\ {Y_{\rm{T}}} = \left[ {1 - \left( {\sqrt {{V_{\rm{f}}}} - {V_{\rm{f}}}} \right)\left( {1 - {E_{\rm{m}}}/{E_{{\rm{f2}}}}} \right)} \right]{X_{{\rm{mt}}}},\\ {Y_{\rm{C}}} = \left[ {1 - \left( {\sqrt {{V_{\rm{f}}}} - {V_{\rm{f}}}} \right)\left( {1 - {E_{\rm{m}}}/{E_{{\rm{f2}}}}} \right)} \right]{X_{{\rm{mc}}}},\\ {S_{12}} = {S_{13}} = {S_{\rm{f}}}{V_{\rm{f}}} + {S_{\rm{m}}}{V_{\rm{m}}},\\ {S_{23}} = \left[ {1 - \left( {\sqrt {{V_{\rm{f}}}} - {V_{\rm{f}}}} \right)\left( {1 - {G_{\rm{m}}}/{G_{{\rm{f12}}}}} \right)} \right]{S_{\rm{m}}}。\end{array} $ | (30) |
式中:下标m代表基体,下标f代表纤维,下标t为拉伸,下标c为压缩,1、2、3代表局部坐标轴。这样,根据纤维和基体的材料属性以及体积分数,就可以求得Tsai-Wu准则中的全部系数。
4 编织复合材料结构渐进失效分析复合材料失效后,基于Tsai-Wu准则的刚度折减模式可以分为:瞬间折减模型,常应力折减模型和逐渐折减模型。这里选取瞬间折减模型对顶盖中横梁进行渐近失效分析。在加载过程中,如果满足失效判据,材料工程弹性常数根据表 1进行折减。
| 表 1 工程弹性常数折减方案 Table 1 Weight-coefficient compromise method for engineering elasticity constants |
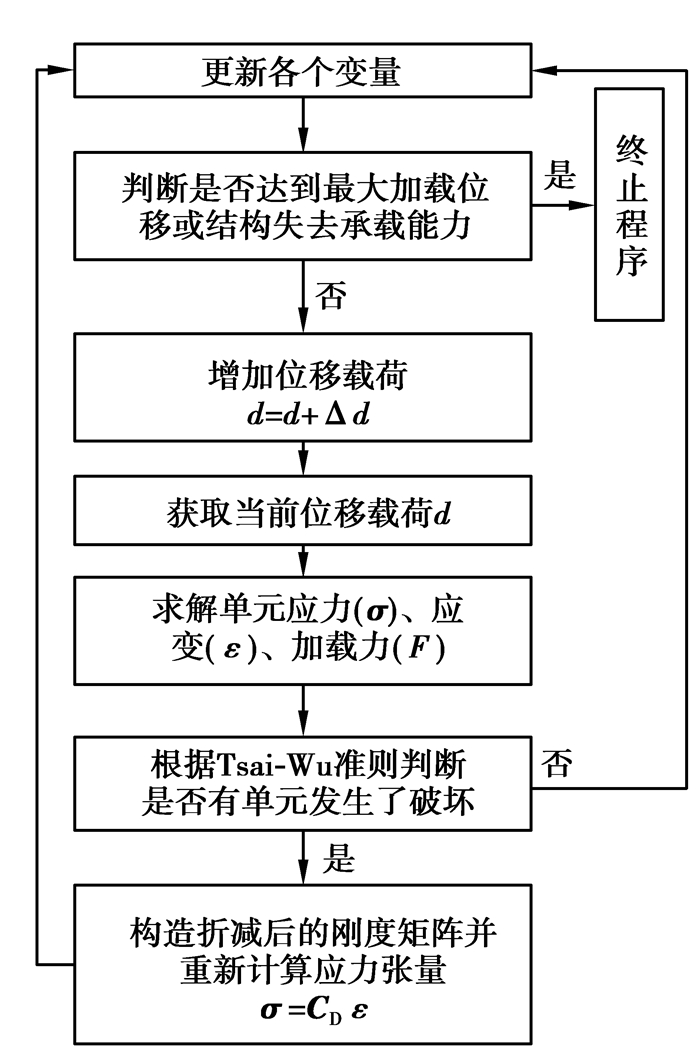
编织复合材料结构渐近失效分析流程如图 4所示,具体步骤如下:
|
图 4 编织复合材料结构渐进失效分析计算流程图 Figure 4 Flow chart of progressive failure analysis in 2DTBC |
1) 施加位移载荷(d)后,求解当前情况下结构各单元的应力(σ)、应变(ε)、加载力(F)。
2) 根据Tsai-Wu准则判断二维三轴编织复合材料结构中是否有单元破坏。
3) 如果没有出现破坏进入步骤(5),否则将失效单元的工程弹性常数按照表 1进行折减。
4) 更新应力张量,σ=CDε,CD为折减后的刚度矩阵,分析加载力。
5) 增加位移载荷,d=d+Δd。
6) 重复步骤1~5,直至达到最大加载位移或结构失去承载能力。得到的最大加载力即为结构强度极限。
5 数值仿真为了验证碳纤维/玻璃纤维二维三轴编织复合材料弹性预测模型和强度理论的正确性,首先根据标准ASTM D3039和ASTM D7078对该二维三轴编织复合材料(具体参数见表 2)进行了轴向拉伸、横向拉伸和面内剪切实验,实验过程如图 5~7所示。轴向拉伸的试件为250 mm×15 mm×2 mm的矩形长片(含夹持部分);横向拉伸的试件为130 mm×15 mm×2 mm的矩形长片(含夹持部分);面内剪切的试件为76 mm×56 mm×2 mm的上下带Ⅴ形切口的矩形方片。根据解析模型和实验数据得到的材料刚度、强度如表 3所示。可以发现:解析模型预测的刚度、强度与实验结果一致。
| 表 2 试件编织参数列表 Table 2 Properties of braided composites |

|
图 5 轴向拉伸实验示意图 Figure 5 Schematic diagram of uniaxial tensile test |

|
图 6 横向拉伸实验示意图 Figure 6 Schematic diagram of transverse tensile test |

|
图 7 面内剪切实验示意图 Figure 7 Schematic diagram of in-plane shear test |
| 表 3 编织材料理论模型和实验结果 Table 3 Comparison of predictions and experiments |
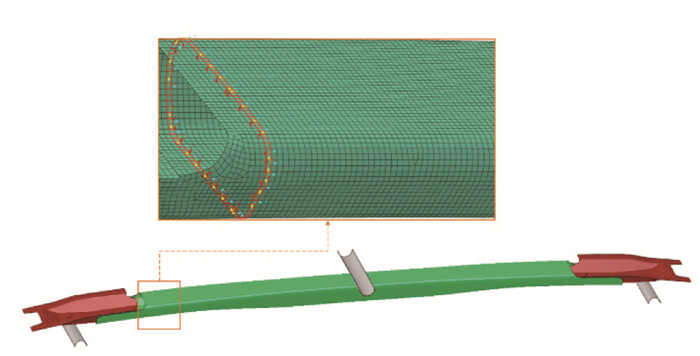
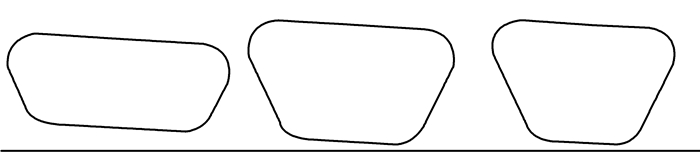
目标编织复合材料顶盖中横梁为组装体,左右两端为金属制连接头,中段为碳纤维/玻璃纤维混编二维三轴编织复合材料。金属接头与编织复合材料结构通过胶体连接。顶盖中横梁无约束放置于两个半圆柱刚体支座上,中部受半圆柱刚体压头作用。支座直径为20 mm,约束6个自由度。压头为直径25 mm,在其上施加10 mm的-z方向的位移载荷。顶盖中横梁三点弯有限元模型如图 8所示。该模型的编织材料部分是横截面连续变化的筒形对称结构,长870 mm,最大宽度62 mm,最大高度38 mm,可大致视为两端细中间粗的方筒,其上表面与侧面的连接区域即整个模型的曲率最大区域(图 9中各横截面的左上端和右上端区域)。
|
图 8 加载及材料方向示意图 Figure 8 Schematic diagram of the applied load and material orientation |
|
图 9 横截面示意图(编织材料部分沿轴向1/6处2/6处3/6处) Figure 9 Schematic diagram of the cross section at 1/6, 2/6, 3/6 of the length of braided structure from one end |
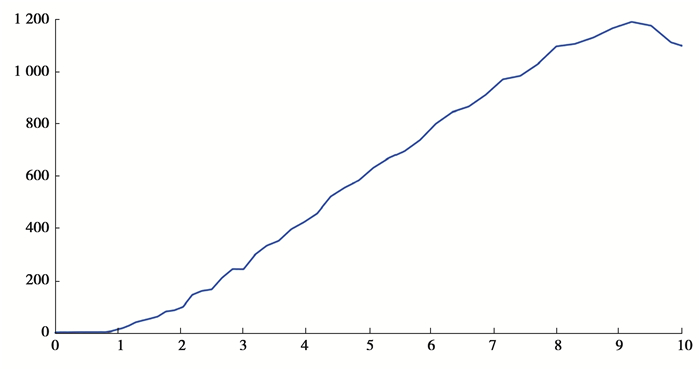
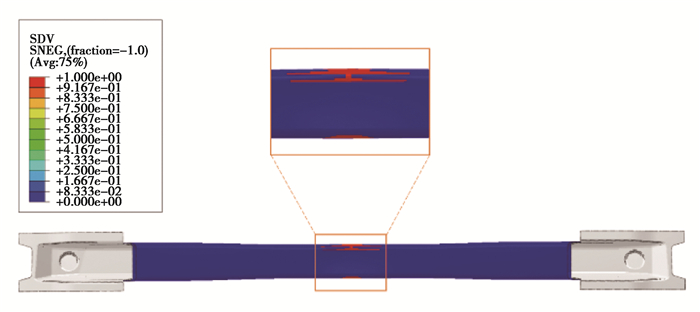
盖中横梁三点弯曲加载过程曲线如图 9所示。可以发现,在第一个极值点之前,曲线都相对平滑,可以视为弹性阶段。取前部分数据做线性回归即可得到复合材料件三点弯曲线性刚度,为169.0 N/mm;最大支反力1 190.5 N(此时加载位移为9.2 mm)即为顶盖中横梁三点弯强度。加载位移9.2 mm时顶盖中横梁的应力云图和损伤分布图如图 10、图 11所示。可以发现:此时已经有部分单元发生了破坏,并且破坏多出现在两侧转角位置;破坏后的单元承载能力下降,从而导致主要承载部位发生变化,即陷入“单元失效—承载转移”的循环;顶盖中横梁与压头接触部位容易出现应力集中。
|
图 10 复合材料件三点弯曲加载过程曲线 Figure 10 Loading curve of braided structure in three-point bending |

|
图 11 加载位移9.2 mm时的应力云图 Figure 11 Stress nephogram at the loading displacement of 9.2 mm |
|
图 12 加载位移9.2 mm时的损伤分布图 Figure 12 Damage nephogram at the loading displacement of 9.2 mm |
1) 根据碳纤维/玻璃纤维混编二维三轴编织复合材料中碳纤维束和玻璃纤维束的空间几何特征, 建立了碳纤维/玻璃纤维混编二维三轴编织复合材料刚度预报模型,并基于Tsai-Wu准则建立了相应的强度预报模型,最后设计材料实验验证了理论分析模型的有效性。
2) 材料参数的理论值与试验结果误差最大的一项是x向的拉伸强度,相对误差为14.7%,仍处于可以接受的范围。
3) 横梁容易发生破坏的位置集中在压头与模型的接触位置和模型曲率较大的,说明在弯曲过程中模型发生了一定的对称挤压变形,符合方筒在三点弯情形下的一般规律,一定程度上反应了仿真的可信性。
| [1] |
Potluri P, Manan A. Mechanics of non-orthogonally interlaced textile composites[J]. Composites Part A:Applied Science and Manufacturing, 2007, 38(4): 1216-1226. DOI:10.1016/j.compositesa.2006.04.008 |
| [2] |
Aggarwal A, Ramakrishna S, Ganesh V K. Predicting the in-plane elastic constants of diamond braided composites[J]. Journal of Composite Materials, 2001, 35(8): 665-688. DOI:10.1177/002199801772662046 |
| [3] |
Johnson W, Masters J, O'Brien T, et al. Mechanical properties of triaxially braided composites:experimental and analytical results[J]. Journal of Composites Technology & Research, 1993, 15: 112-122. |
| [4] |
Byun J H. The analytical characterization of 2-d braided textile composites[J]. Composites Science and Technology, 2000, 60(5): 705-716. DOI:10.1016/S0266-3538(99)00173-6 |
| [5] |
Quek S C, Waas A M, Shahwan K W, et al. Analysis of 2D triaxial flat braided textile composites[J]. International Journal of Mechanical Sciences, 2003, 45(6/7): 1077-1096. |
| [6] |
Kier Z T, Salvi A, Theis G, et al. Estimating mechanical properties of 2D triaxially braided textile composites based on microstructure properties[J]. Composites Part B:Engineering, 2015, 68: 288-299. DOI:10.1016/j.compositesb.2014.08.039 |
| [7] |
Shokrieh M M, Mazloomi M S. An analytical method for calculating stiffness of two-dimensional tri-axial braided composites[J]. Composite Structures, 2010, 92(12): 2901-2905. DOI:10.1016/j.compstruct.2010.04.016 |
| [8] |
严雪, 许希武, 张超. 二维三轴编织复合材料的弹性性能分析[J]. 固体力学学报, 2013, 34(2): 140-151. YAN Xue, XU Xiwu, ZHANG Chao. Analysis of elastic properties of 2D triaxial braided composites[J]. Chinese Journal of Solid Mechanics, 2013, 34(2): 140-151. (in Chinese) |
| [9] |
张芳芳, 刘才. 二维三轴编织复合材料强度及渐进损伤数值预测[J]. 机械工程学报, 2015, 51(8): 84-91. ZHANG Fangfang, LIU Cai. Progressive damage simulation and strength prediction of 2D triaxial braided composites[J]. Journal of Mechanical Engineering, 2015, 51(8): 84-91. (in Chinese) |
| [10] |
张超, 许希武. 二维二轴编织复合材料几何模型及弹性性能预测[J]. 复合材料学报, 2010, 27(5): 129-135. ZHANG Chao, XU Xiwu. Geometrical model and elastic properties prediction of 2D biaxial braided composites[J]. Acta Materiae Compositae Sinica, 2010, 27(5): 129-135. (in Chinese) |
| [11] |
张平, 桂良进, 范子杰. 三向编织复合材料弹性性能研究[J]. 工程力学, 2009, 26(1): 31-36. ZHANG Ping, GUI Liangjin, FAN Zijie. Study on the elastic properties of triaxially braided composites[J]. Engineering Mechanics, 2009, 26(1): 31-36. (in Chinese) |
| [12] |
Tsai S W, Wu E M. A general theory of strength for anisotropic materials[J]. Journal of Composite Materials, 1971, 5(1): 58-80. DOI:10.1177/002199837100500106 |
 2019, Vol. 42
2019, Vol. 42


