1b. 重庆大学 机械工程学院, 重庆 400044;
3. 重庆文理学院 机电工程学院, 重庆 402160
1b. College of Mechanical Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. College of Mechanical and Electrical Engineering, Chongqing University of Arts and Sciences, Chongqing 402160, P. R. China
为了在设计制造中更好地控制机床质量,需要对机床的性能技术指标进行分解,首先将整机的关键质量特性映射到更小的单元,然后进行基于单元的设计与分析。从整机功能(性能)到元动作单元的映射采用的是分步映射的方式,将整机关键质量特性映射到部件的运动层,再将运动层的关键质量特性映射到元动作单元[1]。文中主要研究从整机关键质量特性映射到部件运动层的映射方法。
目前国内外对于数控机床性能分解方面的研究主要集中在产品设计方面,通过质量功能展开(QFD, quality function deploy)和公理化设计(AD, axiomatic design)方法,将产品的性能通过用户域—功能域—物理域—过程域这样一个过程映射到产品设计的整个过程中。刘志林等[2-3]提出了一种基于QFD和DSM的研发项目多级瀑布模型,通过DSM和跨领域映射矩阵DMM将产品的客户需求依次映射到功能域—部件域—流程域;Pang等[4]提出了一种基于粗糙集(RS, rough set)的数控机床质量特性映射研究的方法,将客户需求映射到产品功能层;Diao等[5]提出了一种加权耦合网络(W-CN, weighted-coupled network)的方法,用于解决加工过程中不同质量特性的耦合关系;耿秀丽等[6]采用模糊DEMATEL研究了质量功能展开中产品功能需求之间的相互影响关系。以上研究在建立同代耦合关系方面,不仅只考虑了同代之间的直接影响关系,没有考虑间接影响关系;而且在关键质量特性映射方面大都采用直接映射方式,没有考虑同代耦合关系对下一层单元的影响。
为此,文中在关键质量特性映射过程中:1)采用DEMATEL建立了主运动性能的耦合矩阵;2)引入一种间接映射的方式来代替主运动性能之间的同代耦合关系对二级运动层的影响,并利用FAHP对其进行量化,得到总体的主运动—二级运动性能映射变换矩阵;3)进行矩阵运算映射,完成了关键质量特性在功能—运动层的传递。
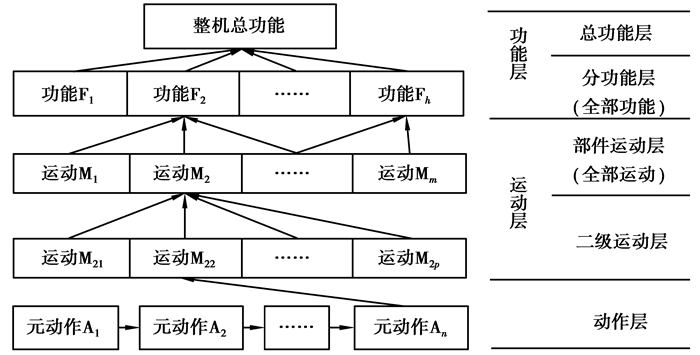
1 主运动性能之间的耦合解耦分析 1.1 机电产品的FMA分解模型根据元动作理论,FMA结构化分解就是通过对机床的功能谱系进行研究,通过功能(function)—运动(movement)—动作(action)这样一个分解过程,将整机功能分解到运动的最小粒度——元动作[7]。其中元动作是指结构关系相对独立、能够实现一定动作目标或达到一定目的、可控可分析不需要(也不能)再细分的动作单元。
FMA结构化分解的核心思想是将数控机床的功能分成一系列最基本的与功能相对应的动作单元,通过对动作的性能特性的控制来保证整个数控机床各项功能和技术特性的实现。FMA结构化分解过程如图 1所示。
|
图 1 FMA结构化分解 Figure 1 FMA structured decomposition |
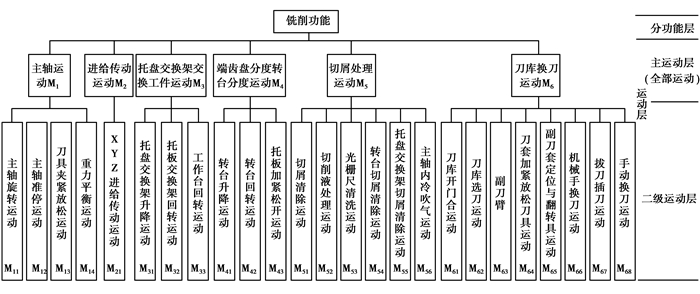
某加工中心为四轴三联动机床,具有直线、圆弧和螺旋插补等功能,属于精密卧式加工中心。以该机床的铣削功能F1为例,对其进行FMA结构化分解。由于只把整机关键质量特性映射到运动层,所以此处分解到运动层,其具体的分解过程如图 2所示。
|
图 2 某加工中心FMA分解模型(部分) Figure 2 FMA decomposition model of a machining center (part) |
数控机床各个主运动性能之间不仅有直接影响关系,而且还有间接影响关系,比如由于转台切屑清除不当,会影响转台的分度运动,所以切屑处理运动M5性能对端齿盘分度转台运动M4性能会产生直接影响;M5性能影响M4性能,而M4性能又影响托盘交换架交换工件运动M3性能,则M5对M3有间接影响关系[8]。所以,采用DEMATEL对这两种影响关系进行耦合解耦分析。
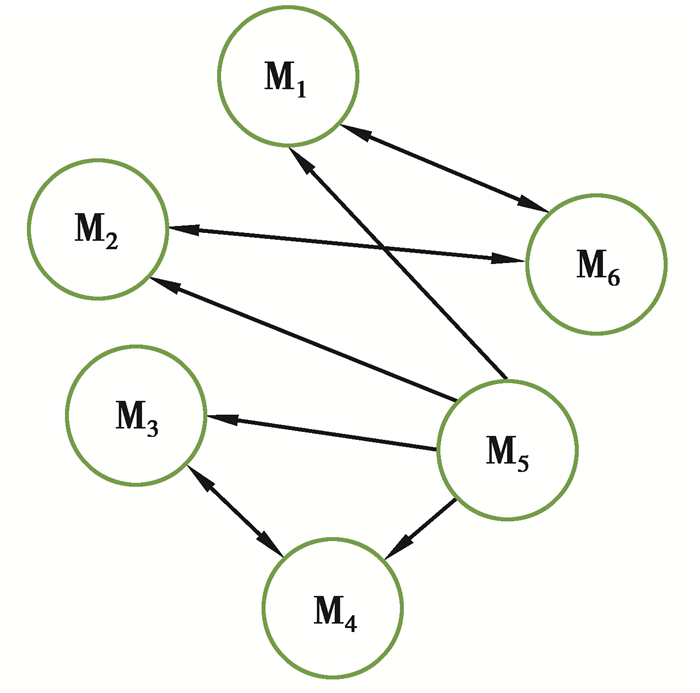
根据图 2的FMA分解模型(部分),结合具体的关联影响统计分析,建立主运动性能影响有向图如图 3所示。
|
图 3 主运动性能影响有向图 Figure 3 Performance influence directed graph of main motions |
根据图 3,可将有向图转化为影响关系矩阵
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&1\\ 1&0&0&0&0&1\\ 0&0&0&1&0&0\\ 0&0&1&0&0&0\\ 1&1&2&2&0&2\\ 1&1&0&0&0&0 \end{array}} \right], $ |
式中,yij为主运动Mi影响主运动Mj的影响次数;i=j时,yii=0。Y的标准化矩阵为
据此可以得到影响因素间直接和间接影响关系组成的综合影响矩阵
| $ \mathit{\boldsymbol{T}} = \mathop {\lim }\limits_{k \to \infty } \left( {\mathit{\boldsymbol{X}} + {2^2} + \cdots + {\mathit{\boldsymbol{X}}^k}} \right) = \mathit{\boldsymbol{X}}{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{X}}} \right)^{ - 1}}, $ |
式中,I是单位矩阵。
Tij为主运动Mi对主运动Mj的综合影响程度,包括直接与间接影响程度。Tij≠0,表示主运动性能间存在相关关系,反之,则无关。故
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 0&{0.14}&0&0&0&{0.33}\\ {0.14}&0&0&0&0&{0.2}\\ 0&0&0&{0.33}&0&0\\ 0&0&{0.33}&0&0&0\\ {0.2}&{0.2}&{0.33}&{0.2}&0&{0.13}\\ {0.33}&{0.2}&0&0&0&0 \end{array}} \right], $ |
得到主运动综合影响程度矩阵T后,确定矩阵中元素取值为
| $ {Z_{ij}} = \left\{ \begin{array}{l} 1,{t_{ij}} > {\lambda _1},\\ 0.5,{\lambda _2} < {t_{ij}} < {\lambda _1},\\ 0,{t_{ij}} < {\lambda _2}, \end{array} \right. $ |
式中:i=1, 2, …, 6; j=1, 2, …, 6;λ1,λ2为给定的阙值,用于系统的简化,根据相关统计经验可得λ1取0.3,λ2取0.15,Z为初始主运动性能耦合矩阵。采用遗传算法[9]对Z进行割裂重组,使主运动性能之间的迭代反馈量最小,从而得到最优的主运动性能耦合矩阵ZMM如表 1所示。
| 表 1 主运动性能耦合矩阵ZMM Table 1 Main motions performance coupling matrix ZMM |
主运动—二级运动映射变换矩阵的作用就是将主运动层的关键质量特性映射到二级运动层,所以应该考虑同代主运动层(M-M,main motion-main motion)性能之间、异代主运动—二级运动(M-S,main motion-secondary motion)层性能之间的耦合依赖关系。
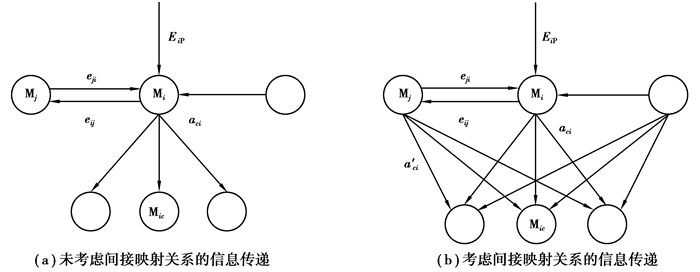
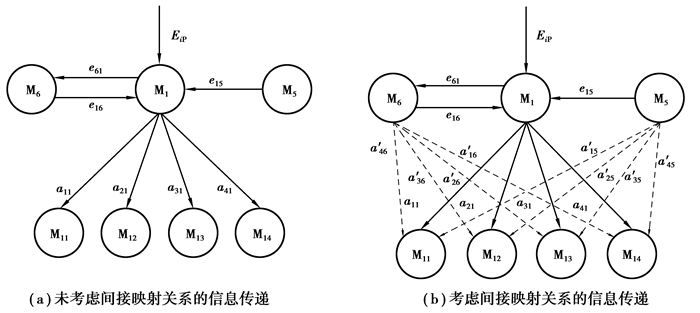
将单独的主运动Mi(i=1, 2, …, N)隔离开来,建立如图 4(a)所示的单一M-S信息传递模型,并采用一种间接映射关系建立和其耦合的其他主运动Mj(j=1, 2, …, N,且j≠i)与二级运动层元素Mic(c=1, 2, …, L)的关系,具体的结果如图 4(b)所示。
|
图 4 单一M-S信息传递模型 Figure 4 Information transfer model of single M-S |
定义1 图 4中EiP为上一层传递过来的输入信息,eij、ej′i为同代节点之间的信息有向边,tij为eij的信息强度(有向边上的权值);aci、a′cj为异代两节点之间的信息有向边,λci为aci的信息强度(有向边上的权值)。对于∀Mi∈M,同代输入信息集合
| $ Z_{\rm{F}}^i = \left\{ {{e_{ij}}\left| {{t_{ij}} > 0} \right.,j = 1,2, \cdots ,N} \right\}, $ |
其维数记为dim(ZFi);异代输入信息集合
| $ Z_{\rm{P}}^i = \left\{ {{E_{i{\rm{P}}}}} \right\}, $ |
其维数记为dim(ZPi);同代输出信息集合
| $ X_{\rm{F}}^i = \left\{ {{e_{j'i}}\left| {{t_{j'i}}} \right. > 0,j' = 1,2, \cdots ,N} \right\}, $ |
其维数记为dim(XFi),异代输出信息集合
| $ X_{\rm{P}}^i = \left\{ {{a_{ci}}\left| {{\lambda _{ci}}} \right. > 0,c = 1,2, \cdots ,L} \right\}, $ |
其维数记为dim(XPi)。则
| $ \begin{array}{*{20}{c}} {\left( {{e_{ij}},{e_{j'i}}} \right)\left( {其中\;{e_{ij}} \in Z_{\rm{F}}^i,{e_{j'i}} \in X_{\rm{F}}^i} \right),}\\ {\left( {{e_{ij}},{a_{ci}}} \right)\left( {其中\;{e_{ij}} \in Z_{\rm{F}}^i,{a_{ci}} \in X_{\rm{P}}^i} \right),}\\ {\left( {{E_{i{\rm{P}}}},{e_{j'i}}} \right)\left( {其中\;{E_{i{\rm{P}}}} \in Z_{\rm{P}}^i,{e_{j'i}} \in X_{\rm{F}}^i} \right),}\\ {\left( {{E_{i{\rm{P}}}},{a_{ci}}} \right)\left( {其中\;{E_{i{\rm{P}}}} \in Z_{\rm{P}}^i,{a_{ci}} \in X_{\rm{P}}^i} \right)} \end{array} $ |
称作信息耦合对,分别记作bjji, bjcia, bPji, bPcia。
对于∀Mi∈M,其信息耦合对集合分别记为
| $ \begin{array}{*{20}{c}} {B_{{\rm{FF}}}^i = \left\{ {\left( {{e_{ij}},{e_{j'i}}} \right)\left| {{e_{ij}} \in Z_{\rm{F}}^i} \right.,{e_{j'i}} \in X_{\rm{F}}^i} \right\};}\\ {B_{{\rm{FP}}}^i = \left\{ {\left( {{e_{ij}},{a_{ci}}} \right)\left| {{e_{ij}} \in Z_{\rm{F}}^i} \right.,{a_{ci}} \in X_{\rm{P}}^i} \right\};}\\ {B_{{\rm{PF}}}^i = \left\{ {\left( {{E_{i{\rm{P}}}},{e_{j'i}}} \right)\left| {{E_{i{\rm{P}}}} \in Z_{\rm{P}}^i} \right.,{e_{j'i}} \in X_{\rm{F}}^i} \right\};}\\ {B_{{\rm{PP}}}^i = \left\{ {\left( {{E_{i{\rm{P}}}},{a_{ci}}} \right)\left| {{E_{i{\rm{P}}}} \in Z_{\rm{P}}^i} \right.,{a_{ci}} \in X_{\rm{P}}^i} \right\}.} \end{array} $ |
故对于主运动Mi,其总的信息耦合对集合为
| $ {B^i} = B_{{\rm{FF}}}^i \cup B_{{\rm{FP}}}^i \cup B_{{\rm{PF}}}^i \cup B_{{\rm{PF}}}^i, $ |
且
| $ \begin{array}{*{20}{c}} {\dim \left( {B_{{\rm{FF}}}^i} \right) = \dim \left( {Z_{\rm{F}}^i} \right) \times \dim \left( {X_{\rm{F}}^i} \right);}\\ {\dim \left( {B_{{\rm{FP}}}^i} \right) = \dim \left( {Z_{\rm{F}}^i} \right) \times \dim \left( {X_{\rm{P}}^i} \right);}\\ {\dim \left( {B_{{\rm{PF}}}^i} \right) = \dim \left( {Z_{\rm{P}}^i} \right) \times \dim \left( {X_{\rm{F}}^i} \right);}\\ {\dim \left( {B_{{\rm{PP}}}^i} \right) = \dim \left( {Z_{\rm{P}}^i} \right) \times \dim \left( {X_{\rm{P}}^i} \right),} \end{array} $ |
主运动Mi的总的信息耦合对集合Bi的维数
| $ \dim \left( {{B^i}} \right) = \dim \left( {B_{{\rm{FF}}}^i} \right) + \dim \left( {B_{{\rm{FP}}}^i} \right) + \dim \left( {B_{{\rm{PF}}}^i} \right) + \dim \left( {B_{{\rm{PP}}}^i} \right)。$ |
耦合度 对于∀bjji, bjcia, bPji, bPcia∈Bi,当eij、EiP发生变化时,引起ej′i、aci发生变化的程度,称为信息耦合度,简称为耦合度,记为djji, djcia, dPji, dPcia。高的耦合度是指eij、EiP变化小时,ej′i、aci变化很大。反之则称低耦合度。
耦合可变度 对于作为研究对象的节点而言,当上游所有输入信息(包括同代输入eij和异代输入EiP)发生变化时,下游输出信息(仅指异代输出aci)可能发生变化的程度,称为耦合可变度,记为ψ(aci)。
根据定义,研究对象主运动节点Mi在建立M-S映射变换矩阵时,由于下属二级运动Mic与该主运动是直接映射关系,需要考虑所有的输入信息变化对该信息依赖关系aci的影响,所以在矩阵中采用耦合可变度ψ(aci)来衡量主运动Mi与下属二级运动Mic之间的定量关系。
非研究对象主运动节点Mj,由于它是通过影响主运动Mi来间接影响其下属的二级运动Mic的,将这种间接映射关系用虚线表示,用来体现非研究对象主运动节点Mj与二级运动Mic之间的关系,记为a′cj, (j=1, 2,…,N,且j≠i), 此时可以采用耦合度djcia来度量这种映射关系。
2.2 耦合可变度的计算在图 4(a)中,对于信息有向边aci,它与研究对象主运动节点Mi的所有输入信息有向边eij、EiP都存在信息耦合关系,它们之间的信息耦合度分别为djcia、dPcia。得到信息有向边aci的耦合可变度为
| $ \psi \left( {{a_{ci}}} \right) = \sum {d_{jc}^{ia}} + \sum {d_{{\rm{P}}c}^{ia}} 。$ | (1) |
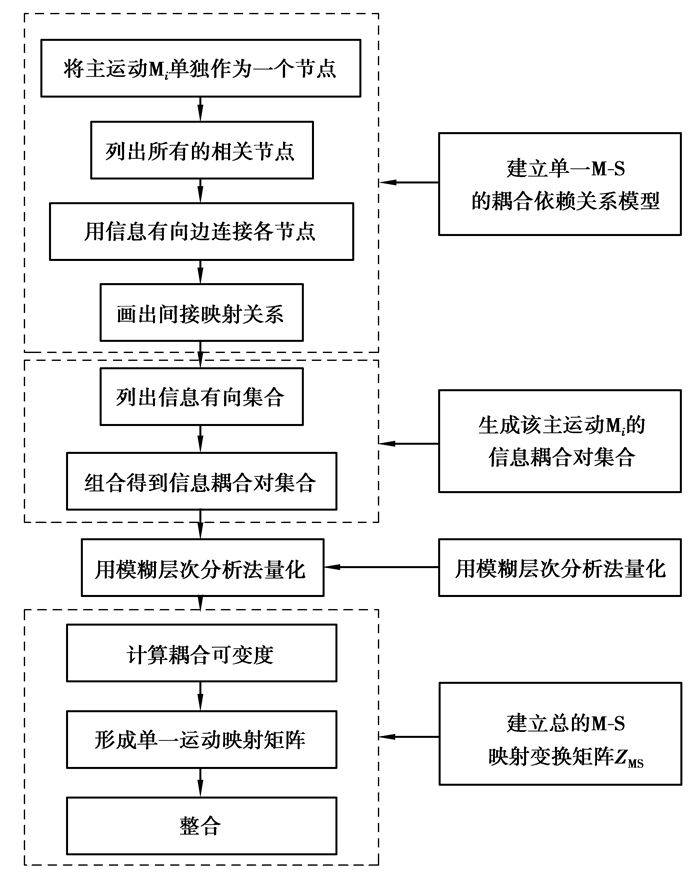
M-S映射变换矩阵ZMS的建立就是构建各主运动层元素与二级运动层元素之间的一种映射关系,然后对其进行量化的一个过程。建立的具体过程如图 5所示。
|
图 5 映射变换矩阵ZMS建立过程 Figure 5 Establishment process of mapping transformation matrix ZMS |
建立信息耦合对就是通过遍历研究对象主运动节点的输入、输出集,将输入、输出集进行组对,形成信息耦合对。
3.2 信息耦合对的量化信息耦合对的量化采用的是FAHP[10-12]。FAHP的主要思想是将一个复杂的多规则量化问题分解为具有递阶结构的量化指标和量化对象,对同一层次上的元素,通过成对的重要程度比较,组成模糊量化矩阵。其具体计算步骤如下:
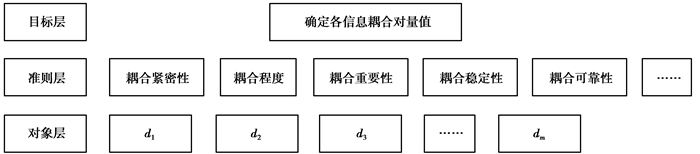
1) 建立信息耦合对层次结构量化模型。主运动Mi的耦合信息对共有M对,集合为Bi={d1,d2,d3,…,dm}。对于信息耦合对的评价,建立的准则层包括H个指标,如耦合紧密性、耦合程度、耦合重要性、耦合稳定性和耦合可靠性等,所以指标集U={u1,u2,u3,…,uh}。量化过程中总共有W个专家,所有专家集V={v1,v2,v3,…,vw}。分析建立如图 6所示的信息耦合对层次结构量化模型。
|
图 6 信息耦合对层次结构量化模型 Figure 6 Hierarchy quantization model of information coupled pairs |
2) 建立模糊层次分析法量化矩阵语言标度。对于建立的这些指标,都是越高越好,所以根据1-9标度法将量化矩阵的语言标度分为9个等级,具体的模糊值分配如表 2所示。
| 表 2 模糊层次分析法量化矩阵语言标度 Table 2 Quantitative matrix language scale of fuzzy analytic hierarchy process |
3) 建立专家量化矩阵。各位专家通过自身的经验,对信息耦合对进行量化,则专家vy认为信息耦合对dx对应满足h个指标要求的程度值表示如下:Tx1y,Tx2y,Tx3y,…,Txhy,其中Txjy为三角模糊数(x=1, 2,…,M;y=1, 2,…,W;j=1, 2,…,H),因此,建立的专家量化矩阵为式(2)所示。
| $ \left[ {\begin{array}{*{20}{c}} {T_{11}^1}&{T_{12}^1}& \cdots &{T_{1h}^1}\\ {T_{21}^1}&{T_{22}^1}& \cdots &{T_{2h}^1}\\ \vdots&\vdots &{}& \vdots \\ {T_{m1}^1}&{T_{m2}^1}& \cdots &{T_{mh}^1} \end{array}} \right] \cdots \left[ {\begin{array}{*{20}{c}} {T_{11}^2}&{T_{12}^2}& \cdots &{T_{1h}^2}\\ {T_{21}^2}&{T_{22}^2}& \cdots &{T_{2h}^2}\\ \vdots&\vdots &{}& \vdots \\ {T_{m1}^2}&{T_{m2}^2}& \cdots &{T_{mh}^2} \end{array}} \right] \cdots \left[ {\begin{array}{*{20}{c}} {T_{11}^w}&{T_{12}^w}& \cdots &{T_{1h}^w}\\ {T_{21}^w}&{T_{22}^w}& \cdots &{T_{2h}^w}\\ \vdots&\vdots &{}& \vdots \\ {T_{m1}^w}&{T_{m2}^w}& \cdots &{T_{mh}^w} \end{array}} \right]。$ | (2) |
由于专家评价带有一定的主观性,所以在这里采用三角模糊数加权平均值公式对量化矩阵进行统一处理,建立信息耦合对模糊量化矩阵,采用直觉模糊熵[13]可以得到专家权重G=(G1,G2, …, Gw)。其三角模糊数加权平均公式为式(3)。
| $ \left\{ \begin{array}{l} L{T_{xh}} = \mathop {\min }\limits_y \left\{ {L{T_{xhy}}} \right\};\\ M{T_{xh}} = \frac{1}{Y}\sum\limits_{y = 1}^Y {M{T_{xhy}}} ;\\ U{T_{xh}} = \mathop {\min }\limits_y \left\{ {U{T_{xhy}}} \right\};\\ {{\tilde T}_{xh}} = \left( {L{T_{xh}},M{T_{xh}},U{T_{xh}}} \right); \end{array} \right. $ | (3) |
式中:Txh为加权平均值。
最后,得到专家量化矩阵为
| $ \left[ {\begin{array}{*{20}{c}} {{{\tilde T}_{11}}}&{{{\tilde T}_{12}}}& \cdots &{{{\tilde T}_{1h}}}\\ {{{\tilde T}_{21}}}&{{{\tilde T}_{22}}}& \cdots &{{{\tilde T}_{2h}}}\\ \vdots&\vdots &{}& \vdots \\ {{{\tilde T}_{m1}}}&{{{\tilde T}_{m2}}}& \cdots &{{{\tilde T}_{mh}}} \end{array}} \right]。$ | (4) |
4) 进行层次单排序,得到信息耦合对量值。根据专家量化矩阵,信息耦合对dx对应满足H个指标的综合重要性程度值为
| $ {S_x} = \sum\limits_{h = 1}^H {{{\tilde T}_{xh}} \otimes {{\left( {\sum\limits_{x = 1}^M {\sum\limits_{h = 1}^H {{{\tilde T}_{xh}}} } } \right)}^{ - 1}}} , $ | (5) |
| $ \sum\limits_{h = 1}^H {{{\tilde T}_{xh}}} = \left( {\sum\limits_{h = 1}^H {L{T_{xh}}} ,\sum\limits_{h = 1}^H {M{T_{xh}}} ,\sum\limits_{h = 1}^H {U{T_{xh}}} } \right), $ | (6) |
| $ {\left( {\sum\limits_{x = 1}^M {\sum\limits_{h = 1}^H {{{\tilde T}_{xh}}} } } \right)^{ - 1}} = \left( {\frac{1}{{\sum\limits_{x = 1}^M {\sum\limits_{h = 1}^H {U{T_{xh}}} } }},\frac{1}{{\sum\limits_{x = 1}^M {\sum\limits_{h = 1}^H {M{T_{xh}}} } }},\frac{1}{{\sum\limits_{x = 1}^M {\sum\limits_{h = 1}^H {L{T_{xh}}} } }}} \right)。$ | (7) |
定义2:2个三角模糊数M1和M2,M2≥M1的可能性为
| $ V\left( {{M_2} \ge {M_1}} \right) = \mathop {\sup }\limits_{y \ge x} \left( {\min \left( {{\mu _{{M_1}}}\left( x \right),{\mu _{{M_2}}}\left( y \right)} \right)} \right), $ |
若存在(x, y),且x>y,μM1(x)=μM2(y)=1,则有V(M2≥M1)=1,其中M1和M2为凸函数,为
| $ V\left( {{M_2} \ge {M_1}} \right) = \left\{ \begin{array}{l} 1,{m_2} \ge {m_1},\\ 0,{l_1} \ge {u_2},\\ \frac{{{l_1} - {u_2}}}{{\left( {{m_2} - {u_2}} \right) - \left( {{m_1} - {l_1}} \right)}},其他。\end{array} \right. $ | (8) |
定义3:一个凸模糊数比其余k个凸模糊数Mi(i=1, 2, …, k)大的可能性程度为
| $ \begin{array}{l} V\left( {M \ge {M_1},{M_2}, \cdots ,{M_k}} \right) = V\left( {\left( {M \ge {M_1}} \right) \cup \left( {M \ge {M_2}} \right) \cup } \right.\\ \left. {\left( {M \ge {M_2}} \right) \cdots \left( {M \ge {M_k}} \right)} \right) = \min V\left( {M \ge {M_i}} \right)。\end{array} $ | (9) |
假设d′(Ax)=minV(Sx≥Sk), k=1, 2, …M; k≠i,Sx为综合重要程度值,Ax表示第x个信息耦合对,则各信息耦合对的量值为W′=(d′(A1),d′(A2),…,d′(Am))T,归一化后,最后的信息耦合对的量值为W=(d′(A1),d′(A2),…,d′(Am))T。
3.3 M-S映射变换矩阵ZM-S的建立M-S映射变换矩阵ZM-S就是M-S之间关系的量化矩阵,分别用耦合可变度ψ和信息耦合度ξ来度量研究对象主运动节点、非研究对象主运动节点与二级运动层元素的定量关系。具体的算法流程如图 7所示。

|
图 7 M-S变换矩阵建立算法流程 Figure 7 Algorithm flow of M-S transformation matrix establishment |
可靠性(R,reliability)、稳定性(S,stability)、精度(P,precision)、精度寿命(A,accuracy life)以及可用性(U,usability)是影响数控机床质量的五大关键质量特性,可靠性可以采用平均故障间隔时间t来度量;对于稳定性,可以采用机器能力指数c[14-15](机器能力指数是指在工序稳定情况下制造设备所具有的保证产品质量的能力)来度量,取值必须大于等于1.33;精度和精度寿命则分别采用精度值p和精度寿命值a来度量;可用性以可用度u[16]来度量,可用度为
| $ u = \frac{u}{{u + {t_{{\rm{MTTR}}}}}}, $ |
式中,tMTTR为平均故障修复时间,故可用度的取值范围为0~1,数值越大,表明机器的可用度越好。
通过对产品客户需求的提取,可以得到功能层关键质量特性值,由于加工中心各功能如铣削、镗孔、钻孔等功能之间不存在耦合依赖关系,所以功能层关键质量特性可以按照直接映射的方式映射到主运动层,得到主运动层关键质量特性矩阵QCMM。
而从主运动层到二级运动层为
| $ {\mathit{\boldsymbol{Q}}_{C{\rm{SM}}}} = {\mathit{\boldsymbol{Q}}_{C{\rm{MM}}}} \cdot \left( {{\mathit{\boldsymbol{Z}}_{{\rm{MM}}}} \cdot \mathit{\boldsymbol{Z}}_{{\rm{M - S}}}^{\rm{T}}} \right), $ | (10) |
式中:QCSM为二级运动层关键质量特性矩阵;QCMM为主运动层关键质量特性矩阵。
按照上述方式就可以将整机关键质量特性映射到二级运动层,得到二级运动层关键质量特性矩阵QCSM。
5 应用实例针对某加工中心的性能分解问题,前面已经得到了主运动性能耦合矩阵ZMM。经过对产品客户需求的提取和量化,得到某加工中心整机t为1 500 h,机器能力指数c为2.2,加工精度p为0.02 mm,精度寿命a为1 800 h,可用度u为0.6,由于加工中心各功能之间不存在耦合关系,可以采用直接映射的方式将功能层的关键质量特性映射到主运动层,得到主运动层关键质量特性矩阵QCMM如表 3所示。
| 表 3 主运动层关键质量特性矩阵QCMM Table 3 Main motion layer key quality characteristic matrix QCMM |
以主轴运动M1为例,建立M-S信息传递模型如图 8所示。通过分析可得主运动M1总的信息耦合对集合为B1={b561,b661,bP61,b511a,b521a,b531a,b541a,b611a,b621a,b631a,b641a,bP11a,bP21a,bP31a,bP41a},信息耦合度量值为D={d561,d661,dP61,d511a,d521a,d531a,d541a,d611a,d621a,d631a,d641a,dP11a,dP21a,dP31a,dP41a}且dim(B1)=dim(BFF1)+dim(BPF1)+dim(BFP1)+dim(BPP1)=15。令B1={b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14,b15}。
|
图 8 M1 M-S信息传递模型 Figure 8 M1 M-S information transfer model |
采用FAHP计算得到各信息耦合对的量值为W={0.044,0.055,0.060,0.070,0.070,0.068,0.067,0.072,0.071,0.070,0.066,0.073,0.072,0.072,0.072}。
根据式(1)计算信息有向边a11,a21,a31,a41的耦合可变度ψ以及非研究对象主运动节点与二级运动层的信息耦合度ξ,然后对主运动M1的映射变换矩阵赋值,得到如表 4所示的矩阵。
| 表 4 主运动M1映射变换矩阵 Table 4 Main motion M1 mapping transformation matrix |
同理可得到该数控机床其他主运动的映射变换矩阵,最后整合得到整个机床的M-S映射变换矩阵ZMS如表 5所示。再按照式(10),可得到二级运动层关键质量特性矩阵QCSM为表 6所示。
| 表 5 数控机床M-S映射变换矩阵ZM-S Table 5 M-S mapping transformation matrix ZM-Sof NC machine tools |
| 表 6 二级运动层关键质量特性矩阵QCSM Table 6 Secondary motion layer key quality characteristic matrix QCSM |
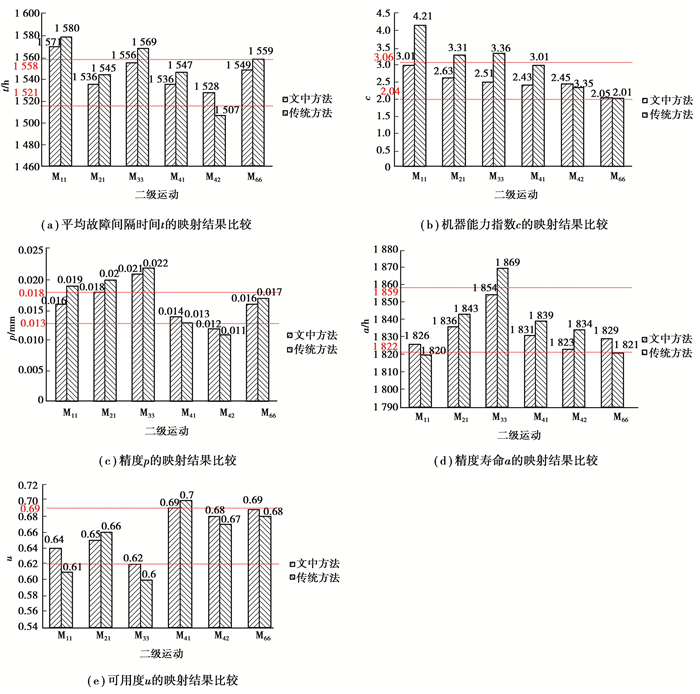
以主轴旋转运动M11、X轴进给传动运动M21、工作台回转运动M33、转台升降运动M41、转台回转运动M42以及机械手换刀运动M66为例,将文中映射得到的结果和传统映射方式(多级QFD瀑布模型[17])映射得到的结果进行对比,结果如图 9所示,其中虚线包含的部分为考虑了开发时间、开发成本和开发质量得到的该数控机床的五大关键质量特性目标区间。
|
图 9 文中映射方法与传统方法对比 Figure 9 Comparison of the mapping method of this paper to the traditional method |
映射得到的加工中心运动层的五大关键质量特性值不能过大,过大将会使得开发成本高、开发时间长,也不能过小,过小会使整机的关键质量特性值达不到要求,所以,根据大量的统计经验分析到了该加工中心运动层五大关键质量特性目标区间为:t(1 521~1 558 h)、c(2.04~3.06)、p(0.013~0.018 mm)、a(1 822~1 859 h)和u(0.62~0.69)。通过以上2种映射方式的对比,可以看出,文中映射得到的结果落在目标区间里的更多,而且相比传统方法,映射的结果更加集中,说明该映射方法的稳定性好,对于数控机床的性能分解,文中提出的映射方法相比于传统的映射方法更加科学合理,更加有效。
6 结论提出了一种数控机床性能分解的新方法,结合FMA分解模型,将整机关键质量特性映射到了二级运动层,相比传统的映射方式,该方法具有如下优势:
1) 采用DEMATEL建立了各主运动性能耦合矩阵,不仅考虑主运动性能之间的直接影响关系,还考虑了间接影响关系,经过对比证明用该方法分析主运动性能之间的耦合关系更加合理;
2) 引入了一种间接映射的方法来代替映射过程中主运动层性能之间的同代耦合关系对二级运动层的影响,并采用模糊层次分析法对映射过程进行了量化;
3) 通过矩阵运算,建立了数控机床关键质量特性从整机到二级运动层的映射机制,为映射到元动作单元,建立映射链和映射链方程提供了依据。
| [1] |
冉琰. 机电产品元动作单元建模及关键质量特性预测控制技术研究[D]. 重庆: 重庆大学, 2016: 23-25. RAN Yan. Research on modeling of meta-actuation unit and predictive control technology for key quality characteristics of mechanical and electrical products[D]. Chongqing: Chongqing University, 2016: 23-25. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1017801788.htm |
| [2] |
刘志林. 复杂研发项目流程和组织的建模与优化研究[D]. 北京: 北京科技大学, 2016: 32-45. LIU Zhilin. Research on modeling and optimization of complex R&D project flow and organization[D]. Beijing: University of Science and Technology Beijing, 2016: 32-45. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10008-1016100135.htm |
| [3] |
杨青, 刘志林, 唐尔玲. 基于DSM和QFD分析功能变更对研发项目的影响[J]. 管理评论, 2015, 27(4): 57-65. YANG Qing, LIU Zhilin, TANG Erling. Analyzing the impact of function modification on r & d projects based on DSM and QFD[J]. Management Review, 2015, 27(4): 57-65. (in Chinese) |
| [4] |
Pang J H. Study on reverse mapping of accuracy design quality characteristics for numerical control machine based on rough set[J]. Journal of Mechanical Engineering, 2012, 48(5): 101. DOI:10.3901/JME.2012.05.101 |
| [5] |
Diao G, Zhao L, Yao Y. A weighted-coupled network-based quality control method for improving key features in product manufacturing process[J]. Journal of Intelligent Manufacturing, 2016, 27(3): 535-548. DOI:10.1007/s10845-014-0887-6 |
| [6] |
耿秀丽, 徐士东, 叶春明. 考虑定量KANO分析的产品功能需求优化设计[J]. 计算机集成制造系统, 2016, 22(7): 1645-1653. GENG Xiuli, XU Shidong, YE Chunming. Optimal design method of product function requirements considering quantitative KANO analysis[J]. Computer Integrated Manufacturing Systems, 2016, 22(7): 1645-1653. (in Chinese) |
| [7] |
张根保, 王新, 冉琰, 等. 复杂机电产品基于元动作分解的可靠性建模及故障诊断[J]. 重庆大学学报, 2017, 40(8): 9-18. ZHANG Genbao, WANG Xin, RAN Yan, et al. Reliability modeling and fault diagnosing method of complex electromechanical products based on meta-action decomposition[J]. Journal of Chongqing University (Natural Science Edition), 2017, 40(8): 9-18. (in Chinese) |
| [8] |
李冬英. 数控机床装配质量建模与诊断技术研究[D]. 重庆: 重庆大学, 2014: 35-46. LI Dongying. Research on quality modeling and diagnosis technology for the assembly process of CNC machine tool[D]. Chongqing: Chongqing University, 2014: 35-46. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1015016987.htm |
| [9] |
Unal M, Onat M, Demetgul M, et al. Fault diagnosis of rolling bearings using a genetic algorithm optimized neural network[J]. Measurement, 2014, 58: 187-196. DOI:10.1016/j.measurement.2014.08.041 |
| [10] |
Han Y, Liu H J. Health evaluation of coal machine equipment gear based on fuzzy analytic hierarchy process[J]. Coal Technology, 2018, 37(5): 279-282. |
| [11] |
Huang K, Zhang Z, Li X. Safety evaluation of connecting structure defects in shipbuilding gantry crane based on fuzzy analytic hierarchy process[J]. Hoisting and Conveying Machinery, 2013(4): 57-60. |
| [12] |
Rodríguez A, Ortega F, Concepción R. An intuitionistic method for the selection of a risk management approach to information technology projects[J]. Information Sciences, 2017, 375: 202-218. DOI:10.1016/j.ins.2016.09.053 |
| [13] |
刘英, 银刚, 张根保, 等. 数控机床质量投影寻踪综合评价方法[J]. 重庆大学学报, 2018, 41(2): 21-28. LIU Ying, YIN Gang, ZHANG Genbao, et al. A comprehensive evaluation method of projection pursuit for CNC machine tool quality[J]. Journal of Chongqing University(Natural Science Edition), 2018, 41(2): 21-28. (in Chinese) |
| [14] |
丁奕. 基于机器能力指数的拧紧设备质量控制方法[J]. 中国设备工程, 2017(23): 43-44. DING Yi. Quality control method of tightening equipment based on machine capability index[J]. China Plant Engineering, 2017(23): 43-44. (in Chinese) DOI:10.3969/j.issn.1671-0711.2017.23.025 |
| [15] |
罗孟然, 丛明, 顾齐芳, 等. 基于Cmk分析的加工中心精度稳定性评估[J]. 组合机床与自动化加工技术, 2015(3): 149-153. LUO Mengran, CONG Ming, GU Qifang, et al. Assessment of precision stability of machining center based on cmk analysis[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(3): 149-153. (in Chinese) |
| [16] |
Hajian-Hoseinabadi H. Availability comparison of various power substation automation architectures[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 566-574. DOI:10.1109/TPWRD.2012.2237185 |
| [17] |
吴小良, 陈春良, 左文涛. 装备保障任务能力的多级QFD需求建模[J]. 火力与指挥控制, 2011, 36(1): 138-142. WU Xiaoliang, CHEN Chunliang, ZUO Wentao. Equipment support task capability requirement modeling in multilevel QFD[J]. Fire Control & Command Control, 2011, 36(1): 138-142. (in Chinese) DOI:10.3969/j.issn.1002-0640.2011.01.036 |
 2019, Vol. 42
2019, Vol. 42


