2. 重庆交通大学 重庆西南水运工程科学研究所, 重庆 400016
2. Southwestern Hydraulic Engineering Research Institute for Waterway, Chongqing Jiaotong University, Chongqing 400016, P. R. China
国际隧道与地下空间协会指出,21世纪是人类走向地下空间的世纪[1]。地下空间是指在岩层或土层中天然形成或经人工开发形成的空间[2],文中主要研究人工开发形成的“地下建筑空间”,如地下住宅、地下商场、地下车库等。地下空间长期处于封闭或者半封闭的状态,与太阳光线和自然空气基本上是隔离的[3],因此,地下空间的空气质量十分糟糕,合理通风尤为重要。当前,地下空间大多采用机械通风,但能耗问题随之产生,违背了建筑与自然的和谐。自然通风不仅可提供健康舒适的室内环境,符合绿色建筑的发展趋势[4-5],引入太阳能烟囱加强地下空间自然通风是一种极具潜力的方法。
太阳能烟囱是被动利用太阳能强化空间自然通风的装置。阳光透过烟囱玻璃板由吸热墙吸收,加热周边空气使之产生密度差,从而在烟囱内产生热浮力自然对流。太阳能烟囱根据结构形式可分为竖直式、倾斜式和Trombe墙体式,文中主要研究竖直式太阳能烟囱对地下空间的强化通风作用。目前,有关竖直式太阳能烟囱的研究已经取得了一些成果。Rodrigues[6]报道了太阳能烟囱的研究重点应该在通风效果和热舒适性上取得平衡。Bansal[7]将小尺寸太阳能烟囱应用于建筑通风,并调查了相应的通风效果。Arce[8]搭建全尺寸实验台调查了太阳能烟囱的自然通风情况,得到温差和进出口压差是影响质量流率的主要因素。李安桂[9]实验验证了太阳能烟囱速度边界层和温度边界层的现象,并得到烟囱通风量随烟囱宽度、热流密度的增大而增大的结论。Ryan[10]进一步研究了太阳能烟囱几何参数、热流密度与通风量的关系并得到相应关系式。戴鹏[11]实验研究了太阳能烟囱自然通风及排烟效果,得到太阳能烟囱的最优空腔间距。尽管实验研究最为直接有效,但其成本高、周期长,相比之下数值模拟研究成本低、周期短,在模型合理的条件下可获得较理想的结果,部分学者开展了相关的数值研究工作。Miyazaki[12]数值模拟了太阳能烟囱加强单层建筑通风的工况,并考虑了热负荷的变化。薛宇峰[13]得到直线渐缩式太阳能烟囱的通风效果要优于曲线渐缩式的结论。Khanal[14]采用实验与数值模拟结合的方式研究了竖直式小尺寸太阳能烟囱的通风效果,并对烟囱结构进行了优化。Zavala-Guillén[15]设计了双通道竖直式太阳能烟囱,并验证了该结构的实用性。此外,杨启容[16]和赵福云[17]研究了二维太阳能烟囱内的流动特性及相应的结构优化措施。
现有研究中涉及竖直式太阳能烟囱强化地下空间自然通风的相关工作较少。华斌[18]、马瑞华[19]报道了太阳能烟囱强化地下车库通风的研究工作,结果表明,引入太阳能烟囱可以满足地下车库的通风要求,但在烟囱内的气体流动特性方面的研究不够深入。基于此,文中对竖直式太阳能烟囱强化地下空间的通风效果进行数值研究。
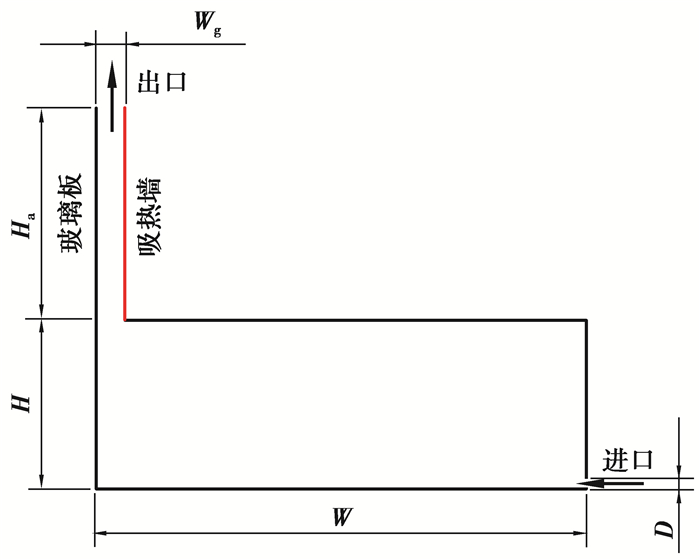
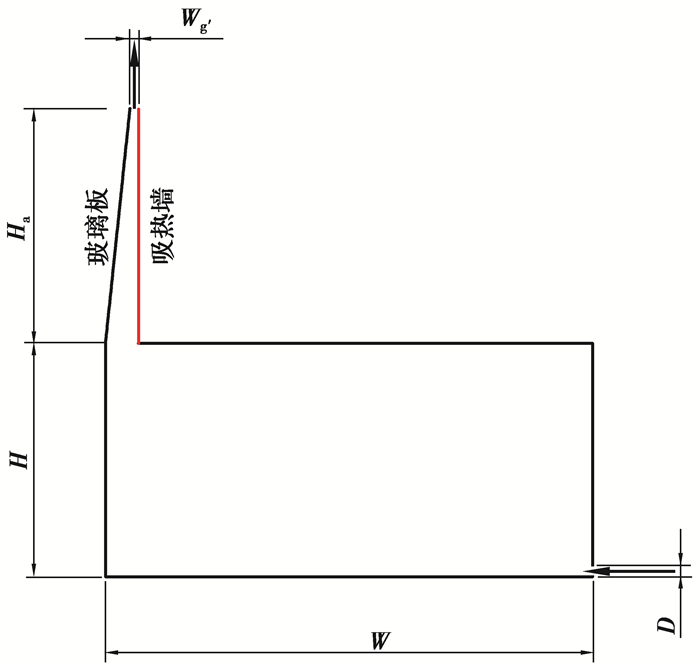
1 问题描述和数值公式 1.1 物理模型文中建立了竖直式太阳能烟囱与地下空间结合的二维物理模型,如图 1所示。图中位于左上角玻璃板与吸热墙相间的部分为烟囱,下方矩形部分为地下空间。烟囱吸热墙高度为Ha,吸热墙和玻璃板之间的宽度为Wg,宽高比As=Wg/Ha,地下空间高度为H,地下空间宽度为W,地下空间进口高度为D。箭头表示气流进出模型的方向。参照相关建筑规范,选用的模型比例为:As=1/7,H/Ha=1,H/W=3/7,H/D=20。
|
图 1 物理模型 Figure 1 Physical model |
为简化计算,对模型做了如下假设:
1) 模型内气体为不可压缩牛顿流体;
2) 气体自然对流采用Boussinesq假设;
3) 不考虑壁面的辐射和烟囱吸热墙的蓄热;
4) 模型内空气流动为层流流动。
1.2 基本控制方程无量纲化的控制方程如下:
| $\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial U}}{{\partial \tau }} + U\frac{{\partial U}}{{\partial X}} + V\frac{{\partial U}}{{\partial Y}} = - \frac{{\partial P}}{{\partial X}} + Pr\left( {\frac{{{\partial ^2}U}}{{\partial {X^2}}} + \frac{{{\partial ^2}U}}{{\partial {Y^2}}}} \right)}\\ {\frac{{\partial V}}{{\partial \tau }} + U\frac{{\partial V}}{{\partial X}} + V\frac{{\partial V}}{{\partial Y}} = - \frac{{\partial P}}{{\partial Y}} + Pr\left( {\frac{{{\partial ^2}Y}}{{\partial {X^2}}} + \frac{{{\partial ^2}V}}{{\partial {Y^2}}}} \right) + PaPr\mathit{\Theta }}\\ {\frac{{\partial U}}{{\partial X}} + \frac{{\partial V}}{{\partial Y}} = 0}\\ {\frac{{\partial \mathit{\Theta }}}{{\partial \tau }} + U\frac{{\partial \mathit{\Theta }}}{{\partial X}} + V\frac{{\partial \mathit{\Theta }}}{{\partial Y}} = \frac{{{\partial ^2}\mathit{\Theta }}}{{\partial {X^2}}} + \frac{{{\partial ^2}\mathit{\Theta }}}{{\partial {Y^2}}}} \end{array}} \right.$ |
其中, 引入的无量纲参数如下:Ra=gβHa3Δt/αυ;Pr=υ/α。
相关参数无量纲化,如表 1所示。
| 表 1 无量纲化表格 Table 1 Dimensionless table |
其中,x、y和u,v分别为水平、竖直方向的坐标(m)和速度(m/s);p为压强,Pa;T为温度,K;Tw、T0和ΔT分别表示吸热墙温度、环境温度和温度差;t为时间,s;质量流率q为单位时间内通过太阳能烟囱出口截面的流体质量,kg/s,反映了烟囱的通风效果。以上各物理量的无量纲表达分别为X、Y、U、V、P、Θ、τ和Q。此外,g为重力加速度,m2/s;ρ为密度,kg/m3;S为烟囱出口面积,m2;β和υ分别为空气的热膨胀系数,1/K、热扩散系数,m2/s;和运动粘度,m2/s。
边界条件如下:
进口:压力入口,即P=0,
出口:压力出口,即P=0,
吸热墙:速度无滑移边界,即U=V=0,温度Θ=1。
其余所有墙体:速度无滑移边界,即U=V=0,温度Θ=0。
2 求解方法及网格描述 2.1 数值方法及参数选取整个模型计算区域采用非均匀交错网格,并在进、出口以及墙体壁面处进行加密。数值计算选用基于压力法的求解器进行离散,其中,对流项和扩散项选用二阶中心差分格式,压力与速度耦合采用SIMPLE算法进行处理。除能量方程外所有方程收敛迭代残差取1e-6,能量方程取1e-8。无量纲参数:Ra=104~109。
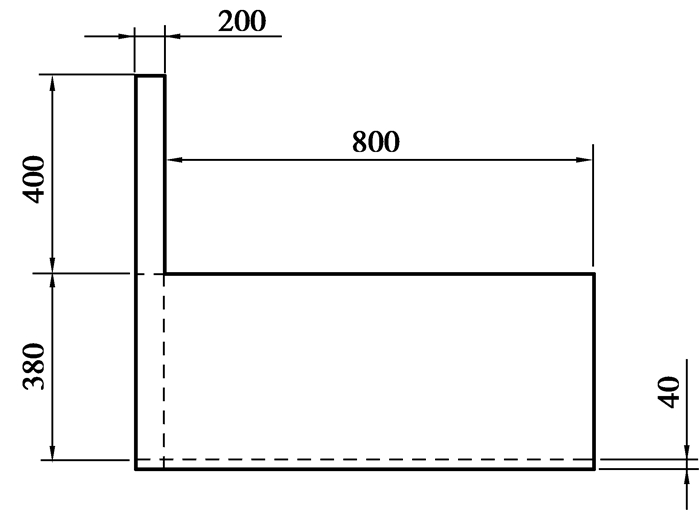
2.2 网格有效性验证模型各边界初始网格设置如图 2所示,总网格量Mesh1为500202。为了验证网格的收敛性,对初始网格进行加密,将模型各边网格量分别增大1.5倍和2倍,得到网格量Mesh2和Mesh3。
|
图 2 网格布置示意图 Figure 2 Grid layout figure |
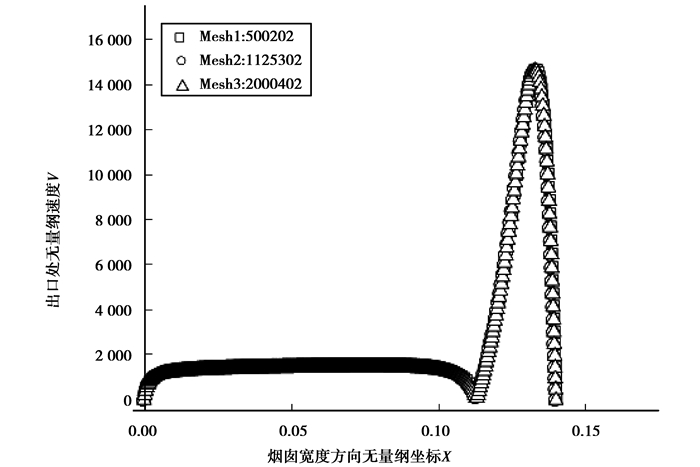
选用研究范围内极限工况Ra=109。采用以上3种网格计算得到烟囱出口处无量纲速度分布,如图 3所示,可以看出,分别采用Mesh1、Mesh2和Mesh3计算所得出口处无量纲速度分布几乎完全重合。网格量Mesh1可以满足计算精度要求,故选用该网格进行后续计算。
|
图 3 不同网格条件下烟囱出口处无量纲速度分布图 Figure 3 Dimensionless velocity distribution at chimney outlet under different grid conditions |
由基本控制方程中浮力项的表示可知,Ra是自然对流驱动力的主要来源之一。太阳能烟囱内部自然对流越强,对烟囱通风效果的影响就越大。Ra是太阳能烟囱通风效果的重要影响因素之一,文中主要分析了低Ra层流条件下太阳能烟囱强化地下空间自然通风特性,Ra取值范围为104≤Ra≤108,主要工况如表 2所示。
| 表 2 计算工况 Table 2 Calculation condition |
1) Ra对烟囱内部气体流动特性的影响
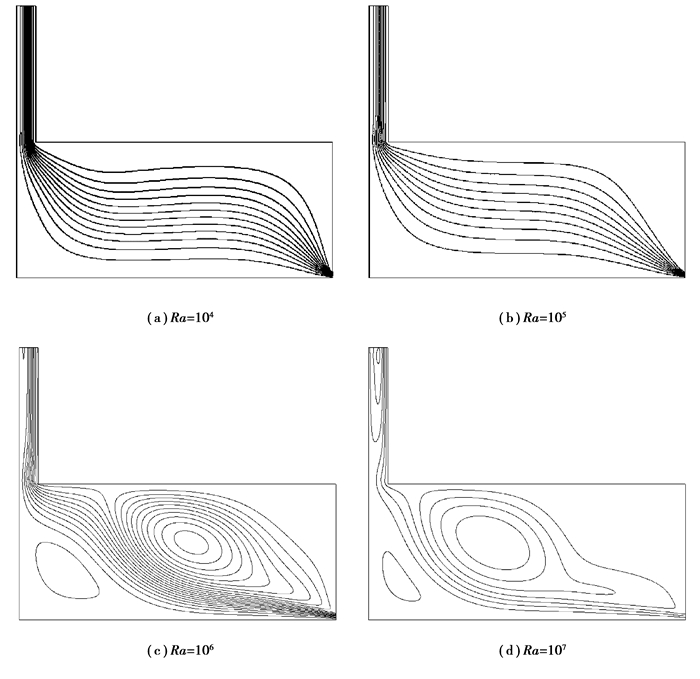
研究了Ra=104、105、106、107和108时太阳能烟囱内部流场。图 4描述了Ra=104、105、106和107时,太阳能烟囱强化地下空间对流通风模型内部气体的流线图。当Ra为104和105时,如图 4(a)和图 4(b)所示,气体在烟囱出口处为完全出流状态,吸热墙附近未形成明显速度边界层,此时,烟囱内传热形式以热传导为主。当Ra增加至106时,如图 4(c)所示,烟囱出口处出现了反向流,此时,为一个过渡阶段。进一步增加Ra至107,如图 4(d)所示,烟囱出口处出现明显的反向流,并且在吸热墙附近形成速度边界层,此时,烟囱内传热形式以对流换热为主。
|
图 4 不同Ra条件下模型内部的流线图 Figure 4 Streamline inside the model under different Rayleigh number |
研究结果表明,随着Ra的增加,太阳能烟囱内气体在出口处由完全出流向出口反向流的流动特征转变,与此同时,吸热墙侧也逐渐由无边界层特性向出现明显的边界层演化。
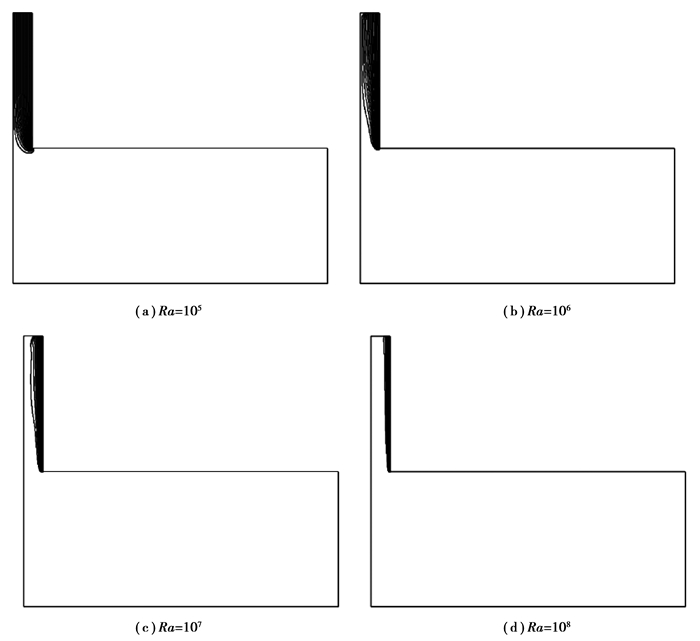
Ra=105、106、107和108时,模型内部的温度等值线也得到描述,如图 5所示。从图 5(a)可以看出,Ra=105时,烟囱内温度等值线几乎覆盖了整个烟囱。当Ra增至106和107时温度边界层逐渐形成,如图 5(b)和图 5(c)所示,此阶段对应烟囱内反向流的形成阶段。当Ra增至108时,如图 5(d)所示,烟囱内形成明显温度边界层。结果表明,Ra越大,烟囱吸热墙附近的温度边界层越明显。
|
图 5 不同Ra下模型内部的温度等值线图 Figure 5 Temperature contours inside the model under different Rayleigh number |
研究不同Ra下烟囱内部的气体流动得到结论如下:随Ra增加,太阳能烟囱出口处气体流动逐渐由完全出流向出口反向流特征转变,与此同时,吸热墙侧也逐渐形成明显速度边界层和温度边界层。
2) Ra对烟囱出口质量流率的影响
为了进一步研究竖直式太阳能烟囱对地下空间通风效果的影响,接下来主要分析不同Ra下烟囱出口质量流率的规律及其影响因素。
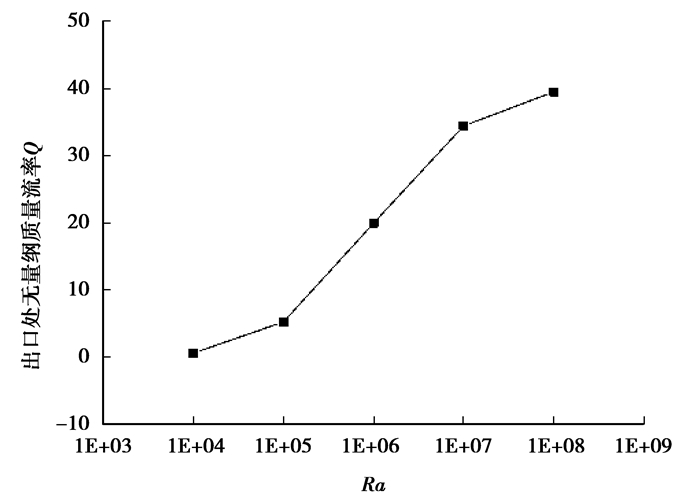
图 6描述了烟囱出口处无量纲质量流率随Ra(104~108)变化的规律。从图中可以看出,烟囱出口处无量纲质量流率呈持续增长趋势,但是,在Ra=106之后,曲线增长速度逐渐变缓。表 3给出了烟囱出口处无量纲质量流率增长率(增长率
| 表 3 出口质量流率增长率 Table 3 Outlet mass flow rate growth rate |
|
图 6 出口处质量流率随Ra变化图 Figure 6 Variation of outlet mass flow rate under Rayleigh number |
结合不同Ra条件下烟囱内部气体流动特性和烟囱出口质量流率规律,当Ra增至106时,烟囱出口处开始出现反向流特性,如图 4(c)所示;而烟囱出口处无量纲质量流率的增长率在此时开始降低。由此可以推论,烟囱出口反向流的出现是影响出口质量流率增长率降低的主要原因。为了明确这一影响因素,接下来将进一步分析烟囱出口质量流率及其内部反向流的关系。
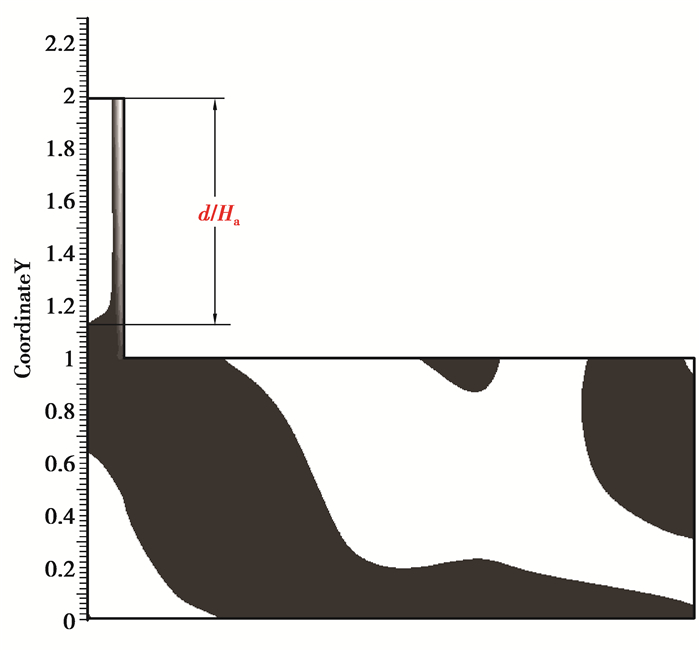
为了描述反向流,用烟囱内纵向负速度区域的最大纵向长度表征反向流深度。图 7为Ra=107时,烟囱内反向流深度示意图,图中所示白色部分为纵向负速度区域,故在该工况下烟囱内存在明显反向流,且反向流深度(d/Ha)为0.78。
|
图 7 Ra=107时反向流深度示意图 Figure 7 Reverse flow depth figure |
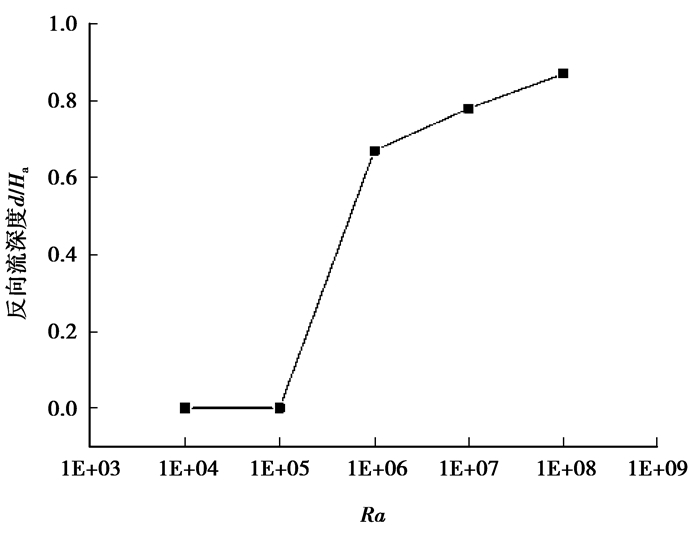
图 8为烟囱内反向流深度随着Ra变化曲线图。从图中可以看出,Ra在105及以下时反向流深度为0;Ra=106时反向流已经出现,随着Ra进一步增加,反向流深度逐渐增加。由图 6、表 3结合分析得到,当Ra=106时,反向流出现,且烟囱出口处无量纲质量流率的增长率减小。反向流深度反映了反向流对整个模型气体流动的影响程度,Ra越大其对出口处无量纲质量流率增长率的影响程度也越大。
|
图 8 反向流深度随Ra变化图 Figure 8 Variation of Reverse flow depth with Rayleigh number |
研究表明,烟囱出口反向流的出现降低了太阳能烟囱强化自然通风效率。因此,抑制反向流的出现可提高出口质量流率,是增强室内通风效果的有效途径。
3.2.3 太阳能烟囱结构优化效果分析优化烟囱结构抑制反向流的出现可加强太阳能烟囱对地下空间的通风效果。针对Ra=108的工况,文中提出太阳能烟囱结构优化方案如下:将太阳能烟囱玻璃板向吸热墙侧倾斜,减小烟囱出口口径以避免烟囱出口反向流的出现。
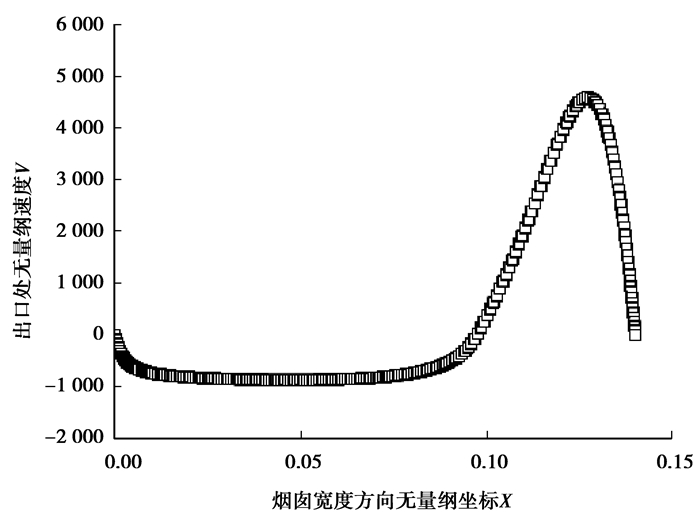
分析了Ra=108时,以上工况下原模型出口处无量纲速度的分布情况,如图 9所示。从图中可以看出,烟囱出口处反向流分布宽度约为0.1。原模型烟囱宽度Wg=0.14,为避免烟囱出口处反向流的出现,优化后的烟囱出口宽度W′g=Wg-0.1=0.04。优化后的模型如图 10所示。
|
图 9 出口处无量纲速度分布图 Figure 9 Outlet dimensionless velocity distribution |
|
图 10 优化后模型 Figure 10 Optimized model |
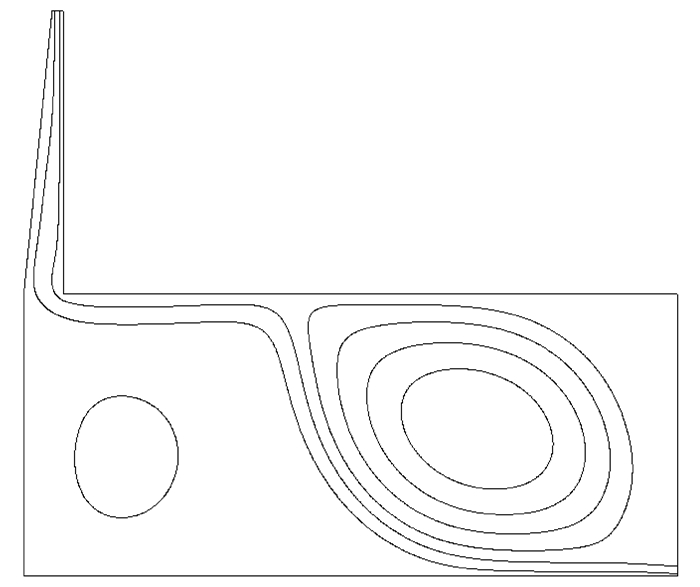
采用优化后的模型,计算得到模型流线图如图 11所示。可以看出,优化后的烟囱内未出现反向流现象。优化后模型出口处无量纲质量流率为106.71,比原模型提高了169.74%。结果表明:倾斜式优化通风结构可有效避免反向流的出现,极大地加强了竖直式太阳能烟囱对于地下空间的通风效果。
|
图 11 优化模型流线图 Figure 11 The streamline of optimized model |
为了研究竖直式太阳能烟囱对地下空间的自然通风效果,文中分析了不同Ra下烟囱内的气体对流特性及出口质量流率规律。
1) 烟囱内气体随着Ra增加由完全出流向出口反向流的特征转变,且Ra=106时,出口处开始出现反向流,吸热墙附近形成边界层;
2) 烟囱出口处无量纲质量流率随着Ra增大而增大,但反向流出现后,出口处无量纲质量流率的增长率随着Ra增大而减小,即反向流是影响太阳能烟囱通风效果的主要因素;
3) 为强化太阳能烟囱对地下空间的通风换气效果,提出倾斜式优化通风结构。通过对比结构优化前后的结果,得到优化后的结构可抑制烟囱出口反向流的出现,有效强化地下空间的通风效果。
| [1] |
陈易. 城市地下空间室内设计[M]. 上海: 同济大学出版社, 2015. CHEN Yi. Interior design of urban underground space[M]. Shanghai: Tongji University Press, 2015. (in Chinese) |
| [2] |
童林旭. 地下建筑学[M]. 北京: 中国建筑工业出版社, 2012. TONG Linxu. Underground architecture[M]. Beijing: China Construction Industry Press, 2012. (in Chinese) |
| [3] |
陈君萍. 地下车库排风量的计算和污染物扩散过程模拟[D]. 西安: 西安建筑科技大学, 2009. CHEN Junping. Calculation of the exhaust volume of an underground garage and simulation on pollutant dispersion process[D]. Xi'an: Xi'an University of Architecture and Technology, 2009. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10703-2009135820.htm |
| [4] |
李楠, 李百战, 沈艳, 等. 住宅建筑自然通风对室内热环境的影响[J]. 重庆大学学报(自然科学版), 2009, 32(7): 736-742. LI Nan, LI Baizhan, SHENG Yan, et al. Impacts of natural ventilation on indoor thermal environment for residential housing[J]. Journal of Chongqing University(Natural Science Edition), 2009, 32(7): 736-742. (in Chinese) |
| [5] |
景星蓉, 张健, 林勇. 绿色生态住宅小区的开发与建设[J]. 重庆大学学报(自然科学版), 2003, 26(6): 105-108. JING Xingrong, ZHANG Jian, LIN Yong. Development and build of green ecological residential guarter[J]. Journal of Chongqing University(Natural Science Edition), 2003, 26(6): 105-108. (in Chinese) |
| [6] |
Rodrigues A M, Canha da Piedade A, Lahellec A, et al. Modelling natural convection in a heated vertical channel for room ventilation[J]. Building and Environment, 2000, 35(5): 455-469. DOI:10.1016/S0360-1323(99)00027-X |
| [7] |
Bansal N K, Mathur J, Mathur S, et al. Modeling of window-sized solar chimneys for ventilation[J]. Building and Environment, 2005, 40(10): 1302-1308. DOI:10.1016/j.buildenv.2004.10.011 |
| [8] |
Arce J, Jiménez M J, Guzmán J D, et al. Experimental study for natural ventilation on a solar chimney[J]. Renewable Energy, 2009, 34(12): 2928-2934. DOI:10.1016/j.renene.2009.04.026 |
| [9] |
李安桂, 郝彩侠, 张海平. 太阳能烟囱强化自然通风实验研究[J]. 太阳能学报, 2009, 30(4): 460-464. LI Angui, HAO Caixia, ZHANG Haiping. Experimental study on solar chimney for natural ventilation[J]. Acta Energiae Solaris Sinica, 2009, 30(4): 460-464. (in Chinese) DOI:10.3321/j.issn:0254-0096.2009.04.011 |
| [10] |
Ryan D, Burek S A M. Experimental study of the influence of collector height on the steady state performance of a passive solar air heater[J]. Solar Energy, 2010, 84(9): 1676-1684. DOI:10.1016/j.solener.2010.05.018 |
| [11] |
戴鹏. 太阳能烟囱建筑自然通风与自然排烟性能的实验研究[D]. 合肥: 中国科学技术大学, 2017. DAI Peng. Experimental study on natural ventilation and smoke exhaust performance of solar chimney buildings[D]. Hefei: University of Science and Technology of China, 2017. (in Chinese) 太阳能烟囱建筑自然通风与自然排烟性能的实验研究 |
| [12] |
Miyazaki T, Akisawa A, Kashiwagi T. The effects of solar chimneys on thermal load mitigation of office buildings under the Japanese climate[J]. Renewable Energy, 2006, 31(7): 987-1010. DOI:10.1016/j.renene.2005.05.003 |
| [13] |
薛宇峰, 苏亚欣. 太阳能烟囱结构对通风效果影响的数值研究[J]. 暖通空调, 2011, 41(10): 79-83. XUE Yufeng, SU Yaxin. Numerical study on impacts of solar chimney structure on ventilation effects[J]. Heating Ventilating & Air Conditioning, 2011, 41(10): 79-83. (in Chinese) DOI:10.3969/j.issn.1002-8501.2011.10.021 |
| [14] |
Khanal R, Lei C W. Flow reversal effects on buoyancy induced air flow in a solar chimney[J]. Solar Energy, 2012, 86(9): 2783-2794. DOI:10.1016/j.solener.2012.06.015 |
| [15] |
Zavala Guillén I, Xamán J, Hernández Pérez I, et al. Numerical study of the optimum width of 2a diurnal double air-channel solar chimney[J]. Energy, 2018, 147: 403-417. DOI:10.1016/j.energy.2017.12.147 |
| [16] |
杨启容, 杜威, 张金翠. 建筑一体化太阳能烟囱的通风性能研究[J]. 太阳能学报, 2010, 31(7): 873-878. YANG Qirong, DU Wei, ZHANG Jincui. Study on ventilation performance of building integrated solar chimney[J]. Acta Energiae Solaris Sinica, 2010, 31(7): 873-878. |
| [17] |
赵福云, 任秀宏, 胡江涛, 等. 太阳能烟囱通风特性及其强化[J]. 武汉大学学报(工学版), 2017, 50(5): 714-719. ZHAO Fuyun, REN Xiuhong, HU Jiangtao, et al. Ventilation performance of solar chimney and its reinforcement[J]. Engineering Journal of Wuhan University, 2017, 50(5): 714-719. (in Chinese) |
| [18] |
华斌. 太阳能烟囱与诱导通风相结合应用于地下车库通风的研究[D]. 南京: 南京师范大学, 2013. HUA Bin. Study on application of solar chimney and induced ventilation in underground garage ventilation[D]. Nanjin: Nanjing normal University, 2013. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10319-1013338373.htm |
| [19] |
马瑞华, 秦堃, 刘黔蜀. 太阳能烟囱在地下车库中强化自然通风的数值模拟[J]. 制冷与空调, 2016, 30(3): 321-324. MA Ruihua, QIN Kun, LIU Qianshu. Numerical study of enhanced natural ventilation of solar chimney in underground garage[J]. Refrigeration & Air Conditioning, 2016, 30(3): 321-324. (in Chinese) DOI:10.3969/j.issn.1671-6612.2016.03.015 |
 2019, Vol. 42
2019, Vol. 42


