人体的血液循环包括体循环、肺循环和微循环,微循环包括微动脉与微静脉之间的血液循环和淋巴循环。淋巴微循环参与淋巴液的生成与转运, 对机体微环境的稳定具有重要意义, 是微循环的重要组成部分。流经毛细血管的血浆有0.5%~2%在动脉端滤出到组织间隙,约有90%的滤出液在静脉端被重吸收,其余约10%(包括滤过的白蛋白分子)进入毛细淋巴管,形成淋巴液[1]。组织间隙滤出液如果不被即时排走,将使内压上升,会对血浆渗透产生影响并可能引起水肿的发生[2]。水肿与微动脉、微静脉的压力、血浆渗透压和淋巴微循环等因素有关[3]。
R.Kh.khafiz’yanva等[4]发现用二甲磷加强淋巴管道的收缩活动,能促进组织液和细胞代谢产物的运输和再吸收。童华生等[5]对重症中暑大鼠肠系膜淋巴微循环变化进行研究,发现重症中暑大鼠的肠系膜淋巴微循环变化具有一定动态规律,可能参与了重症中暑的发病机制。微循环与细胞代谢密切相关,微循环障碍导致组织缺氧是多器官功能障碍综合征的最主要原因。然而,临床中常会面对在宏观血流动力学参数被纠正到正常时,微循环功能障碍、组织缺氧仍继续存在的情况。因此,改善微循环是治疗“难治性休克”的关键,也是治疗难点和尚未攻克的难题[6]。张静等[7]研究发现淋巴微循环在多种休克、多器官功能障碍综合征、多器官衰竭等危重病的发病机制中具有重要作用, 深入研究淋巴微循环在这些疾病发病学中的作用, 有助于全面认识其发病机制, 可以为降低危重病的病死率提出新的防治策略。
王宗银[8]对国内外针灸抢救休克的概况进行了研究,针灸对失血性休克、感染性休克和过敏性休克都有较好的治疗效果,但其原理尚不明确,初步认为与改善血管舒缩的异常状态有关,可以增加重要器官的血流量。赵良举[9]提出了经络呼吸辅助系统假说,认为当内脏器官出现炎症等症状时,代谢加强、CO2产生增多,如果不能及时排出,将使组织间隙压力增大,造成局部微循环障碍。针刺穴位则可以通过经络将组织间隙中多余的CO2排出,从而降低组织间隙压力,使微循环畅通,起到疏经活血的作用。
血液循环在人体正常的生理活动中起着重要作用,而微循环则直接参与养分的输送和代谢废物的带走。本研究将忽略肺循环,直接探讨体循环和微循环的关系。带淋巴微循环的体循环血液流体网络模型,未见文献报导。前期建立的人体血液体循环流体网络模型[10],能较好地模拟每一个体循环分支中血流动力学参数的变化情况。文中将在体循环流体网络中考虑淋巴循环,建立带有淋巴系统的人体血液循环系统网络模型,对淋巴微循环与体循环相互影响机制进行研究。
1 方法 1.1 淋巴系统与血液循环的关系血液通过毛细血管网进入组织间隙形成组织液与组织进行物质交换后,血浆滤出液约10%进入毛细淋巴管成为淋巴液,最后经由淋巴系统回到静脉。胸导管是淋巴系中最粗大的淋巴管道, 引流下肢、盆部、腹部、胸部左侧半、左上肢和头颈部左侧半的淋巴,全身的淋巴流量有5/6汇入胸导管。脾是人体最大的淋巴器官, 因此,在流体网络模型中脾脏上加入胸导管分支(图 1中第10分支),来近似模拟淋巴系统参与血液循环时,人体血液网络血流量和淋巴系统的淋巴液流量变化情况。
|
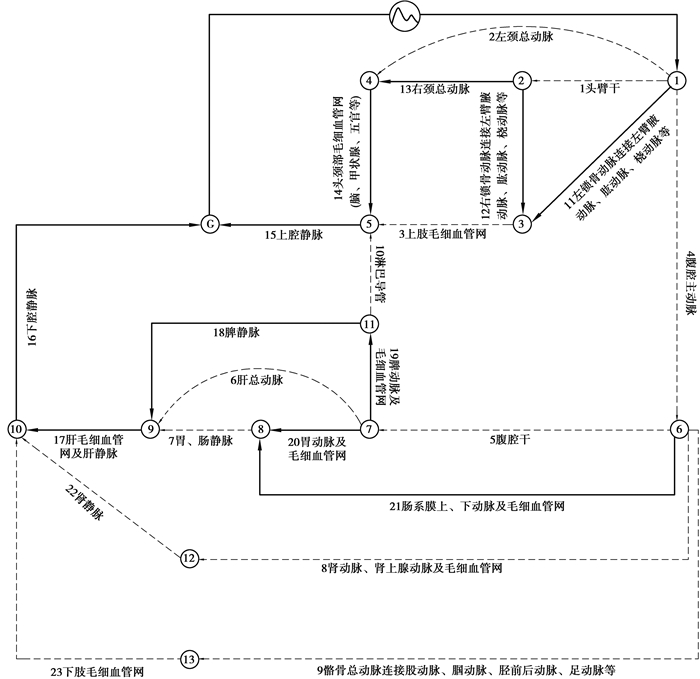
图 1 血液体循环的流体网络模型 Figure 1 Fluid network model of systemic circulation of human blood |
建立一个简化的考虑淋巴系统的血液体循环模型,每一段分支均看作集总参数模型来求解,每条血管分支把同类血管视为并联,不同类血管视为串联,忽视了动脉血流、静脉血流及淋巴系统的生物流体模型的差异性,把人体网络分成若干条血管分支,每条分支代表的血管已在模型中标示。模型中主要反映人体的主动脉及其动脉分支和器官动脉及其毛细血管网分支等,同时,将静脉简化为上下腔静脉回流分支,如图 1所示。网络模型中共有23条分支,独立分支21条,11个独立节点(图中带圆圈的数字)。一个动力执行机构G(相当于血液循环系统中的心脏),1-10分支作为连支(虚线),对应的分支参数的角标为a;11-21分支作为树支,对应的分支参数的角标为c,其中,第10分支为淋巴胸导管分支。
1.3 模型参数和分支流量求解血液在每条分支内的流动可以认为是泊肃叶(Posiseuille)流,则根据泊肃叶定律有:
| $ Q = {\rm{ \mathsf{ π} }} \cdot {r^4} \cdot \frac{{\Delta P}}{{8\mu l}}, $ | (1) |
其中:通过某条分支血液流量Q,mL/s;每条血管分支的压降ΔP,mmHg;血液粘度μ,Pa·s;血管半径r,cm;血管长度l,cm。根据流阻定义计算公式有:
| $ R = \frac{{\Delta P}}{Q} = \frac{{8\mu l}}{{{\rm{ \mathsf{ π} }}{r^4}}}。$ | (2) |
该式表明血流阻力与血液黏度以及血管长度成正比,与血管半径的4次方成反比。定义血液流体阻力系数T值为
| $ T = \frac{{\rho l}}{S}, $ | (3) |
式中,血液密度ρ=1.056 g/cm3;血管横截面积S,cm2。根据前期工作[10]总结的各血管构型的长度和内压、人体安静状态下各器官的流量,设定血液体循环的流体网络模型中各分支压差、流量,正常成年人安静状态下每小时淋巴流量约有120 mL,设定分支10(淋巴分支)的流量为2 mL/min。由式(2)可得各分支流阻R, 由于在同一血管床内,μ在一段时间内变化不大[11],血管长度l已经设定,在简化的血管分支中r可以看作是R的函数,由式(3)得阻力系数T,分支10作为淋巴分支,其中的流动除了淋巴液在淋巴管道内的流动,还包含血液进入组织间隙进行物质交换之后变成淋巴液进入淋巴分支的过程,该过程整个网络保持质量守恒。此传质过程与各血管分支之间血液的流动不同,不能用求血管流阻的方法求该分支流阻。模拟采用的平均法能得到每条分支流量10次谐波形式的近似解表达式,把人体安静状态下的淋巴液流量2 mL/min代入表达式,用迭代法求得淋巴分支的等效流阻。所有参数如表 1所示,各参数的生理意义:压差是每个血管分支两端的压力差,分支流量是流过该分支的血流量或淋巴液流量,分支流阻是血液在血管中流动受到的阻力。
| 表 1 模型参数初始值 Table 1 Initial parameters of the model |
假设心输出量一定,心脏输出的血液流量或压力波f(t)可分解为各种简谐波的组合[12]。Ck为谐波振幅,心脏输出信号的直流部分为Q0,心脏输出的血流动力学的流量表达式为
| $ {Q_{{\rm{in}}}}\left( t \right) = {Q_0} + \sum\limits_{k = 1}^n {{C_k}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}k}}{{{T_n}}}t + {\varphi _k}} \right)} 。$ | (4) |
流体网络模型状态空间表达式可写为[13]:
| $ {T_j}\frac{{{\rm{d}}{Q_j}}}{{{\rm{dt}}}} = - {R_j}\left| {{Q_j}} \right|{Q_j} + {H_j}, $ | (5) |
式中,Qj是通过分支j的流体流量;Rj是流体阻力;Hj是分支压降;Tj是阻力系数。通过对周期性受迫血液循环流体网络进行网络建模,利用自适应控制方法中的平均法进行分析[14],可得到如下结论。
定义矩阵:
| $ {\mathit{\boldsymbol{T}}_{\bf{0}}}\left( \mathit{\boldsymbol{T}} \right) = {\mathit{\boldsymbol{T}}_\mathit{\boldsymbol{c}}} + \mathit{\boldsymbol{E}}_{Qc}^T{\mathit{\boldsymbol{T}}_\mathit{\boldsymbol{a}}}{\mathit{\boldsymbol{E}}_{Qc}}, $ | (6) |
| $ {\mathit{\boldsymbol{B}}_c}\left( {\mathit{\boldsymbol{T}},\mathit{\boldsymbol{E}}} \right) = - \mathit{\boldsymbol{T}}_0^{ - 1}\mathit{\boldsymbol{E}}_{\mathit{\boldsymbol{Qc}}}^\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{T}}_\mathit{\boldsymbol{a}}}{e_{Qin}}, $ | (7) |
| $ {\mathit{\boldsymbol{B}}_a}\left( {\mathit{\boldsymbol{T}},\mathit{\boldsymbol{E}}} \right) = - \left( {I - {\mathit{\boldsymbol{E}}_{Qc}}\mathit{\boldsymbol{T}}_0^{ - 1}E_{Qc}^T{\mathit{\boldsymbol{T}}_a}} \right){e_{Qin}}, $ | (8) |
| $ \mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{R}},\mathit{\boldsymbol{T}},\mathit{\boldsymbol{E}}} \right) = {\rm{col}}\left\{ {B_{ci}^2{R_{ci}}} \right\} - \mathit{\boldsymbol{E}}_{Qc}^Tcol\left\{ {B_{ai}^2{R_{ai}}} \right\}, $ | (9) |
其中,矩阵Tc和Ta分别代表流体网络连支和树支的阻力系数的对角矩阵;EQc是将EQ=[EQc/EQa]中将EQa化为单位矩阵得到的连支网络系数矩阵。
定义矩阵:
| $ \mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{R}},\mathit{\boldsymbol{E}},{\mathit{\boldsymbol{Q}}_0}} \right) = {\rm{diag}}\left\{ {{\mathit{\boldsymbol{Q}}_{c0i}}{R_{ci}}} \right\} - \mathit{\boldsymbol{E}}_{Qc}^TW, $ | (10) |
| $ W = {\left\{ {{\mathit{\boldsymbol{E}}_{Qcij}}\left( { - {\mathit{\boldsymbol{E}}_{Qci}}{\mathit{\boldsymbol{Q}}_{c0}} - {e_{Qini}}{\mathit{\boldsymbol{Q}}_0}} \right){R_{ai}}} \right\}_{\left( {n = l} \right) \times l}}, $ | (11) |
其中,Qc0(R, E, Q0)表示l维二次方程组的解,即:
| $ \mathit{\boldsymbol{Q}}_{c0D}^2{R_c} - \mathit{\boldsymbol{E}}_{Qc}^T{\rm{diag}}\left\{ {{{\left( {{\mathit{\boldsymbol{E}}_{Qci}}{\mathit{\boldsymbol{Q}}_{c0}} - {e_{Qini}}{\mathit{\boldsymbol{Q}}_0}} \right)}^2}} \right\}{R_a} = 0。$ | (12) |
将上面的计算结果带入下列方程组即可得到流体网络各连支和树支的平均流量谐波形式的近似解矩阵表达式:
| $ {{\mathit{\boldsymbol{\bar Q}}}_c}\left( t \right) = {\mathit{\boldsymbol{Q}}_{c0}} - \left( {\sum\limits_{k = 1}^n {\frac{{C_k^4}}{4}} } \right){\mathit{\boldsymbol{V}}^{ - 1}}\mathit{\boldsymbol{U}} + {\mathit{\boldsymbol{B}}_c}\left( {\sum\limits_{k = 1}^n {{C_k}\sin \left( {k\omega t + {\varphi _k}} \right)} } \right), $ | (13) |
| $ {{\mathit{\boldsymbol{\bar Q}}}_a}\left( t \right) = \left( { - {\mathit{\boldsymbol{E}}_{Qc}}{\mathit{\boldsymbol{Q}}_{c0}} - {\mathit{\boldsymbol{e}}_{Qin}}{\mathit{\boldsymbol{Q}}_0}} \right) + \left( {\sum\limits_{k = 1}^n {\frac{{C_k^4}}{4}} } \right)\\ {\mathit{\boldsymbol{E}}_{Qc}}{\mathit{\boldsymbol{V}}^{ - 1}}\mathit{\boldsymbol{U}} + {\mathit{\boldsymbol{B}}_a}\left( {\sum\limits_{k = 1}^n {{C_k}\sin \left( {k\omega t + {\varphi _k}} \right)} } \right)。$ | (14) |
最后,通过改变分支的流阻来模拟各分支病变[15]。定义流阻比η=R′/R,其中,R′表示变化后的流阻,R表示正常流阻,则η为反映流阻变化的无量纲比值,在计算过程中,η分别取值为0.5、1、1.5、2、2.5、3。在心输出量不变的条件下,分别通过改变模型中淋巴分支10、肝分支17、肾分支8、胃分支20、脾分支19、肠分支21和脑分支14的流阻,计算得到每一个分支流阻分别变化时对其他分支平均血流量的影响。分支流阻的增大代表血液循环或淋巴微循环障碍。
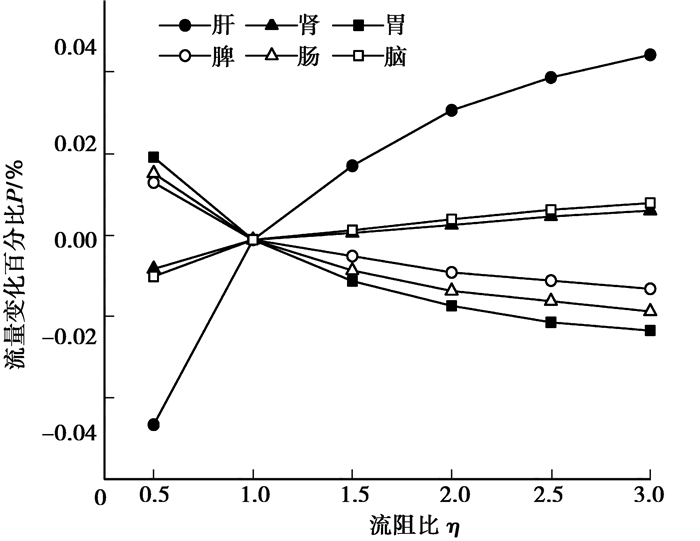
2 计算结果 2.1 淋巴分支流阻变化对其他分支平均流量的影响由图 2可知,随着淋巴分支流阻比η的增大,肝分支、肾分支和脑分支的平均流量略微上升,当η=3时,相对于正常值分别增大0.039%、0.006%和0.008%;随着淋巴分支流阻的增大,胃分支、脾分支、肠分支的平均流量均有略微下降,当η=3时,相对于正常值分别下降0.019%、0.010%和0.015%。
|
图 2 淋巴分支流阻变化对其他分支平均流量的影响 Figure 2 The effect of lymph branch flow resistance change on the average flow ratesof other branches |
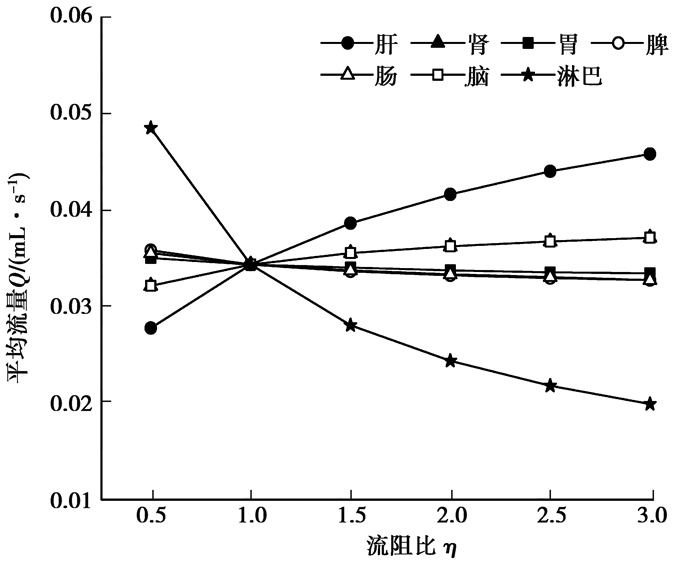
由图 3可知,随着肝分支、肾分支、脑分支流阻比η的增大,淋巴分支的平均流量上升,当η=3时,相对于正常值分别上升33.41%、8.01%和8.07%;随着胃分支、脾分支、肠分支和淋巴分支流阻的增大,淋巴分支的平均流量下降,当η=3时,相对于正常值分别减小2.69%、4.82%、4.65%和42.24%。
|
图 3 分支流阻变化对淋巴分支流量的影响 Figure 3 The effect of other branches flow resistance change on the average flow rates of lymph branches |
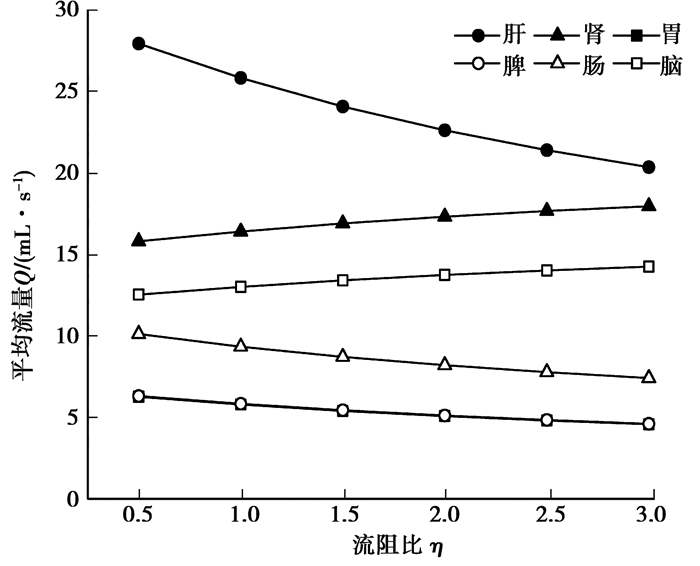
由图 4可知,随着肝分支流阻比η的增大,肝分支的平均流量明显下降,当η=3时,相对于正常值下降21.21%;肾分支和脑分支的平均流量小幅度上升,当η=3时,相对于正常值分别增大9.48%和9.58%;随着肝分支流阻的增大,胃分支、脾分支、肠分支的平均流量均有小幅度下降,当η=3时,相对于正常值分别下降20.90%、21.05%和20.55%。
|
图 4 肝分支流阻变化对其他分支平均流量的影响 Figure 4 The effect of liver branch flow resistance change on the average flow rates of other branches |
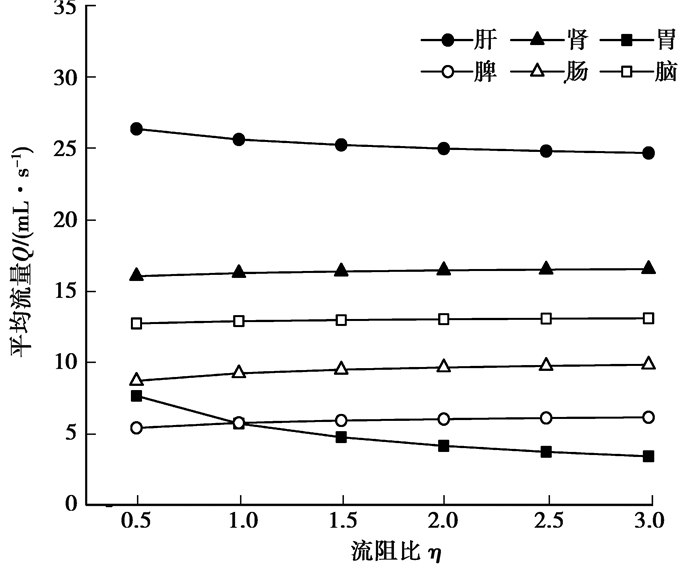
由图 5可知,随着胃分支流阻比η的增大,胃分支的平均流量显著下降,当η=3时,相对于正常值下降39.89%;随着胃分支流阻的增大,肝分支的平均流量小幅度下降,当η=3时,相对于正常值下降3.71%;肾分支、脾分支、肠分支、脑分支的平均流量均有小幅度上升,当η=3时,相对于正常值分别增大1.74%、6.74%、6.52%、1.60%。脾分支和肠分支流阻增大时对其他分支的影响与胃分支相似。
|
图 5 胃分支流阻变化对其他分支平均流量的影响 Figure 5 The effect of stomach branch flow resistance change on the average flow rates of other branches |
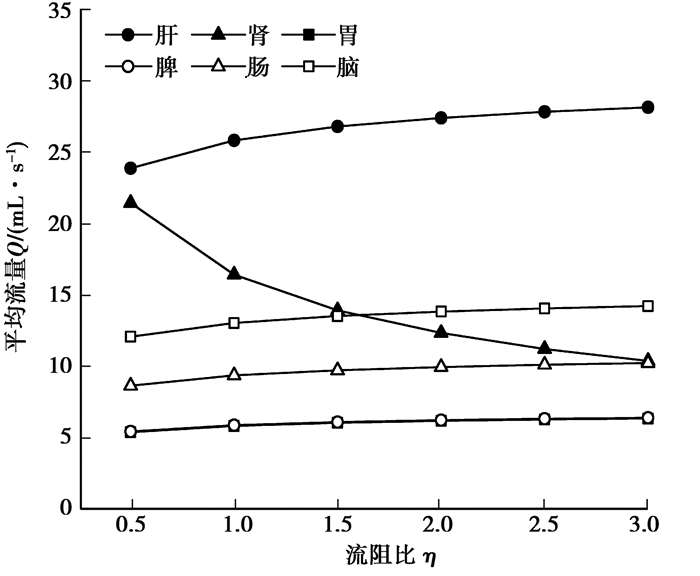
由图 6可知,随着肾分支流阻比η的增大,肾分支的平均流量明显下降,当η=3时,相对于正常值下降36.89%;肝分支、胃分支、脾分支、肠分支和脑分支的平均流量均有小幅度上升,当η=3时,相对于正常值分别增大8.97%、9.08%、9.02%、9.24%和9.15%。
|
图 6 肾分支流阻变化对其他分支平均流量的影响 Figure 6 The effect of kidney branch flow resistance change on the average flow rates of other branches |
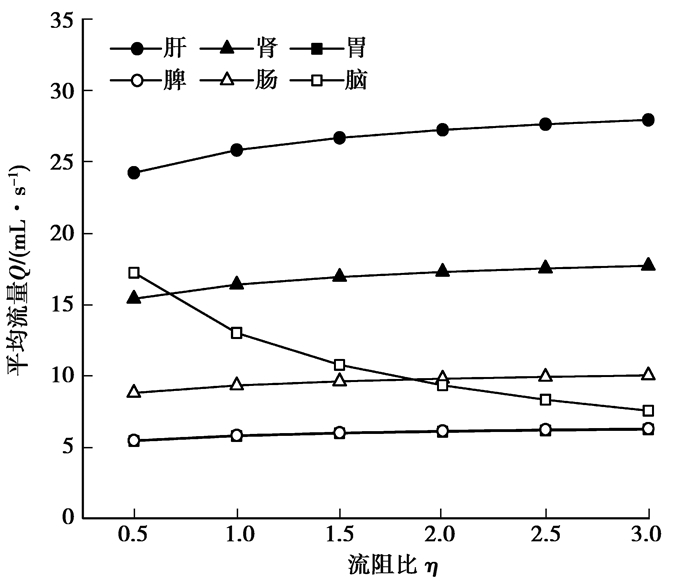
由图 7可知,随着脑分支流阻比η的增大,脑分支的平均流量明显下降,当η=3时,相对于正常值下降41.83%;肝分支、肾分支、胃分支、脾分支和肠分支的平均流量均有小幅度上升,当η=3时,相对于正常值分别增大8.15%、8.04%、7.91%、8.06%和7.54%。
|
图 7 脑分支流阻变化对其他分支平均流量的影响 Figure 7 The effect of brain branch flow resistance change on the average flow rates of other branches |
由图 2可知,淋巴分支流量变化对其他分支流量影响很小;由图 3可知,淋巴分支流阻变化对自身流量影响很大。文献[16]对水肿病人和正常病人的淋巴微循环和体循环观测,未发现明显关联,这与文中的结果是一致的。这也可以解释,实际临床工作中常会面对在宏观血流动力学参数被纠正到正常时,微循环功能障碍依然存在。对宏观循环的调整往往仍难以进一步改善组织灌注[6]。而针刺可以抢救休克病人的原理[8],则可解释为针刺穴位通过经络将组织间隙中多余的CO2排出,从而降低组织间隙压力,淋巴分支阻力减小才使微循环畅通,为机体带去养分使机体恢复活力。
由图 3可知,当分支流阻增大时,除了淋巴分支对自身的影响,对淋巴分支流量影响最大的是肝分支。从人体结构来看,流经腹腔内胃、肠、脾的血液均从各自的静脉汇集到肝门静脉,然后到达肝脏。肝分支流阻增大,血流不畅时,将导致腹腔内血流网络各分支血压升高,毛细血管血压升高,有效滤过压增大,产生更多的淋巴液从淋巴分支回到静脉。结合各器官分支在血液体循环流体网络中的位置,由图 4、图 5可知,肝、胃、脾、肠的相互影响大于对其他分支的影响。肝流阻增大而流量减小时,胃、脾、肠分支的流量有较大的下降。胃、脾、肠分支的流阻增大而流量减少时,肝分支的流量减小,而脑和肾分支的流量增大。由图 6和图 7可知,肾分支和脑分支与另外6条分支相比较为独立,当肾分支或脑分支流量减小时,与之并联的其他网络中的分支平均流量上升。结合图 3可知,当某一分支流阻变化引起淋巴分支所在局部网络流量增大或减小,淋巴分支流量也随之增大或减小。
由于淋巴循环的复杂性,文中模拟仅从生物物理方向研究了淋巴系统对微循环的影响。后续研究将进一步在模型中考虑淋巴系统的生理学功能、细化模型,以期得到更准确的结果。
| [1] |
Michel C C. Immunology of the lymphatic system[M]. NewYork: Springer Science and Business Media, 2013.
|
| [2] |
Cheng H M. Respi-Renal Physiology[C]//Cheng H M. eds. Physiology Question-Based Learning. Cham: Springer International Publishing, 2015: 169-177.
|
| [3] |
Thiriet M. PanVascular medicine[M]. Heidelberg: Springer-Verlag, Berlin, 2015.
|
| [4] |
Khafiz'yanova R K, Mukhutdinov D A. Effect of dimephosphon on lymph circulation and microcirculation, contractility of the wall and cusps of valves in lymphatic microvessels, and cell composition of the lymph during fever[J]. Bulletin of Experimental Biology and Medicine, 2005, 139(6): 680-682. DOI:10.1007/s10517-005-0377-0 |
| [5] |
童华生, 段鹏凯, 张兴钦, 等. 重症中暑大鼠肠系膜淋巴微循环变化[J]. 解放军医学杂志, 2014, 39(4): 329-332. TONG Huasheng, DUAN Pengkai, ZHANG Xingqin, et al. Changes in mesenteric lymph microcirculation in rats suffering from severe heatstroke[J]. Medical Journal of Chinese People's Liberation Army, 2014, 39(4): 329-332. (in Chinese) |
| [6] |
刘大为. 临床血流动力学[M]. 北京: 人民卫生出版社, 2013. LIU Dawei. Clinical hemodynamics[M]. Beijing: People's Medical Publishing House, 2013. (in Chinese) |
| [7] |
张静. 加强危重病发病学的淋巴微循环机制研究[J]. 中国微循环, 2009, 13(1): 5-10. ZHANG Jin. Study on the mechanism of lymphatic microcirculation in the pathogenesis of critical disease[J]. Journal of Chinese Microcirculation, 2009, 13(1): 5-10. (in Chinese) |
| [8] |
王宗银. 国内外针灸抢救休克的概况[J]. 成都医药, 1980(1): 76-86. WANG Zongyin. A survey of shock treatment by acupuncture and moxibustion[J]. Journal of Modern Clinical Medicine, 1980(1): 76-86. (in Chinese) |
| [9] |
Zhao L J. Acupuncture meridian of traditional Chinese medical science:an auxiliary respiratory system[J]. Journal of Acupuncture and Meridian Studies, 2015, 8(4): 209-212. DOI:10.1016/j.jams.2015.04.004 |
| [10] |
徐克, 赵良举, 李明阳. 基于流体网络的人体血液体循环分析[J]. 中国生物医学工程学报, 2017, 36(5): 580-588. XU Ke, ZHAO Liangju, LI Mingyang. The analysis of the systemic circulation of human blood based on fluid network[J]. Chinese Journal of Biomedical Engineering, 2017, 36(5): 580-588. (in Chinese) DOI:10.3969/j.issn.0258-8021.2017.05.010 |
| [11] |
朱大年. 生理学[M]. 北京: 人民卫生出版社, 2013. ZHU Danian. Physiology[M]. Beijing: People's Medical Publishing House, 2013. (in Chinese) |
| [12] |
张修诚, 王唯工, 陈荣洲, 等. 脉搏谐波频谱分析——中医脉诊研究新方法[J]. 中国中西医结合杂志, 1995, 15(12): 743-745. ZHANG Xiucheng, WANG Weigong, CHEN Rongzhou, et al. New method of TCM pulse diagnosis——Analysis of pulse harmonic spectrum[J]. Chinese Journal of Integrated Traditional and Western Medicine, 1995, 15(12): 743-745. (in Chinese) DOI:10.3321/j.issn:1003-5370.1995.12.016 |
| [13] |
Hu Y N, Koroleva O I, Krsti M. Nonlinear control of mine ventilation networks[J]. Systems & Control Letters, 2003, 49(4): 239-254. |
| [14] |
隋金雪, 杨莉. 复杂流体网络分析与控制[M]. 北京: 电子工业出版社, 2013. SUI Jinxue, YANG Li. Analysis and control of complex fluid networks[M]. Beijing: Publishing House of Electronics Industry, 2013. (in Chinese) |
| [15] |
Yang L, Sui J X, Shi H Z. Control modeling and Chinese acupuncture treatment on cerebral circulation[J]. Technology and Health Care, 2015, 23(s1): S77-S82. DOI:10.3233/thc-150934 |
| [16] |
Krupatkin A I. Oscillatory processes in lymph microcirculation in the human skin[J]. Human Physiology, 2014, 40(1): 52-57. DOI:10.1134/S0362119713040087 |
 2019, Vol. 42
2019, Vol. 42


