随着海量商业数据的出现,在很多实际应用中的数据实例通常与多个标签关联[1-2]。如何从多标签商业数据中通过特征选择来降低数据维度成为一项重要而具有挑战性的研究任务[3-4]。针对此类问题的研究取得许多成果,传统算法通过特征和标签之间的相关性准则来选择有效特征子集[5-6]。
Lee等[7]提出了一种基于多元互信息的多标签特征选择算法(MMIFS, feature selection for multi-label classification using multivariate mutual information),通过将高维熵的计算分解为多元互信息的累积和,最大化所选特征和标签之间的相关性来选择有效的特征子集。该算法只考虑特征和标签之间的相关性对特征选择的影响,忽略特征之间冗余性对算法性能的影响。Lin等[8]提出了基于最大依赖性和最小冗余性的多标签特征选择算法(MDMR, multi-label feature selection based on max-dependency and min-redundancy),通过结合最大化特征与标签之间的依赖性,以及最小化候选特征与选择特征之间的冗余性两个准则来进行特征选择,虽然这种策略能更好地提取出重要特征,但是没有考虑特征子空间中样本和标签空间中样本的邻域关系对算法性能的影响,从而影响多标签分类性能。
为了更有效地进行特征选择,文中提出基于邻域维护准则(称为领域关系维护得分NRPS, neighborhood relationship preserving score)的特征选择算法(NPFS,feature selection algorithm based on neighborhood preservation criterion)。首先,利用基于特征子空间的样本相似度矩阵近似基于标签空间样本相似度矩阵来构造相似性维护表达式;其次,通过线性近似,样本相似度的顺序大致保持不变,则具有相似标签空间邻域关系的样本具有相似的特征子空间邻域关系,得到邻域关系维护公式,并计算得出邻域关系维护得分(NRPS)来评估特征子集的重要性;最后,结合贪婪算法[9],设计具有NRPS的多标签特征选择算法(NPFS)。实验结果表明,对比MMIFS算法和MDMR算法,NPFS算法在多标签分类的性能指标上均有提升。
1 基于邻域维护准则的多标签特征评估准则 1.1 相似性维护准则文献[10]中有许多通过保留样本相似性的特征评估标准,例如拉普拉斯分数、Fisher分数和ReliefF。这些标准可以统一成
| $ SC\left( f \right) = {{\mathit{\boldsymbol{\hat f}}}^{\rm{T}}}\mathit{\boldsymbol{\hat K\hat f}}, $ | (1) |
式中:
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{\hat X}}} = \left\| {\mathit{\boldsymbol{\hat K}} - \mathit{\boldsymbol{K}}} \right\|_F^2,\\ \mathit{\boldsymbol{K'}} = {{\mathit{\boldsymbol{\hat X}}}^{\rm{T}}}\mathit{\boldsymbol{\hat X}}, \end{array} $ | (2) |
式中,
| $ {\left\| \mathit{\boldsymbol{M}} \right\|_F} = \sqrt {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\mathit{\boldsymbol{M}}_{ij}^2} } } 。$ | (3) |
为了量化海量多标签商业数据,用
特征选择是选择一个特征子集近似表示所有特征。I⊆{1, …, d}表示所选特征的索引集合,特征选择后的一个实例x∈ℝd近似表示为xI∈ℝ|I|,其中xI是x的子向量。根据训练集T和索引集I,构造基于特征子空间和基于标签空间的2个样本相似度矩阵。对于{x1I, …,xnI},定义基于特征子空间的样本相似度矩阵为FI=[FijI]n×n,FijI=〈xiI, xjI〉。对于{y1, …, yn},定义基于标签空间的样本相似度矩阵为L=[Lij]n×n,Lij=〈yi, yj〉。如果一对样本包含更多相同的标签,则认为它们更相似,根据文献[10]构建相似性维护公式为
| $ \mathop {\min }\limits_I \left\| {{\mathit{\boldsymbol{F}}^I} - \mathit{\boldsymbol{L}}} \right\|_F^2。$ | (4) |
假设子空间中每对样本的相似度近似等于标签空间中的相似度。然而,它们之间的这两种相似可能有不同的尺度。从另一个角度考虑,考虑每种空间中样本相似性的顺序,在每个样本相似度矩阵中,一对样本的相似度越大,则成对样本越接近。因此,样本相似度的顺序能很好地表达样本之间的邻近关系。利用基于特征子空间的样本相似度矩阵来近似基于标签空间样本相似度矩阵并构建相似性维护表达式。通过线性近似,样本相似性的顺序大致保持不变,则表明在标签空间中具有相似邻域关系的样本在特征子空间也具有相似的邻域关系。根据以上分析,构建邻域关系维护表达式为
| $ \mathop {\min }\limits_{I,a,b} \frac{1}{2}\left\| {a{\mathit{\boldsymbol{F}}^I} + b{\bf{1}} - \mathit{\boldsymbol{L}}} \right\|_F^2, $ | (5) |
式中,a和b是求解的2个变量,1=ℝn×n表示所有元素均为1的矩阵。为了从该公式获得特征评估标准,假设I已知,得:
| $ \begin{array}{*{20}{c}} {\arg \mathop {\min }\limits_{a,b} \frac{1}{2}\left\| {a{\mathit{\boldsymbol{F}}^I} + b{\bf{1}} - \mathit{\boldsymbol{L}}} \right\|_F^2 = \arg \mathop {\min }\limits_{a,b} \frac{1}{2}{\rm{tr}}\left[ {{{\left( {a{\mathit{\boldsymbol{F}}^I} + b{\bf{1}} - \mathit{\boldsymbol{L}}} \right)}^{\rm{T}}}\left( {a{\mathit{\boldsymbol{F}}^I} + b{\bf{1}} - \mathit{\boldsymbol{L}}} \right)} \right] = }\\ {\arg \mathop {\min }\limits_{a,b} \frac{1}{2}{\rm{tr}}\left( {{a^2}{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I} + 2ab{\mathit{\boldsymbol{F}}^I}1 + {b^2}{{\bf{1}}^2} - 2a{\mathit{\boldsymbol{F}}^I}\mathit{\boldsymbol{L}} - 2b{\bf{1}}\mathit{\boldsymbol{L}} + {\mathit{\boldsymbol{L}}^2}} \right)。} \end{array} $ | (6) |
令ℤ=
| $ \frac{{{\text{d}}\mathbb{Z}}}{{{\text{d}}a}} = a{\text{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right) + b{\text{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right) - {\text{tr}}\left( {{\mathit{\boldsymbol{F}}^I}\mathit{\boldsymbol{L}}} \right) = 0, $ | (7) |
| $ \frac{{{\text{d}}\mathbb{Z}}}{{{\text{d}}b}} = a{\text{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right) + b{\text{tr}}\left( {{{\bf{1}}^2}} \right) - {\text{tr}}\left( {\mathit{\boldsymbol{L}}{\bf{1}}} \right) = 0, $ | (8) |
根据式(7)和式(8),推出
| $ \left( {\begin{array}{*{20}{c}} \begin{array}{l} {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right)\\ {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right) \end{array}&\begin{array}{l} {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right)\\ {\rm{tr}}\left( {{{\bf{1}}^2}} \right) \end{array} \end{array}} \right)\left( {\begin{array}{*{20}{c}} a\\ b \end{array}} \right) = \left( \begin{array}{l} {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}\mathit{\boldsymbol{L}}} \right)\\ {\rm{tr}}\left( {\mathit{\boldsymbol{L}}{\bf{1}}} \right) \end{array} \right)。$ | (9) |
求解式(9),引入引理1和推论1。
引理1:柯西不等式[11]:假设α1, …, αn, β1, …, βn∈ℝ,然后,
| $ {\left[ {\sum\limits_{i = 1}^n {{\alpha _i}{\beta _i}} } \right]^2} \le \sum\limits_{i = 1}^n {\alpha _i^2} \sum\limits_{i = 1}^n {\beta _i^2} 。$ | (10) |
当且仅当βi=0或αi=cβi(i=1, …, n; c∈ℝ)时,等号成立。
推论1:如果A和B都是对称矩阵,那么
| $ {\left( {{\rm{tr}}\left( {\mathit{\boldsymbol{AB}}} \right)} \right)^2} \le {\rm{tr}}\left( {{\mathit{\boldsymbol{A}}^2}} \right){\rm{tr}}\left( {{\mathit{\boldsymbol{B}}^2}} \right), $ | (11) |
当且仅当B=0或A=cB(c∈ℝ)时,等号成立。
显然,样本间的相似性在实际应用中并不完全相同。因此,FI≠c1(c∈ℝ),那么
| $ {\left( {{\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right)} \right)^2} < {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right){\rm{tr}}\left( {{{\bf{1}}^2}} \right), $ | (12) |
所以
| $ \left| {\begin{array}{*{20}{c}} \begin{array}{l} {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right)\\ {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right) \end{array}&\begin{array}{l} {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right)\\ {\rm{tr}}\left( {{{\bf{1}}^2}} \right) \end{array} \end{array}} \right| \ne 0。$ | (13) |
根据式(9)和式(13)
| $ a = \frac{{{\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}\mathit{\boldsymbol{L}}} \right){\rm{tr}}\left( {{\bf{11}}} \right) - {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right){\rm{tr}}\left( {\mathit{\boldsymbol{L}}{\bf{1}}} \right)}}{{{\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right){\rm{tr}}\left( {{\bf{11}}} \right) - {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right){\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right)}}, $ | (14) |
| $ b = \frac{{{\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right){\rm{tr}}\left( {\mathit{\boldsymbol{L}}{\bf{1}} - {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right){\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}\mathit{\boldsymbol{L}}} \right)} \right.}}{{{\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\mathit{\boldsymbol{F}}^I}} \right){\rm{tr}}\left( {{\bf{11}}} \right) - {\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right){\rm{tr}}\left( {{\mathit{\boldsymbol{F}}^I}{\bf{1}}} \right)}}, $ | (15) |
然后,得到一个称为邻域关系维护得分(NRPS)的特征评估标准,评估每个特征子集的重要性。对于每个索引集合I,计算索引集I对应的特征子集的NRPS为
| $ {\rm{NRPS}}\left( I \right) = \left\| {a{\mathit{\boldsymbol{F}}^I} + \mathit{\boldsymbol{b}}{\bf{1}} - \mathit{\boldsymbol{L}}} \right\|_F^2, $ | (16) |
该值越小,特征子集越重要。
2 NPFS算法令SC(r)为第r个特征的邻域关系维护得分。对于第r个特征(r=1, …, d,其中d是特征的数量),其分数值SC(r)=NRPS({r})。应用NRPS度量每个特征子集的重要性,使用传统的前向搜索策略来选择特征,设计一个用于特征选择的贪婪算法。首先,将选择的特征索引集合I初始化为∅,特征索引集合D初始化为{1, …, d}。其次,基于以下函数将D的元素逐一放入I中, 有
| $ \arg \mathop {\min }\limits_{r \in D} {\rm{NRPS}}\left( {I \cup \left\{ r \right\}} \right). $ | (17) |
要选择k个特征,NPFS算法需要运行k次迭代,算法的计算复杂度为O(kdn2)。
NPFS算法代码如下:
输入:数据矩阵X∈Rn×d,多标签Y∈Rn×m,K(被选择的特征数目)。
输出:所选特征的索引集合I⊆{1, …, d},且|I|=K。
1:计算基于标签空间的相似度矩阵L,L=YYT;
2:I=∅,D={1, …, d},FI=0;//初始化I, D, FI
3:X=XG-1,其中G=
4:Cn=In-11T/n; //计算中心矩阵
5:X=CnX; //零均值化
6:重复
7:如果r∈D
8:计算Fr,其中Fr=FI+F{r};
9:
10:
11:SC(r)=‖αFr+b1-L‖F2;
12:结束;
13:I←I∪{r*},D←D-{r*},FI←Fr*,其中
14:直到|I|=K;
15:返回特征索引集I。
整个算法的具体过程如下:
Step1:构建样本相似矩阵
| $ {\mathit{\boldsymbol{F}}^I} = {\mathit{\boldsymbol{X}}^I}{\left( {{\mathit{\boldsymbol{X}}^I}} \right)^{\rm{T}}},\mathit{\boldsymbol{L}} = \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}, $ |
Step2:构建邻域维护公式
| $ \arg \mathop {\min }\limits_{I,a,b} \frac{1}{2}\left\| {a{\mathit{\boldsymbol{F}}^I} + \mathit{\boldsymbol{b}}1 - \mathit{\boldsymbol{L}}} \right\|_F^2, $ |
Step3:获取特征评估标准
| $ {\rm{NRPS}}\left( I \right) = \mathop {\min }\limits_{a,b} \frac{1}{2}\left\| {a{\mathit{\boldsymbol{F}}^I} + \mathit{\boldsymbol{b}}1 - \mathit{\boldsymbol{L}}} \right\|_F^2, $ |
Step4:设计特征选择算法。
3 仿真分析 3.1 数据集和评价指标为了验证所提出的算法,文中选取来自Mulan Library[12-13]商业领域的多标签数据集进行实验,给定一个多标签数据集T={(xi, Yi)|1≤i≤p},用dim(T),L(T),|T|分别表示特征数量,总标签数量和实例数量。表 1为仿真数据集详细信息。
| 表 1 仿真数据集 Table 1 The simulation dataset |
多标签学习系统的性能评估不同于单标签系统,多标签学习系统评估指标更复杂。对指标进行预定义,一个测试数据集S={(xi, Yi)|1≤i≤p},给定一个实例xi,由多标签分类器预测的标签集合表示为h(xi),标签y预测的排序表示为ranki(y)。文中选用5个常用多标签学习算法评价指标。
1) 平均准确率(AP, average precision)
| $ {\rm{AP}}\left( S \right) = \frac{1}{p}\sum\limits_{i = 1}^p {\frac{1}{{\left| {{Y_i}} \right|}}} \sum\limits_{y \in {Y_i}} {\frac{{{\rm{pre}}{{\rm{c}}_i}\left( y \right)}}{{{\rm{ran}}{{\rm{k}}_i}\left( y \right)}}} , $ | (18) |
其中
| $ {\rm{Pre}}{{\rm{c}}_i}\left( y \right) = \left| {\left\{ {y'\left| {{\rm{ran}}{{\rm{k}}_i}\left( {y'} \right) \le {\rm{ran}}{{\rm{k}}_i}\left( y \right),y' \in {Y_i}} \right.} \right\}} \right|, $ |
该指标评估平均有多少实际标签比给定测试样本包含的标签高。值越大则算法越优。
2) 覆盖率(CV, coverage)
| $ {\rm{CV}}\left( S \right) = \frac{1}{p}\sum\limits_{i = 1}^p {\arg \max {\rm{ran}}{{\rm{k}}_i}\left( y \right) - 1} , $ | (19) |
该指标评估要囊括测试样本实际包含的标签平均需要的最大排序距离。值越小则算法越优。
3) 汉明损失(HL, Hamming loss)
| $ {\rm{HL}}\left( S \right) = \frac{1}{p}\sum\limits_{i = 1}^p {\frac{1}{m}\left| {h\left( {{x_i}} \right) \otimes {Y_i}} \right|} , $ | (20) |
其中⊗表示2个集合的对称差异,该指标评估有多少实例标签对被错误分类。也就是说,属于该实例的标签不被预测或者不属于该实例的标签被预测。值越小则算法越优。
4) 1-错误率(OE, one-error)
| $ {\rm{OE}}\left( S \right) = \frac{1}{p}\sum\limits_{i = 1}^p {\delta \left( {\arg \min {\rm{ran}}{{\rm{k}}_i}\left( y \right) \notin {Y_i}} \right)} , $ | (21) |
该指标评估排名最高的标签不在相关标签集中的次数。值越小则算法越优。
5) 排名损失(RL, ranking loss)
| $ {\rm{RL}}\left( S \right) = \frac{1}{p}\sum\limits_{i = 1}^p {\frac{1}{{\left| {{Y_i}} \right|\left| {{{\bar Y}_i}} \right|}}} \times \left| {\left\{ {\left( {y,y'} \right) \in {Y_i} \times {{\bar Y}_i}\left| {{\rm{ran}}{{\rm{k}}_i}\left( y \right) > {\rm{ran}}{{\rm{k}}_i}\left( {y'} \right)} \right.} \right\}} \right|, $ | (22) |
式中Yi表示Yi相对于C的互补集合。该指标评估有多少不相关标签排名高于相关标签的标签对。值越小则算法越优。
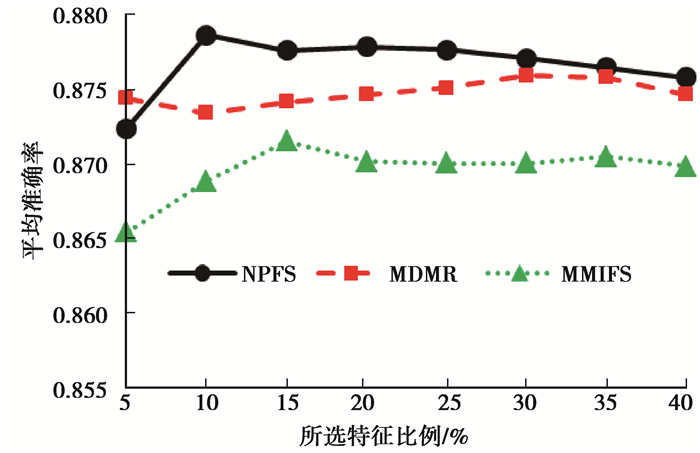
3.2 算法对比仿真分析将所提出的NPFS算法与MMIFS算法和MDMR算法进行实验,并选择分类算法ML-KNN [14]作为评估的分类器,将最近邻K的数量和平滑值S分别被设置为10和1。使用所有特征的5%~40%范围内的选定特征进行实验,间隔为5%。图 1~图 5分别给出3种算法在Business数据集的5项评价指标随着特征数K增加的变化曲线。
|
图 1 不同算法平均准确率对比图 Figure 1 Comparing average precision in different algorithms |
|
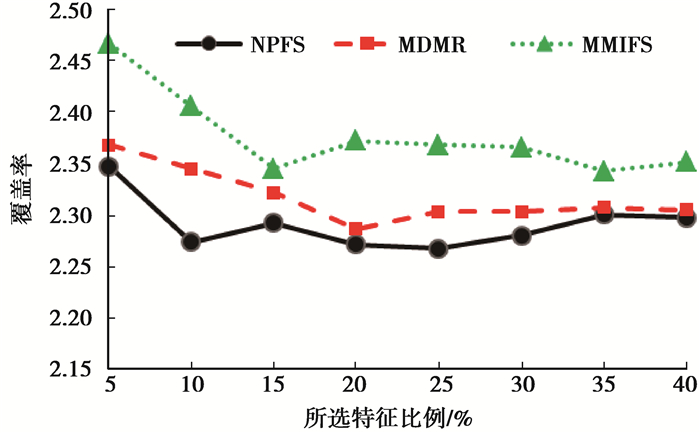
图 2 不同算法覆盖率对比图 Figure 2 Comparing coverage in different algorithms |
|
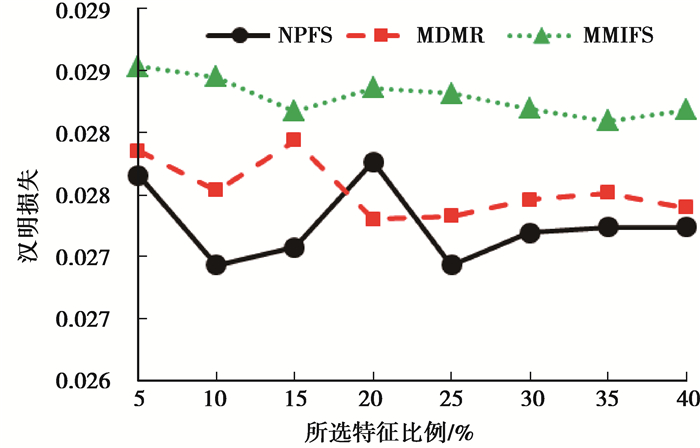
图 3 不同算法汉明损失对比图 Figure 3 Comparing Hamming loss in different algorithms |
|
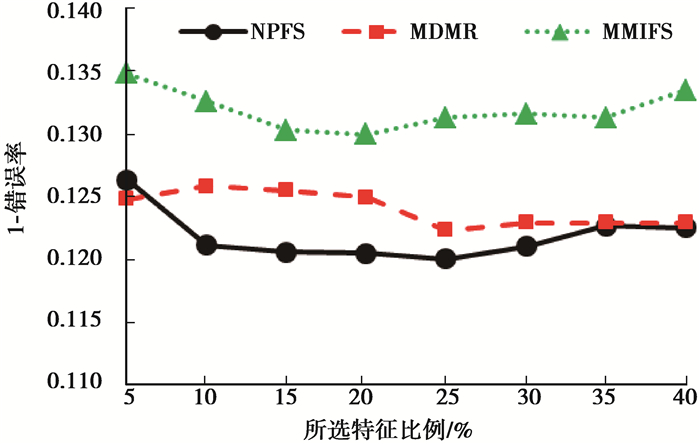
图 4 不同算法1-错误率对比图 Figure 4 Comparing one-error in different algorithms |
|
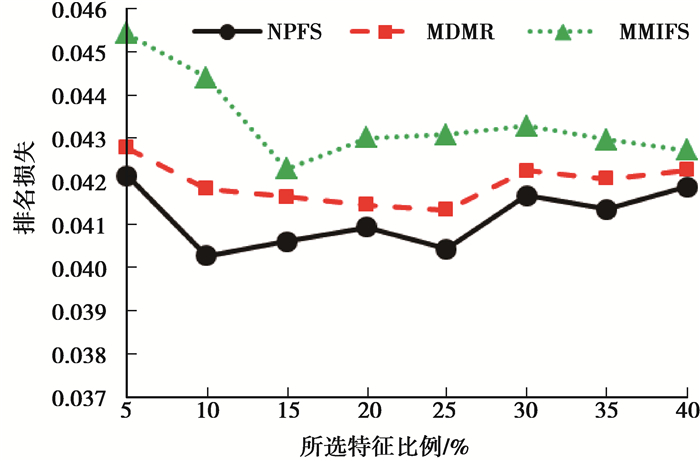
图 5 不同算法排名损失对比图 Figure 5 Comparing ranking loss in different algorithms |
如图 1所示,随着所选特征数目增加,NPFS算法的平均准确率最高,MDMR算法平均准确率次之,MMIFS算法平均准确率最低。
如图 2所示,随着所选特征数目增加,NPFS算法覆盖率最小,MDMR算法覆盖率次之,MMIFS算法覆盖率最高。
如图 3所示,随着所选特征数目增加,NPFS算法的汉明损失最小,MDMR算法平均准确率次之,MMIFS算法汉明损失最大。
如图 4所示,随着所选特征数目增加,NPFS算法的1-错误率最小,MDMR算法1-错误率次之,MMIFS算法1-错误率最大,特征比例增加到30%后,虽然错误率有所增加,但相比于另外2种算法性能也是最好的。
如图 5所示,随着所选特征数目增加,NPFS算法的排名损失最小,MDMR算法排名损失次之,MMIFS算法排名损失最大。
4 结论为了从海量商业多标签数据中有效地选择重要特征来降低数据维度,提出一种基于邻域维护准则的特征选择算法(NPFS)。首先,通过近似基于特征子空间和基于标签空间的2个相似度矩阵来构建相似性维护表达式;其次,通过线性近似扩展相似性维护公式得到邻域关系维护公式,并计算得出邻域关系维护得分(NRPS)来评估特征子集的重要性;最后,结合贪婪方法设计具有NRPS的多标签特征选择算法。实验结果表明,对比MMIFS算法和MDMR算法,在标准商业数据集中,NPFS算法在平均准确率、覆盖率、汉明损失、1-错误率、排名损失5个性能指标上均有提升。文中使用简单的线性关系构造样本相似度矩阵,下一步工作将尝试扩展一般非线性关系构造样本相似度矩阵。
| [1] |
Zhang M L, Wu L. Lift:multi-label learning with label-specific features[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(1): 107-120. DOI:10.1109/TPAMI.2014.2339815 |
| [2] |
Zhang M L, Zhou Z H. A review on multi-label learning algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819-1837. DOI:10.1109/TKDE.2013.39 |
| [3] |
Huang J, Li G R, Huang Q M, et al. Learning label-specific features and class-dependent labels for multi-label classification[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3309-3323. DOI:10.1109/TKDE.2016.2608339 |
| [4] |
Glinka K, Woźniak R, Zakrzewska D. Improving multi-label medical text classification by feature selection[C]//2017 IEEE 26th International Conference on Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), Poznan, 2017: 176-181.
|
| [5] |
He Z F, Yang M, Liu H D. Multi-task joint feature selection for multi-label classification[J]. Chinese Journal of Electronics, 2015, 24(2): 281-287. DOI:10.1049/cje.2015.04.009 |
| [6] |
Xu C, Liu T L, Tao D C, et al. Local rademacher complexity for multi-label learning[J]. IEEE Transactions on Image Processing, 2016, 25(3): 1495-1507. |
| [7] |
Lee J, Kim D W. Feature selection for multi-label classification using multivariate mutual information[J]. Pattern Recognition Letters, 2013, 34(3): 349-357. DOI:10.1016/j.patrec.2012.10.005 |
| [8] |
Lin Y J, Hu Q H, Liu J H, et al. Multi-label feature selection based on max-dependency and min-redundancy[J]. Neuro computing, 2015, 168: 92-103. |
| [9] |
Pathania A, Venkatramani V, Shafique M, et al. Optimal greedy algorithm for many-core scheduling[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2017, 36(6): 1054-1058. DOI:10.1109/TCAD.2016.2618880 |
| [10] |
Zhao Z, Wang L, Liu H, et al. On similarity preserving feature selection[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(3): 619-632. DOI:10.1109/TKDE.2011.222 |
| [11] |
Mutuk H. A physical proof for cauchy's inequality[J]. The American Mathematical Monthly, 2016, 123(8): 843. DOI:10.4169/amer.math.monthly.123.8.843 |
| [12] |
李峰, 苗夺谦, 张志飞, 等. 基于互信息的粒化特征加权多标签学习k近邻算法[J]. 计算机研究与发展, 2017, 54(5): 1024-1035. LI Feng, MIAO Duoqian, ZHANG Zhifei, et al. Mutual information based granular feature weighted k-nearest neighbors algorithm for multi-label learning[J]. Journal of Computer Research and Development, 2017, 54(5): 1024-1035. (in Chinese) |
| [13] |
Xu H T, Xu L Y. Multi-label feature selection algorithm based on label pairwise ranking comparison transformation[C]//2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, 2017: 1210-1217.
|
| [14] |
Zhang M L, Zhou Z H. ML-KNN:a lazy learning approach to multi-label learning[J]. Pattern Recognition, 2007, 40(7): 2038-2048. DOI:10.1016/j.patcog.2006.12.019 |
 2019, Vol. 42
2019, Vol. 42

