无绝缘轨道电路JTC主要由主轨道电路和调谐区2部分构成,作为中国列控系统的重要组成部分对保障行车安全和运输效率具有重要作用。主轨道电路通过在钢轨间隔并联一定容值的补偿电容来抵消钢轨的高感抗,从而使钢轨整体上呈现阻性。调谐区通过调谐单元BA1、BA2以及空心线圈SVA与信号频率的谐振关系实现相邻轨道电路之间的电气隔绝[1]。补偿电容故障(断线或容值严重下降)会缩短JTC信号的有效传输距离,并且降低最小分路电流,导致轨道电路红光带发生;调谐区设备故障(BA1、BA2和SVA断线)则会引起相邻区段信号之间的相互串扰[2-3]。因此,当JTC补偿电容与调谐区设备发生故障时,轻则会影响信号的正常传输,重则造成轨道电路红光带,甚至危及行车安全。目前,对补偿电容及调谐区设备主要通过电务检测车进行定期巡检,但此种方法存在检测成本高,时效性差的问题[4]。现有研究主要集中于对补偿电容故障进行诊断[5-10],诊断精度与效率也较好,但是并没有将调谐区故障考虑在内,导致这些方法的应用具有很大的局限性,从而不能对JTC故障实现全面综合的诊断。因此,完善JTC综合故障诊断方法是一项亟待解决的工作。
定性趋势分析(QTA, qualitative trend analysis)就是用符号语言从定量数据中表示所提取的定性信息,是一种半定量分析技术,在故障诊断中得到了广泛的应用。由于趋势的定性属性会使趋势类型的识别变得复杂困难,将定性趋势分析与模糊理论相结合,通过模糊逻辑技术进行趋势匹配可以有效解决趋势识别困难的问题[11]。鉴于模糊定性趋势分析强大的趋势识别能力以及JTC补偿电容与调谐区设备故障的仿真曲线特点,提出一种基于模糊定性趋势分析的JTC综合故障诊断方法,以实际与仿真的分路电流幅值包络为分析对象,利用模糊定性趋势分析对JTC故障进行诊断。
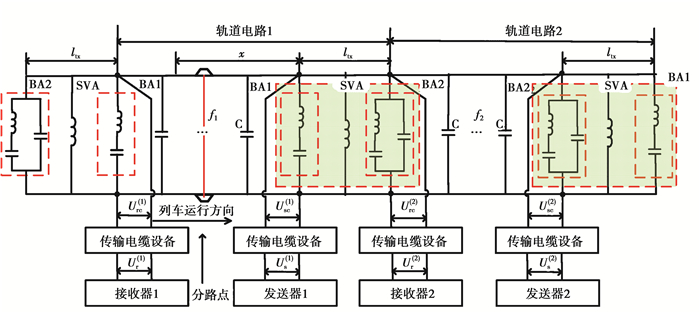
1 补偿电容与调谐区设备故障对分路电流的影响 1.1 包含补偿电容的调谐区建模JTC主要由发送、接收端设备与本区段的钢轨线路等几部分组成。发送端部分主要是指送端处的调谐区设备、送端电缆设备以及发送器;同理接收端部分主要有收端处的调谐区设备、收端电缆设备以及接收器;钢轨线路包括送端至收端之间的钢轨以及等间隔并联于钢轨间的补偿电容[5]。当列车运行于轨道区段1时,其分路情况下的JTC如图 1所示。
|
图 1 JTC分路状态结构示意图 Figure 1 JTC shunt status stnicture diagram |
根据文献[5]可知,分路电流与分路点的关系为
| $ I\left( x \right) = \frac{{{U_S}\left( t \right)}}{{\left| {{G_{11}}\left( x \right){R_f} + {G_{12}}\left( x \right)} \right|}}, $ | (1) |
此时机车信号记录的感应电压幅值包络信号Avg(x)为
| $ {A_{vg}}\left( x \right) = \frac{{\alpha {U_S}\left( t \right)}}{{\left| {{G_{11}}\left( x \right){R_f} + {G_{12}}\left( x \right)} \right|}}, $ | (2) |
| $ \mathit{\boldsymbol{G}}\left( x \right) = \left[ {\begin{array}{*{20}{c}} {{G_{11}}\left( x \right)}&{{G_{12}}\left( x \right)}\\ {{G_{21}}\left( x \right)}&{{G_{22}}\left( x \right)} \end{array}} \right] = {\mathit{\boldsymbol{T}}_p}{\mathit{\boldsymbol{T}}_t}{\mathit{\boldsymbol{T}}_g}\left( x \right), $ | (3) |
式中:α=α1α2,α1可近似为常数,通过接收线圈的安装位置及其特性参数以及JTC信号频率等相关因素决定;α2为常数,由机车信号的内部电路决定。US(t)为发送器1输出的移频信号;Rf为分路电阻;G (x)为分路点至发送器1的四端网传输矩阵;Tp为发送端设备四端网传输矩阵;Tt为发送端调谐区四端网传输矩阵;Tg(x)为列车分路点至发送端调谐区轨面的钢轨线路四端网传输矩阵。
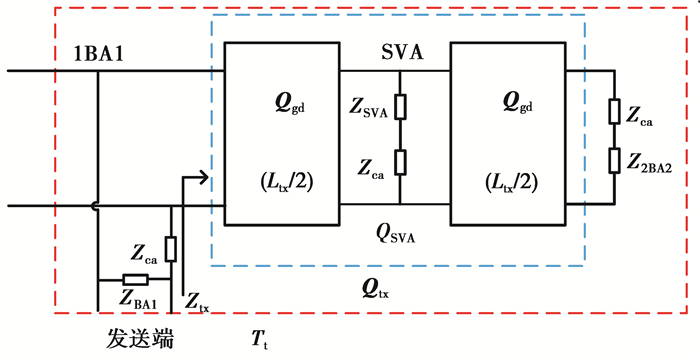
调谐区通过BA1、BA2、SVA对本区段信号呈现串并联的谐振关系有效隔绝了相邻轨道电路之间的信号传输[1]。调谐区等效电路模型如图 2所示
|
图 2 调谐区正常时等效电路模型 Figure 2 The equivalent circuit model when tuning area is normal |
图中:ZBA1,ZBA2和ZSVA分别表示BA1,BA2和SVA在本区段频率信号时所表现的阻抗值;Zca表示各设备与钢轨连接时的阻抗值;Qgd(ltx/2)为调谐区钢轨线路1/2长度的四端网传输矩阵ltx为调谐区钢轨长度[8]。将BA2当作调谐区负载,则虚线框内的四端网传输矩阵Qtx为
| $ {\mathit{\boldsymbol{Q}}_{{\rm{tx}}}} = {\mathit{\boldsymbol{Q}}_{{\rm{gd}}}}{\mathit{\boldsymbol{Q}}_{{\rm{SVA}}}}{\mathit{\boldsymbol{Q}}_{{\rm{gd}}}} $ | (4) |
其中:QSVA为SVA等效阻抗ZSVA及其与钢轨连接阻抗Zca之和的四端网传输矩阵。Ztx表示BA1向BA2的视入阻抗,据此由传输线理论可得
| $ {Z_{{\rm{tx}}}} = \frac{{{\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {1,1} \right)\left( {{Z_{{\rm{BA2}}}} + {Z_{{\rm{ca}}}}} \right) + {\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {1,2} \right)}}{{{\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {2,1} \right)\left( {{Z_{{\rm{BA2}}}} + {Z_{{\rm{ca}}}}} \right) + {\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {2,2} \right)}}。$ | (5) |
则发送端调谐区四端网传输矩阵Tt为
| $ {\mathit{\boldsymbol{T}}_{\rm{t}}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ {1/{Z_{{\rm{BA1}}}}}&1 \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} 1&{{Z_{{\rm{ca}}}}}\\ 0&1 \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} 1&0\\ {1/{Z_{{\rm{tx}}}}}&1 \end{array}} \right]。$ | (6) |
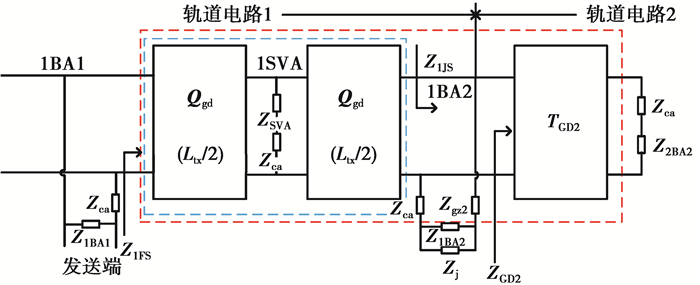
补偿电容与BA1、BA2和SVA通过钢轨引接线与钢轨连接,现场复杂多变的应用环境以及人为破坏等原因会导致补偿电容出现断线或容值下降故障以及调谐区设备断线的故障。当BA2断线时,其等效电路模型如图 3所示
|
图 3 BA2故障时等效电路模型 Figure 3 BA2 fault equiralent circuit model |
式中:ZGD2为从轨道电路1接收端处调谐区向轨道电路2发送端的视入阻抗
| $ {Z_{{\rm{GD2}}}} = \frac{{{\mathit{\boldsymbol{T}}_{{\rm{GD2}}}}\left( {1,1} \right)\left( {{Z_{{\rm{2BA2}}}} + {Z_{{\rm{ca}}}}} \right) + {\mathit{\boldsymbol{T}}_{{\rm{GD2}}}}\left( {1,2} \right)}}{{{\mathit{\boldsymbol{T}}_{{\rm{GD2}}}}\left( {2,1} \right)\left( {{Z_{{\rm{2BA2}}}} + {Z_{{\rm{ca}}}}} \right) + {\mathit{\boldsymbol{T}}_{{\rm{GD2}}}}\left( {2,2} \right)}}, $ | (7) |
Z1JS为BA1向BA2的视入阻抗
| $ {Z_{1{\rm{JS}}}} = \left[ {{Z_{{\rm{ca}}}} + {Z_{{\rm{gz2}}}} + \left( {{Z_{\rm{j}}}//{Z_{{\rm{2BA2}}}}} \right)} \right]//{Z_{{\rm{GD2}}}}, $ | (8) |
Z1FS为从BA2向轨道电路2的视入阻抗
| $ {Z_{1{\rm{FS}}}} = \frac{{{\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {1,1} \right){Z_{{\rm{1JS}}}} + {\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {1,2} \right)}}{{{\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {2,1} \right){Z_{{\rm{1JS}}}} + {\mathit{\boldsymbol{Q}}_{{\rm{tx}}}}\left( {2,2} \right)}}, $ | (9) |
Tt为轨道电路1发送端处调谐区并联阻抗等效四端网络传输矩阵
| $ {\mathit{\boldsymbol{T}}_{\rm{t}}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ {1/{Z_{{\rm{BA1}}}}}&1 \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} 1&{{Z_{{\rm{ca}}}}}\\ 0&1 \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} 1&0\\ {1/{Z_{{\rm{1FS}}}}}&1 \end{array}} \right]。$ | (10) |
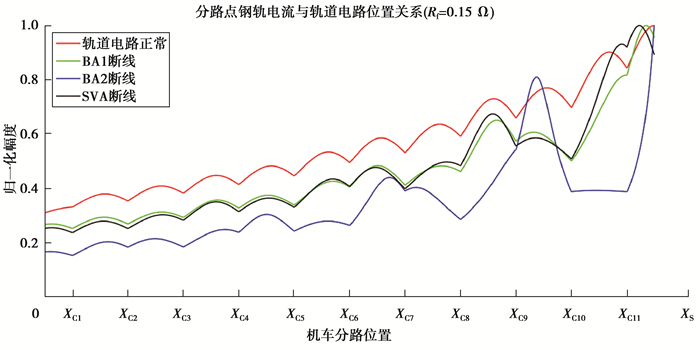
利用式(1)~(10), 根据JTC电气参数[8],选取一段轨道电路并分别对调谐区设备断线故障、补偿电容断线、容值下降至一半以及道砟电阻变化的情况进行仿真,对应的仿真条件设置为:轨道电路1, 2信号载频为f1=2 000 Hz, f2=2 600 Hz; 轨道电路1、2长度为lg1=1 099 m, lg2=1 442 m; 补偿电容个数分别为nc1=11, cv1=40 μF, nc2=18, cv2=50 μF; 分路电阻Rf=0.15 Ω,道砟电阻Rg=1 Ω·km,仿真结果如图 4、5、6和7所示
|
图 4 BA1、BA2和SVA断线时分路电流曲线 Figure 4 Short circuit current when BA1, BA2 and SVA are broken |
|
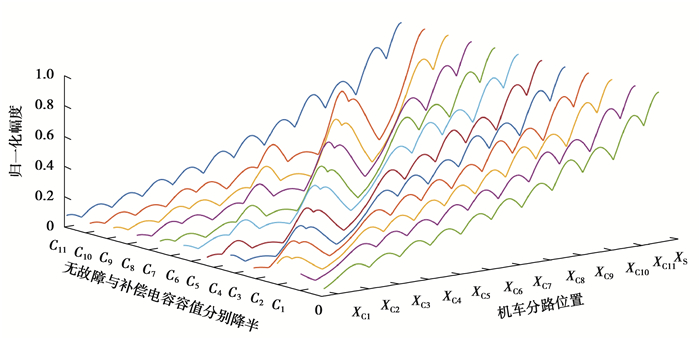
图 5 补偿电容正常与其分别断线时分路电流曲线 Figure 5 Short circuit current when compen sation capacitor is normal and disconnected respe ctively |
|
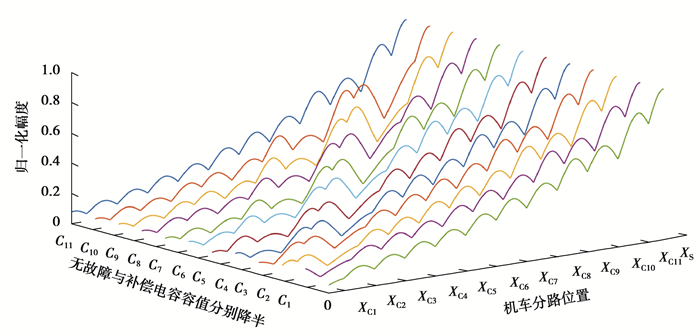
图 6 补偿电容正常与其容值降半时分路电流曲线 Figure 6 Short circuit current when compensation capacitor is normat and disconnected respectively |
|
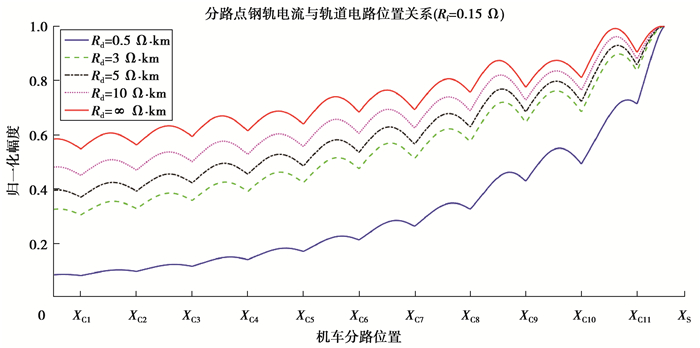
图 7 道砟电阻变化时的分路电流曲线 Figure 7 Short circuit current when ballast resistance changes |
由图 4、5、6和7可知当轨道电路正常时,补偿电容使分路电流从接收端至本区段发送端呈现“波浪式”上升。补偿电容断线及容值下降至一半以及BA1、BA2或SVA断线都会改变分路电流曲线趋势,且各为不同,当补偿电容容值下降和断线时,在分路电流曲线故障点处会有不同程度的衰减。由图 7可知,道砟电阻变化会对分路电流曲线衰减速率造成影响,道砟电阻越大,衰减速率越小,反之越大,但道砟电阻的变化不会改变信号趋势。
2 模糊定性趋势分析定性趋势分析(QTA)基本思想是用一阶和二阶导数表示从定量数据中提取的定性信息,其首要环节就是趋势的提取和识别[12-14]。以补偿电容为界,将原信号划分为若干区间,并对区间进行最小二乘法拟合,通过区间多项式导数符号可以对趋势进行识别。
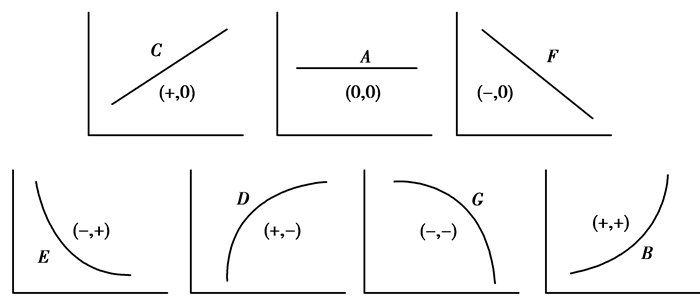
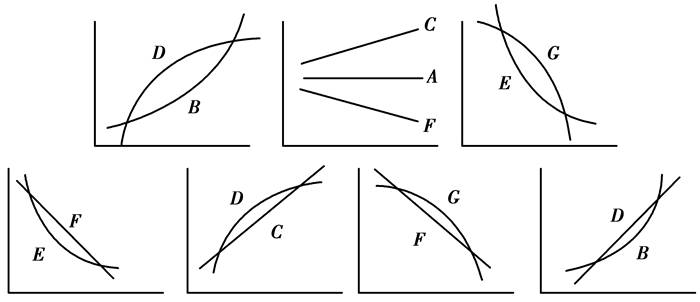
2.1 趋势提取1991年Janus和Venkatasubramanian用一阶和二阶导数符号定义了7种基元,以此提出了定性趋势描述语言[15],如图 8所示:
|
图 8 基元符号 Figure 8 Primitive symbols |
将原信号y(x)以补偿电容所在位置为界划分为若干个单峰区间,用二次多项Qk(x), k∈{1, 2, …, M}对其进行拟合并提取其基元符号,从而实时数据被转换为基元序列
| $ y\left( x \right) \approx \left\{ {{Q_1}\left( x \right),{Q_2}\left( x \right), \cdots ,{Q_M}\left( x \right)} \right\}, $ | (11) |
| $ \left\{ {{Q_1}\left( x \right),{Q_2}\left( x \right), \cdots ,{Q_M}\left( x \right)} \right\} \subseteq \left\{ {{\rm{A}},{\rm{B}},{\rm{C}},{\rm{D}},{\rm{E}},{\rm{F}},{\rm{G}}} \right\}, $ | (12) |
则可将第k个单峰区间表示为
| $ {Q_k}\left( x \right) = \beta _0^k + \beta _1^kx + \beta _2^k{x^2},x \in \left( {{x_{C - 1}},{x_C}} \right), $ | (13) |
原信号拟合完成后,将相应的基元分配给拟合的单峰区间,令Qk(x)的一阶和二阶导数分别如下
| $ {\rm{d}}{s^1} = {\rm{sign}}\left[ {\frac{{{\rm{d}}{Q_k}\left( x \right)}}{{{\rm{d}}x}}} \right] = {\rm{sign}}\left[ {\beta _1^k + 2\beta _2^kx} \right], $ | (14) |
| $ {\rm{d}}{s^2} = {\rm{sign}}\left[ {\frac{{{{\rm{d}}^2}{Q_k}\left( x \right)}}{{{\rm{d}}{x^2}}}} \right] = {\rm{sign}}\left[ {\beta _2^k} \right], $ | (15) |
式中:ds1, 2∈{+, 0, -},Qk(x)的一阶和二阶导数值由于受到噪声等潜在因素的影响通常不会等于零,因此用T-test对其进行显著性检验[9],若检验结果不显著,则设置导数值为零,经过上述步骤,实时数据就被转换为基元序列。
| $ y\left( x \right) \approx \left\{ {{Q_1}\left( x \right),{Q_2}\left( x \right), \cdots ,{Q_M}\left( x \right)} \right\} \subseteq \left\{ {{\rm{A}},{\rm{B}},{\rm{C}},{\rm{D}},{\rm{E}},{\rm{F}}} \right\}。$ |
对于同一故障模式,由于故障程度不同,噪声特性不一等原因,信号数据所表现出的趋势则不尽相同。若为每种潜在的故障构建知识库,则会造成知识库的冗余庞大,因此选取每种故障模式的一条典型故障趋势存储至知识库,提取信号趋势,将其用模糊逻辑技术与知识库中的经典故障趋势进行匹配,以此判断JTC是否故障。基于提出方法的诊断过程包括基元匹配和趋势匹配。
2.2.1 基元匹配从图 9可以看出7种基元之间具有一定的相似性,通过把基元模糊化,可以减少由于噪声等其它干扰因素对基元的误识别。
|
图 9 基元间的模糊化 Figure 9 Fuzification between primitives |
基元匹配度矩阵如表 1所示
| 表 1 基元匹配度矩阵 Table 1 The matching matrix of the primitives |
趋势匹配就是通过对比实际信号与知识库中经典故障模式曲线的趋势,并计算出二者间匹配度的过程。
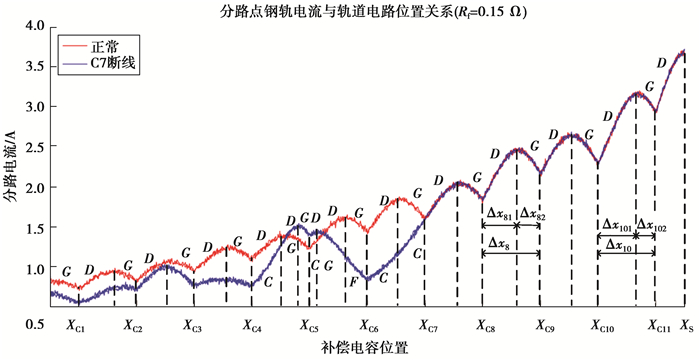
假定知识库中的样本信号与实际信号趋势分别为Qcy和Qcz,则定义其匹配度为
| $ H\left( {{Q_{cy}},{Q_{cz}}} \right) = \frac{1}{{N + 1}}\sum\limits_{C = 0}^N {\sum\limits_{i = 1}^M {{Q_{C_i^yC_i^z}}\frac{{\Delta {x_{Ci}}}}{{\Delta {x_C}}}} } , $ | (16) |
(0≤H(Qcy, Qcz)≤1)以信号极值点所对应的位置将其趋势分割为若干片段,QCiyCiz则为实际信号与样本信号在第C+1与第C个补偿电容区段内的第i段的匹配度,ΔxCi=xCi-xC(i-1)(ΔxCi为第i段的长度),i∈{1, …, M}(M为相邻补偿电容间的划分段数);ΔxC=xC+1-xC(ΔxC为第C至第C+1个补偿电容间的轨道区段长度),C∈{1, …, N}(N为补偿电容个数)。
3 基于模糊定性趋势分析的JTC综合故障诊断 3.1 故障检测规则知识库通过模式识别技术可以实现模糊定性趋势分析的故障诊断方法。首先保存轨道电路无故障以及各种故障情况下的历史数据,并从中提取可以明确区别于其它类型的某种故障类型的趋势特征,同时以基元序列的方式将这种趋势特征保存至故障检测规则知识库;然后,提取实际信号的曲线趋势并与知识库中的经典故障模式进行趋势匹配;最后分析趋势匹配情况,给出故障诊断结果。
| 表 2 规则知识库 Table 2 Rules know ledge base |
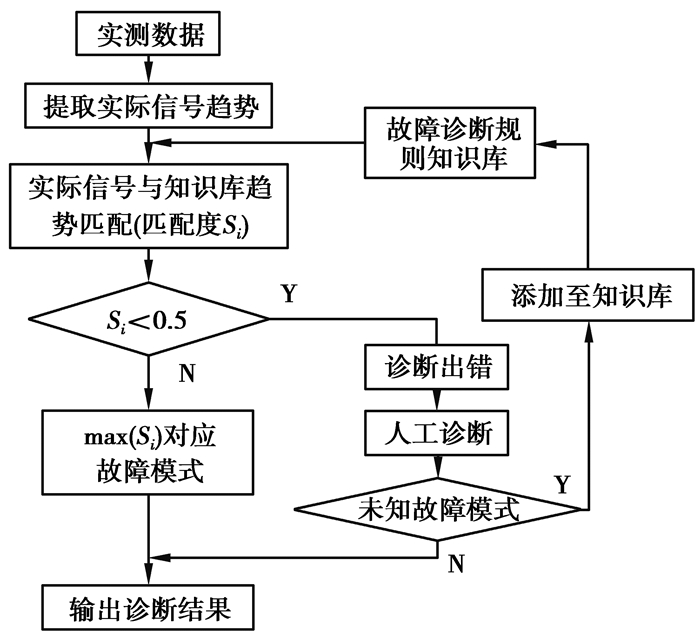
基于模糊定性趋势分析的JTC综合故障诊断流程图如图 11所示。
|
图 11 基于模糊定性趋势分析的JTC综合故障诊断流程图 Figure 11 JTC integrated fault diagnosis flowchart bosed on fuzzy qualitative trend analysis |
算法实现步骤如下
Step1:构建知识库。分别提取JTC调谐区、补偿电容故障以及无故障情况的信号趋势,构建以基元序列方式存在的故障诊断规则知识库。
Step2:提取待检信号序列。以补偿电容所在位置为区间分割点,提取待检测信号的基元序列。
Step3:趋势匹配。依次将提取的基元序列与知识库中的经典故障模式进行匹配,求出其匹配度。
Step4:故障诊断。若知识库中的经典故障模式与待检信号匹配度均小于0.5,则启用人工诊断,若诊断出为知识库中未列入的故障模式则将此种故障模式的基元序列添加至知识库,以便下次遇到同种故障模式时快速诊断。
Step5:当匹配度不完全小于0.5 h,则选取匹配度最大的基元序列所对应的故障模式作为JTC当前状态。
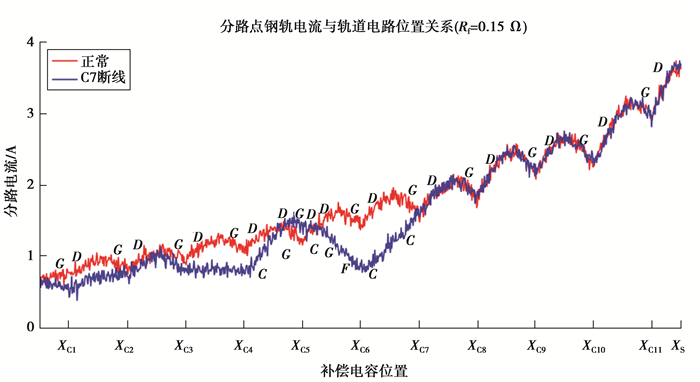
4 结果验证 4.1 实例分析通过定义的区间分割方法分别提取JTC正常状态下和C7断线时的信号趋势,提取结果如图 12所示。相应仿真参数值设置如下:信噪比SNR=60 dB, 道砟电阻Rg=1 Ω·km, T-test显著性水平α=0.05。其余故障模式的提取结果与此类似,共得到26组样本数据,按图 10所示的故障诊断流程图对获得的样本数据进行诊断,诊断结果如表 3所示。表 3中的第一至第三诊断故障分别表示匹配度第一至第三大所对应的故障模式,其中25组样本数据所对应的故障模式由第一诊断故障正确判断得出,诊断正确率达96.2%。对于空心线圈SVA断线的故障模式,其第一诊断故障判断为BA1断线,第二诊断故障为SVA断线,且2者间匹配度差值较小。结合图 4可知BA1和SVA分别断线时的信号趋势序列差异很小,因此出现误诊情况,通过引入的第二诊断故障,人工诊断能够更好的定位故障。对于补偿电容断线及容值严重下降故障,2者匹配度相差较小,结合第一与第二诊断故障可以准确的判断是哪个补偿电容故障以及其故障程度。
|
图 12 JTC正常与C7断线的趋势提取结果 Figure 12 Trend extraction result of normal JTC and CT disconnection |
|
图 10 亲和度匹配图 Figure 10 Affinity match diagram |
| 表 3 第一、二和三诊断故障结果 Table 3 First, second and third diagnosis failure results |
为了验证所提方法在不同信噪比及道砟电阻波动情况下对JTC故障诊断的准确性,根据上述仿真模型,依照轨道电路调整表[16],设置仿真参数T-test假设检验的显著性水平α=0.05,信噪比SNR分别为30,40,50,60 dB,道砟电阻分别为0.5,1,3,5,100,∞ Ω·km,选取每种参数所对应故障模式的6组样本数据,总共获得包含各种故障模式在内的3 744组样本数据,最后得到了不同信噪比及不同道砟电阻情况下的故障诊断正确率如表 4所示。由表 4可知:①信噪比越大,诊断正确率越高,当信噪比增大到50 dB时, 平均故障诊断正确率达到了95.1%;②道砟电阻越大其波动幅度越小,当Rg分别为100 Ω·km和∞ Ω·km时,故障诊断率相差很小。根据表 4实验结果可知,当道砟电阻增大至1 Ω·km及以上时,其对诊断正确率影响很小,因此道砟电阻变化基本不影响信号趋势的识别。
| 表 4 信噪比不同及道砟电阻波动情况下的故障诊断正确率 Table 4 The accuracy of fault diagnosis under different signal to noise ratios and fluctuations in ballast resistance |
研究通过仿真得到JTC补偿电容及调谐区设备故障时的分路电流曲线,根据获得的仿真曲线趋势特点,提出基于模糊定性趋势分析的JTC综合故障诊断方法,实现JTC包括补偿电容及调谐区设备在内的综合故障诊断。实验结果表明,模糊定性趋势分析在信噪比较大的情况下具有较高的诊断正确率,诊断结果基本不受道砟电阻波动的影响,从而很好的实现了JTC的综合故障诊断。模糊定性趋势分析克服了以往方法只能对JTC局部故障进行诊断的弊端,相比于模拟退火算法,模糊定性趋势分析具有更好的灵活性和适用性。同时由于以补偿电容所在位置为区间分割点将信号趋势划分为若干单峰区间的区间分割方法比区间半分法具有更快的收敛速度,因此模糊定性趋势分析能够很好的用于JTC综合故障诊断。
| [1] |
董昱. 区间信号与列车运行控制系统[M]. 北京: 中国铁道出版社, 2008. DONG Yu. Wayside signaling and train operation control system[M]. Beijing: China Railway Publishing House, 2008. (in Chinese) |
| [2] |
赵林海, 任磊. JTC邻区段干扰对TCR的影响研究[J]. 铁道学报, 2013, 35(12): 52-56. ZHAO Linhai, REN Lei. Study on influence of JTC adjacent section interference on TCR[J]. Journal of the China Railway Society, 2013, 35(12): 52-56. (in Chinese) |
| [3] |
Zhao L H, Shi W S. Induction coupling between jointless track circuits and track circuit reader Antenna[J]. Progress in Electromagnetics Research-PIER, 2013, 138: 173-196. DOI:10.2528/PIER13012904 |
| [4] |
孙上鹏, 赵会兵. 基于相空间重构的无绝缘轨道电路补偿电容故障检测方法[J]. 铁道学报, 2012, 34(10): 79-84. SUN Shangpeng, ZHAO Huibing. The method of fault detection of compensation capacitor in jointless track circuit based on phase space reconstruction[J]. Journal of the China Railway Society, 2012, 34(10): 79-84. (in Chinese) DOI:10.3969/j.issn.1001-8360.2012.10.013 |
| [5] |
Oukhellou L, Debiollles A, Denoeux T, et al. Fault diagnosis in railway track circuits using dempstershafer classifier fusion[J]. Engineering Applications of Artificial Intelligence, 2010, 23(1): 117-128. DOI:10.1016/j.engappai.2009.06.005 |
| [6] |
Mariscotti A, Ruscelli M, Vanti M. Modeling of audiofrequency track circuits for validation, tuning, and conducted interference prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1): 52-60. DOI:10.1109/TITS.2009.2029393 |
| [7] |
赵林海, 毕延帅, 刘伟宁. 基于分层免疫机制的无绝缘轨道电路补偿电容故障诊断系统[J]. 铁道学报, 2013, 35(10): 73-81. ZHAO Linhai, BI Yanshuai, LIU Weining. Fault diagnosis system for compensation capacitors of jointless track circuit based on layered immune mechanism[J]. Journal of the China Railway Society, 2013, 35(10): 73-81. (in Chinese) DOI:10.3969/j.issn.1001-8360.2013.10.011 |
| [8] |
张才林.基于神经网络的无绝缘轨道电路调谐区故障诊断方法的研究[D].北京: 北京交通大学, 2013. ZHANG Cailin. A fault diagnosis method for the tuning area of jointless track circuits using neural networks[D]. Beijing: Beijing Jiaotong University, 2013.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10004-1013278284.htm |
| [9] |
Zhao L H, Zhang C L, Qiu K M, et al. A fault diagnosis method for the tuning area of jointless track circuits using neural networks[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2013, 227(4): 333-343. DOI:10.1177/0954409713480453 |
| [10] |
张友鹏, 常高武, 赵斌. 基于SA算法的无绝缘轨道电路故障检方法[J]. 铁道学报, 2017, 39(4): 68-72. ZHANG Youpeng, CHANG Gaowu, ZHAO Bin. A comprehensive fault detection method for jointless track circuit based on SA algorithm[J]. Journal of the China Railway Society, 2017, 39(4): 68-72. (in Chinese) DOI:10.3969/j.issn.1001-8360.2017.04.010 |
| [11] |
Sourabh D, Raghunathan R, Vnkatasubramanian V. Fuzzy-logic based classification for fault diagnosis of chemical processes[J]. Computers and Chemical Engineering, 2003, 27(3): 347-362. DOI:10.1016/S0098-1354(02)00214-4 |
| [12] |
Janusz M E, Venkatasubramanian V. Automatic generation of qualitative descriptions of process trends for fault detection and diagnosis[J]. Engineering Application of Artificial Intelligence, 1991, 4(5): 329-339. DOI:10.1016/0952-1976(91)90001-M |
| [13] |
Dash S, Rengaswamy R, Venkatasubramanian V. Fuzzy-logic based trend classification for fault diagnosis of chemical process trends[J]. Computers & Chemical Engineering, 2003, 27(3): 347-362. |
| [14] |
Dash S, Maurya M R, Venkatasubramanian V, et al. A novel inter-halving framework for automated identification of process trends[J]. AIChE Journal, 2004, 50(1): 149-162. DOI:10.1002/(ISSN)1547-5905 |
| [15] |
张海洋.定性趋势分析在故障诊断中的应用研究[D].北京: 北京化工大学, 2007. ZHANG Haiyang. Applied research of qualitative trend analysis in process fault diagnosis[D]. Beijing: Beijing University of Chemical Technology, 2007.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10010-2007161522.htm |
| [16] |
中华人名共和国铁道部. 铁路信号维护规则技术标准Ⅱ[M]. 北京: 中国铁道出版社, 2008. Ministry of railways of the People's Republic of China. Technical standard for railway signal maintenance rules Ⅱ[M]. Beijing: China Railway Publishing House, 2008. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

