时间序列是按时间顺序排列的一系列观察值,广泛地应用于天文学、生物学、气象学、金融、医药、和工业等众多领域中[1-3]。一维时间序列是某事物发展过程中一种量的描述,从纯数学角度看,是一维的离散函数,也就是说,一维时间序列有着显著的几何形态特性[4-5]。通过其几何形态的相似性,可以判断2个一维时间序列在某些时段量的雷同,进一步可以判断2时间序列描述特征的雷同,从而达到数据挖掘的目的[6]。但是,时间序列除了是时间的离散函数外,一般没有其他限制条件。若直接用线段连接时间序列点,其几何形态就复杂了,这种描述时间序列的方式误差为0,但线段个数最多,不易发现实质性的几何形态变化规律,所以一般不采用。也有用一条线段近似表示时间序列,如最小二乘法,这种方法所用线段最少,因此在一些统计领域中仍被应用[7-8]。但是离散函数较复杂,用一条线段近似时间序列,产生的误差较大,不能反映出时间序列的变化。Keogh[9]提出一种时间序列分段表示理论,用一条折线来逼近时间序列,也就是时间序的分段线性表示。这种方法能够在一定程度上反映时间序列的变化趋势,对时间序列进行有效压缩。把时间序列分段线性表示,关键要找到时间序列的关键点,许多学者对此作了大量的研究[10-12],认为关键点为序列趋势的转折点。但是对趋势是什么有着各自的理解和表达,根据数据点局部变化情况进行判断,达到局部最佳情况。
研究在对多尺度的时间序列固定分段数线性表示[13]及一阶滤波下的线性表示[14]研究的基础上,分析时间序列的几何形态特征,研究时间序列向上、向下趋势的几何形态,提出上、下滤波点及上、下滤波线概念,利用上下滤波点线对趋势的几何特性进行了分析,提出基于全局趋势判断方法,基于趋势的时间序列分段线性表示方法,该方法的复杂度为o(n),便于编程实现。
1 上下滤波点线设p(ti)(i=1, 2, …, n)为时间序列,ti为某时刻,p(ti)=pi(i=1, 2, …, n)为ti时刻某量的值。
定义1.1 对于i=1, 2, …, n中某一个i,若pi≥pi-1(i=2, 3, …, n)或pi≥pi+1(i=1, 2, …, n-1), 则称pi为上滤波点。若pi≤pi-1(i=2, 3, …, n)或pi≤pi+1(i=1, 2, …, n-1),则称pi为下滤波点。
值得注意的是,∀i(i=1, 2, …, n), pi不是上滤波就是下滤波,而且,pi可能是上滤波点同时也是下滤波点。
性质1.1 对于某i=2, …, n-1若pi < pi-1且pi < pi+1,则pi为下滤波点。
性质1.2 对于某i=2, …, n-1, 若pi>pi-1且pi>pi+1,则pi为上滤波点。
由此可见,这种纯粹的上滤波点和下滤波点有着一定的极值性质。
定义1.2 按时间序列顺序把上(下)滤波点连接起来的折线叫上(下)滤波线。
性质1.3 时间序列的上滤波线在下滤波线上方,除了可能有公共部分外,不会出现交叉现象。
一般的时间序列除了这些性质外,没有其他限制,上滤波线与下滤波线之间相互关系比较复杂。对于上升趋势的时间序列段,上滤波线向上发展时,下滤波线也跟着向上发展,2者距离不会超过某范围;同样,下滤波线向下发展时,上滤波线也跟着向下发展,2者距离不会超过某范围,从而形成向上或者向下趋势。
定义1.3 若时间序列在某时间段T内,上滤波线都单调向上,同时在任意时刻t∈T, 上下滤波线保持在一定距离范围内,则在时间段T内,时间序列是向上发展趋势。同样,在某时间段T内,下滤波线都单调下降,同时上下滤波线又保持距离在一定范围内,则是向下发展趋势。
定理1.1 设A为时间序列p(tj)(i=1, 2, …, n)在时间段[tl, ts]中上滤波点的下标集,B为这时间段[tl, ts]中下滤波点的下标集,满足下面2条件:
① 若∀ti, tj∈A, ti < tj则p(ti)≤p(tj);
② 对于ti, ti+1∈A, s∈B.若ti < s < ti+1,则
| $ \left| p({{t}_{i}})+\frac{p({{t}_{i+1}})-p({{t}_{i}})}{{{t}_{i+1}}-{{t}_{i}}}(s-{{t}_{i}})-p\left( s \right) \right|~<\mathit{K }, $ | (1) |
其中,K为某给定阈值,则时间序列p(ti)在此时间段是向上发展趋势。
证明:由条件①知,p(ti) < p(tj)(ti < tj)为上滤波点,上滤波点在此时间段内单调上升。其次,对于ti, ti+1∈A, .ti < s < ti+1(s∈B),在[ti, ti+1]的上滤波线在s点为
| $ p\left( {{t}_{i}} \right)+\frac{p\left( {{t}_{i+1}} \right)-p\left( {{t}_{i}} \right)}{{{t}_{i+1}}-{{t}_{i}}}\left( s-{{t}_{i}} \right), ~ $ |
上下滤波线保持在一定范围内,故时间序列在此时间段有向上发展趋势,证毕。
同样,对于向下发展趋势也有下面结果。
定理1.2 设A为时间序列p(tj)(i=1, 2, …, n)在时间段[tl, ts]中下滤波点的下标集,B为这时间段[tl, ts]中上滤波点的下标集,满足下面2条件
① 若∀ti, tj∈A, ti < tj则p(ti)≥p(tj);
② 对于ti, ti+1∈A, s∈B.若ti < s < ti+1,则
| $ \left| p\left( {{t}_{i}} \right)+\frac{p\left( {{t}_{i+1}} \right)-p\left( {{t}_{i}} \right)}{{{t}_{i+1}}-{{t}_{i}}}\left( s-{{t}_{i}} \right)-p\left( s \right) \right|<\mathit{K}, $ | (2) |
其中,K为某给定阈值,则时间序列p(ti)在此时间段是向下发展趋势。
2 关键点的提取和分段表示PLR_WFTP算法用分段线性近似表示时间序列,要确定分段线性线的关键点,就是分段线性线段的各端点。从上面分析知,时间序列从上升趋势到下降趋势或者从下降趋势到上升趋势是不同的过程,应当用不同的线段刻划,因此,上升趋势线到下降趋势线的转折点应该是分段线性线的关键点。也就是上滤波线转折处是转折点,称为高转折点;下滤波线的转折处为转折点,称为低转折点。
综上分析,提出一种分段线性表示的PLR_WFTP算法:
设p(ti)是时间序列在ti时刻的值(i=1, 2, …, n),
① 提取上、下滤波点
设gao_x[high_k]为上滤波点,di_x[low_k]为下滤波点。High_k、low_k是上下滤波点对应的时间点,初始化为High_k=low_k=0。
for(i=1;i < =n; i++)
{
if((p[i]>p[i-1])||(p[i]>p[i+1]))
{
gao_x[high_k]=x[i];
gao_weizhi[high_k]=i;
high_k++;
}
}
for(i=1;i < =n; i++)
{
if((p[i] < p[i-1])||(p[i] < p[i+1]))
{
di_x[low_k]=x[i];
di_weizhi[low_k]=i;
low_k++;
}
}
② 提取转折点
设gaozhuan_x[number1]是高转折点数组,number1用于高转折点的计数。
number1=0;//注意,是从0开始的。
for(int i=1;i < high_k-1;i++)
{
if((gao_x[i]>=gao_x[i-1]) & & (gao_x[i]>gao_x[i+1]))
{
gaozhuan_x[number1]=(int)gao_x[i];
gaozhuan_weizhi[number1]=gao_weizhi[i];
number1++;
}
}
设dizhuan_x[number2]是低转折点数组, number2用于低转折点的计数。
Number2=0;
for(int i=1;i < low_k-1;i++)
{
if((di_x[i] < =di_x[i-1]) & & (di_x[i] < di_x[i+1]))
{
dizhuan_weizhi[number2]=di_weizhi[i];
dizhuan_x[number2]=(int)di_x[i];
number2++;
}
}
③ 高低转折点合并排序,得到转折点集;
④ 连线转折点。
从上面算法可以看出,在①提取上、下滤波点中只涉及到加减运算,在②提取转折点里也是加减运算,所以这个PLR_WFTP算法的复杂度为O(n),是多项式算法,具有速度快,实现简单等特点。
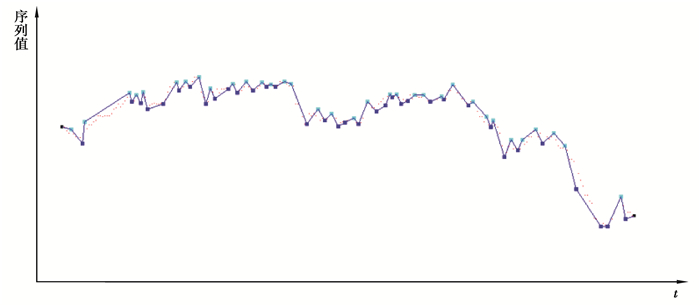
3 实验分析实验在一般的微机上运行,使用的开发工具是VS2010,图 1是对IBM common stock closing prices: daily, 29th June 1959 to 30th June 1960 (N=255)(IBM)数据进行的,其中红点是原始数据,为了讨论一致性,也对数据进行了归一化处理,即对所有数据作变换
|
图 1 PLR_WFTP算法在IBM数据集上的运行结果 Figure 1 Results of the PLR_WFTP algorithm on the IBM data set |
| $ x\left[ i \right]=\frac{x\left[ i \right]-\text{min}}{\text{max}-\text{min}}, $ |
其中,max是时间序列中数据最大者,min是时间序列中数据最小者。于是,所有x[i]都在[0, 1]中。
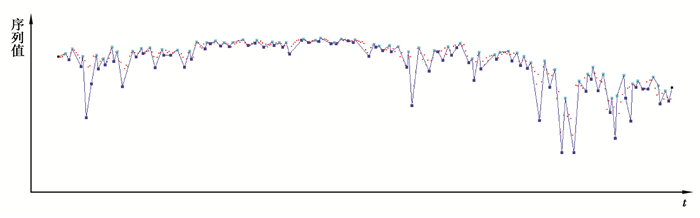
图 2是对Shartes traded in oil and mining stock, TSE数据进行的,也进行了归一化处理,其中红点是原始数据点。得到的线段数是127条。
|
图 2 PLR_WFTP算法在TSE数据集上的运行结果 Figure 2 Results of the PLR_WFTP algorithm on the TSE data set |
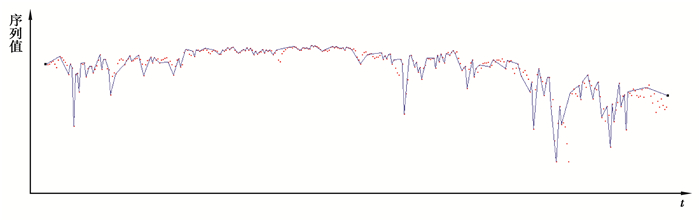
对PLR_TP算法[10]进行编程,如图 3所示。其中数据也是Shartes traded in oil and mining stock, TSE,这里也是归一化处理的,红点是原始数据点。其中,阈值k取为1.5,得到的线段数是171条。
|
图 3 PLR_TP算法在TSE数据集上的运行结果 Figure 3 PLR_TP algorithm running results on the TSE data set |
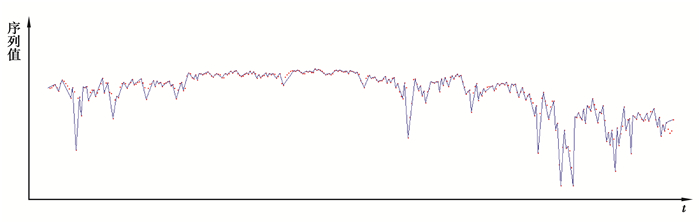
对PLR_ITTP算法[11]进行编程,如图 4所示。其中数据也是Shartes traded in oil and mining stock, TSE,这个算法可以对波动幅度进行描述,这里也是归一化处理的,红点是原始数据点。其中的阈值取为0.05,得到的线段数是206。
|
图 4 PLR_ITTP算法在TSE数据集上的运行结果 Figure 4 Results of the PLR_ITTP algorithm on the TSE data set |
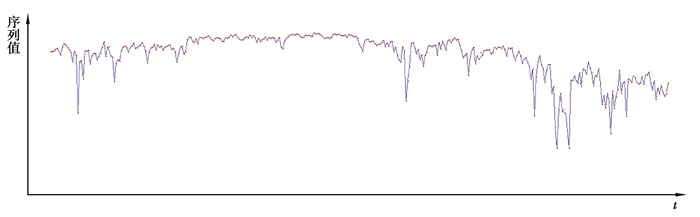
对PLR_SEEP算法[15]进行编程,如图 5所示。其中数据也是Shartes traded in oil and mining stock, TSE,这个算法可以对波动幅度进行描述,这里也是归一化处理的。其中的阈值取为0.001,得到的线段数是347。
|
图 5 PLR_SEEP算法在TSE数据集上的运行结果 Figure 5 Results of the PLR_SEEP algorithm on the TSE data set |
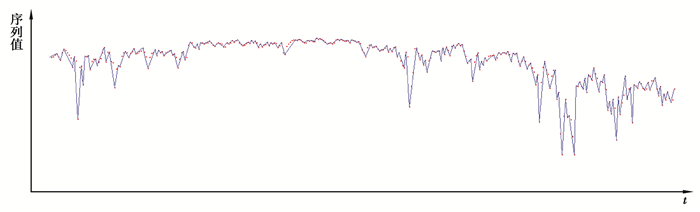
对PLR_TEP算法[16]进行编程,如图 6所示。其中数据也是Shartes traded in oil and mining stock, TSE,这里也是归一化处理的,红点是原始数据点。其中的阈值取为0.000 000 000 1,得到的线段数是208。
|
图 6 PLR_TEP算法在TSE数据集上的运行结果 Figure 6 Results of the PLR_TEP algorithm on the TSE data set |
对比几个实验可以看出,PLR_TP算法、PLR_ITTP算法、PLR_TEP算法、PLR_SEEP算法及PLR_WFTP算法等都较好的用分段线段描述了时间序列,分别用到的线段数是172、206、347及208,而PLR_WFTP用到的是127。
4 结论从实验看,利用上滤波点和下滤波点关系,能够描述时间序列的走向,反映出时间序列的发展趋势,并有较好的逼近性。但是,有些向上(下)发展过程较长,2个转折点之间的数据较多,此时,转折点间的线段最好用最小二乘法求,这样逼近度会更好。其次,有些时间段中数据变化趋势很短,而且,数据变化也不大,此时可以进一步进行优化,以减少线段数量。当然,如何判断出现这情况还需要进一步研究。总之,时间序列数据向上的或向下的趋势是时间序列的形态外貌,通过对两个时间序列的形态外貌进行比较,可以得到时间序列的某些相似性,在数据挖掘中可得到应用。
| [1] |
Bogusz J, Klos A, Bos M S, et al. On the impact of a quadratic acceleration term in the analysis of position time series[C]//EGU General Assembly Conference. US: IEEE, 2016.
|
| [2] |
Mann M E. On smoothing potentially non-stationary climate time series[J]. Geophysical Research Letters, 2013, 31(7): 10-1029. |
| [3] |
Ziegel E R. Analysis of financial time series[J]. Technometrics, 2010, 44(4): 408-408. |
| [4] |
Jaeger H. Observable operator models for discrete stochastic time series[J]. Neural Computation, 2014, 12(6): 1371-1398. |
| [5] |
张晓琴, 陈蜀宇. 新颖的面向网络服务的动态信任模型[J]. 重庆大学学报, 2013, 36(4): 56-63. ZHANG Xiaoqin, Chen S. A novel dynamic trust model for network service[J]. Journal of Chongqing University, 2013, 36(4): 56-63. (in Chinese) |
| [6] |
Tokinaga S, Moriyasu H, Miyazaki A, et al. Forecasting of time series with fractal geometry by using scale transformations and parameter estimations obtained by the wavelet transform[J]. Electronics & Communications in Japan, 2015, 80(8): 20-30. |
| [7] |
Fuentes J, Poncela P, Rodriguez J. Sparse partial least squares in time series for macroeconomic forecasting[J]. Journal of Applied Econometrics, 2015, 30(4): 576-595. DOI:10.1002/jae.v30.4 |
| [8] |
Holst U, Hössjer O, Björklund C, et al. Locally weighted least squares kernel regression and statistical evaluation of lidar measurements[J]. Environmetrics, 2015, 7(4): 401-416. |
| [9] |
KEOGH E. A fast and robust method for pattern matching in time series databases[C]//proceedings of the 9th International conference on Tools with Artificial Intelligence. Newport Beach: IEEE, 1997: 578-584.
|
| [10] |
尚福华, 孙达辰. 基于时间序列趋势转折点的分段线性表示[J]. 计算机应用研究, 2010, 27(6): 2075-2077. SHANG Fuhua, SUN Dachen. PLR based on time series tendency turning point[J]. Application Research of Computers, 2010, 27(6): 2075-2074. (in Chinese) DOI:10.3969/j.issn.1001-3695.2010.06.022 |
| [11] |
周黔, 吴铁军. 基于重要点的时间序列趋势特征提取方法[J]. 浙江大学学报(工学版), 2007, 41(11): 1782-1787. ZHOU Qian, WU Tiejun. Trend feature extraction method based on important points in time series[J]. Journal of Zhejiang University, 2007, 41(11): 1782-1787. (in Chinese) DOI:10.3785/j.issn.1008-973X.2007.11.003 |
| [12] |
Li L, Su X, Zhang Y, et al. Trend modeling for traffic time series analysis:an integrated study[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3430-3439. DOI:10.1109/TITS.2015.2457240 |
| [13] |
林意, 孔斌强. 基于多尺度的时间序列固定分段数线性表示[J]. 计算机工程与应用, 2016, 52(21): 81-87. LIN Yi, KONG Binqiang. Time series piecewise linear representation of fixed section number based on multi scale[J]. Computer Engineering & Applications, 2016, 52(21): 81-87. (in Chinese) DOI:10.3778/j.issn.1002-8331.1501-0327 |
| [14] |
林意, 王智博. 基于一阶滤波的时间序列分段线性表示方法[J]. 计算机工程, 2016, 42(9): 151-157. LIN Yi, WANG Zhibo. Time series piecewise linear representation method based on first-order filtering[J]. Computer Engineering, 2016, 42(9): 151-157. (in Chinese) DOI:10.3969/j.issn.1000-3428.2016.09.027 |
| [15] |
詹艳艳, 徐荣聪, 陈晓云. 基于斜率提取边缘点的时间序列分段线性表示方法[J]. 计算机科学, 2006, 33(11): 139-142. ZHAN Yanyan, XU Rongcong, CHEN Xiaoyun. Time series piecewise linear representation based on slope extract edge point[J]. Computer Science, 2006, 33(11): 139-142. (in Chinese) DOI:10.3969/j.issn.1002-137X.2006.11.038 |
| [16] |
戴爱明, 高学东. 时间序列三角极值点线性分段算法[J]. 南昌航空大学学报(自然科学版), 2009, 23(2): 25-28. DAI Aiming, GAO Xuedong. A linear segmentation algorithm for time series based on triangle extreme points[J]. Journal of Nanchang Hangkong University, 2009, 23. (in Chinese) DOI:10.3969/j.issn.1001-4926.2009.02.006 |
 2019, Vol. 42
2019, Vol. 42

