随着社会的快速发展,国家经济建设和公共事业中出现了大量的大型工程项目。大型工程项目具有工期长、任务多、费用高等特点,单一承包商因受人力、物力、财力等因素限制,无法独立、较好地将其完成,故工程实践中往往需要将大型工程项目的任务指派给多个承包商,以达到缩短工期、降低成本等目的。现有关于工程项目优化的研究聚焦于项目调度[1-4],优化目的聚焦于工期、成本、质量和资源均衡等方面[5-7],而对于项目任务指派的研究极少。在工程项目任务指派问题中,工期最短化是决策者最为关注的优化目标。一个工程项目在将任务指派给多个承包商时存在两类成本,一类是委托方支付给承包商的委托成本,另一类是承包商的执行成本。工程实践中,委托方的资金往往受限,故不能为了缩短工期而只选择任务时间短的承包商,否则,可能导致委托成本超过委托方资金上限;同理,承包商的资金往往受限,故不能无限制地将多个任务指派给同一个承包商,否则会导致任务执行成本超过承包商资金上限。工程实践中,不同承包商由于工作习惯等不同,可能采用不尽相同的工作日历(混合工作日历)。基于此,混合工作日历下资金受限工程项目工期最短化任务指派研究具有重要意义。
混合工作日历下资金受限工程项目工期最短化任务指派本质上属于单目标任务指派问题。单目标任务指派问题的常用求解方法有精确方法和近似方法。精确方法能找到问题的最优解,主要有匈牙利法[8]、削高排除法[9]、缩阵分析法[10]、Munkers法[11]、一次分配算法[12]、目标值子矩阵法[13]、生长树法[14]、分枝定界法[15]、单调迭代算法[16]等,但仅适用于求解小规模指派问题。近似方法基于启发式原理寻找问题的近优解(满意解),主要有遗传算法[17]、蚁群算法[18]、粒子群算法[19]等智能搜索算法,可用于求解较大规模指派问题。
混合工作日历下资金受限工程项目工期最短化任务指派又不同于传统单目标任务指派问题,它比传统单目标任务指派问题更复杂,主要表现在两个方面:1)项目工期的确定过程复杂。在承包商采用混合工作日历的情况下,项目工期的确定需基于“关键路径法”,根据任务时间和承包商各自的工作日历进行准确推算。现有研究对项目工期的确定方法未考虑工作日历[20-22],不能用于确定混合工作日历下的项目工期。2)资金受限约束增加了指派难度。究竟如何指派任务既能保证各承包商执行成本不超过其资金上限、项目委托成本不超过委托方资金上限,又能使项目工期最短,这是一个高度复杂的NP难问题。基于以上原因,解决单目标任务指派问题的精确方法并不适用于求解混合工作日历下资金受限工程项目工期最短化任务指派问题,而近似方法无疑才是求解该问题的有效方法。其中,遗传算法作为一种有效的全局搜索方法,具有鲁棒性、并行性,以及在求最优化问题时可以不必给出目标函数的解析式等优点,可以作为求解混合工作日历下资金受限工程项目工期最短化任务指派的理想方法。
文中针对一类混合工作日历下资金受限工程项目工期最短化任务指派问题,考虑委托方、承包商资金受限约束,提出了一种基于遗传算法(GA, genic algorithm)的优化方法。
1 问题描述某工程项目有n项任务J={J1,J2,…,Jn},要将其指派给m个承包商E={E1,E2,…,Em}执行。假设:①一项任务由一个承包商独立执行,一个承包商在技术可行、资金充足的情况下可执行多项任务。②各项任务由不同承包商执行的时间、委托成本、执行成本事先已被确定,并分别用时间数组、委托成本数组、执行成本数组给出;若某项任务不能由某个承包商执行,则时间数组、委托成本数组、执行成本数组中对应元素被赋为空值。③任务的执行不能违反任务之间的紧前紧后约束关系。④各承包商被指派任务的执行成本总额不能超过其资金上限。⑤项目委托成本总额不能超过委托方资金上限。⑥承包商能做好随时开工的准备,指派给某承包商的任务一旦满足开始执行条件(紧前任务已被完成),则该承包商应能立即开始执行该任务。⑦任务一旦开始执行则不可中断去执行另一项任务。⑧各承包商按自己的工作日历(工作制和工作时段的合称)施工。工作制表征承包商在工程周期内哪些日期是工作日、哪些日期是休息日;工作时段表征工作日各个工作时段的开工、停工起止时间段。⑨当承包商按其工作日历停工时,正在执行的任务停止执行,待承包商重新开工时继续执行此任务后续未完成的工作。⑩项目的开始时刻不能早于委托方指定的项目起始时刻。要求:在以上假设条件下进行合理指派使项目工期最短。显然,该问题是一个复杂的巨组合优化问题,适合采用智能搜索算法求解。
2 遗传算法设计针对研究问题的特点,以Excel VBA为平台设计了遗传算法(GA, genetic algorithm)对其求解。
2.1 类型及变量、数组定义根据算法需要,定义了如图 1所示的自定义类型Chrom及表 1所示的变量及数组。其中,T、EC、IC为n×(m+1)的数组,第1列为任务代码;N为n×4的数组,从左到右依次为任务代码、任务名称、以逗号分隔的紧前任务列表、紧前任务数;E为m×5的数组,从左到右依次为承包商号、名称、资金上限、工作制、工作时段;GZZ为工作制数组,用于存储调度承包商用到的所有工作制,每种工作制占2列,第1列第1行元素为工作制名称、其他行元素为非周末休息日,第2列第1行元素为空、其他各行元素为周末加班日;GZSD为工作时段数组,用于存储调度承包商用到的所有工作时段,每种工作时段占7列,第1列第1行元素为工作时段名称、第2行元素为周一的工作时段个数、其他相邻两行元素对应一个工作时段的开工时刻和停工时刻,第2列第1行元素为空、第2行元素为周二的工作时段个数,其他相邻2行元素对应一个工作时段的开工和停工时刻,依此类推。

|
图 1 自定义类型 Figure 1 Customized types of chromosomes |
| 表 1 变量及数组定义 Table 1 Definition of variables and arrays |
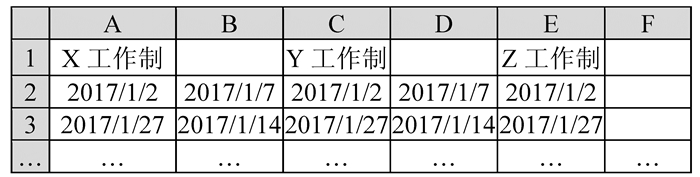
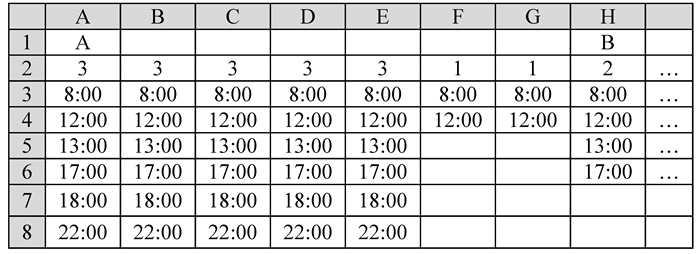
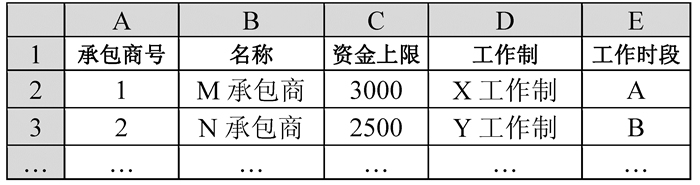
按照假设条件⑧,用Excel设计了“工作制”“工作时段”工作表,表中内容将在算法中分别赋给数组GZZ和GZSD,其结构如图 2和图 3所示。在“承包商”工作表中,将工作制和工作时段名称指定给承包商。如图 4所示,以M承包商为例,当前被指定的工作制为“X工作制”,工作时段名称为“A”。最后,利用VBA编写函数实现基于工作日历的时间推算,分别是Isworkday、Nextworkday、Getsd、Forwardwd、Backwd、Getat1和Getat2。
|
图 2 “工作制”工作表 Figure 2 'Working system' sheet |
|
图 3 “工作时段”工作表 Figure 3 Spreadsheet of work-time periods |
|
图 4 “承包商”工作表 Figure 4 Spreadsheet of contractors |
该函数有2个参数即md(Date型)和wds(String型),其作用是根据承包商工作制wds判断日期md是否为其工作日,若是工作日则返回1,否则返回0。
2.2.2 Nextworkday函数该函数有3个参数即md(Date型)、x(Integer型)和wds(String型),其作用是获得根据承包商工作制wds从日期md推算x天后的工作日,x>0时为正向推算,x < 0时为反向推算。
2.2.3 Getsd函数该函数有3个参数即t(Double型)、cbsh(Integer型)、xqj(Integer型),其作用是根据某承包商cbsh的工作时段名称,获得时间t在该承包商某工作日(一周内第xqj天)的0:00—24:00时间段所处的位置,其返回值为数组A。该数组有2个元素,A(2)是标志元素,其值为0表示时间t属于承包商cbsh某工作日第A(1)个非工作时段,其值为1则表示时间t属于承包商cbsh某工作日第A(1)个工作时段。在图 5中,该承包商某工作日有2个工作时段,8:00—12:00(编号为1)和13:00—17:00(编号为2),把时间0:00—24:00划分成5个时间段,另外3个时间段为非工作时段(编号为0、1、2)。

|
图 5 某承包商某工作日的工作时段与非工作时段 Figure 5 Work-time and non-work-time periods of a contractor's work day |
该函数有3个参数即mdt(Date型)、tt(Double型)和cbsh(Integer型),其作用是根据承包商cbsh的工作日历获得从某个工作时刻mdt正向推算tt小时后的工作时刻。
2.2.5 Backwd函数该函数有3个参数即mdt(Date型)、tt(Double型)和cbsh(Integer型),其作用是根据承包商cbsh的工作日历获得从某个工作时刻mdt反向推算tt小时后的工作时刻。
2.2.6 Getat1函数该函数有2个参数即mdt(Date型)和cbsh(Integer型),其作用是根据承包商cbsh的工作日历获得从某个时刻mdt正向推算得到的最早工作时刻。
2.2.7 Getat2函数该函数有2个参数即mdt(Date型)和cbsh(Integer型),其作用是根据承包商cbsh的工作日历获得从某个时刻mdt反向推算得到的最早工作时刻。
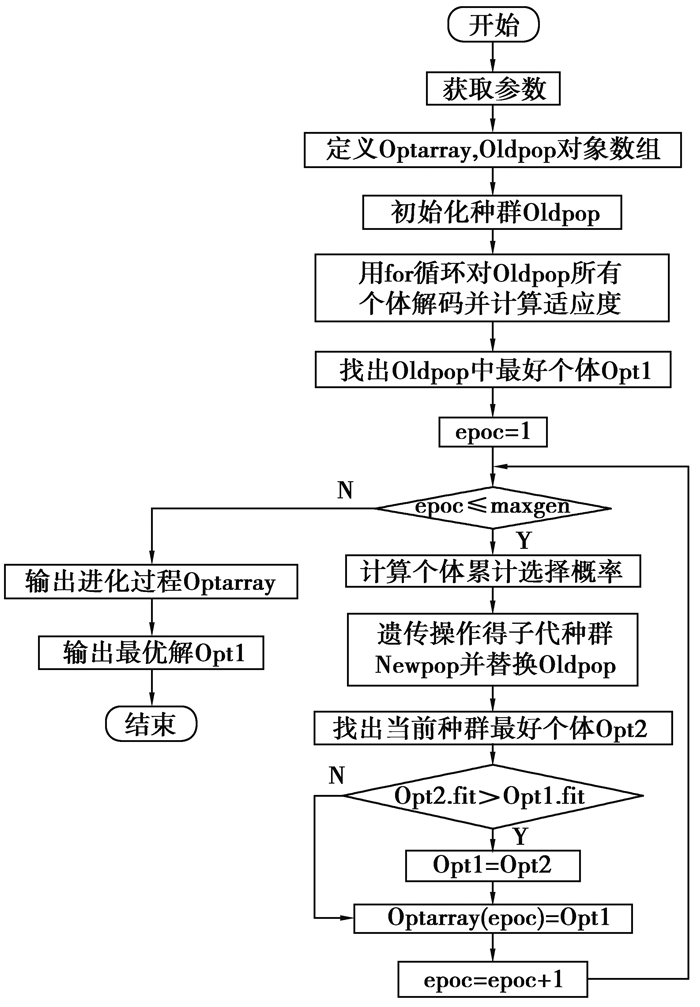
2.3 算法流程文中设计的算法流程如图 6所示。算法中用Opt1存放迭代到每代为止的最优个体,用Optarray对象数组记录迭代过程中每代对应的Opt1。
|
图 6 算法流程 Figure 6 Flow chart of the algorithm |
设计工作表“网络计划表”“承包商”“任务时间”“任务委托成本”“任务执行成本”“其他参数”。算法分别从这些工作表读取相应数据赋给数组N、E、T、EC、IC、GZZ、GZSD和表 1中的其他变量。
2.5 编码方式采用“基于承包商号的整数编码方式”对个体进行编码。式(1)中属性F即为个体Chr(i)的一种编码,表示任务1~n依次被指派给承包商号为3、2、2、1、2、4、5、6…的承包商。
| $ \text{Chr}\left( i \right).F=\left( 3\ 2\ 2\ 1\ 2\ 4\ 5\ 6\ldots \right)。$ | (1) |
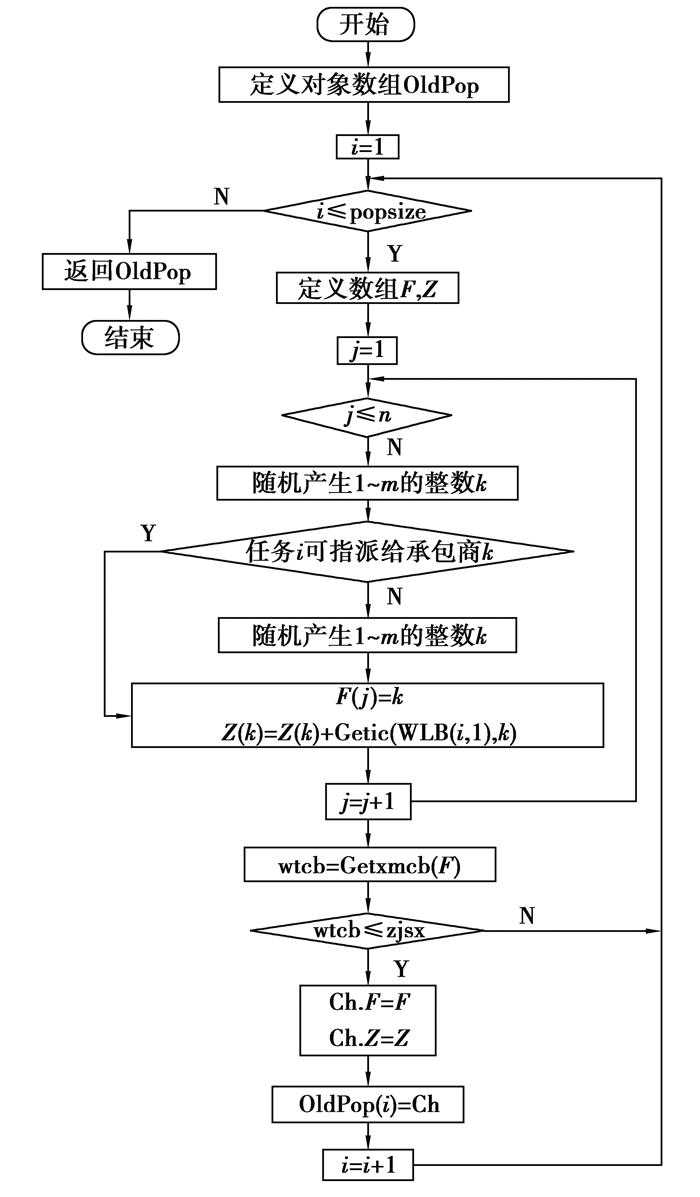
按照图 7所示的流程产生规模为popsize的初始随机种群OldPop。其中,判断任务i是否可指派给承包商k的方法如下:若T(i, k+1)、EC(i, k+1)、IC(i, k+1)为空值,则不可指派,否则,若承包商已被指派任务的执行成本与任务i由承包商k执行的执行成本之和大于承包商k的资金上限,则不可指派,否则可指派。当把任务i指派给承包商k后,需累计承包商k的执行成本。图 7中自定义函数Getic用于获得任务i由承包商k执行的执行成本。当产生了F之后,需根据F利用自定义函数Getwtcb获得项目委托成本总额wtcb,若wtcb≤zjsx,表明项目委托成本总额不超过委托方资金上限,将F、Z赋给Ch.F、Ch.Z并将Ch加入种群Oldpop,否则需重新产生F。从图 7可见,通过While循环保证数组F的每个元素是可行承包商号,从而保证个体Ch是可行的,进而保证初始种群OldPop的所有个体均是可行个体。
|
图 7 种群初始化 Figure 7 Population initialization |
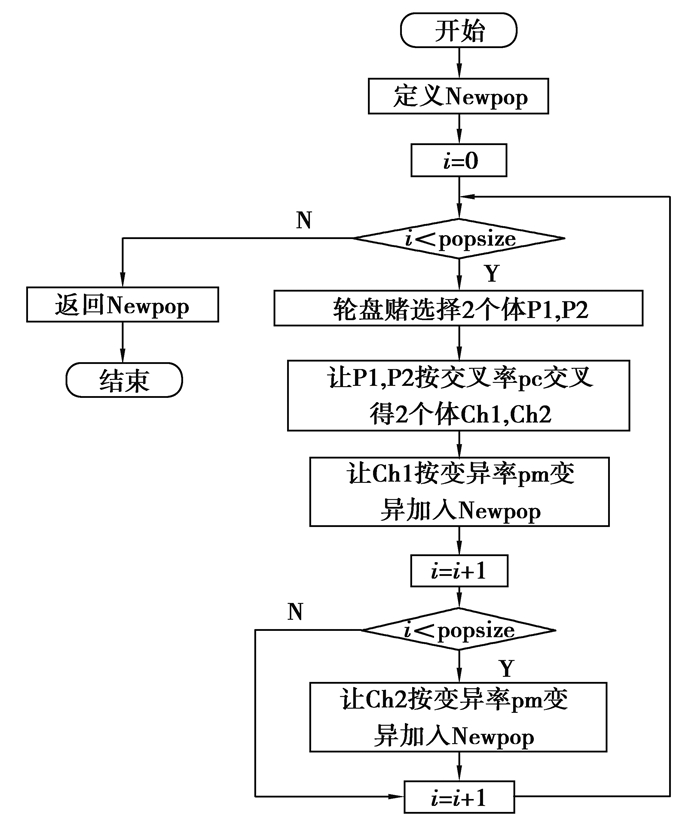
通过选择、交叉、变异操作产生规模为popsize的子代种群Newpop,遗传操作流程如图 8所示。用轮盘赌随机选择2个个体P1、P2,让P1、P2进行交叉操作得到2个个体Ch1、Ch2,先让Ch1变异将得到的子代个体加入Newpop,计数器i增加1,若Newpop中个体数不足popsize,则继续让Ch2变异并将得到的子代个体加入Newpop,计数器i增加1,进入下一循环,直到i=popsize时退出循环,从而得到规模为popsize的子代种群Newpop。
|
图 8 遗传操作 Figure 8 Genetic operation |
针对编码特点,采用“交叉算子改进策略”和“两点交叉方式”进行交叉。虽然交叉前个体可行,考虑到资金受限约束,直接交叉后的个体不一定可行。为保证交叉后的个体仍是可行个体,算法采取的策略是在对换某基因值之前,判断2个父代个体对换基因值之后对应承包商执行成本是否超过其资金上限且2个子代个体的总成本是否超过委托方资金上限,若不超过,则将其对换,否则不对换。具体方法如下:首先,产生2个不相等的1~n的随机整数k1, k2,若k2 < k1则彼此交换使k1 < k2;然后,令k=k1,k1+1, …, k2,依次对基因座k进行如下处理:从父体1的属性F中取出基因值a,从父体2的属性F中取出基因值b,判断a和b是否相等,若相等,不对换基因值,否则,判断父体1中承包商b的执行成本与任务k由承包商b执行的执行成本之和是否超过承包商b的资金上限,且父体2中承包商a的执行成本与任务k由承包商a执行的执行成本之和是否超过承包商a的资金上限,且父体1和2对换基因座k之后各自的委托成本总额是否超过委托方资金上限zjsx,若以上条件都不超过,则对换基因座k的值,更新父体1、2中承包商a、b的执行成本;最后,返回2个子个体Ch1、Ch2。如式(2)所示的2个父代个体P1、P2,若交叉点分别为3、5,若经判断交叉后2新个体中承包商的执行成本均不超过对应的资金上限,则交叉后的2个子代个体如式(3)所示。
| $ \begin{align} &P1.F=\left( 2\ 1\ 2\ 2\ 1\ 3\ 1\ 3 \right), \\ &\text{ }P2.F=\left( 1\ 1\ 3\ 4\ 2\ 4\ 2\ 1 \right), \\ \end{align} $ | (2) |
| $ \begin{align} &\text{Ch1}.F=\left( 2\ 1\ 3\ 4\ 2\ 3\ 1\ 3 \right), \\ &\text{Ch2}.F=\left( 1\ 1\ 2\ 2\ 1\ 4\ 2\ 1 \right) 。\\ \end{align} $ | (3) |
针对编码特点,采用“拒绝策略”和“单点变异方式”进行变异。以Ch1为例,具体变异方法如下:产生1个1~n的随机整数mp作为变异点,再产生1~m且不等于Ch1.F(mp)的随机整数k,判断任务mp是否能指派给承包商k,若任务mp不能指派给承包商k(承包商已被指派任务的执行成本与任务mp由承包商k执行的执行成本之和超过承包商k的资金上限,或变异后的项目委托成本总额超过委托方资金上限zjsx),则重新产生k直到可以指派为止;此时,将Ch1.F(mp)变为k,更新承包商Ch1.F(mp)和k的执行成本,更新项目委托成本。如式(3)所示的父代个体Ch1,若变异点mp=3,若产生的可行承包商号k=5,则变异后的新个体OFF的F属性如式(4)所示。需要说明的是,变异后需要重新解码,然后将其返回。
| $ \text{OFF}.F=(2\ 1\ 5\ 4\ 2\ 3\ 1\ 3)。$ | (4) |
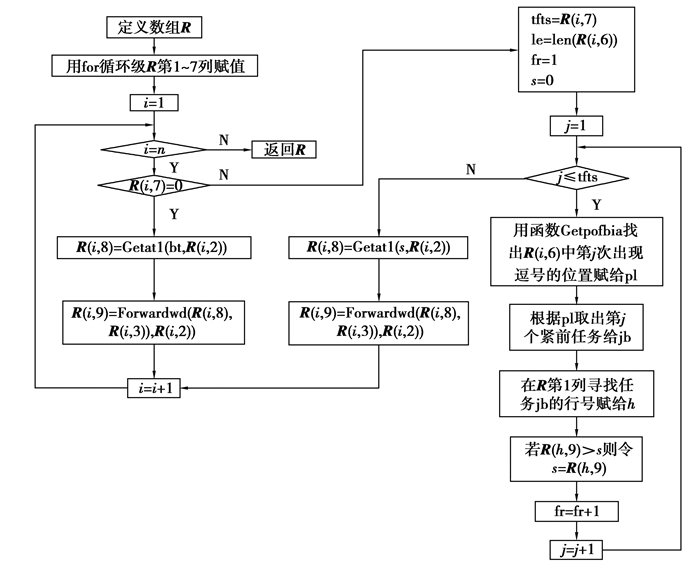
以个体Ch为例说明解码操作过程。基于“关键路径法”,根据指派数组Ch.F采用正向顺推函数FC获得矩阵R (共9列,1~9列依次为任务代码、承包商号、任务时间、任务委托成本、任务执行成本、紧前任务列表、紧前任务数、任务最早开工时刻、任务最早完工时刻);用R第9列的最大值减去第8列的最小值得到项目工期赋给Ch.o。函数FC的流程如图 9所示,其中用到了2.2节设计的时间推算函数进行时间推算。矩阵R第3列的任务时间由自定义函数Getjt获取。该函数有2个参数即jb(String), cbsh(Integer),其作用是在任务时间数组T中查出并返回任务代码为jb的任务由承包商cbsh执行的时间;同理,矩阵R第4列的任务委托成本由自定义函数Getjec获取;矩阵R第5列的任务执行成本由自定义函数Getjic获取。自定义函数Getpofbina有3个参数即a(String), b(String), k(Integer),其作用是返回非空字符串a中第k次出现字符串b的位置,若没有找到,则返回字符串a的长度。
|
图 9 FC函数流程 Figure 9 Flow chart of function FC |
本文优化目标是求工期的最小值,故需采用某种转化方法将其转化为最大化值从而得到适应度。转化的方法通常有2种,一种是取倒数,另一种是用足够大的正数减去目标值。文中采用第二种方法计算适应度,用大数ds减去目标值Ch.o得到适应度,即令Ch.fit=ds-Ch.o。
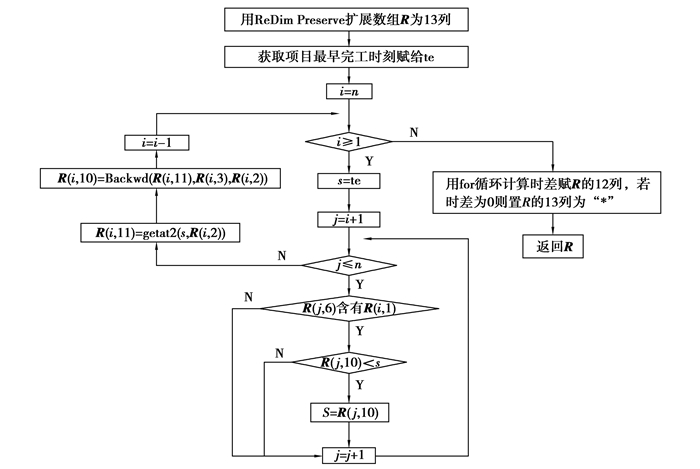
2.10 输出进化过程和最优解将算法得到的进化过程数组Optarray输出到工作表“进化过程”;根据最优解Opt1推算矩阵R并将其输出到工作表“指派表”。其中,推算矩阵R的步骤如下:首先,根据指派数组Opt1.F采用函数FC进行正向推算得到矩阵R的第1~9列;然后,根据R采用函数BC进行逆向推算得到R的10~13列,依次是任务最迟开工时刻、任务最迟完工时刻、时差(单位:h)、关键任务标志(若为关键任务则置符号“*”,否则置空)。函数BC的流程如图 10所示,其中用到了2.2节设计的时间推算函数进行时间推算。
|
图 10 BC函数流程 Figure 10 Flow chart of function BC |
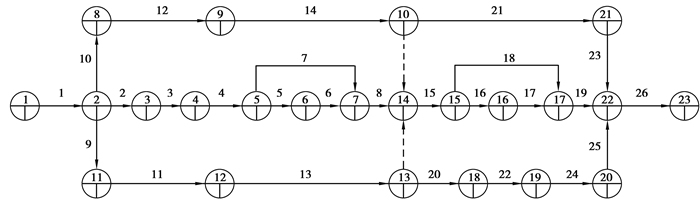
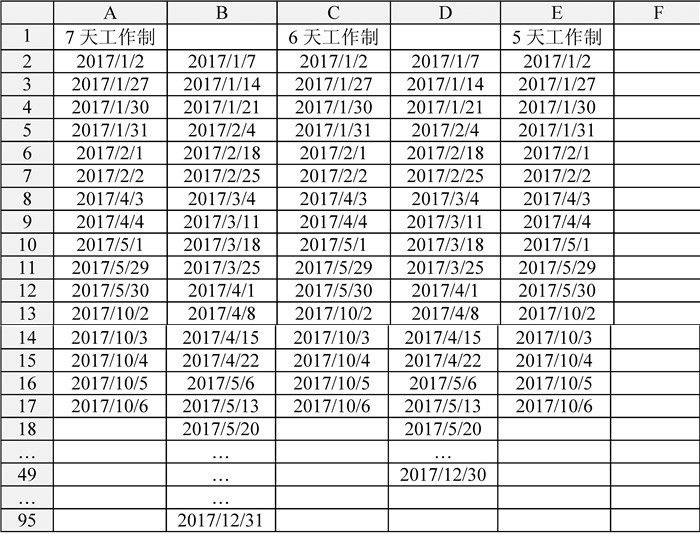
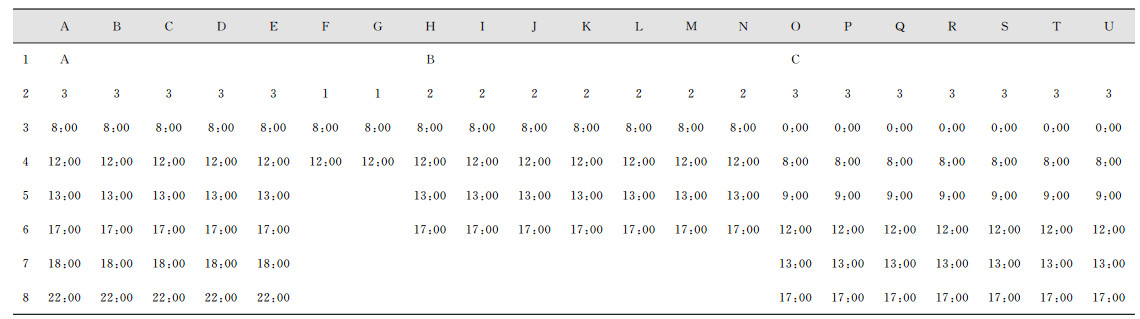
某工程项目网络计划图如图 11所示。该项目共有26项任务,要将其指派给7个承包商,使得项目工期最短。根据图 11转化得到的网络计划表如表 2所示,承包商信息如表 3所示,任务时间如表 4所示,任务委托成本如表 5所示,任务执行成本如表 6所示,其他参数如表 7所示。承包商所用工作制共有3个,即“5天工作制”“6天工作制”和“7天工作制”,“工作制”工作表的设置内容如图 12所示。承包商所用工作时段共有3个,即“A”“B”和“C”,“工作时段”工作表的设置内如图 13所示。
|
图 11 项目网络计划图 Figure 11 Project network plan |
| 表 2 网络计划表 Table 2 Network schedules |
| 表 3 承包商 Table 3 Contractors |
| 表 4 任务时间 Table 4 Task time |
| 表 5 任务委托成本 Table 5 Task commission cost |
| 表 6 任务执行成本 |
| 表 7 计算参数 Table 7 Calculation parameters |
|
图 12 “工作制”工作表设置内容 Figure 12 Spread sheet of working systems |
|
图 13 “工作时段”工作表设置内容 Figure 13 Spreadsheet of work-time periods |
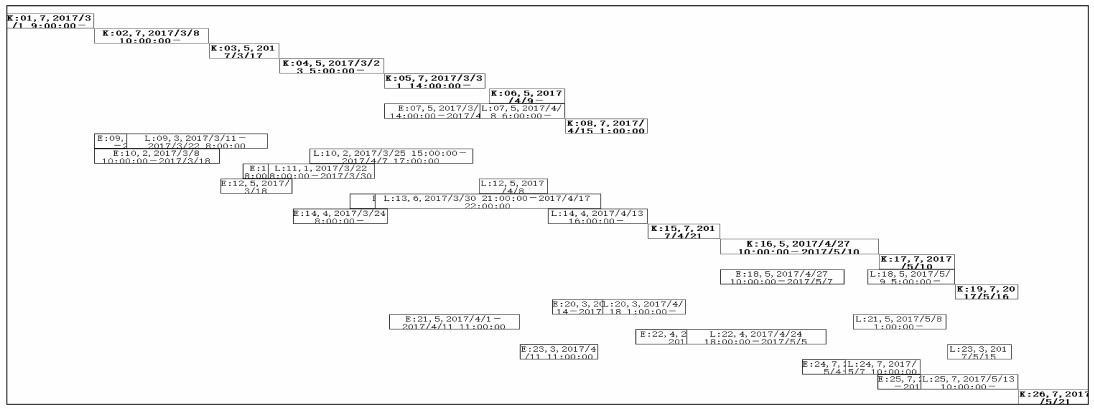
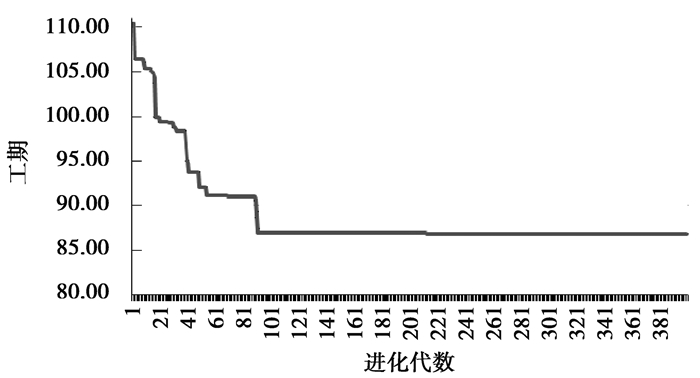
利用算法独立运行20次,均能得到收敛值(最短工期)86.875 d,表明算法收敛效果好。图 15是某次进化过程图,表 8是本次进化得到的最优指派方案对应的指派表,图 14是最优指派方案对应的任务甘特图。
|
图 14 最优指派方案对应的任务甘特图 Figure 14 The Gantt chart of the optimal assignment scheme |
|
图 15 某次进化过程图 Figure 15 Evolutionary process |
| 表 8 最优指派方案对应的指派表 Table 8 The assignment table of the optimal assignment schemes |
图 14中,带E标识符的方框表示任务最早开工时刻与完工时刻之间的时间段,带L标识符的方框表示任务最迟开工时刻与最迟完工时刻之间的时间段,带K标识符的方框表示时差为0的关键任务的开工时刻与完工时刻之间的时间段。左上角第1个方框中“01, 7 2017/3/1 9:00:00—2017/3/8 10:00:00”(方框短未显示完全,从表 8可以看出)表示任务01被指派给承包商号为7的承包商,最早(最迟)开工时刻为2017/3/1 9:00:00,最早(最迟)完工时刻为2017/3/8 10:00:00。由表 3可知承包商7采用“7天工作制”、工作时段采用“C”。由表 4或表 8知,任务01由承包商7执行的时间为106 h,虽然2017/3/1 9:00:00—2017/3/8 10:00:00之间的日历时间为169 h,但由承包商7的工作时历可知,2017/3/1 9:00:00—2017/3/8 10:00:00之间的工作时间正好为106 h。这表明任务01的最早(早迟)开工时刻、最早(最迟)完工时刻是按承包商7的工作日历进行准确推算的。可以检验,其他任务的最早(早迟)开工时刻、最早(最迟)完工时刻也是按相应承包商的工作日历进行准确推算的。从表 8可见,最优指派方案中体现了“能者多劳”的特点,即在任务时间、委托成本、执行成本方面具有优势的承包商可能被指派较多的任务,如承包商7被指派了10项任务,而在任务时间、委托成本、执行成本方面不具优势的承包商可能被指派较少的任务,如承包商1、2、6仅各自被指派了1项任务。
将表 3中承包商的资金上限分别设置为3 000、2 000、4 000、3 000、3 000、4 000、3 000,重新计算得到最短工期为92.96 d,比86.875 d延长了6.085 d。表明在承包商资金上限越小的情况下,指派空间缩小,最优解的质量劣化。
进一步,将委托方资金上限由20 000万元减少为18 500万元,重新计算得到最短工期为95.25 d,比92.96 d又延长了2.29 d。表明委托方资金上限越小的情况下,指派空间进一步缩小,最优解的质量进一步劣化。
4 结论为解决混合工作日历下资金受限工程项目工期最短化任务指派的困难,提出了一种基于遗传算法的优化方法。
1) 提出时间推算方法,能在项目指派过程中准确推算任务的最早(最迟)开工时刻、最早(最迟)完工时刻,从而保证工期按各承包商对应的工作日历进行准确推算,保证了最优指派方案的有效性。
2) 承包商资金上限、委托方资金上限的约束使得解空间缩小,导致最优解的质量劣化。对于大型工程项目,增加委托方资金并选择具有资金实力的承包商进行指派是确保项目工期目标得以改善的有效途径。
利用文中提出的方法可有效解决承包商采用混合工作日历的情况下资金受限工程项目工期最短化任务指派问题。在工程实践中,从优化目标的角度看,决策者除了考虑工期最短化外,还可能考虑成本低、质量高、资源均衡等目标;从约束条件的角度看,除了资金受限外,还可能存在其他资源约束,下一步研究方向为混合工作日历下资源受限工程项目多目标任务指派问题研究。
| [1] |
寿涌毅, 彭晓峰, 李菲, 等. 抢占式资源受限项目调度问题的遗传算法[J]. 浙江大学学报(工学版), 2014, 48(8): 1473-1480. SHOU Yongyi, PENG Xiaofeng, LI Fei, et al. Genetic algorithm for the preemptive resource-constrained project scheduling problem[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(8): 1473-1480. (in Chinese) |
| [2] |
靳金涛, 聂兰顺, 战德臣, 等. 基于人工蜂群的空间资源受限项目调度算法[J]. 计算机集成制造系统, 2014, 20(5): 1088-1098. JIN Jintao, NIE Lanshun, ZHAN Dechen, et al. Spatial-resource constrained project scheduling algorithm based on artificial bee colony[J]. Computer Integrated Manufacturing Systems, 2014, 20(5): 1088-1098. (in Chinese) |
| [3] |
Beşikci U, Bilge Ü, Ulusoy G. Multi-mode resource constrained multi-project scheduling and resource portfolio problem[J]. European Journal of Operational Research, 2015, 240(1): 22-31. DOI:10.1016/j.ejor.2014.06.025 |
| [4] |
Almeida B F, Correia I, Saldanha-Da-gama F. Priority-based heuristics for the multi-skill resource constrained project scheduling problem[J]. Expert Systems with Applications, 2016, 57: 91-103. DOI:10.1016/j.eswa.2016.03.017 |
| [5] |
何立华, 张连营. 基于资源波动成本的工程项目资源均衡优化[J]. 管理工程学报, 2015, 29(2): 167-174. HE Lihua, ZHANG Lianying. Resource leveling optimization based on resource fluctuation cost in construction projects[J]. Journal of Industrial Engineering and Engineering Management, 2015, 29(2): 167-174. (in Chinese) |
| [6] |
张连营, 岳岩. 工期:成本:质量的模糊均衡优化及其Pareto解[J]. 同济大学学报(自然科学版), 2013, 41(2): 303-308, 316. ZHANG Lianying, YUE Yan. Fuzzy trade-off of time-cost-quality in construction project and pareto solution[J]. Journal of Tongji University(Natural Science), 2013, 41(2): 303-308, 316. (in Chinese) DOI:10.3969/j.issn.0253-374x.2013.02.026 |
| [7] |
Chakrabortty R K, Sarker R A, Essam D L. Multi-mode resource constrained project scheduling under resource disruptions[J]. Computers & Chemical Engineering, 2016, 88: 13-29. |
| [8] |
Kuhn H W. The Hungarian method for the assignment problem[J]. Naval Research Logistics Quarterly, 1955, 2(1-2): 83-97. DOI:10.1002/(ISSN)1931-9193 |
| [9] |
周良泽. 削高排除法求解指派问题[J]. 系统工程学报, 1992, 7(2): 97-105. ZHOU Liangze. Solving assignment problem with the method of cutting top and exclusion[J]. Journal of Systems Engineering, 1992, 7(2): 97-105. (in Chinese) |
| [10] |
丁文仁. 缩阵分析法——求解指派问题的新方法[J]. 系统工程理论与实践, 1988, 8(3): 38-86. DING Wenren. New method to solve assignment problem-reduced matrix analyzing method[J]. Systems Engineering theory & Practice, 1988, 8(3): 38-86. |
| [11] |
Zhu H B, Liu D N, Zhang S Q, et al. Solving the Many to Many assignment problem by improving the Kuhn-Munkres algorithm with backtracking[J]. Theoretical Computer Science, 2016, 618: 30-41. DOI:10.1016/j.tcs.2016.01.002 |
| [12] |
周莉, 张维华, 徐射雕. 求解指派问题的一次性分配算法[J]. 计算机工程与应用, 2011, 47(18): 135-138, 152. ZHOU Li, ZHANG Weihua, XU Shediao. One-time assignment algorithm to solve assignment problem[J]. Computer Engineering and Applications, 2011, 47(18): 135-138, 152. (in Chinese) |
| [13] |
赵洪刚, 杨竹君, 孟庆华, 等. 指派问题新解法:目标值子矩阵法[J]. 浙江大学学报(理学版), 2010, 37(5): 501-504. ZHAO Honggang, YANG Zhujun, MENG Qinghua, et al. New method of solving assignment problem-target value submatrix method[J]. Journal of Zhejiang University (Science Edition), 2010, 37(5): 501-504. (in Chinese) DOI:10.3785/j.issn.1008-9497.2010.05.004 |
| [14] |
李珍萍, 王亮. 最短时限缺省指派问题的一种解法[J]. 运筹与管理, 2000, 9(2): 55-61. LI Zhenping, WANG Liang. The absent assignment problem to the shortest time limit and its algorithm[J]. Operations Research and Management Science, 2000, 9(2): 55-61. (in Chinese) |
| [15] |
Mazzola J B, Neebe A W. Resource-constrained assignment scheduling[J]. Operations Research, 1986, 34(4): 560-572. DOI:10.1287/opre.34.4.560 |
| [16] |
郭强. 人数少于任务数的全指派问题的迭代算法[J]. 计算机工程与应用, 2007, 43(24): 91-93, 103. GUO Qiang. Iterative algorithm of total assignment problem on persons less than jobs[J]. Computer Engineering and Applications, 2007, 43(24): 91-93, 103. (in Chinese) DOI:10.3321/j.issn:1002-8331.2007.24.025 |
| [17] |
Choi K, Kim G, Suh Y, et al. Assignment of collaborators to multiple business problems using genetic algorithm[J]. Information Systems and e-Business Management, 2017, 15(4): 877-895. DOI:10.1007/s10257-016-0328-5 |
| [18] |
Myszkowski P B, Skowroński M E, Olech Ł P, et al. Hybrid ant colony optimization in solving multi-skill resource-constrained project scheduling problem[J]. Soft Computing, 2015, 19(12): 3599-3619. DOI:10.1007/s00500-014-1455-x |
| [19] |
Myszkowski P B, Skowroński M E, Olech Ł P, et al. Hybrid ant colony optimization in solving multi-skill resource-constrained project scheduling problem[J]. Soft Computing, 2015, 19(12): 3599-3619. DOI:10.1007/s00500-014-1455-x |
| [20] |
王维博, 冯全源. 基于改进粒子群算法的工程项目综合优化[J]. 西南交通大学学报, 2011, 46(1): 76-83. WANG Weibo, FENG Quanyuan. Synthesis optimization for construction project based on modified particle swarm optimization algorithm[J]. Journal of SouthWest JiaoTong University, 2011, 46(1): 76-83. (in Chinese) DOI:10.3969/j.issn.0258-2724.2011.01.012 |
| [21] |
Gonçalves J F, Mendes J J M, Resende M G C. A genetic algorithm for the resource constrained multi-project scheduling problem[J]. European Journal of Operational Research, 2008, 189(3): 1171-1190. DOI:10.1016/j.ejor.2006.06.074 |
| [22] |
Ma W M, Che Y Y, Huang H, et al. Resource-constrained project scheduling problem with uncertain durations and renewable resources[J]. International Journal of Machine Learning and Cybernetics, 2016, 7(4): 613-621. DOI:10.1007/s13042-015-0444-4 |
 2019, Vol. 42
2019, Vol. 42

