气体绝缘金属封闭输电线路(GIL, gas insulated transmission lines)在长距离和大容量输电系统中具有显著优势,但在实际运行过程中不可避免地产生金属微粒,这种金属微粒能使GIL的绝缘性能降低40%以上[1]。微粒陷阱和电极覆膜是抑制金属微粒污染危害的有效措施,而研究金属微粒在GIL中的运动是优化上述措施的理论基础[2]。在运动过程中,金属微粒会与GIL电极碰撞,因此,微粒与电极的碰撞恢复系数是研究微粒运动规律的关键参数。在较早的研究中,绝大多数学者在模拟计算微粒运动时将碰撞恢复系数简化为常数,这在一定程度上将降低仿真的准确度[2-3]。在近期的研究中,律方成等[4]通过实验手段研究了微粒粒径、碰撞速度和材料特性对碰撞恢复系数的影响,但没有从理论层面对实验结果进行深入解释。
因此,文中基于弹塑性变形理论,推导了法向恢复系数和切向恢复系数与碰撞参数间的计算公式,并搭建了金属微粒与电极碰撞恢复系数测量平台,通过实验验证了理论计算公式的可靠性。
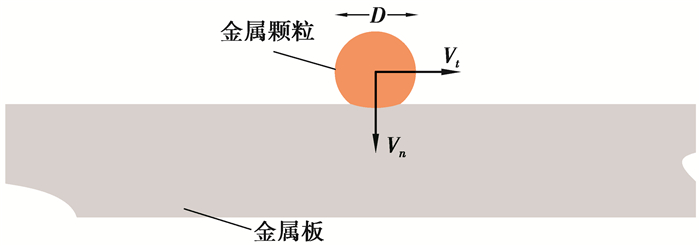
1 碰撞恢复系数计算 1.1 法向恢复系数球形金属微粒(直径为D)以法向分量大小为Vn的速度与金属平板发生斜碰撞,如图 1所示。以弹塑性变形理论为基础,在以下假设条件下对碰撞法向恢复系数进行了推导:
|
图 1 金属颗粒和金属板碰撞示意图 Figure 1 Configuration of collision simulation model |
1) 金属平板与金属微粒均为均匀、各向同性的理想弹塑性体,满足各向同性本构关系;
2) 忽略金属微粒与金属平板表面粗糙度对碰撞的影响。
金属微粒与金属平板间首先发生塑性变形过程,微粒在此过程中受到的阻力Fp[5]可表示为
| $ {F_p} = {P_p}{\rm{ \mathsf{ π} }}Dh, $ | (1) |
式中:Pd为平均接触压力; h为金属平板变形深度,其最大值hmax为
| $ \frac{1}{2}mV_n^2 = \int_0^{{h_{\max }}} {{F_p}dh} = \frac{{{P_d}{\rm{ \mathsf{ π} }}Dh_{\max }^2}}{2}, $ | (2) |
其中,m为金属微粒质量。
当微粒与平板间的塑性变形达到最大值hmax后,微粒开始弹性回弹,根据Herzian接触理论,回弹过程中微粒受到的力FE[6]为
| $ {F_E} = \frac{{16{Y^2}}}{{9{\rm{ \mathsf{ π} }}{P_d}}}{h^2}, $ | (3) |
| $ Y = {\left( {\frac{{1 - {\nu _1}}}{{{E_1}}}} \right)^2} + {\left( {\frac{{1 - {\nu _2}}}{{{E_2}}}} \right)^2}, $ | (4) |
式中:Y为等效弹性模量;E1、E2分别为金属微粒与金属平板的弹性模量;ν1、ν2分别为金属微粒与金属平板的泊松比。当残余法向变形量hr为(hmax-h1)时,法向荷载卸载到0,故式(3)可转换为[7]
| $ {F_E} = \frac{{16{Y^2}}}{{9{\rm{ \mathsf{ π} }}{P_d}}}{\left( {h - {h_{\max }} + {h_1}} \right)^2}, $ | (5) |
式中,h1表示弹性回弹长度。
当h=hmax时,FE|h=hmax=FP| h=hmax,可推知
| $ {h_1} = \frac{{3{\rm{ \mathsf{ π} }}{P_d}}}{{4Y}}\sqrt {D{h_{\max }}} 。$ | (6) |
金属微粒与金属平板碰撞后的法向回弹速度大小Vref[8]为
| $ \frac{1}{2}mV_{{\rm{ref}}}^2 = - \int_{{h_1}}^{{h_{\max }} - {h_1}} {\frac{{16{Y^2}}}{{9{\rm{ \mathsf{ π} }}{P_d}}}{{\left( {h - {h_{\max }} + {h_1}} \right)}^2}{\rm{d}}h} = \frac{{16{Y^2}}}{{27{\rm{ \mathsf{ π} }}{P_d}}}h_1^3。$ | (7) |
因此,由式(1)至式(7)可推知法向恢复系数en为
| $ {e_n} = \frac{{{V_{{\rm{ref}}}}}}{{{V_n}}} = \frac{{{\pi ^{\frac{3}{4}}}{P_d}\frac{1}{4}{m^{\frac{1}{8}}}}}{{\sqrt 2 {Y^{\frac{1}{2}}}{D^{\frac{1}{2}}}V_n^{\frac{1}{4}}}}。$ | (8) |
球形金属微粒(直径为D)以切向分量大小为Vt的速度与金属平板发生斜碰撞,如图 1所示。在切向荷载Q作用下,切向接触变形δ[9]为
| $ \delta = \frac{{3\mu P}}{{16}}\left( {\frac{{2 - \nu }}{G}} \right)\left[ {1 - {{\left( {1 - \frac{Q}{{\mu P}}} \right)}^{\frac{2}{3}}}} \right], $ | (9) |
式中:
由牛顿第二定律可推知切向荷载Q与切向接触变形δ同样满足
| $ \frac{1}{m}Q = \frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{t^2}}}, $ | (10) |
由式(9)和(10)可推知[10]
| $ m\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{t^2}}} = \mu P\left\{ {1 - {{\left[ {1 - \frac{{16}}{{3\mu P}}{{\left( {\frac{{2 - \nu }}{G}} \right)}^{ - 1}}\delta } \right]}^{\frac{3}{2}}}} \right\}。$ | (11) |
式(11)两边关于δ积分,且根据
| $ \frac{1}{2}V_t^2 = \frac{{\mu P}}{m}{\delta _{\max }} + \frac{{3{{\left( {\mu P} \right)}^2}}}{{40m}}\left( {\frac{{2 - \nu }}{G}} \right) \cdot {\left[ {1 - \frac{{16}}{{3\mu P}}{{\left( {\frac{{2 - \nu }}{G}} \right)}^{ - 1}}{\delta _{\max }}} \right]^{\frac{5}{2}}}, $ | (12) |
并根据式(9)计算最大切向荷载Qmax为
| $ {Q_{\max }} = \mu P\left\{ {1 - {{\left[ {1 - \frac{{16}}{{3\mu P}}{{\left( {\frac{{2 - \nu }}{G}} \right)}^{ - 1}}{\delta _{\max }}} \right]}^{\frac{3}{2}}}} \right\}。$ | (13) |
当微粒与平板间的切向变形达到最大后,回弹变形δ1[13-14]为
| $ {\delta _1} = \frac{{3\mu P}}{{16}}\left( {\frac{{2 - \nu }}{G}} \right) \cdot \left[ {2\left( {1 - \frac{{{Q_{\max }} - Q}}{{2\mu P}}} \right) - {{\left( {1 - \frac{Q}{{\mu P}}} \right)}^{\frac{2}{3}}} - 1} \right]。$ | (14) |
切向恢复系数et可根据金属微粒切向可恢复能量Wt1与切向输入能量Wt的比值[15]为
| $ {e_t} = \sqrt {\frac{{{W_{t1}}}}{{{W_t}}}} , $ | (15) |
| $ {W_t} = \int_0^{{\delta _{\max }}} {\mu P\left\{ {1 - {{\left[ {1 - \frac{{16}}{{3\mu P}}{{\left( {\frac{{2 - \nu }}{G}} \right)}^{ - 1}}\delta } \right]}^{\frac{3}{2}}}} \right\}{\rm{d}}\delta } , $ | (16) |
| $ {W_{t1}} = \int_0^{{Q_{\max }}} {\left\{ {{\delta _{\max }} - \frac{{3\mu P}}{{16}}\left( {\frac{{2 - \nu }}{G}} \right) \cdot \left[ {2\left( {1 - \frac{{{Q_{\max }} - Q}}{{2\mu P}}} \right) - {{\left( {1 - \frac{Q}{{\mu P}}} \right)}^{\frac{2}{3}}} - 1} \right]} \right\}{\rm{d}}Q} 。$ | (17) |
法向恢复系数和切向恢复系数计算中的相关参数见表 1[16-18]。
| 表 1 恢复系数计算参数 Table 1 Calculation parameters of recovery coefficients |
由于在GIL中通常会存在不同材质、不同粒径的金属微粒以不同速度撞击电极或壳体的情况,微粒与电极或壳体间的碰撞恢复系数是研究微粒运动规律的关键参数,因此,分别测量了恢复系数的微粒材质效应、微粒直径效应和碰撞速度效应,以验证理论公式用于计算恢复系数的可行性。
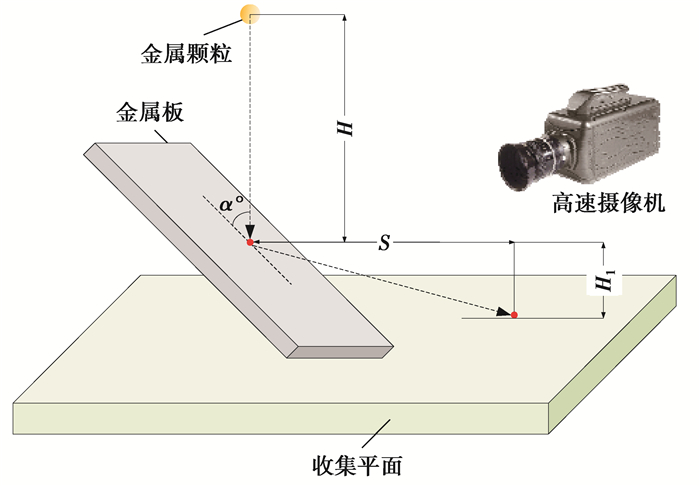
2.1 实验装置文中搭建的金属微粒与金属板碰撞恢复系数测量平台示意图如图 2所示。金属板的材料为铝合金,金属微粒的材料分别为铝合金、铜和钢。金属微粒从一个竖直放置的透明塑料管口自由下落,以斜碰撞角度α与金属板发生碰撞后,被微粒收集平台上涂抹的胶水粘附。用高速摄像机(500 fps)测量微粒与板碰撞到被胶水粘附住的过程所用时间Δt。
|
图 2 金属微粒与金属板碰撞恢复系数测量平台示意图 Figure 2 Platform for measuring impact recovery coefficient between metal particle and metal plate |
通过改变金属微粒种类和直径研究微粒特性对恢复系数的影响,通过改变微粒初始位置与金属板撞击点间的垂直距离H研究碰撞速度对恢复系数的影响。为减小偶然误差对测量结果的影响,每次实验重复20次。设实验中微粒与板斜碰撞后水平位移测量值为S,撞击点与收集平板间的垂直距离为H1则可以通过下列公式计算微粒与板间的碰撞恢复系数。
| $ {e_n} = \frac{{S\cos \alpha - \left( {{H_1} - 0.5g{t^2}} \right)\sin \alpha }}{{\sqrt {2gH} \Delta t\sin \alpha }}, $ | (18) |
| $ {e_t} = \frac{{S\sin \alpha + \left( {{H_1} - 0.5g{t^2}} \right)\cos \alpha }}{{\sqrt {2gH} \Delta t\cos \alpha }}。$ | (19) |
考虑GIL中常见金属微粒种类有铝、铜和铁,文中在研究微粒材质对碰撞恢复系数的影响时,选用上述3种金属微粒进行研究。金属微粒直径取为2 mm,金属板材质为铝合金,金属微粒与金属板碰撞点间的垂直距离恒为0.25 m,a恒为45°。
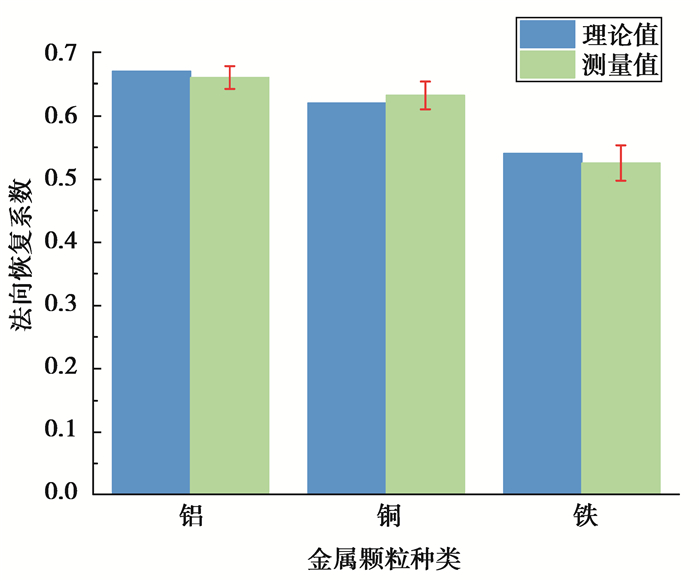
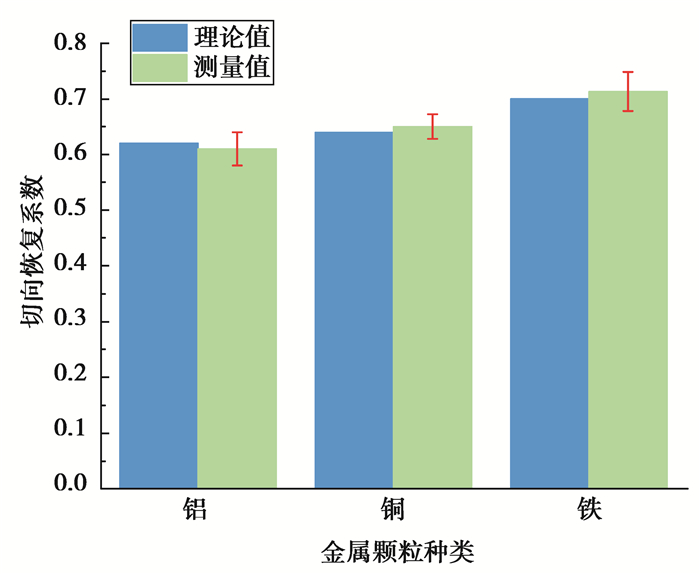
图 3和图 4分别为理论计算和实验测量得到的不同种类金属微粒的法向碰撞恢复系数和切向恢复系数。可以看出,理论计算值和实验测量值基本相符,并且按金属材质铝、铜、钢的顺序,法向碰撞恢复系数逐渐减小,切向碰撞恢复系数逐渐增大。
|
图 3 金属微粒材质对法向恢复系数的影响 Figure 3 Effect of particle properties on normal impact recovery coefficient |
|
图 4 金属微粒材质对切向恢复系数的影响 Figure 4 Effect of particle properties on tangential impact recovery coefficient |
金属微粒与金属平板均属于弹塑性材料,在金属微粒与金属平板碰撞过程结束时,即当法向载荷和切向载荷下降到0时,法向和切向2个方向分别存在残余法向变形量hr和残余切向变形量δr,其值分别为[19-20]
| $ {h_r} = {h_{\max }} - {h_1} = \sqrt {\frac{\rho }{{6{P_d}}}} {V_n}D - \frac{{3{\rm{ \mathsf{ π} }}{P_d}D}}{{4Y}}\sqrt {\sqrt {\frac{\rho }{{6{P_d}}}} {V_n}} , $ | (20) |
| $ {\delta _r} = \frac{{3\mu P\left( {2 - \nu } \right)}}{{16G}}\left\{ {1 - {{\left[ {1 - \frac{{16}}{{3\mu P}}\left( {\frac{{2 - \nu }}{G}} \right){\delta _{\max }}} \right]}^{\frac{3}{2}}}} \right\}。$ | (21) |
由式(20)可以看出,残余法向变形量hr与等效弹性模量Y正相关,其原因在于等效弹性模量表征材料抵抗弹性变形的能力,即弹性形变会随等效弹性模量的增大而减小,等效弹性模量增加,材料弹性回弹长度减小,从而导致残余法向变形量增加。由于等效剪切模量G表征材料抵抗切应变的能力,故最大切向接触变形δmax与等效剪切模量G负相关。由式(21)可以推知,残余切向变形量δr与等效剪切模量G负相关。上述2种等效模量均按金属微粒材质铝、铜、钢的顺序逐渐增大。并且,残余变形量与碰撞过程能耗呈正相关,碰撞过程耗能越大,相应的恢复系数越小[21]。因此,按金属材质铝、铜、钢的顺序,残余法向变形量逐渐增大导致法向碰撞恢复系数逐渐减小;残余切向变形量逐渐减小导致切向碰撞恢复系数逐渐增大。
3.2 碰撞恢复系数的微粒直径效应在实际生产或运行过程中GIL会产生粒径不同的金属微粒,文中选用直径分别为1、2、3 mm的铜微粒研究碰撞恢复系数的微粒直径效应,金属板材质为铝合金,且金属微粒与金属板碰撞点间的垂直距离恒为0.25 m,α恒为45°。
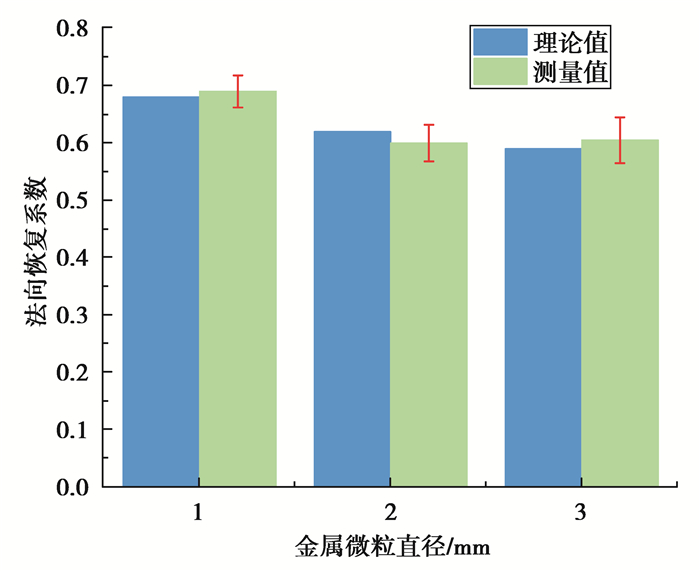
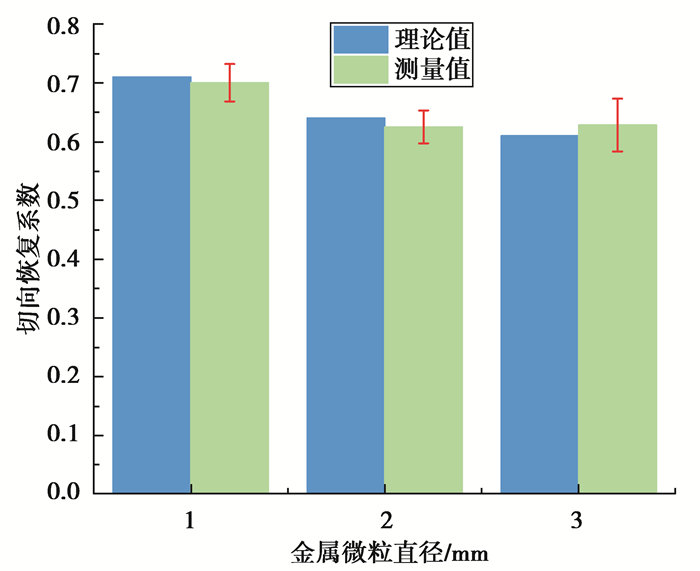
图 5和图 6分别为理论计算和实验测量得到的不同种类金属微粒的法向碰撞恢复系数和切向恢复系数。可以看出,理论计算值和实验测量值基本相符,并且法向碰撞恢复系数和切向碰撞恢复系数均随微粒直径的增加而减小。
|
图 5 金属微粒直径对法向恢复系数的影响 Figure 5 Effect of particle diameter on normal impact recovery coefficient |
|
图 6 金属微粒直径对切向恢复系数的影响 Figure 6 Effect of particle diameter on tangential impact recovery coefficient |
金属微粒与金属平板均属于弹塑性材料,当碰撞回弹结束时在法向和切向均存在残余变形量。由式(20)和式(21)可推知,法向残余变形量与微粒直径呈正相关;由于最大切向接触变形δmax与微粒直径呈正相关,导致切向残余变形量与微粒直径呈正相关,即微粒直径越大,碰撞过程中微粒在法向和切向的能量损耗越大,其原因在于微粒直径越大,其质量越大,则碰撞时产生的惯性力越大,引起的塑性变形增加,可恢复能量减小,残余变形量的增加导致能量损耗越大[22]。因此,法向碰撞恢复系数和切向碰撞恢复系数均与微粒直径呈负相关。
3.3 碰撞恢复系数的碰撞速度效应对于不同运行电压等级的GIL,金属微粒可能会以不同的速度与电极发生碰撞。文中设定铜微粒(直径2 mm)与铝合金板碰撞点间的垂直距离分别为0.10、0.15、0.25、0.50 m,α分别为30°、45°和60°,以此研究碰撞恢复系数的碰撞速度效应。
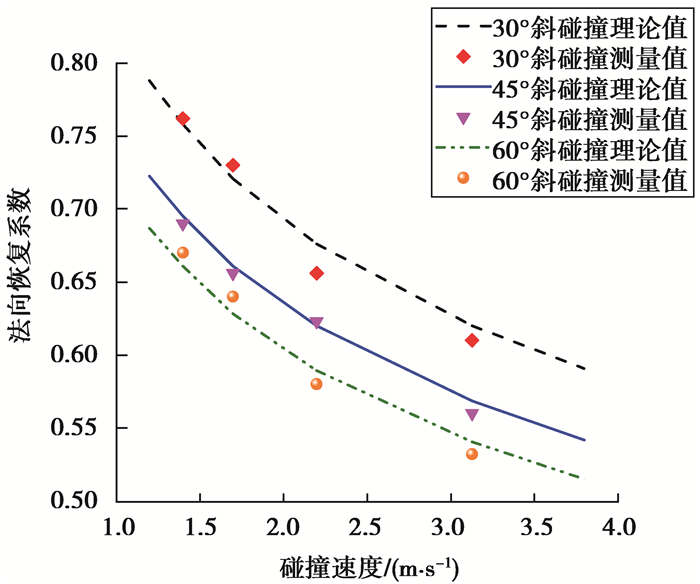
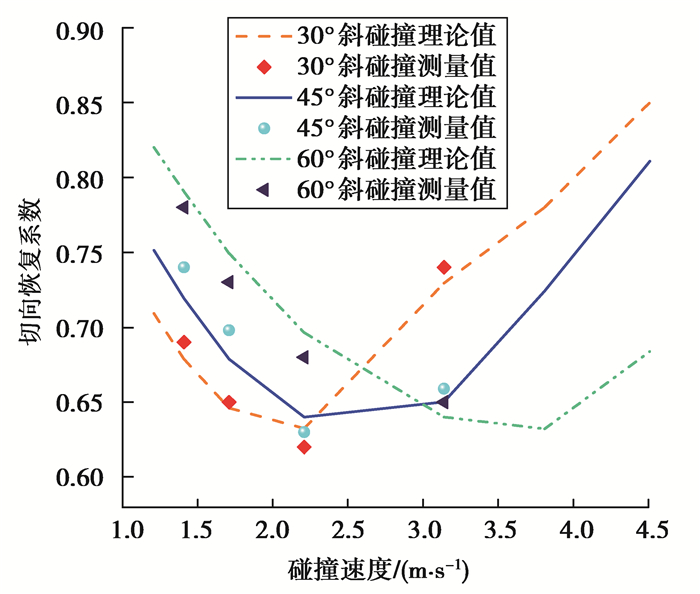
图 7和图 8分别为理论计算和实验测量得到的不同碰撞速度下的法向碰撞恢复系数和切向恢复系数。可以看出,理论计算值和实验测量值基本相符:在同一斜碰撞角度α下,法向碰撞恢复系数随碰撞速度的增加呈负幂指数规律减小,切向碰撞恢复系数随碰撞速度的增加先减小后增加,并且不同斜碰撞角度α下的法向碰撞恢复系数或切向碰撞恢复系数变化规律类似。
|
图 7 碰撞速度对法向恢复系数的影响 Figure 7 Effect of impact velocity on normal impact recovery coefficient |
|
图 8 碰撞速度对切向恢复系数的影响 Figure 8 Effect of impact velocity on tangential impact recovery coefficient |
对于微粒与金属板间的法向碰撞过程,由式(20)可推知,同一斜碰撞角度α下,法向残余变形量正相关于碰撞速度,其原因在于碰撞速度越大,碰撞冲击能量越大,引起的材料塑性变形增加,可恢复能量减小,导致法向残余变形量增加。由于碰撞过程的能量耗散与残余变形量呈正相关,因此,法向碰撞恢复系数随碰撞速度的增加而减小。
对于微粒与金属板间的切向碰撞过程,由式(12)可知,同一斜碰撞角度α下,最大切向接触变形δmax随碰撞速度的增加先增加后减小,其原因在于碰撞速度较小时,碰撞瞬间为静摩擦,碰撞速度增加,最大切向接触变形δmax增加;碰撞速度较大时,碰撞瞬间为动摩擦,碰撞速度增加,可能由于接触时间缩短等原因导致最大切向接触变形δmax减小[15-16]。结合式(21)可得δr和碰撞能耗随碰撞速度的增加先增加后减小,因此,切向碰撞恢复系数随碰撞速度的增加先减小后增加。
4 结论1) 基于弹塑性变形理论,给出了法向恢复系数和切向恢复系数计算公式,并通过碰撞恢复系数测量平台验证了理论计算公式的可靠性。
2) 按金属材质铝、铜、钢的顺序,法向碰撞恢复系数逐渐减小,切向碰撞恢复系数逐渐增大。
3) 法向碰撞恢复系数和切向碰撞恢复系数均与微粒直径呈负相关。
4) 同一斜碰撞角度下,法向碰撞恢复系数随碰撞速度的增加而减小,切向碰撞恢复系数随碰撞速度的增加先减小后增加;并且不同斜碰撞角度下的法向碰撞恢复系数或切向碰撞恢复系数变化规律类似。
5) 文中关于金属微粒与金属平板碰撞恢复系数的计算方法可为微粒陷阱等工程设计提供理论支撑。
| [1] |
李庆民, 王健, 李伯涛, 等. GIS/GIL中金属微粒污染问题研究进展[J]. 高电压技术, 2016, 42(3): 849-860. LI Qingmin, WANG Jian, LI Botao, et al. Review on metal particle contamination in GIS/GIL[J]. High Voltage Engineering, 2016, 42(3): 849-860. (in Chinese) |
| [2] |
Wang J, Li Q M, Li B T, et al. Theoretical and experimental studies of air gap breakdown triggered by free spherical conducting particles in DC uniform field[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(4): 1951-1958. DOI:10.1109/TDEI.2016.7556466 |
| [3] |
Hama H, Okabe S. Factors dominating dielectric performance of real-size gas insulated system and their measures by dielectric coatings in SF6 and potential gases[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(5): 1737-1748. DOI:10.1109/TDEI.2013.6633704 |
| [4] |
律方成, 齐玉娟, 汪佛池, 等. GIS中导电颗粒与电极碰撞系数的测量与分析[J]. 高压电器, 2017, 53(5): 7-13. LYU Fangcheng, QI Yujuan, WANG Fochi, et al. Measurement and analysis of the coefficient of restitution between conducting particles and electrodes in GIS[J]. High Voltage Apparatus, 2017, 53(5): 7-13. (in Chinese) |
| [5] |
Mangwandi C, Cheong Y S, Adams M J, et al. The coefficient of restitution of different representative types of granules[J]. Chemical Engineering Science, 2007, 62(1/2): 437-450. |
| [6] |
Chau K T, Wong R H C, Wu J J. Coefficient of restitution and rotational motions of rockfall impacts[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(1): 69-77. DOI:10.1016/S1365-1609(02)00016-3 |
| [7] |
Aryaei A, Hashemnia K, Jafarpur K. Experimental and numerical study of ball size effect on restitution coefficient in low velocity impacts[J]. International Journal of Impact Engineering, 2010, 37(10): 1037-1044. DOI:10.1016/j.ijimpeng.2010.04.005 |
| [8] |
Thornton C. Coefficient of restitution for collinear collisions of elastic-perfectly plastic spheres[J]. Journal of Applied Mechanics, 1997, 64(2): 383-386. DOI:10.1115/1.2787319 |
| [9] |
Brizmer V, Kligerman Y, Etsion I. The effect of contact conditions and material properties on the elasticity terminus of a spherical contact[J]. International Journal of Solids and Structures, 2006, 43(18/19): 5736-5749. |
| [10] |
Seifried R, Schiehlen W, Eberhard P. Numerical and experimental evaluation of the coefficient of restitution for repeated impacts[J]. International Journal of Impact Engineering, 2005, 32(1/2/3/4): 508-524. |
| [11] |
Vu-Quoc L, Lesburg L, Zhang X. An accurate tangential force-displacement model for granular-flow simulations:Contacting spheres with plastic deformation, force-driven formulation[J]. Journal of Computational Physics, 2004, 196(1): 298-326. DOI:10.1016/j.jcp.2003.10.025 |
| [12] |
Thornton C, Cummins S J, Cleary P W. An investigation of the comparative behaviour of alternative contact force models during inelastic collisions[J]. Powder Technology, 2013, 233: 30-46. DOI:10.1016/j.powtec.2012.08.012 |
| [13] |
Sommerfeld M. Modelling of particle-wall collisions in confined gas-particle flows[J]. International Journal of Multiphase Flow, 1992, 18(6): 905-926. DOI:10.1016/0301-9322(92)90067-Q |
| [14] |
姚文莉, 岳嵘. 有争议的碰撞恢复系数研究进展[J]. 振动与冲击, 2015(19): 43-48. YAO Wenli, YUE Rong. Advance in controversial restitution coefficient study for impact problems[J]. Journal of Vibration and Shock, 2015(19): 43-48. (in Chinese) |
| [15] |
牛佳佳, 王锁芳, 李洁琼, 等. 粒子撞击树脂涂层/铝/合金钢板的反弹特性试验[J]. 航空动力学报, 2018, 33(4): 928-935. NIU Jiajia, WANF Suofang, LI Jieqiong, et al. Experiment of particle rebound characteristics for impingement on resin coated/Al/alloy steel plate[J]. Journal of Aerospace Power, 2018, 33(4): 928-935. (in Chinese) |
| [16] |
牛佳佳, 王锁芳, 董伟林. 100/200/460/700μm粒子撞击铝板的试验研究[J]. 重庆理工大学学报(自然科学版), 2018, 32(2): 118-126, 246. NIU Jiajia, WANG Suofang, DONG Weilin. Experimental investigation on 100/200/460/700μm particles impinging al plate[J]. Journal of Chongqing Institute of Technology, 2018, 32(2): 118-126, 246. (in Chinese) DOI:10.3969/j.issn.1674-8425(z).2018.02.017 |
| [17] |
Tabakoff W. Measurements of particles rebound characteristics on materials used in gas turbines[J]. Journal of Propulsion and Power, 1991, 7(5): 805-813. DOI:10.2514/3.23395 |
| [18] |
Johnson K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985.
|
| [19] |
Abe K, Matsuoka S, Kumada A, et al. Plastic deformation of electrode at collision with particles in vacuum gap[C]//20153rd International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), 25-28 Oct. 2015, Busan, South Korea, 2015: 277-281.
|
| [20] |
何思明, 吴永, 李新坡. 滚石冲击碰撞恢复系数研究[J]. 岩土力学, 2009, 30(3): 623-627. HE Siming, WU Yong, LI Xinpo, et al. Research on restitution coefficient of rock fall[J]. Rock and Soil Mechanics, 2009, 30(3): 623-627. (in Chinese) DOI:10.3969/j.issn.1000-7598.2009.03.008 |
| [21] |
叶阳, 曾亚武, 金磊, 等. 砂岩球体法向恢复系数实验研究[J]. 爆炸与冲击, 2017, 37(5): 813-821. YE Yang, ZENG Yawu, JIN Lei, et al. Normal restitution coefficient of sandstone spheres[J]. Explosion and Shock Waves, 2017, 37(5): 813-821. (in Chinese) |
| [22] |
Xie J, Dong M, Li S. Dynamic impact model of plastic deformation between micro-particles and flat surfaces without adhesion[J]. Aerosol Science and Technology, 2016, 50(4): 10. |
 2019, Vol. 42
2019, Vol. 42

