2. 杭州前进齿轮箱集团股份有限公司, 杭州 311203
2. Hangzhou Advance Gearbox Group Co., Ltd., Hangzhou 311203, P. R. China
新能源电动汽车高速轮边驱动系统,相比传统燃油汽车,舍弃了复杂的主减差速离合传动系统,采用分散驱动布置,传动链大大缩短,结构更为紧凑,具有更好的动力性。高速电机和轮边减速器直接相连,效率相较于传统燃油汽车有较大提高,但传动系统的功率损失仍是电动车主要的功率损失,直接影响电动汽车整车能耗指标,因此开展高速轮边减速器传动效率与功率损失分析具有重要的意义[1]。
当前国内外学者对齿轮传动效率问题进行了一些研究[2-5]。Shen等[2]通过对来源不同的模型进行比较,选择组合形成了一个齿轮箱系统的联合整体模型,同时运用经典参数识别方法和算法确定了最有影响力的参数;Buerkle[3]通过实验的方法测得了不同温度和不同润滑油情况下齿轮啮合的动力损失变化情况;Yin[4]分析讨论了电动汽车传动系统的参数匹配方法和基于最佳电机效率的换挡规则生成方法,并建立了仿真模型,基于仿真结果分析了所提出的换挡原则对车辆性能的影响;Yang等[5]建立了直齿轮啮合效率模型,从啮合传动过程中的功率损失入手,推导出了直齿轮的啮合效率计算公式。综上,现有效率研究多集中针对齿轮副啮合损失或轴承功率损失单方面进行分析,而针对电动车轮边减速器系统效率分析的相关研究较少。
笔者以某电动车高速轮边减速器为研究对象,建立了该减速器的系统效率计算模型,编制计算程序,研究了减速器的设计参数和工况参数对效率的影响规律,为减速器的优化设计提供理论依据。
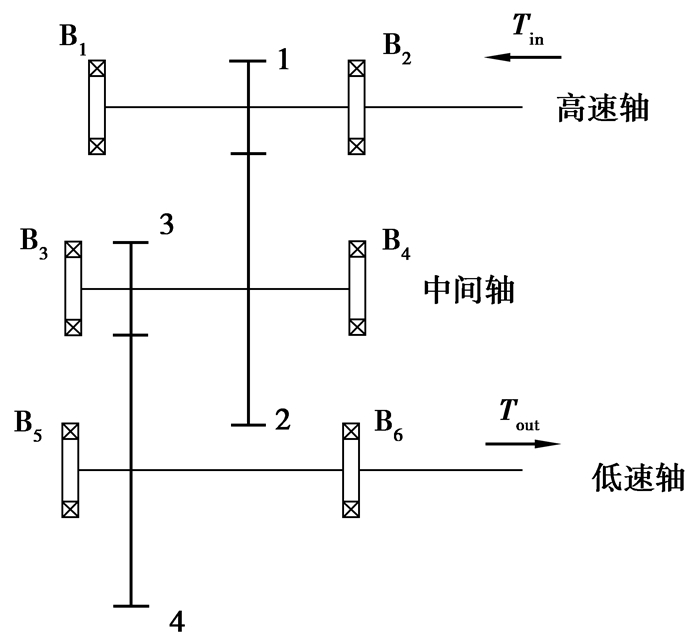
1 电动车轮边减速器效率计算模型 1.1 传动原理某电动车高速轮边减速器采用二级斜齿轮传动形式,具体结构如图 1所示。图中齿轮1和齿轮2构成输入级齿轮副,齿轮3和齿轮4构成输出级齿轮副,减速器所选轴承,其均采用滚动轴承。扭矩从高速轴输入,经过中间轴,从低速轴输出,实现减速增扭作用。
|
图 1 轮边减速器传动原理图 Figure 1 Transmission system of the wheel reducer |
该减速器的基本设计参数如表 1所示。
| 表 1 齿轮的基本设计参数 Table 1 Main gear design parameters |
该减速器设计工况参数如表 2所示。
| 表 2 减速器工况参数 Table 2 Working conditions for the wheel reducer |
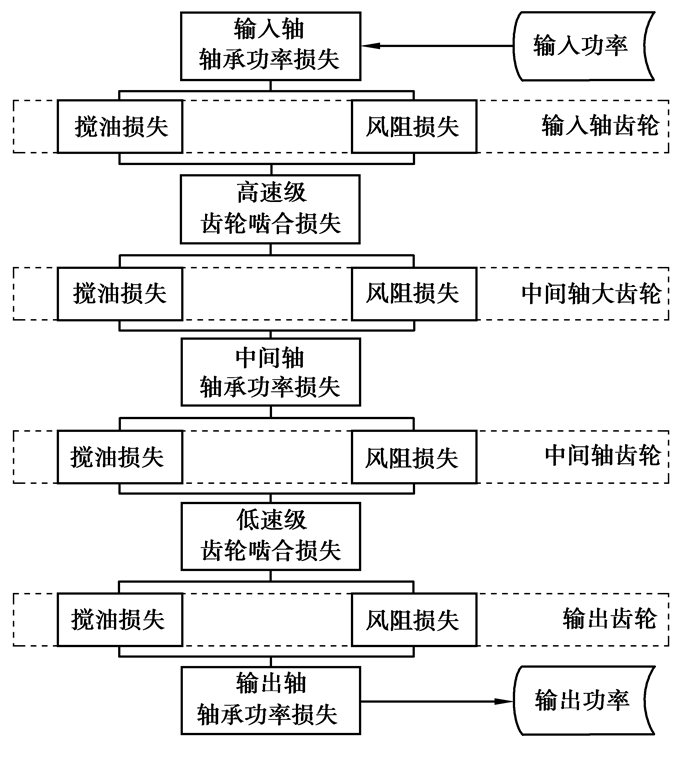
基于该减速器的传动原理与结构,绘制如图 2所示的功率损失流程图。
|
图 2 轮边减速器功率损失流程图 Figure 2 Flow chart for the power loss of the wheel reducer |
功率损失产生于能量流动路线上的元件连接处,在整个流程中,齿轮的搅油损失和风阻损失并联存在,并与啮合损失和轴承损失串联于整个过程中,建立该减速器的总效率计算模型为
| $ \eta = \prod\nolimits_{i = 1}^a {{\eta _{{\rm{B}}i}}} \prod\nolimits_{j = 1}^b {{{\left( {{\eta _{\rm{F}}}{\eta _{\rm{Y}}}{\eta _{\rm{Z}}}} \right)}_j}} , $ | (1) |
式中:ηBi、ηF、ηY、ηZ分别为减速器的轴承效率、啮合效率、搅油效率和风阻效率;a和b分别为减速器内轴的数量和级数。
利用二重积分法推导出斜齿轮啮合传动的平均效率公式[6]
| $ {\eta _{\rm{F}}} = \frac{1}{i}\left[ {U\left( {{Q_1}{R_1} + {Q_2}{R_2}} \right) - 1} \right], $ | (2) |
其中:
| $ {Q_1} = \cos {\beta _{\rm{b}}}/f + \tan {\alpha _{\rm{n}}}/\cos \beta , $ | (3) |
| $ {Q_2} = \cos {\beta _{\rm{b}}}/f - \tan {\alpha _{\rm{n}}}/\cos \beta , $ | (4) |
| $ \begin{array}{*{20}{c}} {U = \left( {{z_1} + {z_2}} \right)\cos {\alpha _{\rm{t}}}/B\left[ {\sqrt {{{\left( {{z_1} + 2h_{{\rm{an}}}^ * \cos \beta } \right)}^2} - {{\left( {{z_1}\cos {\alpha _{\rm{t}}}} \right)}^2}} + } \right.}\\ {\left. {\sqrt {{{\left( {{z_2} + 2h_{{\rm{an}}}^ * \cos \beta } \right)}^2} - {{\left( {{z_2}\cos {\alpha _{\rm{t}}}} \right)}^2}} - \left( {{z_1} + {z_2}} \right)\sin {\alpha _{\rm{t}}}} \right],} \end{array} $ | (5) |
| $ {R_1} = \int_0^B {\ln \left[ {1 + \frac{{{m_{\rm{n}}}\left( {\sqrt {{{\left( {{z_1} + 2h_{{\rm{an}}}^ * \cos \beta } \right)}^2} - {{\left( {{z_1}\cos {\alpha _t}} \right)}^2}} - {z_1}\sin {\alpha _t}} \right)}}{{{z_1}{m_{\rm{n}}}{Q_1}\cos {\alpha _t} - 2y\sin \beta \cos {\alpha _{\rm{t}}}}}} \right]{\rm{d}}y} , $ | (6) |
| $ {R_2} = \int_0^B {\ln \left[ {1 + \frac{{{m_{\rm{n}}}\left( {\sqrt {{{\left( {{z_2} + 2h_{{\rm{an}}}^ * \cos \beta } \right)}^2} - {{\left( {{z_2}\cos {\alpha _{\rm{t}}}} \right)}^2}} - {z_2}\sin {\alpha _{\rm{t}}}} \right)}}{{{z_2}{m_{\rm{n}}}{Q_2}\cos {\alpha _{\rm{t}}} - 2y\sin \beta \cos {\alpha _{\rm{t}}}}}} \right]{\rm{d}}y} , $ | (7) |
式中:z1、z2为齿轮齿数,下标1,2分别为小齿轮与大齿轮;αt、β、βb分别为齿轮的端面压力角、螺旋角和基圆螺旋角;B为齿轮齿宽;f为滑动摩擦系数;mn、han*分别为法面模数和法面齿顶高系数。
减速器的搅油损失主要由元件与油液的摩擦产生能量损失,影响搅油损失的因素主要包括齿形、齿轮直径、元件转速、润滑油黏度和减速器工作温度等[7]。英国标准AGMA ISO14179-1[8]提供了计算高转速下的搅油损失的模型,该模型将搅油损失分为:轴与润滑油摩擦带来的搅油损失PC1;润滑油与齿轮侧面摩擦产生的搅油损失PC2;齿轮轮齿对油池油液的搅拌并使油液飞溅造成的搅油损失PC3。搅油损失的总功率PC可以表示为
| $ {P_{\rm{C}}} = \frac{{7.37{f_{\rm{g}}}\nu n_i^3D_0^{4.0}L}}{{{A_{\rm{g}}}{{10}^{26}}}} + \frac{{1.474{f_{\rm{g}}}\nu n_i^3D_0^{5.7}}}{{{A_{\rm{g}}}{{10}^{26}}}} + \frac{{7.37{f_{\rm{g}}}\nu n_i^3D_0^{4.7}B\left( {\frac{{{R_{\rm{f}}}}}{{\sqrt {\tan \beta } }}} \right)}}{{{A_{\rm{g}}}{{10}^{26}}}}, $ | (8) |
式中:fg为齿轮浸没系数;ν为润滑油运动黏度;ni为元件工作转速;D0、L分别为元件的直径和长度;Ag为配置常数;Rf为粗糙度因子。搅油效率可表示为
| $ {\eta _{\rm{Y}}} = \frac{{{P_i} - {P_{\rm{c}}}}}{{{P_i}}}, $ | (9) |
式中Pi为该级齿轮输入功率。
风阻损失是由于减速器中元件的旋转与空间中的油雾摩擦产生了功率损失[9]。影响风阻损失的因素主要有元件的转速、元件的直径和减速器内油雾的浓度。转速较低时,元件与油雾之间几乎不存在摩擦损失,但在高速运转的轮边驱动系统中,分析减速器的风阻损失更符合实际情况,风阻损失功率计算模型为[10]
| $ {P_{\rm{w}}} = 2.82 \times {10^{ - 7}}\left( {1 + 2.3\frac{B}{r}} \right){n^{2.8}}{r^{4.6}} \times {\left( {0.028\mu + 0.019} \right)^{0.2}}, $ | (10) |
式中:r为齿轮分度圆半径;n为齿轮转速;μ为减速器内油雾的动力黏度。
风阻效率可表示为
| $ {\eta _{\rm{Z}}} = \frac{{{P_i} - {P_{\rm{W}}}}}{{{P_i}}}。$ | (11) |
影响轴承功率损失的因素复杂多变,不同的轴承影响因素也不同。Palmgren研究轴承损失功率归纳总结出轴承的摩擦力矩主要分为2个部分:关于轴承负载的摩擦力矩M0和被齿轮箱工况参数影响的阻力矩M1。英国标准AGMA ISO14179-1[8]提出了和元件转速有关的密封件摩擦力矩M3,最后得到减速器轴承摩擦功率损失为
| $ \begin{array}{*{20}{c}} {{P_{\rm{B}}} = 0.33 \times {{10}^{ - 4}}{\rm{ \mathsf{ π} }}n\left[ {{f_1}{f_{\rm{p}}}\left( {X{F_{\rm{r}}} + Y{F_{\rm{a}}}} \right){d_{\rm{m}}} + } \right.}\\ {\left. {{{10}^{ - 10}}{f_0}{{\left( {{\mu _0}n} \right)}^{\frac{2}{3}}}{d_{\rm{m}}} + \frac{{2\left( {\frac{{{d_{\rm{m}}}}}{{{f_3}}}} \right) + {f_4}}}{{1\;000}}} \right],} \end{array} $ | (12) |
式中:fp为轴承载荷系数;f1为轴承摩擦系数;X、Y分别为径向和轴向载荷系数;Fr、Fa分别为轴承支座的径向和轴向载荷;dm为轴承的平均直径;f0为与润滑油、轴承型号有关的摩擦系数;f3、f4分别为第一、第二轴承密封件系数。
轴承效率可表示为
| $ {\eta _{\rm{B}}} = \frac{{{P_i} - {P_{\rm{B}}}}}{{{P_i}}}。$ | (13) |
将公式(2)~(13)代入到公式(1)中可得到该轮边减速器总效率模型为
| $ \begin{array}{*{20}{c}} {\eta = \frac{{{P_1} + {P_{{\rm{B1}}}}}}{{{P_1}}}\frac{{{P_2} - {P_{{\rm{c1}}}} - {P_{{\rm{w1}}}}}}{{{P_2}}}}\\ {{\eta _{{\rm{F1}}}}\frac{{{P_3} - {P_{{\rm{B2}}}}}}{{{P_3}}}\frac{{{P_4} - {P_{{\rm{c2}}}} - {P_{{\rm{w2}}}}}}{{{P_4}}}{\eta _{{\rm{F2}}}}\frac{{{P_5} - {P_{{\rm{B3}}}}}}{{{P_5}}},} \end{array} $ | (14) |
式中P1~P5为对应处输入的功率。
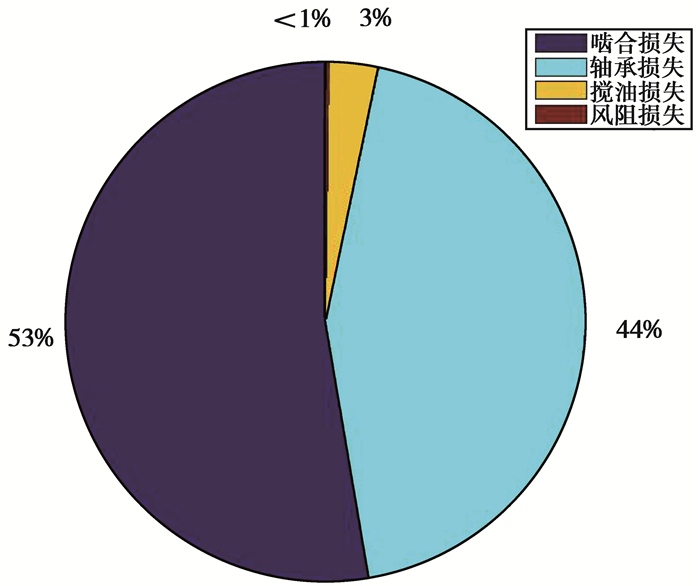
2 系统效率参数化影响分析基于上述模型,采用Matlab软件编制该电动车高速轮边减速器效率计算程序,按表 1和表 2所示减速器的设计和工况参数计算得到该减速器的总效率为94.38%,绘制出各种功率损失在功率总损失的占比情况如图 3所示。分析可知,啮合损失和轴承损失在功率总损失中占据了绝大部分,分别达到了53%和44%,搅油损失和风阻损失占比较小,仅占到3.0%和0.3%。
|
图 3 各部分损失占比 Figure 3 The proportion for various parts of efficiency loss |
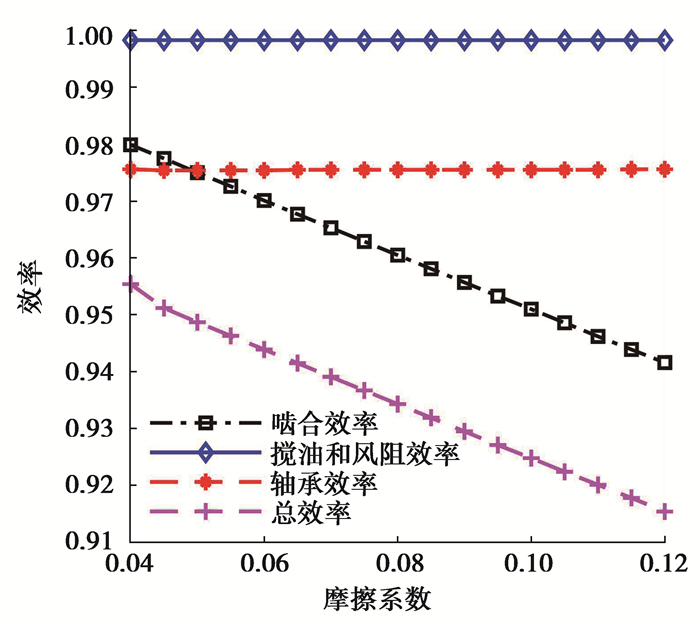
计算得到摩擦系数对系统总效率的影响规律如图 4所示。
|
图 4 摩擦系数对效率的影响 Figure 4 Effect of friction coefficient on efficiency |
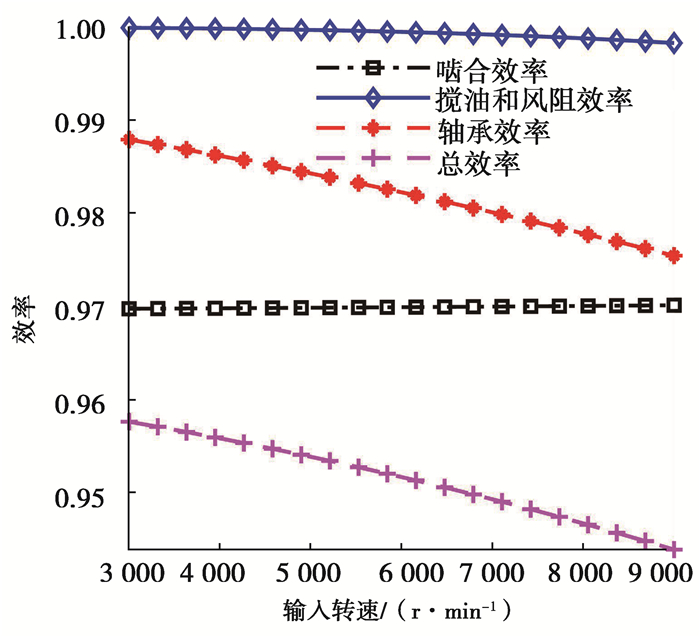
从图 4可以看出,在给定区间内,总效率随着摩擦系数的增加而减小,关系近似为线性。滑动摩擦系数主要通过对啮合效率的影响进而影响总效率。输入转速对系统效率的影响规律如图 5所示。
|
图 5 输入转速对效率的影响 Figure 5 Effect of input speed on efficiency |
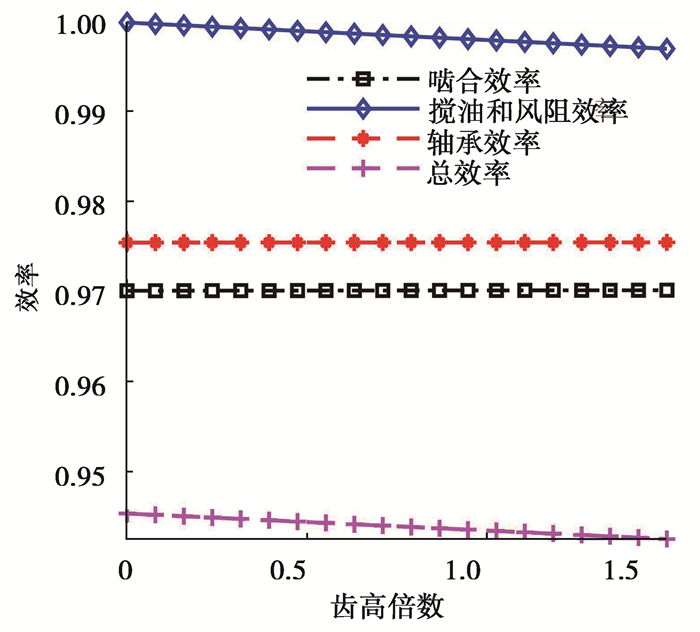
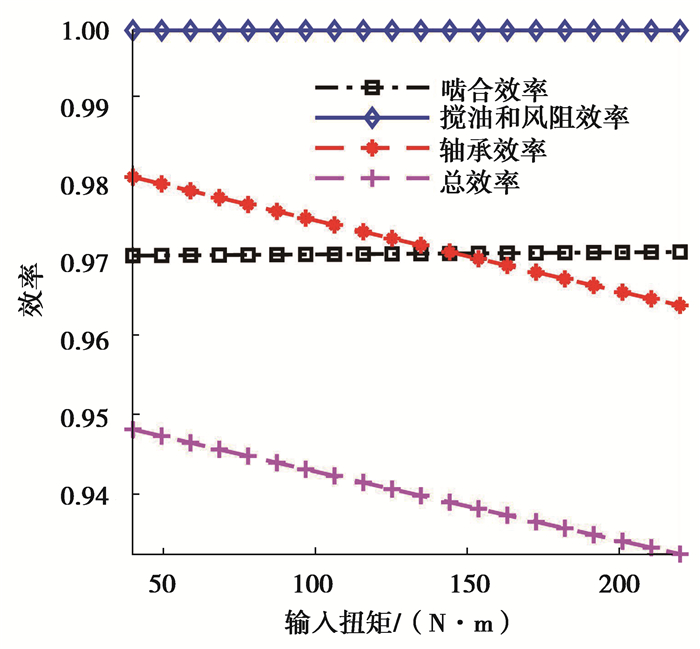
从图 5可以看出,总效率随着转速的增加而减小,变化关系呈线性关系。转速越高,搅油越剧烈,所以随着转速的提高,搅油和风阻效率降低。转速是影响轴承效率的重要因素之一,且轴承效率随着转速的增加而减小。计算得到运动黏度对系统效率的影响规律如图 6所示,齿高倍数对系统效率的影响规律如图 7所示,输入扭矩对系统效率的影响规律如图 8所示。

|
图 6 运动黏度对系统效率的影响 Figure 6 Effect of kinematic viscosity on efficiency |
|
图 7 齿高倍数对系统效率的影响 Figure 7 Effect of Addendum coefficient on efficiency |
|
图 8 输入扭矩对系统效率的影响 Figure 8 Effect of torque on efficiency |
从上述计算结果可以看出,总效率随着运动黏度的增加而减小,变化关系呈线性关系。运动黏度是润滑油的基本特性,通过影响搅油效率和轴承效率对系统效率产生影响。总效率随着齿高倍数的增加而减小。齿高倍数仅对搅油效率有影响,所以齿高倍数对总效率的影响规律和齿高倍数对搅油效率的影响规律一致。输入转矩对搅油效率影响较小,仅对轴承效率有影响。系统总效率与轴承效率随着输入转矩的增加呈线性减小趋势。
2.2 设计参数对效率的影响分析计算得到主动轮齿数对系统效率的影响规律如图 9所示,螺旋角对系统效率的影响规律如图 10所示。

|
图 9 主动轮齿数对效率的影响 Figure 9 Effect of tooth number on efficiency |

|
图 10 螺旋角对效率的影响 Figure 10 Effect of helix angle on efficiency |
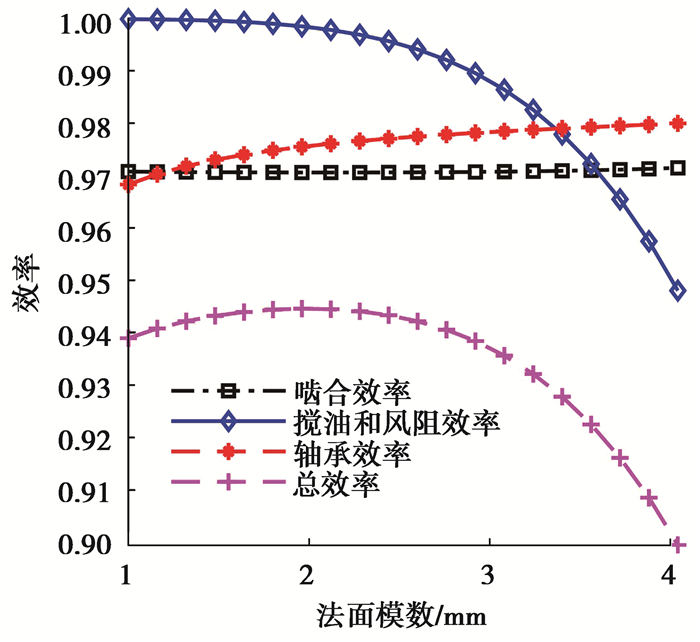
从图 9、10可以看出,系统总效率随齿数的增加先增大后减小,在齿数达到25左右时出现拐点,之后随齿数增加,系统总效率下降的速度逐渐加快。啮合效率随着齿数的增加而变大,但变化幅度较小;轴承效率则先增大再减小,但变化幅度较小;搅油和风阻效率受影响较大,且齿数越多,搅油风阻效率的减小越明显。随着螺旋角的增大,系统总效率呈非线性增大趋势。螺旋角主要通过影响啮合效率影响系统总效率,其对轴承效率、搅油和风阻效率影响较小。计算得到法面模数对系统效率的影响规律如图 11所示。
|
图 11 法面模数对效率的影响 Figure 11 Effect of module on efficiency |
从计算结果可以看出,法面模数在1~4变化区间内,总效率先增加后减小,在法面模数为2时出现拐点。其中,法面模数对啮合效率影响较小;法面模数的变化导致齿轮直径的变化,在同等扭矩的情况下,轴承的受力变小,进而导致轴承效率变大;对搅油和风阻效率,法面模数的变化和齿数的变化相似,使得齿轮直径变化,进而导致搅油和风阻效率的降低。
3 结论1) 以某电动车高速轮边减速器为研究对象,建立了该减速器的效率模型,推导了各部分功率损失的公式,利用Matlab编制计算程序分析了不同工况参数和设计参数对系统效率的影响规律。
2) 随着工况参数转速、转矩、摩擦系数、齿高倍数和运动黏度的增大,系统效率均减小,其中转速、转矩和摩擦系数对总效率影响较大,齿高倍数和运动黏度对总效率的影响较小。研究结果为后续基于加载啮合特性分析,研究完整啮合周期内摩擦系数变化对系统效率的影响奠定基础。
3) 减速器设计参数主动轮齿数和法面模数的变化均导致总效率先增加后减小,螺旋角的增加可明显提高系统效率。研究结果为后续考虑系统效率的齿轮副宏观几何设计参数优化与微观修形奠定基础。
| [1] |
Al-Shibl K, Simmons K, Eastwick C N. Modelling windage power loss from an enclosed spur gear[J]. Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy, 2007, 221(3): 331-341. DOI:10.1243/09576509JPE344 |
| [2] |
Shen Y, Rinderknecht S, Hoppert M. General modelling method of power losses in transmission with parameter identification[J]. Forschung Im Ingenieurwesen, 2017, 81(2/3): 117-123. |
| [3] |
Buerkle M S. Examination of high-speed helical gear mesh efficiency and influences[D]. Ann Arbor, MI: University of Michigan, 2005.
|
| [4] |
Yin X F, Xue D L, Cai Y. Application of time-optimal strategy and fuzzy logic to the engine speed control during the gear-shifting process of AMT[C]//Fouth International Conference on Fuzzy Systems and Knowledge Discovery(FSKD 2007), August 24-27, 2007, Haikou, China. IEEE, 2007: 468-472.
|
| [5] |
杨世平, 范辉, 朱广辉. 直齿圆柱齿轮啮合效率的计算与分析[J]. 机械传动, 2017, 41(2): 148-151. YANG Shiping, FAN Hui, ZHU Guanghui. Calculation and analysis of the meshing efficiency of spur gear[J]. Journal of Mechanical Transmission, 2017, 41(2): 148-151. (in Chinese) |
| [6] |
姚建初, 陈义保, 周济, 等. 齿轮传动啮合效率计算方法的研究[J]. 机械工程学报, 2001, 37(11): 18-21, 27. YAO Jianchu, CHEN Yibao, ZHOU Ji, et al. Study on a method for calculating gearing meshing efficiency[J]. Chinese Journal of Mechanical Engineering, 2001, 37(11): 18-21, 27. (in Chinese) DOI:10.3321/j.issn:0577-6686.2001.11.004 |
| [7] |
Hill M J. A computational investigation of gear windage[D]. University Park, PA: The Pennsylvania State University, 2010.
|
| [8] |
Seetharaman S, Kahraman A, Moorhead M D, et al. Oil churning power losses of a gear pair:experiments and model validation[J]. Journal of Tribology, 2009, 131(2): 022202. DOI:10.1115/1.3085942 |
| [9] |
Anderson N E, Loewenthal S H. Design of spur gears for improved efficiency[J]. Journal of Mechanical Design, 1982, 104(4): 767. DOI:10.1115/1.3256434 |
| [10] |
Dawson H. Windage loss in larger high-speed gears[J]. Proceedings of the Institution of Mechanical Engineers, Part A:Power and Process Engineering, 1984, 198(1): 51-59. DOI:10.1243/PIME_PROC_1984_198_007_02 |
| [11] |
王成, 崔焕勇, 张清萍, 等. 齿轮啮合效率的理论研究进展[J]. 济南大学学报(自然科学版), 2015, 29(3): 229-235. WANG Cheng, CUI Huanyong, ZHANG Qingping, et al. Theoretical research progress of gear meshing efficiency[J]. Journal of University of Jinan (Science and Technology), 2015, 29(3): 229-235. (in Chinese) |
| [12] |
Ariura Y, Ueno T, Sunaga T, et al. The lubricant churning loss in spur gear systems[J]. Transactions of the Japan Society of Mechanical Engineers, 1972, 38(313): 2403-2413. DOI:10.1299/kikai1938.38.2403 |
| [13] |
Seetharaman S, Kahraman A. Load-independent spin power losses of a spur gear pair:model formulation[J]. Journal of Tribology, 2009, 131(2): 022201. DOI:10.1115/1.3085943 |
| [14] |
Moldovean G, Butuc B R, Bozan C A. On the Power Losses of Cylindrical and Bevel Gears Used in Wind Turbines and Tracking Systems for Photovoltaic Platforms[M]//Moldovean G, Butuc B R, Bozan C A. eds. SYROM 2009. Dordrecht: Springer Netherlands, 2009: 337-350.
|
| [15] |
Spitas C, Spitas V, Rajabalinejad M. Dynamical simulation and calculation of the load factor of spur gears with indexing errors and profile modifications for optimal gear design[C]//Power Transmissions: Proceedings of the 4th International Conference, June 20-23, 2012, Sinaia, Romania. Springer, Dordrecht, 2013: 183-196.
|
 2019, Vol. 42
2019, Vol. 42


