为了节约资源、减少环境污染,汽车的轻量化设计作为提高整车燃油经济性的重要手段,已成为国内外学者的研究热点[1-8]。而驱动桥作为汽车的主要承载件,其质量对汽车的操控性和乘坐舒适性有直接的影响,因此驱动桥的轻量化设计具有非常重要的实际意义[9-11]。Zhu等[1]提出了一种基于鲁棒性的轻量化优化方法,使汽车车身质量减轻了7.8 kg。Jang等[2]使用拓扑结构优化和拖车板厚度优化相结合的方法,使拖车车身质量减轻29%。高云凯等[3]将序列Kriging模型应用到车身轻量化设计中,采用粒子群算法所得到的优化结果表明,在满足耐撞性约束的同时所选部件的质量降低了23.35%。丁晓明等[10]在典型工况下对悬架后桥进行了有限元分析,然后用惯性释放的方法完成了悬架后桥壳的轻量化设计。马石磊等[11]基于疏网格理论建立驱动桥壳4个响应量的近似模型,采用非支配排序遗传算法得到三组Pareto最优解集,降低驱动桥壳质量3.94 kg。
现在新能源汽车的电驱动桥基本都是在燃油车车桥的基础上额外增置驱动电机[12-14]。由于电机偏置会导致驱动桥钢板座承受额外的倾覆力矩,进而引起车身振动,降低驾驶舒适性。针对电驱动桥电机偏置问题,罗玉涛等[12]提出了双转子电动机电驱动桥设计,在保证汽车动力性的前提下有效避免了非同轴布置产生的问题,但是双转子电动机电驱动桥造价昂贵、控制复杂且非同轴。因此,新能源汽车电驱动桥的同轴设计非常重要。同时,如何在满足汽车使用性能的要求下,实现电驱动桥的轻量化设计,降低簧下质量提高乘坐舒适性,是亟需解决的另一难题。
针对电驱动桥非同轴问题、为减少环境污染,笔者提出一种纯电动汽车同轴一体化电驱动桥结构,建立其有限元模型进行强度、刚度以及性能分析;根据仿真分析结果,实现了电驱动桥的轻量化设计。
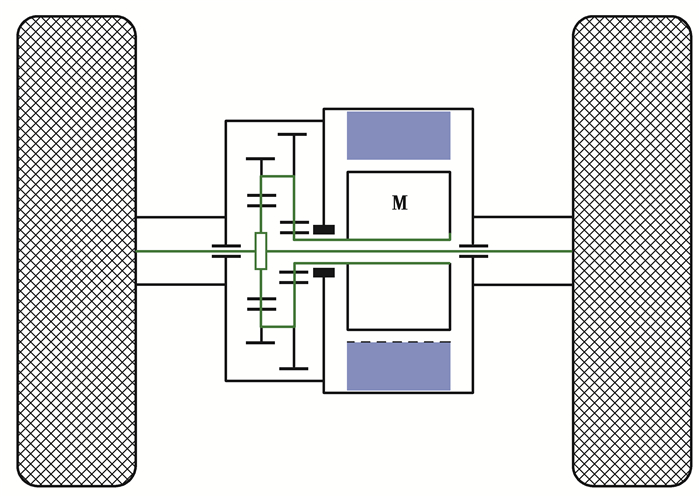
1 电驱动桥结构设计及其有限元模型 1.1 纯电动汽车电驱动桥结构设计为了克服电机悬挂所产生倾覆力矩的影响,提出一种同轴一体化电驱动桥结构,其结构原理图如图 1所示。
|
图 1 同轴一体化驱动桥结构示意图 Figure 1 Schematic diagram of a coaxial integrated electric drive rear axle |
该电驱动桥采取同轴式结构,主要由电机、二级减速器、差速器和半轴组成,电机输出轴通过花键带动减速器的输入轴旋转,经两级齿轮减速后将动力传递给差速器,而半轴穿过空心电机轴插入差速器,最后动力经半轴输出到车轮。
1.2 驱动桥有限元模型建立电驱动桥桥壳有限元模型,如图 2所示。

|
图 2 电驱动桥桥壳有限元模型 Figure 2 Finite element model of electric drive rear axle shell |
电动汽车一体化电动桥壳的主要参数为满轴载荷1.9 t,轮距1 490 mm,板簧距1 016 mm。材料设定为40Cr,将桥壳进行调质处理,处理后的40Cr参数如表 1所示。
| 表 1 桥壳材料参数 Table 1 Material parameters for rear axle shell |
某电动商用车基本参数及驱动系统参数如表 2所示。
| 表 2 整车基本参数及驱动系统参数 Table 2 Basic vehicle parameters and driving system parameters |
汽车实际受力情况较为复杂,按最大冲击工况、最大驱动力工况、紧急制动工况以及最大侧向力工况[15]进行分析。如电动汽车在上述4种极限工况下驱动后桥桥壳达到强度刚度使用条件,则可以确定驱动桥满足电动汽车实际使用要求。
2.1 最大冲击工况下的桥壳强度刚度分析当汽车满载行驶在不平路面受冲击载荷的极限工况下时,桥壳除承受汽车自身的满载重力G、驱动电机和减速器重力G1作用外,还需承受冲击载荷的作用。
弹簧钢板座处受垂直力为:
| $ F = \frac{{G + {F_1}}}{2}。$ | (1) |
其中弹簧钢板座处的冲击载荷为:
| $ {F_1} = {k_{\rm{d}}} \cdot G。$ | (2) |
电机与减速器在冲击作用下的总载荷为:
| $ {F_2} = {G_1} + {k_{\rm{d}}} \cdot {G_1}, $ | (3) |
式中kd为动载荷系数。
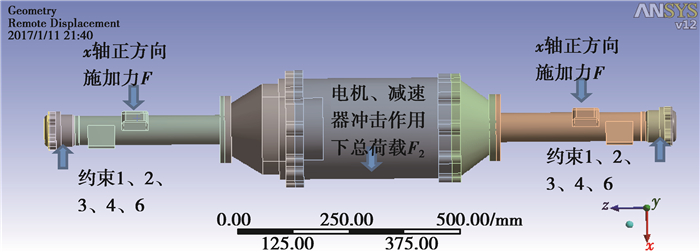
桥壳不平路面冲击载荷约束如图 3所示。加载载荷:在弹簧座处施加3.213 kN垂直力;在电机及减速器重心位置施加2.45 kN力。约束条件:约束一体化桥壳一端x、y、z方向的移动及x、y方向的转动,另一端约束x、y方向的移动及x、y方向的转动。
|
图 3 最大冲击载荷工况桥壳的加载约束 Figure 3 Load and constraints of the bridge shell under the maximum impact load |
将不平路面冲击下的边界仿真载荷施加在图 2所示的有限元模型上,得到的等效应力云图如图 4所示,等效位移云图如图 5所示。

|
图 4 桥壳应力云图 Figure 4 Stress nephogram of bridge shell |
|
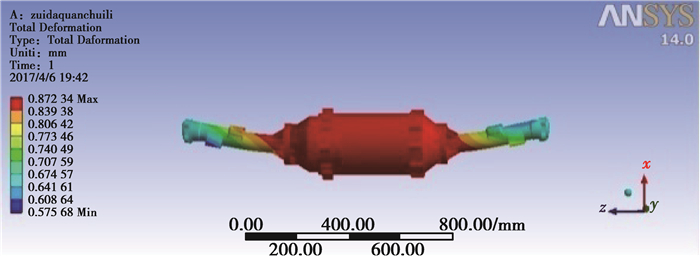
图 5 桥壳位移云图 Figure 5 Displacement nephogram of bridge shell |
由图 4可知,驱动桥桥壳最大应力位于半轴套管约束处,最大应力234.22 MPa,小于40Cr的屈服强度785 MPa。因此,驱动桥满足强度要求。
由图 5可知,驱动桥桥壳的位移较大区域位于两板簧座之间区域的电机和减速部分。最大变形量0.872 mm,位于中间电机和减速器连接的区域。每米轮距变形量0.585 mm/m,小于国家标准规定值1.5 mm/m。因此,该驱动桥满足刚度要求。
2.2 最大驱动力工况下的桥壳强度刚度分析当汽车满载以最大驱动力行驶时,桥壳除承受汽车自身的满载重力G、驱动电机和减速器重力G1作用外,还要承受电机驱动力对桥壳的反扭矩作用。
弹簧钢板座处受垂直力为:
| $ {F_{\rm{t}}} = \frac{{m'' \cdot G}}{2}, $ | (4) |
式中m″为车桥载荷转移系数。
单侧所受旋转反扭矩为:
| $ T = \frac{{{T_{\max }} \cdot i \cdot {\eta _{\rm{T}}}}}{2}, $ | (5) |
式中:Tmax为驱动电机最大输出扭矩;i为驱动后桥减速器传动比;ηT为后桥传动系统效率。
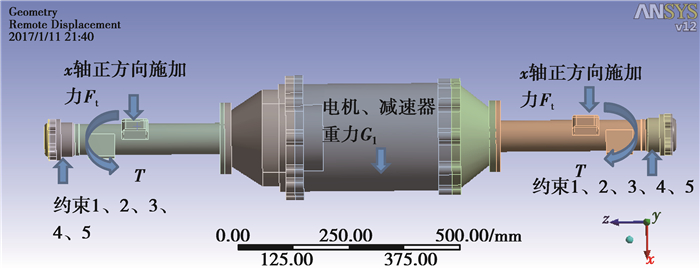
桥壳最大驱动力工况下的载荷约束如图 6所示,加载载荷:在弹簧座处施加22.285 kN垂直力;在电机和减速器重心位置施加0.98 kN力;在弹簧座处施加807.225 Nm扭矩。约束条件:约束桥壳两端x、y、z方向的移动及y、z方向转动。
|
图 6 最大驱动力工况下桥壳的加载约束 Figure 6 Load and constraints of the bridge shell under the maximum driving force |

|
图 7 桥壳应力云图 Figure 7 Stress nephogram of bridge shell |

|
图 8 桥壳位移云图 Figure 8 Displacement nephogram of bridge shell |
由图 7可知,驱动桥桥壳最大应力位于半轴套管约束处,最大应力219.25 MPa,满足强度要求。
由图 8可知,桥壳最大变形量0.739 mm,位于左板簧座和凸包之间的区域;每米轮距变形量0.496 mm/m,满足刚度要求。
2.3 紧急制动工况下的桥壳强度刚度分析当汽车满载处于紧急制动极限工况时,桥壳除承受汽车自身的满载重力G、驱动电机和减速器重力G1作用外,还要承受地面对车轮的制动力矩。
弹簧钢板座处受垂直力为:
| $ {F_{\rm{v}}} = \frac{{k' \cdot G}}{2}, $ | (6) |
式中k′为汽车制动时的质量转移系数。
制动力矩为:
| $ {M_{\rm{h}}} = k' \cdot G \cdot \varphi \cdot r, $ | (7) |
式中:φ为车轮与地面间的附着系数,r为驱动车轮的滚动半径。
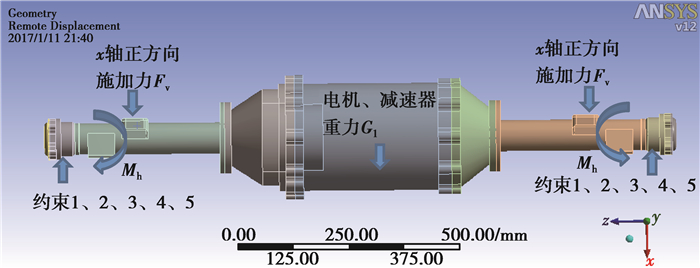
桥壳紧急制动载荷约束如图 9所示。加载载荷:在弹簧座处施加6.964 kN垂直力;在电机及减速器重心位置施加0.98 kN力;在弹簧座处施加1 970.8 Nm制动力矩。约束条件:约束桥壳两端x、y、z方向移动及y、z方向的转动。
|
图 9 紧急制动工况下桥壳的加载约束 Figure 9 Load and constraint of the bridge shell under emergency braking condition |
对应得到的等效应力云图如图 10所示,等效位移云图如图 11所示。

|
图 10 桥壳应力云图 Figure 10 Bridge shell stress nephogram |

|
图 11 桥壳位移云图 Figure 11 Displacement nephogram of bridge shell |
由图 10可知,驱动桥桥壳最大应力位于半轴套管约束处,最大应力179.4 MPa,满足强度要求。
由图 11可知,桥壳最大变形量为0.901 mm,位于在左板簧座和凸包之间;每米轮距变形量为0.605 mm/m,满足刚度要求。
2.4 最大侧向力工况下的桥壳强度刚度分析当汽车处于最大侧向力极限工况时,桥壳除承受汽车自身的满轴载荷G、驱动电机和减速器重力G1作用外,还要承受侧向力P。
汽车驱动桥的侧滑条件为汽车承受的侧向力大于等于轮胎的侧向附着力,即
| $ P \ge {Y_{\rm{L}}} + {Y_{\rm{R}}} = G \cdot \varphi , $ | (8) |
式中:P为汽车桥所受的侧向力,此时最大侧向力P=G·φ;YL、YR分别为地面给左右驱动车轮的侧向反作用力。
假设汽车右侧滑移时,左、右驱动车轮的支撑反力分别为
| $ {F_{\rm{L}}} = \frac{G}{2} - G \cdot \varphi \cdot \frac{H}{B}, $ | (9) |
| $ {F_{\rm{R}}} = \frac{G}{2} + G \cdot \varphi \cdot \frac{H}{B}, $ | (10) |
式中:H为汽车满轴载荷时的质心高度;B为汽车驱动车轮轮距。
当
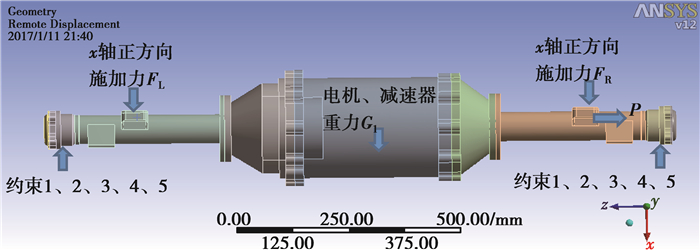
桥壳最大侧向力工况下的载荷约束如图 12所示。加载载荷:在右侧弹簧座处施加18.571 kN垂直支撑反力;在电机及减速器重心位置施加0.98 kN力;在右侧弹簧座处施加18.571 kN右侧向力。约束条件:约束桥壳一端x、y、z方向的平动及z方向的转动,另一端约束x、y方向的平动及z方向的转动。
|
图 12 最大侧向力工况下桥壳的加载约束 Figure 12 Load and constraint of the bridge shell under maximum lateral force |
将最大侧向力工况下的载荷及约束边界条件施加到驱动桥桥壳上,获得等效应力云图如图 13所示,等效位移云图如图 14所示。

|
图 13 桥壳应力云图 Figure 13 Stress nephogram of bridge shell |

|
图 14 桥壳位移云图 Figure 14 Displacement nephogram of bridge shell |
由图 13可知,桥壳最大应力位于轴套管约束处,最大应力201.9 MPa,满足强度要求。
由图 14可知,驱动桥桥壳的最大变形量1.246 9 mm,位于左板簧座和凸包之间的区域。每米轮距变形量0.837 mm/m,满足刚度要求。
3 同轴一体化电驱动桥轻量化设计根据一体化电驱动桥的有限元仿真分析结果,建立了驱动后桥桥壳轻量化优化模型,对其进行轻量化设计。
3.1 驱动桥桥壳结构轻量化模型的建立 3.1.1 优化变量从电驱动后桥的应力云图可知,驱动桥桥壳位于半轴套管和电机外筒处有较大富裕量,设半轴套管、电机外壳的厚度分别为T1、T2。因此,桥壳轻量化优化变量可表示为:
| $ \mathit{\boldsymbol{X}} = {\left[ {{T_1},{T_2}} \right]^{\rm{T}}}。$ | (11) |
1) 最大应力约束。从应力云图可知,汽车在4种极限工况下后桥桥壳上的应力都不相同。而在实际行驶中,车辆承受不平路面冲击载荷工况在所有工况中占比最多,因此对该工况下的最大应力进行约束。
| $ {\sigma _{\max }} \le \left[ \sigma \right], $ | (12) |
式中:σmax为桥壳最大应力,[σ]为材料屈服强度。
2) 最大变形约束。国家标准规定驱动后桥的最大变形不能超过1.5 mm/m。与最大应力约束类似,对车辆承受不平路面冲击载荷工况下的驱动桥桥壳位移变形进行约束。
| $ \frac{{{D_{\max }}}}{{1.49}} \le 1.5\;{\rm{mm}}/{\rm{m,}} $ | (13) |
式中Dmax为桥壳最大变形位移。
3) 桥壳厚度约束。根据桥壳生产实际和加工桥壳钢板的厚度规格,取桥壳最小值为4 mm,最大值为6 mm,则将其约束范围设定为:
| $ 4\;{\rm{mm}} \le {T_1} \le 6\;{\rm{mm}}, $ | (14) |
| $ 4\;{\rm{mm}} \le {T_2} \le 6\;{\rm{mm}}。$ | (15) |
电驱动桥桥壳轻量化优化的目标是桥壳质量M达到最小
| $ \min F\left( \mathit{\boldsymbol{X}} \right) = M\left( \mathit{\boldsymbol{X}} \right)。$ | (16) |
综上所述,驱动桥壳优化模型为:
| $ \begin{array}{*{20}{c}} {\min F\left( \mathit{\boldsymbol{X}} \right) = M\left( {{{\left[ {{T_1},{T_2}} \right]}^{\rm{T}}}} \right)}\\ {{\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {\sigma _{\max }} \le \left[ \sigma \right]\\ \frac{{{D_{\max }}}}{{1.49}} \le 1.5\;{\rm{mm}}/{\rm{m}}\\ 4\;{\rm{mm}} \le {T_1} \le 6\;{\rm{mm}}\\ 4\;{\rm{mm}} \le {T_2} \le 6\;{\rm{mm}} \end{array} \right.} \end{array}。$ | (17) |
首先使用目标驱动优化方法设计样本,计算样本的目标函数值,然后构造输入变量与最大应力、最大位移及最大质量之间的响应曲面关系,最后利用响应曲面求出最终解。
3.2.1 桥壳厚度与位移变形的响应关系将轻量化优化模型导入到Workbench中,输入变量为X=[T1,T2]T,输出变量为桥壳质量,输出约束条件为最大位移变形、最大应力,构造桥壳不同部位厚度与输出变量及输出约束之间的响应曲面。图 15为输入变量T1、T2对驱动桥位移变形的综合响应三维曲面。由图 15可知,随着两变量桥壳厚度的变薄,桥壳的整体位移变形有增大的趋势。

|
图 15 桥壳壳体厚度与后桥位移变形之间的响应关系 Figure 15 Response relation between the bridge shell thickness and the displacement deformation of the rear axle |
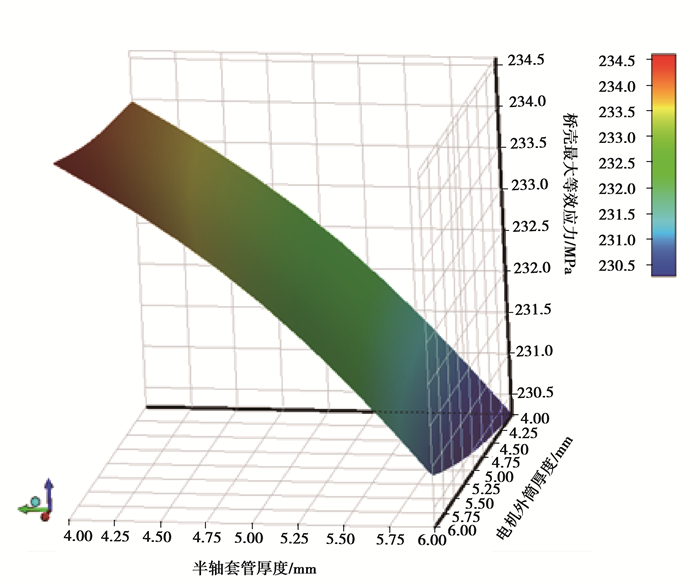
与桥壳位移变形分析类似,将T1、T2分别作为输入变量,获得如图 16所示的桥壳最大应力与T1、T2之间的三维响应关系图。由图 16可知,桥壳最大应力随着桥壳厚度T1、T2的减小有递增的趋势。
|
图 16 桥壳壳体厚度与后桥最大应力之间的响应关系 Figure 16 Response relation between the bridge shell thickness and the maximum stress of the rear axle |
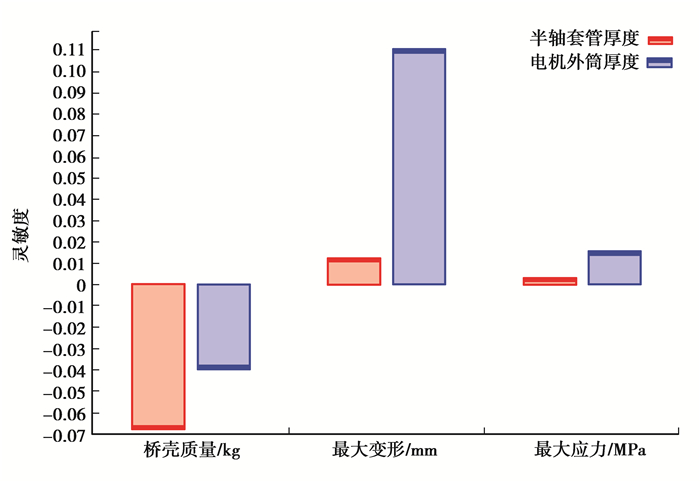
由以上分析可知桥壳不同部位的厚度不同,对桥壳最大应力、最大位移变形及桥壳质量的影响程度均不相同。因此为了确定桥壳不同部位的厚度对桥壳最大应力和最大位移变形的影响程度,构建如图 17所示的各输入变量与各输出变量之间的灵敏度关系图。
|
图 17 输出变量对桥壳不同部位厚度之间敏感关系 Figure 17 Sensitivity of the output variable to the thickness of the different parts of the bridge shell |
由图 17可知,桥壳质量对半轴套管处厚度T1与电机外壳厚度T2敏感度不同,电机外壳厚度T2对桥壳质量较为敏感。这是由于电机外壳径向尺寸较大,因此电机外壳厚度变化对桥壳质量的影响大于半轴套管处厚度的变化对桥壳质量的影响,这与实际情况相符。半轴套管厚度T1对桥壳的最大应力较为敏感,而电机外壳厚度T2对桥壳的最大应力不敏感。最大位移变形与桥壳最大应力的影响较为相似,半轴套管处厚度T1对桥壳的最大位移变形较为敏感,而电机外壳厚度T2对桥壳的最大位移变形不敏感。因此在设计驱动桥时,如果桥壳出现位移变形过大或桥壳应力过大的问题,只须增加半轴套管处的厚度进行改善。
3.2.4 驱动桥桥壳厚度最优解根据以上分析对桥壳进行优化求解,获得轻量化模型的3个最优候选解,如表 3所示。
| 表 3 桥壳轻量化结果 Table 3 Optimization results of lightweight bridge shell |
由表 3可知,当桥壳X=[4.015,4.032]T时,桥壳质量最小、最大变形位移和最大应力都在许用范围内,因此A为最优解。圆整为X=[4,4]T,此时桥壳质量为45.511 kg,比原模型质量49.667 kg减小4.156 kg,轻量化幅度为8.4%。
4 驱动桥壳轻量化验证为了验证桥壳轻量化后的结构是否满足使用要求,在4种极限工况下对轻量化设计后的驱动桥桥壳进行有限元仿真分析。桥壳优化前后的强度分析结果如表 4所示,刚度分析结果如表 5所示。
| 表 4 桥壳优化前后最大应力对比分析 Table 4 Comparison and analysis of maximum stress before and after the optimization of the bridge shell |
| 表 5 桥壳轻量化优化前后最大位移变形对比 Table 5 Comparison of maximum displacement and deformation before and after lightweight optimization of bridge shell |
由表 4可知,轻量化后的驱动桥桥壳在各种工况下的最大应力均有一定幅度的增大,其中最大侧向力工况应力的增大幅度最大,而其他工况下的应力增大不明显。
这是由于最大侧向力工况下最大应力在半轴套管的中间截面处,而其他工况下的最大应力位于半轴套管靠近轮胎处。因此半轴套管处的厚度减小将影响最大侧向力的最大应力分布,而对其他工况下的应力影响较小。因此,在最大侧向力工况时应力增加幅度最大是合理的。
由表 5可知,轻量化后的驱动桥桥壳在各种工况下的最大变形量均有一定幅度的增加,其中最大冲击工况增加幅度为0.215 6 mm。
在最大冲击工况下,施加的垂直方向载荷在驱动桥弹簧钢板处最大,电机减速部分的载荷也是最大;同时由图 17可知,半轴套管处桥壳厚度对变形影响最大。因此,在最大冲击工况下桥壳变形幅度最大是合理的。
综上所述,轻量化设计后的驱动桥桥壳虽然在强度和刚度上均有一定的减弱,但是仍能满足驱动后桥的使用要求,因此轻量化设计是合理的。
5 结论1) 结合生产实际需求提出了一种同轴一体化电动汽车驱动后桥新构型。
2) 对电驱动桥进行了4种极限工况下的强度和刚度仿真分析,获得了电驱动桥的应力和位移分布规律。
3) 建立了驱动后桥桥壳轻量化模型,利用目标驱动方法构建了响应曲面关系,求解优化模型,桥壳减重8.4%。驱动桥桥壳轻量化验证,结果表明轻量化设计后的驱动桥桥壳仍能满足使用要求。
| [1] |
Zhu P, Zhang Y, Chen G L. Metamodel-based lightweight design of an automotive front-body structure using robust optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2009, 223(9): 1133-1147. DOI:10.1243/09544070JAUTO1045 |
| [2] |
Jang G W, Yoon M S, Park J H. Lightweight flatbed trailer design by using topology and thickness optimization[J]. Structural and Multidisciplinary Optimization, 2010, 41(2): 295-307. DOI:10.1007/s00158-009-0409-x |
| [3] |
高云凯, 郭其飞, 方剑光, 等. 基于序列Kriging模型的车身轻量化设计[J]. 汽车工程, 2015, 37(4): 460-465. GAO Yunkai, GUO Qifei, FANG Jianguang, et al. Lightweight design of car body based on sequential kriging model[J]. Automotive Engineering, 2015, 37(4): 460-465. (in Chinese) DOI:10.3969/j.issn.1000-680X.2015.04.016 |
| [4] |
Liu Z, Lu J H, Zhu P. Lightweight design of automotive composite bumper system using modified particle swarm optimizer[J]. Composite Structures, 2016, 140: 630-643. DOI:10.1016/j.compstruct.2015.12.031 |
| [5] |
Delogu M, Maltese S, del Pero F, et al. Challenges for modelling and integrating environmental performances in concept design:the case of an automotive component lightweighting[J]. International Journal of Sustainable Engineering, 2018, 11(2): 135-148. DOI:10.1080/19397038.2017.1420110 |
| [6] |
Park J H, Kim K J, Lee J W, et al. Light-weight design of automotive suspension link based on design of experiment[J]. International Journal of Automotive Technology, 2015, 16(1): 67-71. DOI:10.1007/s12239-015-0007-4 |
| [7] |
Zhao Q H, Chen X K, Lin Y. Reliability-Based Topology Optimization of Control Arm of Suspension for Lightweight Design[M]//Zhao Q H, Chen X K, Lin Y. eds. Lecture Notes in Electrical Engineering. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1129-1138.
|
| [8] |
谢晖, 王品健, 王杭燕. 某电动汽车前舱轻量化设计[J]. 塑性工程学报, 2018, 25(3): 1-7. XIE Hui, WANG Pinjian, WANG Hangyan. Lightweight design for an electric vehicle front cabin[J]. Journal of Plasticity Engineering, 2018, 25(3): 1-7. (in Chinese) |
| [9] |
Lennström D, Johnsson R, Agren A, et al. The influence of the acoustic transfer functions on the estimated interior noise from an electric rear axle drive[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2014, 7(1): 413-422. DOI:10.4271/2014-01-9124 |
| [10] |
丁晓明, 吕俊成, 王伟. 基于典型工况的汽车后桥壳结构轻量化优化设计[J]. 中国机械工程, 2016, 27(8): 1047-1052. DING Xiaoming, LYU Juncheng, WANG Wei. Light weight design of automobile rear axle housing based on typical conditions[J]. China Mechanical Engineering, 2016, 27(8): 1047-1052. (in Chinese) DOI:10.3969/j.issn.1004-132X.2016.08.010 |
| [11] |
马石磊, 李方义, 李剑峰, 等. 基于稀疏网格的近似模型及其在轻量化设计中的应用[J]. 机械工程学报, 2013, 49(7): 43-50. MA Shilei, LI Fangyi, LI Jianfeng, et al. Approximate model using sparse grid approach and its application in lightweight design[J]. Journal of Mechanical Engineering, 2013, 49(7): 43-50. (in Chinese) |
| [12] |
罗玉涛, 周斯加, 邓志君, 等. 基于双转子电动机的混合四轮驱动系统[J]. 机械工程学报, 2007, 43(8): 123-128. LUO Yutao, ZHOU Sijia, DENG Zhijun, et al. Four wheel driving hybrid system based on dual-rotor electric motor[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 123-128. (in Chinese) DOI:10.3321/j.issn:0577-6686.2007.08.022 |
| [13] |
比亚迪公司.电驱动桥总成及具有该电驱动桥总成的车辆: 中国, CN 102658770 A[P]. 2016-06-22. BYD Co., Ltd. Electric drive axle assembly and have the electric vehicle drive axle assembly: China, CN 102658770 A[P]. 2016-06-22. |
| [14] |
长城汽车股份有限公司.电机以及电驱动桥: 中国, 207910605U[P]. 2018-09-25. Great Wall Motor Co., Ltd. Motor and electric drive axle: China, CN 207910605U[P]. 2018-09-25. |
| [15] |
刘惟信. 汽车车桥设计[M]. 北京: 清华大学出版社, 2004. LIU Weixin. Automobile axle design[M]. Beijing: Tsinghua University Press, 2004. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

