中国大学生方程式赛事(Formula SAE,简称FSAE)从2010年开始举办,随着赛车的底盘与动力等技术的发展日趋稳定,空气动力学成为FSAE赛车设计的重要环节,并密切影响着赛车的动力性、经济性与操控稳定性。基于弯道多、转弯半径小、平均速度约为50 km/h的赛道特点,FSAE赛车空气动力学套件开发的主要目的是在低速时产生尽可能多的负升力,提高轮胎侧偏刚度与侧向加速度以提高弯道极限[1]。尾翼是安装在赛车后部的空气动力学部件之一,是重要的负升力来源,其产生的负升力约占整车空气动力学套件的35%左右[2]。文献[3]论证了CFD技术在该赛事运用的优异性,并为赛车设计了全套空气动力学套件,提升了其性能;文献[4]对赛车进行了圈速仿真,表明下压力可以显著提升赛车的弯道极限;文献[5]对FSAE赛车尾翼气动性能进行了研究;文献[6]对比分析了翼面造型对前翼尾翼性能的影响。从目前国内外的研究来看,对FSAE赛车空气动力学分部件及其组合性能的研究较多,而对各气动部件在整车流场中受到的影响、变化规律以及相应的优化方式研究较少。
针对上述问题,笔者利用有限元方法(CFD)分析影响大学生方程式赛车尾翼负升力的内部和外部因素,探究并总结出提高赛车尾翼负升力效率的有效方法。
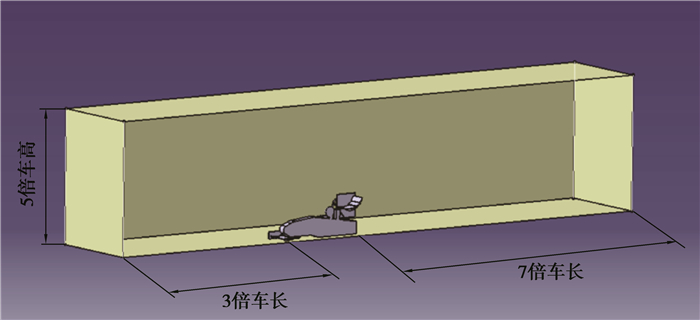
1 计算模型 1.1 整车计算域及网格划分选取FSAE赛事中典型的赛车外观并利用三维建模软件CATIA建立了赛车的三维模型,省略了车辆悬架杆件,简化了车辆侧箱、座舱内部细节和车轮,以便于网格划分和流场计算;建立流场计算域,车辆前部距离流场入口为车长的3倍,尾部距离出口为车长的7倍,计算域高度为车高的5倍,宽度为半车宽的5倍,同时考虑到模型具有对称面,取整车模型的半边以减小计算量[7],如图 1所示。
|
图 1 整车半边模型及计算域模型 Figure 1 Vehicle half-side model and calculation domain model |
利用ICEMCFD网格划分软件,采用Robust(Octree)方法进行四面体非结构网格的划分;对车辆附近的体网格,以及各翼片前缘、后缘和车身表面复杂曲面进行加密,同时全局网格基于曲率和近似度加密;在流体计算软件Fluent中将四面体网格转换为多面体网格以节省计算资源。
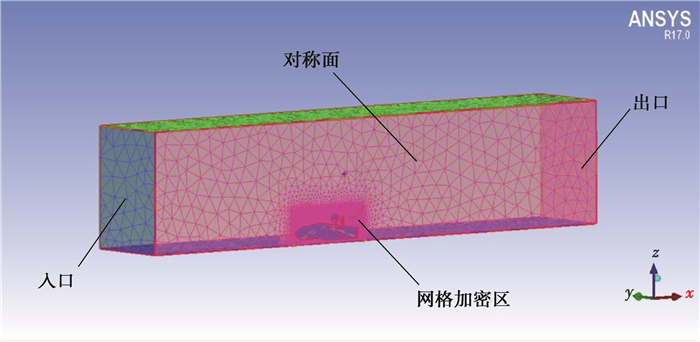
网格划分结果如图 2所示,网格节点总数为754 082,单元总数为3 037 990。
|
图 2 计算域整体网格划分 Figure 2 Computing domain overall meshing |
大学生方程式赛车流场的仿真属于求解湍流流动的问题,马赫数 < 0.3,首先给出适用于任何复杂湍流流动的流体运动的控制方程即N-S方程。
连续方程
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0, $ | (1) |
动量方程
| $ \rho \frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial t}} + \rho {\mathit{\boldsymbol{u}}_i}\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\mu _{eff}}\left( {\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial {x_j}}} + \frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial {x_i}}}} \right)} \right] - \frac{{\partial p'}}{{\partial {x_i}}}, $ | (2) |
式中:ui、uj为速度张量;ρ为空气密度;p′为修正压力;有效粘度系数μeff=μ+μt。
1.2.2 湍流模型需要附加湍流方程对式(1)(2)进行求解,考虑到赛车车身空套的壁面高应变率和大程度的流线弯曲,为尽可能详细地模拟赛车周围流场细节,选取Realizable k-ε模型,该模型被证明在车辆外流场仿真中能给出相对精确的结果。
湍动能方程k
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {\mathit{x}_i}}} = \frac{\partial }{{\partial {\mathit{x}_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon , $ | (3) |
湍动能耗散方程ε
| $ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {\mathit{x}_i}}} = \frac{\partial }{{\partial {\mathit{x}_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{\varepsilon }{k}\left( {{C_{\varepsilon 1}}{C_k} - {C_{\varepsilon 2}}\rho \varepsilon } \right), $ | (4) |
式中:μ为层流粘性系数;μt为湍流粘性系数,且μt=ρCμk2/ε;Cε1、Cε2、σk、σε均为经验常数,软件中的取值分别为1.44,1.92,1.00和1.30;Gk为由层流速度梯度产生的湍流动能[8]。
1.3 参数设置流场计算域入口设置为速度入口(velocity inlet),流速u=20 m/s;出口设置为压力出口;地面设置为滑移壁面,滑移速度为20 m/s,方向与流速方向相同;采用压力基求解器,空气温度T=288 K,静压p0=101.325 kPa,空气密度ρ=1.225 kg/m3,运动黏度ν=1.460 7×10-5m2/s;求解方法为压力耦合方程组的半隐式方法,压力离散格式为standard,动量、湍流强度、湍流耗散率的离散格式为2阶迎风[9]。
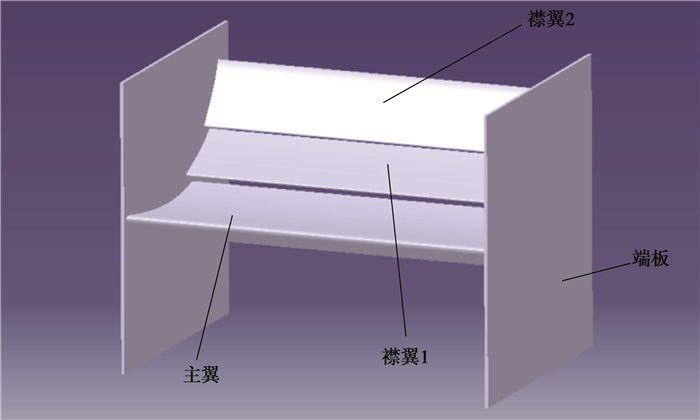
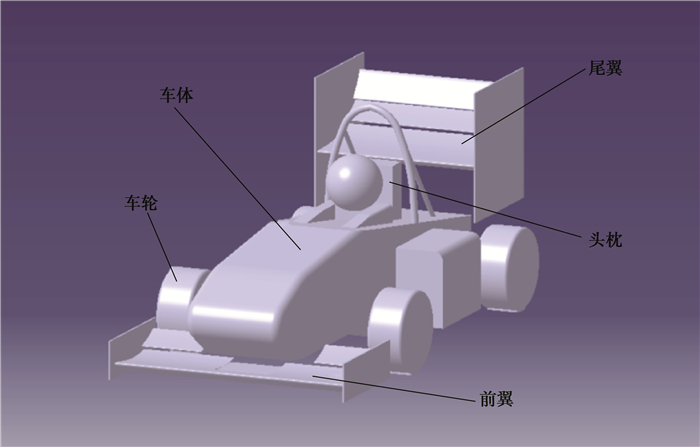
1.4 大学生方程式赛车三维模型尾翼,又称后定风翼,是安装于赛车后部的具有翼片作用特性的气动特征部件,作用为在赛车后部产生下压力并提供一定俯仰力矩,通常由翼片和端板2种基本结构组成,如图 3、4所示。
|
图 3 尾翼结构示意图 Figure 3 Schematic diagram of the tail structure |
|
图 4 整车简化计算模型示意图 Figure 4 Schematic diagram of the simplified vehicle |
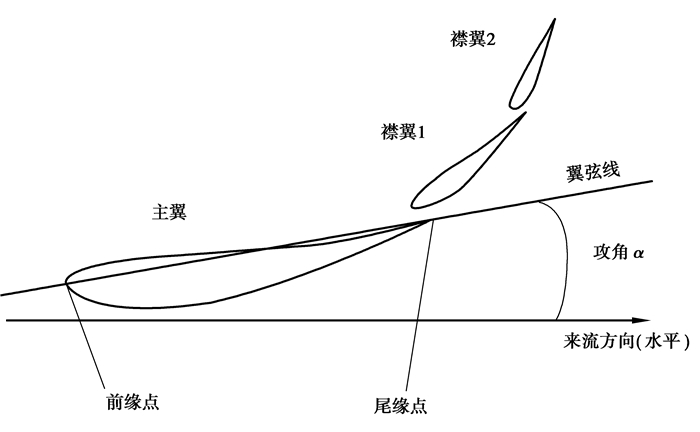
笔者采用尾翼模型为赛事中常见的三翼片布置形式[10],具体参数如图 5、6和表 1所示。
|
图 5 尾翼结构布置示意图 Figure 5 Schematic diagram of the tail structure |
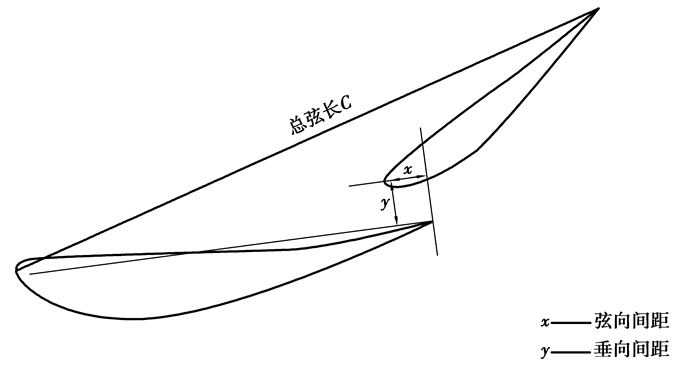
|
图 6 组合翼片缝道参数示意图 Figure 6 Schematic diagram of the combined airfoil seam parameters |
| 表 1 尾翼结构参数 Table 1 Tail structure parameters |
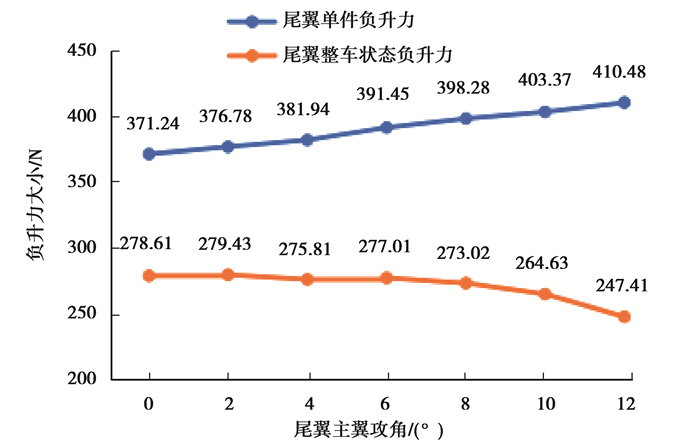
在所有翼片均不发生失速的情况下,进行尾翼主翼攻角单一变量的调整,对比其在单件状态和整车状态中对尾翼负升力数值的影响,结果如图 7所示(单件状态即仅保留三维尾翼实体,并保持与整车相同的在计算域中的相对位置)。
|
图 7 尾翼负升力特性随主翼攻角变化情况 Figure 7 The negative lift characteristics with the angle of attack of the main wing |
用式(5)来描述尾翼整车状态下负升力特性与单件状态负升力特性的关系:
| $ {F_r} = {F_{{\rm{r0}}}} \times \eta , $ | (5) |
式中:Fr为整车状态下尾翼负升力,Fr0为单件状态下尾翼负升力;定义η为尾翼剩余负升力系数,η值越大,则整车状态下尾翼负升力损失越小,负升力产生效率越高。图 8给出了尾翼主翼攻角在0°~12°变化区间内相应的剩余负升力系数值及变化趋势。
由以上可知,单件状态下尾翼负升力随主翼攻角的变化近似是线性的[11],而在整车状态下变化趋势不再满足线性,并且相较于单件状态,在整车状态时负升力下降明显,仅为单件状态下的60%~75%,造成这些差异的原因是整车流场中,尾翼受到了赛车其他部件的影响,并且在不同的尾翼主翼攻角下,尾翼受到影响的程度是不同的。
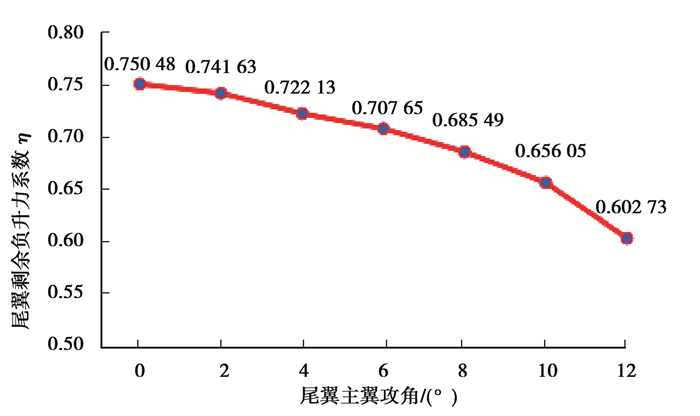
|
图 8 尾翼主翼攻角0°~12°区间剩余负升力系数变化趋势 Figure 8 Trend of residual negative lift coefficient in the range of 0° to 12° angle of attack of the main wing of the tail |
定义:
| $ \eta = {\eta _1} \times {\eta _2}, $ | (6) |
η1记作受遮挡剩余负升力系数,η2记作受前翼影响剩余负升力系数,有:
| $ {\eta _1} = \frac{{仅在车身影响下的尾翼负升力数值}}{{尾翼单件状态负升力数值}}, $ | (7) |
| $ {\eta _2} = \frac{{前翼和车身共同影响下的尾翼负升力数值}}{{仅在车身影响下的尾翼负升力数值}}。$ | (8) |
由此计算得到尾翼的受遮挡剩余负升力系数η1数值及其随主翼攻角的变化趋势如表 2所示。
| 表 2 主翼攻角0°~12°区间尾翼受遮挡负升力与剩余负升力系数 Table 2 Absorbing negative lift and remaining negative lift coefficient of the tail of the main wing angle of attack from 0° to 12° |
车身的存在遮挡了尾翼,对尾翼造成相应影响,同时还会对前翼的下游气流造成干扰,因此系数η2的定义中包含了车身遮挡的部分,以使前翼对尾翼的影响情况更接近实际,故受前翼影响剩余负升力系数η2需要由η和η1共同导出,具体结果如表 3~5所示。
| 表 3 前翼襟翼15°~35°区间两种尾翼设置下的负升力情况 Table 3 Negative lift conditions of the two types of tail fins in the 15° to 35° range of the front wing flaps |
| 表 4 0°尾翼主翼攻角时系数η2与前翼襟翼角度变化关系 Table 4 Relationship between the coefficient η2 and the angle of the front wing flap at the angle of attack of the main wing of 0° tail |
| 表 5 10°尾翼主翼攻角时系数η2与前翼襟翼角度变化关系 Table 5 Relationship between the coefficient η2 and the angle of the front wing flap during the attack angle of the main wing of the 10° tail |
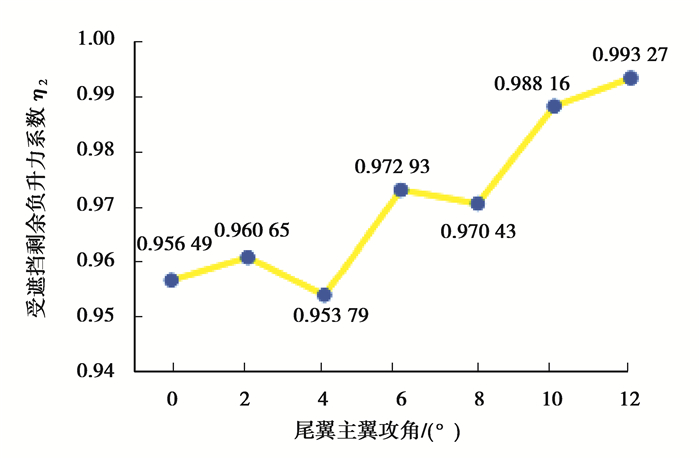
保持前翼参数不变,前翼襟翼攻角设为30°,选取尾翼主翼攻角0°~12°范围进行仿真,受前翼影响剩余负升力系数η2变化趋势如图 9所示。
|
图 9 30°前翼襟翼设置下尾翼攻角0°~12°区间系数η2变化趋势 Figure 9 30° front wing flap setting under the angle of attack angle η2 of the tail angle of 0° to 12° |
由以上结果可知,2个系数随尾翼主翼攻角的变化趋势近似是相反的,而两者的乘积即尾翼剩余负升力系数η总体上随着尾翼主翼攻角的增大而减小。
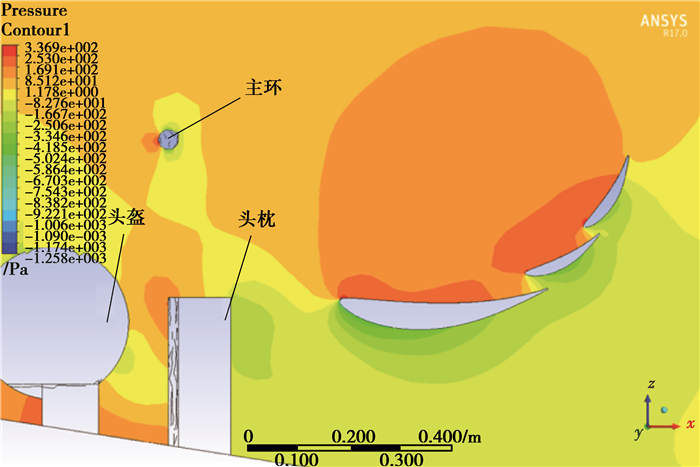
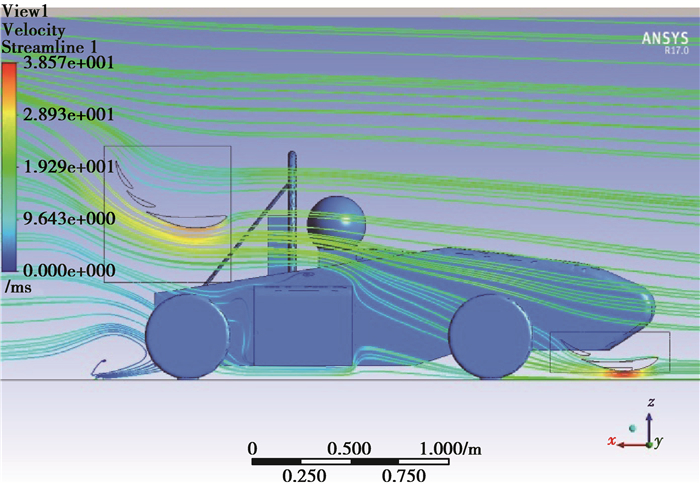
气流在绕过头枕、头盔等特征时会在其后方形成分离涡(如图 10),该部分涡流在一定区域内低速自旋,其位置通常正好位于尾翼翼片下方,分离涡对翼片下表面负压造成扰动并使负压减小,从而使尾翼损失负升力[12];将该部分影响归纳为分离涡引起的尾翼面负压区的破坏。前翼和车身的干扰使气流在其下游形成升流[13],这部分到达尾翼的气流相比远处的直匀流有了一定的角度,从而使尾翼翼片的等效攻角减小[14](如图 11),绕翼环量值发生变化,尾翼产生负升力的能力降低;将该部分影响归纳为上升气流引起的尾翼实际攻角降低。尾翼的负升力特性是二者共同作用的结果。
|
图 10 头枕、头盔等遮挡物对尾翼的影响压力云图 Figure 10 Pressure shadow of the impact of the headrest, helmet and other coverings |
|
图 11 赛车前部升流对尾翼的影响流线图 Figure 11 Flow chart of the influence of the front lift of the car on the tail |
| 表 6 主翼攻角0°~12°区间尾翼迎风面积(X方向) Table 6 Main wing angle of attack 0° to 12° interval tail windward area (X direction) |
由表 7数据可知,随着尾翼主翼攻角的增大,尾翼的迎风面积增加,但受限于规则尾翼最高点始终需要与地面保持1 200 mm的距离,因此主翼片将更加靠近头枕等遮挡部件的气流分离区,尾翼的负升力损失增加,故η1值随尾翼主翼攻角增大而减小;前翼襟翼攻角的增大使其下游气流上升趋势更加显著,从而使尾翼翼片的等效攻角减小,产生负升力的能力因此下降,增大尾翼主翼的攻角即增大了等效攻角,因此尾翼产生负升力的能力重新得到提升,故η2值随主翼攻角增大而增大。
| 表 7 分段式尾翼与常规尾翼负升力特性对比 Table 7 Comparison of negative lift characteristics between segmented tail and conventional tail |
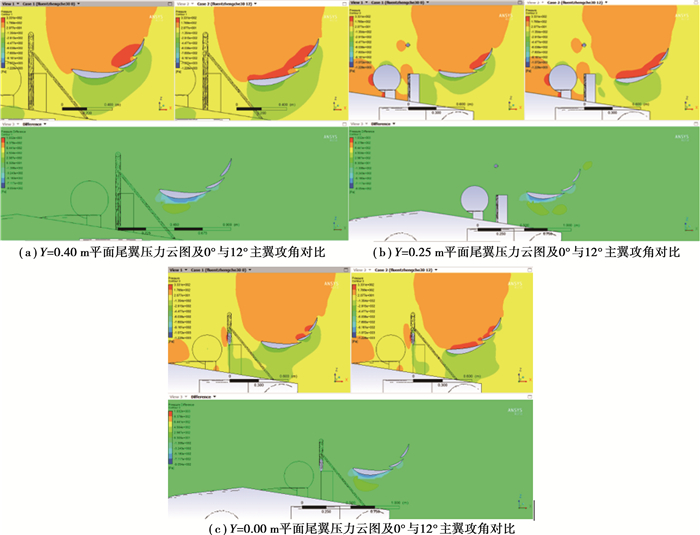
对比如图 12所示的尾翼翼展方向不同位置的压力云图可以发现,尾翼外端未被前方车体部件遮挡的分段其上下表面压差随尾翼主翼攻角的增大而增大,即产生负升力的能力得到增强;而在被遮挡的中间分段则呈现出相反的趋势,产生负升力的能力被削弱[15]。
|
图 12 尾翼翼展向不同位置压力云图对比情况 Figure 12 Comparison of pressure cloud maps of different wings at different positions |
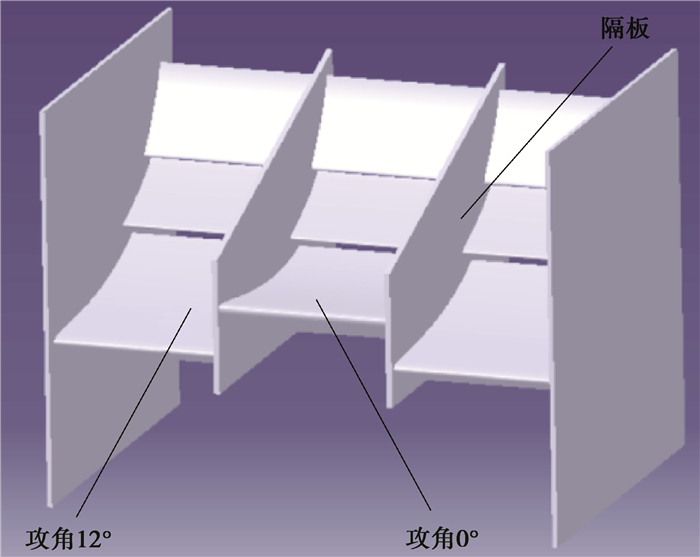
在不同的分段内对不同的影响方式作出相应的优化,如图 13所示,将尾翼按翼展向分作3段,对于翼展中段,减小翼片攻角以适应受遮挡剩余负升力系数的变化规律;对于外侧段调大攻角以适应受前翼影响剩余负升力系数的变化规律,不同分段之间增加隔板加以分割和连接。
|
图 13 带隔板的分段式尾翼设计示意图 Figure 13 Schematic diagram of the segmented tail design with partition |
表 7给出了0°主翼尾翼、12°主翼尾翼和分段式尾翼3种方案在单件状态和整车状态下的负升力以及在整车中的剩余负升力系数。由表 8数据可知,分段处理增强了应对相应干扰的针对性,在总体系数上得到了提升。
将隔板拆除,保留现有分段参数并以平滑曲面过渡连接,得到如图 14的多截面曲面主翼式尾翼方案,在表 8中给出了该方案与上述3种尾翼方案的负升力特性对比。

|
图 14 多截面曲面主翼式尾翼设计示意图 Figure 14 Schematic diagram of multi-section curved main wing tail design |
| 表 8 多截面曲面主翼式尾翼负升力特性 Table 8 Negative lift characteristics of main wing tail of multi-section curved surface |
在本案例中,尽管分段式尾翼和多截面主翼式尾翼在单件负升力和整车负升力绝对数值上较常规方案并没有突破,但在适应整车状态下各种干扰因素的能力明显优于常规尾翼;在FSAE赛车中尾翼前方的各种干扰是不可避免的,现实中的赛车对尾翼的干扰因素更是远多于简化的仿真模型,因此提升优化尾翼在整车状态中的效率比提高单件状态的负升力数值更有意义。
4 结论1) 尾翼在整车流场中的负升力特性不同于单件状态下的特性,单一的增大主翼攻角以增大尾翼所产生负升力的方法在整车状态下不适用。
2) 在整车状态时车身遮挡和前翼下游气流对尾翼负升力的影响均与尾翼主翼攻角近似呈线性关系,但变化趋势相反。
3) 针对不同干扰,通过分段优化得到的分段式尾翼和多截面曲面尾翼是提升尾翼在整车状态中负升力产生效率的较优方案。
| [1] |
潘小卫.赛车CFD仿真及风洞试验研究[D].长沙: 湖南大学, 2009. PAN Xiaowei. Analysis and optimization of some racing car on aerodynamic characteristics[D]. Changsha: Hunan University, 2009.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10532-2009164505.htm |
| [2] |
柏秋阳, 王辉, 李嘉凡, 等. FSAE赛车空气动力学套件组合设计分析[J]. 合肥工业大学学报(自然科学版), 2016, 39(5): 592-597, 676. BAI Qiuyang, WANG Hui, LI Jiafan, et al. Combinational design and analysis of aerodynamics devices of FSAE racing car[J]. Journal of Hefei University of Technology(Natural Science), 2016, 39(5): 592-597, 676. (in Chinese) DOI:10.3969/j.issn.1003-5060.2016.05.004 |
| [3] |
张璇.基于CFD技术的FSC赛车外流场分析及优化[D].锦州: 辽宁工业大学, 2017. ZHANG Xuan. Analyze and optimize FSC racing outflow field based on CFD[D]. Jinzhou: Liaoning University of Technology, 2017.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10154-1017050946.htm |
| [4] |
孙文.基于CFD的低速赛车前后翼设计[D].长沙: 湖南大学, 2016. SUN Wen. The design of low-speed racecar inverted wings based on CFD[D]. Changsha: Hunan University, 2016.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10532-1016252133.htm |
| [5] |
俞凯南, 谢世滨. 基于CFD的FSAE赛车尾翼设计及优化研究[J]. 机电工程, 2018, 35(1): 16-21. YU Kainan, XIE Shibin. Raer wing design and optimization for formula sae car based on CFD[J]. Journal of Mechanical & Electrical Engineering, 2018, 35(1): 16-21. (in Chinese) DOI:10.3969/j.issn.1001-4551.2018.01.003 |
| [6] |
周涛, 曾忠. FSAE赛车新型曲面前翼尾翼气动优化设计[J]. 重庆大学学报, 2017, 40(10): 40-52. Zhou Tao, Zeng Zhong. Optimal aerodynamic design for formula SAE car using curved wings[J]. Journal of Chongqing University, 2017, 40(10): 40-52. DOI:10.11835/j.issn.1000-582X.2017.10.005 |
| [7] |
周涛.基于CFD的大学生方程式赛车空气动力学套件设计[D].重庆: 重庆大学, 2017. ZHOU Tao. Aerodynamics kits design for formula SAE race car based on CFD[D]. Chongqing: Chongqing University, 2017.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1017722123.htm |
| [8] |
Hetawal S, Gophane M, Ajay B K, et al. Aerodynamic study of formula SAE car[J]. Procedia Engineering, 2014, 97: 1198-1207. DOI:10.1016/j.proeng.2014.12.398 |
| [9] |
Soliman A, Martins M, Schommer A.Formula SAE Aerodynamics: Design process with focus on drivability[J/OL]. SAE International, 2015: 2015-36-0359.(2015-09-22).[2018-10-12].https://doi.org/10.4271/2015-36-0359.
|
| [10] |
毛旭, 吴宁宁. FSAE赛车新型定风翼型气动性能的提升[J]. 机械科学与技术, 2014, 33(9): 1397-1402. MAO Xu, WU Ningning. Aerodynamic performance improvement of a new type wing for formula SAE car[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(9): 1397-1402. (in Chinese) |
| [11] |
Mcbeath S. Competition car aerodynamics 3rd edition[M]. Dorset: Veloce Publishing Ltd, 2015.
|
| [12] |
朱发旺. FSC赛车车身空气动力学特性分析研究[D].太原: 中北大学, 2017. ZHU Fawang. Aerodynamics characteristics analysis on FSC racing car[D]. Taiyuan: North University of China, 2017.(in Chinese) |
| [13] |
Gabbasa A, Arslan S, Jawad B, et al. Aerodynamic shape optimization for a 3-D multi-element airfoil[J/OL]. SAE International, 2014: 2014-01-0296. (2014-04-01)[2018-10-31].https://doi.org/10.4271/2014-01-0296.
|
| [14] |
Zhang Y, Yang C, Wang Q, et al.Aerodynamics of Open Wheel Racing Car in Pitching Position[J/OL]. SAE International, 2018: 2018-01-0729.(2018-04-03)[2018-10-06].https://doi.org/10.4271/2018-01-0729.
|
| [15] |
Anderson J D Jr. Fundamentals of aerodynamics[M]. 5th ed. New York: McGraw-Hill, 2009.
|
 2019, Vol. 42
2019, Vol. 42


