动态摄影测量技术是综合应用摄影测量、计算机视觉和数字图像处理知识来测量对象动态性能的一种新兴技术,具有非接触、无附加质量、全场测量及操作简易等优点[1-2]。人工标志具有显著图像特征,通常用人工标志辅助测试,使被测结构具有清晰且辨识度高的纹理特征,可有效提高测量精度。随着测量对象结构大型化、复杂化(例如风力机叶片、飞机机翼等),所需人工标志和拍摄图像数量急剧增多。快速、准确地实现目标标志的识别、定位和匹配成为自动化测量的关键。人工标志分为编码标志与非编码标志两大类。编码标志通过纹理的设计与排列可以产生不同的编码信息与各个纹理唯一对应[3],尤其适用于大尺寸拼接测量和动态测量场合,可以克服摄像机分辨率限制、视场遮挡运动引起目标偏移等因素影响,实现自动化测量。
摄影振动测量的本质是通过单目在时域上的多目标匹配以及双目在空间域上的多目标匹配,最终实现时空域联合的多目标自动识别、定位、追踪和匹配,获得目标点的时域振动响应[4]。现有的摄影测振方法主要是通过在物体表面粘贴特征标志或者喷涂纹理的方式实现特征点或者特征区域的动态追踪匹配。文献[5]对摄影测量技术的最新发展趋势进行了综述,并将摄影测量技术与结构动力学中使用的其他测量技术进行了比较,总结了各种方法的优缺点。文献[6-8]中应用摄影测量技术分别对薄膜结构、Gwangan大桥悬索和风力机叶片进行了动态变形测试;Sarrafi等[9]提出了一种基于相位运动估计和运动放大的风力机叶片振动损伤检测方法;Hassan等[10]研究了基于摄影测量的二维数字图像相关非接触式测量方法;Poozesh等[11]提出了一种基于动态空间数据拼接的多摄像机测量系统用于分布大尺寸全场测量;徐秀秀[12]和Romaszko等[13]利用单相机对悬臂梁进行振动测量;王彤等[14]基于视频测量实现了轻质风扇叶片、若干树叶等结构的几何建模,并进一步结合商业软件进行运行模态分析;Poozesh等[15]采用光学摄影方法跟踪风力机叶片表面的标志点实现位移测量,并提出了融合盲源信号分离和最小二乘复频域模态辨识的运行模态分析方法。以上研究表明摄影测量技术广泛用于动态应变测试、振动测量和模态分析等领域。在已有的基于点追踪方法的研究中,采用非编码圆形标志,识别定位简单但标志特征不具有唯一性,动态测量时易发生错误匹配情况,不适用于多标记点自动追踪匹配;采用圆点或环型组合的编码标志,识别和定位算法复杂且受拍照角度影响易发生变形,识别误差较大。在大尺寸动态测量的实际应用中,需要根据被测对象大小布设相当数量的标志点,因此,研究具有唯一辨识特征纹理的简单标志及其追踪识别方法具有重要意义,用于目标的自动识别、精确定位和快速匹配,能够大大提高大尺寸结构动态测量的效率与精度。
笔者提出一种简易可靠的字符编码标志,应用于摄影振动测量进行大尺寸结构多目标的自动化测量。基于图像特征提取技术与BP神经网络训练模型识别解码字符标志,并采用灰度质心法获取相应编码标志的亚像素坐标,通过码值匹配实现动态测量的目标追踪,进一步实现时空域联合的多目标自动识别、定位、追踪和匹配,获得目标点的精确时域振动响应。以某型风力机叶片为测试对象,对冲击激励下的标志进行字符识别追踪,获得时域振动响应后进行频谱分析,并与锤击实验结果进行对比验证。
1 编码标志识别定位方法字符编码标志设计示意图如图 1所示,不同字符图案对应唯一的码值,实心圆与字符部分灰度具有显著的差异,字符形状与实心圆叠加组合构成一个字符编码标志。通过对字符编码标志上的字符进行识别,可实现快速精确解码,圆形标志易于精确定位,适用于动态匹配以及大视场拼接等场合。
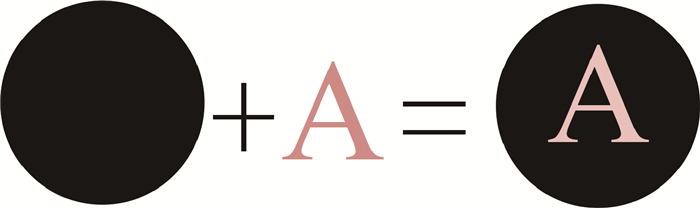
|
图 1 编码标志设计示意图 Figure 1 Design scheme of the proposed coded target |
字符特征提取是保证字符识别准确率的关键步骤之一。在实际测量中,背景噪声、标签的反射等因素都会降低标志图像的成像质量,所以需要对采集的图像进行预处理与图像复原等,为后续的特征分割、字符提取提供保障。
1.1 字符识别首先采用自适应维纳滤波方法[16]对采集的图像进行复原,降噪的同时保留了特征的细节边缘。由于现场测试背景光强不能保证均匀,对复原后的图像分块处理,采用自适应局部阈值法根据灰度分布选取合理阈值进行字符特征分割,获得待识别的字符。
基于BP神经网络训练的字符识别,首先要生成一个训练模型,训练样本包括拟应用于编码的字符形状及其相应的旋转、倾斜、噪声、局部变形、径向变形、笔画宽度变化、放大、缩小后的变体样本库,大量的变形样本可提高分类器的正确识别率。在BP神经网络训练的过程中,会自动提取字符形状的特征向量,例如字符的笔划宽度、笔划方向、噪声程度、灰度值等,映射到某一个输出结果,并根据目标向量与输出结果的误差反向调节字符识别网络的权值,训练得到最理想的网络模型。选取“王”、“开”、“中”、“十”、“又”等汉字为编码字符,设计出相应的编码标志,用手机拍摄的编码标志原始图像如图 2所示。图 3给出了图像预处理、阈值分割以后获得的字符区域及字符识别结果,表明字符识别完全正确。

|
图 2 原始图像 Figure 2 Original image |

|
图 3 字符分割及识别结果 Figure 3 Character segmentation and recognition results |
分割图像获得字符区域Achar和不含字符的圆区域Acircle,对实心圆的内部缺失部分进行填充修复,得到完整的圆形标志区域。由于不同字符具有形状差异,为了进行精确的标志中心定位,对整体区域进行灰度平滑。对两部分区域的灰度求平均,引入平滑因子灰度均值M,计算式为
| $ M = \frac{1}{2}\left( {\frac{1}{M}\sum {{I_{{\rm{char}}}}\left( {x,y} \right)} + \frac{1}{2}\sum {{I_{{\rm{circle}}}}\left( {x,y} \right)} } \right), $ | (1) |
式中:Ichar(x, y)、Icircle(x, y)分别代表区域Achar和Acircle的像素灰度值;m、n分别代表相应区域的像素个数。
则区域Achar和Acircle灰度平滑后的像素点灰度值I′char和I′circle分别为
| $ {{I'}_{{\rm{char}}}} = {I_{{\rm{char}}}} - M,{{I'}_{{\rm{circle}}}} = {I_{{\rm{circle}}}} + M。$ | (2) |
采用灰度质心法求取标志的中心坐标,可以达到亚像素级的定位精度,计算公式为
| $ {X_c} = \frac{{\sum {{P_i}{x_i}} }}{{\sum {{P_i}} }},{Y_c} = \frac{{\sum {{P_i}{y_i}} }}{{\sum {{P_i}} }}, $ | (3) |
式中:(xi, yi)表示区域中第i点的像素坐标;Pi表示区域Achar和Acircle灰度平滑以后的各个像素点的灰度值。
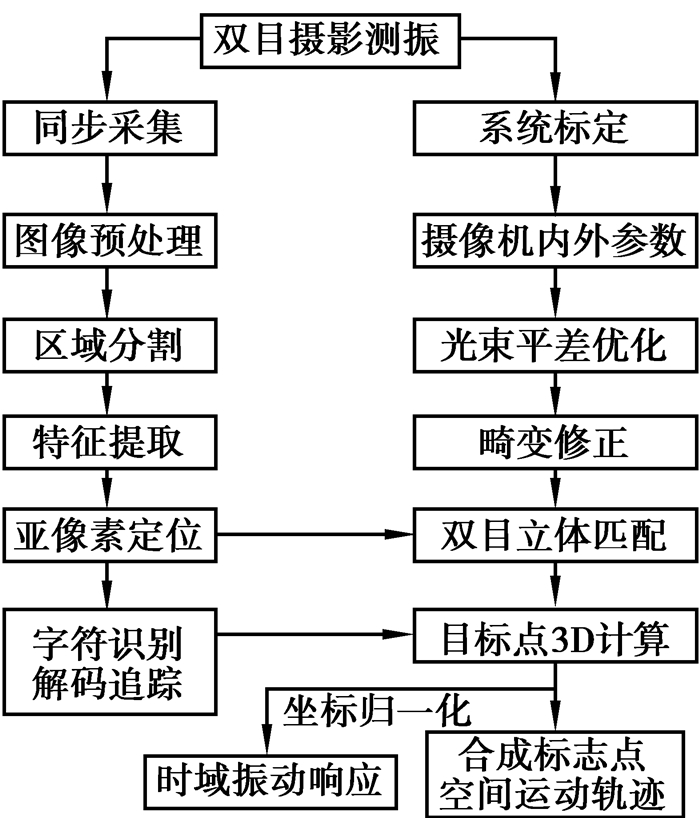
2 双目摄影振动测量原理基于字符编码标志识别追踪的双目摄影测振方法的具体技术路线如图 4所示,分3步实现。首先是测量系统标定,即对2个摄像机的内、外参数求解;其次是标志中心定位与字符识别追踪;最后是目标(特征)的立体匹配成像三维坐标计算及振动响应求解。
|
图 4 双目摄影测振方法流程图 Figure 4 Flow chart of vibration measurement with binocular photogrammetry |
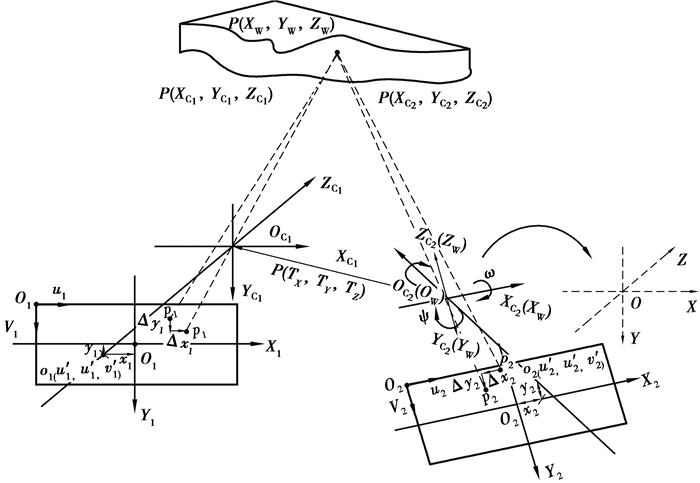
采用考虑径向畸变和切向畸变的小孔非线性成像模型,图 5给出了双摄像机空间交会立体成像模型。为了完整描述理论,做如下定义:下标1和2分别代表左、右摄像机,P点在三维世界坐标系(OW-XWYWZW)、左摄像机坐标系(OC1-XC1YC1ZC1)、右摄像机坐标系(OC2-XC2YC2ZC2)中相应的坐标为P(XW, YW, ZW)、P(XC1, YC1, ZC1)、P(XC2, YC2, ZC2)。
|
图 5 双目立体成像模型 Figure 5 Stereo imaging model of binocular system |
进一步以左摄像机为例,定义摄像机坐标系(OC1-XC1YC1ZC1)中原点OC1为摄像机光学中心,ZC1轴与光轴重合;计算机像素坐标系(o1-u1v1)中u1、v1轴分别平行于XC1、YC1轴,横坐标和纵坐标值分别代表图像的列和行,单位为像素(pixel);图像平面坐标系(O1-X1Y1),O1为理想的主点,在像素坐标系中坐标值为(u01, v01),点P在左图像平面的理想像点为P1(xP1, yP1),因摄像机和光学镜头存在加工和装配误差,实际像点为P′1(x′P1, y′P1),实际主点为o′1(u′1, v′1),则
1) 图像坐标系中,实际像点坐标
| $ \left\{ \begin{array}{l} {{x'}_{{P_1}}} = {x_{{P_1}}} + \Delta {x_1} = {x_{{P_1}}}\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right) + 2{p_1}{x_{{P_1}}}{y_{{P_1}}} + {p_2}\left( {{r^2} + 2x_{{P_1}}^2} \right),\\ {{y'}_{{P_1}}} = {y_{{P_1}}} + \Delta {y_1} = {y_{{P_1}}}\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right) + 2{p_2}{x_{{P_1}}}{y_{{P_1}}} + {p_1}\left( {{r^2} + 2y_{{P_1}}^2} \right), \end{array} \right. $ | (4) |
式中:r2=xP12+yP12;Δx1、Δy1为畸变误差;k1、k2、k3为镜头径向畸变系数;p1、p2为切向畸变系数。
2) 图像平面坐标系到计算机像素坐标系的变换
| $ \left\{ \begin{array}{l} {u_{{P_1}}} = {{u'}_1} + {{x'}_{{P_1}}}/{d_{{x_1}}},\\ {v_{{P_1}}} = {{v'}_1} + {{y'}_{{P_1}}}/{d_{{y_1}}}, \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} {{u'}_1} = {u_1} + {x_1},\\ {{v'}_1} = {v_1} + {y_1}, \end{array} \right. $ | (6) |
式中:dx1和dy1分别表示一个像素在横轴x和纵轴y的宽度,单位mm/pixel;x1、y1为主点误差,可通过系统标定计算。
3) 摄像机坐标系到图像平面坐标系的变换
| $ \left\{ \begin{array}{l} {x_{{P_1}}} = {f_1}\frac{{{X_{{{\rm{c}}_1}}}}}{{{Z_{{{\rm{c}}_1}}}}},\\ {y_{{P_1}}} = {f_1}\frac{{{Y_{{{\rm{c}}_1}}}}}{{{Z_{{{\rm{c}}_1}}}}}, \end{array} \right. $ | (7) |
式中f1为摄像机焦距。
从图 5中可知,右摄像机坐标系(OC2-XC2YC2ZC2)即三维世界坐标系, 依次绕XC2、YC2、ZC2轴旋转ε、ψ、κ角度后得到的坐标系(O-XYZ)与左摄像机坐标系(OC1-XC1YC1ZC1)平行,原点OC1通过平移T与原点OC2重合,其中R为依次绕XC2、YC2、ZC2轴旋转ε、ψ、κ角度的旋转矩阵,可知:
| $ \mathit{\boldsymbol{R}} = \\ \left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}}\\ {{r_4}}&{{r_5}}&{{r_6}}\\ {{r_7}}&{{r_8}}&{{r_9}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \psi \cos k}&{ - \cos \psi \sin k}&{\sin \psi }\\ {\sin \varepsilon \sin \psi \cos k + \cos \varepsilon \sin k}&{ - \sin \varepsilon \sin \psi \sin k + \cos k\cos \varepsilon }&{ - \cos \psi \sin \varepsilon }\\ { - \sin \psi \cos \varepsilon \cos k + \sin \varepsilon \sin k}&{\sin \psi \sin k + \cos k\sin \varepsilon }&{\cos \psi \cos \varepsilon } \end{array}} \right] 。$ | (8) |
4) 三维世界坐标系到左摄像机坐标系的变换
| $ \left[ {\begin{array}{*{20}{c}} {{X_{{{\rm{C}}_1}}}}\\ {{Y_{{{\rm{C}}_1}}}}\\ {{Z_{{{\rm{C}}_1}}}} \end{array}} \right] = \mathit{\boldsymbol{R}} \cdot \left[ {\begin{array}{*{20}{c}} {{X_{{{\rm{C}}_2}}}}\\ {{Y_{{{\rm{C}}_2}}}}\\ {{Z_{{{\rm{C}}_2}}}} \end{array}} \right] + \mathit{\boldsymbol{T}}。$ | (9) |
运用齐次坐标,将式(9)写成矩阵形式,如下:
| $ \left[ \begin{array}{l} {X_{{{\rm{C}}_1}}}\\ {Y_{{{\rm{C}}_1}}}\\ {Z_{{{\rm{C}}_1}}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}}&{{T_X}}\\ {{r_4}}&{{r_5}}&{{r_6}}&{{T_Y}}\\ {{r_7}}&{{r_8}}&{{r_9}}&{{T_Z}} \end{array}} \right] \cdot \left[ \begin{array}{l} {X_{{{\rm{C}}_2}}}\\ {Y_{{{\rm{C}}_2}}}\\ {Z_{{{\rm{C}}_2}}}\\ 1 \end{array} \right]。$ | (10) |
根据公式(3)~(9)可得到计算机像素坐标到三维世界坐标的映射关系
| $ {z_{{{\rm{c}}_1}}}\left[ \begin{array}{l} {u_{{P_1}}}\\ {v_{{P_1}}}\\ 1 \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {1/{d_{{x_1}}}}&0&{{{u'}_1}}\\ 0&{1/{d_{{y_1}}}}&{{{v'}_1}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{f_1}}&0&0\\ 0&{{f_1}}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}}&{{T_X}}\\ {{r_4}}&{{r_5}}&{{r_6}}&{{T_Y}}\\ {{r_7}}&{{r_8}}&{{r_9}}&{{T_Z}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{\rm{w}}}}\\ {{Y_{\rm{w}}}}\\ {{Z_{\rm{w}}}}\\ 1 \end{array}} \right]。$ | (11) |
同理,可得右摄像机的计算机像素坐标到三维世界坐标的映射关系
| $ {z_{{{\rm{C}}_2}}}\left[ \begin{array}{l} {u_{{P_2}}}\\ {v_{{P_2}}}\\ 1 \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {1/{d_{{x_2}}}}&0&{{{u'}_2}}\\ 0&{1/{d_{{y_2}}}}&{{{v'}_2}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{f_2}}&0&0\\ 0&{{f_2}}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{\rm{w}}}}\\ {{Y_{\rm{w}}}}\\ {{Z_{\rm{w}}}} \end{array}} \right]。$ | (12) |
联合求解公式(11)(12),可计算出空间点P的三维坐标为
| $ \left\{ \begin{array}{l} {X_W} = {Z_W}{X_1}/{f_1},{Y_W} = {Z_W}{Y_1}/{f_1}\\ {Z_W} = \frac{{{f_l}\left( {{f_2}{T_Y} - {Y_2}{T_Z}} \right)}}{{{Y_2}\left( {{r_7}{X_1} + {r_8}{X_1} + {f_1}{r_9}} \right) - {f_2}\left( {{r_4}{X_1} + {r_5}{X_1} + {f_1}{r_6}} \right)}} \end{array} \right., $ | (13) |
其中
| $ \left\{ \begin{array}{l} {X_1} = \left( {{u_{{P_1}}} - {{u'}_1}} \right) \cdot {d_{{x_1}}},{Y_1} = \left( {{v_{{P_1}}} - {{v'}_1}} \right) \cdot {d_{{y_1}}},\\ {X_2} = \left( {{u_{{P_2}}} - {{u'}_2}} \right) \cdot {d_{{x_2}}},{Y_2} = \left( {{v_{{P_2}}} - {{v'}_2}} \right) \cdot {d_{{y_2}}}。\end{array} \right. $ | (14) |
对测点进行光束平差,以共线方程式作为数学模型,像点的像平面坐标观测值为未知数,使用Levenberg-Marquardt算法进行非线性优化估计得到精确的三维坐标。
3 实验与结果分析 3.1 摄影测量实验如图 6所示,系统硬件具体由大华A5131MU210工业摄像机(配computar 25 mm定焦镜头和三脚架)、图形图像工作站、触发控制器、棋盘格标定板、LED光源、合作标志贴及各种控制线、数据线、电源线若干组成,测试对象为1.6 m长、2.8 kg的某型3 kW风力机叶片实体模型,通过螺栓固定在地面钢架支撑结构上。摄像机的分辨率为1 280×1 024,像元尺寸是4.8 μm×4.8 μm,为保证测量精度,选取叶片末端一段约30 cm长度的部分进行动态测量,在叶片表面粘贴10个字符编码标志,调整摄像机的空间位置保证叶片的振动过程清晰成像,采用硬件TTL电平触发控制,确保双摄像机实现同步采集。

|
图 6 实验测试平台 Figure 6 Experimental test rig |
定义三维世界坐标系与左摄像机坐标系重合,原点在左摄像机光学中心点,采用棋盘格平面板进行测量系统参数标定,单个棋盘格的尺寸为30 mm×30 mm,两摄像机前方交会拍摄,标定板遍历整个视场区域,共取8个位置,可以有效矫正镜头畸变。采用张正友标定算法[17]计算得到系统外部参数为
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {0.961\;5}&{0.027\;1}&{0.273\;4}\\ { - 0.029\;0}&{0.999\;6}&{0.003\;0}\\ { - 0.273\;2}&{ - 0.010\;8}&{0.961\;9} \end{array}} \right],\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} { - 482.955\;3}\\ {0.659\;0}\\ {22.774\;5} \end{array}} \right], $ | (15) |
式中:平移矩阵T的结果表明左摄像机的光心与右摄像机的光心在水平(X)方向相距482.955 3 mm, 垂直(Y)方向相距0.659 0 mm,深度(Z)方向相距22.774 5 mm,与实验现场左、右摄像机的空间相对位姿情况相符,表明标定结果可靠。
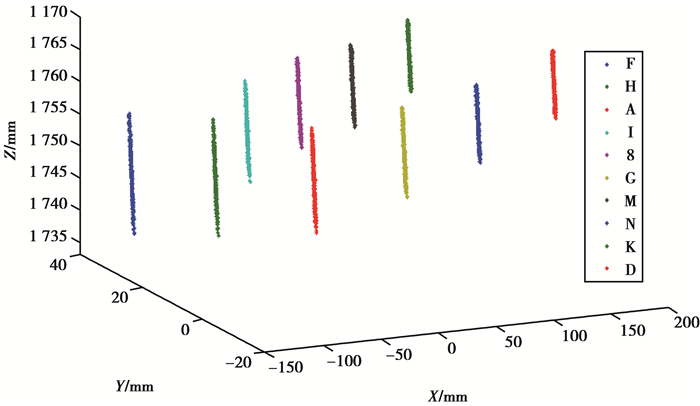
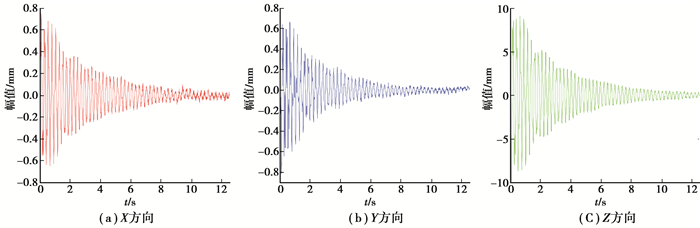
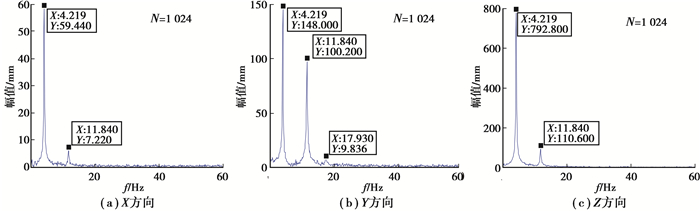
用力锤敲击叶片使其振动,摄像机采样频率设定为120 Hz,连续采集并存储1 500幅动态图像序列。基于数字图像处理技术分割字符,BP神经网络训练模型识别字符,如图 7所示,准确识别出了10个编码字符。对各个字符标志进行定位获取标志中心的图像坐标,通过字符解码对各编码标志实现追踪匹配,结合系统标定参数,计算各编码标志(即测点)的时域空间坐标,获得10个测点的空间运动轨迹如图 8所示,叶片主要沿着Z方向做往复运动且靠近叶尖的标志振幅最大。对每个测点的时域运动轨迹进行坐标归一化,使各测点的初始状态坐标变换到空间坐标系原点上,即可获得各测点的真实振动位移响应,图 9(a)~(c)分别为字符F编码标志在X、Y、Z方向上的振动响应。从图 9可知,叶片在X、Y、Z 3个方向都表现为有阻尼自由衰减振动,且Z方向振幅远远大于X、Y方向。进一步对测点F进行FFT频域分析,从图 10(a)~(c)中可知:3个方向的前2阶振动频率一致,1阶频率为4.219 Hz,2阶频率为11.840 Hz;在Y方向上峰值拾取得到3阶频率为17.930 Hz。

|
图 7 字符标志识别结果 Figure 7 Character recognition result |
|
图 8 编码标志空间运动轨迹 Figure 8 Trajectories of the coded targets in 3D space |
|
图 9 测点F的振动位移 Figure 9 Vibration displacement curves of target F |
|
图 10 FFT分析结果 Figure 10 FFT analysis results |
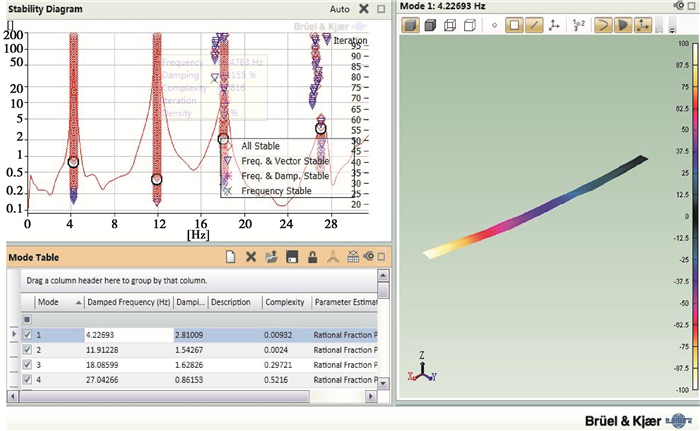
对叶片进行锤击法模态测试,采用B & K公司的测试系统,硬件包括8206-002力锤、4514B-001加速度传感器和3053-B-120采集卡,软件为PULSE的MTC Hammer模块和Reflex后处理模块。选用1个传感器粘贴在距离叶根30 cm处,建立叶片测试模型,敲击点均匀分布;对照模型对叶片上相应点进行敲击,力锤遍历模型上所有测点,采集卡同时采集力锤的输入信号与传感器的输出响应;利用最小二乘法复频域方法[18]计算得到模态稳定图,软件自动识别出叶片的前3阶模态频率,分别是4.227,11.912和18.086 Hz(见图 11)。
|
图 11 锤击法模态分析结果 Figure 11 Modal analysis results of hammer testing |
将字符追踪摄影法获得的叶片频率与锤击实验法的测量结果进行对比分析,可知前3阶固有频率的最大绝对误差为0.156 Hz,相对误差均小于0.9%,验证了提出的方法具有可行性且测量结果可靠。
4 结论笔者设计了一种由字符和圆叠加组合的编码标志,既有圆形特征的简单标志特性,通过字符编码又具有唯一性,满足人工编码标志的唯一辨识性要求且结构简单。引入该字符编码标志用于大尺寸结构动态摄影测量中,可通过字符识别解码进行目标的快速追踪匹配。在图像滤波和阈值分割的基础上采用BP神经网络训练模型进行字符分类识别能够实现准确解码,基于灰度平滑后的特征中心定位精度稳定可靠,提出的基于字符编码标志的摄影振动测量方法有效可行,可实现大尺寸结构中多目标的自动化、高精度测量。
| [1] |
Gwashavanhu B, Oberholster A J, Heyns P S. Rotating blade vibration analysis using photogrammetry and tracking laser Doppler vibrometry[J]. Mechanical Systems and Signal Processing, 2016, 76/77: 174-186. DOI:10.1016/j.ymssp.2016.02.019 |
| [2] |
Al-Kaff A, Martín D, García F, et al. Survey of computer vision algorithms and applications for unmanned aerial vehicles[J]. Expert Systems with Applications, 2018, 92: 447-463. DOI:10.1016/j.eswa.2017.09.033 |
| [3] |
XU Zhongxiong, Shao Guiwei, Wu Liang, et al. Automatic UAV positioning with encoded sign as cooperative target[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2017, 34(6): 669-679. |
| [4] |
Wang W Y, Li X J, Ahmat Y, et al. Vibration measurement method based on point tracking for irregular structures[J]. Optik, 2019, 176: 482-490. DOI:10.1016/j.ijleo.2018.09.100 |
| [5] |
Baqersad J, Poozesh P, Niezrecki C, et al. Photogrammetry and optical methods in structural dynamics-A review[J]. Mechanical Systems and Signal Processing, 2017, 86: 17-34. |
| [6] |
Jurjo D L B R, Magluta C, Roitman N, et al. Analysis of the structural behavior of a membrane using digital image processing[J]. Mechanical Systems and Signal Processing, 2015, 54/55: 394-404. DOI:10.1016/j.ymssp.2014.08.010 |
| [7] |
Kim S W, Kim N S. Dynamic characteristics of suspension bridge hanger cables using digital image processing[J]. NDT & e International, 2013, 59: 25-33. |
| [8] |
Yang J S, Peng C Y, Xiao J Y, et al. Application of videometric technique to deformation measurement for large-scale composite wind turbine blade[J]. Applied Energy, 2012, 98: 292-300. DOI:10.1016/j.apenergy.2012.03.040 |
| [9] |
Sarrafi A, Mao Z, Niezrecki C, et al. Vibration-based damage detection in wind turbine blades using Phase-based Motion Estimation and motion magnification[J]. Journal of Sound and Vibration, 2018, 421: 300-318. DOI:10.1016/j.jsv.2018.01.050 |
| [10] |
Hassan G M, Dyskin A V, MacNish C K, et al. A comparative study of techniques of distant reconstruction of displacement and strain fields using the DISTRESS simulator[J]. Optik, 2016, 127(23): 11288-11305. DOI:10.1016/j.ijleo.2016.09.026 |
| [11] |
Poozesh P, Baqersad J, Niezrecki C, et al. Large-area photogrammetry based testing of wind turbine blades[J]. Mechanical Systems and Signal Processing, 2017, 86: 98-115. DOI:10.1016/j.ymssp.2016.07.021 |
| [12] |
徐秀秀, 郭毓, 余臻, 等. 基于机器视觉的柔性臂振动测量研究[J]. 华中科技大学学报(自然科学版), 2013, 41(z1): 129-132. XU Xiuxiu, GUO Yu, YU Zhen, et al. Vibration measurement of flexible beam based on machine vision[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2013, 41(z1): 129-132. (in Chinese) |
| [13] |
Romaszko M, Sapiński B, Sioma A. Forced vibrations analysis of a cantilever beam using the vision method[J]. Journal of Theoretical and Applied Mechanics, 2015, 243. DOI:10.15632/jtam-pl.53.1.243 |
| [14] |
王彤, 李俊坡, 夏遵平, 等. 基于视频测量的运行状态模态分析[J]. 振动与冲击, 2017, 36(5): 157-163, 220. WANG Tong, LI Junpo, XIA Zunping, et al. Operational modal analysis based on videogrammetric technique[J]. Journal of Vibration and Shock, 2017, 36(5): 157-163, 220. (in Chinese) |
| [15] |
Poozesh P, Sarrafi A, Mao Z, et al. Modal parameter estimation from optically-measured data using a hybrid output-only system identification method[J]. Measurement, 2017, 110: 134-145. DOI:10.1016/j.measurement.2017.06.030 |
| [16] |
沈希忠, 叶秋泽. 基于维纳滤波的超声增强实现方法[J]. 数据采集与处理, 2018, 33(3): 455-460. Sheng Xizhong, Ye Qiuze. Implementation of ultrasonic enhancement based on wiener filtering[J]. Journal of Data Acquisition and Processing, 2018, 33(3): 455-460. (in Chinese) |
| [17] |
Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 |
| [18] |
Chu Z G, Huang D, Wang J, et al. Development of online detection system for natural frequency of brake discs based on the improved least squares complex frequency domain method[J]. Journal of Vibroengineering, 2017, 19(4): 2795-2805. DOI:10.21595/jve.2017.17798 |
 2019, Vol. 42
2019, Vol. 42


