2. 广东华路交通科技有限公司, 广州 510420
2. Guangdong Hualu Transportation Technology Co. Ltd., Guangzhou 51042, P. R. China
截至2018年底,我国高速公路通车里程突破1.4×105 km,高速公路建设从建设期转入养护期。高速公路沥青路面使用性能是结构设计、材料性能、施工质量、行车荷载、自然因素与养护维修等多方面综合作用的结果[1]。路面使用性能预测模型则是表征路面使用性能随时间、材料、行车荷载等因素变化的关系式[2]。精确的预测模型可辅助决定后期的养护决策与养护资金的合理分配,同时随着养护大数据时代的来临,养护数据的机器学习是人工智能的趋势,小样本预测模型亦可为养护大数据预测提供模型基础。因此,科学地建立路面使用性能预测模型对沥青路面养护具有重要意义。
目前,国内外路面使用性能预测模型有不确定性模型、确定性模型、动态模型和仿生模型4类[3]。常用的不确定性模型为灰色理论模型,该模型研究数据量少、预测精度高、计算方法简单,所以在路面使用性能预测中运用广泛,如Wang等[4]将该模型运用到路面平整度预测中。但该模型只是从已有的检测数据出发,没有考虑未来可能影响数据趋势的因素[5],随着预测周期增长,预测的稳定性和精度大大降低;同时该模型只考虑到时间对路面使用性能的影响,没有考虑自然环境、交通荷载等因素。确定性模型如孙立军等[6]提出的沥青路面性能衰变PPI方程,该模型主要利用沥青路面初始性能指数、路龄等因素,使用十分简单便利,但只利用初始的路面使用性能,无法合理利用动态数据,只能预测短期和大致的数据。运用最多的仿生模型为遗传神经网络模型,该模型可考虑各种影响因素,并且预测精度高,如Yang等[7]将该模型运用于车辙、行驶质量的预测中。但该模型过于依赖初值,收敛速度慢,且易于局部收敛。动态预测模型是在传统灰色模型的基础上建立的,如汪海年等[8]把美国PME模型和灰色预测理论与力学经验法结合起来,提出了动态灰色预测模型,并建立了DGM-PME组合模型,对车辙进行预测,该模型可以将后期的数据充分利用起来,可预测更长周期的数据,但该模型操作起来较为复杂。路面养护周期不需要太长,普通模型即可满足。
本研究综合考虑了国内外各类沥青路面使用性能预测模型,为弥补各类模型的缺陷,提出了基于灰色关联度分析(grey relation analysis,GRA)和支持向量机回归(support vector machine regression,SVR)的沥青路面使用性能预测模型,首先利用灰色模型中灰色关联度分析将影响沥青路面使用性能的因素进行属性预处理,找出主要影响因素,再利用支持向量机回归, 实现结构风险最小化,提高泛化性能,通过建立一个超平面作为决策曲面,最终建立沥青路面使用性能预测模型,为养护决策与后期养护资金投入提供依据,同时为未来大数据养护研究提供模型基础。
1 GRA-SVR基本原理 1.1 GRA灰色系统理论认为复杂的客观系统都是整体有序的,离散的数据必然蕴含着内在规律[9]。影响沥青路面使用性能的因素很多,但各因素对沥青路面使用性能的作用效果不是很清晰,呈现出灰色性。使用GRA可定量地反映沥青路面使用性能与各因素之间的关联度,可从影响沥青路面使用性能的众多因素中找到主要影响因素。其主要方法是将系统中的影响因素对应统计数据转化为几何曲线,根据灰色系统理论,曲线几何形状越接近,其关联程度越大[10]。
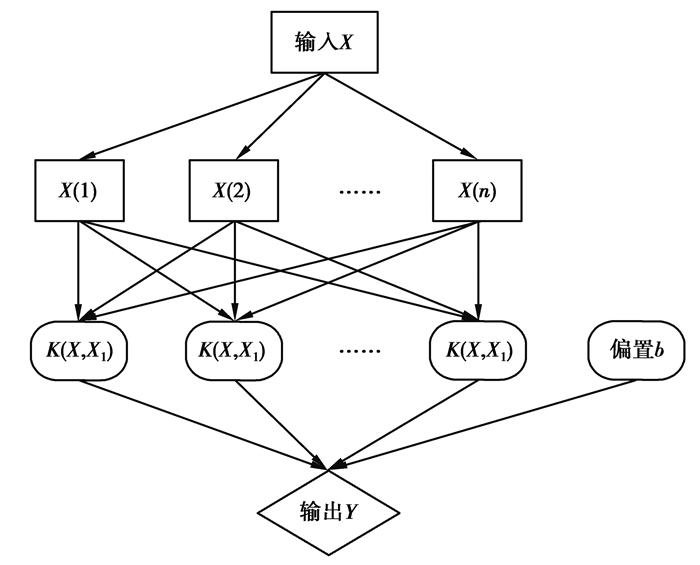
1.2 SVR支持向量机回归(SVR)是由支持向量机(support vector machine,SVM)衍生得到的模型。SVM是一种分类模型,是由VAPNIK所提出的一种机器学习方法,可解决小样本、非线性、高维数等问题[11-12]。其原理建立在统计学理论的VC维理论和结构风险最小化原理的基础上,通过建立最优的超平面,寻求数据挖掘中的最优解决方法[13-14]。通常我们的思维习惯于把样本进行降维来简化问题,而SVM方法恰恰相反,将样本点进行升维,通过核函数将样本点映射到高维甚至无穷维空间,在高维空间处理线性与非线性问题。支持向量机体系结构如图 1所示。
|
图 1 支持向量机体系结构图 Figure 1 Structure of support vector machine system |
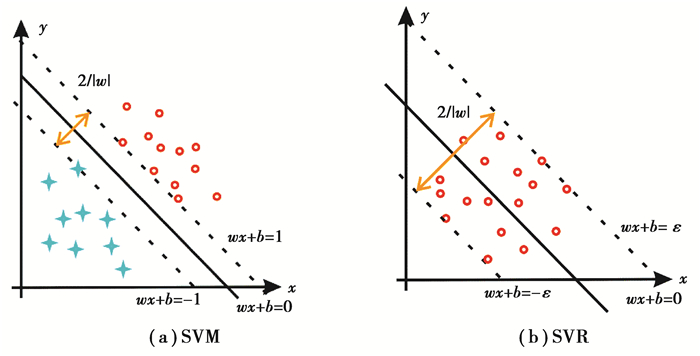
回归和分类从某种意义上讲本质相同,如图 2所示:SVM分类模型是找到一个超平面,让两个分类集合的支持向量或者所有的数据离分类平面最远;SVR回归模型是找到一个回归超平面,让一个集合的所有数据到该平面的距离最近。SVR可以通过建立训练数据中的待测数据与支持向量的非线性关系,对测试数据的预测向量进行预测。
|
图 2 SVM和SVR示意图 Figure 2 Diagrams of SVM and SVR |
SVR具体方法如下。
设样本集:(x1, y1), (x2, y2)…(xl, yl), x ∈ Rn, y ∈ R, R表示实数集。则样本集中y与x可通过方程表示为:
| $ f\left( \mathit{\boldsymbol{x}} \right) = w \cdot \mathit{\boldsymbol{x}} + b, $ | (1) |
式中w和b为超平面的系数。
若原始数据与支持向量机回归拟合良好,则使得
| $ \begin{array}{*{20}{c}} {\min \frac{1}{2}\left\| {{w^2}} \right\|}\\ {{\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} w \cdot {x_i} + b - {y_i} \le \varepsilon \\ {y_i} - w \cdot {x_i} - b \le \varepsilon \end{array} \right.,\;\;\;\;\;\;\;i = 1,2, \cdots ,l,} \end{array} $ | (2) |
式中ε为任意的一个正数。
引入拉格朗日对数对式(1)进行变化得到变形为:
| $ f\left( \mathit{\boldsymbol{x}} \right) = w \cdot \mathit{\boldsymbol{x}} + b = \sum\limits_{i = 1}^l {\left( {{\mathit{\boldsymbol{a}}_i} - \mathit{\boldsymbol{a}}_i^ * } \right)\left( {{x_i} \cdot \mathit{\boldsymbol{x}}} \right) + b} , $ | (3) |
式中ai和ai*为样本支持向量,大多数取值为零。
上述过程为SVR的线性回归原理。在处理SVR的非线性问题时,将样本xi通过Ψ:x→H映射到一个高维空间。为构造出最优的超平面,在Ψ未知的情况下,利用原空间参数实现内积运算。为了解决“维数灾难问题”,当核函数满足Mercer条件[15],便可获得内积核函数K(xi, xj)=Ψ(xi)·Ψ(xj)。同时引入拉格朗日变化得到:
| $ L\left( {w,\xi ,b,a,\beta } \right) = \sum\limits_{i = 1}^l {{a_i}} - \frac{1}{2}\sum\limits_{i,j = 1}^l {{y_i}{y_j}{a_i}{a_j}K\left( {{x_i}{x_j}} \right)} 。$ | (4) |
最后得到变形后的回归函数:
| $ f\left( \mathit{\boldsymbol{x}} \right) = w \cdot \mathit{\boldsymbol{x}} + b = \sum\limits_{i = 1}^l {\left( {{\mathit{\boldsymbol{a}}_i} - \mathit{\boldsymbol{a}}_i^ * } \right)K\left( {{x_i} \cdot \mathit{\boldsymbol{x}}} \right) + b} 。$ | (5) |
这种方法可以避免传统方法造成的过拟合的缺点。SVR非线性回归拟合通过升维的方式对拟合过程进行控制。泛化性能强是SVR的一大优势,而该性能与核函数的选择息息相关。常用核函数有:
1) 线性核函数:K(x, xi)= xTxi;
2) 多项式核函数:K(x, xi)=(μxTxi+r)p, μ>0,这里μ、r、p均为核函数的参数;
3) 径向基核函数:K(x, xi)=exp(-μ‖x -xi‖2), μ>0;
4) 两层感知器核函数:K(x, xi)=tanh(μxTxi+r), μ>0。
2 GRA-SVR沥青路面使用性能模型构建 2.1 最佳参数的选择在使用SVR进行预测时需要选择合适的惩罚参数c和核函数参数g才能保证整个模型的准确率与精度。解决这一问题一般采用交叉验证(cross validation,CV)方法,该方法是用来验证模型性能的统计分析方法,其思想是将原始数据进行分组,分别作为验证集和训练集。该方法可以有效地避免欠学习与过学习状态,最终得到理想的准确率。常见的CV方法如下。
2.1.1 Hold-out method该方法将数据随机分为两组,一组为训练集,一组作为验证集,利用训练集训练模型,然后用验证集验证模型[16],最终的准确率为该模型的性能指标。
2.1.2 LOO-CV假设原始数据有N个样本,那么此模型为N-CV,每个样本都为独立的验证集,其余N-1个样本为训练集,得到N个模型,用N个模型最终验证集的准确率的平均数作为该模型的性能指标。但该模型由于计算成本过高,在实际操作中存在困难。
2.1.3 K-CV将原始数据平均分为K组,将每组数据分别作一次验证集,其余K-1组数据作为训练集,得到K个模型,然后用这K个模型最终验证集的分类准确率的平均数作为此模型的性能指标[16]。此种方法可以有效地避免欠学习和过学习状态,最终结果也较为准确。
本研究采用K-CV模型交叉验证选择最佳的惩罚参数c和函数参数g。具体方法为:使c和g在一定范围内取值,求K-CV模型的分类准确率,取使训练集准确率最高的c和g作为最佳参数。具体使用libsvm3.0工具包来实现。
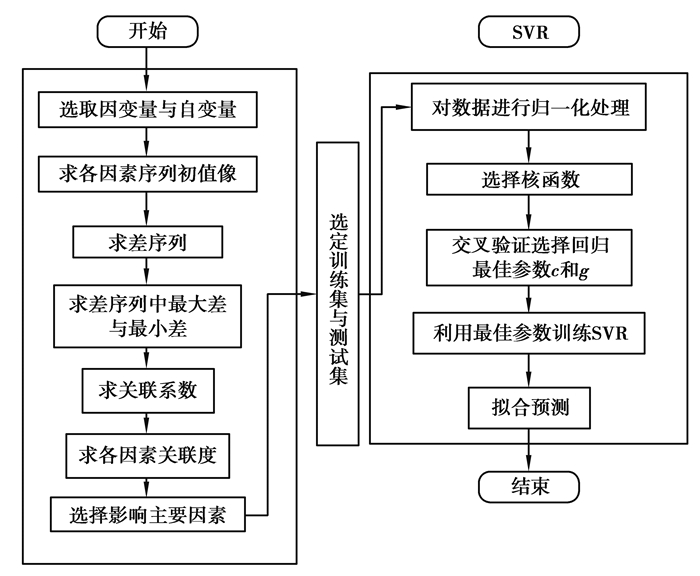
2.2 模型构建沥青路面使用性能受多种复杂因素如降雨量、交通量、最高最低温度等影响,并且影响大多都是非线性的,所以各因素影响下的路面使用性能是一个灰色系统。因此,用灰色关联度分析作为属性处理器,选择出重要的几项影响因素,然后使用SVR进行回归预测,建立一个GRA-SVR综合模型来预测在各种因素影响下路面使用性能的变化趋势。具体建模过程见图 3。
|
图 3 GRA-SVR建模过程流程图 Figure 3 Flowchart of the GRA-SVR modeling process |
具体步骤为:
1) 选取因变量和自变量。
2) 求各序列的初值像。
令Xi(其中i=0, 1, 2, …, n)表示第i种影响因素的n个样本,令
| $ \begin{array}{*{20}{c}} {{{X'}_i} = {X_i}/{x_i}\left( 1 \right) = \left( {{{x'}_i}\left( 1 \right),{{x'}_i}\left( 2 \right), \cdots ,{{x'}_i}\left( n \right)} \right),}&{i = 0,1,2, \cdots ,m。} \end{array} $ | (6) |
3) 求差序列。记
| $ \begin{array}{*{20}{c}} {{\Delta _i}\left( k \right) = \left| {{{x'}_0}\left( k \right) - {{x'}_i}\left( k \right)} \right|,}&{{\Delta _i} = \left( {{\Delta _i}\left( 1 \right),{\Delta _i}\left( 2 \right), \cdots ,{\Delta _i}\left( n \right)} \right),}&{i = 1,2, \cdots ,m。} \end{array} $ | (7) |
4) 求差序列中最大差与最小差。记最大值为M,最小值为N,则
| $ M = \mathop {\max }\limits_i \mathop {\max }\limits_k {\Delta _i}\left( k \right),N = \mathop {\min }\limits_i \mathop {\min }\limits_k {\Delta _i}\left( k \right)。$ | (8) |
5) 求各样本的关联系数:
| $ \begin{array}{*{20}{c}} {{\gamma _{0i}}\left( k \right) = \frac{{m + \xi M}}{{{\Delta _i}\left( k \right) + \xi M}},}&{\xi \in \left( {0,1} \right),k = 1,2, \cdots ,n,i = 1,2, \cdots ,m。} \end{array} $ | (9) |
式中ξ称为分辨系数。当ξ≤0.546 3时,分辨力最好,通常取ξ= 0.5,因此本研究取0.5计算。
6) 计算各影响因素与系统的关联度:
| $ {\gamma _{0i}} = \frac{1}{n}\sum\limits_{k = 1}^n {{\gamma _{0i}}\left( k \right)} ,\;\;\;i = 1,2, \cdots ,m。$ | (10) |
7) 选取影响程度较大的因素。
8) 为了提高模型的精度预训练速度,防止数据在运算过程中大数吃小数,应对数据进行归一化处理,处理至[0, 1]区间,本研究采用MATLAB中自带的mapminmax函数对数据进行归一化处理。
9) 径向基核函数具有很高的精度[17-18],所以我们选择径向基核函数。
10) 采用K-CV模型交叉验证选择最佳的惩罚参数c和函数参数g。
11) 利用最佳参数进行SVR拟合得到函数,最终得到预测数据。
3 沥青路面使用性能预测实例 3.1 原始数据本研究以广云高速为依托工程,采用该高速公路2011年铣刨重铺的GAC-16路面作为研究样本。广东地区年平均气温18.7~21.6℃,极端最高温度42℃;交通流量较大,车辙为该路的主要病害,所以本研究以广云高速车辙指数(RDI)为例,同时调查当地路面使用年限、年交通量、投入的养护资金、年最低温度、年最高温度、年降雨量以及当地日照等影响因素,调查结果见表 1。图 4为各影响因素与车辙深度指数RDI的散点图。
| 表 1 广云高速车辙深度指数(RDI)与各影响因素调查表(2011—2017) Table 1 Datasheet of RDI and various influencing factors of Guangyun Expressway(2011—2017) |

|
图 4 车辙深度指数RDI与主要影响因素散点图 Figure 4 Scatter plots of rutting depth index(RDI)versus main influence factors |
由上图可知各因素与车辙深度指数均为非线性关系。
3.2 影响因素关联度分析对表 1数据进行关联度分析,得出各影响因素的关联度见表 2。
| 表 2 各影响因素关联度 Table 2 Relevance of each influencing factor |
由上表可知各因素对车辙深度的影响程度为:γ4<γ1<γ5<γ7<γ3<γ2<γ6,即最低温度<使用年限<最高温度<日照<养护资金<当量轴次<降雨。因此,剔除关联度小的最低温度与使用年限,我们进行SVR预测。
3.3 数据归一化对降维的数据通过软件进行归一化处理,结果见表 3。
| 表 3 归一化处理标准数据 Table 3 Standardized data after normalization |
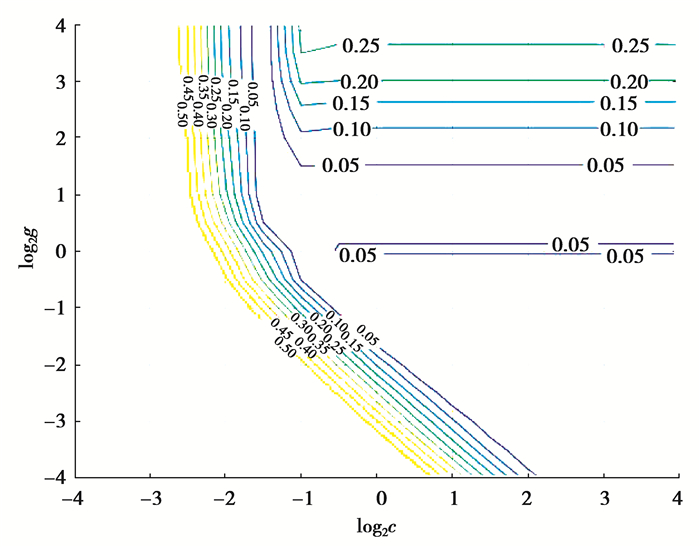
采用K-CV模型交叉验证选择最佳的惩罚参数c和函数参数g。图 5中,等高线表示c和g在2-4~24范围内的均方误差(MSE)。当MSE最小时,相应的c和g为最佳。最终得出最佳惩罚参数c=5.656 9,g=0.062 5。
|
图 5 最佳的惩罚参数终选 Figure 5 Selection of optimal penalty parameters c and g |
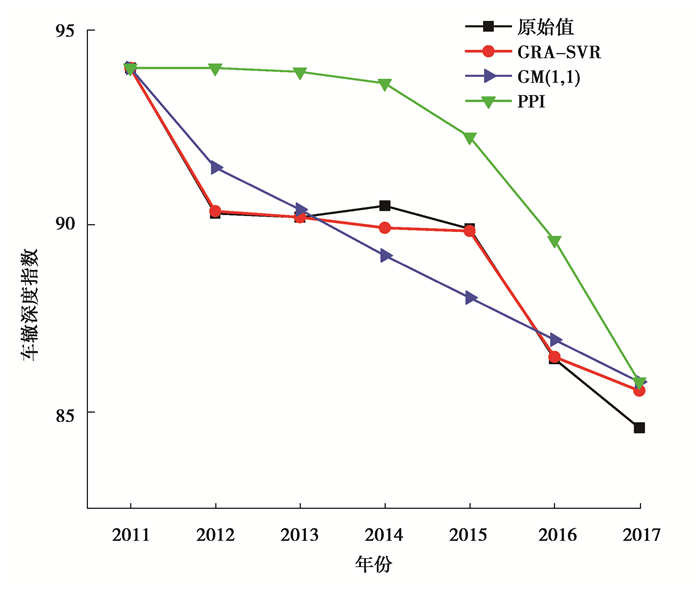
以2011至2016年的各因素以及RDI作为训练集,对2017年的RDI进行预测,同时与GM(1, 1)[19]和PPI模型[6]进行对比分析。不同模型预测值与实际值对比分析见表 4, 相应的变化趋势见图 6。
| 表 4 RDI预测值与实际值对比 Table 4 Comparison of predicted and actual values of RDI |
|
图 6 不同模型车辙深度指数RDI预测值与实际值变化趋势图 Figure 6 Comparison of the values of rutting depth index(RDI)predicted by different models and the actual RDI value |
由表 4可以看出,对于2017年RDI值,GRA-SVR预测值的绝对误差为1.147,GM(1, 1)和PPI预测值的绝对误差均为1.418。GRA-SVR模型的绝对误差最小,预测精度最高。
由图 6可以看出对于历史预测数据GRA-SVR最接近原始数据,GM(1, 1)模型次之,PPI模型最差,表明随着时间的推移GRA-SVR的预测精度变化不大,而其他模型则随着时间的推移,预测精度降低。所以GRA-SVR模型可以长期预测路面使用性能。
4 结论1) GRA-SVR预测模型首先对样本影响因素进行灰色关联度分析,对各因素进行降维处理,然后利用SVR良好泛化性能,处理高维数非线性问题。
2) 使用GRA-SVR建立的预测模型,是一种多因素的综合模型,可以处理各非线性影响因素对沥青路面使用性能的影响。相对于其他模型该模型考虑的影响因素更多。
3) GRA-SVR模型具有良好预测精度,并在长周期的预测中同样精度较高,所以,该模型不仅适合短时间的预测,也适合长时间的预测。
综上所述,GRA-SVR沥青路面使用性能预测模型可以很好地预测路面使用性能,为沥青路面养护决策提供准确依据,同时为养护大数据发展提供模型参考。
| [1] |
李巧茹, 郭知洋, 王耀军, 等. 基于PCA-SVM的高速公路沥青路面使用性能评价[J]. 北京工业大学学报, 2018, 44(2): 283-288. LI Qiaoru, GUO Zhiyang, WANG Yaojun, et al. Evaluation of freeway asphalt pavement performance based on PCA-SVM[J]. Journal of Beijing Polytechnic University, 2018, 44(2): 283-288. (in Chinese) |
| [2] |
周岚.高速公路沥青路面使用性能评价及预测研究[D].南京: 东南大学, 2015. ZHOU Lan. Research of performance evaluation and prediction method of asphalt pavements for highway[D]. Nanjing: Southeast University, 2015.(in Chinese) |
| [3] |
敬超, 张金喜. 沥青路面性能预测研究综述[J]. 中外公路, 2017, 37(5): 31-35. JING Chao, ZHANG Jinxi. Review on the performance prediction research of asphalt pavement[J]. Journal of China & Foreign Highway, 2017, 37(5): 31-35. (in Chinese) |
| [4] |
Wang K C P, Li Q. Gray clustering-based pavement performance evaluation[J]. Journal of Transportation Engineering, 2010, 136(1): 38-44. |
| [5] |
申健民, 党耀国, 周伟杰, 等. 基于指数函数的灰色动态多属性关联决策模型[J]. 控制与决策, 2016, 31(8): 1441-1445. SHEN Jianmin, DANG Yaoguo, ZHOU Weijie, et al. Grey dynamic multiple attribute correlation decision-making model based on exponential function[J]. Control and Decision, 2016, 31(8): 1441-1445. (in Chinese) |
| [6] |
孙立军, 刘喜平. 路面使用性能的标准衰变方程[J]. 同济大学学报(自然科学版), 1995(5): 512-518. SUN Lijun, LIU Xiping. Standard decay equation for pavement performance[J]. Journal of Tongji University(Natural Science), 1995(5): 512-518. (in Chinese) |
| [7] |
Yang J, Lu J J, Gunaratne M. Application of neural models for forecasting or pavement crack index and pavement condition rating[R]. Washington, DC: National Academy of Sciences, 2003.
|
| [8] |
汪海年, 张琛, 尤占平, 等. 基于数理统计方法的MEPDG车辙预估模型校正[J]. 长安大学学报(自然科学版), 2013, 33(6): 1-7. WANG Hainian, ZHANG Chen, YOU Zhanping, et al. Calibration of rutting prediction model in MEPDG based on mathematical statistics method[J]. Journal of Chang'an University(Natural Science Edition), 2013, 33(6): 1-7. (in Chinese) DOI:10.3969/j.issn.1671-8879.2013.06.001 |
| [9] |
Dong M. A grey relational analysis between some selected affective factors and English test performance[J]. Canadian Social Science, 2014, 10(6): 195-200. |
| [10] |
陈可嘉, 李烜楠, 丘永宜. 福建省交通工程材料价格影响因素的灰色关联分析[J]. 公路交通科技, 2018, 35(4): 137-145. CHEN Kejia, LI Xuannan, QIU Yongyi. Grey correlation analysis on influencing factors of traffic engineering material price in Fujian province[J]. Journal of Highway and Transportation Research and Development, 2018, 35(4): 137-145. (in Chinese) |
| [11] |
Abdi M J, Giveki D. Automatic detection of erythemato-squamous diseases using PSO-SVM based on association rules[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 603-608. DOI:10.1016/j.engappai.2012.01.017 |
| [12] |
Liu Z W, Cao H R, Chen X F, et al. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings[J]. Neurocomputing, 2013, 99: 399-410. DOI:10.1016/j.neucom.2012.07.019 |
| [13] |
刘黔会, 张挣鑫, 黄方林, 等. 基于支持向量机的沥青路面使用性能预测探究[J]. 公路工程, 2018, 43(2): 201-205. LIU Qianhui, ZHANG Zhengxin, HUANG Fanglin, et al. Studied on performance prediction of asphalt pavement based on support vector machine[J]. Highway Engineering, 2018, 43(2): 201-205. (in Chinese) DOI:10.3969/j.issn.1674-0610.2018.02.038 |
| [14] |
李嫄源, 袁梅, 王瑶, 等. SVM与PSO相结合的电机轴承故障诊断[J]. 重庆大学学报, 2018, 41(1): 99-107. LI Yuanyuan, YUAN Mei, WANG Yao, et al. Fault diagnosis of motor bearings based on SVM and PSO[J]. Journal of Chongqing University, 2018, 41(1): 99-107. (in Chinese) |
| [15] |
黄啸.支持向量机核函数的研究[D].苏州: 苏州大学, 2008. HUANG Xiao. The study on kernels in support vector machine[D]. Suzhou: Soochow University, 2008.(in Chinese) |
| [16] |
董西伟, 王玉伟, 张广顺, 等. 基于迁移学习的跨公司软件缺陷预测[J]. 计算机工程与设计, 2016, 37(3): 684-689. DONG Xiwei, WANG Yuwei, ZHANG Guangshun, et al. Transfer learning based cross-company software defects prediction[J]. Computer Engineering and Design, 2016, 37(3): 684-689. (in Chinese) |
| [17] |
Aydin I, Karakose M, Akin E. A multi-objective artificial immune algorithm for parameter optimization in support vector machine[J]. Applied Soft Computing, 2011, 11(1): 120-129. DOI:10.1016/j.asoc.2009.11.003 |
| [18] |
de Castro L N, von Zuben F J. Learning and optimization using the clonal selection principle[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(3): 239-251. DOI:10.1109/TEVC.2002.1011539 |
| [19] |
Deng J L. Introduction to grey theory[J]. The Journal of Grey System, 1989, 1: 1-24. |
 2019, Vol. 42
2019, Vol. 42


