b. 重庆大学 城市建设与环境工程学院, 重庆 400030
b. Urban Construction and Environmental Engineering, Chongqing University, Chongqing 400030, P. R. China
换热器是国民经济和工业生产领域中广泛使用的一种通用设备,其中,管壳式换热器凭借其制造简单,工作可靠,能适应高温高压等优点,成为目前国内外换热设备的主要结构形式,市场占有率高达65%,广泛应用于炼油厂、核电站的余热回收以及其他一些大型化工进程中[1]。随着计算机技术的飞速发展,目前对于管式换热器的研究主要采用数值模拟的方法来研究换热器的性能。高绪栋等针对壳侧、管侧换热介质皆为水的管壳式换热器进行了三维数值模拟,讨论了不同折流板形状对换热器性能的影响[2];司子辉等用Fluent数值模拟方法,研究两种翅片(波纹三对称穿孔翅片与波纹翅片)的表面流动性与传热性,得到不同风速表面传热系数的分布[3];北京石油化工学院的俞接成等针对管壳式换热器的壳侧流体流动进行了三维数值模拟,指出壳侧折流板间距的减小大幅增加了换热器壳侧压降,但壳侧换热增加并不明显[4]。由此可见,虽然对于管式换热器的研究有很多,数值模拟的方法也很成熟,但主要都是从换热器的物理结构层面出发,很少从冷热流体的组成成分、入口参数角度来分析它的换热性能。
本研究基于太阳能化学储能——甲醇蒸汽重组反应制取氢气系统[5],利用管式换热器对该反应的产物余热加以回收,产物由高温水蒸气、氢气和二氧化碳等组成[6]。高温混合流体在换热器中的流动过程会受到组分之间的相互作用而发生扩散,这种扩散并不像Fick定律描绘的那样,而有可能发生逆浓度梯度扩散的情况[7];Krishna和Wesselingh基于Maxwell和Stefan理论,发展了用于定量分析多组分系统中各组分扩散过程的适用范围更加广泛的Maxwell-Stefan(以下简称为MS)方程[8]。因此笔者在MS扩散模型和Navier-stokes、k-ε方程模型的基础上,采用COMSOL Multiphysics软件中的浓物质传递、传热和CFD模块,建立了三维稳态扩散耦合流体传热模型,模拟管式换热器在有无扩散作用影响下的温度场和浓度场分布并且对模拟结果进行准确度验证,分析物质扩散对换热性能的影响。对冷热流体在不同的进口温度、速度以及混合流体在不同的混合比等工况下进行模拟,从㶲的角度对各工况结果进行分析,确定管式换热器在该余热回收中的最佳工作状况。
1 数学模型 1.1 计算模型的简化工程所用换热器结构相对复杂,为便于研究,对计算模型进行如下简化:1)忽略折流板与换热管以及壳体的间隙;2)增加冷热流体进入换热器的直管段长度;3)假设流体物性不随温度、压力的变化而改变;4)假设壳体壁面为绝热材料,与外界无热交换;5)为了减少划分网格的数量,提高计算速度,将换热器的对称面设为对称边界。冷热流的动量、能量输运、冷流的质量输运分别遵循牛顿黏性定律、傅里叶定理、菲克定律;热流多组分气体的质量输运遵循MS定律。
1.2 非等温流动模型换热器的流体流动与传热必须满足如下控制方程[9]:
质量守恒方程:
| $ \frac{{\partial \left( {{u_i}} \right)}}{{\partial {x_i}}} = 0。$ | (1) |
动量守恒方程:
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}{u_i}} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _t}} \right)\frac{{\partial {\mathit{u}_i}}}{{\partial {x_j}}}} \right] - \frac{{\partial P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _t}} \right)\frac{{\partial {\mathit{u}_j}}}{{\partial {x_i}}}} \right]。$ | (2) |
能量守恒方程:
| $ \frac{{\partial \left( {\rho T} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}T} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\frac{\mu }{{P{r_t}}} + \frac{{{\mu _t}}}{{{\sigma _T}}}} \right)\frac{{\partial T}}{{\partial {x_j}}}} \right]。$ | (3) |
k-ε两方程:
湍动能方程:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}k} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon 。$ | (4) |
耗散率方程:
| $ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}\varepsilon } \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{\varepsilon }{k}\left( {{C_{1\varepsilon }}{G_k} - {C_{2\varepsilon }}\rho \varepsilon } \right)。$ | (5) |
其中,
| $ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }, $ | (6) |
| $ {G_k} = {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}}。$ | (7) |
式(1)~(7)中:ui和uj为流体在各个方向的速度分量;ρ为流体密度;μ为流体的动力黏度;P为流体压力;T为流体温度;Pr为普朗特数;σk、σε分别是与湍动能k和耗散率ε对应当普朗特数;k为湍动能;ε为湍动能耗散率;C1ε、C2ε为常数;Gk是由平均速度梯度引起的湍动能的产生项。
1.3 Maxwell-Stefan模型对于含有两种组分的物系,它的MS方程[8]为:
| $ {J_i} = - {C_{\rm{t}}}{D_2}\mathit{\Gamma }\nabla {x_i}, $ | (8) |
式中:Ji为i组分的扩散通量,mol/(m2·s);Ct为总浓度,mol/m3;▽xi为浓度梯度,1/m;Г为热力学因子;D2为MS扩散系数,m2/s,可由经验公式(9)计算[10]:
| $ {D_2} = \frac{{0.010\;1{T^{1.75}}\sqrt {\frac{1}{{{M_{\rm{A}}}}} + \frac{1}{{{M_{\rm{B}}}}}} }}{{P{{\left[ {{{\left( {\sum {{v_{\rm{A}}}} } \right)}^{1/3}} + {{\left( {\sum {{v_{\rm{B}}}} } \right)}^{1/3}}} \right]}^2}}}。$ | (9) |
式中:P为气体的总压,Pa;T为气体的温度,K;MA、MB为组分A、B的摩尔质量,kg/kmol;ΣvA、ΣvB为组分A、B的分子扩散体积,cm3/mol,其中H2O的分子扩散体积为13.1 cm3/mol,CO2的分子扩散体积为26.9 cm3/mol,H2的分子扩散体积为6.12 cm3/mol。
| $ \mathit{\boldsymbol{J}} = - {C_{\rm{t}}}{\mathit{\boldsymbol{D}}_n}\mathit{\Gamma }\nabla x = - {C_{\rm{t}}}{\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\Gamma }\nabla x, $ | (10) |
式中Dn为多组分物系传质过程MS扩散系数矩阵,本研究为三元混合气体,则其形式为:
| $ {\mathit{\boldsymbol{D}}_3} = \left[ {\begin{array}{*{20}{c}} {{D_{11}}}&{{D_{12}}}&{{D_{13}}}\\ {{D_{21}}}&{{D_{22}}}&{{D_{23}}}\\ {{D_{31}}}&{{D_{32}}}&{{D_{33}}} \end{array}} \right]。$ | (11) |
矩阵中主对角元素反映某组分的浓度梯度对自身扩散通量的影响, 交叉项元素则反映组分间的浓度梯度交互作用影响,在二组分模型中,Dij=Dji,在多组分模型中,Dij≠Dji,i≠j。式(10)中B为二元组分扩散系数倒数矩阵,矩阵中的元素可通过下式计算求得:
| $ {B_{ii}} = \frac{{{x_i}}}{{{D_{in}}}} + \sum\limits_{k = 1,k \ne i}^n {\frac{{{x_k}}}{{{D_{ik}}}}} , $ | (12) |
| $ {B_{ij}} = {x_i}\left( {\frac{1}{{{D_{ij}}}} - \frac{1}{{{D_{in}}}}} \right), $ | (13) |
式中:Dij为组分i和j组成的二元组分扩散系数,通过上式可求得矩阵B,求解B的逆矩阵可得三组分气体传质过程系数矩阵D3。
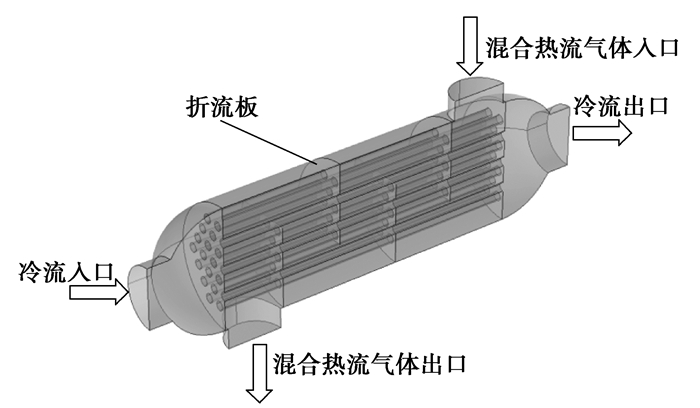
2 物理模型 2.1 几何模型本换热器模型的几何尺寸如表 1所示,换热管中通冷流,壳侧通热流,冷热流体采用逆流的方式流动,如图 1所示。
| 表 1 换热器几何结构尺寸 Table 1 The geometrical structure size of heat exchanger |
|
图 1 换热器几何模型 Figure 1 The geometrical model of heat exchanger |
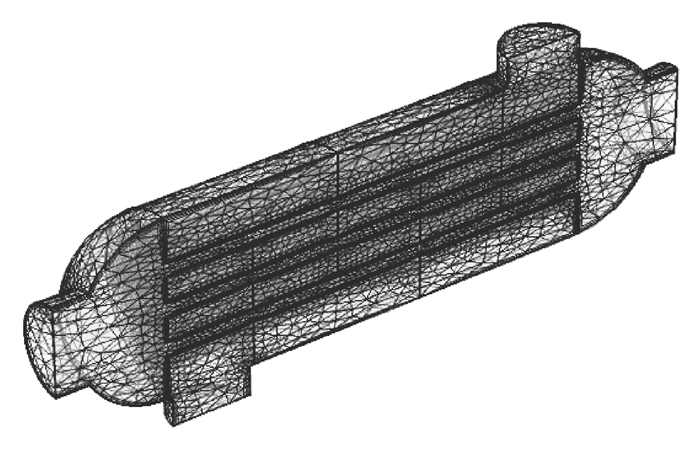
COMSOL软件内预定义了九级划分网格的方法,综合考虑计算精度和运行速度,采用极细化的划分方法,网格形状采用自由四面体,最终划分最大的单元尺寸为54.5 mm,最小的单元尺寸为11.6 mm如图 2所示。
|
图 2 模型网格划分图 Figure 2 Model mesh generation map |
本数值模型涉及3种输运形式。对于湍流流动,模型设为k-ε模型,壁处理采用壁函数;管程和壳程流体均采用速度入口,管程为冷流水,分别模拟速度为0.1,0.2,0.3,0.4,0.5 m/s时的情况,壳程为热流混合气体,分别模拟速度为0.5,1.5,2.5,3.5,4.5 m/s时的情况;出口均采用压力出口设为0 Pa。对于流体传热,热流入口温度为523 K恒定不变,冷流入口温度分别设为298,308,318,328,338 K;出口均设为流出。对于物质浓度分布,扩散模型选择MS方程,扩散系数根据1.3所求;扩散区域为壳程,将管程设为禁用,壳程入口的混合物明细采用摩尔分数,分别模拟水蒸气、二氧化碳和氢气三者的摩尔配比为2 :2 :1,2 :1 :1,1 :1 :1,1 :1 :2,1 :1 :3,壳程出口设为流出。
2.4 准确度验证选取冷流速度0.1 m/s,热流速度1 m/s,冷流温度298 K,热流温度523 K,热流混合气体的混合比1 :1 :1时为验证工况,采用经验公式计算出换热器壳侧的换热系数与模拟结果进行对比。壳侧换热系数采用Kern经验公式求得[14]:
| $ Nu = 0.36\mathit{R}{\mathit{e}^{0.55}}\mathit{P}{\mathit{r}^{0.33}}{\left( {\frac{{{\mu _{\rm{f}}}}}{{{\mu _{\rm{w}}}}}} \right)^{0.14}}。$ | (14) |
式中,定性温度取流体进、出口温度的算术平均值,μf、μw分别为以流体和管壁温度作为定性温度的动力黏度,将验证工况下的参数带入经验公式(14),结果如表 2所示。
| 表 2 数值模拟结果与计算值对比 Table 2 Comparison between numerical simulation and calculated value |
从对比结果可以看出,模拟结果与由经验公式所得理论值误差仅为10.6%,引起误差的原因其一是数值模型做了多方面的简化,其二是经验公式计算结果也有一定的偏差,由此可以看出文中所建数值模型方法合理。
3 结果与讨论 3.1 物质扩散对传热的影响设置两组对照模型,为了保证两组数值模拟结果的差异仅来源于物质扩散,除有无考虑物质浓度分布这一区别外其余条件相同,分析各自的温度场和浓度场的分布,得出物质扩散对换热器换热特性的影响。
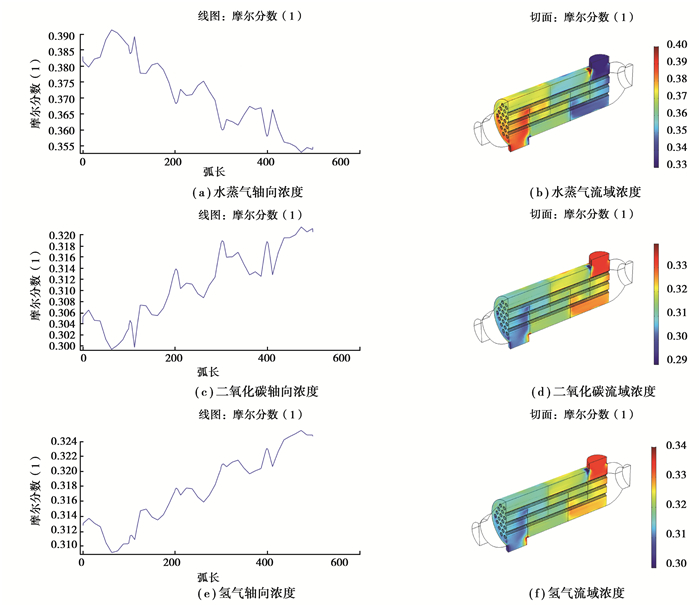
物质扩散发生在换热器壳侧,热流混合气体中各组分的浓度分布变化,影响热流对于冷流的传热特性。在考虑扩散的情况下,混合物质各组分的浓度分布如图 3所示,从图 3中可以看出,各组分沿轴向和在整个流域中的浓度分布趋势一致,其中氢气和二氧化碳的浓度分布大体相同,从壳侧入口到出口递减,这两种物质的同步性符合文献[15]所描述的结论:组分之间的交互作用表现为大分子对小分子的拖带,当拖带作用大于自身的浓度梯度作用时,就会发生回流扩散的现象。本研究中,小分子氢气在大分子二氧化碳的拖带作用下发生回流,浓度沿着流动路径递减,在这三种物质中,氢气的热容和导热系数最大,在传热中起主导作用,其浓度分布会对传热产生重要的影响。当热流临近出口与入口的冷流进行热交换热时,氢气的浓度降至最低,换热效果也随之降低,同时,氢气的回流扩散会使得临近出口的低温热流与入口的高温热流反复换热,降低入口热流的温度,影响对冷流的传热,降低换热效果。
|
图 3 物质浓度分布图 Figure 3 The substance concentration profile |
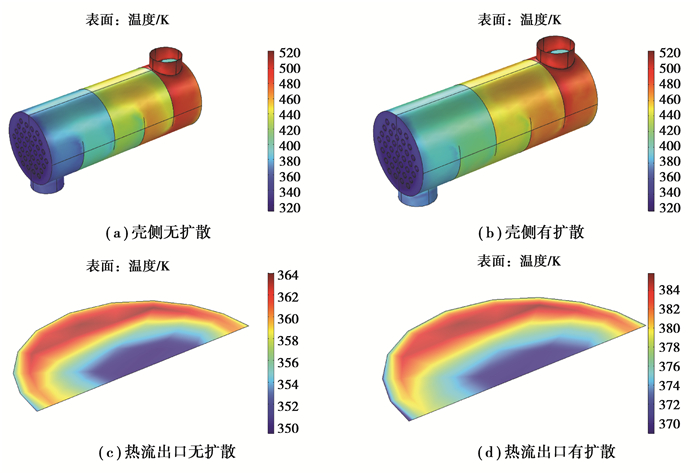
有无物质扩散条件下两种数值模拟的温度场分布如图 4所示,其中(c)和(d)是换热器壳程出口截面的温度场分布。从图 4中可以看出,在忽略物质扩散时,热流的温度整体低于考虑物质扩散的情况,出口平均温度从378.67 K降为357.83 K。
|
图 4 有无扩散条件下温度场分布 Figure 4 The temperature distribution both in the presence and absence of diffusion |
描述换热器特性和效力的参数有很多,其中的一种等效传热系数较为简单,其表达式为:
| $ {h_{{\rm{eq}}}} = \frac{P}{{A\left( {{T_{{\rm{hot}}}} - {T_{{\rm{cold}}}}} \right)}}, $ | (15) |
式中:P为总换热量,W;A为换热面积,m2。由模拟计算可得,考虑物质扩散因素和不考虑物质扩散因素的换热器的热通量分别为3 589.9、3 727 W/m2,等效传热系数分别为15.955、16.564 W/(m2·K),这是因为氢气的回流扩散会使得临近出口的低温热流与入口的高温热流反复换热,降低入口热流的温度,影响对冷流的传热,降低换热效果。
3.2 流体入口条件对传热的影响基于能源利用的合理性对换热器的有效能利用进行评价,即采用㶲的分析方法。其中,㶲效率是指设备对外输出的㶲与所获得的㶲之比,它的计算方法如下[16]:
| $ {\eta _{{\rm{ex}}}} = \frac{{E_{{\rm{out}}}^{\rm{C}} - E_{{\rm{in}}}^{\rm{C}}}}{{E_{{\rm{in}}}^{\rm{H}} - E_{{\rm{out}}}^{\rm{H}}}} = \frac{{\Delta {E^{\rm{C}}}}}{{\Delta {E^{\rm{H}}}}}, $ | (16) |
式中:EoutC为冷流出口,EinC为冷流入口,EinH为热流入口,EoutH为热流出口,ΔEC为冷流㶲变,ΔEH为热流变。推导公式如下[17]。
流体在流动传热过程中,㶲为:
| $ {\rm{d}}E = \left( {{\rm{d}}h - T{\rm{d}}s} \right)。$ | (17) |
由定压传热过程,得:
| $ {\rm{d}}h = {c_p}{\rm{d}}T,{\rm{d}}s = {c_p}\frac{{{\rm{d}}T}}{T}。$ | (18) |
对㶲进行积分,得:
| $ \Delta E = \int\limits_{{T_1}}^{{T_2}} {\left( {{c_p}{\rm{d}}T - {T_0}{c_p}\frac{{{\rm{d}}T}}{T}} \right)} = {c_p}\left( {{T_2} - {T_1} - {T_0}\ln \frac{{{T_2}}}{{{T_1}}}} \right)。$ | (19) |
则冷热流体的㶲变分别为:
| $ \Delta {E^{\rm{C}}} = {c_{p{\rm{C}}}}\left( {{T_{{{\rm{C}}_2}}} - {T_{{{\rm{C}}_1}}} - {T_0}\ln \frac{{{T_{{{\rm{C}}_2}}}}}{{{T_{{{\rm{C}}_1}}}}}} \right), $ | (20) |
| $ \Delta {E^{\rm{H}}} = {c_{p{\rm{H}}}}\left( {{T_{{{\rm{H}}_1}}} - {T_{{{\rm{H}}_2}}} - {T_0}\ln \frac{{{T_{{{\rm{H}}_1}}}}}{{{T_{{{\rm{H}}_2}}}}}} \right)。$ | (21) |
则㶲效率为:
| $ {\eta _{{\rm{ex}}}} = \frac{{{c_{p{\rm{C}}}}\left( {{T_{{{\rm{C}}_2}}} - {T_{{{\rm{C}}_1}}} - {T_0}\ln \frac{{{T_{{{\rm{C}}_2}}}}}{{{T_{{{\rm{C}}_1}}}}}} \right)}}{{{c_{p{\rm{H}}}}\left( {{T_{{{\rm{H}}_1}}} - {T_{{{\rm{H}}_2}}} - {T_0}\ln \frac{{{T_{{{\rm{H}}_1}}}}}{{{T_{{{\rm{H}}_2}}}}}} \right)}}。$ | (22) |
式中:h为流体的焓,kJ/kg;s为流体的熵,kJ/(kg·K);T为流体的温度,K;cp为流体的定压比热容,J/(kg·K);T1,T2为流体的进出口温度,K;T0为环境温度,K。
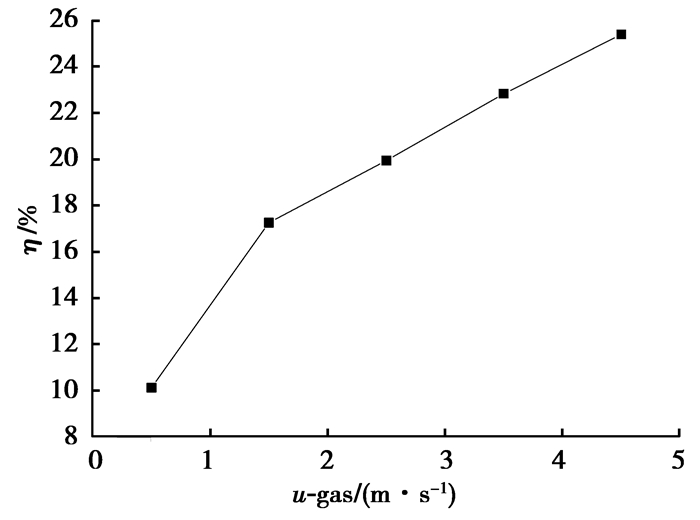
3.2.1 热流入口速度的影响将模型验证工况作为初始工况,保持其他条件一定,分别将热流的入口速度设为0.5,1.5,2.5,3.5,4.5 m/s进行模拟,计算得到热流的出口温度分别为352.73,394.50,413.72,425.60,434.19 K,冷流的出口温度分别为366.54,382.00,383.11,385.24,386.73 K,从㶲的角度对模拟结果进行数据处理,结果如图 5所示。
|
图 5 热流入口速度的影响 Figure 5 The influence of heat flow inlet velocity |
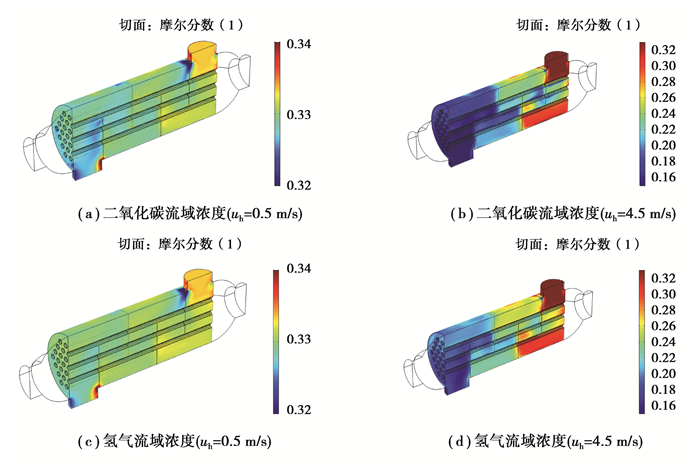
由图 5可以看出,随着热流入口速度的增加,换热器的㶲效率随之提高,在一定的速度范围内,当热流的入口速度增加到4.5㶲效率m/s时,设备的㶲效率达到25.4%。出现这一现象的原因是随着速度的提高,强化了换热系数,同时也加强了氢气的回流效应。如图 6所示分别为热流入口速度为0.5 m/s和4.5 m/s时混合气体的浓度分布,可以看出二氧化碳在扩散中对氢气的拖带作用随着速度的提高越来越强,因此发生回流扩散的程度越来越显著,由于速度流动过快换热不充分,温度仍然很高的下游氢气重新流回上游进行二次换热,因此换热效果提升,设备的㶲效率提高。
|
图 6 物质浓度分布图 Figure 6 The substance concentration profile |
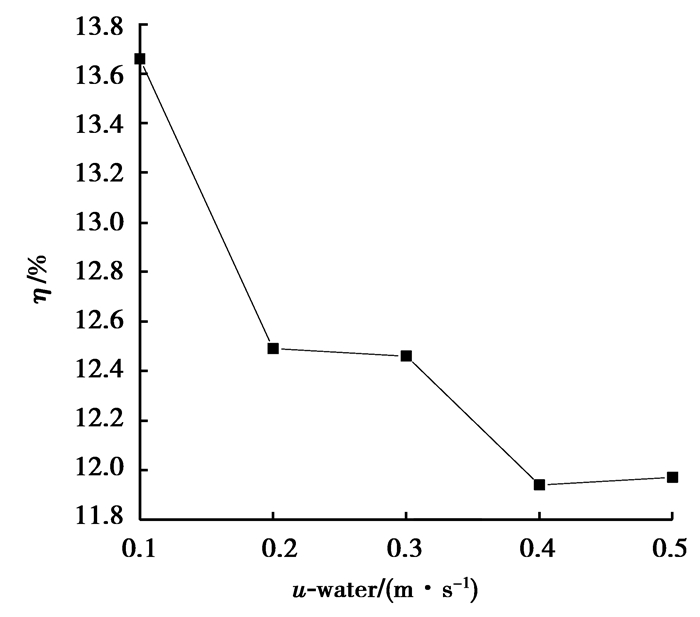
基于验证工况,分别将冷流的入口速度设为0.1,0.2,0.3,0.4,0.5 m/s进行模拟,得到热流的出口温度分别为378.67,376.33,375.36,374.78,374.38 K,冷流的出口温度分别为374.93,371.52,371.61,369.92,370.12 K,从㶲的角度进行分析,模拟数据处理结果如图 7所示。
|
图 7 冷流入口速度的影响 Figure 7 The influence of cold flow inlet velocity |
如图 7所示,随着冷流入口速度的增加,换热器的㶲效率总体呈下降趋势,为防止冷流水紊流程度过大,振荡管壁,应控制冷流体速度,另外,出现这一现象的原因是冷流水的入口速度变化幅度小,所以设备㶲效率变化不是很大,随着冷流水速度的增加,冷热流的换热时间缩短,传热不够充分,换热器的㶲效率降低。
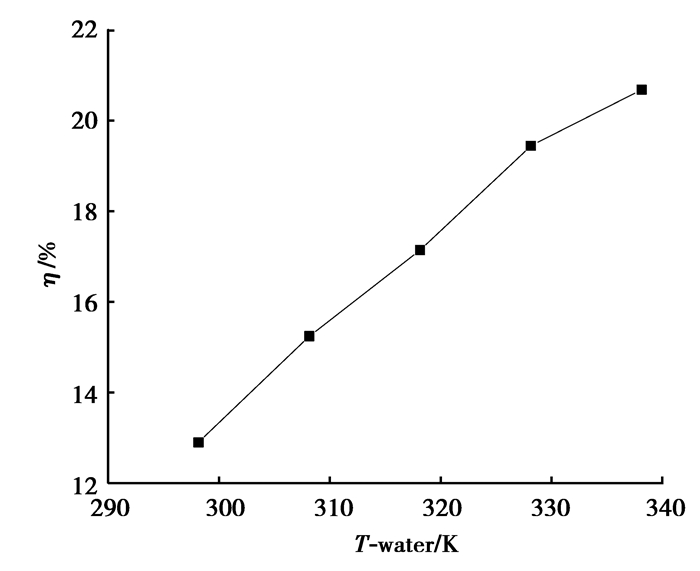
3.2.3 冷流入口温度的影响保持初始工况其他条件一定,分别将冷流水的入口温度设为298.15,308.15,318.15,328.15,338.15 K进行模拟,得到热流的出口温度分别为378.67,385.83,392.90,399.87,406.77 K,冷流的出口温度分别为372.45,380.40,386.85,394.65,400.05 K,采用㶲分析法对模拟结果进行研究,数据处理结果如图 8所示。
|
图 8 冷流入口温度的影响 Figure 8 The influence of cold flow inlet temperature |
如图 8所示,随着冷流入口温度的上升,换热器的㶲效率随之提高,冷流水的温度不宜太高,当冷流水的入口温度达到338.15 K时,换热器的㶲效率提高到20.7%。出现这一结果是因为随着冷流温度的提高,冷热流的温差变小,换热过程的不可逆损失减小,设备的㶲效率提高。
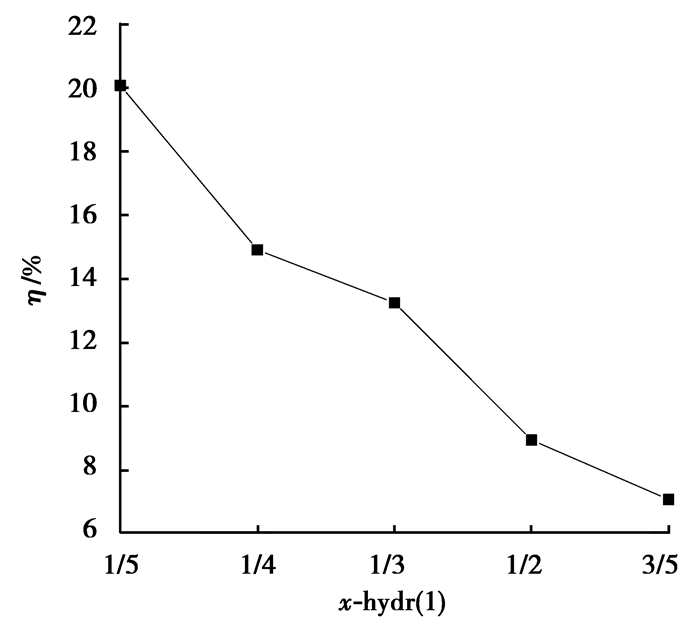
3.2.4 热流混合比的影响保持其他条件一定,分别对混合气体中水蒸气、二氧化碳和氢气的混合比分别为2 :2 :1,2 :1 :1,1 :1 :1,1 :1 :2,1 :1 :3进行模拟,得到热流的出口温度分别为382.18,371.04,378.67,370.83,364.12 K,冷流的出口温度分别为375.65,372.34,373.58,371.65,369.27 K,从㶲的角度对模拟结果进行分析,数据处理结果如图 9所示。
|
图 9 热流混合比的影响 Figure 9 The influence of heat flow mixing ratio |
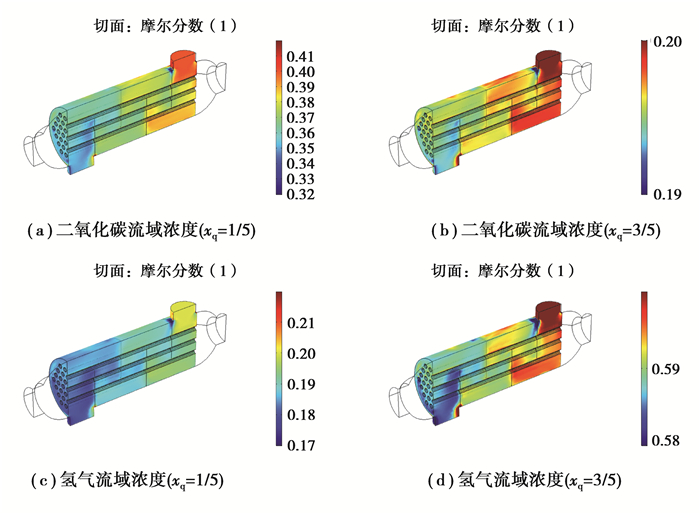
由图 9可以看出,随着氢气摩尔分数的增加,换热器的㶲效率下降,当混合气体中水蒸气、二氧化碳和氢气的混合比达到甲醇蒸汽重组制氢反应的理论比1 :1 :3时,换热器的㶲效率低至7.1%。随着氢气摩尔分数的增加,二氧化碳摩尔分数的减少,其扩散拖带作用逐渐减弱,当氢气的摩尔分数达到3/5时几乎不受二氧化碳的拖带作用影响从而发生回流扩散,如图 10所示,xq表示氢气的摩尔分数。设备的㶲效率下降的原因是采用高品质的氢能来加热低品位的水,能源利用合理性不佳。但是从采用冷流水冷却高温混合气体的角度看,随着氢气摩尔分数的增加,热流的出口温度在下降,符合课题研究的目的。
|
图 10 物质浓度分布图 Figure 10 The substance concentration profile |
对以上结果的分析,可以得出以下结论。
1) 物质扩散会严重影响管式换热器的传热性能,它会改变物质的浓度分布,在本例中,如果忽略物质传递这一因素会使得换热器的换热效果偏强,计算结果偏大,在对管式换热器精确设计时应加以计算。
2) 换热器的㶲效率在10%~30%之间,比较低下,从㶲效率的概念考虑,从流体角度出发,说明在传热过程中,仅需达到少量的冷流水㶲增就可获得可观的热流气体㶲减,降低热流温度,这一㶲效率区间符合论文研究目的。
3) 从设备㶲效率的角度考虑,随着热流入口速度的增加,换热器的㶲效率提高,当热流入口速度为4.5 m/s时,换热器的㶲效率达到25.4%;随着冷流入口速度的增加,换热器的㶲效率降低直至稳定,当冷流入口速度为0.1 m/s时,换热器的㶲效率为13.7%;随着冷流入口温度的增加,换热器的㶲效率提高,当冷流入口温度为338.15 K时,换热器的㶲效率达到20.7%;随着氢气摩尔分数的增加,换热器的㶲效率下降,当混合气体的摩尔配比为2 :2 :1,即氢气的摩尔分数为1/5时,换热器的㶲效率达到20.1%。
| [1] |
Lee H S. Thermal design:Heat sinks, thermoelectrics, heat pipes, compact heat exchangers, and solar cells[M]. Wiley, 2010.
|
| [2] |
高绪栋, 程林, 许明田, 等.管壳式换热器壳侧流体的流动及其熵产分布[C]//中国工程热物理学会2008年传热传质学学术会议.郑州: 中国工程热物理学会, 2008. GAO Xudong, CHENG Lin, XU Mingtian, et al. The flow of fluid and its entropy distribution on the side of shell of tubular heat exchanger[C]//2008 Heat and Mass Transfer Academic Conference of the China Institute of Engineering Thermal Physics. Zhengzhou: China Society of Engineering Thermophysics, 2008. (in Chinese) |
| [3] |
司子辉, 张燕, 康一亭, 等. 翅片管式换热器的数值模拟与优化[J]. 化工进展, 2010, 29(S2): 82-86. SI Zihui, ZHANG Yan, KANG Yiting, et al. Numerical simulation and optimization of finned tube heat exchanger[J]. Chemical Industry and Engineering Progress, 2010, 29(S2): 82-86. (in Chinese) |
| [4] |
俞接成, 诸葛一然. 管壳式换热器流动与传热的三维数值模拟[J]. 北京石油化工学院学报, 2012, 20(2): 60-64. YU Jiecheng, ZHUGE Yiran. A three-dimension numerical study on the heat transfer and fluid flow of a shell-and-tube heat exchanger[J]. Journal of Beijing Institute of Petro-Chemical Technology, 2012, 20(2): 60-64. (in Chinese) DOI:10.3969/j.issn.1008-2565.2012.02.014 |
| [5] |
彭必先, 甘昌胜, 闫天堂. 甲醇水蒸汽催化重整过程的研究进展[J]. 化学进展, 2004, 16(3): 414-421. PENG Bixian, GAN Changsheng, YAN Tiantang. Advances in methanol-steam catalytic reforming process[J]. Progress in Chemistry, 2004, 16(3): 414-421. (in Chinese) DOI:10.3321/j.issn:1005-281X.2004.03.014 |
| [6] |
Liu Q B, Hong H, Yuan J L, et al. Experimental investigation of hydrogen production integrated methanol steam reforming with middle-temperature solar thermal energy[J]. Applied Energy, 2009, 86(2): 155-162. DOI:10.1016/j.apenergy.2008.03.006 |
| [7] |
Duncan J B, Toor H L. An experimental study of three component gas diffusion[J]. AIChE Journal, 1962, 8(1): 38-41. DOI:10.1002/(ISSN)1547-5905 |
| [8] |
Krishna R, Wesselingh J A. The Maxwell-Stefan approach to mass transfer[J]. Chemical Engineering Science, 1997, 52(6): 861-911. DOI:10.1016/S0009-2509(96)00458-7 |
| [9] |
Bassi F, Crivellini A, Rebay S, et al. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ω turbulence model equations[J]. Computers & Fluids, 2005, 34(4/5): 507-540. |
| [10] |
Fuller E N, Schettler P D, Giddings J C. New method for prediction of binary gas-phase diffusion coefficients[J]. Industrial & Engineering Chemistry, 1966, 58(5): 18-27. |
| [11] |
Krishna R. A generalized film model for mass transfer in non-ideal fluid mixtures[J]. Chemical Engineering Science, 1977, 32(6): 659-667. DOI:10.1016/0009-2509(77)80232-7 |
| [12] |
王维德. 多组分物系传质过程扩散系数及其计算[J]. 华侨大学学报(自然科学版), 2002, 23(2): 180-183. WANG Weide. Diffusivity of multicomponent mixture during the process of mass transfer and its calculation[J]. Journal of Huaqiao University(Natural Science), 2002, 23(2): 180-183. (in Chinese) |
| [13] |
Krishna R. Effect of nature and composition of inert gas on binary vapour condensation[J]. Letters in Heat and Mass Transfer, 1979, 6(2): 137-147. DOI:10.1016/0094-4548(79)90006-7 |
| [14] |
王冶.船用换热器流动与传热的三维流场数值模拟研究[D].上海: 上海交通大学, 2013. WANG Ye. Numerical simulation for 3D flow field on flow and heat transfer performance of the marine heat exchangers[D]. Shanghai: Shanghai Jiaotong University, 2013. (in Chinese) |
| [15] |
谷伟, 张虎, 李增耀, 等. 混合气体在典型多孔介质内扩散过程的数值模拟[J]. 西安交通大学学报, 2012, 46(3): 107-112. GU Wei, ZHANG Hu, LI Zengyao, et al. Simulation on diffusion processes of multicomponent gas mixture in typical porous media[J]. Journal of Xi'an Jiaotong University, 2012, 46(3): 107-112. (in Chinese) DOI:10.3969/j.issn.1008-245X.2012.03.017 |
| [16] |
高鑫, 刘超杰. 换热器在核电站的应用及其性能分析[J]. 河南科技, 2015(22): 69-70. GAO Xin, LIU Chaojie. Application and performance analysis of heat exchanger in nuclear power plant[J]. Journal of Henan Science and Technology, 2015(22): 69-70. (in Chinese) DOI:10.3969/j.issn.1003-5168.2015.22.049 |
| [17] |
罗庚. 基于(火用)分析法的换热器性能研究[J]. 企业导报, 2016(10): 113. LUO Geng. Based on exergy analysis method of the heat exchanger performance study[J]. Guide to Business, 2016(10): 113. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

