目前能用于机械密封的材料很多, 如橡胶、金属、高分子材料、石墨、铸铁、Al2O3陶瓷、硬质合金、SiC、CrC等, 但能用于强辐照、耐弱酸, 且能充当金属润滑剂的材料,就非常之少。在核电后处理设备中,常需要使用动密封,但橡胶在辐射环境下会发生断链反应或交联反应等结构变化[1],严重影响材料物理化学性能和使用寿命,最终导致材料失效;金属垫片密封润滑性能差,磨损量大,后处理环境中需用水、酸等清洗,且金属垫圈不耐腐蚀。碳纤维填料由于具有耐高温、耐化学性、耐腐蚀性、耐磨性和低摩擦系数的特性[2],既能满足密封要求,又具有自润滑效果,常用于核电设备中。
现有的密封材料研究多针对橡胶密封的有限元分析[3-4],郭立晓[5]对软填料密封进行了有限元分析,但使用的是选择超弹性单元HYPER84, 一般适用于求解橡胶类的问题,而填料多为石棉、石墨、碳纤维盘根,与橡胶材质特性有区别;仝文科[6]等通过对密封机理的理论分析,得到填料径向压力分布;励行根[7]进行了柔性石墨、编织盘根组合填料密封性能试验研究,但未从理论上找出压力分布与磨损量、泄漏量的联系;秦瑶[8]进行了V型填料密封的力学分析及润滑性能研究,但试验研究用的密封圈是聚四氟乙烯材料。已有研究多从有限元或实验得到压力对密封材料性能的影响,以及预测磨损量、泄漏量的方法[9-13],关于2者与轴向压力的计算方法仍不充分;笔者在填料压力分布的基础上得到磨损量的计算方法,并对碳纤维填料进行实验得到端盖预紧力对密封介质泄漏量的影响,同时还研究了填料磨损量与介质泄漏量的联系。
1 预紧应力与磨损量的关系填料密封使用中,填料与运动件的磨损是影响密封效果、密封有效寿命的关键因素,也是研究密封填料特性的重要部分。密封填料端盖预紧力可使填料变形产生轴向应力和径向应力,分别与轴、填料箱表面紧密贴合,最终达到阻止流体泄漏的目的[14]。预紧力小则填料与轴接触面积小、径向应力小,摩擦磨损较少;预紧力过大会导致径向应力过大,与轴接触力大,填料磨损量增大,缩短填料密封的寿命。通过受力分析与计算,可得到密封填料磨损量与端盖预紧力的联系。
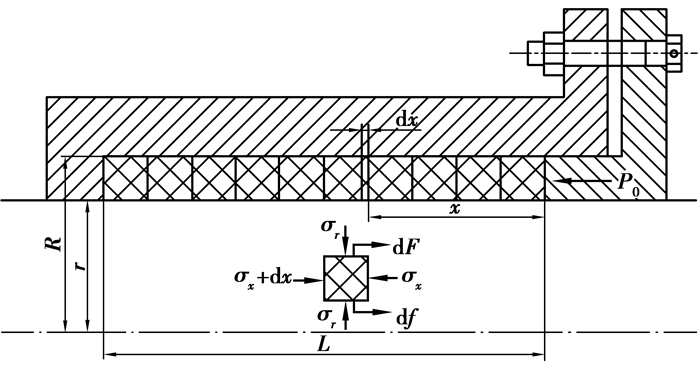
密封填料受轴向压力P0后,除产生轴向应力σx外,径向与轴和密封箱体也产生接触应力σr,侧压系数K为填料径向应力与轴向应力的比值。侧压系数随着预紧力增加而增大,且填料与轴间的侧压系数大于填料与箱体间的侧压系数[15],为简化计算假设填料的侧压系数为常数K。填料与轴的摩擦系数为μi,与箱体内表面的摩擦系数为μo,设填料的径向宽度b=R-r,在距离端盖x处填料的轴向应力为σx,则径向接触应力为σr=Kσx。填料密封的受力情况如图 1所示。
|
图 1 填料密封受力分析图 Fig. 1 Packing seal force analysis diagram |
取填料中宽度为dx,内径为r,外径外R的环形微元体,建立平衡方程
| $ \sigma_{x} \cdot \pi\left(R^{2}-r^{2}\right)=\left(\sigma_{x}+\mathrm{d} \sigma_{x}\right) \cdot \pi\left(R^{2}-r^{2}\right)+\mathrm{d} f+\mathrm{d} F, $ | (1) |
式中:df=μi·σr·2πr·dx为微元对轴表面的摩擦力,N;dF=μo·σr·2πR·dx为微元对箱体内表面的摩擦力,N;dσr为局部径向接触应力在微元dx上的应力变化,Pa。
由于σr=Kσx,并为简化计算假设可将μi=μo=μ,式(1)可化简为
| $ -\left(R^{2}-r^{2}\right) \mathrm{d} \sigma_{x}=2 \mu K \sigma_{x}(R+r) d_{x} $ |
由x积分到L,L为填料密封长度,由σx积分到P0可得
| $ \int_{\sigma_{x}}^{P_{0}} \frac{\mathrm{d} \sigma_{x}}{\sigma_{x}}=-2 \mu K \frac{(R+r)}{\left(R^{2}-r^{2}\right)} \int_{x}^{L} d_{x}, $ | (2) |
将b=R-r代入式(2)可得
| $ {\sigma _x} = {P_0} \cdot e\frac{{2K\mu (L - x)}}{b},{\sigma _{\rm{r}}} = K{\sigma _x} = K{P_0} \cdot e\frac{{2K\mu (L - x)}}{b}, $ | (3) |
填料与轴和箱体的磨损多为黏着磨损,根据阿查德方程[16]得到磨损率
| $ \frac{W_{V}}{S}=K_{\mathrm{m}} \frac{L_{\mathrm{m}}}{H}, $ | (4) |
式中:WV为较软材料上的体积磨损率;S为总滑动距离,m;Km为黏着磨损系数;Lm为法向载荷,Pa;H为较软材料的硬度,即填料硬度,HB;
在此条件下,法向载荷即填料的径向接触应力σr,将式(3)代入式(4)中可得
| $ {W_V} = {K_{\rm{m}}}S\frac{{{\sigma _{\rm{r}}}}}{H} = {K_{\rm{m}}}SK{P_0}\frac{{e\frac{{2K\mu (L - x)}}{b}}}{H}, $ | (5) |
式(5)为轴向某点的磨损率,计算填料总磨损率W为
| $ W = \frac{{2\pi r \cdot {K_{\rm{m}}}SK{P_0}}}{H}\int_0^L e \frac{{2K\mu (L - x)}}{b}{d_x}, $ | (6) |
式中,Km通常称为黏着磨损系数,其值会随载荷变化、摩擦条件和摩擦材料而变化。根据实验经验,黏着磨损系数值在10-2~10-7变化。当表面略有润滑时,Km值为10-4~10-5;当表面润滑较好时,Km值为10-6~10-7。由于研究对象碳纤维填料中的碳纤维具有乱层石墨结构,具有自润滑性,但其具体数值很难确定。密封填料较软,硬度在1~30 HB之间,可通过实验测得不同预紧力下的磨损量后通过曲线拟合得到黏着磨损系数与硬度的比值,从而确定磨损量的计算公式。
2 预紧应力与泄漏量的关系填料的轴向预紧力不仅与磨损量相关,也影响密封介质的泄漏。通过对泄漏原因及机理分析,得到综合因素下的泄漏量计算公式。并用实验得到拟合密封间隙与预紧力关系,得到最终泄漏量计算公式。
常见有间隙泄漏机理、多孔隙泄漏机理、粘附泄漏机理和动力泄漏机理。密封介质为液体时,其特有的泄漏形式是粘附泄漏;当密封介质为气体时,主要为间隙泄漏和多孔隙泄漏。
密封填料的泄漏是3个因素造成的:填料密封内部的缝隙出现流体渗漏;流体通过填料和轴表面之间的间隙泄漏;流体通过填料与箱体内表面的之间的间隙泄漏。填料本身的缝隙泄漏需非接触区域联通形成泄漏通道[17],通过压实填料的方法来消除;填料与箱体内表面之间因为无相对运动,且填料被压紧后与填料箱内表面紧密接触,泄漏量基本可忽略;只有填料与往复运动轴之间,有相对运动,并存在微小间隙,所以泄漏量主要是由填料与轴之间的间隙产生的[18]。
填料的径向应力分布与介质的压力分布呈相反的趋势。当拧紧端盖螺栓时,填料变形并产生径向应力,其由外端向底部递减,且由急剧递减到趋向平缓。密封介质的压力则由底部逐渐向外端递减。当填料外端处介质压力为零时,则密封状态最佳(泄漏量为零);而当外端的介质压力大于零时, 则泄漏量随着介质压力的增大而增大[6],故介质的泄漏与填料和密封介质的压力都有关。
密封介质的泄漏主要有密封材料两端压力差引起的压差流动,和芯轴与填料箱体相对运动引起的剪切流动[19]。压差流动导致的泄漏量为
| $ Q_{1}=\frac{\pi D h^{3}}{12 \mu_{j} L} \Delta p, $ |
式中:h为填料与芯轴间的间隙高度,m;D=2r为芯轴直径,由于芯轴与填料间间隙极小,m;Δp为填料两端的密封介质压力差值, Pa;μj为密封介质的流体动力粘度, Pa·s;
芯轴相对箱体往外运动时流体剪切流动的流量为
当芯轴往内运动时,缝隙间流动的流量
所以芯轴的相对运动引起的剪切流动泄漏量
芯轴一次往复运动(包括内外行程)引起的填料密封的介质泄漏量为
| $ Q=Q_{1}+Q_{2}=\frac{\pi D h^{3}}{12 \mu_{j} L} \cdot p+\frac{\pi D h}{2}\left(v_{\mathrm{o}}-v_{i}\right), $ | (7) |
式(7)基于如下假设计算的
1) 流体为层流流动;
2) 芯轴与密封填料完全同心,密封间隙为环形间隙;
3) 不考虑密封介质在流动过程中加速的影响;
4) 不考虑芯轴运动过程中间隙的形状改变。
当密封介质为液体时,粘附在芯轴表面通过填料与芯轴间的密封间隙泄漏,间隙高度与芯轴粗糙度、填料粗糙度、芯轴径向位移、填料径向位移及预压紧下芯轴径向位移有关[20], 可通过数值模型计算[21-22],也可通过磨损仿真、流体动力学结合进行泄漏预测[23-24];当密封为气体时,气体粘附力小,与液体介质泄漏情况不同,且由于填料为碳纤维预氧化后轴编织而成,其不具备各向同性的特性,受轴向压力后形变量用广义Hooke定律计算不准确,故可采用实验拟合的方法确定间隙高度与预紧力的关系,从而计算泄漏量。
3 磨损量与泄漏量的关系前面求出了预紧应力与磨损量、泄漏量的关系式,表明磨损量与预紧应力成正相关,泄漏量与预紧应力成负相关变化。表明要达到较小的泄漏量,需要较大的预紧应力,而这样会导致磨损量增大,填料的使用寿命缩短。
而这两者本身之间也存在联系,可通过磨损量计算出介质的理论泄漏量。随着往复运动次数增加,填料磨损量增大,与轴之间的间隙增大,密封介质的泄漏也相应增多。可计算出填料的磨损体积为
| $ {V_{\rm{m}}} = V \cdot W。$ | (8) |
填料中各点受径向力不同,磨损率不同,但差异极小,假设填料的磨损为内圆柱面表面均匀磨损,磨损后为同心环形间隙。为简化计算假设磨损的体积是以轴的周长为长边的2πr×h×L的长方体,根据式(8)的体积磨损量, 可计算得到密封间隙近似为
| $ h=\frac{V_{\mathrm{m}}}{2 \pi r L}。$ | (9) |
将式(9)得到的密封间隙带入式(7)中即可得到往复运动行程S后的介质泄漏量为
| $ Q=\frac{\pi D \Delta p}{12 \mu_{j} L}\left[\frac{V_{\mathrm{m}}}{2 \pi r L}\right]^{3}+\frac{\pi D\left(v_{\mathrm{o}}-v_{i}\right)}{2} \frac{V_{\mathrm{m}}}{2 \pi r L}。$ | (10) |
实验将芯轴与TS308碳纤维密封填料装入填料箱体后,安装在疲劳实验机上,由疲劳实验机带动芯轴往复运动;压缩空气通入填料箱,由压力表测得气体压力,由燃气表测量气体流量即泄漏量;采用接近式光电传感器和计数器记录芯轴往复运动次数。
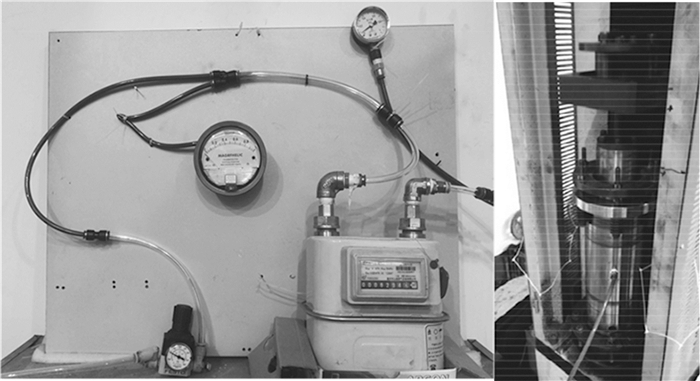
实验装置的设备如图 2所示。
|
图 2 实验设备图 Fig. 2 Diagram of the experimental devoice |
实验参数:往复运动周N=1~10 000次,填料的轴向预紧力P0依次为0.1、0.3、0.5、0.7、1.2 MPa。预紧力不同时填料密封被压缩后高度不同,经测量L1=150.5 mm,L2=140.5 mm,L3=135 mm,L4=130.5 mm,L5=120 mm。当对磨副为淬火45钢时, 稳态摩擦系数约为0.13。芯轴的直径即填料密封内径D=2r=90 mm,填料外径半径R=60 mm,b=R-r=15 mm。侧压系数K在填料不同轴向位置时数值不同,且随预紧力变化,实验中预紧力差值较小K值变化极小,视为常量K=0.3。填料密度为1.26×103 kg/m3。密封介质两端压差Δp=0.07 MPa, 通入的密封介质为压缩空气,其动力粘度为1.81×10-5 Pa·s(环境温度20 ℃)。芯轴往复行程为60 mm,芯轴往外运动速度vo=70 mm/s,往内运动速度vi=50 mm/s,平均速度v设为60 mm/s(即1次/s),故1 s的泄漏量即每次循环运动的泄漏量。
安装填料前去除表面残留的石墨等污染物,并使用电子秤称量实验前的每组填料。填料装入后将螺栓拧紧以达到所需轴向预紧力的扭矩值T,开机预运行100次往复循环后再拧紧螺栓至扭矩值T。正式运行疲劳实验机后,每200次记录气体流量,直至10 000次运行完后用电子秤称量实验后的每组填料,得到磨损量并计算磨损率。
4.2 实验结果 4.2.1 预紧应力与磨损量的关系经过10 000次往复运动后,取出密封填料后计算得到各预紧力下磨损量,由于每次实验的填料高度不同则体积不同,所以计算出磨损率进行比较。
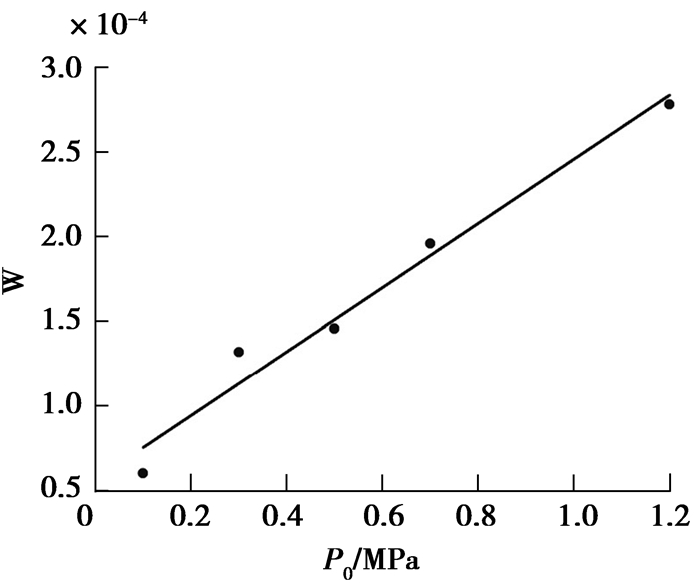
如图 3所示,磨损率与轴向预紧力成线性关系,与式(6)相符。因施加预紧力后,填料的轴向高度不同,故将磨损率带入式(6)分别计算出磨损系数与硬度比值的平均值为
|
图 3 磨损率与预紧力关系图 Fig. 3 Relationship between wear ratio and axial stress |
则填料磨损量计算公式为
| $ W=3.60 \times 10^{-11} \cdot 2 \pi r \cdot S K P_{0} \int_{0}^{L} e \frac{2 K \mu(L-x)}{b} d_{x}。$ | (11) |
如图 4所示,随着轴向预紧力的增大,填料所受的径向应力增大后与芯轴接触更加紧密,密封介质泄漏量减小,密封效果越好,可见泄漏量随轴向预紧力变化的曲线符合理论假设。

|
图 4 不同预紧力泄漏量对比图 Fig. 4 Comparison of the leakage on different axial stress |
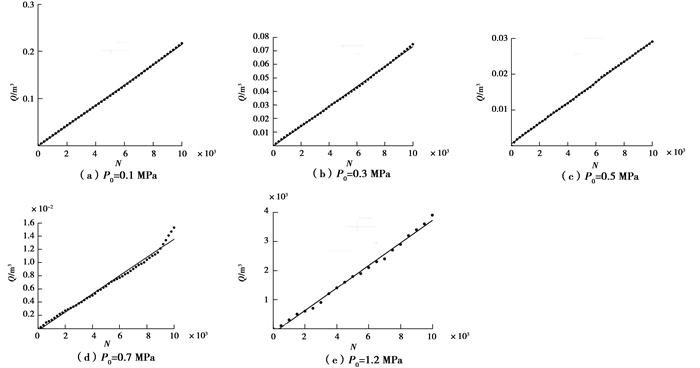
由上图可见,当填料密封的轴向预紧力一定时,介质泄漏量与循环次数成线性关系,通过曲线拟合得到计算公式。以下分别为不同预紧力泄漏量随循环次数增加的变化情况。
如图 5所示,当填料的轴向预紧力为0.1 MPa时,泄漏量与循环次数的关系为
| $ Q_{1}=(2.15 N-16.17) \times 10^{-5}。$ | (12) |
|
图 5 泄漏量与循环次数关系图 Fig. 5 Relationship between leakage and number of cycle |
当填料的轴向预紧力为0.3 MPa时,泄漏量与循环次数的关系为
| $ Q_{2}=(7.34 N-373.08) \times 10^{-6}。$ | (13) |
当填料的轴向预紧力为0.5 MPa时,泄漏量与循环次数的关系为
| $ Q_{3}=(2.86 N+580.85) \times 10^{-6}。$ | (14) |
当填料的轴向预紧力为0.7 MPa时,泄漏量与循环次数的关系为
| $ Q_{4}=(1.38 N-294.34) \times 10^{-6}。$ | (15) |
由于泄漏量1.2 MPa预紧力下极小,故记录间隔增加。如图 4(e)所示,当填料的轴向预紧力为1.2 MPa时,泄漏量与循环次数的关系为
| $ Q_{5}=3.87 \times 10^{-7} N-1.49 \times 10^{-4}。$ | (16) |
从式(12)可以得到预紧力为0.1 MPa时,芯轴每往复运动一次泄漏量为2.15×10-5 m3;同理从式(13)~式(16)中得到其他预紧力下每往复运动一次泄漏量为7.34×10-6、2.86×10-6、1.38×10-6、3.87×10-7 m3。
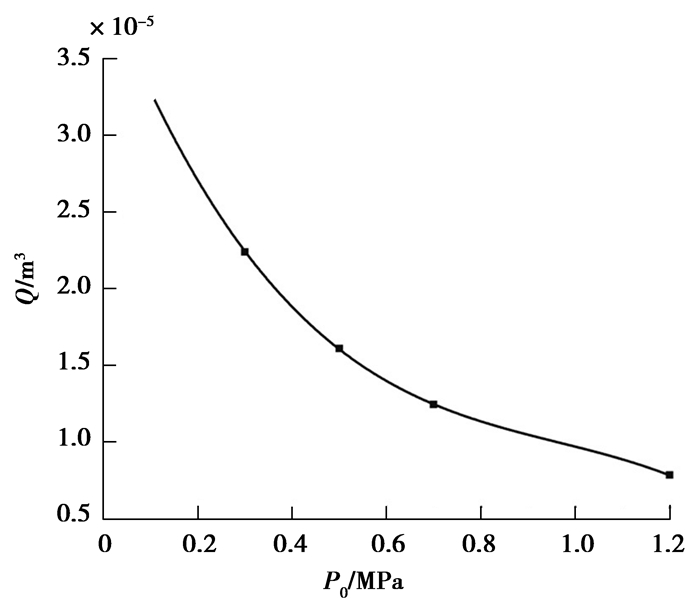
通过式(7)用MATLAB可计算得到不同预紧力下的密封间隙,并经过曲线拟合,如图 6所示。
|
图 6 密封间隙与预紧力关系图 Fig. 6 Relationship between clearance thickness and axial stress |
得到填料密封与芯轴间隙高度与轴向预紧力的关系为
| $ h=\left(3.99-7.78 P_{0}+7.29 P_{0}^{2}-2.52 P_{0}^{3}\right) \times 10^{-5}。$ | (17) |
故不同预紧力下的泄漏量理论计算公式为
| $ \begin{aligned} Q=& \frac{\pi D \Delta p}{12 \mu_{j} L}\left[\left(3.99-7.78 P_{0}+7.29 P_{0}^{2}-2.52 P_{0}^{3}\right) \times 10^{-5}\right]^{3}+\frac{\pi D(v)_{\circ}-v_{i} )}{2} \\ &\left[\left(3.99-7.78 P_{0}+7.29 P_{0}^{2}-2.52 P_{0}^{3}\right) \times 10^{-5}\right]。\end{aligned} $ | (18) |
为验证式(11)是否能预测密封介质的磨损量,进行了另一组实验。与前面的实验条件、设备、参数相同,设置轴向预紧力为1.0 MPa,测得压缩后填料高度L6=126 mm,实验测得磨损率为3.09×10-4。
由式(11)计算得到磨损率理论值为3.26×10-4,误差为5.2%,故认为此计算方法能预测填料密封的磨损量。验证实验的磨损量较理论值偏小,可能是由于碳纤维具有乱层石墨结构,结构赋予其自润滑性[25],密封表面形成了石墨润滑膜减小磨损。
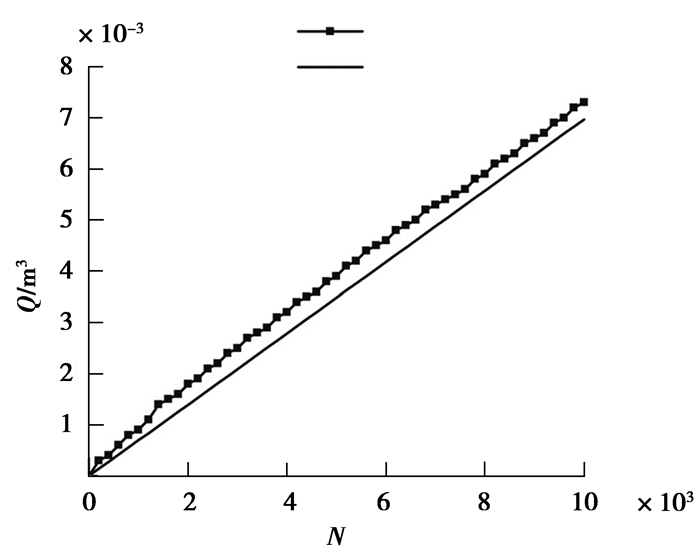
4.3.2 泄漏量验证为验证式(18)是否能预测密封介质的泄漏量,故进行另一组实验。与前面的实验条件、设备、参数相同,设置轴向预紧力为1.0 MPa,测得填料高度L6=126 mm,泄漏量随循环次数变化如图 7所示。
|
图 7 泄漏量理论值与实验值对比图 Fig. 7 Comparison of theoretical leakage with experiment leakage |
而通过式(18)计算得到泄漏量理论值为
| $ Q=7.083 \times 10^{-7} \mathrm{m}^{3} / \mathrm{s}。$ |
填料的理论泄漏量如上图所示,实际泄漏量与理论泄漏量相差较小,可认为该计算方法能有效预测填料的泄漏量。实际测得循环运动的泄漏量比理论计算值偏大并与理论曲线近似平行。密封间隙比理论计算出的间隙偏大,可能是往复运动数次后,填料回弹松弛,未达到设定的预紧力值,所以填料变形量偏小。或可能是由于芯轴与填料摩擦温度升高,密封介质流动速度加快的影响。
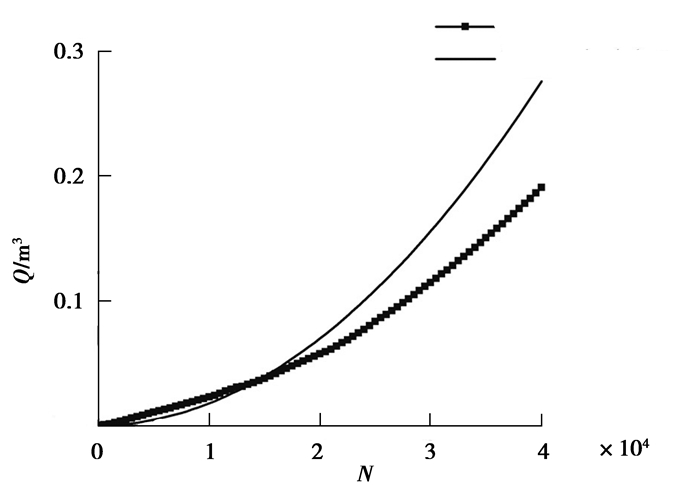
4.3.3 泄漏量与磨损量关系验证前面的实验循环次数均为10 000次,实验中泄漏量与循环次数成线性关系。可能由于实验次数较少,填料磨损引起密封间隙增大导致的泄漏量增大没有明显表现。故增加循环次数至40 000次,为验证填料磨损量计算介质泄漏量的计算方法是否可行,进行另一组实验。与前面的实验条件、设备、参数相同,设置轴向预紧力为0.5 MPa,测得填料高度L6=135 mm,泄漏量随循环次数变化如图 8所示。
|
图 8 磨损量对泄漏量影响图 Fig. 8 Influence of wear on leakage |
密封介质的泄漏量随着循环次数的增加而增大,而且增大速度由缓到急,说明往复运动行程增加后填料磨损量加大,密封间隙随之增大,导致泄漏速度加快。其变化与理论上通过材料磨损量计算介质泄漏量公式变化趋势一致,表明密封材料磨损量增大引起密封介质泄漏量的加速增加。且泄漏量与式(10)通过磨损量计算出理论值对比后发现,实验大约前15 000次实际泄漏量大于理论值,由于式(10)是假设实验初始状态是填料与芯轴无间隙,随着填料磨损间隙增大泄漏量逐渐增大,而实验中填料压紧变形后与芯轴间仍存在微小间隙,故实际泄漏量偏大;实验后期实际泄漏量小于理论值,填料中的石墨经过多次运动在表面形成了较好的润滑,减小了填料的磨损,故泄漏量较理论值偏小。
5 结语1) 填料的磨损量随轴向预紧力增大而增大,且成线性关系;通过密封填料的受力分析和阿查德方程推导出填料的磨损率计算方法,并通过实验确定其中的磨损系数和硬度比值,得到确定的计算公式,且进行另一组实验验证了计算公式的有效性。
2) 填料的密封介质泄漏量随轴向预紧力增大而减小;将密封填料的泄漏视为压差泄漏和剪切流动的共同作用结果,推导出密封填料的泄漏量计算方法;通过实验拟合得到不便于测量和计算的密封间隙与轴向预紧力的关系,并进行实验验证了计算公式可估算介质的泄漏量。
3) 填料密封的磨损随着轴向预紧力的增大而增加,导致间隙增大,密封介质泄漏量增大加剧;密封件运动次数较少时可选用式(18)计算泄漏量,运动次数较多时可选用磨损量与泄漏量关系式计算泄漏量,在实际应用中应合理选用预紧力,保证泄漏率要求并尽量减小磨损,提高密封填料的使用寿命。
| [1] |
黄元昌. γ(Gamma)辐射对橡胶密封材料低温特性的影响[J]. 橡塑技术与装备, 2017, 43(05): 34-38. HUANG Yuanchang. Effect of γ(Gamma) radiation on the rubber sealing material properties at low temperature[J]. China Rubber/Plastics Technology and Equipment (Rubber), 2017, 43(05): 34-38. |
| [2] |
杨家义, 杨博峰, 李香, 等. 全无油往复压缩机用碳纤维增强聚四氟乙烯密封材料的性能研究[J]. 流体机械, 2017, 45(3): 6-10. YANG Jiayi, YANG Bofeng, LI Xiang, et al. Study on properties of carbon fiber reinforced PTFE sealing material appliedin non-lubricated reciprocating compressor[J]. Fluid Machinery, 2017, 45(3): 6-10. (in Chinese) DOI:10.3969/j.issn.1005-0329.2017.03.002 |
| [3] |
Hui Y. Contact stress analysis of metal rubber seals based on finite element[J]//Science and Engineering Research Center. Proceedings of 2016 International Conference on Applied Mechanics, Mechanical and Materials Engineering(AMMME 2016).US: Science and Engineering Research Center, 2016.
|
| [4] |
常洁, 陈同祥. 长寿命航天器结构密封性能仿真分析研究[J]. 航天器工程, 2014, 23(3): 49-53. CHANG Jie, CHEN Tongxiang. Research of performance for silicone rubber seals used in spacecraft structure based on finite element analysis[J]. Spacecraft Engineering, 2014, 23(3): 49-53. (in Chinese) DOI:10.3969/j.issn.1673-8748.2014.03.009 |
| [5] |
郭立晓, 伍开松, 袁新生, 等. 抽油杆盘根密封机理研究[J]. 石油矿场机械, 2008, 37(3): 29-32. GUO Lixiao, WU Kaisong, YUAN Xinsheng, et al. Study of sealing mechanism of sucker rod packer[J]. Oil Field Equipment, 2008, 37(3): 29-32. (in Chinese) DOI:10.3969/j.issn.1001-3482.2008.03.008 |
| [6] |
仝文科, 黄清世, 陈小军, 等. 填料密封机理及其应用的研究[J]. 现代机械, 2006(6): 54-55. TONG Wenke, HUANG Qingshi, CHEN Xiaojun, et al. Study on the principle and appliance of the filler sealing[J]. Modern Machinery, 2006(6): 54-55. (in Chinese) DOI:10.3969/j.issn.1002-6886.2006.06.022 |
| [7] |
励行根, 王成林, 沈明学, 等. 柔性石墨/编织盘根组合填料密封性能试验研究[J]. 润滑与密封, 2014, 39(12): 119-124. LI Xinggen, WANG Chenglin, SHEN Mingxue, et al. Study on sealing performance of combined packing of flexible graphite ring and braided packing ring[J]. Lubrication Engineering, 2014, 39(12): 119-124. (in Chinese) DOI:10.3969/j.issn.0254-0150.2014.12.025 |
| [8] |
秦瑶, 王财生, 周琼, 等. V型填料密封压紧过程受力计算方法[J]. 华东理工大学学报(自然科学版), 2013, 39(1): 108-114. QIN Yao, WANG Caisheng, ZHOU Qiong, et al. Mechanics calculation method for V-seal ring in compression process[J]. Journal of East China University of Science and Technology(Natural Science Edition), 2013, 39(1): 108-114. (in Chinese) DOI:10.3969/j.issn.1006-3080.2013.01.019 |
| [9] |
Wang Z X, Zhi Y J, Hu C Y, et al. Study of seals on long stroke and reciprocating motion condition[J]. Journal of Power and Energy Engineering, 2013, 1(7): 40-44. DOI:10.4236/jpee.2013.17007 |
| [10] |
Miranda S, Molari L, Scalet G, et al. A physically-based analytical relationship for practical prediction of leakage in longitudinally cracked pressurized pipes[J]. Engineering Structures, 2014, 79: 142-148. DOI:10.1016/j.engstruct.2014.08.011 |
| [11] |
Alvarez G A. Finite element solution of the radial load equation for rotary shaft seals[J]. Tribology Transactions, 1992, 35(4): 571-582. DOI:10.1080/10402009208982159 |
| [12] |
Bishnoi L R, Vedula R P. Prediction of air leakage and aerosol transport through concrete cracks with a fractal based crack morphology model[J]. Nuclear Engineering and Design, 2013, 265: 393-401. DOI:10.1016/j.nucengdes.2013.06.032 |
| [13] |
Lee S H, Yoo S S, Kim D E, et al. Accelerated wear test of FKM elastomer for life prediction of seals[J]. Polymer Testing, 2012, 31(8): 993-1000. DOI:10.1016/j.polymertesting.2012.07.017 |
| [14] |
秦博杰, 韩光辉, 励勇, 等. 疏水阀填料泄漏分析与改进[J]. 发电设备, 2017, 31(1): 30-32. QIN Bojie, HAN Guanghui, LI Yong, et al. Analysis and treatment on packing leakage of a steam trap valve[J]. Power Equipment, 2017, 31(1): 30-32. (in Chinese) DOI:10.3969/j.issn.1671-086X.2017.01.007 |
| [15] |
肖光凯, 章兰珠, 王夫清, 等. 石墨填料环力学和密封性能试验研究[J]. 润滑与密封, 2016, 41(11): 10-14, 64. XIAO Guangkai, ZHANG Lanzhu, WANG Fuqing, et al. Study on mechanical and sealing performance of flexible graphite packing rings[J]. Lubrication Engineering, 2016, 41(11): 10-14, 64. (in Chinese) DOI:10.3969/j.issn.0254-0150.2016.11.003 |
| [16] |
王振廷, 孟君晟. 摩擦磨损与耐磨材料[M]. 哈尔滨: 哈尔滨工业大学出版社, 2013. WANG Zhenting, MENG Junsheng. Frictional wear and wear resistant materials[M]. HaErbing: HaErbing industry college book concern, 2013. (in Chinese) |
| [17] |
Bottiglione F, Carbone G, Mantriota G. Fluid leakage in seals:an approach based on percolation theory[J]. Tribology International, 2009, 42(5): 731-737. |
| [18] |
刘尚明, Liu Shangming. 超高压往复式压缩机填料密封的失效及其对策[J]. 化工装备技术, 2016, 37(1): 36-38. LIU Shangming, LIU Shangming. Failure of the packing seal of ultrahigh pressure reciprocating compressor and its countermeasures[J]. Chemical Equipment Technology, 2016, 37(1): 36-38. (in Chinese) |
| [19] |
周志鸿, 闫建辉, 刘连华. 间隙泄漏量的分析计算[J]. 凿岩机械气动工具, 2002(4): 14-17. ZHOU Zhihong, YAN Jianhui, LIU Lianhua. Analysis and calculation of Gap leakage[J]. Tribology Transactions, 2002(4): 14-17. (in Chinese) |
| [20] |
Nikas G K. Elastohydrodynamics and mechanics of rectangular elastomeric seals for reciprocating piston rods[J]. Journal of Tribology, 2003, 125(1): 60. DOI:10.1115/1.1506316 |
| [21] |
Nikas G K, Sayles R S. Computational model of tandem rectangular elastomeric seals for reciprocating motion[J]. Tribology International, 2006, 39(7): 622-634. DOI:10.1016/j.triboint.2005.04.004 |
| [22] |
Thatte A, Salant R F. Transient EHL analysis of an elastomeric hydraulic seal[J]. Tribology International, 2009, 42(10): 1424-1432. DOI:10.1016/j.triboint.2009.05.026 |
| [23] |
Li X, Peng G L, Li Z. Prediction of seal wear with thermal structural coupled finite element method[J]. Finite Elements in Analysis and Design, 2014, 83: 10-21. DOI:10.1016/j.finel.2014.01.001 |
| [24] |
Li X, Peng G L, Liu W J, et al. Research on dynamic simulation method of leakage prediction for hydraulic system[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2015, 229(4): 771-786. DOI:10.1177/0954406214539469 |
| [25] |
陈显明. 碳纤维的性能、发展及应用研究进展[J]. 印染助剂, 2015, 32(7): 1-4. CHEN Xianming. Property, development and application research of carbon fiber[J]. Textile, 2015, 32(7): 1-4. (in Chinese) DOI:10.3969/j.issn.1004-0439.2015.07.001 |
 2019, Vol. 42
2019, Vol. 42

