2. 重庆工商大学 制造装备机构设计与控制重庆市重点实验室, 重庆 400067
2. Chongqing Key Laboratory of Manufacturing Equipment Mechanism Design and Control, Chongqing Technology and Business University, Chongqing 400067, P. R. China
共轭曲线是指两构件上用以实现给定运动规律的连续相切的一对曲线,是计算齿轮齿面、凸轮轮廓等工程问题的理论基础[1],其中由已知齿轮廓形求解其共轭齿形是齿轮设计领域的常见问题。
传统计算共轭齿形的方法有齿廓法线法与包络法两种。齿廓法线法[2]是经典的共轭齿形求解方法,如王家序等[3]基于齿轮啮合原理求解谐波传动的共轭齿形。该方法首先建立啮合方程,再通过坐标变换求解共轭齿形,由于啮合方程复杂,需要采用数值方法进行迭代求解。包络法是近年来研究较多的数字方法,Chiang等[4]基于包络原理提出了一种螺杆加工成形砂轮廓形的几何设计方法,Wu等[5]基于包络原理提出RRS成形磨加工仿真。包络法本质是其中一个齿轮固定不动,另一个齿轮在其上绕着瞬心点纯滚动,形成一系列曲线簇,曲线簇的包络即为共轭齿形,其难点在于包络点的求解。无论齿廓法线法还是包络法,求解的第一步是确定齿廓曲线的法向量,而齿廓上的不可导点,如双圆弧齿轮的两段圆弧连接点[6],渐开线齿轮的齿顶尖点[7]等,采用这两种传统计算方法将出现奇异点问题,表现为求解的共轭齿形不连续。
近年来,国内外学者提出一些无奇异点问题的共轭齿形求解方法,如Radzevich[8]基于微分几何学提出R-映射法,用于计算径向剃齿刀修形齿面,Zhou[9]提出截线式数字模拟包络方法计算砂轮廓形,吴玉仁等[10]在截线法的基础上提出了射线法,用于计算双螺旋压缩机转子的成形刀具廓形,上述方法虽无奇异点问题,然而当齿面较为复杂时求解困难。笔者于文献[11]中提出尖点矢量离散法,用于解决有奇异点的双圆弧齿轮共轭齿形,并在此基础上提出点矢量一次包络算法[12]和点矢量二次包络算法[13],分别用于计算修形齿轮的成型砂轮及蜗杆砂轮廓形。点矢量包络算法无需对齿面建模,通用性好,然而其精度受限于离散点数量。
为此,文中基于共轭曲线的等距偏移特性,提出共轭齿形求解的轮转曲线等距偏移法,在曲率半径变化率较小的齿廓曲线共轭齿形求解时,无奇异点问题,计算简单,且可得到解析解。
1 共轭曲线的等距偏移特性共轭曲线的等距偏移特性可表述为:记A曲线的共轭曲线为A′,B曲线的共轭曲线为B′,若B曲线是A曲线偏移距离为L的等距偏移线,则B′曲线也是A′曲线的等距偏移线,且偏移距离仍为L。
记A曲线的方程为r1,则B曲线的方程r′1可表示为
| $ {{\mathit{\boldsymbol{r'}}}_1} = {\mathit{\boldsymbol{r}}_1} + L{\mathit{\boldsymbol{N}}_1}, $ | (1) |
N1表示r1的单位法向量。将r′1代入啮合方程[14],并用齐次坐标表示:
| $ {\mathit{\boldsymbol{N}}_2} \cdot \mathit{\boldsymbol{V}}_2^{\left( {12} \right)} = 0 \Rightarrow {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_1}}\\ {\bf{1}} \end{array}} \right]^{\rm{T}}}\mathit{\boldsymbol{K}}\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1}}\\ {\bf{1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_1}}\\ {\bf{0}} \end{array}} \right]} \right), $ | (2) |
式中,N2表示B曲线共轭齿形B′的单位法向量,V2(12)表示在与B′固连的坐标系中B曲线对B′的相对运动速度。矩阵K与坐标变换有关,可以表示为
| $ \mathit{\boldsymbol{K}} = \mathit{\boldsymbol{W}}_{21}^{\rm{T}}\frac{{{\rm{d}}{\mathit{\boldsymbol{M}}_{21}}}}{{{\rm{d}}t}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)}^{\rm{T}}}\frac{{{\rm{d}}{\mathit{\boldsymbol{M}}_{21}}}}{{{\rm{d}}t}}}&{{{\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)}^{\rm{T}}}\frac{{{\rm{d}}\mathit{\boldsymbol{a}}}}{{{\rm{d}}t}}}\\ {\bf{0}}&{\bf{0}} \end{array}} \right], $ | (3) |
式中:W21表示法向量的变换矩阵; W21*表示W21的三阶顺序主子式; M21表示位置矢量的变换矩阵,M21的三阶顺序主子式也为W21*; a是位置变换的列向量。根据坐标变换性质,W21*是反对称阵,有(W21*)TW21*=E,对等式两边求导有:
| $ {\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)^{\rm{T}}}\frac{{{\rm{d}}\mathit{\boldsymbol{W}}_{21}^ * }}{{{\rm{d}}t}} = - \frac{{{\rm{d}}{{\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)}^{\rm{T}}}}}{{{\rm{d}}t}}\mathit{\boldsymbol{W}}_{21}^ * , $ | (4) |
利用矩阵转置的性质,式(4)两边同时转置,化简得到:
| $ {\left[ {{{\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)}^{\rm{T}}}\frac{{{\rm{d}}\mathit{\boldsymbol{W}}_{21}^ * }}{{{\rm{d}}t}}} \right]^{\rm{T}}} = - {\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)^{\rm{T}}}\frac{{{\rm{d}}\mathit{\boldsymbol{W}}_{21}^ * }}{{{\rm{d}}t}}, $ | (5) |
则K的三阶顺序主子式为反对称阵,记为K*,代入式(2)中,有:
| $ {\left[ \begin{array}{l} {\mathit{\boldsymbol{N}}_1}\\ {\bf{1}} \end{array} \right]^{\rm{T}}}\mathit{\boldsymbol{K}}\left[ \begin{array}{l} {\mathit{\boldsymbol{r}}_1}\\ {\bf{1}} \end{array} \right] + L\left( {{{\left[ \begin{array}{l} {\mathit{\boldsymbol{N}}_1}\\ {\bf{1}} \end{array} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}^ * }}&{{{\left( {\mathit{\boldsymbol{W}}_{21}^ * } \right)}^{\rm{T}}}\frac{{{\rm{d}}\mathit{\boldsymbol{a}}}}{{{\rm{d}}t}}}\\ {\bf{0}}&{\bf{0}} \end{array}} \right]\left[ \begin{array}{l} {\mathit{\boldsymbol{N}}_1}\\ {\bf{1}} \end{array} \right]} \right) = 0, $ | (6) |
式中:N1是列向量,则N1TK*N1是一阶矩阵,有N1TK*N1=(N1TK*N1)T,展开化简并考虑K*是反对称阵,易知:
| $ \mathit{\boldsymbol{N}}_1^{\rm{T}}{\mathit{\boldsymbol{K}}^ * }{\mathit{\boldsymbol{N}}_1} = 0。$ | (7) |
将式(7)代入式(6),r′1的啮合方程最终化简为
| $ \left[ \begin{array}{c}{\boldsymbol{N}_{1}} \\ {\bf{1}}\end{array}\right]^{\mathrm{T}} \boldsymbol{K} \left[ \begin{array}{c}{\boldsymbol{r}_{1}} \\ {\bf{1}}\end{array}\right]=0。$ | (8) |
式(8)为r1的啮合方程,故等距偏移前后,啮合方程不变,则方程的解不变,曲线A与曲线B坐标变换矩阵均为M21,对曲线r′1进行坐标变换:
| $ \boldsymbol{r}_{2}^{\prime}=\boldsymbol{M}_{21} \boldsymbol{r}_{1}。$ | (9) |
将式(1)代入式(9),最终得到:
| $ \boldsymbol{r}_{2}^{\prime}=\boldsymbol{r}_{2}+L \boldsymbol{N}_{2}, $ | (10) |
式中:r′2表示B曲线的共轭曲线方程;r2表示A曲线的共轭曲线方程。式(10)说明r′2是r2偏移距离为L的等距偏移线,则等距偏移特性得证。
2 轮转曲线等距偏移法 2.1 圆弧曲线的共轭齿形圆弧可看作圆心的等距偏移线,偏移距离为圆弧半径,圆心的共轭齿形本质是点的运动轨迹[2],记圆心的极坐标为(R,ε),其运动轨迹的位置矢量rrc可表示为
| $ \boldsymbol{r}_{\mathrm{rc}}=\boldsymbol{M}_{21}[R \sin \varepsilon \quad R \cos \varepsilon \quad 1]^{\mathrm{T}}。$ | (11) |
根据常见的齿轮传动形式,将变换矩阵M21代入式(11)[15],并进行等距偏移,偏移距离L为圆弧半径,最终得到以下4类轮转曲线等距偏移方程。
1) 由齿轮向齿条传动时,得到摆线类等距偏移方程:
| $ \left\{\begin{array}{c}{\boldsymbol{r}_{\mathrm{oc}}=\left[ \begin{array}{c}{R_{\mathrm{p}} \varphi-R \sin (\varphi-\varepsilon)-L \cos \beta} ,\\ {-R_{\mathrm{p}}+R \cos (\varphi-\varepsilon)-L \sin \beta}\end{array}\right]} \\ {\beta=\arctan \frac{R \sin (\varphi-\varepsilon)}{\left(R_{\mathrm{p}}-R\right) \cos (\varphi-\varepsilon)}}\end{array}\right., $ | (12) |
2) 由齿条向齿轮传动时,得到渐开线类等距偏移方程:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_{{\rm{oc}}}} = \left[ \begin{array}{l} R\sin \left( {\varphi + \varepsilon } \right) + {R_{\rm{p}}}\left( {\sin \varphi - \varphi \cos \varphi } \right) - L\cos \beta \\ R\cos \left( {\varphi + \varepsilon } \right) + {R_{\rm{p}}}\left( {\cos \varphi + \varphi \sin \varphi } \right) - L\sin \beta \end{array} \right],}\\ {\beta = \arctan \frac{{R\sin \left( {\varphi + \varepsilon } \right) - {R_{\rm{p}}}\varphi \cos \varphi }}{{R\cos \left( {\varphi + \varepsilon } \right) + {R_{\rm{p}}}\varphi \sin \varphi }},} \end{array}} \right. $ | (13) |
3) 由齿轮向转向相反的齿轮传动,即外齿轮传动时,得到外摆线类等距偏移方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{{\rm{oc}}}} = \left[ {\begin{array}{*{20}{c}} { - R\sin [(1 + \rho )\varphi - \varepsilon ] + E\sin \rho \varphi - L\cos \beta }\\ {R\cos [(1 + \rho )\varphi - \varepsilon ] - E\cos \rho \varphi - L\sin \beta } \end{array}} \right],}\\ {\beta = \arctan \frac{{(1 + \rho )R\sin ((1 + \rho )\varphi - \varepsilon ) - E\rho \sin \rho \varphi }}{{ - (1 + \rho )R\cos ((1 + \rho )\varphi - \varepsilon ) + E\rho \cos \rho \varphi }},} \end{array}} \right. $ | (14) |
4) 由齿轮向转向相同的齿轮传动,即内齿轮传动时,得到内摆线类等距偏移方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{{\rm{oc}}}} = \left[ {\begin{array}{*{20}{c}} {R\sin [(1 - \rho )\varphi - \varepsilon ] - E\sin \rho \varphi - L\cos \beta }\\ {R\cos [(1 - \rho )\varphi - \varepsilon ] + E\cos \rho \varphi - L\sin \beta } \end{array}} \right],}\\ {\beta = \arctan \frac{{(1 - \rho )R\sin ((1 - \rho )\varphi - \varepsilon ) + E\rho \sin \rho \varphi }}{{(1 - \rho )R\cos ((1 - \rho )\varphi - \varepsilon ) - E\rho \cos \rho \varphi }},} \end{array}} \right. $ | (15) |
式(12)~式(15)中:roc是轮转曲线等距偏移线的位置矢量;φ为自变量;Rp表示分度圆半径;E表示中心距;ρ表示传动比。由共轭曲线等距偏移特性可知,圆弧曲线的共轭曲线为轮转曲线的一段,且偏移距离为圆弧半径。
计算实例为半径1 mm的圆弧齿轮,节圆半径50 mm,则对应的齿条廓形为偏移距离1 mm的长幅摆线等距偏移线,参数方程[Xoc, Yoc]T为
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{X_{{\rm{oc}}}}}\\ {{Y_{{\rm{oc}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {50\varphi - 54.0093\sin (\varphi - 0.0724) - \cos \beta }\\ { - 50 + 54.0093\cos (\varphi - 0.0724) - \sin \beta } \end{array}} \right],}\\ {\beta = - \arctan [13.47140\tan (\varphi - 0.0724)]。} \end{array}} \right. $ | (16) |
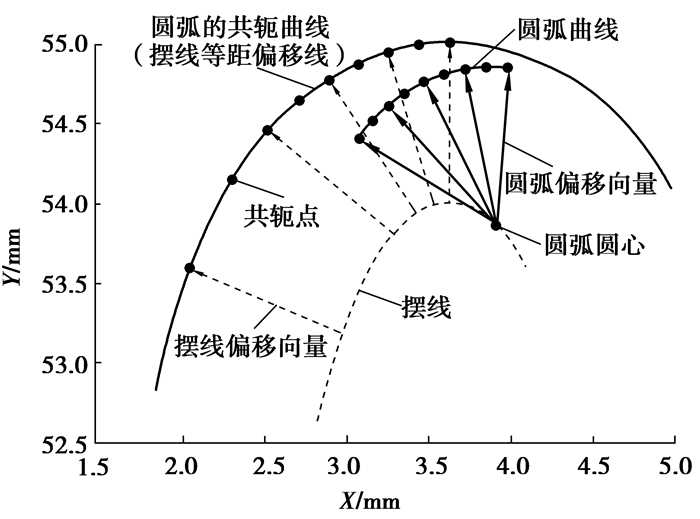
在Matlab中绘制式(16),将结果与传统啮合方程求解的共轭点对比,共轭点在曲线上,如图 1所示。说明圆弧曲线的共轭齿形是长幅摆线等距偏移线。
|
图 1 圆弧的共轭曲线 Fig. 1 The conjugate curve of an arc |
对于由任意曲线构成的齿廓,可将齿廓曲线进行离散处理,用圆弧曲线逼近任意曲线。圆弧圆心为相邻离散点的法向量交点,圆心坐标为
| $ \left\{ {\begin{array}{*{20}{l}} {Y_0^{(i)} - Y_g^{(i)} = \frac{{Ny_{\rm{g}}^{(i)}}}{{Nx_{\rm{g}}^{(i)}}}\left( {X_0^{(i)} - X_0^{(i)}} \right),(i = 1,2, \cdots ,N - 1),}\\ {Y_0^{(i)} - Y_{\rm{g}}^{(i + 1)} = \frac{{Ny_{\rm{g}}^{(i + 1)}}}{{Nx_{\rm{g}}^{(i + 1)}}}\left( {X_0^{(i)} - X_0^{(i + 1)}} \right),(i = 1,2, \cdots ,N - 1),} \end{array}} \right. $ | (17) |
式中:(X0(i),Y0(i))是第i段圆弧的圆心坐标;(Xg(i),Yg(i))是第i个齿廓曲线的离散点坐标;[Nxg(i),Nyg(i)]T是第i个齿廓曲线的离散点法向量,i的取值范围是1~(N-1),N为离散点数。补充曲线端点,当i=N时,有:
| $ \left\{ \begin{array}{l} X_0^{\left( N \right)} = X_g^{\left( N \right)},\\ Y_0^{\left( N \right)} = Y_g^{\left( N \right)}。\end{array} \right. $ | (18) |
圆弧半径为法向量交点到离散点距离,半径大小为
| $ L^{(i)}=\sqrt{\left(X_{\mathrm{g}}^{(i)}-X_{0}^{(i)}\right)^{2}+\left(Y_{\mathrm{g}}^{(i)}-Y_{0}^{(i)}\right)^{2}},(i=1,2, \cdots, N), $ | (19) |
式中,L(i)表示第i段圆弧的半径。
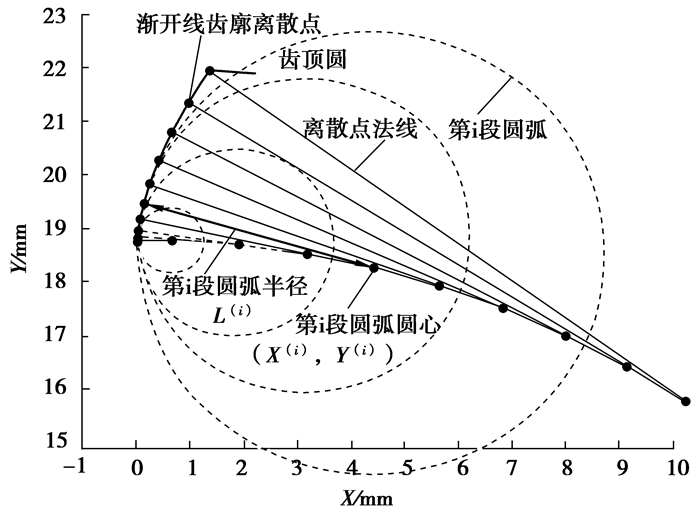
以计算渐开线齿形及齿顶圆为例,齿轮模数2、齿数20的渐开线齿轮,齿顶尖点为不可导的奇异点,将齿顶尖点看作半径为0的圆弧。圆弧逼近结果如图 2所示。
|
图 2 圆弧代替任意曲线 Fig. 2 The curve replaced by arcs |
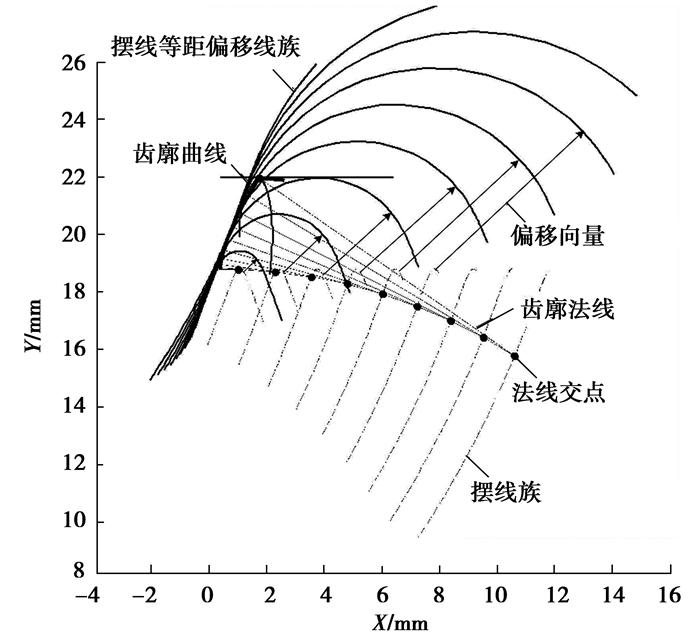
把圆弧坐标(X0(i),Y0(i))化为极坐标(R0(i),ε0(i)),根据传动形式,将R0(i)、ε0(i)、L(i)代入对应的式(12)~式(15),得到一系列轮转曲线等距偏移线族。以齿轮廓形计算齿条廓形为例,代入式(12),得到摆线类等距偏移线族,如图 3所示。
|
图 3 轮转曲线等距偏移线族 Fig. 3 Family of rotation curve equidistant offset line |
令roc(i)=roc(i),求解相邻两段等距偏移线的交点作为临界点,最终共轭曲线由N-1段轮转曲线等距偏移线组成,方程为
| $ \boldsymbol{r}_{\mathrm{w}}=\left\{\begin{array}{l}{\boldsymbol{r}_{\mathrm{oc}}^{(1)}, \varphi=\varphi_{1} \sim \varphi_{2}} ,\\ {\boldsymbol{r}_{\mathrm{oc}}^{(2)}, \varphi=\varphi_{2} \sim \varphi_{3}} ,\\ {\ldots} \\ {\boldsymbol{r}_{\mathrm{oc}}^{(\mathrm{N}-1)}, \varphi=\varphi_{\mathrm{N}-1} \sim \varphi_{\mathrm{N}}}\end{array}\right., $ | (20) |
式中:rw为共轭曲线的位置矢量;roc(i)为第i段轮转曲线等距偏移线,自变量φi通过式(21)确定。
| $ {\left[ {\begin{array}{*{20}{c}} {X_{{\rm{oc}}}^{\left( i \right)}}\\ {Y_{{\rm{oc}}}^{\left( i \right)}} \end{array}} \right]_{\left| {\varphi = \varphi i} \right.}} = {\left[ {\begin{array}{*{20}{c}} {X_{{\rm{oc}}}^{\left( i \right)}}\\ {Y_{{\rm{oc}}}^{\left( i \right)}} \end{array}} \right]_{\left| {\varphi = \varphi \left( {i + 1} \right)} \right.}} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{\varphi _i}}\\ {{\varphi _{i + 1}}} \end{array}} \right.,i = 1,2, \cdots ,N, $ | (21) |
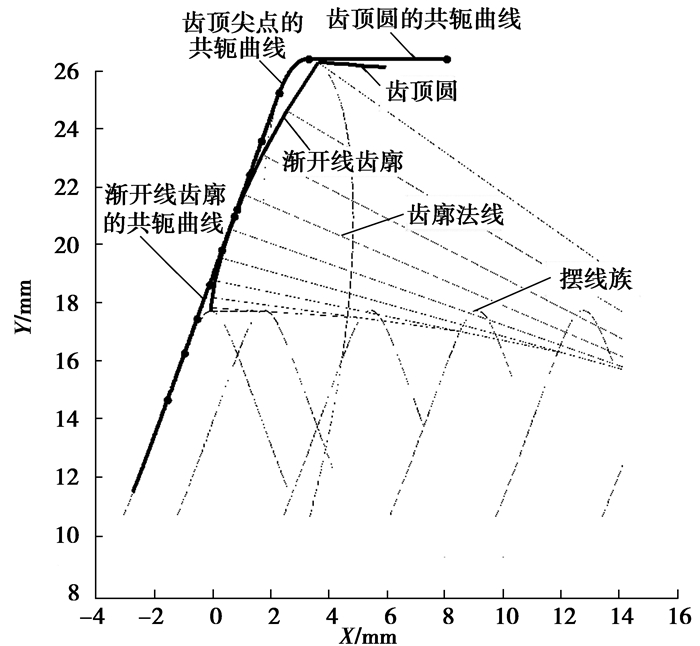
式中,[Xoc(i), Yoc(i)]T是roc(i)的矩阵表示式,联立求解得到φi与φi+1,代入式(20),得到最终齿廓曲线的共轭曲线,齿顶尖点处的共轭齿形由偏移距离为0的摆线等距偏移线组成,齿顶圆处的共轭齿形由圆心坐标为(0, 0)的摆线等距偏移线组成,如图 4所示。
|
图 4 齿廓的共轭曲线 Fig. 4 The conjugate curve of gear profile |
尖点矢量离散是现阶段解决奇异点共轭齿形的常用方法[11],为验证齿顶尖点的共轭齿形,通过尖点矢量离散得到齿顶尖点的共轭点。对齿顶尖点处的点矢量进行离散处理:
| $ {\alpha _i} = \frac{{i - 1}}{{N - 1}}\left( {{\rm{ \mathsf{ π} }} - {\theta _0}} \right) + \frac{{N - i}}{{N - 1}}\arctan \left( {\frac{{Y{g_{\left( {{\theta _0}} \right)}}}}{{X{g_{\left( {{\theta _0}} \right)}}}}} \right),i \in \left[ {1 \sim N} \right], $ | (22) |
式中:αi表示第i个离散点矢量的偏转角度;N表示离散点数;齿顶尖点参数θ0与齿顶圆半径Ra有关,为
| $ {\theta _0} = \sqrt {{{\left( {\frac{{{R_a}}}{{{R_b}}}} \right)}^2} - 1} 。$ | (23) |
将式(22)和式(23)代入啮合方程,并化简,为
| $ {\left( {\left[ {\begin{array}{*{20}{c}} {\cos {\varphi _i}}&{ - \sin {\varphi _i}}&0\\ {\sin {\varphi _i}}&{\cos {\varphi _i}}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos {\alpha _i}}\\ {\sin {\alpha _i}}\\ 1 \end{array}} \right]} \right)^{\rm{T}}}\left( {{\rm{d}}\left[ {\begin{array}{*{20}{c}} {\cos {\varphi _i}}&{ - \sin {\varphi _i}}&{{R_{\rm{p}}}{\varphi _i}}\\ {\sin {\varphi _i}}&{\cos {\varphi _i}}&{ - {R_{\rm{p}}}}\\ 0&0&1 \end{array}} \right]/{\rm{d}}t} \right)\left[ \begin{array}{l} X{g_{\left( {{\theta _0}} \right)}}\\ Y{g_{\left( {{\theta _0}} \right)}}\\ 1 \end{array} \right] = 0。$ | (24) |
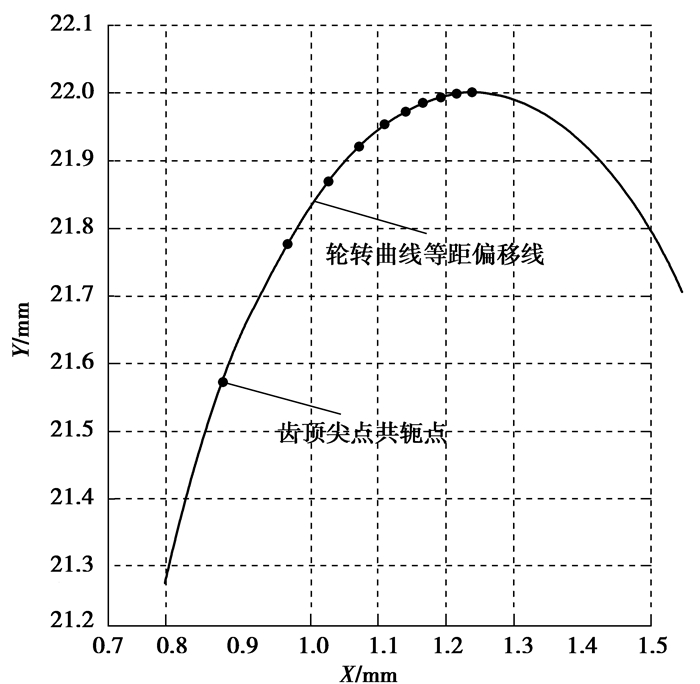
求解式(24),得到齿顶尖点的离散点矢量啮合转角φi,然后对齿顶尖点(Xg(θ0), Yg(θ0))进行坐标变换,最终得到齿顶尖点的一系列共轭点,将这些共轭点代入式(20),结果吻合,点均在曲线上,如图 5所示,说明轮转曲线等距偏移线法求解齿顶尖点的共轭齿形正确。
|
图 5 共轭齿形验证 Fig. 5 Verification of conjugate curve |
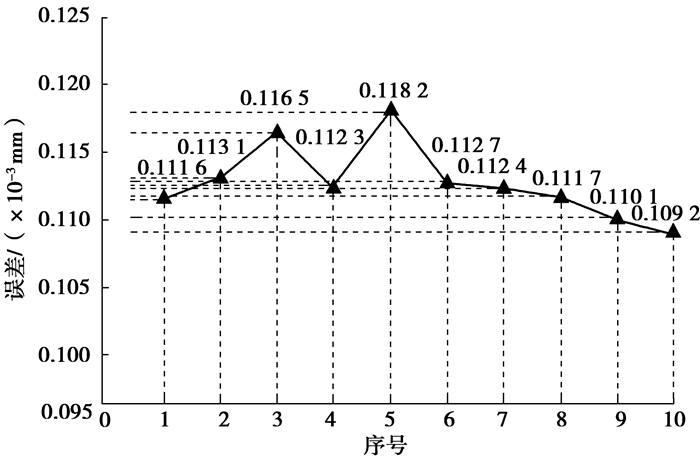
为验证前述的渐开线齿廓的共轭齿形,通过求解啮合方程得到齿廓共轭点,求解过程从略,误差为共轭点到齿廓曲线沿法线方向的距离,齿廓曲线方程由式(20)表示,从齿根到齿顶取10个点并依次标号,绘制误差曲线如图 6所示。
|
图 6 齿廓误差曲线 Fig. 6 Error curve of tooth profile |
通过误差曲线可以看出,各点误差均在0.114 0 mm左右,可见轮转曲线等距偏移法求解渐开线的共轭齿形可行,然而误差较大。
3 误差分析 3.1 误差数学模型轮转曲线等距偏移法采用圆弧曲线替代任意曲线,这一替代过程存在原理误差。
| $ E_{i}=R_{i+1}-R_{i}, $ | (25) |
式中:Ei表示第i段圆弧的逼近误差;Ri表示曲线上第i个离散点的曲率半径,Ri可以通过曲率半径公式计算:
| $ {R_i} = \frac{{{{\left[ {Xg{'}_{\left( {\theta i} \right)}^2 + Yg{'}_{\left( {\theta i} \right)}^2} \right]}^{3/2}}}}{{\left| {X{{g'}_{\left( \theta \right)i}}Y{{g''}_{\left( \theta \right)i}} - Y{{g'}_{\left( \theta \right)i}}X{{g''}_{\left( \theta \right)i}}} \right|}}。$ | (26) |
(Xg,Yg)表示齿廓曲线关于θ的参数方程。将式(26)代入式(25),并通过曲率半径的导数进行化简:
| $ {E_i} = \left( {{\theta _{i + 1}} - {\theta _i}} \right)\frac{{{\rm{d}}{R_{\left( \theta \right)}}}}{{{\rm{d}}\theta }}。$ | (27) |
根据等距偏移的共轭曲线偏移距离相等特性,当Ei取得最大值时表示共轭曲线的误差E,为
| $ E = \Delta \theta {\left. {\left( {R_{(\theta )}^\prime } \right)} \right|_{\max }}。$ | (28) |
曲率半径的变化率R′(θ)为
| $ {R{'}_{\left( \theta \right)}} = \frac{{3\left( {{{X''}_g}{{X'}_g} + {{Y''}_g}{{Y'}_g}} \right)\left( {X{'}_g^2 + Y{'}_g^2} \right)\left| {{{X'}_{\rm{g}}}{{Y''}_g} - X_g^n{{Y'}_g}} \right| - {{\left( {X{'}_g^2 + Y{'}_g^2} \right)}^{1.5}}\left| {{{X'}_{\rm{g}}}{{Y'''}_g} - {{X'''}_g}{{Y'}_g}} \right|}}{{{{\left( {X{'}_g^2 + Y{'}_g^2} \right)}^2}}}。$ | (29) |
由式(28)可知,误差E与2个因素有关:齿廓曲线的曲率半径变化率越小,则误差越小;选取的离散点越密集,自变量差值Δθ越小,则误差越小。
3.2 误差消减方法齿廓曲线确定时,改变自变量差值Δθ,可减少误差E。当Δθ=0时,齿廓离散点重合,在该点的法线方向上任取A、B 2点:
| $ \left[ {\begin{array}{*{20}{c}} {{X_A}}\\ {{Y_A}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_g} + aN{x_g}}\\ {{Y_g} + aN{y_g}} \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {{X_B}}\\ {{Y_B}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_g} + bN{x_g}}\\ {{Y_g} + bN{y_g}} \end{array}} \right], $ | (30) |
式中:(XA,YA)表示A点坐标;(XB,YB)表示B点坐标;(Xg,Yg)表示齿廓离散点坐标;[Nxg,Nyg]T表示齿廓离散点法向量;a与b为任意不相等实数。将A点、B点分别用极坐标(RA,εA)、(RB,εB)表示,根据具体传动形式,选择式(12)~式(15)其中之一代入,得到两段轮转曲线等距偏移线roc(a)、roc(b):
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_{{\rm{oc}}\left( a \right)}} = \left[ \begin{array}{l} {R_{\rm{p}}}{\varphi _a} - {R_a}\sin \left( {{\varphi _a} - {\varepsilon _a}} \right) - a\cos {\beta _a}\\ - {R_{\rm{p}}} + {R_a}\cos \left( {{\varphi _a} - {\varepsilon _a}} \right) - a\sin {\beta _a} \end{array} \right],\\ \beta = \arctan \frac{{{R_a}\sin \left( {{\varphi _a} - {\varepsilon _a}} \right)}}{{\left( {{R_{\rm{p}}} - {R_a}} \right)\cos \left( {{\varphi _a} - {\varepsilon _a}} \right)}}, \end{array} \right. $ | (31) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_{{\rm{oc}}\left( a \right)}} = \left[ \begin{array}{l} {R_{\rm{p}}}{\varphi _b} - {R_b}\sin \left( {{\varphi _b} - {\varepsilon _b}} \right) - b\cos {\beta _a}\\ - {R_{\rm{p}}} + {R_b}\cos \left( {{\varphi _b} - {\varepsilon _b}} \right) - b\sin {\beta _a} \end{array} \right],\\ \beta = \arctan \frac{{{R_b}\sin \left( {{\varphi _b} - {\varepsilon _b}} \right)}}{{\left( {{R_{\rm{p}}} - {R_b}} \right)\cos \left( {{\varphi _b} - {\varepsilon _b}} \right)}}。\end{array} \right. $ | (32) |
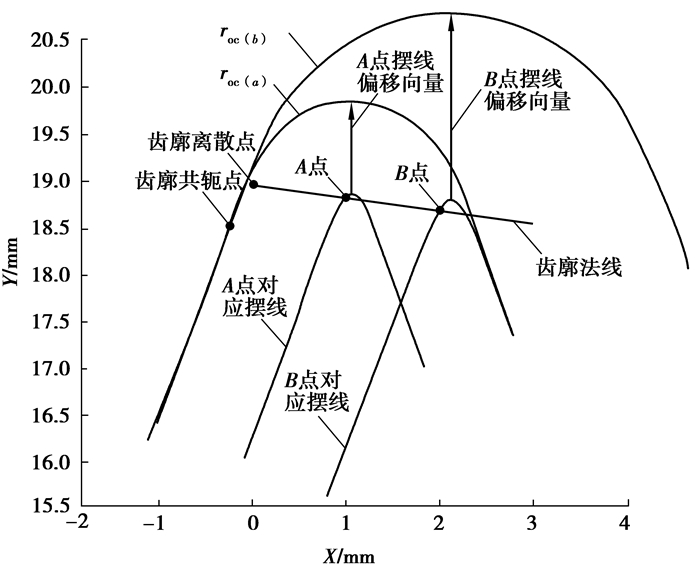
以齿轮齿条传动为例,式(26)和式(27)分别表示A、B 2点对应的摆线等距偏移线。齿廓离散点既可看作A点的等距偏移点,又可看作B点的等距偏移点,则齿廓共轭点既在A点的等距偏移线roc(a)上,又在B点的等距偏移线roc(b)上,故roc(a)与roc(b)的交点即齿廓共轭点,如图 7所示。
|
图 7 齿廓共轭点 Fig. 7 Conjugate points of gear profile |
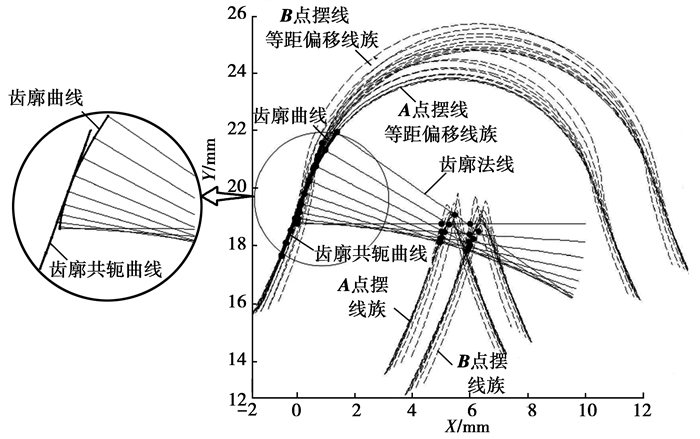
令roc(a)=roc(b),求解得到φa与φb,带入式(31)或式(32),roc(a)或roc(b)则是所求的齿廓共轭点。对齿廓上的每个离散点均采用上述方法优化求解,则最终的共轭齿形可由众多共轭点组成,如图 8所示。
|
图 8 优化后共轭齿形 Fig. 8 Conjugate gear profile without error in principle |
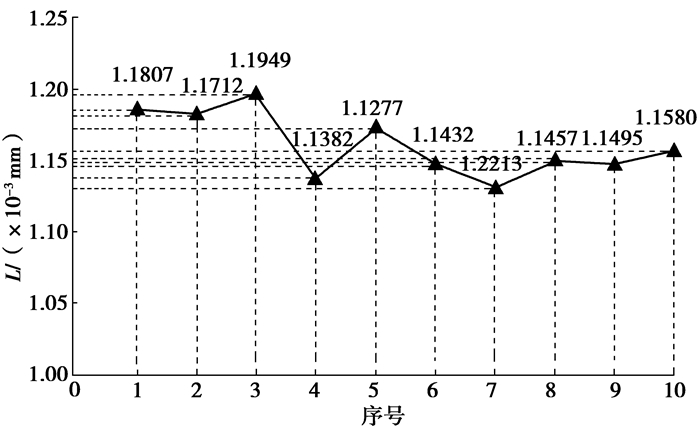
采用上述同样方法计算误差并绘制曲线,如图 9所示,优化后误差已降低到0.001 2 mm以内,结果已较为精确。优化后误差主要由方程求解精度导致,通过优化迭代算法可进一步降低误差。
|
图 9 优化后误差曲线 Fig. 9 The optimized error curve |
1) 针对传统共轭齿形求解方法无法解决奇异点问题,且啮合方程求解困难,提出轮转曲线等距偏移法,通过实例计算说明了该方法的正确性。
2) 分析了轮转曲线等距偏移法的原理误差,说明了该方法适合求解齿廓曲线曲率半径变化率较小的共轭齿形。提出了消除原理误差的方法,实例计算表明优化后的结果已较为精确。
3) 轮转曲线等距偏移法在求解圆弧齿轮、齿顶圆角的共轭齿形时有明显优势:无奇异点问题,计算简单,且可得到解析解。在求解齿廓曲线曲率半径变化率较大的共轭齿形时,可以采用3.2节的误差消减方法进行优化。
目前轮转曲线等距偏移法仅适用于平面啮合问题,如直齿轮啮合或斜齿轮平行轴啮合,下一步研究将针对空间啮合的轮转曲面等距偏移法,进行圆锥齿轮、蜗杆砂轮等廓形计算。
| [1] |
Totolici S, Teodor G, Baroiu N, et al. A new profile for the worm gear drive of a spiral gear[J]. IOP Conference Series:Materials Science and Engineering, 2018, 400: 042057. DOI:10.1088/1757-899X/400/4/042057 |
| [2] |
Litvin F L, Fuentes A. Gear geometry and applied theory[M]. Cambridge: Cambridge University Press, 2004.
|
| [3] |
王家序, 袁攀, 李俊阳, 等. 基于不同啮合原理的谐波传动齿廓研究[J]. 华中科技大学学报(自然科学版), 2017, 45(3): 58-64. WANG Jiaxu, YUAN Pan, LI Junyang, et al. Tooth profile research of harmonic drive based on different engagement theory[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2017, 45(3): 58-64. (in Chinese) |
| [4] |
Chiang C J, Fong Z H. Design of form milling cutters with multiple inserts for screw rotors[J]. Mechanism and Machine Theory, 2010, 45(11): 1613-1627. DOI:10.1016/j.mechmachtheory.2010.06.012 |
| [5] |
Wu Y R, Fong Z H, Zhang Z X. Simulation of a cylindrical form grinding process by the radial-ray shooting (RRS) method[J]. Mechanism and Machine Theory, 2010, 45(2): 261-272. DOI:10.1016/j.mechmachtheory.2009.09.005 |
| [6] |
李阁强, 张龙飞, 韩伟锋, 等. 双圆弧斜齿齿轮泵脉动特性分析及齿形设计[J]. 中国机械工程, 2018, 29(2): 186-192. LI Geqiang, ZHANG Longfei, HAN Weifeng, et al. Pulsation characteristic analysis and tooth profile design of double-circular-arc helical gear pumps[J]. China Mechanical Engineering, 2018, 29(2): 186-192. DOI:10.3969/j.issn.1004-132X.2018.02.009 |
| [7] |
Wen Q, Du Q G, Zhai X C. An analytical method for calculating the tooth surface contact stress of spur gears with tip relief[J]. International Journal of Mechanical Sciences, 2019, 151: 170-180. DOI:10.1016/j.ijmecsci.2018.11.007 |
| [8] |
Radzevich S P. On the accuracy of precision involute hobs:an analytical approach[J]. Journal of Manufacturing Processes, 2007, 9(2): 121-136. DOI:10.1016/S1526-6125(07)70113-5 |
| [9] |
Zhou Y S. Form grinding technology for the mold of powder metallurgy gears[J]. Chinese Journal of Mechanical Engineering, 2005, 41(1): 162. DOI:10.3901/JME.2005.01.162 |
| [10] |
Wu Y R, Fong Z H, Zhang Z X. Simulation of a cylindrical form grinding process by the radial-ray shooting (RRS) method[J]. Mechanism and Machine Theory, 2010, 45(2): 261-272. DOI:10.1016/j.mechmachtheory.2009.09.005 |
| [11] |
李国龙, 孙孟辉, 李先广, 等. 螺旋面截形尖点矢量离散法及其在双圆弧滚刀过渡曲面最小化中的应用[J]. 机械工程学报, 2011, 47(17): 187-192. LI Guolong, SUN Menghui, LI Xianguang, et al. Method of discreting cusp vectors of helicoid and its application in minimization of the relief grinding of double circular-arc gear hob[J]. Journal of Mechanical Engineering, 2011, 47(17): 187-192. (in Chinese) |
| [12] |
李国龙, 林超, 李先广, 等. 成形磨齿砂轮包络计算的双参数点矢量族法[J]. 重庆大学学报, 2013, 36(4): 11-18. LI Guolong, LIN Chao, LI Xianguang, et al. Envelope to a two-parameter family of point vectors method for surface swept by wheel during 5-axis gear form grinding[J]. Journal of Chongqing University (Natural Science Edition), 2013, 36(4): 11-18. (in Chinese) |
| [13] |
He K, Li G L, Li X G. The second envelope method of point-vector and its application on worm wheel grinding modified gear[J]. The International Journal of Advanced Manufacturing Technology, 2017, 88(9/10/11/12): 3175-3184. |
| [14] |
Ji W T, Yao L G, Zhang J. Mathematical modeling and characteristics analysis for the nutation gear drive based on error parameters[J]. Journal of Chongqing University (English Edition), 2016, 15(4): 149-158. |
| [15] |
宋朝省, 樊荣, 刘立斌. 小角度交错轴变厚齿轮齿根应力及影响因素分析[J]. 重庆大学学报(自然科学版), 2014, 37(1): 1-6. SONG Chaosheng, FAN Rong, LIU Libin. Analysis on tooth root stress and influencing factors of crossed beveloid gears with small shaft angle[J]. Journal of Chongqing University(Natural Science Edition), 2014, 37(1): 1-6. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

