洗出算法也称运动提示算法(motion cue algorithm),用来改变真实飞机加速度和角速度进入模拟器平台实现模拟驾驶飞机的目的,改进算法是为了在有限制的模拟器运动空间内达到相对较高的动感逼真度。这是为了向飞行员提供与驾驶真实飞机同样的感觉,达到培养飞行员的目的。洗出算法研究历程经过经典洗出滤波算法、自适应洗出滤波算法和最优控制洗出滤波算法3个阶段[1],其它的算法研究是基于这3种而发展的。Parrish等人[2]引进自适应洗出算法,解决了经典洗出算法参数固定难以调节的问题。Sivan等[3-4]在人体前庭模型的基础上提出最优化洗出算法概念。
在国内,王小亮等[5]以洗出位移和角度作为目标函数,使用遗传算法优化经典洗出算法参数;虽然能够使平台迅速返回到初始位置,但同时降低了算法洗出位移,无法达到充分利用平台空间的目的。王辉、朱道杨[6]等提出基于人体评价的模糊算法,有效改善了相位延迟问题,但对于如何提高洗出位移等缺少描述。在国外,Asadi等人[7]使用遗传算法对滤波器参数进行优化,并且对高通加速度通道作了非线性处理;虽然提高了洗出位移,但是恢复中立位置的时间较长,降低了算法响应逼真度。
针对以上算法的优缺点,笔者提出一种基于人体感官模型的混合算法,结合角加速度二次滤波补偿角位移与模糊逻辑补偿等优点对飞行模拟器洗出算法进行设计。以纵向模式为例对算法进行验证,其它模式类似,不再赘述。
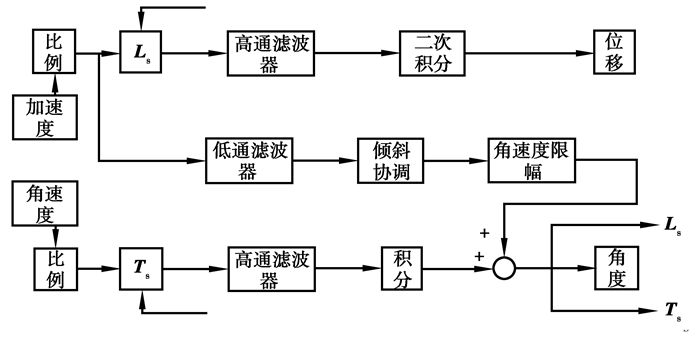
1 体感模拟算法 1.1 经典洗出算法经典洗出算法通常由3个信号通道组成,包括高通加速度通道、倾斜协调通道和高通角速度通道。经典洗出算法如图 1所示。其原理主要是利用高通加速度通道洗出的高频加速度信号来模拟操纵真实飞机产生的突发过载,由于提取的加速度瞬态分量为高频信号,不会使模拟器平台发生损坏,可直接输入;低通滤波器通道也称倾斜协调通道,利用重力加速度分量来模拟飞行员感知的持续加速度感,低频信号幅值可能会超出限制而损坏模拟器平台,因此加入限幅环节进行平台保护;高通角速度通道模拟真实飞机的旋转分量,此分量会对加速度通道产生影响,但对于民用飞机角速度不会太高,因此经典洗出算法忽略此项,直接进行高通角速度输入即可。经典洗出算法由于结构简单而被广泛采用,高通滤波器和低通滤波器的参数截止频率和阻尼比固定,无法在线调节,通常根据飞行员的驾驶经验进行反复试验调整。图中Ls和Ts为转换矩阵。
|
图 1 经典洗出算法 Fig. 1 The classic washout algorithm |
高通加速度通道滤波器传递函数
| $ G = \frac{{{s^3}}}{{\left( {{s^2} + 2{\omega _1}{\xi _1}s + \omega _1^2} \right)\left( {s + {\omega _b}} \right)}}, $ | (1) |
式中:s为拉普拉斯算子;ω1为高通滤波器截止频率,rad/s;ωb为一阶环节系数,rad/s;ξ1为高通滤波器阻尼比,无量纲。
倾斜协调通道滤波器传递函数
| $ G = \frac{{\omega _2^2}}{{{s^2} + 2{\omega _2}{\xi _2}s + \omega _2^2}}, $ | (2) |
式中:s为拉普拉斯算子;ω2为低通滤波器截止频率,rad/s;ξ2为低通滤波器阻尼比,无量纲。
高通角速度通道滤波器传递函数
| $ G = \frac{{{s^2}}}{{{s^2} + 2{\omega _3}{\xi _3}s + \omega _3^2}}, $ | (3) |
式中:s为拉普拉斯算子;ω3为低通滤波器截止频率,rad/s;ξ3为低通滤波器阻尼比,无量纲。
1.2 人体前庭模型前庭系统位于内耳内部,包括半规管和耳石器官[8-9],分别感应角速度和线加速度。人体对于加速度的感知是以比力(相对加速度)的形式呈现的。耳石感知的比力f是通过绝对加速度a减去重力加速度g获得的,为
| $ f = a - g, $ | (4) |
式中:f为人体感官所感受到的线加速度;a为人体的绝对线加速度;g为重力加速度。
耳石模型的传递函数如式(5)所示,对于纵向、侧向以及垂直3个方向具体的参数见文献[6]。
| $ \frac{{\vec f}}{f} = \frac{{K\left( {1 + {\tau _a}s} \right)}}{{\left( {{\tau _L}s + 1} \right)\left( {{\tau _s}s + 1} \right)}}, $ | (5) |
式中:
半规管模型感知角速度信号,其感觉传递函数如式(6)所示,对于俯仰、滚装以及偏航3个自由度具体的参数见文献[6]。
| $ \frac{{\vec \omega }}{\omega } = \frac{{{\tau _a}{\tau _1}{s^2}}}{{\left( {{\tau _a}s + 1} \right)\left( {{\tau _1}s + 1} \right)\left( {{\tau _2}s + 1} \right)}}, $ | (6) |
式中:
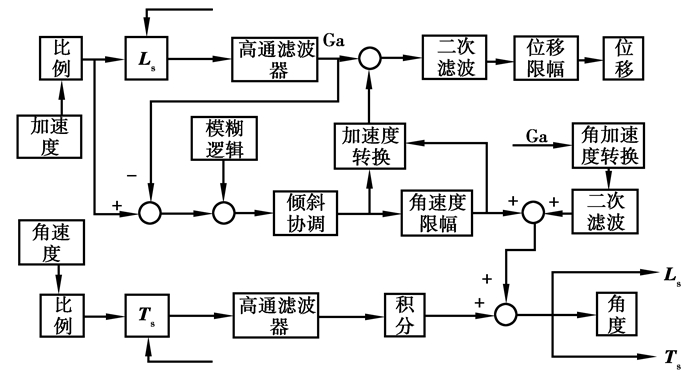
1) 改进洗出算法结构如图 2所示。为解决相位延迟和空间利用率低等问题,采用模糊逻辑补偿思想,以人体感官模型洗出信号误差及变化率作为模糊控制器输入,补偿于倾斜协调通道,达到减小相位误差和提高逼真度的目的。
|
图 2 新型倾斜协调体感算法 Fig. 2 New algorithm of tilting coordination sense of body |
2) 去除原低通滤波器,对倾斜协调通道进行重新设计,用输入的参考模拟信号减去经高通滤波器过滤的高频信号,结合模糊逻辑的补偿信号,使得倾斜洗出效果更加逼近人体感官参考信号,提高模拟逼真度。
3) 洗出算法是为了使飞行员在有限模拟器工作空间内感受到真实飞机中的加速度和角速度。在具体的模拟驾驶中,实际参考加速度与低频输出持续加速度存在较大的感觉误差,增加平动高通角加速度二次滤波补偿角位移,提高飞行员动态逼真感觉。
4) 对于位移洗出部分一方面将角速度限幅前后损失的信号转换成加速度补偿到高通加速度通道,与洗出高频加速度信号合成提高输出位移。另一方面增加二次滤波和位移限幅环节,使得在提高工作空间利用率的同时,平台能够快速回位,为下一次运动做准备,实现高逼真度动感模拟。
2.2 模糊逻辑 2.2.1 模糊补偿控制模糊控制思想:误差有增大趋势时,应采取大的控制量来补偿或消除误差;误差有减少趋势时,应采取小的控制量去补偿。需注意严格控制小误差补偿量,防止平台超限[10-11]。
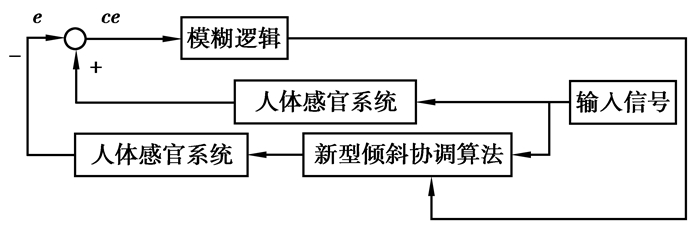
模糊补偿控制主要是利用基于人体感官系统的洗出信号的误差e及其变化率ce,在规则库的基础上,经过归一化、模糊化、模糊推理以及去模糊化一系列模块依照一定的规则补偿给洗出算法的3个滤波器通道如图 3所示。
|
图 3 模糊逻辑补偿模型 Fig. 3 Fuzzy logic compensation model |
由于人体感觉系统受限导致自身无法感受精确的运动,因此模糊规则语言变量在一定程度上设计即可。一般来说,人们总是习惯于将事物分为3个等级。比如速度的快、中、慢;身高的高、中、矮等等[12]。当然设计的模糊子集也分为大、中、小3个等级,具体为FD(负大),FZ(负中),FX(负小),ZX(正小),ZZ(正中),ZD(正大)6个词汇,模糊规则表如表 1所示。
| 表 1 模糊控制规则表 Table 1 Fuzzy control rules table |
隶属函数的设计取决于模糊论域和函数形状的确定。为了进行模糊化处理,必须将输入变量从基本论域转换到相应的模糊集的论域当中,中间将输入变量乘以相应的量化因子,超调量和响应时间随着量化因子的增加而增加,因此量化因子的选择对控制性能有很大影响。通过多组数据仿真,确定选择改进算法前后洗出加速度误差e及其变化率ce的模糊子集论域分别为[-5, 5]和[-1, 1]。函数形状选用三角形状的隶属函数来进行模糊补偿控制[13-14]。式(7)~(12)给出误差e的隶属函数。式(7)中-5和-3分别为隶属函数论域边界,对应的模糊规则为FD(负大),式右边2个隶属函数根据最大最小函数规则取值。式(8)~(11)类似。同理可根据论域和隶属函数形状确定误差变化率ce的隶属函数,不再赘述。
| $ {\mu _{{\rm{FD}}}}(x; - 5, - 3) = {\rm{max}}\left( {{\rm{min}}\left( {1,\frac{{ - 3 - x}}{2}} \right),0} \right), $ | (7) |
| $ {\mu _{{\rm{FZ}}}}(x; - 5, - 3, - 1) = {\rm{max}}\left( {{\rm{min}}\left( {\frac{{x + 5}}{2},\frac{{ - 1 - x}}{2}} \right),0} \right), $ | (8) |
| $ {\mu _{{\rm{FX}}}}(x; - 3, - 1,1) = \max \left( {\min \left( {\frac{{x + 3}}{2},\frac{{1 - x}}{2}} \right),0} \right), $ | (9) |
| $ {\mu _{{\rm{ZX}}}}(x; - 1,1,3) = {\rm{max}}\left( {{\rm{min}}\left( {\frac{{x + 1}}{2},\frac{{3 - x}}{2}} \right),0} \right), $ | (10) |
| $ {\mu _{{\rm{ZZ}}}}(x;1,3,5) = {\rm{max}}\left( {\min \left( {\frac{{x - 1}}{2},\frac{{5 - x}}{2}} \right),0} \right), $ | (11) |
| $ {\mu _{{\rm{ZD}}}}(x;3,5) = {\rm{max}}\left( {\min \left( {\frac{{x - 3}}{2},1} \right),0} \right)。$ | (12) |
飞行员所感受到的比力不仅与模拟器加速度有关,角加速度对比力也有影响。当高通滤波器输出的高频线加速度低于人体感觉阈值时,人体将感受不到这部分信号,但在实际运动中可以感受到。因此需要将平动高通加速度通道高频角加速度信号Ga通过二次滤波转换成补偿角位移,消除动感误差。
角加速度具体转换的思想:平动高通通道洗出小于0的部分加速度输出为人体感觉阈值加速度0.17 m/s2,结合上平台中心到座椅中人体前庭系统的距离计算转换角加速度
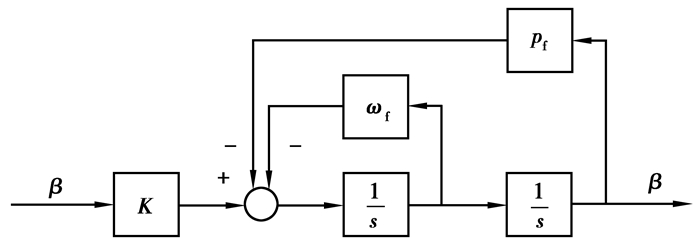
角加速度二次滤波如图 4所示。位移二次滤波同理,不再赘述。
|
图 4 角加速度二次滤波 Fig. 4 Quadratic filtering of angular acceleration |
二次滤波传递函数为
| $ \frac{\beta }{{\ddot \beta }} = \frac{K}{{{s^2} + {\omega _f}s + {p_f}}}, $ | (13) |
式中:ωf=2ξω,pf=ω2;ω为二次滤波截止频率,rad/s;ξ为二次滤波阻尼比,无量纲。
3 仿真分析为了验证改进算法的洗出效果,以纵向模式进行仿真说明,仿真采用ode45算法,仿真时间为20 s。输入参考加速度信号2~10 s内为2 m/s2,输入俯仰角速度为0 rad/s。仿真统计,经典洗出算法响应时间为1.0 ms,改进新型倾斜协调体感算法响应时间为1.4 ms。
图 5为经典洗出算法和改进算法的纵向洗出位移图,从结果可以看出位移有较大改善,经典洗出算法位移幅值为0.018 m,而改进新型倾斜协调体感算法位移幅值为0.108 m,运动平台位移极限为0.15 m,平台空间利用率得到了提高。
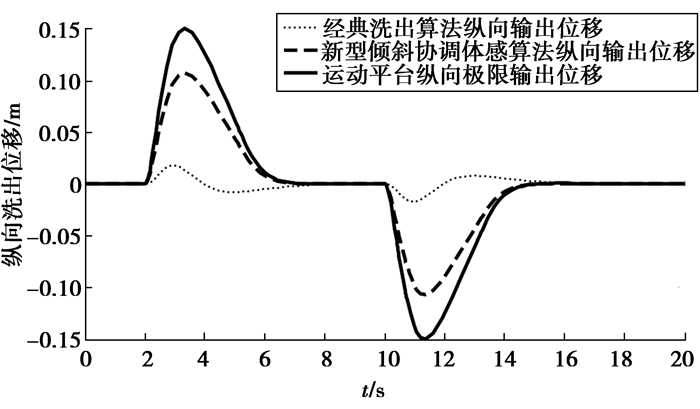
|
图 5 纵向洗出位移 Fig. 5 Longitudinal washout displacement |
图 6为倾斜协调洗出角位移图,从图中得出经典洗出算法在在5 s加速度突变时洗出角位移过小,改进算法通过角加速度二次滤波补偿角位移,使得洗出倾斜角位移在不超限的情况下最大程度模拟俯仰持续加速度,增加运动感知。
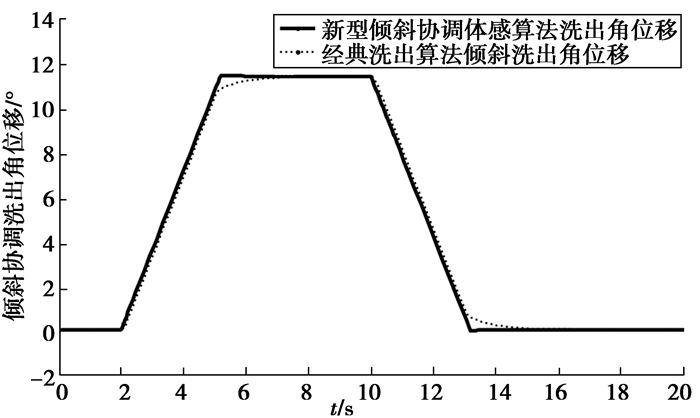
|
图 6 倾斜协调洗出角位移 Fig. 6 The washout angular displacement of tilt coordinate |
图 7为人体评价倾斜感知加速度图,从仿真结果看出,输入参考倾斜感知加速度在4 s达到峰值1.445 (m·s-2),而经典洗出算法仿真出的感知加速度在6 s达到峰值1.318 (m·s-2)。说明经典洗出算法不仅倾斜感知加速度幅值比参考曲线低,而且相位滞后了2 s,逼真度不够。新型倾斜协调体感算法人体评价倾斜感知加速度在4 s达到峰值1.455 (m·s-2),矫正了相位误差,提高了感觉幅值。改进算法通过对倾斜协调通道改进,并且结合模糊逻辑优点,进一步提高了动感逼真效果。
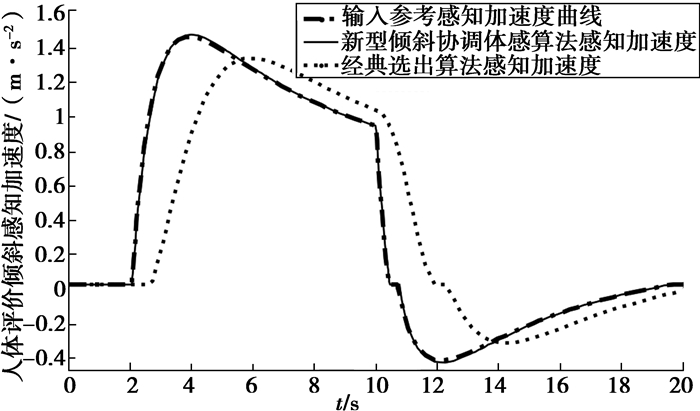
|
图 7 人体评价倾斜感知加速度 Fig. 7 The human body evaluates sensory acceleration of tilt coordinate |
图 8为人体评价倾斜感知加速度误差图,可以看出经典洗出算法误差1.085 (m·s-2);提出的新型倾斜协调体感算法将人体评价感知加速度误差降低0.040 (m·s-2),虚假暗示程度大大降低,使算法的洗出效果更加符合人体感官模型。
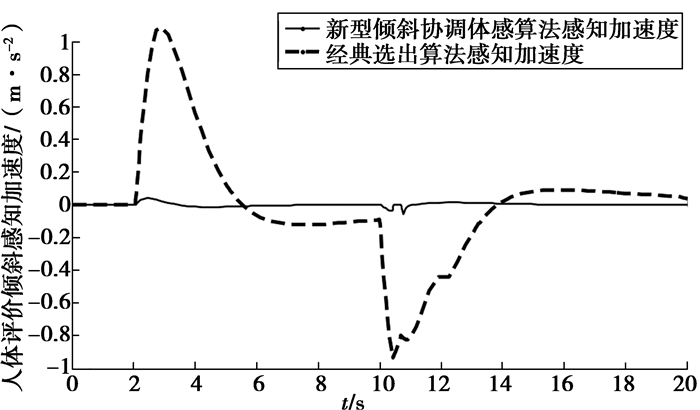
|
图 8 人体评价倾斜感知加速度误差 Fig. 8 The human body evaluates sensory acceleration error of tilt coordinate |
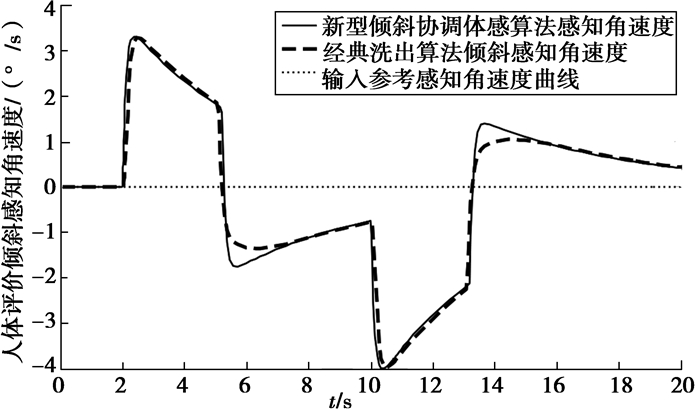
图 9为人体评价倾斜感知角速度图,可以看出经典洗出算法与改进算法感知角速度幅值基本一致,在2 s时改进算法感知角速度并未超过人体感知门限3.6°/s[15],因此在俯仰方向的角速度不会带来虚假暗示。在10 s时两种算法感知角速度由于加速度突变未能回零继续反向运动,俯仰方向的角速度超出了人体感知门限,会带来角速度虚假暗示。在5.6 s和13.6 s处,改进算法感知相比经典洗出算法角速度幅值较大一些,说明改进算法动感性更强一些。
|
图 9 人体评价倾斜感知角速度 Fig. 9 The human body evaluates sensory angular velocity of tilt coordinate |
对飞行模拟器经典洗出算法的研究表明,倾斜协调运动严重影响模拟逼真度。基于经典洗出算法的整体结构进行改进,结合角加速度二次滤波补偿角位移和模糊逻辑以及加速度信号补偿的优点对算法进行优化,仿真结果表明改进算法不仅提高了位移空间利用率、优化了相位延迟和虚假暗示,而且降低了感知误差。提出的算法能够有效提高模拟逼真度,对控制飞行模拟器有一定指导意义。但模糊逻辑隶属函数的选取以及上平台到人体前庭距离的确定也影响着洗出结果,此外人体评价感知角速度超限也是待优化问题。若将其应用于整个六自由度飞行模拟器当中模拟,需要综合考虑平台整体的运动空间范围。并且实际的具体实验情况与仿真有一定的偏差,所以该改进算法的参数在飞行模拟器的生产中仍需不断优化。
| [1] |
罗竹辉, 魏燕定, 周晓军, 等. 六自由度平台车辆运动模拟器变输入洗出算法[J]. 浙江大学学报(工学版), 2013, 47(2): 238-243. LUO Zhuhui, WEI Yanding, ZHOU Xiaojun, et al. Research on variable input washout algorithm for stewart platform vehicle simulator[J]. Journal of Zhejiang University(Engineering Science), 2013, 47(2): 238-243. (in Chinese) DOI:10.3785/j.issn.1008-973X.2013.02.007 |
| [2] |
Parrish R V, Dieudonne J E, Martin D J Jr. Coordinated adaptive washout for motion simulators[J]. Journal of Aircraft, 1975, 12(1): 44-50. DOI:10.2514/3.59800 |
| [3] |
Sivan R, Shalom J, Huang J K. An optimal control approach to the design of moving flight simulators[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1982, 12(6): 818-827. DOI:10.1109/TSMC.1982.4308915 |
| [4] |
Nguyen T A K, DiGiovanna J, Cavuscens S, et al. Characterization of pulse amplitude and pulse rate modulation for a human vestibular implant during acute electrical stimulation[J]. Journal of Neural Engineering, 2016, 13(4): 046023. DOI:10.1088/1741-2560/13/4/046023 |
| [5] |
王小亮, 李立, 张卫华, 等. 列车驾驶模拟器经典洗出算法的参数优化[J]. 中国铁道科学, 2008, 29(5): 102-107. WANG Xiaoliang, LI Li, ZHANG Weihua, et al. Parameters optimization of the classical washout algorithm in locomotive driving simulator[J]. China Railway Science, 2008, 29(5): 102-107. (in Chinese) DOI:10.3321/j.issn:1001-4632.2008.05.019 |
| [6] |
王辉, 朱道扬, 平凡, 等. 基于模糊逻辑的高逼真度运动体感算法研究[J]. 系统仿真学报, 2017, 29(3): 546-551, 558. WANG Hui, ZHU Daoyang, PING Fan, et al. Study on motion cueing algorithm of high-fidelity based on fuzzy logic[J]. Journal of System Simulation, 2017, 29(3): 546-551, 558. (in Chinese) |
| [7] |
Asadi H, Mohamed S, Rahim Zadeh D, et al. Optimisation of nonlinear motion cueing algorithm based on genetic algorithm[J]. Vehicle System Dynamics, 2015, 53(4): 526-545. DOI:10.1080/00423114.2014.1003948 |
| [8] |
Meyer A, Bouchetemblé P, Costentin B, et al. Lateral semicircular canal fistula in cholesteatoma:diagnosis and management[J]. European Archives of Oto-Rhino-Laryngology, 2016, 273(8): 2055-2063. DOI:10.1007/s00405-015-3775-6 |
| [9] |
Asadi H, Mohamed S, Lim C P, et al. A review on otolith models in human perception[J]. Behavioural Brain Research, 2016, 309: 67-76. DOI:10.1016/j.bbr.2016.03.043 |
| [10] |
Dabbaghjamanesh M, Moeini A, Ashkaboosi M, et al. High performance control of grid connected cascaded H-bridge active rectifier based on type Ⅱ-fuzzy logic controller with low frequency modulation technique[J]. International Journal of Electrical and Computer Engineering (IJECE), 2016, 6(2): 484. DOI:10.11591/ijece.v6i2 |
| [11] |
Mesloub H, Benchouia M T, Goléa A, et al. A comparative experimental study of direct torque control based on adaptive fuzzy logic controller and particle swarm optimization algorithms of a permanent magnet synchronous motor[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(1/2/3/4): 59-72. |
| [12] |
Ghosh A, Sen S, Dey C. Rule reduction of a neuro-fuzzy PI controller with real-time implementation on a speed control process[M]. New Delhi: Springer India, 2015: 445-458. DOI:10.1007/978-81-322-2526-3_46
|
| [13] |
Harliana P, Rahim R. Comparative analysis of membership function on mamdani fuzzy inference system for decision making[J]. Journal of Physics:Conference Series, 2017, 930: 12-29. |
| [14] |
Nabipour M, Razaz M, Seifossadat S G, et al. A novel adaptive fuzzy membership function tuning algorithm for robust control of a PV-based dynamic voltage restorer[J]. Engineering Applications of Artificial Intelligence, 2016, 53: 155-175. DOI:10.1016/j.engappai.2016.04.007 |
| [15] |
王辉, 万毅, 平凡. 飞行模拟器洗出算法的优化研究[J]. 科学技术与工程, 2015, 15(29): 83-86, 94. WANG Hui, WAN Yi, PING Fan. Washout algorithm optimization for flight simulator[J]. Science Technology and Engineering, 2015, 15(29): 83-86, 94. (in Chinese) DOI:10.3969/j.issn.1671-1815.2015.29.015 |
 2019, Vol. 42
2019, Vol. 42

