b. 湖南大学 工程结构损伤诊断湖南省重点实验室, 长沙 410082
b. Hunan Provincial Key Lab on Diagnosis for Engineering Structures, Hunan University, Changsha 410082, P. R. China
为使钢筋混凝土(RC)框架结构在地震作用下具有足够的延性与耗能能力,避免“柱铰机制失效模式”的出现,《建筑抗震设计规范》(GB 50011—2010)[1](以下简称2010版《抗规》)要求框架结构满足“强柱弱梁”而使结构塑性铰出现在梁端而不出现在柱端,使柱具有足够的延性与承载力。为实现“强柱弱梁”的设计预期,各国规范中均采用了人为提高柱端设计受弯承载力的方法,即在梁柱节点与底层柱下端处引入柱端弯矩增大系数(CMAF)的概念。
从汶川地震的震害分析[2]可以看出,中国的RC框架结构在地震作用下很少出现“全梁失效模式”,塑性铰仍多出现在柱端。夏倩[3]通过对框架结构单节点的概率分析指出2001版《抗规》与欧洲规范EC8相比,二、三级抗震等级的CMAF值仍需提高,并建议分别提高为1.3(8度区二级抗震为1.4)、1.2。2010版《抗规》对2001版《抗规》中的CMAF值进行了调整,即将一、二、三级框架结构梁柱节点处的CMAF值由1.4、1.2、1.1调整为1.7、1.5、1.3, 底层柱下端的增大系数由1.5、1.25、1.15调整为1.7、1.5、1.3。
众多学者对CMAF的合理取值进行了研究。文献[4-6]指出,考虑楼板内配筋时CMAF值应大于2.0框架结构才可有效地形成梁铰机制。文献[7]针对美国混凝土设计规范(ACI 318-99),对规范中最小CMAF取值进行了抗震性能分析,指出最小CMAF的值取为2.0是合理的。文献[8]采用多目标抗震设计方法得到的最优CMAF取值均大于ANSI/AISC 341-05的建议取值。文献[9]指出对于8度区0.2 g大震水准,CMAF的合理取值应为1.7。文献[10]建议将二级框架的CMAF值提升至1.85以上。文献[11]表明现行规范给出的CMAF值难以满足二、三、四级抗震等级框架梁实现梁铰。文献[12]指出2010版《抗规》提高CMAF值后对塑性铰分布改善较有限,建议进一步增大系数取值。同时,楼板中纵筋的存在也对CMAF的取值有较大影响。文献[13]讨论了ACI 318-99中的设计方法,并通过数值量化表明,现浇楼板参与梁受力的程度随着结构侧向位移的增大而增大。文献[14]指出由于楼板的存在,结构由梁铰机制变为柱铰机制的概率随着地震作用的增强而变大。文献[15]基于概率分析讨论了不同情况下楼板有效翼缘的取值。目前,对于2010版《抗规》对梁柱节点与底层柱下端CMAF值修改的合理性与该系数的合理取值仍需进一步研究。文中通过对6栋6层钢筋混凝土RC框架结构进行IDA和易损性分析,得到易损性曲线,从而分析现行规范中梁柱节点与底层柱下端CMAF取值在7度区与8度区设计的合理性。
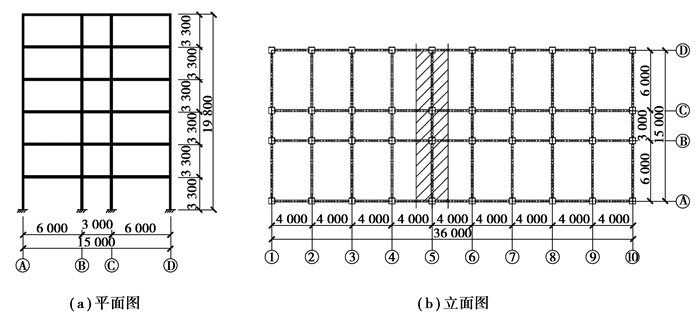
1 RC框架结构模型设计以中国现行2010版《抗规》为基础,设计6栋6层RC框架结构模型,如图 1所示。其中,RC1-7、RC2-7、RC1-7E为7度设防,RC1-8、RC2-8、RC1-8E为8度设防。RC1-7(RC1-8)的梁柱节点与底层柱下端CMAF值为1.3(1.5)。RC2-7(RC2-8)为调整梁柱节点与底层柱下端CMAF值后的框架计算模型,其系数均取1.5(1.8)。RC1-7E、RC1-8E为RC1-7、RC1-8对应的CMAF值相同但不考虑楼板作用的空框架。模型楼板厚度取150 mm,双层双向配筋。相关设计参数如下:设计地震分组为第二组,Ⅱ类场地,丙类结构,混凝土强度等级均为C30,梁柱纵筋采用HRB400级钢筋,箍筋采用HPB300级钢筋,板筋采用HPB300级钢筋,楼板导荷按双向板处理。楼、屋面恒载标准值为6 kN/m2,走廊处荷载标准值取3.5 kN/m2,其余各处荷载均取2 kN/m2,梁上荷载取值为9 kN/m。由于结构对称,文中取中间(即⑤轴线)框架进行设计和分析,设计时从PKPM软件中导出梁上分布荷载与柱顶集中荷载,并按照《抗规》对各模型进行配筋设计。在设计时保持相同抗震设防烈度模型梁配筋相同,通过柱配筋体现梁柱节点与底层柱下端的CMAF值变化。计算得到的梁柱尺寸及配筋情况,如表 1所示。
|
图 1 框架结构模型示意图 Fig. 1 Sketch of frame structure model |
| 表 1 模型基本参数 Table 1 Parameter details of models |
对于RC1-7、RC2-7、RC1-8、RC2-8模型,建模时考虑楼板对结构的影响,按《混凝土结构设计规范》(GB50010—2010)中的有效翼缘宽度建议取值,即框架梁两侧6倍板厚,将模型中梁截面设计为两侧翼缘宽度均为900 mm的T形梁,每侧翼缘上下各配5根直径为8 mm的纵筋以模拟有效翼缘宽度范围内板筋的作用,各板筋间距200 mm。对于RC1-7E、RC1-8E模型,则在建模时不考虑有效翼缘与板筋作用。
2 框架结构增量动力分析 2.1 地震波的选取在进行增量动力分析时,应对模型输入多条地震波来获取较精确的地震反映。文献[16]指出,选取10~20条地震波记录进行增量动力分析,能够较好地对中等高度建筑进行地震需求估计。选取了10条不同震级地震波以对应模型可能遇到的各强度地震作用,所选地震波信息如表 2所示。选取的地震波满足以下要求:剪切波速260 m/s<Vs30<510 m/s,对应国内的Ⅱ类场地[17];震中距大于20 km且小于100 km,排除近场地震动记录[17]。
| 表 2 地震波基本信息 Table 2 Basic information of seismic waves |
IDA分析过程基于SAP2000有限元分析软件,在软件中建立各有限元分析模型,并将地面运动峰值加速度apg(单位:m/s2)作为地震强度参数,最大层间位移角θmax(单位:rad)作为结构性能参数进行增量动力分析。在SAP2000中输入10条地震波,得到多条θmax-apg曲线,并对曲线进行分析,从而对各模型的抗震性能进行评估。
SAP2000分析模型中各级钢筋材料参数,如表 3所示,混凝土采用C30混凝土,弹性模量取30 GPa,线膨胀系数取1×10-5/℃。形成IDA曲线时,地震动调幅基准由0.098 m/s2开始,每级调幅动力“加载”步长取0.980 m/s2,调幅基准增加至6.958 m/s2后每级调幅动力“加载”步长取为0.490 m/s2。
| 表 3 模型钢筋材料参数 Table 3 Material parameters of REBAR in models |
为了对各性能水准进行量化评估,通过最大层间位移角来定义各性能水准。李应斌等[18]通过总结国内外结构性能的评价指标,给出了RC框架各性能水准对应的层间位移角限值,结合2010版《抗规》将各性能水准下对应的最大层间位移角取值如表 4所示。
| 表 4 各性能水准下的层间角 Table 4 Interstory drift corresponding to different levels |
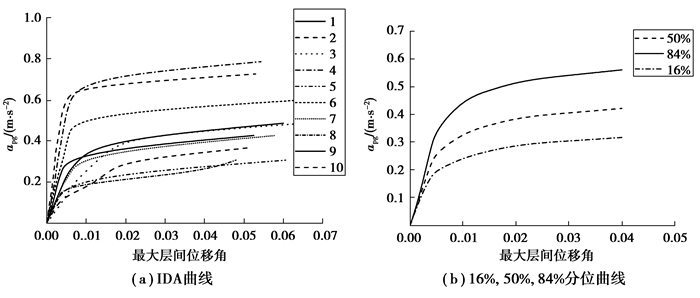
运用SAP2000软件对上述模型进行动力弹塑性分析,各材料的本构模型均采用软件默认的本构关系,每栋模型得到10条θmax-apg曲线。假定每条θmax-apg曲线均服从正态分布, 则可以通过16%、50%、84%分位曲线来体现曲线的分布情况,其中,50%曲线体现均值,16%、84%曲线体现离散程度。图 2为RC1-7框架的IDA曲线及对应的IDA分析曲线,其余框架的IDA曲线数据反映于能力点分析中。
|
图 2 RC1-7模型IDA曲线 Fig. 2 IDA curves forRC1-7 model |
对各θmax-apg曲线进行统计分析后,即可由各性能水准下对应的层间位移角得到结构的轻微破坏点、严重破坏点、倒塌破坏点所对应的apg。认为结构在达到轻微破坏点之后,出现了可修复的轻度破坏;达到严重破坏点后,出现了不可修复的严重破坏;达到倒塌破坏点之后,发生倒塌。通过θmax-apg曲线对应的各能力点apg大小可体现结构在地震作用下的反应。各模型在达到各能力点时apg情况如表 5所示。
| 表 5 各模型能力点对应apg值 Table 5 Value for apg corresponding to ability point of each model |
通过对比IDA分析的结果,可以得到以下结论:
1) 7度设防时,将CMAF值由1.3提升至1.5可以有效提高各能力点对应的apg值,且轻微破坏点对应提升幅度较小,严重破坏点与倒塌破坏点对应提升幅度较大,平均提高幅度分别为32%、59%、60%。
2) 8度设防时,将CMAF值由1.5提升至1.8对提高各能力点对应的apg值的贡献有限,平均提高幅度基本在15%~35%。
3) 对于有无翼缘模型而言,无翼缘模型在发生轻微破坏时的apg值均小于相应的有翼缘模型5%左右,而在严重破坏与倒塌破坏时的apg值分别大于相应的有翼缘模型5%与10%左右。由于翼缘与板筋的存在,有翼缘模型在弹性阶段抗侧刚度大于无翼缘模型,层间位移较小;而在弹塑性阶段,有翼缘模型更易形成柱铰,产生较大层间位移。RC1-7E模型部分不符合规律数据是IDA分析数据的离散性造成的。
3 地震易损性分析 3.1 易损性分析基本过程参见文献[19]的分析过程,假定地震动参数服从正态分布,对地震需求参数的估计用式(1)来表达:
| $ \begin{array}{*{20}{c}} {d = a{I^b}}\\ {即{\rm{ln}}(d) = {\rm{ln}}(a) + b{\rm{ln}}(I) = A + B{\rm{ln}}(I), } \end{array} $ | (1) |
其中,A、B、a、b为线性回归系数。文中用θmax表示参数d,用apg/g表示I,代入式(1)中得到
| $ {\rm{ln}}\left( {{\theta _{\max }}} \right) = A + B{\rm{ln}}\left( {{a_{{\rm{rs}}}}/g} \right), $ | (2) |
结构反应的概率函数可表示为对数正态分布函数,其形式为
| $ {\mu _{\rm{d}}} = \ln \left( {{{\tilde \mu }_{\rm{d}}}, {\beta _{\rm{d}}}} \right), $ | (3) |
其中,
结构承载力概率函数可表示为对数正态分布函数,其形式为
| $ {\mu _{\rm{c}}} = \ln \left( {{{\tilde \mu }_{\rm{c}}}, {\beta _{\rm{c}}}} \right), $ | (4) |
其中,
结构反应μd大于结构承载力μc时的概率公式可表示为
| $ {P_{\rm{f}}} = {P_{\rm{f}}}\left( {{\mu _{\rm{c}}}/{\mu _{\rm{d}}} \le 1} \right), $ | (5) |
由于μd和μc均服从对数正态分布,故失效概率Pf可表示为
| $ {P_{\rm{f}}} = {\rm{\Phi }}\left( {\frac{{ - {\rm{ln}}\left( {{{\tilde \mu }_{\rm{c}}}/{{\tilde \mu }_{\rm{d}}}} \right)}}{{\sqrt {\beta _{\rm{c}}^2 + \beta _{\rm{d}}^2} }}} \right), $ | (6) |
将式(3)代入式(6)可得:
| $ {P_{\rm{f}}} = {\rm{\Phi }}\left( {\frac{{{\rm{ln}}\left[ {{e^A}{{\left( {{a_{{\rm{pg}}}}/g} \right)}^B}/{{\tilde \mu }_{\rm{c}}}} \right]}}{{\sqrt {\beta _{\rm{c}}^2 + \beta _{\rm{d}}^2} }}} \right)。$ | (7) |
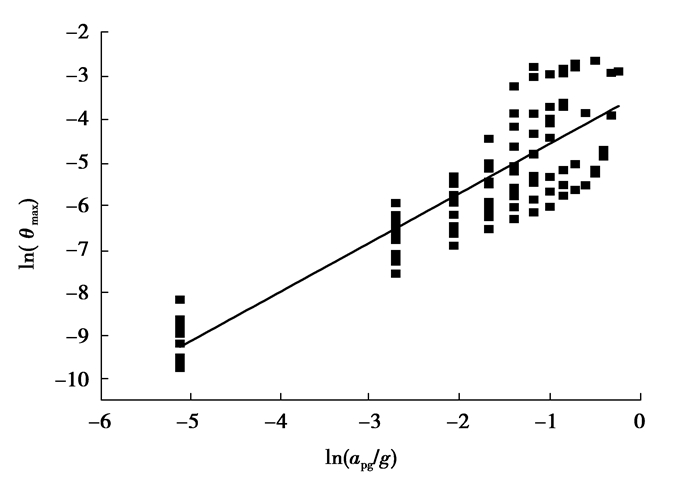
基于IDA分析的计算结果,以apg/g为自变量,结构反应θmax为因变量,按照易损性分析进行线性回归分析。使用Origin数据处理软件将结果绘制如图 3所示。
|
图 3 RC1-7模型回归曲线 Fig. 3 Regression curves forRC1-7model |
得到RC1-7模型回归公式为
| $ \ln \left( {{\theta _{{\rm{max}}}}} \right) = 1.1425{\rm{ln}}\left( {{a_{{\rm{pg}}}}/g} \right) - 3.4336, $ | (8) |
将式(8)代入式(7)可得:
| $ {P_{\rm{f}}} = {\rm{\Phi }}\left( {\frac{{{\rm{ln}}\left[ {{e^{ - 3.4336}}{{\left( {{a_{{\rm{pg}}}}/g} \right)}^{1.1425}}/{{\tilde \mu }_{\rm{c}}}} \right]}}{{\sqrt {\beta _{\rm{c}}^2 + \beta _{\rm{d}}^{\rm{2}}} }}} \right)。$ | (9) |
当易损性曲线以apg/g为自变量时,
其余各框架根据上述分析过程,可得到各自的回归公式与失效概率公式,并可根据失效概率公式得到3种破坏形态对应的超越概率。表 6给出其余各框架回归公式中线性回归系数A、B的取值。
| 表 6 其余模型回归系数取值 Table 6 Value for regression coefficient corresponding to each model |
通过定义各地震设防烈度所对应的apg值,可得到易损性曲线在不同条件下各烈度水平性能点的超越概率。为了全面覆盖结构在使用阶段可能遭遇的不同地震烈度,考虑结构可能遭遇到特大地震,计算了罕遇地震与特大地震在7、8度设防烈度下的超越概率,其中罕遇地震对应的apg值参照2010版《抗规》,特大地震对应的apg值采用文献[20]中建议的apg值,具体如表 7所示。
| 表 7 各地震水准的烈度水平 Table 7 Intensity corresponding to each earthquake standards |
将罕遇地震、特大地震对应的7、8度设防烈度的apg值代入各模型的失效概率公式,可算出各模型在各烈度水平下不同性能点的破坏概率,如表 8所示。
| 表 8 各结构在不同设防烈度下破坏概率 Table 8 Failure probabilitycorrespondingtodifferent seismic intensityof each structure |
对于结构的可靠指标,ATC-63报告认为结构在大震作用下有低于10%的倒塌概率是可以接受的,表明结构可以满足抗震要求。因此,可以通过考察不同性能点的倒塌概率等破坏概率来反映结构是否满足抗震要求。
由表 8可以得到以下结论:
1) 按照现行规范设计的7度设防与8度设防框架在罕遇地震作用下倒塌破坏概率较小,可以满足大震不倒的抗震要求,但其在特大地震作用下仍有一定的倒塌破坏概率。
2) 提高CMAF值后,7度与8度设防框架在罕遇地震作用下发生严重破坏的概率均减小60%,发生倒塌破坏的概率均减小77%,提高CMAF值可有效减小倒塌概率;而在特大地震下7度与8度设防框架发生严重破坏概率分别减小32%与38%,倒塌破坏概率分别减小55%与63%,虽对减小严重破坏概率效果较有限,但对减小倒塌破坏概率较有效。
3) 对于有无翼缘模型而言,2种模型发生轻微破坏的概率基本相同,而发生严重破坏与倒塌破坏的概率分别小于相应的有翼缘模型10%与15%左右。有翼缘模型由于易产生柱铰机制,在弹塑性阶段发生严重破坏与倒塌破坏的概率均大于无翼缘模型。RC1-7E模型部分不符合规律数据是分析数据的离散性造成的。
4 结论对调整CMAF值的框架模型的IDA与易损性分析,得出以下结论:
1) 按照现行规范设计的7度设防与8度设防框架可以满足大震不倒的设防要求,2010版《抗规》对梁柱节点与底层柱下端处CMAF值的提高是合理的。
2) 根据现行规范设计的框架在特大地震作用下仍有较大的倒塌概率,若在7度设防时,将梁柱节点与底层柱下端处CMAF值均由1.3提升至1.5,8度设防时均由1.5提升至1.8,可以使特大地震发生时结构的倒塌概率减小至可接受范围内,对于7度设防框架效果明显。
3) 在进行框架梁柱设计时,应按规范要求充分考虑有效翼缘的影响,若忽略此影响,则会低估结构破坏发生的概率,该种低估在非线性阶段更加明显。
| [1] |
GB/T 50011-2010建筑抗震设计规范[S].北京: 中国建筑工业出版社, 2010. GB/T 50011-2010 Code for seismic design of buildings[S]. Beijing: China Architecture and Building Press, 2010. (in Chinese) |
| [2] |
清华大学土木工程结构专家组, 西南交通大学土木工程结构专家组, 北京交通大学土木工程结构专家组, 等.汶川地震建筑震害分析[J].建筑结构学报, 2008, 29(4): 1-9. Civil and Structural Groups of Tsinghua University, Southwest Jiaotong University and Beijing Jiaotong University, et al. Analysis on seismic damage of buildings in the Wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(4): 1-9.(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-JZJB200804002.htm |
| [3] |
夏倩. 钢筋混凝土框架结构强柱弱梁的概率分析[J]. 四川建筑科学研究, 2010, 36(3): 13-16. XIA Qian. Probability analysis is for strong column-weak beam design of reinforced concrete frames[J]. Building Science Research of Sichuan, 2010, 36(3): 13-16. (in Chinese) DOI:10.3969/j.issn.1008-1933.2010.03.004 |
| [4] |
蔡健, 周靖, 方小丹, 等. 柱端弯矩增大系数取值对RC框架结构抗震性能影响的评估[J]. 土木工程学报, 2007, 40(1): 6-14. CAI Jian, ZHOU Jing, FANG Xiaodan, et al. Evaluation of influences of various moment magnifying coefficients at column ends of RC frames on seismic performance[J]. China Civil Engineering Journal, 2007, 40(1): 6-14. (in Chinese) DOI:10.3321/j.issn:1000-131X.2007.01.002 |
| [5] |
管民生, 杜宏彪, 韩大建. RC矩形柱框架结构不同柱[XC半字线.TIF, JZ]梁抗弯强度比的Pushover分析[J]. 建筑结构, 2009, 39(4): 14-16, 42. GUAN Minsheng, DU Hongbiao, HAN Dajian. Pushover analysis on rectangular column frames with different column-to-beam strength ratios[J]. Building Structure, 2009, 39(4): 14-16, 42. (in Chinese) |
| [6] |
朱宏锋, 黄珊珊, 张敏, 等. 考虑现浇楼板的柱端弯矩增大系数可靠指标分析[J]. 工程抗震与加固改造, 2016, 38(3): 73-77, 129. ZHU Hongfeng, HUANG Shanshan, ZHANG Min, et al. Reliable indicator analysis of CMAF considering the cast-in-place floor slab[J]. Earthquake Resistant Engineering and Retrofitting, 2016, 38(3): 73-77, 129. (in Chinese) |
| [7] |
Dooley K L, Bracci J M. Seismic evaluation of column-to-beam strength ratios in reinforced concrete frames[J]. ACI Structural Journal, 2001, 98(6): 843-851. |
| [8] |
Choi S W, Kim Y, Lee J, et al. Minimum column-to-beam strength ratios for beam-hinge mechanisms based on multi-objective seismic design[J]. Journal of Constructional Steel Research, 2013, 88: 53-62. DOI:10.1016/j.jcsr.2013.05.004 |
| [9] |
于晓辉, 吕大刚, 郑浩琴. 基于典型失效模式可靠度分析的柱端弯矩增大系数概率评定[J]. 建筑结构学报, 2014, 35(4): 169-176. YU Xiaohui, LYU Dagang, ZHENG Haoqin. Probabilistic evaluation of column overdesign factor through reliability analysis for typical failure modes[J]. Journal of Building Structures, 2014, 35(4): 169-176. (in Chinese) |
| [10] |
李伯维, 张耀庭. 基于Pushover的多层钢筋混凝土框架结构设计与抗震性能分析[J]. 建筑技术, 2016, 47(5): 392-395. LI Bowei, ZHANG Yaoting. Design and seismic performance analysis of multi story reinforced concrete frame structure based on pushover analysis[J]. Architecture Technology, 2016, 47(5): 392-395. (in Chinese) DOI:10.3969/j.issn.1000-4726.2016.05.002 |
| [11] |
张敏, 朱宏锋. 传统框架及楼板局部设缝框架柱端弯矩增大系数分析[J]. 结构工程师, 2015, 31(1): 21-27. ZHANG Min, ZHU Hongfeng. The CMAF parameter analysis for the traditional frame and the frame with local gaps in slabs[J]. Structural Engineers, 2015, 31(1): 21-27. (in Chinese) DOI:10.3969/j.issn.1005-0159.2015.01.004 |
| [12] |
杨红, 任小军, 白绍良, 等. 双向水平地震下7度区框架结构的"强柱弱梁"措施[J]. 振动与冲击, 2016, 35(13): 42-50. YANG Hong, REN Xiaojun, BAI Shaoliang, et al. "Strong column weak beam"measures for RC frame structures in 7 seismic intensity area under bi-directional horizontal seismic excitations[J]. Journal of Vibration and Shock, 2016, 35(13): 42-50. (in Chinese) |
| [13] |
Pantazopoulou S J, French C W. Slab participation in practical earthquake design of reinforced concrete frames[J]. ACI Structural Journal, 2001, 98(4): 479-489. |
| [14] |
Yuan J, Hu D. Influence of steel bars in monolithic floor slabs on the yielding-damage mechanism of frame structures[J]. Earthquake Resistant Engineering Structure, 2009, 104: 27-37. |
| [15] |
Ning N, Qu W J, Ma Z J. Design recommendations for achieving "strong column-weak beam" in RC frames[J]. Engineering Structures, 2016, 126: 343-352. DOI:10.1016/j.engstruct.2016.07.053 |
| [16] |
Shome N, Cornell C A. Probabilistic seismic demand analysis of nonlinear structures[R]. Report No.RMS-35. Stanford, California: Stanford University. PMS Program, 2004: 16-50.
|
| [17] |
张耀庭, 刘昌芳, 王晓伟. 结构非线性时程分析中的地震动参数选择[J]. 地震工程与工程振动, 2016, 36(4): 153-162. ZHANG Yaoting, LIU Changfang, WANG Xiaowei. Parameter selection of ground motion in nonlinear time history analysis of structure[J]. Earthquake Engineering and Engineering Vibration, 2016, 36(4): 153-162. (in Chinese) |
| [18] |
李应斌, 刘伯权, 史庆轩. 结构的性能水准与评价指标[J]. 世界地震工程, 2003, 19(2): 132-137. LI Yingbin, LIU Boquan, SHI Qingxuan. Performance levels and estimation indices of structures[J]. World Earthquake Engineering, 2003, 19(2): 132-137. (in Chinese) DOI:10.3969/j.issn.1007-6069.2003.02.024 |
| [19] |
张耀庭, 马超, 郭宗明, 等. 不同弯矩增大系数钢筋混凝土框架结构地震易损性分析[J]. 建筑结构学报, 2014, 35(2): 29-37. ZHANG Yaoting, MA Chao, GUO Zongming, et al. Seismic fragility analysis for RC frame structures with various moment magnifying coefficients[J]. Journal of Building Structures, 2014, 35(2): 29-37. (in Chinese) |
| [20] |
施炜, 叶列平, 陆新征, 等. 不同抗震设防RC框架结构抗倒塌能力的研究[J]. 工程力学, 2011, 28(3): 41-48, 68. SHI Wei, YE Lieping, LU Xinzheng, et al. Study on the collapse-resistant capacity of RC frames with different seismic fortification levels[J]. Engineering Mechanics, 2011, 28(3): 41-48, 68. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

