2. 重庆大学 土木工程学院, 重庆 400045
2. School of Civil Engineering, Chongqing University, Chongqing 400044, P. R. China
随着浅埋资源逐渐耗尽,大型深部能源勘探在全球范围正变得越来越重要[1-2],深部工程中的岩体力学问题成为当前研究中的热点,尤其是岩石受拉破坏机理。岩石抗拉特性是岩石的重要特性。在地下巷道周边经常存在拉应力,岩石抗压强度明显高于抗拉强度,拉伸破坏成为岩石损伤中最常见的类型之一[3]。地下矿产开采等地下工程中也存在大量拉伸破坏现象,比如,顶板岩石冒落,已成为施工安全事故中最重要的原因之一[4]。研究拉伸破坏过程中的声发射特性,通过判断岩体顶板或隔层岩石在弯曲状态下的Kaiser效应特征,对于巷道顶板的稳定性监测、预警及预报具有重要的科学价值和工程意义[5]。
早在1950年,德国科学家Kaiser便发现了著名的凯撒效应现象,即受单向拉伸力作用的金属材料,当应力达到材料所受过的最大先期应力时,会有明显的声发射现象出现[6-7]。而Goodman等将其运用到岩石压缩试验中,并成功证实了岩石存在Kaiser效应现象。不少学者对不同岩石在各种条件下,对Kaiser效应的影响进行了研究,比如,应力水平[9-12]、湿度[13-14]、时间延迟[15-22]、受荷状态[23]等。而加载速度对岩石Kaiser效应的影响与岩石损伤过程中的声发射信号特征直接相关,但该问题研究较少,Lavrov A[24]和陈勉[25]分别研究了砂岩单轴受压试验和砂岩、泥岩有围压受压试验的加载速度对Kaiser效应影响,但不够深入。而受拉应力状态下的加载速度对岩石Kaiser效应影响及机理,几乎未有相关研究。文中将从3种加载速度下的三点弯曲声发射试验出发,研究加载速度变化下,受拉应力状态砂岩Kaiser效应特征。借助RFPA2D从微裂纹开展角度,对试验过程中Kaiser效应随加载速度变化呈现的差异进行了机理分析。最后,运用小波分析方法获取不同加载速度的砂岩Kaiser点频谱分布区间,量化其宏观现象的判断标准。
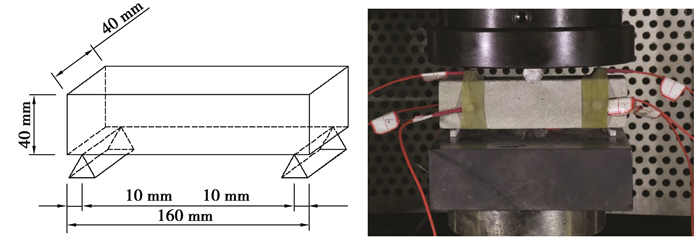
1 试验系统和试件制备 1.1 试验系统声发射采集系统为PCI-2声发射仪,AE硬件参数设置为前置放大40 dB,门槛值设置为45 dB,探头谐振频率为100~400 kHz,采样频率为1 MSPS。加载系统采用WAW-1000型微机控制电液伺服万能试验机。试验过程中收集AE事件、能量等参数信息和波形信息。试验装置如图 1所示。

|
图 1 试验系统 Fig. 1 Test system |
砂岩采自重庆市某矿区,按照国际岩石力学学会试验建议方法(ISRM),将砂岩母料加工成标准试件。棱柱体试件尺寸为40 mm×40 mm×160 mm,端面平整度误差控制在0.02 mm以内,端面平整度允许偏差范围为±0.25°。每个试验中试件固定6个探头,如图 2所示,棱柱体试件除支承面外,每个表面左右对称布置2个,探头表面耦合剂采用凡士林。为减少砂岩表面岩石颗粒破碎错动产生的噪音,在试压设备与试件接触面之间增加1层橡胶垫片,使加载初期声发射振铃累计计数曲线变得平缓。
|
图 2 三点弯曲试验加载方式 Fig. 2 Loading ways of the three-point bending test |
试验加载速度分3组,分别为10、20、40 N/s,每组5个试件(平行试验),均采用连续循环加卸载方式。每次循环加载至指定荷载时稳载10 s,每次加载完成后以40 N/s的速度卸载至0.1 kN。试验过程中采集应力、声发射特征参数和波形数据。
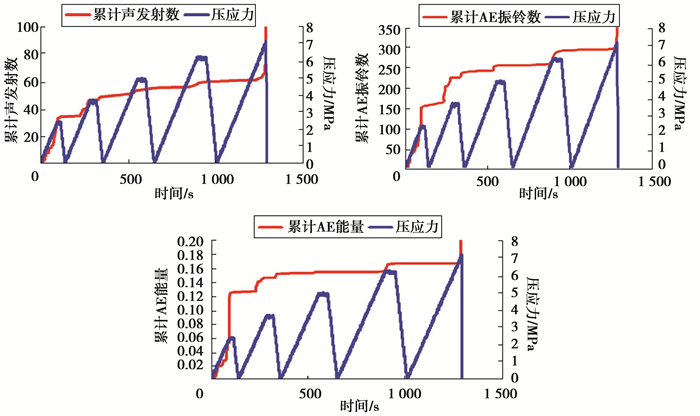
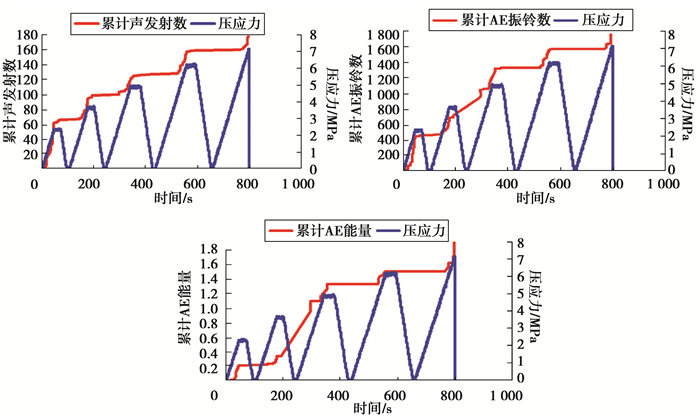
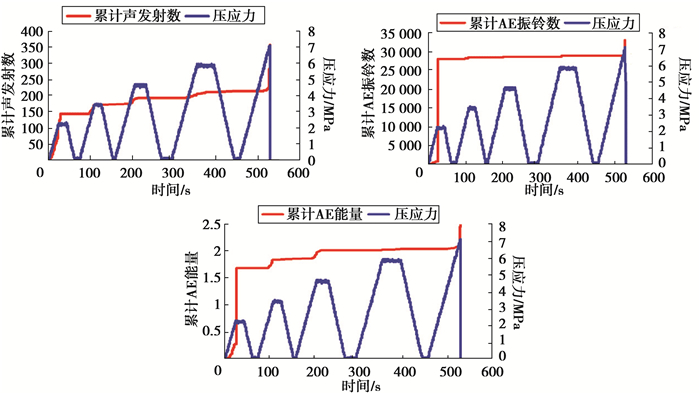
2 加载速度变化对Kaiser效应影响每组分别选取其中1个试件为代表进行分析说明,编号分别为B5、B10、B17,试验结果如图 3~图 5所示。通过声发射特征曲线图可发现:1)砂岩在连续循环加载条件下的Kaiser现象存在,加载速度越高,试样产生总的累计声发射事件数、累计AE振铃数和累计声发射能量越大,试件在破坏时的累计AE声发射事件、累计AE振铃数和累计能量与加载速度成正比关系。2)从能量时间关系曲线可知,加载速度越高,Kaiser效应越明显,拐点也越清晰。3)从累计声发射事件数时间关系曲线可知,加载速度为20 N/s的Kaiser效应比10 N/s和40 N/s的Kaiser效应明显,说明加载速度与Kaiser效应明显程度并非一定正相关。
|
图 3 试件B5声发射特征曲线(10 N/s) Fig. 3 AE characteristic curve of B5 (10 N/s) |
|
图 4 试件B10声发射特征曲线(20 N/s) Fig. 4 AE characteristic curve of B10 (20 N/s) |
|
图 5 试件B17声发射特征曲线(40 N/s) Fig. 5 AE characteristic curve of B17 (40 N/s) |
由此可见,砂岩破坏时的声发射事件数多少可以用于评价岩石破坏过程的发展程度,但判断过程中最好采用能量时间关系曲线进行分析。同时表明,加载速度变化对岩石的受拉破坏模式有重要影响。
3 受拉条件Kaiser效应机理分析为研究加载速度变化对岩石Kaiser效应的影响,基于Kaiser效应源于裂纹发展过程中所产生的应力波原理,裂纹发展过程、数量与声发射参数特征有一一对应关系,将通过加载速度变化下,裂纹演化规律的差异来对其机理进行研究。因裂纹扩展能量显著高于裂纹错动,故假定Kaiser效应由裂纹扩展引起[26]。模拟方法采用RFPA2D,RFPA2D是一种基于有限元理论和统计损伤理论,能准确模拟材料非线性断裂破坏的数值试验工具[27]。
3.1 模拟参数设定试件尺寸与试验一致为:160 mm×40 mm×40 mm,材料参数设定,如表 1所示。材料参数只有加载速度即单步增量1个变量,其他参数均一致。
| 表 1 材料参数设定 Table 1 Material parameter setting |
1) 当单步增量为1 μm/步时,第1次先加载40步,然后卸载5步,第2次再加载25步,然后卸载5步,以后每次都按照第2次加载方式循环至试件破坏。
2) 当单步增量为2 μm/步的时候,第1次先加载20步,然后卸载5步,第2次再加载15步,然后卸载5步,以后每次都按照第2次加载方式循环至试件破坏。
3) 当单步增量为4 μm/步的时候,第1次先加载10步,然后卸载5步,第2次再加载10步,然后卸载5步,以后每次都按照第2次加载方式循环至试件破坏。
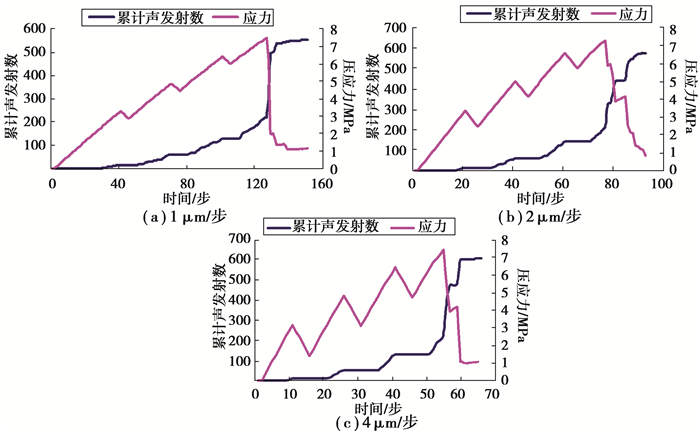
3.2 模拟过程与结果分析计算结果如图 6~图 9所示,3种速度条件下的三点弯曲试验破坏现象均较明显。
|
图 6 Kaiser效应模拟图(1 μm/步、2 μm/步、4 μm/步) Fig. 6 Simulation of Kaiser effect(1 μm/step, 2 μm/step, 4 μm/step) |

|
图 7 破坏过程图(1 μm/步) Fig. 7 Failure process renderings(1 μm/step) |

|
图 8 破坏过程图(2 μm/步) Fig. 8 Failure process renderings(2 μm/step) |

|
图 9 破坏过程图(4 μm/步) Fig. 9 Failure process renderings(4 μm/step) |
1) 单步增量为1 μm/步的试样在第28步时出现声发射现象(有裂纹出现),在第141步进入裂纹贯通破坏阶段。
2) 单步增量为2 μm/步试样在第15步开始出现声发射现象(有裂纹出现),在第75步进入裂纹贯通破坏阶段。单步增量为1 μm/步和单步增量为2 μm/步的破坏形式基本一致,裂纹延展方向均由试件中下部向上延伸。
3) 单步增量为4 μm/步的试件在第9步出现声发射现象(有裂纹出现),在第54步进入裂纹贯通破坏阶段,裂纹延展方向总体由试件中下部向上延伸,但出现了偏转。
将裂纹数等价衡量声发射数,加载速度越快,声发射事件数越大,如图 6所示,加载速度为1 μm/步, 120加载步总声发射数约560个,而4 μm/步,60加载步总声发射数达700个。3种加载速度下的Kaiser效应明显程度为4 μm/步高于1 μm/步,表明加载速度越快,Kaiser效应越明显,但Kaiser点的精度会降低,岩石破坏过程中的裂纹开展规律性会变得越不明显。
深入分析加载速度变化下,Kaiser效应差异性的影响机理,发现在较低加载速度下,试件处于纯拉应力状态,微裂纹可充分扩展后贯通为竖直裂缝。而随着加载速度的增加,试件应变能在局部快速聚集并至裂纹增生,微裂纹没有充分时间发育,裂纹会沿着开裂难度最小方向扩展,裂纹发展随机性增强,破坏强度加大,受荷状态可能向复合应力状态转化。加载速度变化,会引起裂纹竞争起裂趋势的变化,进而改变体内裂纹面方向与受力单元体远场应力方向的夹角大小,使裂纹开裂应力随之减小或增大,即减弱或增强裂纹开裂难易程度。导致裂纹发展方向向着开裂难度最小方向偏转,造成声发射事件出现时间提前或延迟,影响Kaiser效应反映岩石记忆先期荷载值的准确度。因此,加载速度越快,由于岩石裂纹开展的随机性变大,Kaiser效应明显程度会呈非线性变化,这样与试验结论相吻合。
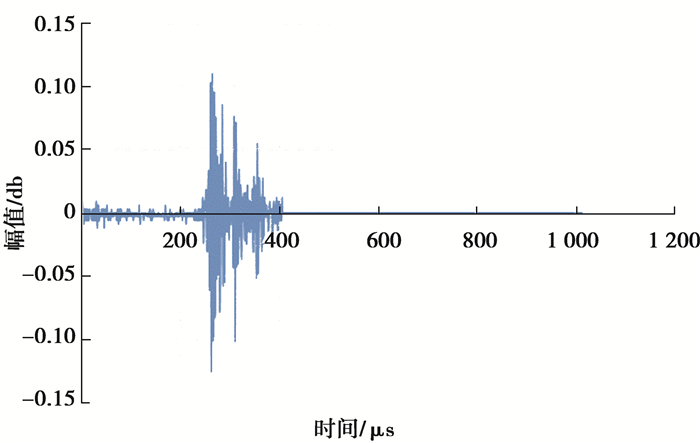
4 Kaiser点的频谱变化规律加载速度变化会影响Kaiser效应辨识度。为更好地认识和识别加载速度不同的Kaiser点特征,进而正确评价Kaiser效应,将通过对试件B5、B10、B17在第二循环中的Kaiser点波形数据进行小波分析,以确定受拉应力状态下的砂岩Kaiser点频谱变化规律。B10波形数据,如图 10所示,
|
图 10 B10样本Kaiser点信号图 Fig. 10 Kaiser point signals of sample B10 |
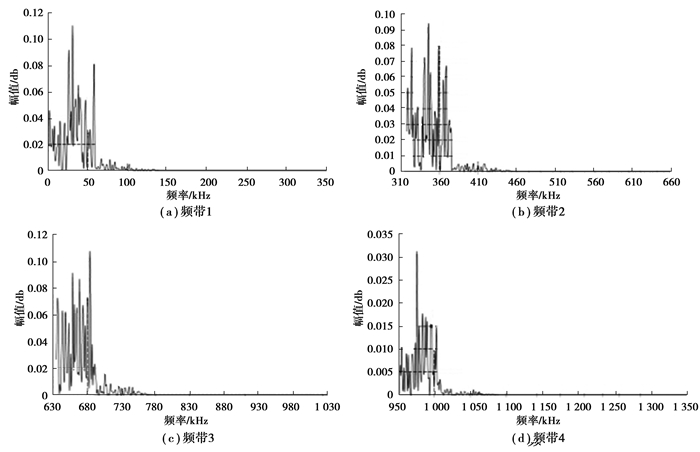
由于岩石破裂声发射频率范围主要集中在20~1 000 kHz间,故只对B5、B10、B17号样本信号图以构造小波函数为基础函数,作频带宽度1 250 kHz的2层小波分解,共4个频段。B10频带能量,如图 11所示,各试件能量比重占比,如表 2和图 12所示。
|
图 11 B10样本两次小波分解 Fig. 11 Two layer wavelet decomposition of sample B10 |
| 表 2 样本B7试验Kaiser点小波包分解各频段能量百分比汇总表 Table 2 Energy percentage summary for Kaiser point wavelet decomposition of sample B10 |
|
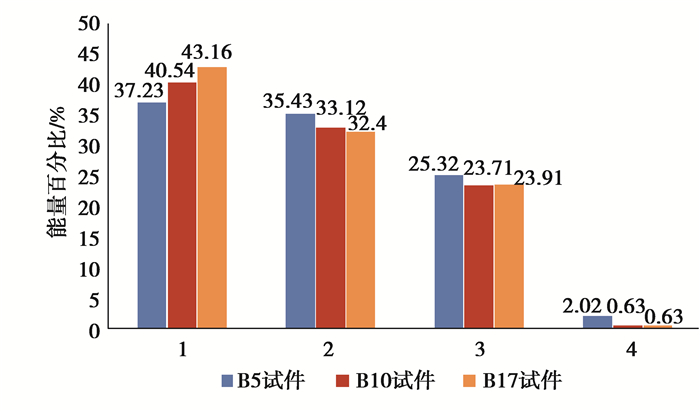
图 12 不同加载速度Kaiser点能量百分比分布图 Fig. 12 Energy percentage distribution of Kaiser point with different loading rates |
由表 2可知,样本声发射信号频谱范围主要集中在0~315.50 kHz频率,能量最大段范围为40.54%,而频带范围315.50~605.50 kHz的能量占比达到33.12%,同时,605.50~925.50 kHz频带能量占比也接近23%。说明受拉应力状态下的砂岩Kaiser点频谱特征以高频为主,并且集中在300 kHz附近,低频声发射能量并不占有绝对优势。
由图 12可知,不同加载速度Kaiser点能量百分比,在同频段范围的数值大小不同,整体趋势为:频带1(0~315.50 kHz)的能量百分比随着加载速度的增加而增加,频带2(315.50~605.50 kHz)、频带3(605.50~925.50 kHz)、频带4(925.50~1 250.00 kHz)的能量百分比均递减。说明加载速度的增加,Kaiser点能量分布会向着高频集中,这主要是由于能量在短时间内增大,微裂纹无法充分扩展所致,这一规律也可以用于反演辨识岩石受荷冲击强度变化。
5 结论通过3种加载速度下的三点弯曲声发射试验,观测了加载速度变化下的受拉应力状态砂岩Kaiser效应变化规律;并通过RFPA2D数值模拟,探讨了该Kaiser效应变化规律机理;同时,借助小波分析手段,获得了其可控因素,具体结论如下:
1) 从试验现象表明,加载速度越高,Kaiser效应越明显,拐点也越清晰,但并非一定正相关。
2) 通过RFPA2D数值模拟发现,受拉加载速度变化对砂岩Kaiser效应影响机理为:加载速度变化影响了裂纹扩展路径。裂纹加载速度越快,声发射事件数越大,岩石破坏规律性越不明显,纯拉应力状态可能向复合应力状态转化。由于加载速度增大,会引起裂纹竞争起裂趋势的改变,岩石裂纹开展的随机性变大,Kaiser效应明显程度呈现非线性特征。
3) 运用小波分析,获得了加载速度变化对砂岩Kaiser效应影响的频率可控因素,递增加载速率下的Kaiser点频带分布特征呈现一致性变化规律。随着加载速度的增加,Kaiser点能量分布会向着高频集中,这主要是由于能量在短时间内增大,微裂纹无法充分扩展所致,这一规律也可用于反演辨识岩石受荷冲击强度变化。
| [1] |
Sellers E J, Klerck P. Modelling of the effect of discontinuities on the extent of the fracture zone surrounding deep tunnels[J]. Tunnelling and Underground Space Technology, 2000, 15(4): 463-469. DOI:10.1016/S0886-7798(01)00015-3 |
| [2] |
谢和平. "深部岩体力学与开采理论"研究构想与预期成果展望[J]. 工程科学与技术, 2017(2): 1-16. XIE Heping. Research framework and anticipated results of deep rock mechanics and mining theory[J]. Advanced Engineering Sciences, 2017(2): 1-16. (in Chinese) |
| [3] |
余贤斌, 谢强, 李心一, 等. 直接拉伸、劈裂及单轴压缩试验下岩石的声发射特性[J]. 岩石力学与工程学报, 2007, 26(1): 137-142. YU Xianbin, XIE Qiang, LI Xinyi, et al. Acoustic emission of rocks under direct tension, brazilian and uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 137-142. (in Chinese) DOI:10.3321/j.issn:1000-6915.2007.01.019 |
| [4] |
李果, 艾婷, 于斌, 等. 不同岩性巴西劈裂试验的声发射特征[J]. 煤炭学报, 2015, 40(4): 870-881. LI Guo, AI Ting, YU Bin, et al. Acoustic emission characteristics of different lithologies under Brazilian splitting[J]. Journal of China Coal Society, 2015, 40(4): 870-881. (in Chinese) |
| [5] |
谢强, 王志委, 余贤斌, 等. 四点弯曲试验条件下页岩的声发射特性[J]. 重庆大学学报(自然科学版), 2010, 33(6): 72-76, 90. XIE Qiang, WANG Zhiwei, YU Xianbin, et al. Acoustic emission behavior of shale under four-point bending test[J]. Journal of Chongqing University(Natural Science Edition), 2010, 33(6): 72-76, 90. (in Chinese) |
| [6] |
Kaiser J. Erkenntnisse und Folgerungen aus der Messung von Geräuschen bei Zugbeanspruchung von metallischen Werkstoffen[J]. Archiv Für Das Eisenhüttenwesen, 1953, 24(1/2): 43-45. |
| [7] |
Barr S P, Hunt D P. Anelastic strain recovery and the kaiser effect retention span in the carnmenellis granite, U.K.[J]. Rock Mechanics and Rock Engineering, 1999, 32(3): 169-193. DOI:10.1007/s006030050031 |
| [8] |
Goodman R E. Subaudible noise during compression of rocks[J]. Geological Society of America Bulletin, 1963, 74(4): 487. DOI:10.1130/0016-7606(1963)74[487:SNDCOR]2.0.CO;2 |
| [9] |
Feerineis N. Anwendung der schallemissionanalyse(SEA) als zerstorungsfreies Prufverfahren fur Beton[J]. Dissertation TH Darmstadt, 1982, 511-524. |
| [10] |
纪洪广, 李造鼎. 混凝土材料凯塞效应与Felicity效应关系的实验研究[J]. 应用声学, 1997, 16(6): 30-33. JI Hongguang, LI Zaoding. Experimental study on the relationship of kaiser and felicity effect in concrete material[J]. Applied Acoustics, 1997, 16(6): 30-33. (in Chinese) |
| [11] |
李庶林, 唐海燕. 不同加载条件下岩石材料破裂过程的声发射特性研究[J]. 岩土工程学报, 2010, 32(1): 147-152. LI Shulin, TANG Haiyan. Acoustic emission characteristics in failure process of rock under different uniaxial compressive loads[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(1): 147-152. (in Chinese) |
| [12] |
卢运虎, 陈勉, 金衍, 等. 碳酸盐岩声发射地应力测量方法实验研究[J]. 岩土工程学报, 2011, 33(8): 1192-1196. LU Yunhu, CHEN Mian, JIN Yan, et al. Experimental study on stress measurement for sound emission in carbonate formation[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(8): 1192-1196. (in Chinese) |
| [13] |
Kurita K, Fujii N. Stress memory of crystalline rocks in acoustic emission[J]. Geophysical Research Letters, 1979, 6(1): 9-12. DOI:10.1029/GL006i001p00009 |
| [14] |
Yoshikawa S, Mogi K. A new method for estimation of the crustal stress from cored rock samples:Laboratory study in the case of uniaxial compression[J]. Tectonophysics, 1981, 74(3/4): 323-339. |
| [15] |
Li C, Nordlund E. Experimental verification of the Kaiser effect in rocks[J]. Rock Mechanics and Rock Engineering, 1993, 26(4): 333-351. DOI:10.1007/BF01027116 |
| [16] |
Goodman R E. Subaudible noise during compression of rocks[J]. Geological Society of America Bulletin, 1963, 74(4): 487. DOI:10.1130/0016-7606(1963)74[487:SNDCOR]2.0.CO;2 |
| [17] |
Holcomb D J. Using acoustic emission to determine in situ stress:problems and promise[J]. Geomechanics, 1983, 57: 11-21. |
| [18] |
Yoshikawa S, Mogi K. Experimental studies on the effect of stress history on acoustic emission activity-apossibility for estimation of rock stress[J]. J Acoust Emission, 1989, 8(4): 113-123. |
| [19] |
Koerner R M, Lord A E. AE detection of prestress in soil and rock[C]//Proceedings of the Fourth Conference on AE/MA in Geologic Structures and Materials. ClausthalZellerfeld: Trans Tech Publications, 1989: 73-86.
|
| [20] |
Filimonov Y L, Lavrov A V, Shkuratnik V L. Prospects of memory effects for stress measurement applications in rock salt[C]//Proceedings of EUROCK'2001 Symposium. Rotterdam: A A Balkema, 2001: 59-63.
|
| [21] |
Shin K, Kanagawa T. Kaiser effect of rock in acousto-elasticity, AE and DR[C]//Proceedings of the Fifth Conference on AE/MA in Geologic Structures and Materials. Clausthal-Zellerfeld: Trans Tech Publications, 1995: 197-204.
|
| [22] |
Michihiro K, Hata K, Yoshioka H, et al. Determination of the initial stresses on rock mass using acoustic emission method[J]. J Acoust Emission, 1991/1992, 10(1/2): 63-76. |
| [23] |
Fu X, Xie Q, Liang L. Comparison of the Kaiser effect in marble under tensile stresses between the Brazilian and bending tests[J]. Bulletin of Engineering Geology and the Environment, 2015, 74(2): 535-543. DOI:10.1007/s10064-014-0707-4 |
| [24] |
Lavrov A. Kaiser effect observation in brittle rock cyclically loaded with different loading rates[J]. Mechanics of Materials, 2001, 33(11): 669-677. DOI:10.1016/S0167-6636(01)00081-3 |
| [25] |
陈勉, 张艳, 金衍, 等. 加载速率对不同岩性岩石Kaiser效应影响的试验研究[J]. 岩石力学与工程学报, 2009, 28(S1): 2599-2604. CHEN Mian, ZHANG Yan, JIN Yan, et al. Experimental study of influence of loading rate on kaiser effect of different lithological rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 2599-2604. (in Chinese) |
| [26] |
傅翔, 谢强, 江小城, 等. 受拉加载方向变化对Kaiser效应点准确度的影响[J]. 岩土工程学报, 2014, 36(7): 1365-1370. FU Xiang, XIE Qiang, JIANG Xiaocheng, et al. Influence of tensile loading direction on accuracy of determining Kaiser effect point[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1365-1370. (in Chinese) |
| [27] |
唐春安, 赵文. 岩石破裂全过程分析软件系统RFPA2D[J]. 岩石力学与工程学报, 1997, 16(5): 507-508. TANG Chunan, ZHAO Wen. RPFA2D system for rock failure process analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(5): 507-508. (in Chinese) DOI:10.3321/j.issn:1000-6915.1997.05.018 |
 2019, Vol. 42
2019, Vol. 42


