由边坡失稳破坏而引起的灾害是世界范围内破坏性极大的一类灾害[1],制定有效的灾害预防与治理措施是目前密切关注的问题[2]。了解边坡失稳破坏引起的影响范围有多大、滑体的运动速度有多快,才能定量地确定受灾体的数量和可能的损坏程度,全面地评估发生此类灾害的风险[3]。因此,有效的边坡失稳影响范围模拟及失稳运动过程分析,是此类灾害风险量化评价的核心问题之一[4]。
边坡发生失稳运动的机理较为复杂,诱因多样,发生失稳破坏后运动状态与过程具有不确定性[5],因而,有效地模拟边坡失稳过程及影响范围一直是边坡模拟的重点与难点。边坡失稳运动过程及影响范围模拟常用方法可分为4类:简化分析模型[6-7]、流体力学模型[8-10]、统计信息模型[11-13]和基于质量和动量守恒的数值模拟预测模型[14-16]。简化分析模型是此类研究初期提出的模型,但过于抽象与简单,计算结果误差较大;流体力学模型通常应用在流动型滑坡、碎屑流等灾害体的失稳运动过程模拟和影响范围模拟中,其可行性与有效性已经得到了验证,但模型中流动参数不易获取,且只针对固定类型的滑坡适用;统计信息模型为预测边坡失稳后影响范围提供了一个实用工具,但其精度受限于历史数据的完整性与准确性,需累计大量、不同环境和条件下的案例及数据;基于质量和动量守恒的数值模拟模型逐渐成为分析此类问题的主要方式,目前,国内外基于各种数值方法建立的相关模型在基础理论研究中取得了阶段性进展。Tang[17]、Quecedo[18]、杨长卫[19]、毕钰璋[20]等运用离散元方法(DEM)模拟了地震诱发滑坡、高速滑坡、岩质滑坡、碎屑流等全过程,取得了较好的结果;Wu[21]、Beyabanaki[22]、殷坤龙[16]、邬爱清[23]等运用非连续变形分析方法(DDA)对地震诱发的流动型滑坡、岩质滑坡等进行了模拟,验证了该方法在滑坡模拟中的适用性;孙玉进等[24]运用物质点法对滑坡的全过程进行动态模拟分析;杜娟等[25]基于有限体积法对滑坡-碎屑流三维运动过程进行了模拟分析;Huang[26]、Hu[27]等利用光滑粒子流体动力学方法(SPH)对地震滑坡、流动型滑坡、土质滑坡进行了模拟分析,模拟结果与现场数据符合较好。综上所述,基于各种数值方法建立的相关计算模型是当前研究的重点,种类较多但各类方法侧重点不一,例如,离散元方法可用于各类边坡变形及运动的模拟,但计算中一些参数不易确定,且计算规模受算法理论与计算机能力限制;其他无网格方法,如非连续变形分析方法(DDA, discontinuous deformation analysis),在模拟计算中一些算法引入的非物理参数不易确定,若取值不当将给数值计算带来较大问题,并且力学表达难以直接描述模型的应力应变关系[28]。
随着计算机能力的提升及各类算法模型的发展,基于质量动量守恒定律的数值模型已经成为分析边坡失稳运动特征与模拟影响范围的主要手段。传统有限元与基于网格划分的数值方法难以进行大变形问题的计算,网格大变形畸变是数值解不精确甚至中断的原因。鉴于传统网格方法局限性,无网格方法成为解决此类问题的研究热点。其中,SPH方法是目前发展最成熟的无网格方法,开始逐步应用于土体变形、岩石破裂、滑坡运动、泥石流过程等研究领域。Pastor等基于Biot-Zienkiewicz模型提出了流动型滑坡深度影响的SPH模型,实现了一些流动型滑坡失稳运动过程模拟[29]。McDougall和Hungr提出了复杂地形滑坡运动过程快速模拟的平均深度模型[30]。Huang等采用了SPH框架下的非牛顿流体模型对汶川地震引发流动型滑坡过程及影响范围进行了模拟,数值结果与现场采集数据基本吻合[26, 31]。Bui等采用弹塑性土体本构模型与德鲁克普拉格屈服准则,提出了适合模拟岩土材料大变形运动的SPH模型,并验证了模型的精确性[31]。Huang[32]、Hu[33]等在流体本构模型基础上建立了三维SPH模型,用于流动型滑坡的模拟。其中,基于GIS平台建模提出了考虑土体弹塑性本构关系的二维SPH模型[34-35]。然而,该二维模型在边界条件的确定上难以适用于实际滑坡问题的模拟,并且在模拟粘性土时,所采用的人工应力技术存在应力较大的问题。
文中采用弹塑性土本构关系的SPH模型模拟边坡失稳后的行为,在GIS平台上构建滑坡模型并进行适当的边界处理,去除了计算过程中的人工应力技术。最后,以美国华盛顿州Oso滑坡为例,将数值模拟结果与现场数据进行对比,两者能较好地吻合,验证了此方法的可行性。
1 研究模型 1.1 光滑粒子流体动力学(SPH)方法基础SPH方法是一种无网格拉格朗日粒子法。在SPH方法中,系统计算域的状态基于若干粒子进行表述,计算粒子被赋予了材料的各类性质信息,且遵循控制方程的规律运动。核函数近似逼近与质点近似逼近是构造SPH方程的2个关键步骤。其核近似可用下式积分表示场函数[37]:
| $ \langle f(x)\rangle=\int_{\Omega} f\left(x^{\prime}\right) W\left(x-x^{\prime}, h\right) \mathrm{d} x, $ | (1) |
式中:W表示核函数; h是光滑长度。核函数的构造与选择很大程度决定了SPH算法的计算精度和效率。文中采用的核函数为式(2)所示三次样条函数。
| $ W\left( {R,h} \right) = {\alpha _d} \times \left\{ \begin{array}{l} \frac{2}{3} - R2 + \frac{1}{2}{R^3},\;\;\;\;\;0 \le R < 1,\\ \frac{1}{6}{\left( {2 - R} \right)^3},\;\;\;\;\;\;\;\;\;\;1 \le R < 2,\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R \ge 2; \end{array} \right. $ | (2) |
其中,R=|x-x′|/h, 在二维和三维空间,αd分别取15/(7πh2)和3/(2πh3)。
另外,近似将粒子信息用光滑域内的其他粒子表示,其特征如下:
| $ \left\langle f\left(x_{i}\right)\right\rangle=\sum\limits_{j=1}^{N} \frac{m_{j}}{\rho_{j}} f\left(x_{j}\right) \cdot W_{i j}, $ | (3) |
其中,Wij=W(xi-xj, h), m和ρ分别表示粒子的质量和密度。
1.2 控制方程根据质量守恒定律,连续性方程可以写为
| $ \frac{{{\rm{d}}\rho }}{{{\rm{d}}t}} = - \rho \frac{{\partial {v^\beta }}}{{\partial {x^\beta }}}, $ | (4) |
式中, v表示速度。依据所述SPH粒子近似方法,式(4)可改写为
| $ \frac{{{\rm{d}}{\rho _i}}}{{{\rm{d}}t}} = {\rho _i}\sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}\left( {\nu _i^\beta - \nu _j^\beta } \right) \cdot \frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}} , $ | (5) |
其中:m为粒子质量; v是粒子速度; x代表粒子的坐标位置。参考连续性密度法的推导过程,控制方程中动量方程的粒子近似可以写为
| $ \frac{{D\nu _i^\alpha }}{{Dt}} = \sum\limits_{j = 1}^N {{m_j}\left( {\frac{{\sigma _i^{\alpha \beta }}}{{\rho _i^2}} + \frac{{\sigma _j^{\alpha \beta }}}{{\rho _j^2}}} \right)\frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}} + g, $ | (6) |
式中,g是外力作用(此时为重力),式(6)即是SPH框架下的动量方程。
1.3 弹塑性力学本构在固体力学中,理想弹塑性材料全应力张量可以写为静水压力球形张量与剪应力偏张量两部分之和:
| $ \sigma^{\alpha \beta}=-p \delta^{a \beta}+s^{\alpha \beta}, $ | (7) |
在SPH方法计算框架中,静水压力p通常由状态方程(equation of state)求得,文中p直接根据其标准定义求得,写为
| $ p=-\frac{1}{3} I_{1}=-\frac{1}{3}\left(\sigma^{x x}+\sigma^{y y}+\sigma^{z z}\right), $ | (8) |
式中压应力为负。对于理想弹塑性材料, 应变率张量
| $ {\dot \varepsilon ^{\alpha \beta }} = \dot \varepsilon _e^{\alpha \beta } + \dot \varepsilon _P^{\alpha \beta }, $ | (9) |
根据虎克定律与塑性流动法则,式(9)可写为
| $ {\dot \varepsilon ^{\alpha \beta }} = \frac{{{{\dot S}^{\alpha \beta }}}}{{2G}} + K{\dot \sigma ^{\gamma \gamma }}{\delta ^{\alpha \beta }} + \dot \lambda \frac{{\partial f}}{{\partial {\sigma ^{\alpha \beta }}}}, $ | (10) |
式中:
文中使用理想弹塑性本构与德鲁克普拉格(DP, Drucker-Prager)屈服准则描述土体的应力应变关系及屈服状态,该屈服条件可表示为
| $ f\left( {{I_1},{j_2}} \right) = \sqrt {{J_2}} + {\alpha _\phi }{I_1} - {k_c} = 0, $ | (11) |
其中, I1和j2是应力张量的第一和第二不变量,表示为
| $ {I_1} = {\sigma ^{xx}} + {\sigma ^{yy}} + {\sigma ^{zz}}\;和\;{j_2} = \frac{1}{2}{s^{\alpha \beta }}{s^{\alpha \beta }}, $ |
式中,αϕ和kc是常量, 两者可以通过土体摩尔库伦参数粘聚力c与内摩擦角ϕ计算求得。对于平面应变问题,常量αϕ和kc为
| $ {\alpha _\phi } = \frac{{\tan \phi }}{{\sqrt {9 + 12{{\tan }^2}\phi } }},\;\;\;\;{k_c} = \frac{{3c}}{{\sqrt {9 + 12{{\tan }^2}\phi } }}。$ |
考虑塑性流动下的非关联流动法则,塑性屈服函数可表示为
| $ {\dot \sigma ^{\alpha \beta }} = 2G{\dot e^{\alpha \beta }} + K{\dot \varepsilon ^{\gamma \gamma }}{\delta ^{\alpha \beta }} - \dot \lambda \left( {9K\sin \psi {\delta ^{\alpha \beta }} + \frac{G}{{\sqrt {{J_2}} }}{s^{\alpha \beta }}} \right)。$ | (12) |
式(12)表达了理想弹塑性土体材料模型在DP屈服准则下,考虑非关联流动塑性状态的应力变化率张量。
1.4 关键问题处理 1.4.1 人工粘性在SPH算法框架下通常会采用人工粘性的数值处理方法增强数值模拟的稳定性。固体问题SPH方法通常将人工粘性引入到数值计算处理中,因此, 方程(6)可写成[37]:
| $ \frac{{D\nu _i^a}}{{Dt}} = \sum\limits_{j = 1}^N {{m_j}} \left( {\frac{{\sigma _i^{a\beta }}}{{\rho _i^2}} + \frac{{\sigma _j^{a\beta }}}{{\rho _j^2}} + {\mathit{\Pi }_{ij}}} \right)\frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }} + g, $ | (13) |
式(13)中Πij表示为
| $ {\mathit{\Pi }_{ij}} = \frac{{ - a\bar c{\mu _{ij}} + b\mu _{ij}^2}}{{\bar \rho }}, $ | (14) |
其中,
| $ {\mu _{ij}} = \frac{{h\left( {{v_i} - {v_j}} \right) \cdot \sqrt {\left( {{x_i} - {x_j}} \right)2 + {{\left( {{y_i} - {y_j}} \right)}^2}} }}{{{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2} + 0.01{h^2}}}, $ |
| $ \bar c = \left( {{c_i} + {c_j}} \right)/2\bar \rho = \left( {{\rho _i} + {\rho _j}} \right)/2。$ |
式中:a和b是常数; c是岩土材料中的声速。
1.4.2 饶曼应力率SPH方法在模拟大变形问题时,增量的刚度矩阵难以求解,为解决此问题,数值计算中引入了饶曼应力率。饶曼应力率张量
| $ {{\dot{\hat{\sigma }}}^{a\beta }}={{\dot{\sigma }}^{a\beta }}-{{\dot{\omega }}^{a\beta }}{{\sigma }^{a\beta }}-{{\sigma }^{a\beta }}{{\left( {{{\dot{\omega }}}^{a\beta }} \right)}^{\text{T}}}, $ | (15) |
其中,
| $ {\dot \omega ^{a\beta }} = \frac{1}{2}\left( {\frac{{\partial {v_\alpha }}}{{\partial {x_\beta }}} - \frac{{\partial {v_\beta }}}{{\partial {x_\alpha }}}} \right)。$ | (16) |
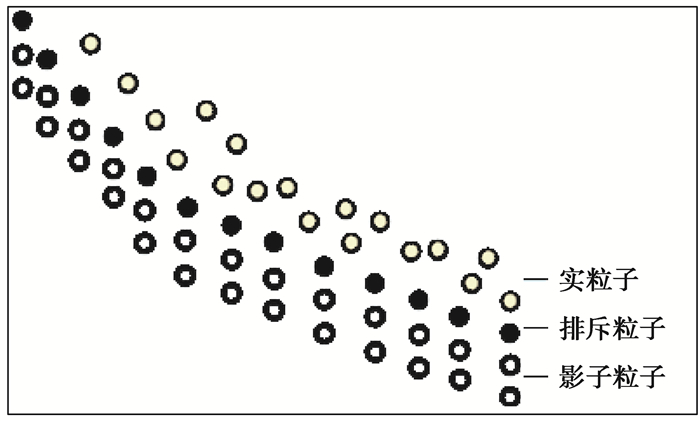
边界条件是SPH数值计算中的一个重要部分,与SPH计算的精确性密切相关。SPH文献中最常用的方法仍然是基于虚粒子的边界处理方法。由于在边坡失稳后运动模拟中,实粒子底部常常由于过大的应力引起较大的加速度,进而速度过大从边界逸出,文中结合了排斥粒子与影子粒子,提出如图 1所示的耦合边界,在速度无滑移边界条件(No-slip boundary)的基础上,增加排斥粒子,以阻止实粒子由于过大的速度引起的逃逸。通过赋予影子粒子一定的速度,实现边界上速度无滑移的效果,如图 1所示。
|
图 1 耦合边界条件算法示意图 Fig. 1 Illustration of coupled boundary algorithm |
真实的边界与影子粒子之间的相对速度为
| $ v_{\mathrm{AB}}=v_{\mathrm{A}}-v_{\mathrm{B}}=\beta\left(v_{\mathrm{B}}-v_{\mathrm{wall}}\right), $ | (17) |
| $ v_{\mathrm{A}}=(1-\beta) v_{\mathrm{B}}+\beta v_{\mathrm{wall}}, $ | (18) |
其中,
| $ \sigma_{j}^{\alpha \beta}=\sigma_{i}^{\alpha \beta}。$ | (19) |
得益于无网格法的特性,SPH计算框架摆脱了网格划分对计算带来的局限,文中通过将边坡体离散成为SPH粒子,并将边坡表面地形与滑动面地形创建边界粒子来实现边坡模型的建立。借助地表与滑面轮廓线与内部插值,通过编程实现了整个边坡粒子模型的构建。二维边坡SPH粒子模型的构建步骤如下:1)收集边坡基础资料,在特征剖面线中提取地形、滑面、地层分界线、地下水位等位置轨迹线;2)在地理信息系统(GIS)平台或计算机辅助设计(CAD)平台上,沿各位置轨迹线将均匀插入粒子,并遵循竖向对齐的原则;3)在竖向对齐的粒子间进行等距离插入新的SPH粒子,并赋予SPH粒子质量、密度、位置、速度等参数;4)对于边界粒子可增加层数且错位铺设。将此过程通过计算机编程实现,提高了计算分析的效率。
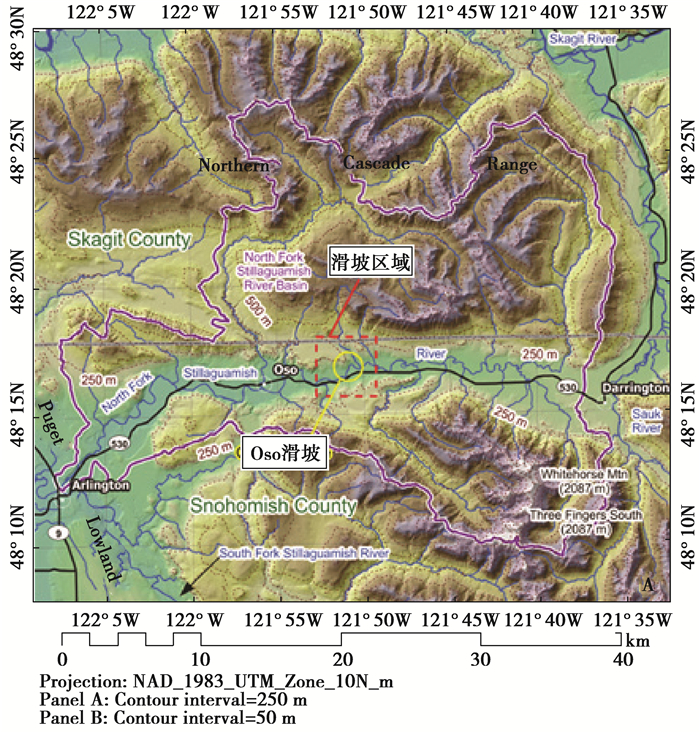
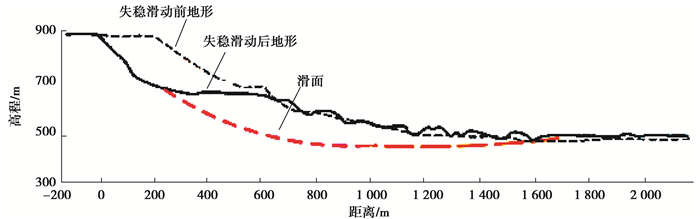
2 实例分析2014年3月22日上午,美国华盛顿州Oso镇的大面积山体滑坡,灾害共造成43人死亡,并有10人受伤,灾后估计经济损失高达5 000万美元[1]。Oso山体滑坡位于Cascade Range北部的一个向西延伸的峡谷,滑坡发生在山谷最狭窄的位置,如图 2所示。调查报告显示,滑坡失稳前3周内的强降雨(降雨量达到约760 mm)是此次滑坡的主要原因。图 3是Oso滑坡发生前后的航拍对比图,图 4显示了在主剖面上边坡失稳滑动前后的地形对比。
|
图 2 Oso滑坡附近地形 Fig. 2 landform near the Oso landslide |

|
图 3 边坡失稳前后对比图 Fig. 3 before and after the slopefailure |
|
图 4 边坡失稳前后剖面图 Fig. 4 Profile map before and after the slope failure |
根据前节所提出的粒子模型方法,结合图 4边坡失稳前后剖面图创建了二维Oso滑坡SPH粒子模型。以此滑坡SPH粒子模型为例,模型共包含4 229个实粒子,这些实粒子均匀填充在滑坡体中;模型中共包含1 911个虚粒子构成滑面边界,计算中初始光滑长度为7.5 m。计算中所使用的岩土材料参数见文献[1],模拟参数如表 1所示。此外,模拟计算过程中应用了张力裂缝处理及应力重新调整等数值技术[35]。
| 表 1 Oso滑坡SPH计算模拟参数 Table 1 Simulation parameters of Oso Landslide |
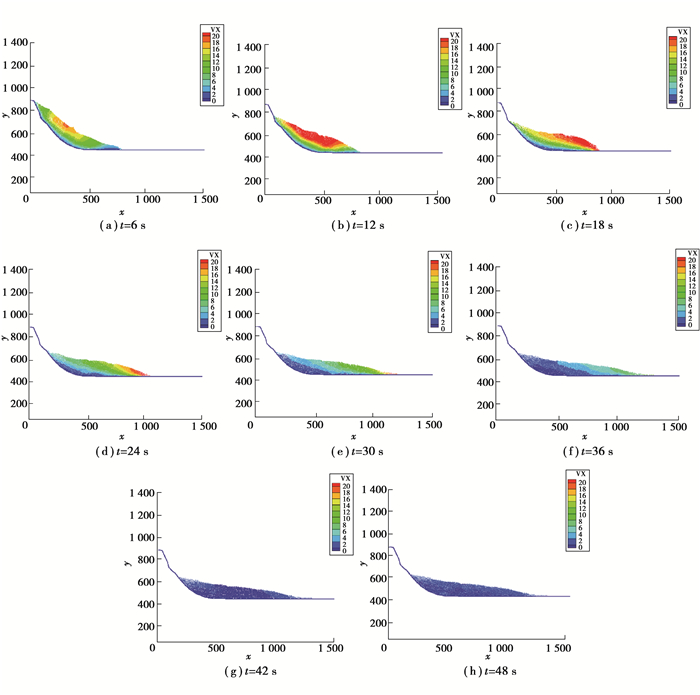
计算结果展现出滑坡失稳运动的整个过程,图 5显示了Oso滑坡在此过程中具有代表性时刻的地形特征,滑坡体沿滑动方向上的速度,如图 5所示。可以看出,当t=6 s时,边坡处于失稳运动前期,在滑坡体的中后部沿滑动方向上的速度最大;随着时间的推移,滑坡体前面部分沿滑动方向上速度越来越大,到达速度最大后转而减小,直到整个运动过程结束,所有SPH粒子在沿滑动方向上的速度都等于零,在48 s的时候基本停止,整个运动过程结束。
|
图 5 Oso滑坡失稳运动过程模拟 Fig. 5 Simulated run-out process of Oso landslide |
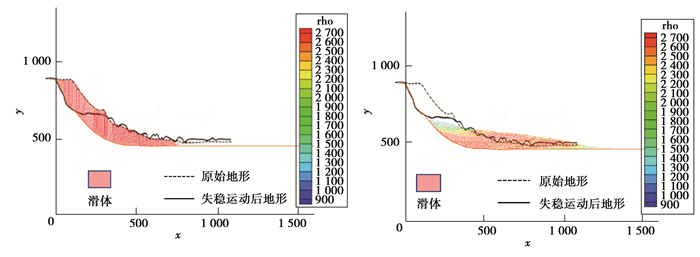
由图 6可知,最后模拟结果得到的滑坡影响范围地表轮廓线与实际雷达测出的轮廓线较为吻合。然而,若对现场数据和仿真结果进行比较,地形特征略有差异,部分差异可能是滑坡体中的不均匀土质或岩土层信息缺乏造成的。滑坡的模拟影响范围与实际影响范围大致相同,说明基于SPH的模拟方法能得到较为准确的结果,对边坡失稳影响范围模拟有一定的适用性。
|
图 6 模拟结果与实际边坡失稳影响范围前后对比 Fig. 6 Comparison of influenced areabetween simulation results and landslide |
针对边坡失稳破坏后的影响范围模拟是边坡调查与风险评价中重要环节,有助于定量确定受灾体的数量和可能的损坏程度,减少此类地质灾害造成的损失。采用基于DP屈服准则和非关联流动法则的SPH方法,在弹塑性本构模型的核心下,改进了边界粒子的分布方式,更加精确和便捷地模拟边坡失稳破坏后影响范围。以美国华盛顿州Oso滑坡为例,经建模模拟其失稳破坏过程与影响范围,与现场雷达收集数据对比,结果较为符合,验证了SPH方法及所述运动模型在此类问题研究中的可行性,较好地模拟对边坡失稳影响范围。
| [1] |
Wartman J, Montgomery D R, Anderson S A, et al. The 22 march 2014 oso landslide, washington, USA[J]. Geomorphology, 2016, 253: 275-288. DOI:10.1016/j.geomorph.2015.10.022 |
| [2] |
Lee E M. Landslide risk assessment:the challenge of communicating uncertainty to decision-makers[J]. Quarterly Journal of Engineering Geology and Hydrogeology, 2016, 49(1): 21-35. DOI:10.1144/qjegh2015-066 |
| [3] |
吴越, 刘东升, 周忠浩, 等. 考虑滑动过程内部崩解耗散的滑坡体运动模型[J]. 岩土工程学报, 2015, 37(1): 35-46. WU Yue, LIU Dongsheng, ZHOU Zhonghao, et al. Mobility assessment model for landslide mass considering disintegration energy consumption in slipping process[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 35-46. (in Chinese) |
| [4] |
吴树仁. 滑坡风险评估理论与技术[M]. 北京: 科学出版社, 2012. WU Shuren. Landslide risk assessment theory and technology[M]. Beijing: Science Press, 2012. (in Chinese) |
| [5] |
姜波, 柴波, 方恒, 等. 万州孙家荆竹屋基滑坡滑动模型研究[J]. 长江科学院院报, 2015, 32(8): 103-109. JIANG Bo, CAI Bo, FANG Heng, et al. Sliding model of jingzhuwuji landslide in sunjia town, Wanzhou district[J]. Journal of Yangtze River Scientific Research Institute, 2015, 32(8): 103-109. (in Chinese) |
| [6] |
王家鼎, 张倬元. 地震诱发高速黄土滑坡的机理研究[J]. 岩土工程学报, 1999, 21(6): 670-674. WANG Jiading, ZHANG Zhuoyuan. A study on the mechanism of high-speed loess landslide induced by earthquake[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 670-674. (in Chinese) DOI:10.3321/j.issn:1000-4548.1999.06.008 |
| [7] |
张倬元. 工程地质分析原理[M]. 北京: 地质出版社, 2009. ZHANG Zhuoyuan. Analysis principle of Engineering geology[M]. Beijing: Geology Press, 2009. (in Chinese) |
| [8] |
Sousa J, Voight B, Sousa J. Continuum simulation of flow failures[J]. Géotechnique, 1991, 41(41): 515-538. |
| [9] |
Chen H, Lee C F. Numerical simulation of debris flows[J]. Canadian Geotechnical Journal, 2000, 37(1): 146-160. DOI:10.1139/t99-089 |
| [10] |
Huang X, García M H. A Herschel-Bulkley model for mud flow down a slope[J]. Journal of Fluid Mechanics, 1998, 374: 305-333. DOI:10.1017/S0022112098002845 |
| [11] |
Heim A. Landslide and human lives[M]. Vancouver: Bitech Press, 1989.
|
| [12] |
Scheidegger A E. On the prediction of the reach and velocity of catastrophic landslides[J]. Rock Mechanics Felsmechanik mCanique des Roches, 1973, 5(4): 231-236. DOI:10.1007/BF01301796 |
| [13] |
王念秦, 张倬元, 王家鼎. 一种典型黄土滑坡的滑距预测方法[J]. 西北大学学报(自然科学版), 2003, 33(1): 111-114. WANG Nianqin, ZHANG Zhuoyuan, WANG Jiading. A forecasting method of sliding distance on typical loess lands-lides[J]. Journal of Northwest University(Natural Science Edition), 2003, 33(1): 111-114. (in Chinese) DOI:10.3321/j.issn:1000-274X.2003.01.030 |
| [14] |
Tang C L, Hu J C, Lin M L, et al. The Tsaoling landslide triggered by the Chi-Chi earthquake, Taiwan:Insights from a discrete element simulation[J]. Engineering Geology, 2009, 106(1/2): 1-19. |
| [15] |
Wu J H, Chen C H. Application of DDA to simulate characteristics of the Tsaoling landslide[J]. Computers and Geotechnics, 2011, 38(5): 741-750. DOI:10.1016/j.compgeo.2011.04.003 |
| [16] |
殷坤龙, 姜清辉, 汪洋. 滑坡运动过程仿真分析[J]. 地球科学, 2002, 27(5): 632-636. YIN Kunlong, JIANG Qinghui, WANG Yang. Simulation of landslide movement process by discontinuous deformation analysis[J]. Earth Science, 2002, 27(5): 632-636. (in Chinese) DOI:10.3321/j.issn:1000-2383.2002.05.026 |
| [17] |
Tang C L, Hu J C, Lin M L, et al. The Tsaoling landslide triggered by the Chi-Chi earthquake, Taiwan:Insights from a discrete element simulation[J]. Engineering Geology, 2009, 106(1/2): 1-19. |
| [18] |
Quecedo M, Pastor M, Herreros M I, et al. Numerical modelling of the propagation of fast landslides using the finite element method[J]. International Journal for Numerical Methods in Engineering, 2004, 59(6): 755-794. DOI:10.1002/(ISSN)1097-0207 |
| [19] |
杨长卫, 张建经, 张明, 等. 双面高陡岩质边坡地震滑坡机制的研究[J]. 岩土力学, 2013, 34(11): 3261-3268. YANG Changwei, ZHANG Jianjing, ZHANG Ming, et al. Analysis of landslide mechanisms of a high steep rock hill with two-side slopes under ground shaking[J]. Rock and Soil Mechanics, 2013, 34(11): 3261-3268. (in Chinese) |
| [20] |
毕钰璋, 付跃升, 何思明, 等. 牛眠沟地震滑坡碎屑化全过程离散元模拟[J]. 中国地质灾害与防治学报, 2015, 26(3): 17-25. BI Yuzhang, FU Yuesheng, HE Siming, et al. Simulation of the whole process of Niumiangou creek rock avalanche triggered by the earthquake using a distinct element method[J]. The Chinese Journal of Geological Hazard and Control, 2015, 26(3): 17-25. (in Chinese) |
| [21] |
Wu J H, Chen C H. Application of DDA to simulate characteristics of the Tsaoling landslide[J]. Computers and Geotechnics, 2011, 38(5): 741-750. DOI:10.1016/j.compgeo.2011.04.003 |
| [22] |
Beyabanaki S A R, Bagtzoglou A C, Liu L B. Applying disk-based discontinuous deformation analysis (DDA) to simulate Donghekou landslide triggered by the Wenchuan earthquake[J]. Geomechanics and Geoengineering, 2016, 11(3): 177-188. DOI:10.1080/17486025.2015.1082647 |
| [23] |
邬爱清, 丁秀丽, 李会中, 等. 非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程[J]. 岩石力学与工程学报, 2006, 25(7): 1297-1303. WU Aiqing, DING Xiuli, LI Huizhong, et al. Numerical simulation of startup and whole failure process of Qianjiangping landslide using discontinuous deformation analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1297-1303. (in Chinese) DOI:10.3321/j.issn:1000-6915.2006.07.001 |
| [24] |
孙玉进, 宋二祥. 大位移滑坡形态的物质点法模拟[J]. 岩土工程学报, 2015, 37(7): 1218-1225. SUN Yujin, SONG Erxiang. Simulation of large-displacement landslide by material point method[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1218-1225. (in Chinese) |
| [25] |
杜娟, 殷坤龙, 王佳佳, 等. 基于有限体积法的滑坡—碎屑流三维运动过程模拟分析[J]. 岩石力学与工程学报, 2015, 34(3): 480-488. DU Juan, YIN Kunlong, WANG Jiajia, et al. Simulation of three-dimensional movement of landslide-debris flow based on finite volume method[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 480-488. (in Chinese) |
| [26] |
Huang Y, Zhang W J, Xu Q, et al. Run-out analysis of flow-like landslides triggered by the Ms 8.02008 Wenchuan earthquake using smoothed particle hydrodynamics[J]. Landslides, 2012, 9(2): 275-283. DOI:10.1007/s10346-011-0285-5 |
| [27] |
Hu M, Liu M B, Xie M W, et al. Three-dimensional run-out analysis and prediction of flow-like landslides using smoothed particle hydrodynamics[J]. Environmental Earth Sciences, 2015, 73(4): 1629-1640. DOI:10.1007/s12665-014-3513-1 |
| [28] |
黄雨, 郝亮, 谢攀, 等. 土体流动大变形的SPH数值模拟[J]. 岩土工程学报, 2009, 31(10): 1520-1524. HUANG Yu, HAO Liang, XIE Pan, et al. Numerical simulation of large deformation of soil flow based on SPH method[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1520-1524. (in Chinese) DOI:10.3321/j.issn:1000-4548.2009.10.007 |
| [29] |
Pastor M, Haddad B, Sorbino G, et al. A depth-integrated, coupled SPH model for flow-like landslides and related phenomena[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(2): 143-172. DOI:10.1002/nag.v33:2 |
| [30] |
McDougall S, Hungr O. A model for the analysis of rapid landslide motion across three-dimensional terrain[J]. Canadian Geotechnical Journal, 2004, 41(6): 1084-1097. DOI:10.1139/t04-052 |
| [31] |
Bui H H, Fukagawa R, Sako K, et al. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic-plastic soil constitutive model[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(12): 1537-1570. DOI:10.1002/nag.v32:12 |
| [32] |
Huang Y, Dai Z L. Large deformation and failure simulations for geo-disasters using smoothed particle hydrodynamics method[J]. Engineering Geology, 2014, 168: 86-97. DOI:10.1016/j.enggeo.2013.10.022 |
| [33] |
Hu M, Liu M B, Xie M W, et al. Three-dimensional run-out analysis and prediction of flow-like landslides using smoothed particle hydrodynamics[J]. Environmental Earth Sciences, 2015, 73(4): 1629-1640. DOI:10.1007/s12665-014-3513-1 |
| [34] |
胡嫚, 谢谟文, 王立伟, 等. 基于弹塑性土体本构模型的滑坡运动过程SPH模拟[J]. 岩土工程学报, 2016, 38(1): 58-67. HU Man, XIE Mowen, WANG Liwei, et al. SPH simulations of post-failure flow of landslides using elastic-plastic soil constitutive model[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 58-67. (in Chinese) |
| [35] |
许波, 谢谟文, 胡嫚, 等. 基于GIS空间数据的滑坡SPH粒子模型研究[J]. 岩土力学, 2016, 37(9): 2696-2705. XU Bo, XIE Mowen, HU Man, et al. SPH landslide model based on GIS spatial data[J]. Rock and Soil Mechanics, 2016, 37(9): 2696-2705. (in Chinese) |
| [36] |
Liu G R, Liu M B. Smoothed Particle Hydrodynamics-AMeshfree particle method[M]. World Scientific Publishing Co. Pte. Ltd., 2003.
|
 2019, Vol. 42
2019, Vol. 42

