2. 中交第二公路勘察设计研究院有限公司, 武汉 430056
2. The Second Highway Survey and Design Institute Co. Ltd. of China Communications, Wuhan 430074, P. R. China
混凝土被广泛应用于工程建设,其内部缺陷的准确预测与预报,对于确保结构物的正常工作和避免建筑物的灾难性损伤具有重大意义。目前,混凝土缺陷检测技术主要有超声脉冲法[1]、雷达扫描法[2]、红外热谱法[3]等。这些方法应用广泛,但均存在一定的局限性。如混凝土对超声的强吸收问题影响了超声脉冲技术在混凝土检测中的应用。雷达法检测仪器多采用国外进口,成本较高,且无法对原始数据进行分析,该技术在国内尚处于起步阶段。红外热谱法应用较多,但其主要应用于定性判断和表面质量检测,难以实现对缺陷定量及目标内部的可视化检测。
近年来,电阻率成像技术(ERT, electrical resistance tomography)因其成本低、无损伤及功能成像等优点[4]被广泛用于工程检测领域[5]。ERT技术是一种新型的图像重建技术。ERT技术是通过向被测对象注入电流,测量边界电压(或电势),经过反演计算,重构被测对象内部的电导率,进而显示物体内部状态的一种成像技术。但是,ERT是一个病态反问题[6],存在着非线性、欠定性、严重不适定性和计算量大等难点,成像的精度和稳定性很难保证。为提高图像重建质量,文献[7]提出阈值修正法,可去除部分图像伪影,改善成像质量,但选取阈值大小时,主观因素影响较大,难以寻找到合理阈值。董峰等[8]在阈值修正法基础上提出一种快速自适应稀疏重建算法,研究了噪声对图像重建效果的影响,获得了较好效果。肖理庆[9]提出一种改进牛顿拉夫逊绝对图像重建算法,采用灵敏度矩阵自动更新的策略,结合图像结果自动选取阈值修正电阻率,可有效降低图像的相对误差。Cheney等[10]提出牛顿单步残差法(NOSER, Newton’s one-step error reconstructor),设定均匀分布的电导率为初值,用一次牛顿迭代后的结果进行成像,可实现快速成像,但其成像伪影较大,电阻率与真实值相差较大,仅能定性分析,无法实现定量分析。
将ERT技术应用于混凝土检测领域时,由于混凝土自身电导率较小,测量受外界因素影响较大,且混凝土基体与缺陷间的电导率为突变而不是渐变关系等原因,用于医学检测的传统ERT算法很难将缺陷与基体间的锐利边界重构出来,限制了ERT技术在混凝土无损检测中的应用。
采用ERT技术进行混凝土缺陷检测时,被测对象有两个特点:基体与缺陷有明显边界(即电导率发生突变而不是渐变);混凝土的电导率可事先测量。针对这些特点和上述算法的问题,文中提出一种优化算法——约束牛顿迭代算法(NCRM, Newton’s constrained reconstruction method),依据被测对象的这些信息作为先验条件,结合上一次迭代结果来调整初始向量,逐次递进反算初值,通过进一步迭代来得到较为准确的内部电导率分布,实现混凝土缺陷无损检测目的。
1 ERT工作原理ERT技术实质上是低频电流场的反问题计算,主要包括正问题和反问题的研究。正问题为已知场域电阻率分布,求解边界电极处电压值,计算过程稳定,有唯一解;而其反问题是已知边界电压,通过反运算推测场域内各单元的电阻率分布,一般情况下能获得的边界电压值有限,而单元数远多于电压数量,计算呈现明显的病态性和欠定性,数学上的解决方案多采用Newton-Raphson迭代和正则化方法来降低病态性,用最小二乘法获得近似解。
从物体表面注入低频恒定电流,忽略介电常数,将场域内的电流场认为是准静态场,则电阻率σ与电势分布函数φ满足Laplace方程[11],即
| $ \mathit{\Omega }:\nabla \cdot (\sigma \nabla \varphi ) = 0, $ | (1) |
| $ {\mathit{\Gamma }_1}:\mathit{\boldsymbol{\varphi }} + {z_l}\sigma \frac{{\partial \varphi }}{{\partial \mathit{\boldsymbol{\bar n}}}} = {U_l}, $ | (2) |
| $ {\mathit{\Gamma }_2}:\int \sigma \frac{{\partial \varphi }}{{\partial \mathit{\boldsymbol{\bar{n}}}}}d\mathit{\Gamma } = - {I_l}, $ | (3) |
式中:φ为场域Ω内的电势分布函数;zl代表第l个测量电极的接触阻抗;Ιl是电极处的电流密度;n为外法向单位矢量;σ为场域内的电导率分布函数。
正问题是根据边界条件与场域内电导率分布σ求解电势分布φ。采用有限元法求解时,可写成矩阵形式
| $ \mathit{\boldsymbol{S\varphi }} = \mathit{\boldsymbol{F}}, $ | (4) |
式中:S为系数矩阵,是由单元系数矩阵Sije组装而成,里面包含单元的电导率,此处假设每个单元的电导率为常数,Sije可由单元形函数推导得到;F为电流列向量,电流注入流出的位置分别为I和-I,其余项均为0。
ERT的反问题是由边界测量电压计算被测物内部的电导率分布,一般采用最小二乘法搜索出一合适的电导率分布σ,使在此电导率分布的计算电压Ui(σ)与测量电压Vi足够接近,即(Vi-Ui(σ))(i=1, 2, …, N)达到最小,即:
| $ E(\sigma)=\sum\limits_{i=1}^{N}| | V_{i}-U_{i}(\sigma)| |^{2}=\sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N}\left(V_{i j}-U_{i j}(\sigma)\right)^{2}, $ | (5) |
式中:E(σ)是电导率分布σ的函数;vij是第i次激励第j次测量得到的测量电压;Uij(σ)是在电导率分布为σ时由ERT正运算得到第i次激励第j次计算电压;N是电极数量。
寻找电导率分布σ时,使E(σ)达到最小,可令其偏导数为零,即
| $ {F_m}\left( \sigma \right) = \frac{{\partial E\left( \sigma \right)}}{{\partial {\sigma _m}}} = - 2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left( {{V_{ij}} - {U_{ij}}\left( \sigma \right)} \right)} } \frac{{\partial {U_{ij}}\left( \sigma \right)}}{{\partial {\sigma _m}}} = 0,\left( {m = 1,2, \cdots ,M} \right)。$ | (6) |
根据牛顿迭代法,有
| $ \sigma^{(k+1)}=\sigma^{(k)}-\left[\boldsymbol{J}\left(\sigma^{(k)}\right)\right]^{-1} \cdot F\left(\sigma^{(k)}\right),(k=0,1, \cdots), $ | (7) |
式中:k为迭代次数,一直到满足精度要求为止;J(σk)为雅克比矩阵,计算公式为
| $ {J_{n,m}}\left( {{\sigma ^{\left( k \right)}}} \right) = \frac{{\partial {F_N}\left( {{\sigma ^{\left( k \right)}}} \right)}}{{\partial {\sigma _m}}},\left( {n,m = 1,2, \cdots ,M} \right)。$ | (8) |
以上是ERT正问题和反问题的数学表示,反问题求解的关键是尽量找到较好的、与真实电导率分布相近的初值σ(k)。
2 NCRM算法图像重构原理当采用牛顿类算法计算时,如果初始电导率分布接近真实电导率分布,那么迭代次数就会减少很多。NOSER方法[12]用整个区域的平均电导率作为迭代的初值,仅通过一次迭代来实现ERT成像,结果虽不精确,但能从重建电图像中得到场域内目标的位置和大致尺寸,可实现快速成像。采用的NCRM算法在此基础上,利用已知的先验条件来多次调整初值,以获得更为准确的结果,由于被测物体内电导率分布未知,初值仍是假设场域内电阻率均匀分布,计算出第一次的初值X1,即X1=c(1, 1, …, 1)T, 设l(0)=(1, 1, …, 1)T,向量l(0)为所有元素等于1的单位向量,计第k次迭代l(k)。c的大小利用最小二乘法确定,代入E(σ)中求得
| $ E\left( {c{\mathit{\boldsymbol{l}}^{(k)}}} \right) = \sum\limits_{i = 1}^N | |{V_i} - {U_i}\left( {c{\mathit{\boldsymbol{l}}^{(k)}}} \right)|{|^2} = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{\left( {{V_{ij}} - {U_{ij}}\left( {c{\mathit{\boldsymbol{l}}^{(k)}}} \right)} \right)}^2}} } , $ | (9) |
式中:c为初始电导率分布中基体的电导率; l(k)为第k次迭代时对单位向量l(0)的修正向量;Vi为相邻电极上的测量电压值;Ui(cl(k))为利用有限元方法计算的相邻电极电压值; c为常数,可转换为Uij(cl(k))=cUij(l(k)),求得c值为
| $ c = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left( {{V_{ij}}{U_{ij}}\left( {{\mathit{\boldsymbol{l}}^{(k)}}} \right)} \right)} } /\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{\left( {{U_{ij}}\left( {{\mathit{\boldsymbol{l}}^{(k)}}} \right)} \right)}^2}} } ,{(i,j = 1,2, \cdots ,N)}。$ | (10) |
利用式(10)求解系数c,将X1=c(1, 1, …, 1)T作为初值带入方程(7)求得近似电导率分布Y1=(σ1(1), σ2(1), …, σm(1))T,同时也获得第一次重构图像,由结果可以确定最有可能是缺陷的位置(单元),但伪影较多,原因是均匀分布的电导率与实际电导率分布相差较大,没有很好地满足牛顿法对初值的要求。从实验结果看,缺陷的识别范围也明显大于实际尺寸,缺陷的中心位置可由此判定,试验证明中心位置与实际缺陷中心位置也基本一致。以该近似电导率分布Y1为基础,NCRM算法将混凝土基体及缺陷的电导率(σc、σf)作为先验信息,依据第一次重构图像确定的缺陷中心位置,将混凝土电导率σc和缺陷电导率σf作为先验条件代入算法中,调整分布向量l(0)为l(1),即由第一次的均匀分布l(0)=(1, 1, …, 1, …, 1)T调整为l(k)=(1, 1, …,
需要指出的是,如果测量电压不含噪音,是理想的数据源时,由于有严格的数学推演,采用文中方法可基本消除伪影,获得数学上最优, 并与实际相符的反运算结果。该算法原理也适用于多目标成像,如试件中含有多种缺陷(如孔洞、裂缝或其他异物等),σf即该缺陷的测量电导率值,将
为对比施加约束前后重构图像性能指标,文中拟采用相对误差及相关系数进行量化评价。研究中混凝土基体电导率以实测值作为先验条件,所以,在图像指标评定中,试件真实电导率可假设为缺陷位置电导率为0 ms/cm,其余部分为均匀基体,电导率为实测值。因实验中试件采用的是细集料,均匀性较高,所以假设的真实电导率分布具有参考价值。
相对误差:
| $ R_{\mathrm{E}}=\frac{\left\|x^{*}-x\right\|}{\left\|x^{*}\right\|_{2}}, $ | (11) |
相关系数:
| $ C_{\mathrm{C}}=\frac{\sum\nolimits_{i}^{N}\left(x_{i}-\overline{x}\right)\left(x_{i}^{*}-\overline{x}^{*}\right)}{\left\|x_{i}-\overline{x}\right\|_{2}\left\|x_{i}^{*}-\overline{x}^{*}\right\|_{2}}, $ | (12) |
式中:x为电导率分布测试结果;x*为与测试结果对应的真实电导率分布(假设值);“-”符号表示平均值。相对误差越小、相关系数越高则成像质量越好。
3 实验材料与方法实际混凝土检测中,由于模型误差、接触阻抗、测量误差是不可避免的,输入的测量电压一定含有噪音数据。为验证NCRM约束算法的可行性和实用性,文中采用预设孔洞的圆盘形水泥试件模拟混凝土缺陷。在重构算法迭代过程中,利用缺陷与混凝土电导率的比值作为先验条件,该缺陷为孔洞,其电导率趋近于0,计算时直接采用σf=0作为先验条件干预反运算的迭代过程,即可获得较为理想的重构图像。
3.1 试样制作水泥砂浆试件的材料为P42.5普通硅酸盐水泥和标准砂(粒径范围0.25~0.65 mm, 密度2.59 g/cm3),其中,水灰比为0.5。实验中共有2组试件,如图 1所示。第1组试件为圆盘形试件,直径10 cm,高2 cm,分别预设1个和2个直径为9 mm的圆孔,用于模拟混凝土缺陷的电阻成像检测实验。第2组试件为方块形试件,尺寸为5 cm×5 cm×2 cm,用于检测混凝土电导率,为电阻成像检测试验提供先验信息。2组试件采用同种配比同时浇筑,在相同条件下养护。

|
图 1 水泥砂浆试件 Fig. 1 Cement mortar specimen |
电阻层析成像系统主要由电极组件、电流源及数据采集系统、数据处理系统组成。文中采用自行搭建的电阻成像系统,如图 2所示。硬件部分包括:①计算机(包含数据处理和成像算法程序);②可编程控制转换开关;③电流源(美国吉时利Model 6221,能够为各种元件和材料的交流特征分析提供2 pA~100 mA的交流电流源);④电压采集仪(安捷伦34 970 A);⑤电极夹具。软件部分是基于Matlab环境下自编译的NCRM约束算法程序。工作原理为注入激励电流,用可编程控制转换开关实现相邻激励模式[13],计算机通过接口将指令传达给控制开关和电压采集仪,控制开关执行指令从16个电极中选择激励电极对,同时电压采集仪测量其他电极对电压并将电压测量值返回计算机作为图像重建的原始数据。

|
图 2 电阻成像系统 Fig. 2 Experimental setup of ERT system |
因混凝土表面粗糙且坚硬,为保证电压测量精度,在电极接触方面尤其重要。考虑混凝土表面特性,自制电极夹具可有效减小电极之间的接触阻抗差。每个电极端部用导电泡沫(导电布包裹泡沫),导向杆采用激光钻孔精确定位(见图 2),通过弹簧施加压力,使导电泡沫与混凝土试件表面接触良好并受力均匀。
4 实验与结果分析 4.1 试件电阻检测试验NCRM约束算法利用了缺陷电导率及混凝土电导率范围的先验信息,试验中的缺陷为孔洞,室内环境下空气电导率接近零,在计算中缺陷电导率选取为σf=0 ms/cm。混凝土电导率采用LCR精密电桥(Applent AT2818)测得,如图 3所示。

|
图 3 试件电阻抗测量 Fig. 3 Impedance measurement of the specimen |
电阻层析成像中交流电频率需尽可能低,以避免由于连接到测量单元的电缆过长而产生的电极电感效应,另外,频率必须足够高,以避免电极极化效应。对于电阻成像来说,当相位角最小时,电阻抗虚部最小,对应的交流电频率最为合适。将试件从标准养护箱中取出置于实验室12 h,实验室环境为23 ℃,相对湿度70%,此时,试件中含水率较高,电阻较干燥状态小,有利于验证NCRM约束算法的可行性。利用LCR仪器检测试件电阻抗时采用1~300 kHz的交流电压,检测结果如表 1所示,根据相位角的大小,采用激励电流频率为50 kHz。实验测得电阻抗为4.082 kΩ,相位角8.48°,电阻为4.037 kΩ,根据试件尺寸计算其电导率为σc=0.123 ms/cm。
| 表 1 试件电阻抗测量 Table 1 Impedance of cement mortar specimen |
与电阻抗测量试件一致,试件从标准养护箱中拿出来后置于室内环境下12 h后开始试验,室内湿度70%,温度23 ℃,实验中电极布置方式如图 4(a)所示。重构成像在Matlab平台上进行,有限元模型如图 4所示。单元数量256个,节点数145,16个电极均匀分布在试件边缘。

|
图 4 有限元模型 Fig. 4 Finite element model |
实验采用直径为10 cm的混凝土试件,设置了1个直径为9 mm的空心孔来模拟单个缺陷(见图 4(a)),设置2个直径为9 mm的空心孔来模拟多个缺陷(见图 4(b)),将前面测得的混凝土试件电导率(0.123 ms/cm)作为先验信息,得到缺陷与混凝土机体的电导率比值
|
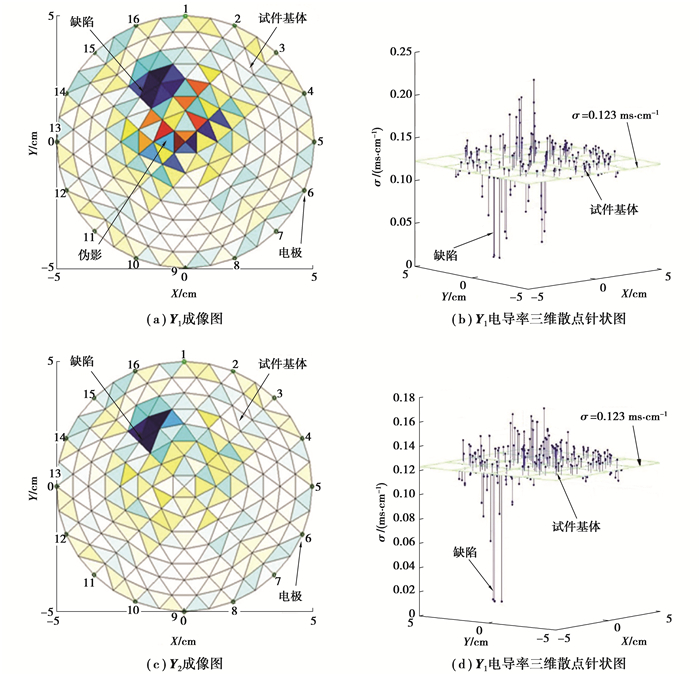
图 5 NCRM算法计算结果(单孔缺陷) Fig. 5 The result of experimental elements'conductivity by NCRM (one flaw) |
图 5为NCRM算法进行试样缺陷检测的2次计算结果Y1和Y2的成像图和电导率散点图。图 5(a)和图 5(b)为Y1的结果,图 5(c)和图 5(d)为Y2的结果。当采用均匀电导率分布为初值计算时,Y1成像图有较多的伪影,但可以准确定位缺陷的中心位置,由对应的图 5(b)针状图可以看出,反运算后电导率的分布呈阶梯状逐渐变化,虽可以定位缺陷位置,但无法分辨缺陷与基体的边界,也就无法判断缺陷的大小程度、分布范围;当对初值X1进行约束一次后,计算结果Y2成像图明显减少了伪影,显示的缺陷位置集中分布在实际孔洞处,对应针状图(图 5(d))可以看出,基体与缺陷的电导率呈大致的二值性,梯度渐变的趋势减弱,反映在成像图(见图 5(c))上即出现了更符合真实情况的较为锐利的边界过渡。对于单目标缺陷检测,仅迭代2次即可获得较为满意的结果。
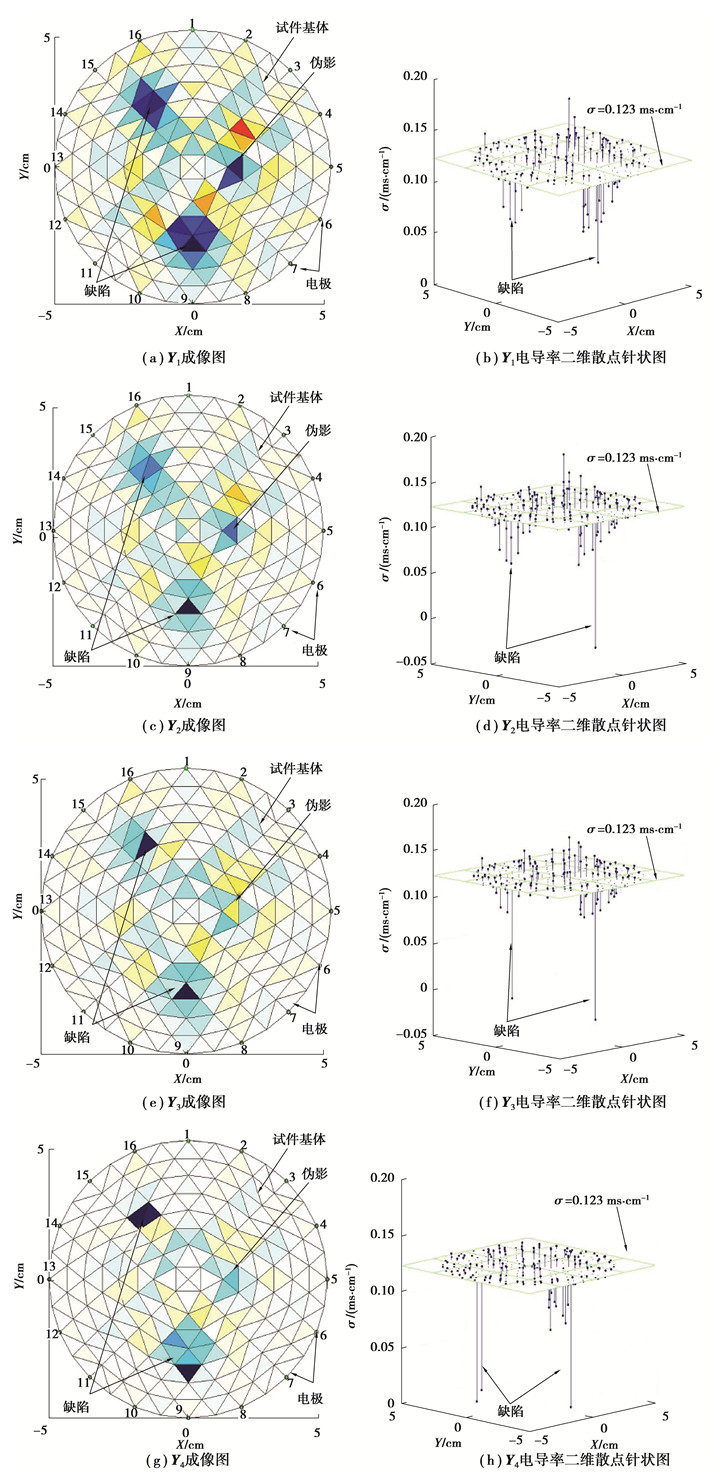
图 6为NCRM算法进行试样缺陷检测的4次计算结果Y1,Y2,Y3及Y4的成像图和电导率散点图。图 6(a)、图 6(c)、图 6(e)、图 6(g)为电导率重构图像,图 6(b)、图 6(d)、图 6(f)、图 6(h)为电导率二维散点图。当采用均匀电导率分布为初值计算时,Y1成像图有较多的伪影,如图 6(a)所示,但可以准确定位缺陷的中心位置,由对应的图 6(a)针状图可以看出,逆运算后电导率的分布呈阶梯状逐渐变化,虽可以定位缺陷位置,但无法分辨缺陷与基体的边界,也就无法判断缺陷的大小程度、分布范围;对初值X依次进行3次约束后,可以看到,计算结果Y2,Y3及Y4成像图的伪影成递减状态,显示的缺陷位置集中分布在实际孔洞处,虽然重构得到的缺陷中心与实际有一定的偏差,但是相对于不加约束前的重构图像,成像质量有了明显的改善。同样,从对应图 6(d)、图 6(f)、图 6(h)可以看出,基体与缺陷的电导率呈大致的二值性,梯度渐变的趋势减弱,反映在成像图上即出现了更符合真实情况的较为锐利的边界过渡。对于2个目标缺陷检测,经过3次迭代可获得较为满意的结果。
|
图 6 NCRM算法计算结果(两孔缺陷) Fig. 6 The result of experimental elements'conductivity by NCRM(two flaws) |
按照式(11)和式(12)分别计算2组实验每次迭代计算后的相对误差和相关系数,结果如表 2和表 3所示。
| 表 2 重构图像评价指标(单孔) Table 2 Quality evaluation parameters for reconstructed image (one flaw) |
| 表 3 重构图像评价指标(两孔) Table 3 Quality evaluation parameters for reconstructed image (two flaws) |
由表 2和表 3可以看出,施加约束后,电导率分布重构图像的相对误差明显减小,单孔缺陷施加1次约束就得到了较好的成像结果。两孔缺陷在施加3次约束后,相对误差的减小较为显著,图像相关系数也明显提高,说明NCRM约束方法可以用于多目标缺陷的检测。通过实验, 验证了文中提出的NCRM约束算法相对传统算法能够更好地进行混凝土试件缺陷检测。计算结果仍含有部分伪影,主要原因有:
1) 原始测量数据无法完全消除噪音,因为测量误差及接触阻抗在各电极间的差异客观存在;
2) 数值建模采用三角形单元,单元划分是任意的,不能事先考虑缺陷的位置和范围,并且有限元分析中假设同一单元内的电导率是常数,不可避免地出现某些单元同时跨越了实际被测对象的基体和缺陷,而这些单元的电导率应该同时包含两者信息,这些系统误差也会影响成像精度;
3) 逆运算并不是单元越密效果越好,对于16电极系统,独立有效的测量数据为104个,通过这些独立测量数据反演模型中各个单元的电导率本身就是一个欠定问题,单元数越大,问题欠定性越强,结果越不可控。
因此,NCRM算法增加的约束条件即为降低反问题病态性,相当于增加了一些有效数据给逆运算系统。
5 结论对于混凝土检测来说,由于ERT传统算法偏重于解决稳定性问题,不能很好地反映机体与缺陷之间锐利的边界,使得重建图像与真实情况有较大差别。NCRM算法利用先验信息对ERT反问题进行优化,重建结果表明该方法是有效的,可以降低伪影,提高目标位置的定位精度,迭代次数少,计算速度快。
该算法增加了约束条件来干预反演过程,需要事先获知被测对象及缺陷的电导率范围,且只适用于缺陷与基体间有较明显的电导率突变现象的情况。因此,文中NCRM算法用于混凝土孔洞、裂缝的ERT检测效果较好。对于混凝土渗水检测,因其内部电导率在干湿界面处是渐变的,与约束条件不符,故不能用此算法求解。
| [1] |
王满丰, 刘福生. 超声法检测混凝土缺陷技术的发展概况[J]. 黑龙江交通科技, 2008, 31(7): 70-70. WANG Manfeng, LIU Fusheng. Development of ultrasonic testing of concrete defects[J]. Communications Science and Technology Heilongjiang, 2008, 31(7): 70-70. (in Chinese) DOI:10.3969/j.issn.1008-3383.2008.07.046 |
| [2] |
Molyneaux T C K, Millard S G, Bungey J H, et al. Radar assessment of structural concrete using neuralnetworks[J]. Ndt& E International, 1995, 28(5): 281-288. |
| [3] |
黄莉.基于红外热像的碳纤维混凝土损伤分析与研究[D].武汉: 武汉理工大学, 2005. HUANG Li. Research on damage of carbon fiber reinforced concrete based on infrared thermography[D]. Wuhan: Wuhan University of Technology, 2005.(in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10497-2005127973.htm |
| [4] |
Daily W, Ramirez A, Binley A, et al. Electrical resistance tomography[J]. The Leading Edge, 2004, 23(5): 409-512. |
| [5] |
Zhou X Y, Bhat P, Ouyang H, et al. Localization of cracks in cementitious materials under uniaxial tension with electrical resistance tomography[J]. Construction and Building Materials, 2017, 138: 45-55. DOI:10.1016/j.conbuildmat.2017.01.128 |
| [6] |
Borcea L. Electrical impedance tomography[J]. Inverse Problems, 2002, 18: 99-136. DOI:10.1088/0266-5611/18/6/201 |
| [7] |
陈晓艳, 张静. 采用阈值修正法改善电阻抗图像质量[J]. 中国生物医学工程学报, 2011, 30(4): 481-486. CHEN Xiaoyan, ZHANG Jing. Using threshold correction method to improve the image quality of EIT[J]. Chinese Journal of Biomedical Engineering, 2011, 30(4): 481-486. (in Chinese) DOI:10.3969/j.issn.0258-8021.2011.04.001 |
| [8] |
董峰, 赵佳, 许燕斌, 等. 用于电阻层析成像的快速自适应硬阈值迭代算法[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(4): 305-310. DONG Feng, ZHAO Jia, XU Yanbin, et al. A fast adaptive iterative hard threshold algorithm for electrical resistance tomography[J]. Journal of Tianjin University(Science and Technology), 2015, 48(4): 305-310. (in Chinese) |
| [9] |
肖理庆. 一种改进牛顿-拉夫逊ERT绝对图像重建算法[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(8): 734-741. XIAO Liqing. A modified newton-raphson absolute image reconstruction algorithm for ERT[J]. Journal of Tianjin University(Science and Technology), 2015, 48(8): 734-741. (in Chinese) |
| [10] |
Cheney M, Isaacson D, Newell J C, et al. NOSER:An algorithm for solving the inverse conductivity problem[J]. International Journal of Imaging Systems and Technology, 1990, 2(2): 66-75. DOI:10.1002/(ISSN)1098-1098 |
| [11] |
徐桂芝, 李颖. 生物医学电阻抗成像技术[M]. 北京: 机械工业出版社, 2010. XU Guizhi, LI Ying. Electrical impedance tomography in biomedical engineering[M]. Beijing: China Machine Press, 2010. |
| [12] |
罗辞勇.基于快速牛顿一步误差重构的电阻抗成像算法和实验研究[D].重庆: 重庆大学, 2005. LUO Ciyong. Algorithm of electrical impedance tomography and experiment research based on fast newton's one-step error reconstructor[D]. Chongqing: Chongqing University, 2005.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-2005145199.htm |
| [13] |
Heikkinen L M, Vauhkonen M, Savolainen T, et al. Modelling of internal structures and electrodes in electrical process tomography[J]. Measurement Science and Technology, 2001, 12(8): 1012-1019. DOI:10.1088/0957-0233/12/8/304 |
 2019, Vol. 42
2019, Vol. 42


