b. 河北工程大学 土木工程学院, 河北 邯郸 056038
b. College of Civil Engineering, Hebei University of Engineering, Handan 056038, Hebei, P. R. China
群体智能算法具有简单性、分布式、鲁棒性好、扩展性和广泛的适用性等特点,在不存在集中控制并缺少局部信息和模型的情况下,为解决复杂分布式问题提供了思路。群体智能算法已经逐渐成为当前智能优化领域的研究热点。具有代表性的蚁群算法[1-2]、遗传算法[3-4]、粒子群算法[5-7]、人工蜂群算法[8-11]等,已被广泛应用于多个领域并被广大学者进行了大量的研究[12]。
海豚群算法(DSA, dolphin swarm algorithm)是浙江大学伍天骐教授[13]于2016年提出的一种新型的群体智能优化算法,该算法模拟海豚回声定位、信息交流、分工合作等生物特性和生活习性,通过搜索、呼叫、接收和捕食4个关键阶段实现海豚群算法的寻优。传统群体智能优化算法只是采用了前进式的解决方案,而海豚群算法利用回声定位,采取不同的策略,更易求得最优解。
海豚群算法作为一种新的算法,也存在着一定缺陷,如易陷入局部最优和早熟收敛。对此,李卫忠等[14]将混沌搜索策略引入海豚群算法以提高算法全局最优能力,其他学者也对其进行了改进[15-16]。文中针对算法易陷入局部最优和早熟收敛的缺陷,提出信息熵策略对算法进行改进。以信息熵的值表示算法搜索过程中的不确定性,控制路径的选择概率,通过算法的自适应调节调整搜索重点,将改进后的算法在结构优化设计中进行应用,为解决结构优化问题提供了新的思路和手段。
1 基本海豚群算法海豚群算法主要是通过模拟海豚实际捕食过程中所表现出的生物学特性和生活习性来实现的。在该算法中,海豚群通过搜索阶段、呼叫阶段、接收阶段和捕食阶段4个关键阶段完成捕食。分别模拟这4个阶段的行为,设计相应的搜索环节,通过迭代进而获得问题的解。
1.1 初始化在优化问题中,每一个海豚代表一个可行解。在D维解空间内,定义海豚在公式中简称为Xi=[x1, x2, …, xD]T(i=1, 2, …, N),即一个可行D维解,其中,N是海豚的数量,xj(j=1, 2, …, D)是i在第j维的取值。对于每个Xi(i=1, 2, …, N),有2个相应的变量Li(i=1, 2, …, N)和Ki(i=1, 2, …, N),其中,Li表示个体最优解,即Xi自身搜索找到的最优解;Ki表示领域最优解,即Xi自身或从其他海豚那里发现并比较后得到的最优解。在DSA算法中,适应度表示为E(X),越接近零越好。算法中共使用3种距离:Xi和Xj之间的距离Xi, j=||Xi-Xj||, i, j=1, 2, …, N, i≠j;Xi和Ki之间的距离YDKi=||Xi-Ki||, i=1, 2, …, N;Li和Ki之间的距离YDKLi=||Li-Kj||, i=1, 2, …, N。
1.2 关键阶段 1.2.1 搜索阶段在搜索阶段,每只海豚通过声波来搜索附近的区域。设Vi=[v1, v2, …, vD]T(i=1, 2, …, M)为个体i随机在M个方向发出的声波。其中,M是声音的数量,Vj(j=1, 2, …, D)是声音的方向属性。声音满足||Vi||=Vspeed(i=1, 2, …, M),其中,Vspeed是一个常量,代表声音的速度属性。设最大搜索时间为T1,则声波Vj在时间t搜索到的新解可定义为
| $ {X_{ijt}} = {X_i} + {V_{jt}}。$ | (1) |
适应度Eijt为
| $ E_{i j t}=E\left(X_{i t j}\right)。$ | (2) |
如果Eiab=minj=1, 2, …, M; t=1, 2, …, T1,Eijt=minj=1, 2, …, M; t=1, 2, …, T1,E(Xijt)认为Xiab为Xi的个体最优解,即Li=Xiab;如果E(Li) < E(Ki),以Li取代Ki;否则,Ki不变。
1.2.2 呼叫阶段在呼叫阶段,每个海豚都会发出声音,通知其他海豚其搜索结果,包括是否找到更好的解决方案,以及更好的解决方案的位置。
1.2.3 接收阶段其他海豚将接收到的最优解信息与自身最优解比较,选择较优的解作为领域最优解Ki。
在DSA中,交换过程(包括呼叫阶段和接收阶段)是由一个名为“传输时间矩阵”TTS的N×N阶矩阵来实现的。在TTS中,TTSij代表了声音从Xj到Xi的剩余时间。对于Ki,Kj和TTSij,如果E(Ki) < E(Kj),且
在捕食阶段,每只海豚需要计算环绕半径R2,根据已知信息确定海豚邻域最优解与捕食阶段后的位置之间的距离,得到一个新的位置。
2 基于信息熵的算法改进由于海豚群算法搜索阶段海豚搜索选择的不确定性,导致海豚群算法在迭代过程中易陷入局部最优和早熟收敛。针对该算法的缺陷,提出将信息熵引入算法搜索阶段的策略,提高搜索效率,最终实现算法的自适应调节。
2.1 信息熵信息熵为一个物理概念,最早是由克劳修斯在热力学中提出的,用以描述系统的状态。而后被引入多个领域,从而产生了玻尔兹曼熵、信息熵、概率测度熵等。其中,信息熵由Shannon将热力学熵引入信息论,是描述系统不确定性的一个重要概念[17-21]。
离散型随机变量的熵值为
信息熵具有以下性质[22]:①对称性:p1, p2, …, pn的顺序改变,熵值不变。即S(p1, p2, …, pn)=S(pn, pn-1, …, p1); ②非负性:S(p1, p2, …, pn)≫0。③可加性:相对独立的状态,其熵的和等于和的熵。④极值性:
由于海豚群算法搜索阶段具有不确定性,而信息熵本身可作为不确定性的一种度量,因此,将息熵引入算法,通过控制信息熵的值来控制海豚群搜索阶段选择概率,实现算法自适应调节的目的。
2.2 算法改进定义每个海豚的位置的概率分布值为
| $ p_{i}=E_{i} / \sum\limits_{i=1}^{N} E_{i},$ | (3) |
式中,Ei即为基本海豚群算法中的E(Ki)。
定义信息熵值为
| $ H\left(E_{i}\right)=-\sum\limits_{i=1}^{N} p_{i} \ln p_{i},$ | (4) |
式中,
在算法运行初期,各方向的搜索概率相同,信息熵值最大,但随着某方向搜索概率的增强,熵值逐渐减小,此时,如不加以控制,熵值将最终变为零,即最终只有一个方向搜索概率最大,被误认为是最终的解,造成早熟。
因此,引入
| $ \alpha=1-\left(H_{\max }-H\right) / 2 H_{\max },$ | (5) |
| $ \beta=\left(H_{\max }-H\right) / H_{\max },$ | (6) |
式中:α为最优解被选择的概率;β为允许适当小范围内搜索猎物的海豚占总海豚群的比例;Hmax为最大熵值。
将α,β引入(1)式和式(3)中,可以得到
| $ p_{i}=\beta E_{i} / \sum\limits_{i=1}^{n} E_{i},$ | (7) |
| $ X_{i j t}=X_{i}+\frac{V_{j}}{\alpha} t。$ | (8) |
在算法运行初期β较小,使海豚尽量均匀地分布于初始解空间,后期随着β增大,算法的局部搜索能力增强,可避免早熟收敛。对于α,在算法初期,α值较小,保证海豚尽可能地寻找最优解;后期随着熵值的变化而增大,缩小步长,提高搜索精度。
将该参数引入搜索阶段,由信息熵的变化控制参数α和β的大小,进而控制搜索过程,提高搜索效率,最终实现算法的自适应调节。改进的算法选择信息熵作为算法的终止标准,通过仿真实验确定,当信息熵的值H≪0.000 1时,算法结束,输出结果。
改进后的海豚群算法基本流程如下:
步骤1 初始化,确定海豚种群数量及D维空间海豚个体。
步骤2 搜索阶段海豚随机向M个方向发出声波。期间计算每个海豚适应度的熵、α和β值,更新α和β。通过式(7)和式(8)对最优猎物进行选择。并将信息熵的值设置为稍大于0的值作为选择的停机条件。
步骤3 联系阶段海豚通过呼叫将自身寻找的个体最优解向外传播,其他海豚则将收到的最优解信息同自身寻找的个体最优解比较,选择较好的解作为邻域最优解K。
步骤4 捕食阶段联系阶段完成后海豚个体根据邻域最优解K,更新自己的位置进行捕食。
对于每个海豚,已知信息包含自己的位置、个体最优解L、邻域最优解K、距离YDK和距离YDKL和表示搜索阶段的最大范围的搜索半径R1=T1×Vspeed。包围半径R2的计算和海豚位置的更新分为3种情况。下面以Xi(i=1, 2, …, N)为例来说明这3种情况。
1) 如果YDKi≪R1,即Xi的邻域最优解Ki在搜索范围内,如图 1所示。则将个体最优解Li视为Ki。
| $ {R_2} = \left( {1 - \frac{2}{e}} \right){Y_{{\rm{DK}}i}}, $ | (9) |
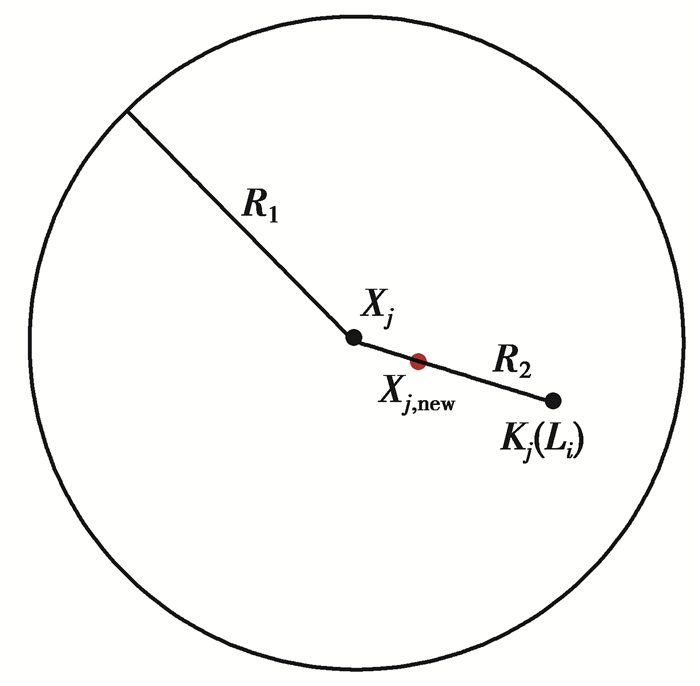
|
图 1 情况(1)中Xi移动的结果 Fig. 1 The result of Xi movement in case (1) |
式中,e是一个常数,称为“半径修正系数”,大于2,通常设为3或4。可知,R2逐渐收敛于零。
| $ {X_{i,{\rm{ new }}}} = {K_i} + \frac{{{X_i} - {K_i}}}{{{Y_{{\rm{DK}}i}}}}{R_2}, $ | (10) |
即Xi向Ki方向移动,并停止在离Ki距离为R2的位置。
2) 如果YDKi > R1, 并且YDKi≫YDKLi, 即邻域最优解Ki在搜寻范围之外,且Li比Ki更接近Xi,如图 2所示。
| $ {R_2} = \left( {1 - \frac{{\frac{{{Y_{{\rm{D}}{{\rm{K}}i}}}}}{{E\left( {{K_i}} \right)}} + \frac{{{Y_{{\rm{D}}{{\rm{K}}i}}} - {Y_{{\rm{DK}}{{\rm{L}}i}}}}}{{E\left( {{L_i}} \right)}}}}{{e \cdot {Y_{{\rm{DK}}i}}\frac{1}{{E\left( {{K_i}} \right)}}}}} \right){T_{{\rm{DK}}}}, $ | (11) |
| $ {X_{i,{\rm{new}}}} = {K_i} + \frac{{{Z_{{\rm{Random}}}}}}{{\left\| {{Z_{{\rm{Random}}}}} \right\|}}{R_2}, $ | (12) |
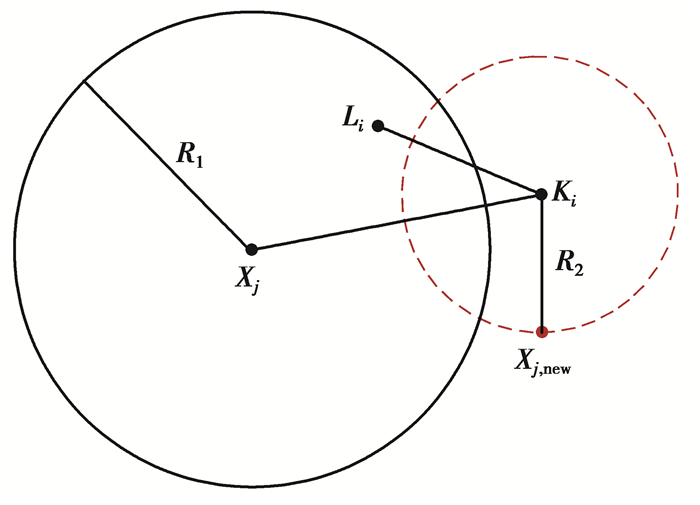
|
图 2 情况(2)中Xi移动的结果 Fig. 2 The result of Xi movement in case (2) |
即Xi移动到与Ki距离为R2的随机位置。
3) 如果YDKi > R1,且YDKi < YDKLi,即邻域最优解Ki在搜寻范围之外, 且Xi比Li更接近Ki,如图 3所示。
| $ {R_2} = \left( {1 - \frac{{\frac{{{Y_{{\rm{D}}{{\rm{K}}i}}}}}{{E\left( {{K_i}} \right)}} - \frac{{{Y_{{\rm{DKL}}i}} - {Y_{{\rm{DK}}i}}}}{{E\left( {{L_i}} \right)}}}}{{e \cdot {Y_{{\rm{DK}}i}}\frac{1}{{E\left( {{K_i}} \right)}}}}} \right){T_{{\rm{DK}}i}}, $ | (13) |
| $ {X_{i,{\rm{new}}}} = {K_i} + \frac{{{Z_{{\rm{Random}}}}}}{{\left\| {{Z_{{\rm{Random}}}}} \right\|}}{R_2}, $ | (14) |

|
图 3 情况(3)中Xi移动的结果 Fig. 3 The result of Xi movement in case (3) |
即Xi移动到距离Ki为R2的随机位置。
在Xi移动到Xi, new的位置之后,比较Xi, new和Ki的适应度,如果:
| $ E\left( {{X_{i,{\rm{new}}}}} \right) < E\left( {{X_i}} \right), $ | (15) |
则用Xi, new替换Ki,即Ki=Xi, new; 否则,Ki不变。海豚进入新一轮搜索,直到满足终止条件。
图 4给出了改进后的算法流程图。

|
图 4 基于信息熵的改进海豚群算法流程图 Fig. 4 Flow chart of improved dolphin algorithm based on information entropy |
为了验证改进算法的有效性,选择3个标准测试函数来测试改进海豚群算法的性能。另外,选取TSP问题进行仿真实验,并与海豚群算法和蚁群算法进行了比较。
3.1 函数测试选择Rosenbrock函数、Sphere函数、Rastrigin函数进行测试。
第1个是Rosenbrock函数,如图 5所示。
| $ \begin{array}{*{20}{c}} {{f_1}\left( x \right) = 100{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_1} - 1} \right)}^2},}\\ { - 5.12 \ll {x_i} \ll 5.12。} \end{array} $ | (16) |

|
图 5 Rosenbrock函数 Fig. 5 Rosenbrock function |
第2个是Sphere函数:
| $ \begin{array}{*{20}{c}} {{f_2}(x) = \sum\limits_{i = 1}^n {x_i^2} },\\ { - 2.048 \ll {x_i} \ll 2.048。} \end{array} $ | (17) |
第3个是Rastrigin函数
| $ \begin{array}{*{20}{c}} {{f_3}(x) = \sum\limits_{i = 1}^n {\left( {x_i^2 - 10\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right) + 10} \right)} ,}\\ { - 5.12 \ll {x_i} \ll 5.12}。\end{array} $ | (18) |
海豚群算法的基本控制参数:T1=3,T2=100,VSpeed=1,M=3,e=4,A=5。随机初始化,当信息熵值H≪0.000 1时,算法结束。经过30次运行后取得平均值,结果见表 1所示。
| 表 1 函数运算结果(平均值)及比较 Table 1 The result of function operation (average value) and comparison |
由表 1可以看出,基于信息熵的改进海豚群算法在标准测试函数上的表现优于标准海豚群算法。该改进算法是可行且有效的。
3.2 TSP问题旅行商问题(TSP, traveling salesman problem)是路径规划和组合优化领域中最著名的NP-hard问题。文中对TSP Chn31问题、bayes29问题、d1291问题、d2103w问题、fl3795问题和fnl14461问题进行了计算,并将其与基本海豚群算法进行比较。参数设置同上,最大迭代次数200。计算结果见表 2。
| 表 2 算法性能对比实验结果 Table 2 Experimental results of algorithm performance comparison |
由表 2可知,改进后的海豚群算法结果优于其他算法,改进后的海豚群算法求得的解已非常接近最优解。
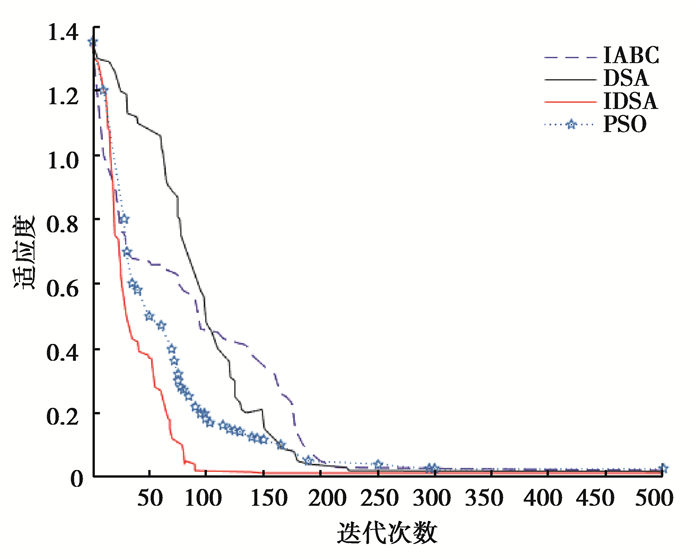
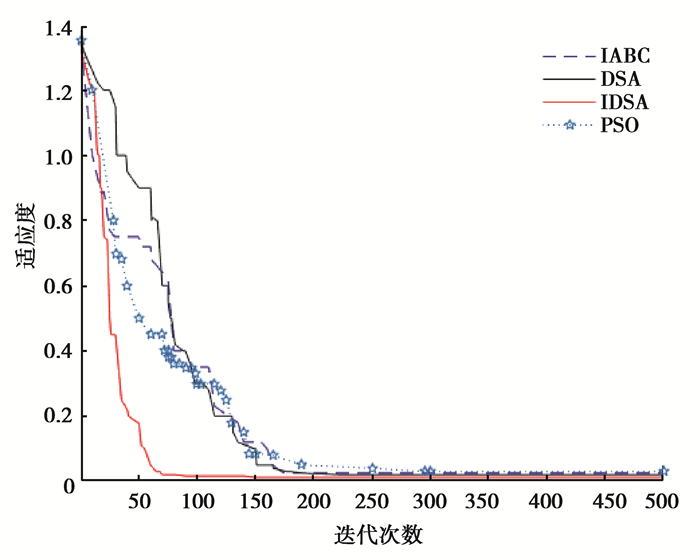
3.3 算法迭代曲线对比为了进一步测试改进算法的性能,更加直观地比较算法的运行时间,图 6~图 8是改进的海豚群算法(IDSA, improved dolphin swarm algorithm)、基本海豚群算法(DSA)、粒子群算法(PSO, particle swarm optimization)及基于信息熵的改进人工蜂群算法[22](IABC, improved artificial bee colony algorithm)在上述3种基准函数下的收敛曲线图。算法采用同上的参数设置,500次迭代,运行30次并取得最后结果的平均值。
|
图 6 算法在Sphere函数下的迭代曲线 Fig. 6 The iteration curves under Sphere function |

|
图 7 算法在Rosenbrock函数下的迭代曲线 Fig. 7 The iteration curves under Rosenbrock function |
|
图 8 算法在Rastrigin函数下的迭代曲线 Fig. 8 The iteration curves underRastrigin function |
通过迭代曲线的对比可以看出,在大多数情况下,IDSA可以比其他3种算法更快地达到最优解,即搜索速度更快,所用时间更少。并且IDSA求得的最优解更接近函数理想最优解,收敛精度比其他算法更高。上述结果证明了IDSA的搜索策略更加良好稳定,改进的算法是可行有效的。
4 改进的算法对桁架结构的优化 4.1 桁架结构优化模型 4.1.1 优化模型以截面积为设计变量的桁架优化模型问题可以描述为
| $ \begin{array}{*{20}{c}} {\min F = W\left( x \right),}\\ {{\rm{s}}.\;{\rm{t}}.{g_i}\left( x \right) \le 0,i = 1,2, \cdots ,m,} \end{array} $ | (19) |
式中:gi(x)为约束函数;m为约束个数。
4.1.2 目标函数| $ W\left( A \right) = \sum\limits_{i = 1}^n {\rho {A_i}{L_i}} , $ | (20) |
式中:W(A)为结构的重量;Ai为第i根杆件的截面积;Li为第i根杆件长度;ρ为材料密度;n为设计变量个数。
4.1.3 约束条件各杆必须满足强度、刚度、稳定性及截面尺寸的要求,约束条件如下
| $ \begin{array}{*{20}{c}} {\frac{{{\sigma _i}}}{{\left[ \sigma \right]}} - 1 \le 0,}\\ {\frac{{{\mu _j}}}{{{\mu _{\max }}}} - 1 \le 0,}\\ {{A_{\min }} \le {A_i} \le {A_{\max }}。} \end{array} $ | (21) |
式中:σ为第i杆的轴向正应力;[σ]为材料的许用应力;μj为节点j的位移;μmax为节点j的许用位移;Amin、Amax分别为杆件截面的上限、下限。
4.2 算例分析建立25杆空间桁架结构模型(见图 9),荷载工况见表 3,应力约束[-275.8, 275.8]MPa, 材料密度ρ=2 678 kg/m3, 弹性模量E=68 950 MPa, 1、2节点的最大竖向位移dmax=8.889 mm, L=635 mm。

|
图 9 25杆空间桁架结构示意图 Fig. 9 25-bar space truss structure diagram |
| 表 3 25杆空间桁架工况 Table 3 Load cases of the 25-bar spatial truss structure |
| 表 4 25杆空间桁架分类 Table 4 The classification of the 25-bar spatial truss structure |
| 表 5 25杆空间桁架优化结果比较 Table 5 Comparison of optimal designs for the 25-bar spatial truss structure |
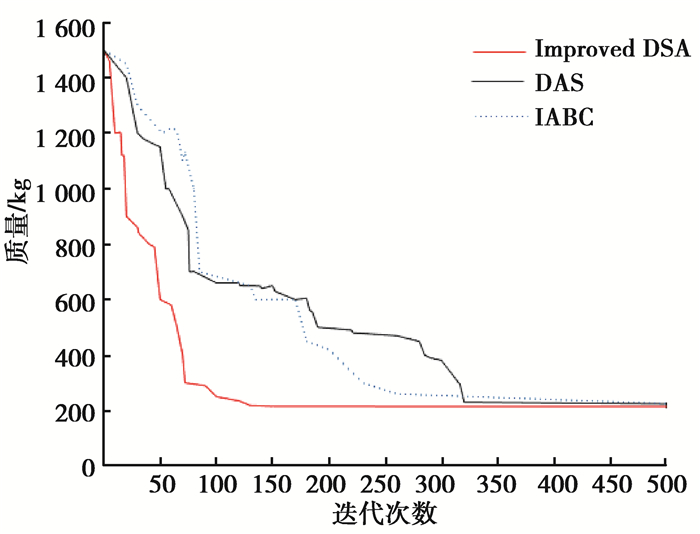
由于该桁架结构模型为经典算例模型,通过比较可以看出,改进算法在该算例中求解速度和求解精度表现更加良好,能够更快速地求解出最优解,达到节省时间和材料的目的。
采用Matlab软件得到改进的海豚群算法对桁架优化的迭代曲线(图 10),并与基本海豚群算法和改进信息熵的人工蜂群算法[22]对比,可以看出改进的海豚群算法有较高的收敛速度和收敛精度。
|
图 10 改进的海豚群算法迭代曲线示意图 Fig. 10 Iterative curve diagram of improved dolphin swarm algorithms |
针对基本海豚群算法易陷入局部最优和早熟收敛的缺点,提出一种基于信息熵的改进海豚群算法。该算法在迭代过程中,利用信息熵对不确定的度量,在海豚搜索阶段引入信息熵和变量α和β控制海豚搜索阶段,有效避免了算法陷入局部最优和早熟的缺陷。通过仿真实验和方法对比,验证了文中提出的改进海豚群算法是可行、有效的,将其应用于桁架结构优化设计中,经过更少的迭代次数求得目标函数值,达到结果重量最轻的目的。
| [1] |
Dorigo M, Maniezzo V, Colorni A. Ant system:optimization by a colony of cooperating agents[J]. IEEE Transactionson Systems, Man andCybernetics, Part B (Cybernetics), 1996, 26(1): 29-41. DOI:10.1109/3477.484436 |
| [2] |
Deepa O, Senthilkumar A. Swarm intelligence from natural to artificial systems:ant colony optimization[J]. International Journal on Applications of Graph Theory in Wireless Ad Hoc Networks and Sensor Networks, 2016, 8(1): 9-17. DOI:10.5121/jgraphhoc |
| [3] |
Reid C R, Latty T. Collective behaviour and swarm intelligence in slime moulds[J]. FEMS Microbiology Reviews, 2016, 40(6): 798-806. DOI:10.1093/femsre/fuw033 |
| [4] |
张金梦, 刘慧君. 遗传算法优化BP神经网络的泊车位数量预测[J]. 重庆大学学报, 2018, 41(3): 76-81. ZHANG Jinmeng, LIU Huijun. Prediction of parking space based on BP neural network optimized by genetic algorithm[J]. Journal of Chongqing University, 2018, 41(3): 76-81. (in Chinese) |
| [5] |
Strasser S, Goodman R, Sheppard J. A new discrete particle swarm optimization algorithm[C]. Genetic and Evolutionary Computation Conference, Denver, CO, 2016: 53-60. http://www.sciencedirect.com/science/article/pii/S0020025514009657
|
| [6] |
Rahmat-Samii Y, Gies D, Robinson J. Particle swarm optimization (PSO):A novel paradigm for antenna designs[J]. URSI Radio Science Bulletin, 2003(306): 14-22. |
| [7] |
Wang G G, Gandomi A H, Alavi A H, et al. A hybrid method based on krill herd and quantum-behaved particle swarm optimization[J]. Neural Computing & Applications, 2016, 27(4): 989-1006. |
| [8] |
Renaudineau H, Donatantonio F, Fontchastagner J, et al. A PSO-based global MPPT technique for distributed PV power generation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1047-1058. DOI:10.1109/TIE.2014.2336600 |
| [9] |
Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report-TR06, Erciyes University, Turkey, 2005.
|
| [10] |
Akay B, Karaboga D. A modified Artificial Bee Colony algorithm for real-parameter optimization[J]. Information Sciences, 2012, 192: 120-142. DOI:10.1016/j.ins.2010.07.015 |
| [11] |
郭一君, 周杰, 王时龙, 等. 基于改进人工蜂群算法和极限学习机的刀具磨损监测[J]. 重庆大学学报, 2018, 41(6): 1-8. GUO Yijun, ZHOU Jie, WANG Shilong, et al. Tool wearmonitoring based on improved artificial bee colony algorithm and extreme learning machine[J]. Journal of Chongqing University (Natural Science Edition), 2018, 41(6): 1-8. (in Chinese) |
| [12] |
Mavrovouniotis M, Li C, Yang S. A survey of swarm intelligence for dynamic optimization:algorithms and applications[J]. Swarm & Evolutionary Computation, 2017, 33: 1-17. |
| [13] |
Wu T Q, Yao M, Yang J H. Dolphin swarm algorithm[J]. Frontiers of Information Technology & Electronic Engineering, 2016, 17(8): 717-729. |
| [14] |
李卫忠, 李志鹏, 江洋, 等. 混沌海豚群优化灰色神经网络的空中目标威胁评估[J]. 控制与决策, 2018, 33(11): 1997-2003. LI Weizhong, LI Zhipeng, JIANG Yang, et al. Air-targets threat assessment using grey neural network optimized by chaotic dolphin swarm algorithm[J]. Control and Decision, 2018, 33(11): 1997-2003. (in Chinese) |
| [15] |
Kaveh A, Farhoudi N. A new optimization method:dolphin echolocation[J]. Advances in Engineering Software, 2013, 59(5): 53-70. |
| [16] |
Wang Y, Wang T, Zhang C Z, et al. A new stochastic optimization approach:dolphin swarm optimization algorithm[J]. International Journal of Computational Intelligence and Applications, 2016, 15(2): 1650011. DOI:10.1142/S1469026816500115 |
| [17] |
Shannon C E. Prediction and entropy of printed English[J]. Bell System Technical Journal, 1951, 30(1): 50-64. DOI:10.1002/bltj.1951.30.issue-1 |
| [18] |
Arieh Ben-Naim. Entropy, Shannon's measure of information and boltzmann'sh-theorem[J]. Entropy, 2017, 19(2): 48. DOI:10.3390/e19020048 |
| [19] |
Nemzer L R. Shannon information entropy in the canonical genetic code[J]. Journal of Theoretical Biology, 2017, 415: 158-170. DOI:10.1016/j.jtbi.2016.12.010 |
| [20] |
Wang H, Yao X. Objective reduction based on nonlinear correlation information entropy[J]. Soft Computing, 2016, 20(6): 2393-2407. DOI:10.1007/s00500-015-1648-y |
| [21] |
Ye G, Pan C, Huang X, et al. A chaotic image encryption algorithm based on information entropy[J]. International Journal of Bifurcation & Chaos, 2018, 28(1): 1850010. |
| [22] |
李彦苍, 彭扬. 基于信息熵的改进人工蜂群算法[J]. 控制与决策, 2015, 30(6): 1121-1125. LI Yancang, PENG Yang. Improved artificial bee colony algorithm based on information entropy[J]. Control and Decision, 2015, 30(6): 1121-1125. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

