在工业控制中,常常会伴随大量的模拟量数据采样。模拟量采样时,由于待采量本身、传感器和传输过程中的外界干扰,特别是非稳态干扰信号等因素的影响,采样值中通常含有各种周期性和非周期性的噪声和干扰。为得到稳定、准确的测量值以便实现精确控制,必须消除被测信号中的各种噪声和干扰。在广泛使用的工业控制器S7-1200序列PLC(programmable logic controller)中,可通过启用PLC自身AI(analogy input)端口的滤波器功能,再配合另行设计的数字滤波,也可借助外部滤波设备以最大限度去除噪声和干扰。
数字滤波器具有以下优点:精度与准确度高;可编程性与适应性好;相位与延迟控制精确;鲁棒性好;与其他数字子系统兼容性好;成本低、功耗小;可靠性、可复用性好[1]。常用的数字滤波算法主要有算术平均值滤波、加权平均值滤波[2-3]、滑动平均值滤波[4]、中值滤波[5-7]、程序判断滤波等。对于PLC中的AD(analog to digital)采样滤波需要结构简单、高效、可靠的滤波算法,其中算术平均值滤波、加权平均值滤波、中值滤波可适用。中值滤波算法最为简便,但可靠性不如前两者;算术平均值滤波较加权平均值滤波算法计算步骤少,但滤波结果可靠性不如后者。为降低成本,提高控制精度,一种高效、简单的数字滤波器设计在工业应用中是非常必要的。
1 适用于PLC的典型数字滤波器数字滤波器主要有两大类:一类是有限冲激响应(FIR, finite impulse response)滤波器;另一类是无限冲激响应(IIR, infinite impulse response)滤波器[8]。其中,FIR滤波器结构简单,在许多情况下是最为重要的数字滤波器。常见的FIR滤波器设计方法有窗函数法[9-10]、最小均方(LMS, least mean square)法[10-13]、等波纹设计法[14-15]等。
S7-1200属于小型PLC,是使用较为广泛的工业控制器,其编程语言包括梯形图(LAD, ladderlogic programming language)、函数块图(FBD, function block diagram)、结构化控制语言(SCL, structured control language)3种。其中,LAD是图像型描述性语言,形象而直观,类似于继电器控制原理,易于掌握和开发[16];函数块图FBD使用类似于数字电路的图形逻辑符号来表示控制逻辑,鲜有人使用;结构化控制语言SCL是一种基于Pascal的高级编程语言,尤其适用于数据管理、过程优化配方管理、数学计算等。
文中需在一定时间内连续采样,不宜使用梯形图编程。采用Siemens STEP 7编程软件中的SCL语言对西门子1200PLC进行编程,可实现一定时间内连续采样,并通过滤波计算后输出,使用更灵活、方便。
对于模拟信号,经过采样和A/D变换后得到的数字序列,数据处理速率要求很高,因此,需要结构简单、高效的数字滤波器。
以下几种数字滤波器设计方法适用于PLC。
1.1 窗函数设计法窗函数法亦称傅里叶级数法,属于一种在时域设计FIR数字滤波器的方法,是最简单最普遍使用的方法。
对于理想低通滤波器具有非因果脉冲响应,即:
| $ h(t) = \sin \left( {\frac{{{\rm{ \mathsf{ π} }}t}}{2}} \right)/{\rm{ \mathsf{ π} }}t。$ | (1) |
式中:h(t)为脉冲响应函数。此滤波器在时域中持续时间无限长,在物理上无法实现。式(1)所示的理想脉冲响应在有限区间可近似。利用N点采样矩形窗或取样函数ωN(t)可从理想脉冲响应中提取并得到有限N点采样的近似脉冲响应。
| $ {\omega _N}(t) = \left\{ \begin{array}{l} 1, |t| \le \frac{{(N - 1)}}{2}, \\ 0, 其他。\end{array} \right. $ | (2) |
式中,ωN(t)为矩形窗的取样函数,可应用于定义一个有限区间的时间序列hN(t)=ω(t)×h(t)。由于hN(t)在时间轴的负半轴取值,因此,hN(t)是非因果型窗口滤波器,不能应用于实时领域。为了将有限非因果型FIR转换为因果型FIR,取样窗口内的脉冲响应曲线在时间轴上右移L=(N-1)/2个采样周期,由此产生的因果脉冲响应为
| $ {h_c}(t) = \frac{{\sin \left( {\left( {\frac{{\rm{ \mathsf{ π} }}}{2}} \right)\left( {t - \frac{{N - 1}}{2}} \right)} \right)}}{{{\rm{ \mathsf{ π} }}\left( {t - \frac{{N - 1}}{2}} \right)}}, t = 0, 1, 2, \cdots , (N - 1)。$ | (3) |
式中,hc(t)为因果脉冲响应函数。由于是对hN(t)进行开窗口操作,所以这种设计方法称为窗函数法。所谓开窗口即把信号的观察时间限制在一定的时间间隔内,对其进行分析,取有限个数据。对信号数据截断的过程,也就等于将信号进行加窗函数操作。窗函数不仅会影响原信号在时域上的波形,也会影响到频域内的形状。
常用的窗函数很多,例如矩形窗、三角窗、Hanning窗、Poisson窗,等等。窗函数在光谱分析、滤波器设计以及音频数据压缩等方面有着广泛的应用。窗函数滤波器设计法可应用于频谱分析、功率谱分析等信号处理中。对于具有时变性的AD采样数据,该滤波器结构过于复杂、计算量大、输出信号会有明显的滞后,故不推荐使用此方法。
1.2 最小均方设计法最小均方(LMS)设计准则是使误差平方最小化,通过最小化误差信号的均方值来修正滤波器系数,模拟所需理想滤波器,是一种算法简单、应用广泛的自适应滤波算法。
在求解超定方程组时,通过最小二乘法使每个方程产生的误差平方和最小。经典的最小二乘估计方法可以用于解决FIR滤波器设计问题。考虑按加权最小平方误差的要求,需设计一个线性相位FIR:
| $ \sigma = \sum\limits_{i = 1}^K {{{\left\{ {W\left( {{\omega _i}} \right)\left[ {e\left( {\overline {{\omega _l}} } \right)} \right]} \right\}}^2}} = \sum\limits_{i = 1}^K {{{\left\{ {W\left( {\overline {{\omega _l}} } \right)\left[ {H\left( {\overline {{\omega _l}} } \right) - {H_d}\left( {\overline {{\omega _l}} } \right)} \right]} \right\}}^2}} , $ | (4) |
式中:H(
误差权值W(ωi)是LMS法区别于窗函数的特征之一。与窗函数相比,权值能够提高重要频率段的比重,降低非重要频率段的影响。
1.3 滑动平均滤波器滑动平均FIR滤波器,属于无乘法器FIR滤波器的一种,是在时域输出N个连续采样的平均值。其传递函数为
| $ \begin{array}{l} {H_{MA}}(z) = \frac{1}{N}\sum\limits_{m = 0}^{N - 1} {{z^{ - m}}} = \frac{1}{N}\sum\limits_{m = 0}^\infty {{z^m}} = - \frac{1}{N}\sum\limits_{m = 0}^{ - \infty } {{z^m}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{N}\frac{1}{{1 - {Z^{ - 1}}}} - \frac{1}{N}\frac{{{Z^{ - N}}}}{{1 - {Z^{ - 1}}}} = \frac{1}{N}\frac{{{Z^{ - N}}}}{{1 - {Z^{ - 1}}}} = \frac{1}{N}\frac{{\left( {{Z^{ - N}} - 1} \right)}}{{{Z^{N - 1}}(Z - 1)}}。\end{array} $ | (5) |
滑动平均值法把N点采样数据看作一个队列,队列长度固定为N,每进行一次采样,把其放人队尾,同时舍去队首数据,这样队列中始终有N个“最新”数据。计算滤波值时,把队列中的N个数据进行平均,得到新的滤波值。
滑动平均值法对周期性干扰有良好的抑制作用,平滑度高、灵敏度低,但对非周期性的冲击干扰(如回路中有磁性负载的启停)、随机干扰抑制作用差。
文中的A/D采样处理时,若采用此方法,可使输出曲线更为平滑。但文中旨在一段时间内得到稳定、准确的输出值,以便正确读取和模拟量换算,因此,不推荐使用该方法。
1.4 改进型加权平均法基于LMS法,提出一种改进型加权平均滤波算法,相对算术平均滤波算法,该方法增加采样值在平均值中的比重,并且去掉若干疑似超调峰值(即将峰值权重配置为0),使输出有效值更接近实际值。
对于一个N项加权平均式为
| $ Y = \sum\limits_{K = 1}^N {{C_K}} X(K), $ | (6) |
其中加权系数CK应满足:
| $ \sum\limits_{K = 1}^N {{C_K}} = 1。$ | (7) |
加权平均法适用于包含随机干扰信号的滤波,这种信号有平均值,对于温度、压力、液位等缓变量,可通过该方法快速获得稳定、准确的测量值。
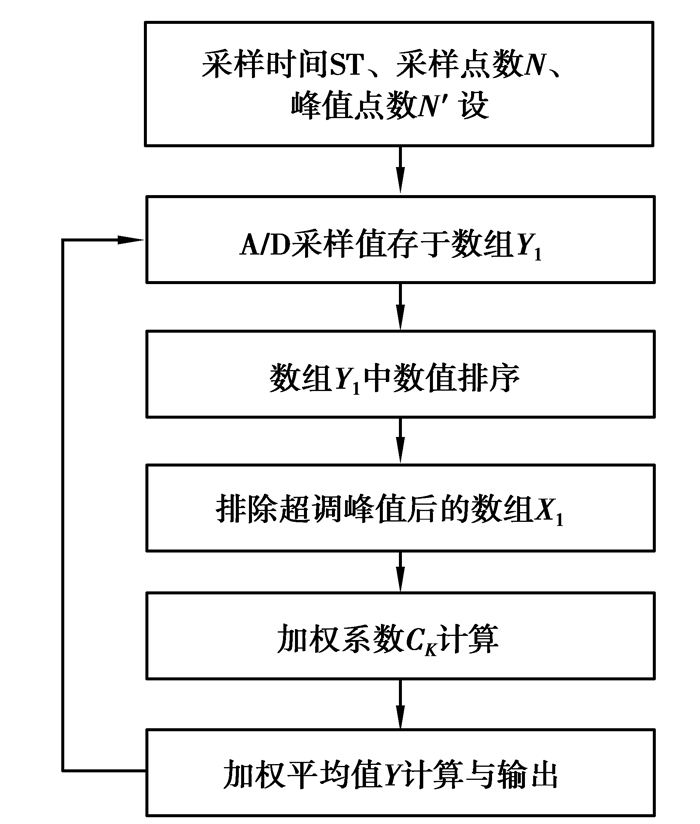
文中对该算法加以改进,将在一定时间ST内采得的N个值存于数组Y1中,对采样值进行排序,去除N'个最大值与最小值(即去掉了疑似超调的峰值),将余下采样值存储到一个新的数组X1中,并计算加权系数CK,计算加权平均值输出,实现在此段时间内模拟量采样值的数字滤波。依此类推进入下一次滤波循环,其滤波流程如图 1所示。
|
图 1 采样滤波流程 Fig. 1 Theprocess of sampling and filtering |
改进后的算法整理为
| $ Y = \sum\limits_{K = 1}^{N - 2N'} {{C_K}} {X_1}(K), $ | (8) |
式中:
| $ {C_k} = \frac{{I(k)}}{{\sum I (k)}}, $ | (9) |
其中,I(k)为数据X1(K)在采样组中出现次数。需注意,采样个数N应为偶数。
2 改进型加权平均滤波算法的可靠性分析对于S7-1200等小型工业控制器,考虑到内存局限性及AD采样的时变性,所用滤波算法不宜过于复杂。可用算法有算术平均值滤波算法、加权平均值滤波算法、中值滤波算法。其中,中值滤波(即取采样值的中间值)结构最简单,但所得结果的可靠性相对较差。
2.1 各算法可靠性比较为验证算法的有效性与可靠性,比较几种滤波算法的优劣,在Matlab中模拟各算法滤波效果。分别计算各算法滤波值,并根据LMS设计准则,计算各算法滤波值的误差平方和。
S7-1200PLC采样模拟量为无符号型0~27 648的整数。在Matlab中随机生成元素个数为500、范围为[11 000, 12 000]的数组,模拟一个采样周期内模拟量的连续采样值。在实际AD采样中,往往会有较大的随机干扰,即在采样值中会产生突变值。因此,在生成的数组中随机替代插入若干突变值。为了更清晰地比较改进型算法与未改进型原始算法、加权平均值算法与算术平均值滤波算法,另外加入一种去掉峰值的算术平均值滤波算法(改进型算术平均值滤波算法)。下面将算术平均值、加权平均值、改进型算术平均值以及文中所提出的改进型加权平均值4种滤波算法进行比较。
为了考虑权重因素,分别计算剔除峰值与未剔除峰值2组数据的加权系数,如图 2所示。计算改进型加权平均值、算术平均值、改进型算术平均值、加权平均值,结果如图 3所示。并将模拟数组a1与各滤波值绘制成线图,如图 4(a)所示。

|
图 2 权重计算 Fig. 2 Weight calculation |

|
图 3 各算法计算值 Fig. 3 Calculated value of each algorithm |

|
图 4 滤波值线图 Fig. 4 Filtered value curve |
图 4(a)中,数据在一定范围内波动,且数据有较大峰值,基本符合AD数据采样实际情况。但各滤波数据值较为接近,需放大区分,如图 4(b)所示。从上至下依次为算术平均值、改进型算术平均值、加权平均值、改进型加权平均值。
基于LMS准则,需计算各滤波值误差平方和,考虑加权最小平方误差的要求,计算结果如图 5所示。

|
图 5 各算法误差平方和 Fig. 5 Error sum of squares for each algorithm |
经验证e1 < e3 < e2 < e4,改进型算法优于未改进型原始算法,加权平均值算法优于算术平均值算法,即改进型加权平均算法误差平方和最小。但由于加权平均值算法需要计算每个变量的权值,故算术平均值算法较加权平均值算法结构更为简单。在存储器空间允许的条件下,选择加权平均值更为理想,且改进后的算法去除了疑似超调的峰值,结果更为合理。
2.2 采样时间与采样个数对结果的影响采样后对数据进行了大量运算,为验证4种算法的运算效率,将计算过程写成FC(Function)块,并调用RUNTIME指令分别检查不同采样个数时的运算时间。4种算法在不同采样个数时的运算时间为表 1所示。
| 表 1 运算时间对比 Table 1 Operation time comparisonms |
S7-1200CPU最大程序循环时间为150 ms,超过其最大程序循环时间的2倍,即300 ms时,CPU会停止运行。由于运算时间有一定范围的波动,为保证CPU正常运行,改进型加权平均值算法采样个数应保持在130个以内;加权平均值算法采样个数应保持在160个以内;改进型算术平均值算法采样个数应保持在260个以内;由于算术平均值算法无排序及计算权值过程,所用时间最少,采样个数可达2 000以上。
文中设计的数字滤波器在一个采样周期内其采样个数与采样周期时间均可自由设定。为比较一个周期内不同采样个数对滤波结果的影响,将3.1节方法中元素个数改为300和100,并分别计算其滤波值以及各滤波值误差平方和,如图 6所示。

|
图 6 不同元素误差平方和 Fig. 6 Error sum of squares of different element |
经验证e1 < e20 < e30,即元素个数越多滤波值误差平方和越小,在一个周期内滤波采样值越多所求滤波结果越准确。
综上所述,文中所提出的方法适用于存储空间足够,且模拟量变化率不是很快的时变系统。滤波周期与采样个数可根据实际情况进行设定。
3 S7-1200 PLC中数字滤波器的设计在程序块中建立一个SCL语言的FC块,在此FC块中编写滤波程序,供main主程序块中调用。另外,需要为其添加一个全局DB(datablock)块,用于数据存储。
3.1 变量定义与功能分配数字滤波器的变量定义如表 2所示。
| 表 2 变量定义表 Table 2 Variable definition |
加权平均值的计算过程可理解为一个求和过程,定义数组S[#n9]最后一个元素为所求加权平均值。此程序中数组限值均设置为0~199,即该数组元素个数为200个,若采样个数N≤200,多余的元素可不计入运算;若采样个数N>200,需要在编程时将此函数块对应数组限值扩大到需要值,如图 7所示。

|
图 7 数组限值修改 Fig. 7 Array limit modification |
在编写程序前需在main主程序中调用定时器,供滤波程序使用,否则滤波程序中的定时器无法识别。此程序不可编写为FB(function block)函数块,在编写多个滤波程序时,需编写另一个FC块,并调用不同的定时器。
本程序中求和程序如下:
#S[0] := 0;
FOR #n9 := 1TO #N-2*#"N′"-1 DO
#S[#n9] := #S[#n9-1] + #C[#n9];
END_FOR;
本语句采用数组求和,而非实数型变量直接累加求和,若采用累加求和语句应为:
FOR #n9 := 0 TO #N-2*#"N′"-1 DO
#S := #S + #C[#n9];
END_FOR;
此程序更简洁,但PLC中执行的求和结果数据变大,并不准确。原因在于PLC在执行“#S := #S + #C[#n9]”时,会重复扫描执行多次,造成数值过大。若在指定时间段内执行该语句,所求值S将远超出实际所求值。文中所用数组求和的方法可避免该问题。
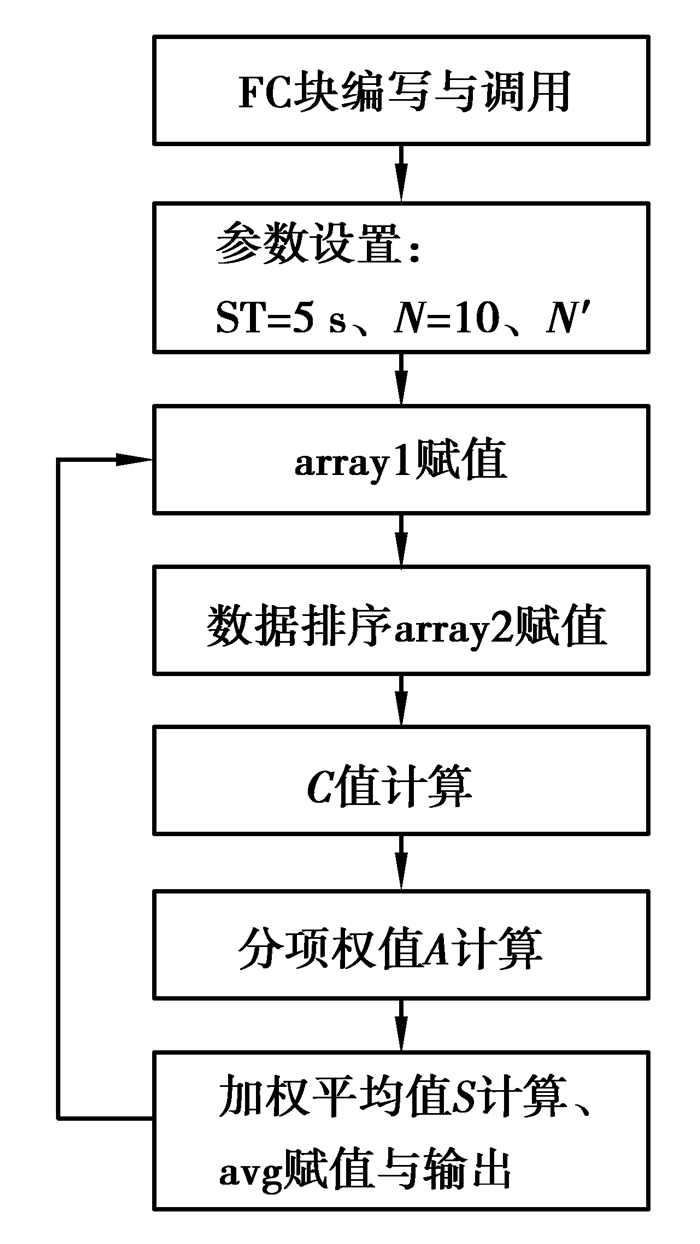
4 S7-1200 AD采样实验与结果验证 4.1 程序可行性初步检验通过S7-12001214C DC/DC/DC PLC自带AI接口接收电压信号,用直流稳压电源作为模拟量输入,手动调节来模拟采样时模拟量的变化。为方便观察,分别取N=10,N′=2,ST=5 s,即在5 s内采样10个数据,分别剔除最大、最小值各2个,剩余6个数据求平均值输出。滤波程序设计流程如图 8所示。
|
图 8 滤波流程 Fig. 8 Filtering process |
为检验采样数据是否排序以及选取情况,在该函数块TEMP变量中添加REAL实数型变量“1~10”“11~16”“21~26”。“1~10”记录与显示所采样数据排序后情况;“11~16”记录与显示排除疑似超调值后所选取数据情况;“21~26”记录与显示各项加权系数计算情况。
PLC在线状态下,监视变量的赋值情况。表 3为采样的变量由软件按升序排列的结果。表 4为表 2剔除最大、最小值后的结果。表 5为各项加权系数设置,加权系数之和为1。
| 表 3 排序检查 Table 3 Sorting check |
| 表 4 数据选取检查 Table 4 Data selection check |
| 表 5 权重计算 Table 5 Weight calculation |
经验证,此程序对采样数据排序情况正常,去除峰值结果正常,权重计算正常。达到此程序对计算上的要求。
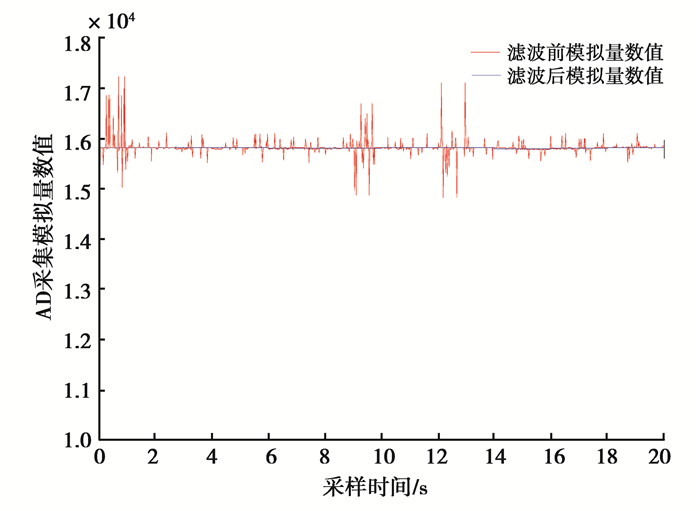
4.2 AD采样实验与结果验证课题组研制的一套温度调控装置,装置中含压缩机、变频器等强干扰负载,如图 9所示。为检验此函数在实际AD采样的效果,此装置将温度传感器PT100检测到的实时温度值,经变送器模块转换成4~20 mA的电流信号,通过模拟量输入模块SM1231送给1214PLC。将此滤波程序写入到PLC中,分别取N=100,N′=20,ST=2 s,将20 s所采样数据与滤波值导入到Matlab中,生成图像便于观察与比较。如图 10为所生成图像,红线为滤波前曲线,蓝线为滤波后曲线。

|
图 9 温控设备 Fig. 9 Temperature control device |
|
图 10 模拟量滤波曲线 Fig. 10 Analog filter curve |
在实际工程应用中,为使传感器所测工程量在上位机中准确显示,需要对传感器进行标定。标定过程中读取模拟量时,数据抖动会给操作人员带来很大不便。一些环境下干扰较大,而通过自身AI端口滤波一般仅能滤除周期性的高频信号干扰,显然无法满足其稳定性要求。如果回路中存在大功率三相异步电机或伺服电机时,以及开关电源、电机启停等随机干扰情况下,仅靠PLC自身端口滤波器均无法滤除全部干扰信号。
图 10为滤波前后模拟量采样值,从图上不难发现:经过文中的数字滤波器滤波后的曲线相比滤波前的曲线更为平稳,有效地解决了此过程数据抖动的问题。
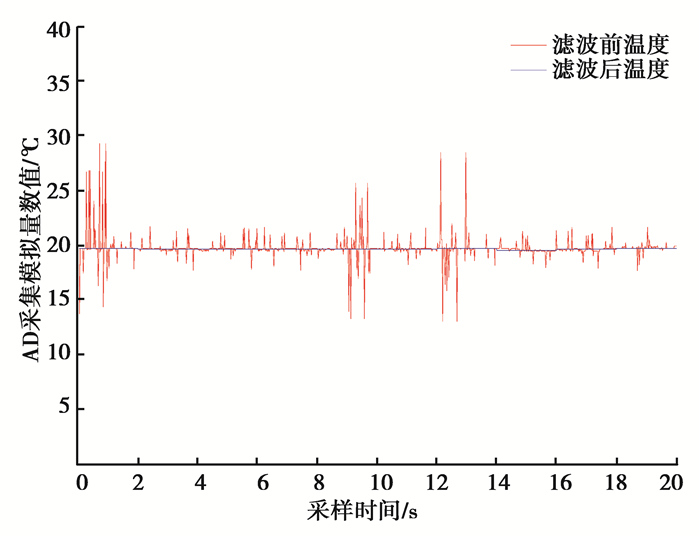
分别将滤波前后的模拟量计算为实际温度后导入到Matlab中,并生成实际温度滤波线图,如图 11所示,其中红线为滤波前曲线,蓝线为滤波后曲线。
|
图 11 实际温度曲线 Fig. 11 Actual temperature curve |
在实际工程应用中所测工程量一般在上位机显示,或程序内进行逻辑判断。以文中温度为例,抖动过大不宜操作人员读取,而在比较精准的控制程序中,亦不利于程序判断,特别在临界温度判断有可能造成程序判断上的错误。经滤波后曲线更为平稳,从读取上更直观,也可避免程序判断上的错误。
5 结束语针对西门子1200序列等工业控制器PLC,在模拟量AD采样与数据处理过程中,针对外界干扰所引起的扰动,设计了一种新型数字滤波器。由于控制器自身AI端口滤波无法确保采样数据平稳的要求,增加外部滤波器时又提高了设备的成本、电路变得复杂。采用的滤波算法使用SCL语言编程,解决了常用梯形图方法采样与处理多个模拟量过于繁琐的问题;使用数组求和方法,解决了累加求和由于程序重复扫描无法求出正确值的问题。该方法中数据采样点数与滤波周期可调,为工业上模拟量的采样提供了一种简单、可靠、高效、实用而灵活的方法,又无需增加外部设备,节约了成本。由于剔除了若干最大与最小值,对于干扰多、波动大的模拟量提供了更为稳定可靠的数据。
但文中的算法有以下几点不足:
1) 滤波周期内采样数据量不宜过大,否则在周期时间内PLC无法完成数据运算,会发生运行错误;
2) 因算法采用数组存储采样和运算数据,考虑PLC存储空间限制,所以总体数据量不宜过大。
3) 因算法程序调用了定时器,故而无法编写为FB块,在多路AD采样时需编写多个FC块并调用不同的定时器。
4) 由于该算法需连续采样多个值后进行加权运算,有一定滞后,在实时性要求较高的场合不宜使用,比如振动、速度、加速度信号的采样等。
因此,下一步研究工作重点在于寻求一种更为简便的方法,以节省更多的存储空间;为统一滤波时间的程序寻求一种可以编写为FB块的方法,应用将会更为简便;寻求一种新的采样与计算方法,以便适于变化频率较快的数据采样。
| [1] |
泰勒.数字滤波器原理及应用(借助MATLAB)[M].程建华, 袁书明, 译.北京: 国防工业出版社, 2013. Fred J. Digital filters principles and applications with MATLAB[M]. CHENG Jianhua, YUAN Shuming, translate. Beijing: National Defense Industry Publishing House, 2013. |
| [2] |
Panetta K, Bao L, Agaian S. Sequence-to-sequence similarity-based filter for image denoising[J]. IEEE Sensors Journal, 2016, 16(11): 4380-4388. DOI:10.1109/JSEN.2016.2548782 |
| [3] |
Hong Y, Shi T L, Wang X, et al. Weighted adaptive spatial filtering in digital holographic microscopy[J]. Optics Communications, 2017, 382: 624-631. DOI:10.1016/j.optcom.2016.08.056 |
| [4] |
程兰, 王志远, 陈杰, 等. 基于粒子滤波和滑动平均扩展Kalman滤波的多径估计算法[J]. 电子与信息学报, 2017, 39(3): 709-716. CHENG Lan, WANG Zhiyuan, CHEN Jie, et al. An improved multipath estimation algorithm using particle filter and sliding average extended kalmanfilter[J]. Journal of Electronics & Information Technology, 2017, 39(3): 709-716. (in Chinese) |
| [5] |
Erkan U, Gökrem L, Enginoǧlu S. Different applied median filter in salt and pepper noise[J]. Computers & Electrical Engineering, 2018, 70: 789-798. |
| [6] |
Kang X G, Stamm M C, Peng A J, et al. Robust median filtering forensics using an autoregressive model[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(9): 1456-1468. DOI:10.1109/TIFS.2013.2273394 |
| [7] |
胡妍, 王柯俨, 许宁, 等. 利用分割中值滤波和透射率补偿的图像去雾[J]. 西安电子科技大学学报(自然科学版), 2018, 45(4): 99-105. HU Yan, WANG Keyan, XU Ning, et al. Image dehazing by thesegmenting median filter and transmission compensation[J]. Journal of Xidian University (Natural Science), 2018, 45(4): 99-105. (in Chinese) DOI:10.3969/j.issn.1001-2400.2018.04.018 |
| [8] |
常乃超, 刘思旭, 余高旺, 等. 动态条件下同步相量测量装置的数字滤波器及计算优化[J]. 电力系统自动化, 2017, 41(20): 92-96. CHANG Naichao, LIU Sixu, YU Gaowang, et al. Digital filter and computational optimization of synchronized phasor measurement unit under dynamic conditions[J]. Automation of Electric Power Systems, 2017, 41(20): 92-96. (in Chinese) DOI:10.7500/AEPS20170424003 |
| [9] |
Wang J, Meng X H, Liu H, et al. Optimization of finite difference forward modeling for elastic waves based on optimum combined window functions[J]. Journal of Applied Geophysics, 2017, 138: 62-71. DOI:10.1016/j.jappgeo.2017.01.005 |
| [10] |
曹磊, 赵庆生, 王旭平, 等. 基于改进泰勒加权最小二乘法的相量测量算法[J]. 电力系统保护与控制, 2018, 46(7): 24-30. CAO Lei, ZHAO Qingsheng, WANG Xuping, et al. A phasor measurement algorithm based on improved Taylor weighted least squares[J]. Power System Protection and Control, 2018, 46(7): 24-30. (in Chinese) |
| [11] |
Jin D Q, Chen J, Richard C, et al. Model-driven online parameter adjustment for zero-attracting LMS[J]. Signal Processing, 2018, 152: 373-383. DOI:10.1016/j.sigpro.2018.06.020 |
| [12] |
赵知劲, 金明明. 基于块自适应滤波的核最小均方算法[J]. 计算机工程, 2017, 43(9): 162-166. ZHAO Zhijin, JIN Mingming. Kernaelleast mean square algorithm based on block adaptive filtering[J]. Computer Engineering, 2017, 43(9): 162-166. (in Chinese) DOI:10.3969/j.issn.1000-3428.2017.09.029 |
| [13] |
Tobar F A, Kung S Y, Mandic D P. Multikernelleast mean square algorithm[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(2): 265-277. DOI:10.1109/TNNLS.2013.2272594 |
| [14] |
Falissard F. Chebyshev-like generalized Shapiro filters for high-accuracy flow computations[J]. Journal of Computational Physics, 2017, 336: 595-607. DOI:10.1016/j.jcp.2017.01.067 |
| [15] |
刘佳, 唐小明, 宋洪良. 基于分布式协同模式的MTI滤波器设计与仿真[J]. 现代电子技术, 2017, 40(17): 79-82. LIU Jia, TANG Xiaoming, SONG Hongliang. Design and simulation of MTI filter based on distributed cooperation mode[J]. Modern Electronics Technique, 2017, 40(17): 79-82. (in Chinese) |
| [16] |
邱盛成, 蔡启仲, 李克俭, 等. PLC梯形图转化为多操作数逻辑指令的设计与实现[J]. 计算机测量与控制, 2016, 24(6): 202-205, 217. QIU Shengcheng, CAI Qizhong, LI Kejian, et al. Design and realization of transformation from PLC ladder diagram to multiple operands logic instruction[J]. Computer Measurement & Control, 2016, 24(6): 202-205, 217. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42


