2. 重庆清平机械有限责任公司, 重庆 401123
2. Chongqing Qingping Machinery CO., Ltd., Chongqing 401123, P. R. China
海洋平台用于海上油气资源勘探和开发,分为移动式平台和固定式平台。移动式海洋平台又分为坐底式、半潜式和自升式等多种不同的结构型式,其中自升式海洋平台由于具有作业灵活、耗材少、建造成本低及可移动性能好等优势而成为海洋油气资源开发的重要工程装备。目前市场上使用较多的是齿轮齿条升降式海洋平台,其中提升齿轮箱起到提升和支撑平台的作用。但由于海洋平台的工作环境复杂恶劣,提升齿轮箱的动作涉及平台的作业状态包括下降桩腿、升降和支撑平台、预压、提桩等,所以其工况非常复杂,且由于采用多级NGW行星传动串联,其结构上仅第1级太阳轮轴和输出齿轮轴处有轴承和箱体接触支撑,内部各构件彼此相互支撑,结构极为紧凑,其啮合机理极为复杂,因此对提升齿轮箱进行啮合特性分析研究具有重要的意义。
当前国内外学者对单对齿轮副、行星轮系的啮合特性和行星齿轮箱传动特性进行了一些研究。在单对齿轮啮合特性分析方面,Mohamad等[1]将轮齿啮合刚度考虑为特定弹簧,建立准无限弹性模型,进行啮合特性分析,研究传递误差对汽车传动齿轮的振动和噪声;Fuentes等[2]在平面铣刀的基础上提出两种不同几何形状的圆弧齿形,并对其进行啮合接触分析;国内学者Mao[3]采用精确非线性有限元的方法研究齿轮接触行为,并通过微观修形的方式降低齿轮的疲劳磨损;Wu[4]等提出一种考虑啮合齿对、载荷弹性和接触变形以及滑动摩擦等因素的动态啮合有限元分析方法,较真实地对齿轮进行啮合特性分析。Liu等[5]和Ni等[6]在前人的基础上研究齿轮修形对小倾角锥齿轮啮合特性的影响。在行星轮系啮合特性分析方面,Yang等[7]考虑齿轮啮合刚度、传递误差等因素建立行星齿轮箱齿裂故障非线性动力学模型;曹洪[8]将自升式海洋平台4级NGW行星传动齿轮副的时变啮合刚度考虑进该齿轮箱耦合系统扭转动力学模型中进行分析;林腾蛟等[9-10]以某型提升齿轮箱为研究对象,综合考虑齿轮副时变啮合刚度、齿侧间隙和传递误差等内部激励构建4级行星减速器耦合系统纯扭转动力学模型,进行系统优化及噪声分析。在行星轮系宏观参数优化方面,国内外学者对多级行星传动多目标进行大量研究,多采用建立多目标方程进行求解[11-14];以提升齿轮箱为对象,许登科等[13]以海工平台提升齿轮箱的传动比作为优化对象,研究如何使其结构更为紧凑,成本更低;张氢等[14]以可靠性和轻量化为目标,建立多目标数学模型,对自升式海洋平台提升齿轮箱进行优化,提出一种协调可靠性和经济性的方法。综上,现有文献对单对齿轮副的啮合特性的研究多为参数变化对齿轮啮合特性的影响;行星轮系的啮合特性研究多和系统的动态特性结合研究。目前对自升式海洋平台提升齿轮箱系统啮合特性相关研究较少。
笔者采用MASTA建立提升齿轮箱啮合分析模型,针对正常提升和预压提升工况下的提升齿轮箱啮合特性进行分析,开展了以重合度为目标的宏观参数优化研究,分析比较优化前后该齿轮箱的啮合特性变化规律。
1 提升齿轮箱结构与分析模型 1.1 提升齿轮箱的结构与传动原理自升式海洋平台拥有4条桩腿,每条桩腿上有18个提升齿轮箱,共72个提升齿轮箱,提升齿轮箱布局如图 1所示。平台到达指定工作地点后,所有提升齿轮箱输出齿轮与桩腿上齿条啮合共同带动4条桩腿向下运动至海底,同时使平台脱离海平面向上运动到达预压高度,锁紧平台进行预压工作;预压结束后,锁紧装置松开桩腿,提升齿轮箱带动平台升至作业高度,并锁紧齿条后平台进行作业操作。

|
图 1 自升式海洋平台提升齿轮箱布局 Fig. 1 Layout of jack-up offshore platforms promote gearbox |
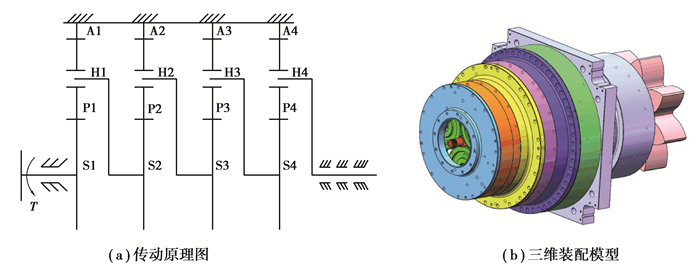
笔者所分析提升齿轮箱采用4级NGW行星传动,其传动原理图如图 2(a)所示,利用SOLIDWORKS建立的三维模型如图 2(b)所示。图中齿轮均为渐开线直齿轮,内齿圈A和箱体固定,各级太阳轮S为扭矩T输入端,经过行星架H并通过行星级功率分流,最终由第4级行星架H4输出驱动输出齿轮轴与桩腿上齿条啮合带动平台升降或支撑平台。该提升齿轮箱的基本参数如表 1所示。
|
图 2 提升齿轮箱传动系统 Fig. 2 Transmission system of the promote gearbox |
| 表 1 提升齿轮箱的基本参数 Table 1 Main parameters of the promote gearbox |
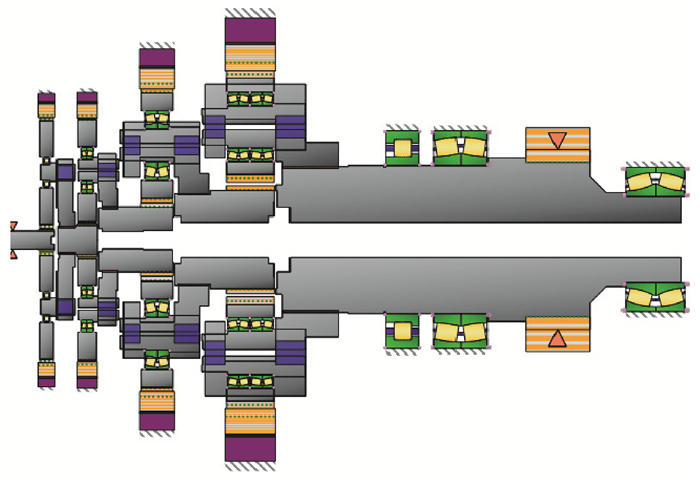
由表 1中提升齿轮箱的基本参数在MASTA中建立传动系统分析模型如图 3所示。基于此模型进行以重合度为优化目标的宏观参数优化和啮合特性分析。
|
图 3 分析模型 Fig. 3 The mechanical analysis model |
提升齿轮箱的工况复杂,在设计分析的过程中主要分析5种工况,分别是正常提升、预压提升、正常支撑、预压支撑和风暴支撑。因为提升齿轮箱在正常支撑、预压支撑和风暴支撑3种工况下静止,所以在正常提升和预压提升2种工况进行提升齿轮箱啮合特性分析,表 2为2种工作工况参数。
| 表 2 提升齿轮箱工况参数 Table 2 Working conditions for the promote gearbox |
基于MASTA考虑齿轮的微观几何特性、轴等零部件的变形,以重合度为优化目标,在不改变齿数、模数、压力角和中心距等参数的条件下,以齿顶厚等为约束条件对提升齿轮箱进行优化。其中齿顶厚约束为:齿顶厚/模数>0.3, 考虑到第一行星齿轮系在设计时的齿顶厚较小,这里不进行重合度优化,避免齿顶厚过小。
由重合度的计算公式可知,外啮合齿轮重合度由式(1)进行计算,内啮合齿轮重合度由式(2)进行计算。
| $ {\varepsilon _{\alpha {\rm{S - P}}i}} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\left[ {{z_{{\rm{Si}}}}\left( {\tan {\alpha _{{\rm{aS}}i}} - \alpha _{{\rm{S - P}}i}^\prime } \right)} \right] + {z_{{\rm{P}}i}}\left( {\tan {\alpha _{{\rm{aP}}i}} - {{\alpha '}_{S - {P_i}}}} \right), i = 2, 3, 4 $ | (1) |
| $ {\varepsilon _{\alpha {\rm{P}} - {\rm{A}}i}} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\left[ {{z_{{\rm{P}}i}}\left( {\tan {\alpha _{{\rm{a}}{P_i}}} - \alpha _{{\rm{P}} - {\rm{A}}i}^\prime } \right)} \right] - {z_{{\rm{A}}i}}\left( {\tan {\alpha _{{\rm{aA}}i}} - \alpha _{{\rm{P}} - {\rm{A}}i}^\prime } \right), $ | (2) |
式中:εαS-Pi,εαP-Ai分别为第i级行星轮系太阳轮行星轮(S-P)和行星轮内齿圈(P-A)齿轮副的重合度;zSi,zPi,zAi分别为第i级行星轮系太阳轮、行星轮和内齿圈的齿数;αaSi,αaPi,αaAi分别为第i级行星轮系太阳轮、行星轮和内齿圈齿顶圆压力角;α′S-Pi和α′P-Ai分别为第i级行星轮系太阳轮行星轮(S-P)和行星轮内齿圈(P-A)啮合副的啮合角。优化模型的数学描述为:
| $ \left\{ \begin{array}{l} X = \left[ {{h_{{\rm{S}}i}}, {h_{{\rm{P}}i}}, {h_{{\rm{A}}i}}} \right], \\ \max {\varepsilon _{\alpha {\rm{S}} - {\rm{P}}i}}(X), \\ \max {\varepsilon _{\alpha {\rm{S}} - {\rm{A}}i}}(X), \\ \begin{array}{*{20}{l}} {{\rm{ s}}{\rm{.t}}{\rm{. }}{s_{{\rm{ aS }}i}}(X)/{m_i} > 0.3, }\\ {{s_{{\rm{ aP }}i}}(X)/{m_i} > 0.3, }\\ {{s_{{\rm{ aAi }}}}(X)/{m_i} > 0.3。} \end{array} \end{array} \right. $ | (3) |
式中:hSi,hPi,hAi分别为第i级行星轮系太阳轮、行星轮和内齿圈的齿顶高系数;saSi(X),saPi(X),saAi(X)分别为第i级行星轮系太阳轮、行星轮和内齿圈的齿顶厚,是关于各齿轮齿顶高系数的函数;mi为第i级行星轮系各齿轮模数。
2 啮合特性分析与优化优化前后各齿轮副重合度见表 3,表中Sa为齿顶厚,ε为齿轮副重合度。
| 表 3 优化前后行星轮系各齿轮重合度 Table 3 The contact ratio of planetary gear train before and after optimization |
优化后各齿轮的齿顶厚会在一定程度上减小,全齿高增大,但仍然满足约束条件。由表 3可知,经过宏观参数优化后,各齿轮副的重合度增大,第2级太阳轮行星轮(S2-P2)和行星轮内齿圈(P2-A2)的重合度分别增加了14.58%和15.56%;第3级太阳轮行星轮(S3-P3)和行星轮内齿圈(P3-A3)的重合度分别增加了14.36%和15.48%;第4级太阳轮行星轮(S4-P4)和行星轮内齿圈(P4-A4)的重合度分别增加了17.56%和20.03%。重合度的增大必将引起各齿轮副传递误差与时变啮合刚度的改善。
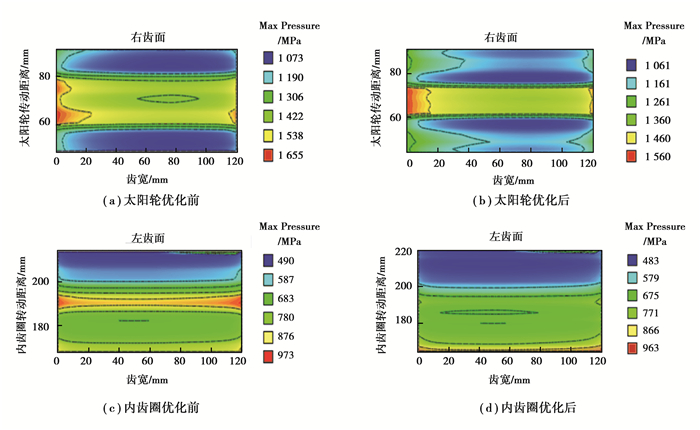
2.1 接触特性分析图 4为正常提升和预压提升2种工况下,优化前后太阳轮和内齿圈齿面最大接触应力。各太阳轮和内齿圈的许用接触应力为1 500 MPa和750 MPa,从图 4(a)可以看出,在预压提升时,第3级和第4级太阳轮的最大接触应力均超出了许用接触应力,因为各齿轮都未经过齿顶修缘处理,优化后太阳轮在2种工况下的最大接触应力均有小幅减小,但优化前后差距较小。由图 4(b)可以看出,优化前后内齿圈在2种工况下的最大接触应力基本不变,第4级内齿圈在正常提升和预压提升时最大应力均大于许用接触应力。第4级太阳轮和内齿圈在预压提升工况下的接触斑点如图 5所示,从图中可以看出齿轮副存在偏载,有必要对其进行修形,以改善齿面应力分布情况,且优化后,太阳轮的接触斑点区变窄,内齿圈的最大接触应力区向下移动。

|
图 4 太阳轮和内齿圈齿面最大接触应力 Fig. 4 Max contact pressure of sun gears and annular gears |
|
图 5 预压提升第4级太阳轮和内齿圈接触斑点 Fig. 5 Contact pattera of the fourth stage sun gear and annulus gear |
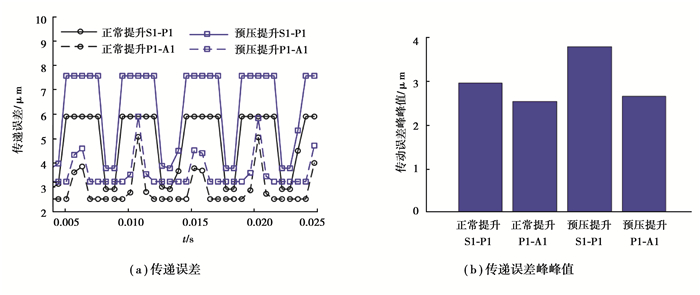
图 6为第1级行星轮系各齿轮副的传递误差,图 7,8和9分别为第2级、第3级和第4级行星轮系各齿轮副的传递误差,图 10为整个行星传动系统的传递误差,表 4为优化前后各齿轮副及系统的传递误差峰峰值对比。该4级NGW行星传动的传递误差定义为输出齿轮理论转角和实际转角的差值。
|
图 6 第1级行星轮系各齿轮副传递误差 Fig. 6 Transmission error of first stage gear pairs |
|
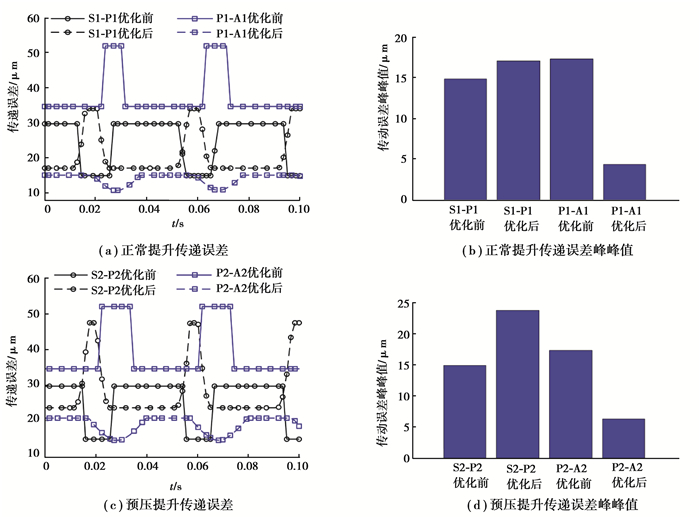
图 7 第2级行星轮系各齿轮副传递误差 Fig. 7 Transmission error of second stage gear pairs |
|
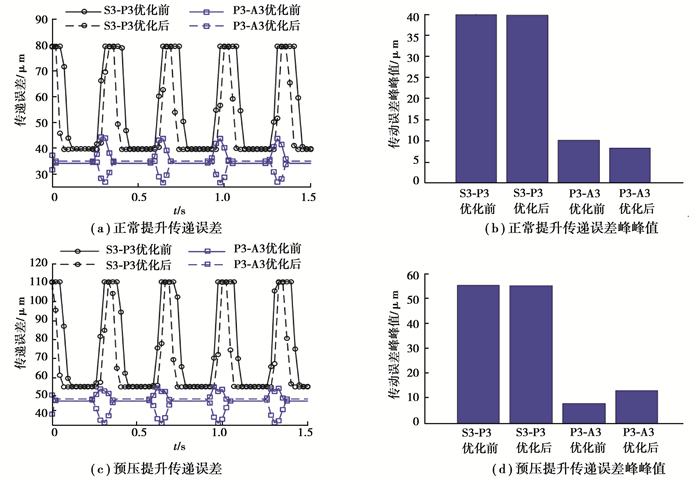
图 8 第3级行星轮系各齿轮副传递误差 Fig. 8 Transmission error of third stage gear pairs |
|
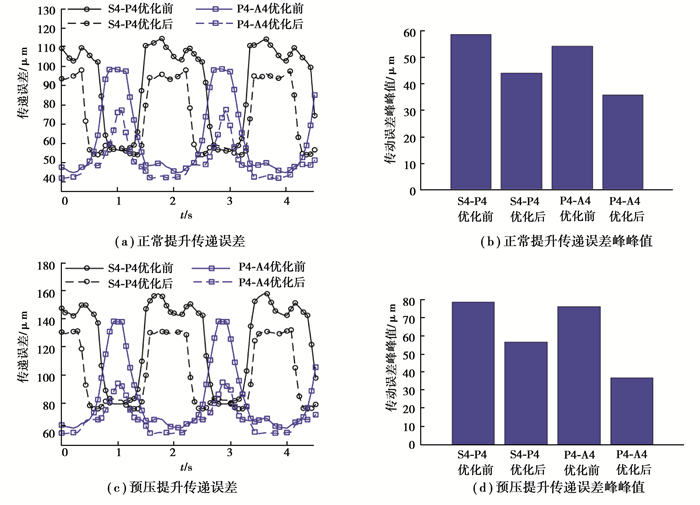
图 9 第4级行星轮系各齿轮副传递误差 Fig. 9 Transmission error of fourth stage gear pairs |
|
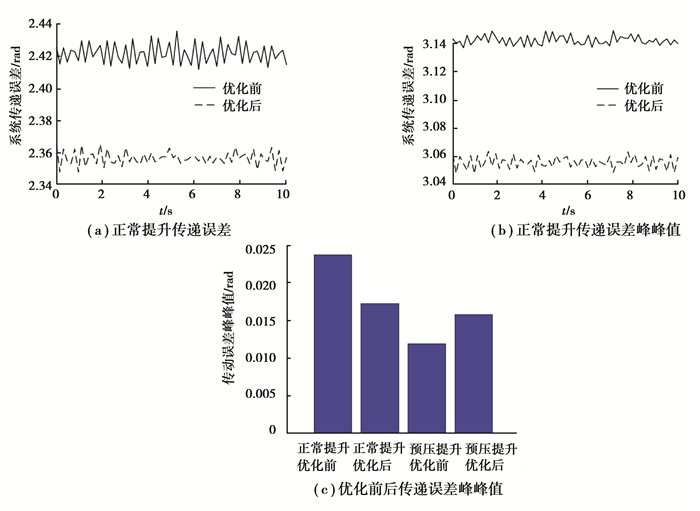
图 10 优化前后系统传递误差 Fig. 10 Transmission error of system before and after optimization |
| 表 4 优化前后的传递误差峰峰值 Table 4 Peak-to-peak value of TE before and after optimization |
结合表 4,从图 6~10可以看出,正常提升工况下,第1级太阳轮行星轮(S1-P1)的传递误差峰峰值大于行星轮内齿圈(P1-A1)的传递误差峰峰值。第2级太阳轮行星轮(S2-P2)的传递误差峰峰值优化后增大14.9%,行星轮内齿圈(P2-A2)的传递误差峰峰值优化后减小75.2%。第3级太阳轮行星轮(S3-P3)的传递误差峰峰值优化前后基本不变,行星轮内齿圈(P3-A3)的传递误差峰峰值优化后减小18.5%。第4级太阳轮行星轮(S4-P4)的传递误差峰峰值优化后减小24.7%, 行星轮内齿圈(P4-A4)的传递误差峰峰值优化后减小33.9%。4级NGW行星传动传递误差峰峰值优化后减小29.2%。预压提升工况下,第1级太阳轮行星轮(S1-P1)的传递误差峰峰值大于行星轮内齿圈(P1-A1)的传递误差峰峰值。第2级太阳轮行星轮(S2-P2)的传递误差峰峰值优化后增大60%,行星轮内齿圈(P2-A2)的传递误差峰峰值优化后减小63.8%,第3级太阳轮行星轮(S3-P3)的传递误差峰峰值优化前后基本不变,行星轮内齿圈(P3-A3)的传递误差峰峰值优化后增大70%,第4级太阳轮行星轮(S4-P4)的传递误差峰峰值优化后减小28%, 行星轮内齿圈(P4-A4)的传递误差峰峰值优化后减小52%。4级NGW行星传动传递误差峰峰值优化后增大33.3%。
正常提升和预压提升两种工况下,优化后,各齿轮副和4级NGW行星传动传递误差峰峰值总体上减小,且优化后各齿轮副曲线有一个较小的滞后量,主要是重合度增大使双齿啮合区增长引起的。
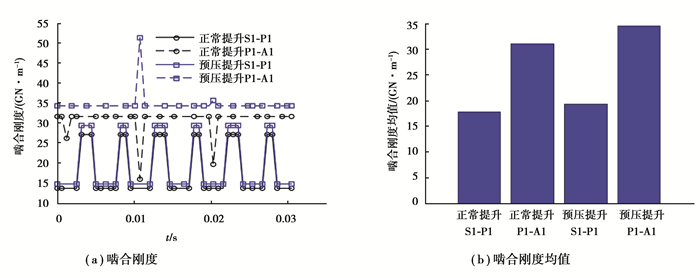
2.3 啮合刚度分析在齿轮啮合的过程中,实际参与啮合的齿轮对数时刻在改变,轮齿的弹性变形、几何误差等因素导致啮合刚度的变化进而导致轮齿动态啮合力的变化是齿轮传动产生振动的主要原因之一。自升式海洋平台提升齿轮箱有14对外啮合和14对内啮合齿轮副,图 11为第1级行星轮系各齿轮副之间的啮合刚度,图 12,13和14分别为第2级、第3级和第4级行星轮系各齿轮副啮合刚度,表 5为优化前后各齿轮副的啮合刚度均值对比。
|
图 11 第1级行星轮系齿轮副啮合刚度 Fig. 11 Meshing stiffness of the first stage gear pairs |
|
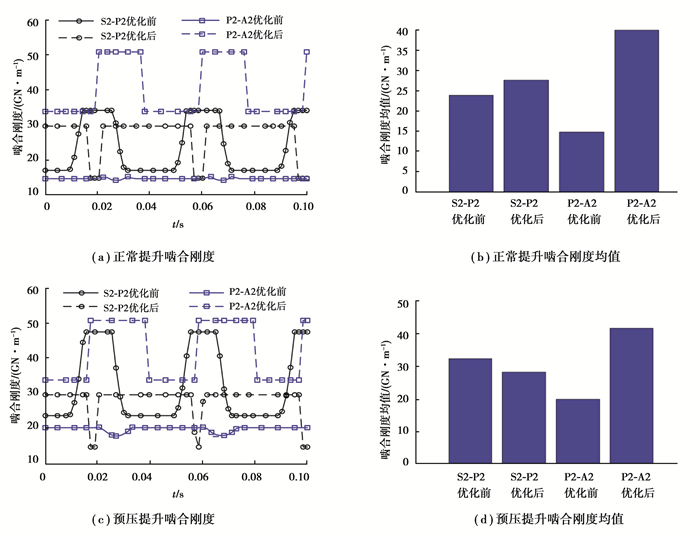
图 12 第2级齿轮副啮合刚度 Fig. 12 Meshing stiffness of the second stage gear pairs |
|
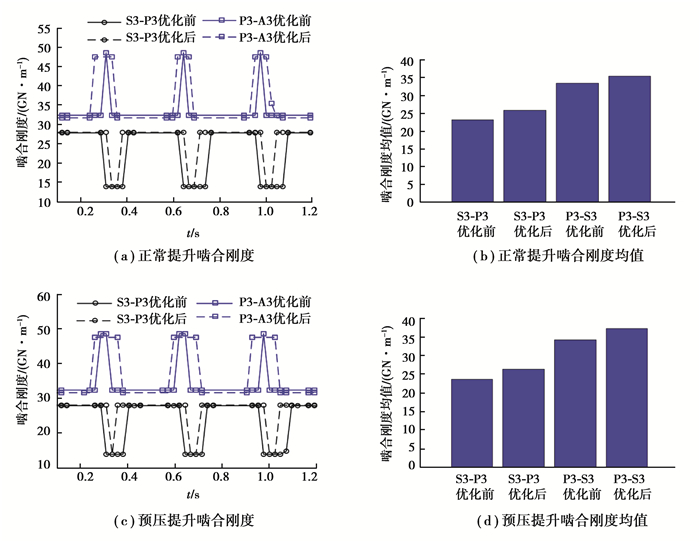
图 13 第3级齿轮副啮合刚度 Fig. 13 Meshing stiffness of the third stage gear pairs |
|
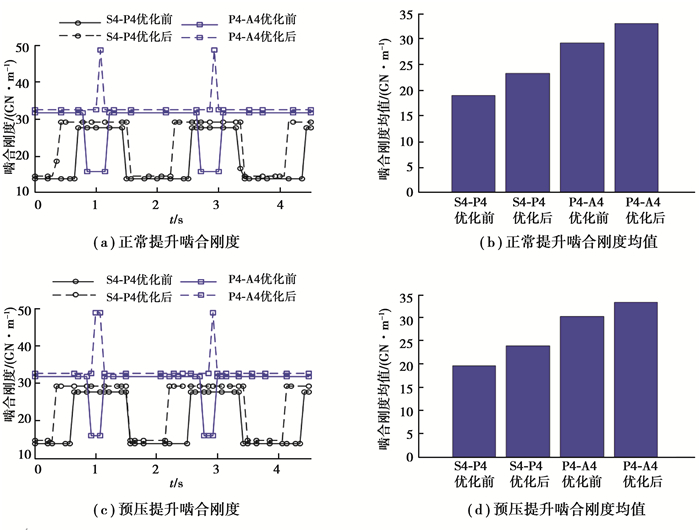
图 14 第4级齿轮副啮合刚度 Fig. 14 Meshing stiffness of the fourth stage gear pairs |
| 表 5 优化前后啮合刚度均值 Table 5 The mean of meshing stiffness before and after optimization |
结合表 5,从图 11~14可以看出,正常提升工况下,第1级太阳轮行星轮(S1-P1)的啮合刚度均值小于行星轮内齿圈(P1-A1)的啮合刚度均值;第2、第3和第4级太阳轮行星轮(S-P)的啮合刚度均值优化后分别增大16.1%,11.7%和22.5%,行星轮内齿圈(P-A)的啮合刚度均值优化后分别增大172.0%,6.3%和13.5%。预压提升工况下,第1级太阳轮行星轮(S1-P1)的啮合刚度均值小于行星轮内齿圈(P1-A1)的啮合刚度均值;第2级太阳轮行星轮(S2-P2)的啮合刚度均值减小12.5%;第3、第4级太阳轮行星轮(S-P)的啮合刚度均值优化后分别增大11.4%和21.9%;第2、第3和第4级行星轮内齿圈(P-A)的啮合刚度均值优化后分别增大109.0%,8.8%和10.1%。在正常提升与预压提升两种工况下,优化后各齿轮副的啮合刚度均值总体上增大,且第2级行星轮内齿圈(P2-A2)的啮合刚度均值成倍增加。
3 结论1) 以重合度为优化目标,齿顶厚/模数>0.3为主要约束条件,对第2到第4级行星轮系进行宏观参数优化,优化后各齿轮副重合度增大,各齿轮的齿顶厚有所下降,全齿高增大,各齿轮齿面最大接触应力小幅下降。
2) 正常提升和预压提升两种工况下,优化后,各齿轮副和4级NGW行星传动传递误差峰峰值总体上减小。
3) 在正常提升与预压提升两种工况下,优化后,各齿轮副的啮合刚度均值总体上增大,且第2级行星轮内齿圈(P2-A2)的啮合刚度均值成倍增加。
| [1] |
Mohamad E N, Komori M, Murakami H, et al. Analysis of general characteristics of transmission error of gears with convex modification of tooth flank form considering elastic deformation under load[J]. Journal of Mechanical Design, 2009, 131(6): 1-9. |
| [2] |
Fuentes A, Ruiz-Orzaez R, Gonzalez-Perez I. Computerized design, simulation of meshing, and finite element analysis of two types of geometry of curvilinear cylindrical gears[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 272: 321-339. DOI:10.1016/j.cma.2013.12.017 |
| [3] |
Mao K. Gear tooth contact analysis and its application in the reduction of fatigue wear[J]. Wear, 2007, 262(11/12): 1281-1288. |
| [4] |
Wu Y J, Wang J J, Han Q K. Contact finite element method for dynamic meshing characteristics analysis of continuous engaged gear drives[J]. Journal of Mechanical Science and Technology, 2012, 26(6): 1671-1685. DOI:10.1007/s12206-012-0416-5 |
| [5] |
Liu S Y, Song C S, Zhu C C, et al. Effects of tooth modifications on mesh characteristics of crossed beveloid gear pair with small shaft angle[J]. Mechanism and Machine Theory, 2018, 119: 142-160. DOI:10.1016/j.mechmachtheory.2017.09.007 |
| [6] |
Ni G X, Zhu C C, Song C S, et al. Tooth contact analysis of crossed beveloid gear transmission with parabolic modification[J]. Mechanism and Machine Theory, 2017, 113: 40-52. DOI:10.1016/j.mechmachtheory.2017.03.004 |
| [7] |
Yang W, Jiang D, Han T. Effects of tooth breakage size and rotational speed on the vibration response of a planetary gearbox[J]. Applied Sciences, 2017, 7(7): 3-17. |
| [8] |
曹洪.升降齿轮箱多级行星传动耦合振动分析及动态性能优化[D].重庆: 重庆大学, 2017. CAO Hong. Coupled vibration analysis and dynamic performance optimization of multi-stage planetary transmission of lifting gearbox[D]. Chongqing: Chongqing University, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1017723194.htm |
| [9] |
林腾蛟, 曹洪, 吕和生, 等. 4级行星齿轮箱振动噪声预估及修形效果分析[J]. 重庆大学学报, 2018, 41(2): 1-9. LIN Tengjiao, CAO Hong, LYU Hesheng, et al. Vibration noise prediction and tooth modification effect analysis of a four-stage planetary gearbox[J]. Journal of Chongqing University, 2018, 41(2): 1-9. (in Chinese) |
| [10] |
林腾蛟, 曹洪, 谭自然, 等. 四级行星齿轮减速器耦合系统动态性能优化[J]. 机械工程学报, 2017, 54(11): 162-171. LIN Tengjiao, CAO Hong, TAN Ziran, et al. Dynamic performance optimization of coupled system for four-stage planetary gear reducer[J]. Journal of Mechanical Engineering, 2017, 54(11): 162-171. (in Chinese) |
| [11] |
秦大同, 赵勇. 盾构机刀盘驱动多级行星齿轮传动系统的多目标优化[J]. 中国机械工程, 2012, 23(1): 12-17. QIN Datong, ZHAO Yong. Multi-objective optimization of multi-stage planetary gear train used in shield machine cutter driver[J]. China Mechanical Engineering, 2012, 23(1): 12-17. (in Chinese) DOI:10.3969/j.issn.1004-132X.2012.01.003 |
| [12] |
魏静, 杨攀武, 秦大同, 等. 重载行星齿轮传动等强度优化设计方法[J]. 北京工业大学学报, 2018, 44(7): 979-986. WEI Jing, YANG Panwu, QIN Datong, et al. Equal strength optimal design method in heavy-load planetary gear transmission[J]. Journal of Beijing University of Technology, 2018, 44(7): 979-986. (in Chinese) |
| [13] |
许登科, 曹科名, 彭锐涛, 等. 海工平台提升齿轮箱传动比优化设计[J]. 中国海洋平台, 2016, 31(4): 1-6. XU Dengke, CAO Keming, PENG Ruitao, et al. Optimal design of the transmission ratio lifting gearbox of offshore platform[J]. China Offshore Platform, 2016, 31(4): 1-6. (in Chinese) DOI:10.3969/j.issn.1001-4500.2016.04.001 |
| [14] |
张氢, 李冉, 张小杰, 等. 自升式海洋平台抬升减速器的优化设计[J]. 机械传动, 2015, 39(2): 51-54. ZHANG Qing, LI Ran, ZHANG Xiaojie, et al. Optimal design for the lifting gearbox of self-elevating offshore platform[J]. Journal of Mechanical Transmission, 2015, 39(2): 51-54. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42


