2. 甘肃省物流及运输装备信息化工程技术研究中心, 兰州 730070
2. Engineering Technology Center for Informatization of Logistics & Transport Equipment, Lanzhou 730070, P. R. China
动车制动系统结构和功能复杂,其可靠性对动车行驶的安全性有重要影响。在实际工作环境中,制动系统各个组成部分不是简单地服从某种规律,而是相互间存在着顺序相关性、功能相关性和优先性等动态特点,而且非精确统计和主观原因等不确定性因素会造成对系统零部件实际状态的误判,致使不易取得基本事件的精确故障率,因此根据实际工况所建立的系统模型比较复杂,存在失效数据难以获取等问题。
对于动车制动系统的可靠性问题,文献[1]通过分析制动系统结构和制动力构成的特点, 应用旁联结构构造制动系统的可靠性模型,但局限于系统整体计算分析。文献[2]对CRH3高速列车制动系统的故障和现象进行分析,进一步针对各部件对系统的影响提出了主动预防性维护措施。文献[3]应用热机械摩擦分析,提出一种评估制动盘热裂纹的方法。文献[4]根据列车制动的实时检测数据,将线性矩阵不等式结合分散式控制理论,构建了在途故障诊断方法。文献[5]采用反向最近邻技术检测离群点算法,并利用K近邻技术识别支持向量机中分类超平面的边界点,提出一种计算估计误差代价的新方法,应用于制动系统故障检测,降低了数据的复杂度。文献[6]建立了列车制动系统半实物仿真试验台,避免了制动系统现场试验的高成本,保证了试验结果的可靠性。文献[7]采用AMESim与Simulink软件对列车制动系统仿真模型与性能参数分析模型进行构建,比较了3种不同备用系统的优劣差异。文献[8]将故障树分析方法(fault tree analysis,FTA)与层次分析法相结合, 对制动系统进行安全和风险的综合评估。文献[9]基于高速列车制动系统中电磁阀的特性在小样本和无失效数据的情况下提出了一种新的贝叶斯(Bayesian network,BN)方法,避免了主观信息的误导。但文献[8-9]没有对系统故障的动态性特点进行研究。文献[10]对轴控式与架控式制动系统分别构建了动态故障树(dynamic fault tree,DFT)的可靠性模型来对比分析,但针对动态子树使用Markov链求解,求解过程较复杂。文献[11]根据制动系统结构,利用AMESim建立了系统的各功能块,模拟系统的动态特性对几种仿真场景出现的故障进行了研究,但没有针对故障概率的不确定性进行研究。
目前对于动车制动系统故障的模糊动态可靠性的相关研究相对较少,笔者在现有研究的基础上提出一种基于模糊FTA的动态贝叶斯(dynamic Bayesian network, DBN))可靠性分析方法,主要内容包括:1)应用模糊数学理论对底事件的故障率模糊化,考虑故障率的不确定性;2)引入BN模型解决FTA建模难以确定最小割集的问题, 并且清晰地表征事件之间的因果逻辑关系;3)采用BN条件概率表(conditional probability table, CPT)表示变量之间的联系,解决了Markov方法中因变量状态数过多而导致组合爆炸问题。
1 故障数据的处理对于系统故障可靠性分析中的数据处理,往往不能得到一个确定准确的事件故障率,因此应用模糊集理论和扩展原理对其进行模糊处理,得到事件故障率的模糊区间,使得到的数据更加符合实际故障率特性。
1.1 模糊集对于论域U里的集合
| $ \begin{array}{*{20}{c}} {{\mu _{\tilde A}}:U \to [0, 1], }\\ {u| \to {\mu _{\tilde A}}{{(u)}_0}。} \end{array} $ |
根据隶属函数定义[12],得到典型的三角模糊数为
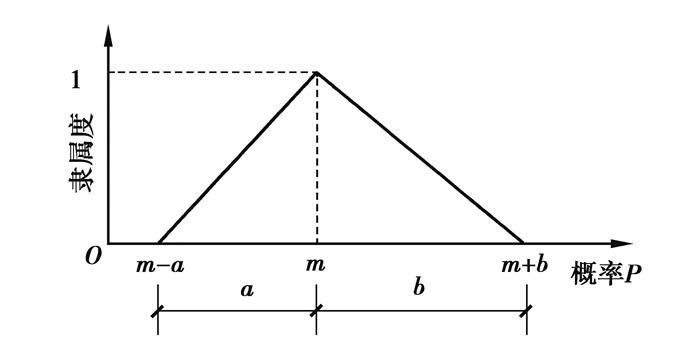
| $ {\mu _{\tilde A}} = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\frac{{x - m + a}}{a}\quad , m - a \le x < m;}\\ {1\qquad , x = m;} \end{array}\\ \frac{{m + b - x}}{b}\quad , m < x \le m + b;\\ 0, \quad 其他。\end{array} \right. $ | (1) |
典型的三角模糊数图形如图 1所示。
|
图 1 三角模糊数的隶属函数 Fig. 1 The membership function of trigonometric fuzzy numbers |
给定论域Ri(i=1, 2, …, n)中的模糊数
| $ {U_{\tilde Y}}(y) = \mathop {\sup }\limits_{\begin{array}{*{20}{c}} {{X_i} \in {R_i}(i = 1, \ldots , n)}\\ {y = f\left( {{X_1}, {X_2}, \cdots , {X_n}} \right)} \end{array}} \min \left( {{u_{{{\tilde X}_1}}}\left( {{X_1}} \right), {u_{{{\tilde X}_2}}}\left( {{X_2}} \right), \cdots ;{u_{{{\tilde X}_n}}}\left( {{X_n}} \right)} \right)。$ | (2) |
由扩展原理,模糊数
| $ \begin{array}{l} {{\tilde Y}_a}(y) = \left[ {\mathop {\min }\limits_{1 \le i \le n} f\left( {X;{\mu _{{{\tilde X}_i}}}\left( {{X_i}} \right)} \right.} \right. \ge \alpha ), \mathop {\max }\limits_{1 \le i \le n} f\left( {X;{\mu _{{{\tilde X}_i}}}\left( {{X_i}} \right) \ge \alpha } \right)] = \\ \left[ {\tilde Y_\alpha ^{\rm{L}}, \tilde Y_a^{\rm{R}}} \right], \end{array} $ | (3) |
式中:α表示任意大于零的实数:
因此, 可以将求解模糊数
| $ \begin{array}{*{20}{c}} {\tilde Y_a^{\rm{L}} = \mathop {\min }\limits_{1 \le i \le n} f\left( {{X_1}, {X_2}, \cdots , {X_n}} \right), }\\ {{\rm{subject}}\;\;\;{\rm{to}}}\\ {\tilde X_{1\alpha }^{\rm{L}} \le {X_1} \le \tilde X_{1\alpha }^{\rm{R}}, }\\ {\tilde X_{2\alpha }^{\rm{L}} \le {X_2} \le \tilde X_{2\alpha }^{\rm{R}}, }\\ \vdots \\ {\tilde X_{n\alpha }^{\rm{L}} \le {X_n} \le {\rm{ }}\tilde X_{n\alpha }^{\rm{R}}。} \end{array}\;\;\;\;\;\begin{array}{*{20}{c}} {\tilde Y_\alpha ^{\rm{R}} = \mathop {\max }\limits_{1 \le i \le n} \left( {{X_1}, {X_2}, \cdots , {X_n}} \right), }\\ {{\rm{subject}}\;\;\;{\rm{to}}}\\ {\tilde X_{1\alpha }^{\rm{L}} \le {X_1} \le \tilde X_{1a}^{\rm{R}}, }\\ {\tilde X_{2\alpha }^{\rm{L}} \le {X_2} \le \tilde X_{2\alpha }^{\rm{R}}, }\\ \vdots \\ {\tilde X_{na}^{\rm{L}} \le {X_n} \le \tilde X_{n\alpha }^{\rm{R}}。} \end{array} $ | (4) |
根据以上扩展原理得到模糊数在不同截集下的区间边界。
2 DBN分析方法FTA在分析大型复杂系统时往往表达能力不足,DFT在FTA表示整个系统中存在静态逻辑关系的基础上借助动态逻辑门来描述系统间的动态关系。但应用DFT进行分析时,要求获取最小路集或最小割集,使计算过程变得复杂[13]。而BN变量节点间具有条件独立性,在分析过程中不需要上述条件,避免了大量的计算,故把DFT转化为DBN分析。
2.1 BN模型BN通过有向无环图来构建,它由代表变量的节点及连接这些节点的有向边构成。其中,节点表示论域中的变量,有向边表示变量间的关系[14]。
BN结构具有条件独立关系,在给定某个节点的父节点时,除该节点的后代节点外,它与其他所有节点之间条件独立。即对任意Xi,如果存在P(Xi)
| $ P\left( {{X_1}, {X_2}, \cdots , {X_n}} \right) = \prod\limits_{i = 1}^n P \left( {{X_i}|P\left( {{X_i}} \right)} \right), $ | (5) |
式中P(Xi)为节点Xi所有父节点的变量集合。
用Yi表示节点Xi的父节点,根据全概率公式得到节点Xi的边缘概率为
| $ P(X) = \sum\limits_{i = 1}^n P \left( {X|{Y_i}} \right)P\left( {{Y_i}} \right), $ | (6) |
式中:P(X)为X的边缘概率;P(X|Yi)为X的条件概率;P(Yi)为父节点Yi的先验概率;n为父节点的个数。
根据贝叶斯公式得出BN条件概率值的推理过程可以表示为
| $ P\left(Y_{i} | X\right)=\frac{P\left(Y_{i}, X\right)}{P(X)}=\frac{P\left(X | Y_{i}\right) P\left(Y_{i}\right)}{P(X)}, $ | (7) |
式中P(Yi|X)表示Yi的后验概率。
2.2 离散时间BN模型将模型的整段时长[0,+∞]细化分割为n+1个时间段,一般把系统任务时长(0,T)划分为n个时间段,剩下的(T,+∞)作为第n+1个时间段。当某个节点Xi对应的部件在T内第i个时间段[(i-1)Δ, iΔ)内失效,则称节点Xi为状态i。若节点Xi在时间段[T, +∞)内失效,则称节点Xi为状态n+1。由上述定义可得离散时间BN中全部节点的状态空间的n+1个子区间:{[0, Δ], (Δ, 2Δ], ((n-1)Δ, nΔ], (nΔ, +∞) },简记为{1, 2, …, n, n+1}[15]。若DBN中包含m个节点,非叶节点表示为Ui(1≤i≤m-1),则求解顶事件UT在任务时间T内发生的概率为
| $ \begin{array}{l} P(T) = \sum\limits_{0 \le x \le n} P \left( {{U_T} = ((x - 1)\Delta , x\Delta )} \right) = \\ \sum\limits_{0 \le x \le n{U_1}} {\sum\limits_{, , \ldots , {U_{m - 1}}} P } \left( {{U_1} = {u_1}, \cdots , {U_{m - 1}} = {u_{m - 1}}, {U_T} = ((x - 1)\Delta , x\Delta )} \right), \end{array} $ | (8) |
式中:T代表任务时长;ui表示Ui的发生区间,ui属于{[0, Δ), [Δ, 2Δ), …, [(n-1)Δ, nΔ), [nΔ, +∞)};Δ代表时间间隔(Δ=T/n,n表示间隔数目)。
若部件的故障概率分布函数服从指数分布,则求解可靠度和不可靠度的计算式为
| $ R(t)=\mathrm{e}^{-\lambda t}, F(t)=1-R(t)=1-\mathrm{e}^{-\lambda t}, $ | (9) |
式中:R(t)为部件的可靠度; F(t)为不可靠度; λ为故障率。结合式(9),若节点Xi为状态i时,即该节点在[(i-1)Δ, iΔ]时间段内出现故障的先验概率为
| $ \begin{array}{l} P\left( {{X_i} = i} \right) = \int\limits_{(i - 1)\Delta }^{i\Delta } {} {f_{{X_i}}}(t){\rm{d}}t = \int\limits_{(i - 1)\Delta }^{i\Delta } {} \frac{{{\rm{d}}{F_{{X_i}}}(t)}}{{{\rm{d}}t}}{\rm{d}}t = \\ {\lambda _{{X_i}}}\int\limits_{(i - 1)\Delta }^{i\Delta } {} {{\rm{e}}^{ - {\lambda _{Xi}}t}}{\rm{d}}t = \left( {{{\rm{e}}^{ - {\lambda _{Xi}}\Delta }} - 1} \right){{\rm{e}}^{ - {\lambda _{Xi}}t\Delta }}。\end{array} $ | (10) |
若节点Xi为状态n+1时,那么此节点在[T, ∞]时间段内出现故障的先验概率为
| $ P\left( {{X_i} = n + 1} \right) = \int\limits_T^\infty {} {f_{{X_i}}}(t){\rm{d}}t = \int\limits_T^\infty {} \frac{{{\rm{d}}{F_{{X_i}}}(t)}}{{{\rm{d}}t}}{\rm{d}}t = {{\rm{e}}^{ - {\lambda _{{X_i}}}T}}, $ | (11) |
式中:fXi(t)代表节点Xi的故障概率密度函数;FXi(t)代表节点Xi的累积故障概率分布函数;λXi代表故障率。
2.3 逻辑门输出事件CPT的确定在DBN定量分析过程中需要确定网络节点的CPT,下面主要介绍几种在制动系统分析过程中常遇到的逻辑门的CPT的确定。
1) 与门。
令Xg=[X1, X2, …, Xm],其中m代表与门的输入事件个数,g=1, 2, …, m代表输入事件的状态变量,令Y代表输出的状态变量, 所有变量的状态空间都为{1, 2, …, m+1}。令k=max(X1, X2, …, Xm), 则Y的条件概率分布为
| $ P(Y = j|X) = \left\{ {\begin{array}{*{20}{l}} {1, j = k;}\\ {0, j \ne {k_0}。} \end{array}} \right. $ | (12) |
该分布表明与门输出节点的CPT表中,每行对应的输入事件全部发生时列上的值为1,其他值为0。
2) 或门。
令r=min(X1, X2, …, Xm),则Y的条件概率分布为
| $ P(Y = j|X) = \left\{ {\begin{array}{*{20}{l}} {1, j = r;}\\ {0, j \ne {r_0}。} \end{array}} \right. $ | (13) |
该分布表明或门输出节点的CPT表中,每行对应一个或一个以上输入事件发生时列上的值为1,其他值为0。
3) 备件门。
冷备件门是指备件S在主件A工作时不工作,故障率为零,只有主件A发生故障时备件S才工作,当备件S也发生故障时冷备件门顶事件发生。其条件概率分布为
| $ {P_{j{\rm{ }}i}} = P(S = i{\rm{ }}|{\rm{ }}A = j) = \left\{ \begin{array}{l} \frac{{P(S = i, A = j)}}{{P(A = j)}}, i > j;\\ 0, 其他。\end{array} \right. $ | (14) |
热备件门和温备件门同与门的CPT分布一样,不再说明。
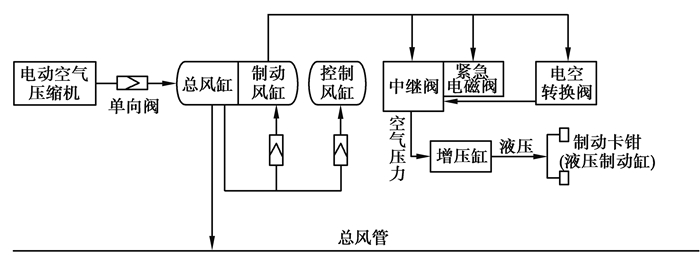
3 动车制定系统可靠性分析空气供给系统工作原理:由电动空气压缩机产生压缩空气,经过滤器过滤后通过布置于整个列车的总风管输送到各车的总风缸,再由单向阀分配给控制风缸和制动风缸。各车制动风缸中的压缩空气提供给电空转换阀、中继阀和紧急电磁阀使用。空气制动系统简图如图 2所示。
|
图 2 空气制动系统简图 Fig. 2 Sketch of air brake system |
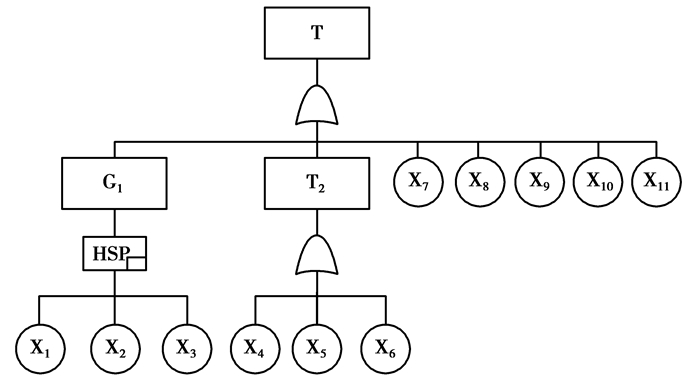
建立故障树选定制动空气供给系统故障为顶事件,各子系统的工作状态影响着整个制动控制系统的运作,即任意子系统出现问题,就会造成动车制动系统无法正常工作。所创建的故障树如图 3所示。
|
图 3 制动空气供给系统DFT Fig. 3 Dynamic fault tree of brake control system |
应用第1节的模糊数学方法结合专家调查问卷法对兰州动车所积累的制动空气供给系统运行的全部风险事件故障数据进行整理分析,获得基本事件模糊故障率如表 1所示,给出了用三角模糊数表示的风险事件故障率及故障树中各底事件编号所匹配的故障名称。设定系统和部件的工作状态只包含正常和故障两种状态,零部件失效服从指数分布。
| 表 1 底事件名称对应的编号及故障率 Table 1 The number and failure rate corresponding to the name of the bottom event |
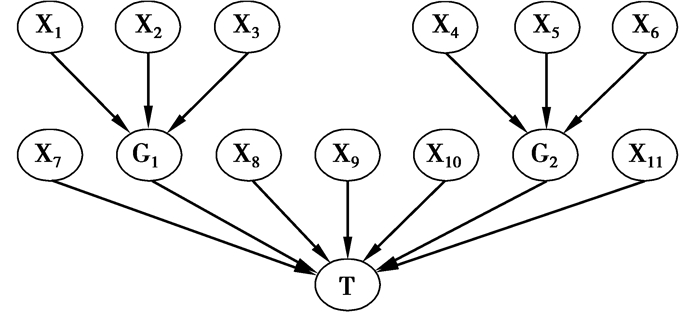
根据系统和部件之间的失效机理,按照BN模型的规则得到对应的BN,如图 4所示。
|
图 4 制动空气供给系统BN模型 Fig. 4 BN model of brake air supply system |
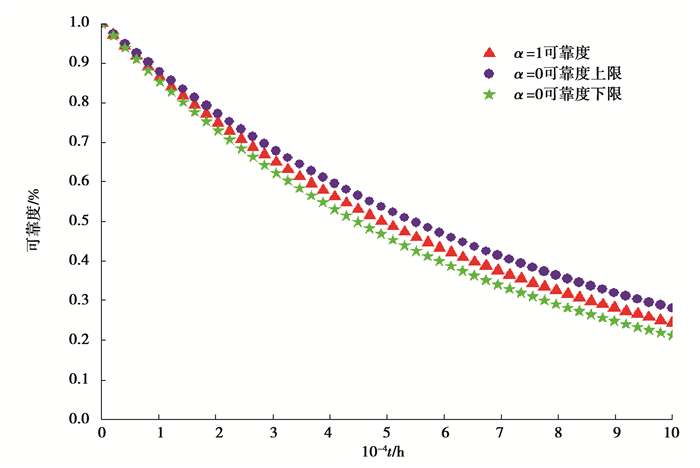
假设任务时间t=15 000 h,取n等于5,即计算的时间间隔为3 000 h,运用推理算法根据2.3节DBN逻辑门的CPT分布以及式(10)(11)可得叶节点在15 000 h内的不同区间时刻的模糊故障概率在不同截集下的上下限,如表 2所示。系统可靠度随时间的变化曲线如图 5所示。
| 表 2 叶节点故障概率 Table 2 Fault probability of leaf node |
|
图 5 水平截集α=0及α=1时的系统模糊可靠度 Fig. 5 System fuzzy reliability of horizontal intercepting α=0 and α=1 |
根据图 5得出,随着时间的不断推移,制动系统的可靠度逐渐下降,且图中分布的3条曲线的纵向距离逐渐变大,原因是部件的故障率随时间的增长而增加,导致制动供风系统可靠度的不确定性也逐渐增大。
当系统故障时,应用BN的反向推理计算,根据式(7)可以得到所有底事件的后验失效概率如表 3所示。
| 表 3 根节点后验故障概率 Table 3 Posteriori fault probability of root node |
通过表 3获取的数据,分析结果可知,根节点X8,X10的后验概率最大,因此安全阀和单向阀属于制动空气供给系统的薄弱环节,最可能对系统可靠性造成影响,应为重点高频检修对象;底事件X1,X2,X3的后验概率最小,因此主压缩机、第2压缩机和第3压缩机对于系统的可靠性影响最小,能够合理安排减小检测维护的频次。其他部件可以按照后验概率的大小排序合理安排检修维护的频次。
4 结论1) 将FTA和离散DBN模型结合起来,并应用三角模糊数表示事件的故障率来考虑系统基本事件故障率的不确定性,对列车制动系统可靠性进行分析是可行的。
2) 通过实例分析得出了制动系统的可靠度预测曲线以及各底事件的后验概率,得到了影响系统可靠性的薄弱环节,为制定该线路上运行车辆制动系统的检修策略提供了理论依据。
| [1] |
王孝延, 吴萌岭, 赵惠祥, 等. 2型高速动车组的制动力分配和可靠性建模[J]. 同济大学学报(自然科学版), 2010, 38(9): 1359-1362. WANG Xiaoyan, WU Mengling, ZHAO Huixiang, et al. Braking force distribution of CRH2 and its reliability modeling[J]. Journal of Tongji University(Natural Science), 2010, 38(9): 1359-1362. (in Chinese) DOI:10.3969/j.issn.0253-374x.2010.09.020 |
| [2] |
曹宏发, 周军, 陈伟, 等. 高速列车制动系统运用可靠性综合分析[J]. 铁道机车车辆, 2013, 33(3): 95-99. CAO Hongfa, ZHOU Jun, CHEN Wei, et al. Comprehensive analysis of operational reliability for braking system of high speed train[J]. Railway Locomotive & Car, 2013, 33(3): 95-99. (in Chinese) DOI:10.3969/j.issn.1008-7842.2013.03.22 |
| [3] |
Hong H, Kim M, Lee H, et al. A study on an analysis model for the thermo-mechanical behavior of a solid disc brake for rapid transit railway vehicles[J]. Journal of Mechanical Science and Technology, 2018, 32(7): 3223-3231. DOI:10.1007/s12206-018-0322-6 |
| [4] |
余博, 季常煦, 贾利民, 等. 基于LMI的城轨列车制动系统在途故障诊断方法研究[J]. 交通运输系统工程与信息, 2013, 13(6): 154-160. YU Bo, JI Changxu, JIA Limin, et al. Real-time fault diagnosis of urban train brake system based on LMI[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(6): 154-160. (in Chinese) DOI:10.3969/j.issn.1009-6744.2013.06.024 |
| [5] |
Liu J, Zio E. A scalable fuzzy support vector machine for fault detection in transportation systems[J]. Expert Systems with Applications, 2018, 102: 36-43. DOI:10.1016/j.eswa.2018.02.017 |
| [6] |
Wang Y, Han L, Wu M L, et al. A hardware-in-the-loop simulation test bench for subway train brake systems[J]. Advanced Materials Research, 2014, 1064: 219-224. DOI:10.4028/www.scientific.net/AMR.1064 |
| [7] |
祝露, 王晓东, 吴萌岭, 等. 备用制动系统性能比较[J]. 交通运输工程学报, 2016, 16(1): 80-87, 94. ZHU Lu, WANG Xiaodong, WU Mengling, et al. Performance comparison of backup brake system[J]. Journal of Traffic and Transportation Engineering, 2016, 16(1): 80-87, 94. (in Chinese) DOI:10.3969/j.issn.1671-1637.2016.01.010 |
| [8] |
刘敬辉. 基于FTA-AHP的铁路安全风险综合评估方法[J]. 中国铁道科学, 2017, 38(2): 138-144. LIU Jinghui. Synthesized risk assessment method for railway safety based on FTA-AHP analysis[J]. China Railway Science, 2017, 38(2): 138-144. (in Chinese) DOI:10.3969/j.issn.1001-4632.2017.02.21 |
| [9] |
Yang J W, Wang J H, Huang Q, et al. Reliability assessment for the solenoid valve of a high-speed train braking system under small sample size[J]. Chinese Journal of Mechanical Engineering, 2018, 31(3): 47-57. |
| [10] |
曹吉康, 姚恩涛, 乐珺, 等. 基于动态故障树的轴控式列车制动系统的可靠性分析[J]. 机械制造与自动化, 2016, 45(3): 11-13, 46. CAO Jikang, YAO Entao, LE Jun, et al. Reliability analysis of train axle control braking system based on dynamic fault tree[J]. Machine Building & Automation, 2016, 45(3): 11-13, 46. (in Chinese) DOI:10.3969/j.issn.1671-5276.2016.03.004 |
| [11] |
Wei X, Cheng M, Jia L M, et al. (2014) On simulation of urban rail vehicle electro-pneumatic braking systems[C]//Proceedings of the 2013 International Conference on Electrical and Information Technologies for Rail Transportation (EITRT2013). Berlin: Springer, 2014: 347-356.
|
| [12] |
Lavasani S M, Zendegani A, Celik M. An extension to Fuzzy Fault Tree Analysis (FFTA) application in petrochemical process industry[J]. Process Safety and Environmental Protection, 2015, 93: 75-88. DOI:10.1016/j.psep.2014.05.001 |
| [13] |
Abdo H, Flaus J M. Monte Carlo simulation to solve fuzzy dynamic fault tree[J]. IFAC-PapersOnLine, 2016, 49(12): 1886-1891. DOI:10.1016/j.ifacol.2016.07.905 |
| [14] |
蔡超, 刘艳秋. 基于模糊贝叶斯网络的物流服务供应链系统可靠性分析[J]. 中国流通经济, 2018, 32(4): 49-58. CAI Chao, LIU Yanqiu. Reliability analysis of logistics service supply chain system based on fuzzy bayesian networks[J]. China Business and Market, 2018, 32(4): 49-58. (in Chinese) |
| [15] |
Boudali H, Dugan J B. A discrete-time Bayesian network reliability modeling and analysis framework[J]. Reliability Engineering & System Safety, 2005, 87(3): 337-349. |
 2019, Vol. 42
2019, Vol. 42


