钻孔预抽是煤矿井下瓦斯灾害治理的重要方法之一[1],而钻孔设计参数与抽采效果有着直接的关系,因此对钻孔进行合理的布置显得至关重要[2-4],它不仅可以直接提高钻孔瓦斯抽采效率,而且还能减少钻孔施工的工程量。为考察钻孔布置参数对瓦斯抽采效果的影响,众多学者对钻孔参数优化进行大量的研究,取得了丰富的研究成果。卢平等[5]利用数值模拟方法研究了煤层钻孔周围瓦斯渗流规律及影响钻孔瓦斯抽放率的因素,提出了原始煤层钻孔抽放瓦斯时存在极限抽放时间、极限抽放量和最大的安全抽放钻孔间距。王旭峰等[6]采用物理模拟方法,分析了煤层群不同开采顺序时的采动裂隙演化特征,并运用FLUENT数值模拟软件分析并确定了铁法矿区泄压煤层气抽采钻孔的布置原则。秦伟等[7]以山西新大地煤矿15101综放面为研究对象,针对钻孔在走向和倾向上的具体位置提出了6种优化方案,并利用FLUENT数值模拟软件对优化方案进行模拟分析,确定了15101综放面邻近层穿层钻孔的最佳位置。以上文献主要对钻孔抽采时间效应及钻孔位置等抽采参数进行了优化确定,但未对掩护煤巷掘进时多个穿层钻孔之间的布置方式进行深入研究。刘军等[8]利用COMSOL Multiphysics数值模拟软件对钻孔抽采时间、钻孔间距和瓦斯抽采有效影响半径的关系进行了研究,得出缩短抽采钻孔布置间距可有效消除抽采空白带,预防和消除在掘进过程中煤与瓦斯突出危险性,提高巷道掘进速度,但是由于井下煤层范围较广,缩短钻孔的布置间距又会增加钻孔的工程量。徐青伟等[9]基于几何图形分析提出一种新的钻孔布置方式,既能消除钻孔抽采瓦斯在煤层中形成的空白带,又能减少钻孔的孔数,从而提高钻孔抽采效率,考虑到不同钻孔的长度不一致,因此钻孔的孔数不能完全表征钻孔的工程量。李胜等[10]利用COMSOL Multiphysics软件对成庄矿4321工作面钻孔瓦斯抽采进行数值模拟,得出增大抽采负压对抽采效果影响不明显,并确定穿层钻孔布置的终孔间距为9 m。Liu等[11]利用压力下降系数值来反映钻孔之间的干扰程度,并采用双钻孔模式分析了两个钻孔之间的相互作用,结果表明,随着煤的渗透率增加,压力下降系数值逐渐增大,当煤渗透率过低时,钻孔间的相互作用可以忽略,该研究中对钻孔之间的影响进行了分析,但未深入分析不同钻孔布置方式下所需的钻孔工程量。以上专家学者主要利用专业的模拟软件对钻孔的抽放时间、抽放位置和布置间距等进行了研究,但未定量地比较分析不同钻孔布置方式下留有空白带的面积和消除空白带所需的时间,而且较少对穿层钻孔在不同布置方式下的瓦斯抽采效果和钻孔工程量进行分析。
为了探明潘三煤矿11-2煤穿层钻孔不同布置方式对瓦斯抽采的影响,笔者在建立煤岩瓦斯气固耦合数值模型的基础上,利用有限容积和牛顿迭代法分别对10×5,8×6和7×7钻孔布置方式下的瓦斯抽采过程进行数值模拟,比较不同钻孔布置方式下残留的空白带面积和消除空白带所需的抽采时间;以潘三煤矿下向穿层钻孔预抽2121(1)运顺掘进工作面瓦斯为试验对象,通过现场试验分析不同穿层钻孔布置方式下所需的钻孔工程量和单孔平均抽采瓦斯纯量,并结合数值模拟分析结果,优选出最优的钻孔布置方式,为煤矿现场穿层钻孔瓦斯抽采时钻孔的优化设计提供理论指导。
1 煤岩瓦斯气固耦合数学模型 1.1 基本假设为了便于计算,笔者把钻孔瓦斯抽采物理模型简化为二维模型,并做如下假设[12-13]:
1) 煤层中瓦斯为理想气体;
2) 在裂隙中游离瓦斯流动符合Darcy定律,在孔隙中吸附瓦斯扩散符合Fick定律;
3) 煤层变形为弹性变形,遵从Hooke定律;
4) 煤层介质均匀且各向同性。
1.2 煤层瓦斯渗流和扩散方程煤层介质由裂隙和孔隙构成:裂隙为游离瓦斯的流通通道,其流动符合Darcy定律;孔隙为吸附瓦斯的主要赋存结构,其扩散符合Fick定律。假设在微元体中,裂隙系统和孔隙系统之间的质量交换瞬间完成,则微元体的瓦斯质量守恒方程可以描述为单位时间内裂隙中的游离瓦斯和孔隙中的吸附瓦斯质量变化等于微元体各方向上渗流和扩散至微元体的瓦斯净质量,即[12]:
| $ \frac{\partial(\rho n+C)}{\partial t}+\nabla \cdot(\rho \boldsymbol{V})=\nabla \cdot(D \nabla C)。$ | (1) |
式中:ρ为游离瓦斯的密度,kg/m3,游离瓦斯看成理想气体,可利用理想气体状态方程进行求解,即ρ=β·p;p为瓦斯压力, Pa;β为瓦斯的压缩系数,kg/(m3·Pa),β=1/(Rg·T);Rg为瓦斯气体常数, J/(kg·K);T为煤层温度,K;n为微元体的孔隙率,无量纲,它是与瓦斯压力和煤层应力有关的变量;C为单位体积煤层所含吸附状态瓦斯的质量,kg/m3;D为孔隙系统瓦斯扩散系数, m2/s;V是游离瓦斯渗流速度矢量,m/s,可采用Darcy渗流定律进行计算:
| $ \boldsymbol{V}=-\frac{k}{\mu} \nabla p_{0}。$ | (2) |
式中:k为裂隙系统渗透率,m2,是孔隙率n的函数;μ为瓦斯气体粘度,Pa·s,与温度相关,含瓦斯煤岩在瓦斯渗流过程可视为等温过程,故不考虑温度的影响。
吸附瓦斯浓度C可根据Langmuir进行计算[12, 14]:
| $ C=\frac{a b c p p_{\mathrm{n}}}{(1+b p) R_{\mathrm{g}} T}。$ | (3) |
式中:a为单位质量可燃物在参考压力下的极限吸附量,m3/kg;b为吸附平衡常数,Pa-1;c为单位体积可燃物的质量,满足
与前面裂隙和孔隙系统取同一微元体,二维微元体受力的守恒方程如下:
| $ \frac{\partial \sigma_{x}}{\partial x}+\frac{\partial {\boldsymbol{\tau}}_{y x}}{\partial y}+f_{x}=0, $ | (4) |
| $ \frac{\partial \sigma_{y}}{\partial y}+\frac{\partial {\boldsymbol{\tau}}_{x y}}{\partial x}+f_{y}=0。$ | (5) |
式中:fx和fy分别为x和y方向上的体积力,Pa/m;σx和σy为x和y方向上的正应力,Pa;
以y方向为垂直方向,根据微元体在x,y两个方向上力的平衡关系,把Hooke定律、煤岩变形几何方程及修正的Terzaghi有效应力公式带入应力平衡方程(4)和(5)中,得到以位移为变量的变形场微分方程[14-15]:
| $ E_{\mathrm{s}} \frac{\partial^{2} u}{\partial x^{2}}+G \frac{\partial^{2} u}{\partial y^{2}}+(G+\lambda) \cdot \frac{\partial^{2} v}{\partial x \cdot \partial y}-\frac{\partial(\alpha p)}{\partial x}=0, $ | (6) |
| $ E_{\rm s} \frac{\partial^{2} v}{\partial y^{2}}+G \frac{\partial^{2} v}{\partial x^{2}}+(G+\lambda) \cdot \frac{\partial^{2} u}{\partial y \cdot \partial x}-\frac{\partial(\alpha p)}{\partial y}+\rho_{\rm s} g=0。$ | (7) |
式中:G为剪切模量, 满足
考虑煤体变形和瓦斯压力对固体骨架的作用,忽略温度及煤岩体瓦斯吸附和解吸对孔隙率的影响,根据孔隙率定义有:
| $ n=1-\frac{\left(1-n_{0}\right)}{1+\varepsilon_{\mathrm{v}}}\left(1-\frac{p-p_{0}}{k_{\mathrm{s}}}\right)。$ | (8) |
式中:εv为煤岩体的体应变,无量纲;ks为煤岩固体骨架模量,Pa;n0为初始孔隙率,无量纲;p0为初始瓦斯压力,Pa。
渗透率为孔隙率函数,采用Kozeny-Carman公式求解[14, 16]:
| $ k=\frac{k_{0}}{1+\varepsilon_{\mathrm{v}}}\left[1+\frac{\varepsilon_{\mathrm{v}}}{n_{0}}+\frac{\left(p-p_{0}\right) \cdot\left(1-n_{0}\right)}{k_{\mathrm{s}} \cdot n_{0}}\right]^{3}。$ | (9) |
式中k0为初始瓦斯渗透率,m2,该参数主要通过与现场钻孔瓦斯抽采反演求得。
以上耦合模型包括渗流扩散方程(1)、变形方程(6)(7)和耦合参数方程(8)(9)。在瓦斯渗流扩散方程(1)中,仅含有瓦斯压力p为未知变量的非线性方程,变形方程(6)(7)的未知变量为u和v。瓦斯场和变形场都是强非线性方程,求解时先用有限容积法对守恒方程进行离散,然后采用Newton-Raphson迭代和GMRES法(generalized minimal residual algorithm method)相结合,求解非线性方程组[17-19],最后利用Fortran语言编程实现煤层钻孔瓦斯抽采过程的数值求解。
2 不同钻孔布置的数值模拟及分析 2.1 穿层钻孔布置设计的依据根据潘三煤矿11-2煤瓦斯抽采有效半径的现场测试及相关文献,淮南矿区穿层钻孔瓦斯抽采有效半径为5.0 m左右[20],所以在布孔时尽量考虑终孔之间的最大距离控制在10.0 m以内。目前淮南矿区穿层钻孔的布孔方式主要采用10×5布置,即走向终孔间距为10.0 m,倾向终孔间距为5.0 m。为了保证终孔最大间距在10.0 m范围内,本次选择10×5,8×6(走向终孔间距为8.0 m,倾向终孔间距为6.0 m)、7×7(走向和倾向终孔间距均为7.0 m)3种布孔方式进行现场试验和数值模拟分析。
2.2 物理模型及模拟条件由于各钻孔排列是呈对称分布,所以沿钻孔中心线是绝流的,因此可以对不同穿层钻孔布置进行简化,把4个钻孔之间的区域作为研究对象,3种布孔方式的简化二维模型如图 1所示。
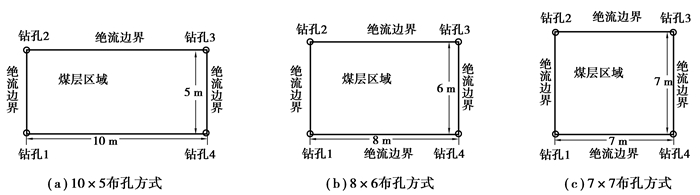
|
图 1 布孔方案示意图 Fig. 1 Schematic diagrams of three borehole layouts |
根据实验室对潘三矿11-2煤的a,b常数实验、力学实验及现场测试,本次模拟使用参数如表 1所示。
| 表 1 11-2煤力学及地质参数 Table 1 Mechanical and geological parameters of 11-2 coal seam |
根据前面物理模型分析,计算区域边界可看成为绝流边界,钻孔边界采用定压边界条件,不考虑钻孔边界的瓦斯扩散,即有:
| $ \left\{\begin{array}{l}{\left.\frac{\partial p(i, j)}{\partial n}\right|_{\Gamma_{\mathrm{s}}}=0}, \\ {p\left.(i, j)\right|_{\Gamma_{\mathrm{r}}}=p_{\text { out }}}。\end{array}\right. $ | (10) |
式中:Γs为计算区域边界;Γr为钻孔边界;pout为钻孔边界实际抽采负压,为pn-1.3 ×104 Pa。
当求解变形场时,计算区域边界位移量为0,钻孔内正应力和剪应力均为0,变形场边界条件如下式:
| $ \left\{\begin{array}{l}{u\left.(i, j)\right|_{\Gamma_{\mathrm{s}}}=0}, \\ {v\left.(i, j)\right|_{\Gamma_{\mathrm{s}}}=0}, \\ {\sigma\left.(i, j)\right|_{\Gamma_{\mathrm{r}}}=0}, \\ {\tau\left.(i, j)\right|_{\Gamma_{\mathrm{r}}}=0。}\end{array}\right. $ | (11) |
本节将主要分析钻孔不同布置方式对瓦斯压力和瓦斯含量(X)分布的影响。为了使模拟结果更具有可比性,除了计算区域及钻孔位置不同之外,所有模拟基础参数都相同,模拟得到3种布孔方式抽采30 d的瓦斯压力和瓦斯含量分布,如图 2~4所示。
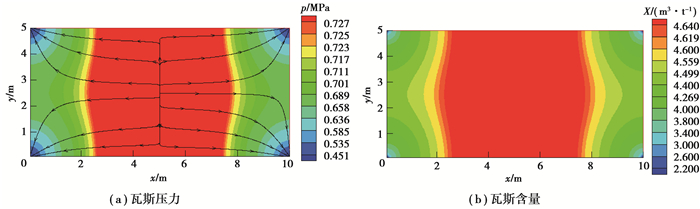
|
图 2 10×5布孔方式下的瓦斯压力和含量分布云图 Fig. 2 Gas pressure and content distribution of the borehole layout of 10×5 |
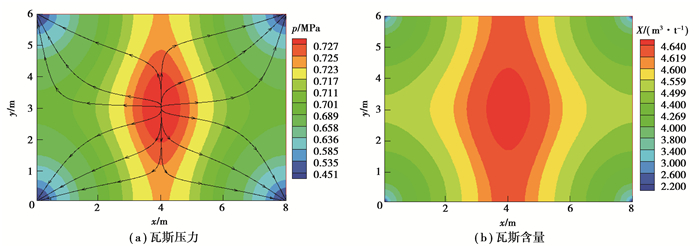
|
图 3 8×6布孔方式下的瓦斯压力和含量分布云图 Fig. 3 Gas pressure and content distribution of the borehole layout of 8×6 |

|
图 4 7×7布孔方式下的瓦斯压力和含量分布云图 Fig. 4 Gas pressure and content distribution of the borehole layout of 7×7 |
从图 2~4可知,计算区域内的瓦斯压力分布不同,越靠近钻孔附近,瓦斯压力越低,这主要是因为在瓦斯抽采条件下,煤层内的瓦斯不断地向钻孔方向运移,从瓦斯压力图中流线的箭头指向(图中黑色带箭头线)可以看出。由于煤层瓦斯压力和含量满足Langmuir方程,所以同一布孔方式下的瓦斯含量和压力的分布具有相似性,也是越靠近钻孔,瓦斯含量越低,离钻孔越远,瓦斯压力越高,瓦斯含量越大。
通过比较图 2~4可知,不同布孔方式下的瓦斯压力和含量分布明显不同。7×7布孔方式下,中间红色区域近似圆形分布,说明瓦斯压力和瓦斯含量分布均匀。而10×5布孔方式下,因钻孔间距过于不均匀,使得相隔较近的钻孔之间出现抽采范围“重叠”现象,而相隔较远的钻孔之间更容易出现空白带。
为了更直观地比较它们之间的异同,需要根据瓦斯抽采有效半径的判据来分别计算抽采30 d后钻孔之间的危险区域面积(也称为空白带面积)。现场测试的初始瓦斯压力为1.4 MPa,带入Langmuir方程中,可求得初始的瓦斯含量为6.552 m3/t。根据防治煤与瓦斯突出规定,若初始瓦斯压力大于0.74 MPa,且初始瓦斯含量大于6.0 m3/t时,则抽采后残余瓦斯压力应低于0.74 MPa,而且瓦斯抽采率应大于70%才为有效抽采范围。所以当抽采后残余瓦斯压力小于0.74 MPa,且瓦斯含量应小于4.59 m3/t才为有效范围。根据模拟结果,采用7×7布孔方式抽采后瓦斯压力最大为0.73 MPa,最大瓦斯含量为4.655 m3/t;采用8×6布孔方式抽采后瓦斯压力最大为0.728 MPa,最大瓦斯含量为4.648 m3/t;采用10×5布孔方式抽采后瓦斯压力最大为0.764 MPa,最大瓦斯含量为4.782 m3/t;若以瓦斯压力0.74 MPa作为危险区域的判据,则只有10×5布孔方式抽采后会存在一定的空白带面积,说明采用10×5布孔方式更容易留有空白带。若以残余瓦斯含量大于4.59 m3/t作为空白带面积,可以得到3种不同布孔方式抽采30 d后的空白带面积,如图 5所示。
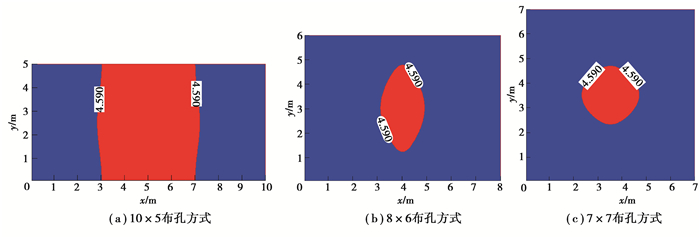
|
图 5 不同布孔方式的空白带分布图 Fig. 5 Blank zones distribution diagram of three borehole layouts |
根据图 5可以计算出采用10×5,8×6和7×7不同布孔方式抽采30 d后的空白带面积分别为21.0,5.08,4.52 m2,由此说明采用7×7与8×6留有空白带的面积相差不大,而采用10×5布孔方式留有空白带面积最大。
从煤矿安全生产角度,最重要的是消突,因此,除了比较相同抽采时间后留有的空白带面积外,还应比较分析3种布孔方式在相同地质条件下消除空白带所需的抽采时间。按照前面分析的消突要求,钻孔周围区域的瓦斯压力应低于0.74 MPa,且残余瓦斯含量低于4.59 m3/t时才算完全消突。以此作为模拟判据,得出采用10×5钻孔布置所需的抽采时间为35.83 d,而7×7与8×6钻孔布置所需的抽采时间分别为31.67,31.92 d,说明采用10×5钻孔布置所需的抽采时间明显长于采用7×7与8×6钻孔布置。
综合上述数值模拟结果分析得出,因10×5布孔方式下钻孔间距过于不均匀,所以在钻孔瓦斯抽采过程中更容易留有空白带,而且消除空白带所需的抽采时间也会更长,这两个方面均说明10×5的布孔方式相对更不利于消突。
3 不同布孔方式的瓦斯抽采效果试验考察 3.1 试验地点及钻孔布置为使试验结果更具有可比性,试验地点都选择在2121(1)运顺瓦斯综合治理巷,该巷道主要是为掩护2121(1)运顺工作面掘进,通过在2121(1)运顺瓦斯综合治理巷的钻场内向2121(1)运顺施工下向穿层钻孔,预抽2121(1)运顺掘进工作面前方的瓦斯,为2121(1)运顺掘进提供安全保障。根据前面数值模拟钻孔的布置方式,共施工6个钻场进行试验,其中1#和2#钻场为10×5布置,4#和5#钻场为8×6布置,7#和8#钻场为7×7布置。每个钻场原则上按照6组进行设计,由于断层和现场施工条件的影响,1#钻场设置了5组钻孔,7#钻场设置了8组钻孔,钻孔布置如图 6所示。从图 6可知,1#和2#钻场总孔数为110个,4#和5#钻场总孔数为96个,7#和8#钻场总孔数为112个。为了考察不同布孔方式下钻孔的瓦斯抽采效率,在3种布孔方式所在的钻场位置分别安设了孔板流量计监测瓦斯抽采流量和瓦斯浓度。
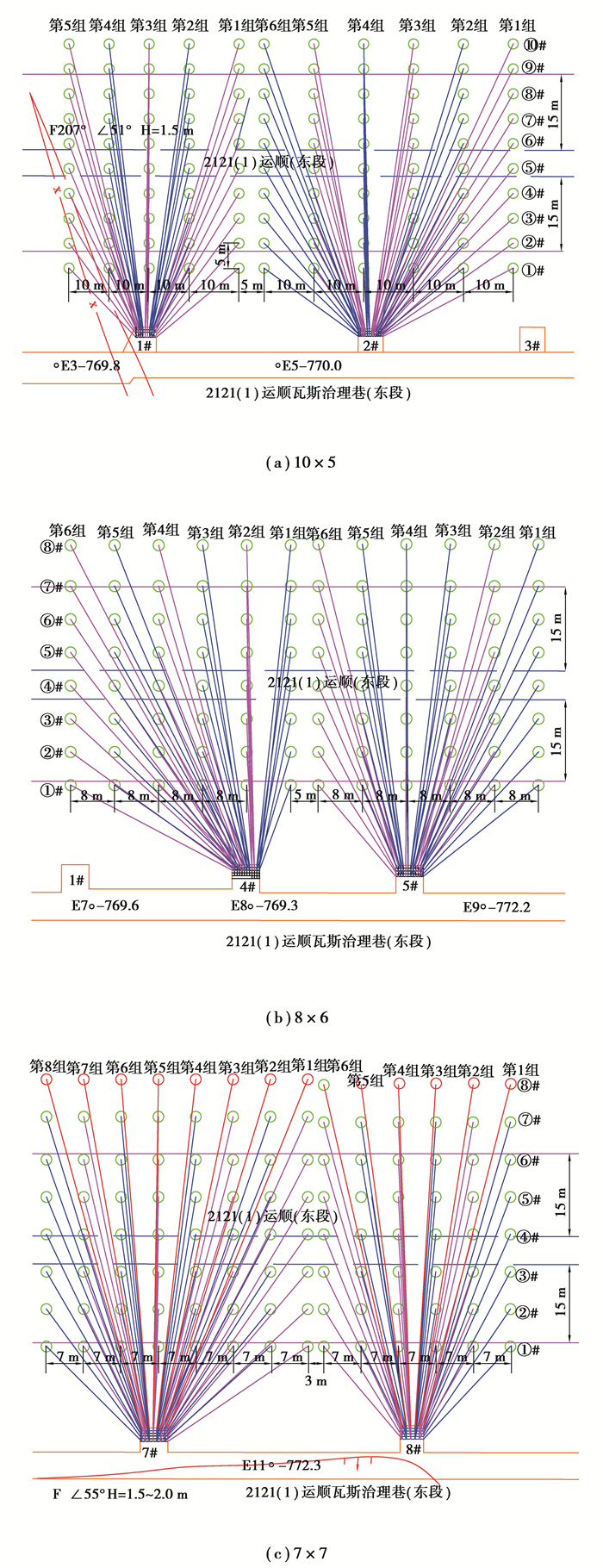
|
图 6 钻场内钻孔布置图 Fig. 6 The borehole layouts of drilling fields |
为了直观地比较不同钻孔布置方式的钻孔工程量,笔者提出每掘进单位长度巷道所需钻孔工程量指标,即为保证钻孔瓦斯抽采在倾向上满足煤巷掘进时泄压范围要求的前提下,每掘进1 m煤巷长度所需要的钻孔工程量。若需要的钻孔工程量越少,则钻孔施工成本就越低,因此可以从钻孔施工方面提高钻孔的抽采效益。
考虑到现场钻孔参数的数据量较大,10×5,8×6和7×7布孔方式分别以2#、5#和8#钻场为例,统计了现场不同钻场的钻孔施工长度,如表 2所示。
| 表 2 钻场中钻孔施工长度 Table 2 Boreholes length in drilling fields |
根据图 6(a)可知,现场10×5钻孔布置通常按照6排设计,每排10孔,每排钻孔终孔间距为10.0 m,每个钻场能够掩护巷道走向长度为50 m;8×6钻孔布置也一般按照6排设计,每排8孔,每排钻孔终孔间距为8.0 m,每个钻场能够掩护巷道走向长度为40.0 m;现场7×7钻孔布置也是按照6排设计,根据条带预抽时煤层倾向宽度要求,至少要保证被掩护煤巷两侧15 m范围内都被预抽。根据防治煤与瓦斯突出规定,⑦#钻孔与煤层顶板相交点距煤巷帮应大于15 m,但受到钻孔偏角的影响,实际⑦#钻孔与煤层顶板的相交点距煤巷帮小于15 m,所以不能够保证煤巷两侧15 m范围内被预抽,需要再补打⑧#钻孔,因此,7×7钻孔布置时每排也需要8个钻孔,每排钻孔终孔间距为7.0 m,每个钻场能够掩护巷道走向长度为35.0 m。由表 2统计得到3种不同布孔方式下对应钻场累计的钻孔施工长度,根据式(12)求得每掘进单位长度巷道所需的钻孔工程量H,计算结果如表 3所示。
| $ H=\frac{\sum\limits_{j=1}^{r} l_{j}}{L}, $ | (12) |
| 表 3 不同钻孔布置下所需钻孔工程量 Table 3 Engineer quantity of boreholes under three borehole layouts |
式中:H为每掘进1 m长度巷道所需的钻孔工程量, m/m;lj为钻场中第j个钻孔的长度, m;L为钻场掩护巷道长度, m;r为钻场中钻孔总个数。
从表 3中可知,采用8×6布孔方式的单位长度巷道所需钻孔工程量最小,为69.0 m/m,而采用7×7布孔方式的单位长度巷道所需钻孔工程量最大,高达77.0 m/m,这主要是因为7×7钻孔布置在煤层倾向上与8×6钻孔布置需要同样多的钻孔数量,但是走向上孔间距比8×6钻孔布置更小(7×7钻孔布置为7.0 m,而8×6钻孔布置为8.0 m)。因此从所需钻孔工程量角度看,8×6布孔方式最优。
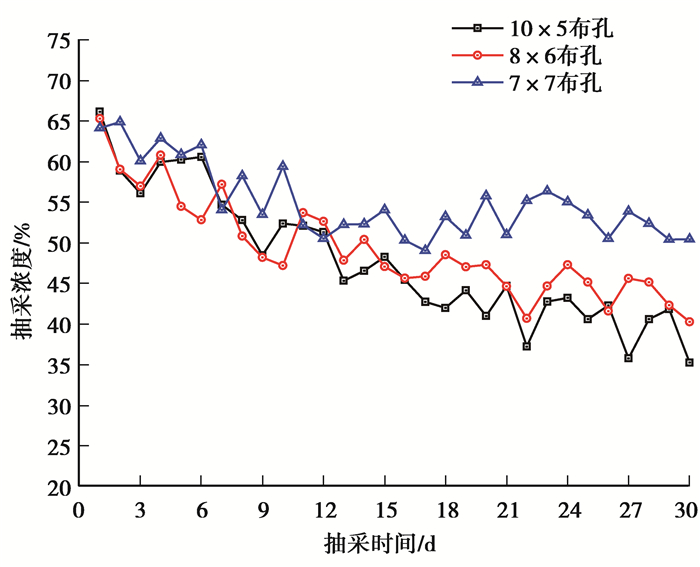
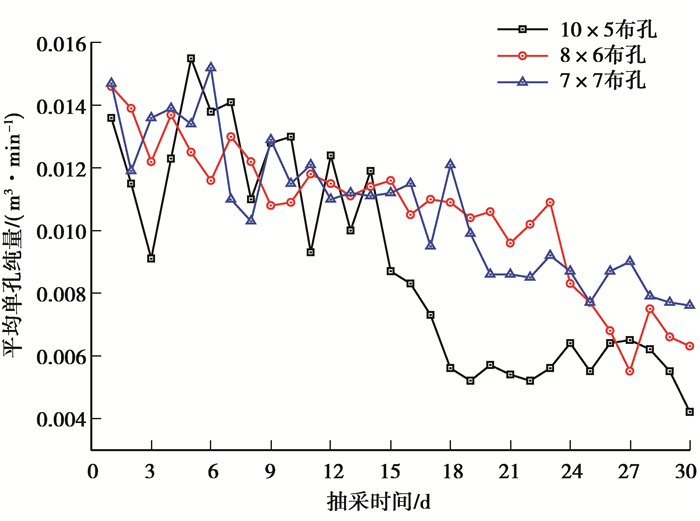
3.3 钻场瓦斯抽采试验根据现场实测数据,统计了6个试验钻场抽采30 d的瓦斯浓度。由于随着抽采时间增加,钻孔瓦斯抽采量及抽采瓦斯浓度具有一定的衰减性,为使实测数据更具有可比性,统计每个钻场所有钻孔都施工完毕后30 d内的瓦斯抽采数据,抽采浓度分布如图 7所示。根据不同布孔方式下的混合流量及钻场内总孔数,可以求出不同抽采时间下单孔日平均抽采瓦斯纯流量,其分布曲线如图 8所示。
|
图 7 不同布孔方式下瓦斯抽采浓度与抽采时间的关系 Fig. 7 Relationship between gas concentration and pumping time under three borehole layouts |
|
图 8 不同布孔方式单孔日均抽采瓦斯纯量与抽采时间的关系 Fig. 8 Relationship between gas flow volume per day and pumping time under three borehole layouts |
从图 7可以看出,不同抽采时间下的瓦斯浓度主要在35%~66%之间上下波动,这主要是由抽采负压波动和地质条件复杂所致。随着抽采时间增加,3种不同布孔方式抽采瓦斯浓度均呈现下降趋势,但7×7布孔方式抽采的瓦斯浓度下降速度最慢,说明采用7×7布孔方式时,瓦斯抽采浓度受钻孔间相互干扰最小。根据图 8可知,随着抽采时间增加,3种布孔方式的单孔日均抽采瓦斯纯量都呈现下降的趋势,但采用10×5布孔方式的单孔日均抽采瓦斯纯量在14~18 d之间下降幅度最大,而8×6和7×7布孔方式在抽采30 d内未出现单孔日均抽采瓦斯纯量下降幅度大的情况,说明若采用10×5布孔时可能会过早地出现“井间干扰”,降低瓦斯抽采的效果。为了进一步直观地比较不同布孔方式下的抽采效果,根据图 7与图 8的数据,计算出不同布孔方式在抽采30 d内的单孔平均浓度及平均抽采瓦斯纯量,结果如表 4所示。
| 表 4 不同布孔方式单孔在抽采30 d内的平均瓦斯数据表 Table 4 Average gas concentration and flow volume per day for 30 days of three borehole layouts |
从表 4可知,抽采30 d内,采用7×7布孔方式的单孔平均抽采瓦斯纯量为0.010 7 m3/min,采用8×6布孔方式的单孔平均抽采瓦斯纯量略低于7×7布孔方式,而10×5布孔方式下的单孔平均抽采瓦斯纯量仅为0.008 9 m3/min。
综合以上分析,从抽采效果角度,10×5布孔方式的瓦斯抽采效果最差,7×7布孔方式的瓦斯抽采效果略优于8×6布孔方式。
4 钻孔布置方式优选根据数值模拟和现场试验结果分析,得到穿层钻孔不同布置方式对瓦斯抽采的影响,如表 5所示。从表 5中可知,相同瓦斯抽采条件下,采用10×5布孔方式留有的空白带面积最大,说明从消突角度,10×5布孔方式最差,7×7与8×6更优;从现场单位长度巷道需要施工的钻孔工程量角度分析,8×6布孔方式所需钻孔工程量最少,10×5布孔方式次之,7×7布孔方式所需的钻孔工程量最大;从试验钻场瓦斯抽采结果分析可知,10×5布孔方式的单孔平均抽采瓦斯纯量最低,效果最差,7×7布孔方式的单孔平均抽采瓦斯纯量略高于8×6;综合以上3个方面分析,可以得出8×6布孔方式最优。
| 表 5 不同钻孔布置方式的数值模拟和现场试验结果 Table 5 Comparison of numerical simulation and experiment results of three borehole layouts |
当然,本次钻孔优化布置研究的具体地点是在潘三矿2121(1)运顺瓦斯综合治理巷,而对于不同矿井,甚至不同煤层,因煤层地质条件不同,瓦斯治理巷所在的位置也不同,而且煤层厚度也存在较大差异,这可能会导致钻孔的角度、长度、煤层瓦斯压力和含量等参数发生明显改变,所以不同钻孔布置方式下所需的钻孔工程量、空白带面积和单孔平均抽采瓦斯纯量可能会有差异,因此若在不同试验地点进行钻孔布置方式的优化时,需要对这些参数进行重新计算和分析。
5 结论为了研究潘三煤矿2121(1)运顺瓦斯综合治理巷中不同穿层钻孔布置对瓦斯抽采的影响,利用建立的煤岩瓦斯气固耦合数值模型对10×5,8×6和7×7钻孔布置方式的瓦斯抽采过程进行数值模拟分析,并通过现场试验对不同穿层钻孔布置方式的钻孔工程量和单孔平均抽采瓦斯纯量进行考察,得出以下主要结论:
1) 在相同抽采条件下,采用10×5布孔方式的空白带面积最大,采用8×6的空白带面积略高于7×7;在消除空白带所需的时间上,10×5所需时间最长,说明10×5布孔方式最不利于消突;
2) 通过现场试验得出,采用7×7布孔方式的单位长度巷道所需钻孔工程量最大,采用8×6布孔方式所需钻孔工程量最小;
3) 根据钻孔抽采30 d数据统计分析得出,采用10×5布孔方式的单孔平均抽采瓦斯纯量最低,抽采效果最差,7×7布孔方式的抽采效果略优于8×6布孔方式;
4) 结合数值模拟分析和现场试验综合比较,确定8×6布孔方式在潘三煤矿2121(1)运顺瓦斯综合治理巷中最优。
因钻孔按照7×7布置时钻孔位置完全对称,可以直观地看出7×7是最优的,但是从潘三煤矿2121(1)运顺瓦斯综合治理巷中3种钻孔布置所需的工程量来看,7×7所需钻孔工程量又是最多的,这将导致现场工程技术人员在选择何种穿层钻孔布置进行瓦斯抽采时存在一定的困难。笔者对潘三煤矿11-2煤穿层钻孔布置从多个方面比较了3种方案的优缺点,可为煤矿现场对穿层钻孔的优化布置提供一定的指导作用。
致谢: 本研究得到淮南矿业(集团)有限责任公司潘三煤矿的领导及现场工作人员大力支持,在此表示衷心感谢。
| [1] |
周福宝, 王鑫鑫, 夏同强, 等. 瓦斯安全抽采及其建模[J]. 煤炭学报, 2014, 39(8): 1659-1666. ZHOU Fubao, WANG Xinxin, XIA Tongqiang, et al. A model of safe drainage of coal seam gas[J]. Journal of China Coal Society, 2014, 39(8): 1659-1666. (in Chinese) |
| [2] |
Karacan C Ö, Diamond W P, Schatzel S J. Numerical analysis of the influence of in-seam horizontal methane drainage boreholes on longwall face emission rates[J]. International Journal of Coal Geology, 2007, 72(1): 15-32. DOI:10.1016/j.coal.2006.12.007 |
| [3] |
Wu B, Hua M, Feng X Y, et al. Study on methods of determining gas extraction radius with numerical simulation[J]. Procedia Engineering, 2012, 45: 345-351. DOI:10.1016/j.proeng.2012.08.169 |
| [4] |
Zhang C, Xu J, Peng S, et al. Dynamic behavior of gas pressure and optimization of borehole length in stress relaxation zone during coalbed methane production[J]. Fuel, 2018, 233: 816-824. DOI:10.1016/j.fuel.2018.06.132 |
| [5] |
卢平, 李平, 周德永, 等. 石门揭煤防突抽放瓦斯钻孔合理布置参数的研究[J]. 煤炭学报, 2002, 27(3): 242-248. LU Ping, LI Ping, ZHOU Deyong, et al. Study on proper layout parameters of the gas drainage drills of outburst prevention in rock cross-cut coal uncovering[J]. Journal of China Coal Society, 2002, 27(3): 242-248. (in Chinese) DOI:10.3321/j.issn:0253-9993.2002.03.005 |
| [6] |
王旭锋, 张东升, 李国君, 等. 铁法矿区高瓦斯低透气性煤层群卸压煤层气抽采钻孔布置[J]. 煤炭学报, 2011, 36(8): 1296-1301. WANG Xufeng, ZHANG Dongsheng, LI Guojun, et al. Boreholes layout of coal mine methane drainage for high gassy and low permeability coal seams in Tiefa coalfield[J]. Journal of China Coal Society, 2011, 36(8): 1296-1301. (in Chinese) |
| [7] |
秦伟, 许家林, 吴仁伦, 等. 基于CFD模拟的邻近层穿层钻孔瓦斯抽采优化设计[J]. 采矿与安全工程学报, 2012, 29(1): 111-117. QIN Wei, XU Jialin, WU Renlun, et al. Gas extraction optimum design of layer-through borehole in adjacent seam based on CFD simulation[J]. Journal of Mining and Safety Engineering, 2012, 29(1): 111-117. (in Chinese) DOI:10.3969/j.issn.1673-3363.2012.01.020 |
| [8] |
刘军, 王兆丰, 李学臣, 等. 消除矿井瓦斯抽采空白带方法的研究[J]. 煤炭科学技术, 2012, 40(12): 59-61, 87. LIU Jun, WANG Zhaofeng, LI Xuechen, et al. Study on the methods of eliminating blank zone of mine gas drainage[J]. Coal Science and Technology, 2012, 40(12): 59-61, 87. (in Chinese) |
| [9] |
徐青伟, 王兆丰. 预抽煤层瓦斯消除空白带钻孔布置方式的优化[J]. 煤矿安全, 2015, 46(8): 152-155. XU Qingwei, WANG Zhaofeng. Optimization of borehole layout to eliminate drainage blind by pre-pumping coal seam gas[J]. Safety in Coal Mines, 2015, 46(8): 152-155. (in Chinese) |
| [10] |
李胜, 毕慧杰, 范超军, 等. 基于流固耦合模型的穿层钻孔瓦斯抽采模拟研究[J]. 煤炭科学技术, 2017, 45(5): 121-127. LI Sheng, BI Huijie, FAN Chaojun, et al. Simulation study of gas drainage with borehole passed through strata based on fluid-solid coupling[J]. Coal Science and Technology, 2017, 45(5): 121-127. (in Chinese) |
| [11] |
Liu Z D, Cheng Y P, Jiang J Y, et al. Interactions between coal seam gas drainage boreholes and the impact of such on borehole patterns[J]. Journal of Natural Gas Science and Engineering, 2017, 38: 597-607. DOI:10.1016/j.jngse.2017.01.015 |
| [12] |
吴世跃. 煤层中的耦合运动理论及其应用:具有吸附作用的气固耦合运动理论[M]. 北京: 科学出版社, 2009. WU Shiyue. Theory and application of coupling behavior in coal-gas-solid coupling motion theory of adsorption[M]. Beijing: Science Press, 2009. (in Chinese) |
| [13] |
Kong X, Wang E, Liu Q, et al. Dynamic permeability and porosity evolution of coal seam rich in CBM based on the flow-solid coupling theory[J]. Journal of Natural Gas Science and Engineering, 2017, 40: 61-71. DOI:10.1016/j.jngse.2017.02.011 |
| [14] |
司鹄, 郭涛, 李晓红. 钻孔抽放瓦斯流固耦合分析及数值模拟[J]. 重庆大学学报, 2011, 34(11): 105-110. SI Hu, GUO Tao, LI Xiaohong. Analysis and numerical simulation of fluid-structure coupling of gas drainage from boreholes[J]. Journal of Chongqing University, 2011, 34(11): 105-110. (in Chinese) DOI:10.11835/j.issn.1000-582X.2011.11.017 |
| [15] |
Wang J G, Liu J, Kabir A. Combined effects of directional compaction, non-Darcy flow and anisotropic swelling on coal seam gas extraction[J]. International Journal of Coal Geology, 2013, 109/110: 1-14. DOI:10.1016/j.coal.2013.01.009 |
| [16] |
王登科, 彭明, 付启超, 等. 瓦斯抽采过程中的煤层透气性动态演化规律与数值模拟[J]. 岩石力学与工程学报, 2016, 35(4): 704-712. WANG Dengke, PENG Ming, FU Qichao, et al. Evolution and numerical simulation of coal permeability during gas drainage in coal seams[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(4): 704-712. (in Chinese) |
| [17] |
Saad Y, Schultz M H. GMRES:a generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869. DOI:10.1137/0907058 |
| [18] |
唐明云, 施安峰, 王晓宏, 等. 含轻质组分稠油油藏蒸汽注采过程自适应网格法[J]. 力学季刊, 2013, 34(1): 25-31. TANG Mingyun, SHI Anfeng, WANG Xiaohong, et al. Adaptive mesh refinement method for thermal recovery of heavy oil with light component using steam injection[J]. Chinese Quarterly of Mechanics, 2013, 34(1): 25-31. (in Chinese) DOI:10.3969/j.issn.0254-0053.2013.01.004 |
| [19] |
Laguna A A, Ozak N, Lani A, et al. Fully-implicit finite volume method for the ideal two-fluid plasma model[J]. Computer Physics Communications, 2018, 231: 31-44. DOI:10.1016/j.cpc.2018.05.006 |
| [20] |
辛明. 利用SF6示踪技术测试煤层瓦斯抽采半径[J]. 安徽理工大学学报(自然科学版), 2012, 32(1): 64-66. XIN Ming. Determination of gas extraction radius in coal seams by tracer technique with SF6[J]. Journal of Anhui University of Science and Technology(Natural Science), 2012, 32(1): 64-66. (in Chinese) DOI:10.3969/j.issn.1672-1098.2012.01.014 |
 2019, Vol. 42
2019, Vol. 42


