随着矿山浅部资源的减少,深部开采势在必行,超千米深井巷道围岩处于高应力状态,构造应力场复杂,开巷后围岩中容易出现很高的集中应力和偏应力[1]。开挖后的应力集中现象已严重影响了许多矿山的正常生产。如,冬瓜山铜矿在基建、生产过程中,局部深部巷道顶板下沉量可达500 mm、帮部鼓出量可达400 mm以上;凡口铅锌矿深部地压显著,部分巷道变形严重,常出现前掘后修的情况。传统上常以工程类比、定性评价结合人为主观判断确定巷道支护方案,而深井巷道支护方案选择是一个多目标决策问题,必须采取科学的方法深入研究。
针对深井巷道支护方式选择遇到的问题,国内外许多学者已进行了深入的研究。郑海力[2]将多级模糊评判与粗糙集理论结合,对巷道支护方案优选进行了研究;Niedbalski等[3]通过层次分析法(AHP)对巷道设计方案进行评价;Mahdevari等[4]研究了人工神经网络在巷道稳定性评价中的应用;Farzi等[5]对城市深基坑支护体系优选进行了研究;王望珍等[6]研究了博弈论在基坑支护方案优选中的应用;Wang等[7]、Cao等[8]对断层、高应力巷道支护设计方案进行了优化;李必红等[9]建立了Fisher判别分析模型(FDA)对基坑支护方案进行了优选;贺永俊等[10]、王宏伟等[11]根据神经网络法,研究了神经网络在锚杆支护方案优选及变形预测中的应用;陈建宏等[12]利用基于优势关系的粗糙集建立巷道支护方案评价体系,评价优选支护方案。唐诗卉[13]基于未确知理论对巷道支护方案进行评价。上述研究用不同理论方法将定性指标转化为定量指标进行分析,评价过程简便、客观性较好。然而,深井巷道支护方式的选择不仅需要灵活定量计算,而且需要反映支护方案属性与其效用之间的非线性关系。
鉴于此,将机巧灵活的TOPSIS[14]法与可反映序列之间非线性关系特征的灰色关联分析法(grey relational analysis,GRA)有机结合,构建加权GRA-TOPSIS[15]综合评价模型优选深井巷道支护方式。采用最优组合权值[16]将主、客观权重优化组合,再进行理想支护方案求解,计算出每个方案的相对贴合度,并以此确定综合评价最优的支护方案。
1 巷道支护方式综合评价指标体系巷道支护方式选择是一个复杂的综合性问题,考虑矿山巷道实际特点并结合国内外同类巷道评价情况,以安全性、经济性、工期性和技术的可行性等方面建立巷道支护综合评价体系[4, 13]。
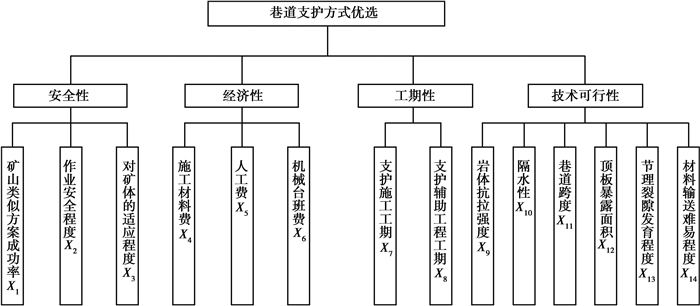
其中一级指标为:安全性、经济性、工期性和技术可行性;一级指标又可分为二级指标,基于支护方案安全性,选取类似方案成功率X1、作业安全程度X2、对矿体的适用程度X3;考虑矿山支护成本、施工工期情况,以指标实测值进行评价,选择施工材料费X4、人工费X5、机械台班费X6、支护施工工期X7和支护辅助施工工期X8;考虑深井巷道具有地压显著、围岩变形严重等特点,基于巷道支护体与巷道围岩共同作用的原理,选择了岩体强度X9、隔水性X10、巷道跨度X11、顶板暴露面积X12以及巷道围岩节理裂隙发育程度X13五个评价指标;最后,基于支护耗材的考虑,选择材料输送的难易程度X14作为评价体系的二级指标。支护方式综合评价指标体系如图 1所示。
|
图 1 支护方式综合评价体系指标关系 Fig. 1 Index relationship of comprehensive evaluation system of support scheme |
针对支护方式综合评价指标体系的特点及评价目的,考虑主、客观因素共同作用,对各指标采用组合赋权,基于GRA与TOPSIS法各自优点,建立GRA-TOPSIS综合评价模型,以定量计算待评估支护方案基于评价指标的贴合度,进而合理比较支护方式的优劣,为决策最佳支护方式提供可靠依据。
2.1 组合赋权 2.1.1 AHP法权重考虑矿山巷道实际特点并结合专家经验,构建指标判断矩阵,进行权值计算与一致性检验,则评价指标的主观权值为wjz=(w1, w2, …, wm),具体计算方法依据文献[15]。
2.1.2 熵权法权重设xij(i=1, 2, …, n; j=1, 2, …, m)为第j个指标的第i个观测数据,采用熵权法确定指标客观权重步骤为:
1) 设tj为第j个评价指标的熵值,依据熵值计算公式,则tj为:
| $ t_{j}=-\frac{1}{\ln n} \sum\limits_{i=1}^{n}\left(x_{i j} / \sum\limits_{i=1}^{n} x_{i j}\right) \ln \left(x_{i j} / \sum\limits_{i=1}^{n} x_{i j}\right); $ | (1) |
2) 设wj*为第j个评价指标的熵权,依据熵权计算公式,则wj*为:
| $ w_{j}^{*}=t_{j} / m-\sum\limits_{j=1}^{m} t_{j}, j=1, 2, \cdots, m_{0}。$ | (2) |
设最优组合权值wj,为使最优组合权值wj与wjz,wj*尽可能接近,依据最小鉴别信息原理,建立如下目标函数[16-17]:
| $ \min F=\sum\limits_{j=1}^{n} w_{j}\left(\ln \frac{w_{j}}{w_{j}^{z}}\right)+\sum\limits_{j=1}^{n} w_{j}\left(\ln \frac{w_{j}}{w_{j}^{*}}\right), $ | (3) |
| $ {\rm{s.t.}}\;\;\;\;\;\sum\limits_{j=1}^{n} w_{j}=1, w_{j}>0。$ | (4) |
采用Lagrange乘子法进行求解,可得最优组合权重:
| $ w_{j}=\frac{\left(w_{j}^{z} w_{j}^{*}\right)^{1 / 2}}{\sum\limits_{j=1}^{n}\left(w_{j}^{z} w_{j}^{*}\right)^{1 / 2}}。$ | (5) |
由最优组合赋权法确定指标权重后,支护方式评价步骤如下:
2.2.1 构建指标矩阵设有m个待评价样本,含有n个评价指标,样本相对应的评估值pij(i=1, 2, …, m;j=1, 2, …, n),则评价指标矩阵P=(pij)m×n为:
| $ \boldsymbol{P}=\left[\begin{array}{cccc}{p_{11}} & {p_{12}} & {\cdots} & {p_{1 n}} \\ {p_{21}} & {p_{22}} & {\cdots} & {p_{2 n}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {p_{m 1}} & {p_{m 2}} & {\cdots} & {p_{m n}}\end{array}\right]。$ |
由于各指标性质、单位、量级存在较大差异,采用改进功效系数法进行向量规范化处理,实现评价指标矩阵归一化。
对效益型指标(指标数值越大越优),令
| $ x_{i j}=(1-\beta)+\beta \times \frac{\left(p_{i j}-p_{\min (j)}\right)}{\left(p_{\max (j)}-p_{\min (j)}\right)}。$ | (6) |
对成本型指标(指标数值越小越优),令
| $ x_{i j}=(1-\beta)+\beta \times \frac{\left(p_{\max j}-p_{i j}\right)}{\left(p_{\max j}-p_{\min (j)}\right)}, $ | (7) |
式中:
由上述处理实现了xij同向化,得到规范化处理后的矩阵
| $ \boldsymbol{P}^{\prime}=\left[\begin{array}{cccc}{x_{11}} & {x_{12}} & {\cdots} & {x_{1 n}} \\ {x_{21}} & {x_{22}} & {\cdots} & {x_{2 n}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {x_{m 1}} & {x_{m 2}} & {\cdots} & {x_{m n}}\end{array}\right]。$ |
将最优组合权值与归一化指标矩阵相乘,得到指标加权规范化矩阵:
| $ \boldsymbol{Y}=\left[\begin{array}{cccc}{y_{11}} & {y_{12}} & {\cdots} & {y_{1 n}} \\ {y_{21}} & {y_{22}} & {\cdots} & {y_{2 n}} \\ {\vdots} & {\vdots} & {} & {\vdots} \\ {y_{m 1}} & {y_{m 2}} & {\cdots} & {y_{m n}}\end{array}\right]。$ |
分析综合评价指标体系中各指标以效益型指标j+的最大值和与支出型指标j-的最小值构成正理想解;以效益型指标j+的最小值和与支出型指标j-的最大值构成负理想解[18]。其中类似方案成功率、作业安全程度、对矿体适应程度、岩体强度和隔水性为效益性指标,其余指标均为支出型。
正理想解:
| $ y_{j}^{+}=\left(\max\limits _{1 <i<m} y_{i j}\left|j \in j^{+}, \min\limits _{1<i<m} y_{i j}\right| j \in j^{-}\right), j=1, 2, \cdots, n_{\circ} $ | (8) |
负理想解:
| $ y_{j}^{-}=\left(\min\limits _{1<i<m} y_{i j}\left|j \in j^{+}, \max \limits_{1<i<m} y_{i j}\right| j \in j^{-}\right), j=1, 2, \cdots, n。$ | (9) |
第i种支护方式与正理想解的欧氏距离:
| $ D_{i}^{+}=\sqrt{\sum\limits_{j=1}^{n}\left(y_{i j}-y_{j}^{+}\right)^{2}}, i=1, 2, \cdots, m。$ | (10) |
第i种支护方式与负理想解的欧氏距离:
| $ D_{i}^{-}=\sqrt{\sum\limits_{j=1}^{n}\left(y_{i j}-y_{j}^{-}\right)^{2}}, i=1, 2, \cdots, m。$ | (11) |
以指标加权规范化矩阵Y为基础,令第i个方案正理想解与负理想解关于第j个指标的灰色关联系数分别为φij+和φij-。
| $ \varphi_{i j}^{+}=\frac{\min\limits _{i} \min \limits_{j}\left|y_{j}^{+}-y_{i j}\right|+\gamma \max\limits _{i} \max\limits _{j}\left|y_{j}^{+}-y_{i j}\right|}{\left|y_{j}^{+}-y_{i j}\right|+\gamma \max\limits _{i} \max\limits _{j}\left|y_{j}^{+}-y_{i j}\right|}, $ | (12) |
| $ \varphi_{i j}^{-}=\frac{\min\limits _{i} \min \limits_{j}\left|y_{j}^{-}-y_{i j}\right|+\gamma \max\limits _{i} \max\limits _{j}\left|y_{j}^{-}-y_{i j}\right|}{\left|y_{j}^{-}-y_{i j}\right|+\gamma \max\limits _{i} \max\limits _{j}\left|y_{j}^{-}-y_{i j}\right|}, $ | (13) |
式中γ是分辩系数,取值为0<γ<1,通常取0.5。
则第i个评价方案与正理想解和负理想解的灰色关联度分别为qi+和qi-。
| $ q_{i}^{+}=\frac{1}{n} \sum\limits_{j=1}^{n} \varphi_{i j}^{+}, i=1, 2, \cdots, m, $ | (14) |
| $ q_{i}^{-}=\frac{1}{n} \sum\limits_{j=1}^{n} \varphi_{i j}^{-}, i=1, 2, \cdots, m_{0}。$ | (15) |
对欧氏距离Di+和Di-,以及灰色关联度qi+和qi-进行量纲一的处理,即
| $ Q{'_i} = \frac{{{Q_i}}}{{\mathop {\max {Q_i}}\limits_{1 \le i \le m} }},{Q_i}分别为D_{i}^{+}, D_{i}^{-}, q_{i}^{+}, q_{i}。$ | (16) |
分析GRA与TOPSIS二者的评价效果,即Di-和qi+的数值越大,表明评价对象越接近正理想解;Di+和qi-的数值越大,则评价对象越偏离正理想解。因此,综合考虑欧氏距离与灰色关联度。
| $ L_{i}^{+}=\alpha D_{i}^{-}+(1-\alpha) q_{i}^{+}, i=1, 2, \cdots, m; $ | (17) |
| $ L_{i}^{-}=\alpha D_{i}^{+}+(1-\alpha) q_{i}^{-}, i=1, 2, \cdots, m; $ | (18) |
式中:α为偏好系数,反映评价者对评价指标的偏好程度;Li+与Li-分别表示第i个评价对象与正、负理想解的接近程度。
2.2.8 计算评价对象的贴合度相对贴合度ξ能综合反映评价对象与理想解的接近程度,计算方法如下:
| $ \xi=\frac{L_{i}^{+}}{L_{i}^{+}+L_{i}^{-}}, i=1, 2, \cdots, m。$ | (19) |
依据式(19)计算结果,采用相对贴合度ξ的数值大小作为方案评价的综合优越度,进行支护方案优劣排序,相对贴合度ξ越大,评价方案越优。
3 应用实例某矿山准备开采位于地表千米以下的深部矿体,开采矿体的顶板为炭质泥岩与中风化泥岩,底板为中风化泥质灰岩与砂质页岩,矿体平均厚度为10.8 m,矿体倾角约为16°~27°,巷道掘进断面为直墙拱形,其断面净宽为4.3 m,净高为3.8 m。巷道围岩平均单轴抗压强度为24.64 MPa。该中段地应力测量结果:最大水平主应力为33.18 MPa,最小水平主应力为15.47 MPa,垂直应力为33.42 MPa。同时,通过现场位移监测,得到巷道开挖后顶底板移近量约0.8 m,其中底鼓量0.55 m以上;巷道左右两帮变形量可达0.68 m。
根据上述开采的基本条件,考虑深部开采中围岩承受极高地应力和三向等压状态,易导致围岩大面积塑性破坏同时伴有大规模动力失稳[1],随着巷道埋深的增加,顶底板位移量迅速增大。结合矿山实际,当巷道埋深超于1 000 m时,巷道底板的底鼓量非常严重,可达顶板位移量的75%,并且深部应力、强度以及结构的不对称使得巷道各部分的变形存在很大差异。因此,为减少巷道顶板下沉量、帮部及底板鼓出量,以维持巷道稳定,需对深井巷道采取全断面、高强度、高预应力的联合支护方式。
矿山以及时、主动、全断面支护以及锚杆与锚索支护优先为原则,拟选如下5种支护方案作为深井巷道备选支护方案:顶、帮锚杆锚索,喷射混凝土(方案①);顶、帮锚杆锚索,喷射混凝土,底板锚索(方案②);顶、帮锚杆锚索,喷射混凝土,底板锚索,并锚索孔注浆(方案③);U型钢支架加反底拱(方案④);U型钢支架加反底拱,顶、帮锚杆锚索(方案⑤)。经统计,对于备选的5种支护方案,类似方案成功率取值范围在75%~92%,材料费为1 500~3 400万元,人工费为320~440万元,机械台班费为900~2 100万元,支护工期的取值范围24~32个月,辅助工程工期的取值范围14~19个月。
3.1 确定评价指标矩阵依据该矿拟选的5种支护方式的特性及经验参数,并以建设规模下的平均估值作为指标体系的基础数据进行计算。由于各指标的含义、单位存在差异,进行指标体系无量纲化处理结果见表 1。
| 表 1 指标体系量纲一的数据 Table 1 Dimensionless data of the indicator system |
定性指标依据赋值的方法将其转变为半定量指标,以得到较为准确的评价结果[19-20],指标具体取值方法见表 2。
| 表 2 巷道支护评价定性指标分级标准 Table 2 Classification criteria for qualitative evaluation of roadway support evaluation |
首先,根据层次分析法,结合巷道实际情况与专家意见及经验,评价指标体系主观权重结果见表 3。
| 表 3 层次分析法指标权重 Table 3 Analytic Hierarchy Process (AHP) indicator weights |
然后,利用式(1)和式(2)计算各指标的客观权重为:
wj*=[0.053, 0.120, 0.061, 0.063, 0.060, 0.066, 0.062, 0.052, 0.078, 0.070, 0.070, 0.064, 0.120, 0.059]。
最后,根据最小鉴别信息原理,利用式(3)和式(5),则各指标的最优组合权重为:
wj=[0.073, 0.086, 0.044, 0.097, 0.133, 0.075, 0.073, 0.054, 0.081, 0.047, 0.060, 0.045, 0.087, 0.045]。
3.3 无量纲矩阵加权化确定组合权重后,对归一化矩阵进行加权处理,则指标加权规范化矩阵为:

|
由式(8)和式(9)分别计算各指标的正、负理想解,构建理想支护方式的正理想解yj+和负理想解yj-:
| $ \begin{array}{c}{y_{j}^{+}=[0.0727, 0.0857, 0.0438, 0.0966, 0.1325, 0.0747, 0.0727, } \\ {0.0538, 0.0807, 0.0468, 0.0598, 0.0448, 0.0867, 0.0448 ]}, \end{array} $ |
| $ \begin{array}{c}{y_{j}^{-}=[0.00015, 0.00017, 0.00009, 0.00019, 0.00027, 0.00015, 0.00015, } \\ {0.00011, 0.00016, 0.00009, 0.00012, 0.00009, 0.00017, 0.00009 ]}。\end{array} $ |
由式(10)(11)和式(12)~(15)分别得到各拟选支护方案与正、负理想支护之间的欧氏距离与灰色关联度,结果见表 4。
| 表 4 支护方案到理想解的欧氏距离与灰色关联度 Table 4 Euclidean distance and grey correlation degree of support scheme to ideal solution |
依据式(16)对5种拟用支护方案的欧氏距离和灰色关联度进行量纲一的处理,由式(17)、式(18)评价对象与正、负理想解的接近程度,取偏好系数α=0,α=0.5,α=1,采用式(19)进行相对贴合度计算,结果见表 5。
| 表 5 支护方案评价结果 Table 5 Evaluation results of support schemes |
由表 5计算结果可知,无论偏好系数取α=0,0.5或者1,③号支护方案的相对贴合度均最大,表明③号支护方案的综合优越度最高,即顶、帮均锚杆锚索、喷射混凝土,底板锚索,并锚索孔注浆的联合支护加固方式可作为该矿深井巷道支护方案的最优决策。当偏好系数α的取值不同时,支护方案对应的正理想解贴合度最大值存在一定差异。例如,当偏好系数α取0时,方案①的正理想解贴合度最大,方案③的正理想解贴合度其次;当偏好系数α取0.5和1时,方案③的正理想解贴合度最大,方案①的正理想解贴合度其次,方案②的正理想解贴合度最小。是由于偏好系数不同,评价模型对GRA和TOPSIS法二者侧重不同,因此评价方案的贴合度发生变化。当偏好系数α=0时,评价体系只采用GRA对支护方案进行评价;当偏好系数α=1时,评价体系只采用TOPSIS法评价支护方案;依据计算结果,总体来看,支护方案的评价结果差异性较小,整体上均保持③>⑤>①>②>④的优选结果。
该矿山实际生产采用的支护方式正为方案③:顶板与两帮均锚杆锚索,喷射混凝土,底板锚索并采取注浆。该方案较适合深井巷道支护,能够有效控制巷道围岩变形,巷道稳定性较好,实现了安全、可靠的生产。经矿山实践表明,加权GRA-TOPSIS能为支护方案决策者提供可靠参考,选择最优支护方案。
4 结论1) 依据最小鉴别信息原理,优化AHP和熵权法所得组合权重,引入能够较好地反映序列之间非线性关系的GRA法和机巧灵活的TOPSIS法,构建了较为客观的深井巷道支护方案优选组合模型。
2) 考虑深井巷道支护的安全性、经济性、工期性和技术可行性4个方面,选取类似方案成功率、作业安全程度等14个评价指标,建立评价指标体系,对某矿深井巷道拟选用的5种支护方案进行优选计算,最终得到其最佳支护方式为顶板及两帮锚杆锚索、喷射混凝土,底板锚索并注浆的联合支护加固方案,与矿山实际现用方案吻合,能够较好地控制巷道围岩变形。
3) 采用该方法优选深井巷道支护方案,综合考虑了巷道支护特性与影响因素,减少了原有评价体系的不确定性和复杂性,实现了巷道支护方案定量评价,评价体系简单易行,可信度较高。为类似矿山选取适当的支护方案提出了一个新的计算方法。
| [1] |
康红普, 范明建, 高富强, 等. 超千米深井巷道围岩变形特征与支护技术[J]. 岩石力学与工程学报, 2015, 34(11): 2227-2241. KANG Hongpu, FAN Mingjian, GAO Fuqiang, et al. Deformation and support of rock roadway at depth more than 1000 meters[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(11): 2227-2241. (in Chinese) |
| [2] |
郑海力. 基于多级模糊评判与嵌套式粗糙集理论的深井巷道支护方案优选体系[J]. 化工矿物与加工, 2012, 41(2): 23-27. ZHENG Haili. Optimization system for the deep roadway support schemes based on multi-stage fuzzy and nested rough sets theory[J]. Industrial Minerals and Processing, 2012, 41(2): 23-27. (in Chinese) DOI:10.3969/j.issn.1008-7524.2012.02.007 |
| [3] |
Niedbalski Z, Majcherczyk T. Indicative assessment of design efficiency of mining roadways[J]. Journal of Sustainable Mining, 2018, 17(3): 131-138. DOI:10.1016/j.jsm.2018.04.003 |
| [4] |
Mahdevari S, Shahriar K, Sharifzadeh M, et al. Stability prediction of gate roadways in longwall mining using artificial neural networks[J]. Neural Computing and Applications, 2017, 28(11): 3537-3555. DOI:10.1007/s00521-016-2263-2 |
| [5] |
Farzi M, Pakbaz M S, Aminpour H A. Selection of support system for urban deep excavations:A case study in Ahvaz geology[J]. Case Studies in Construction Materials, 2018, 8: 131-138. DOI:10.1016/j.cscm.2018.01.004 |
| [6] |
王望珍, 陈翼飞, 李素芹, 等. 基于博弈论和相对熵的基坑支护方案优选[J]. 数学的实践与认识, 2015, 45(6): 165-171. WANG Wangzhen, CHEN Yifei, LI Suqin, et al. Optimization of supporting schemes for foundation pit based on game theory and relative entropy evaluation method[J]. Mathematics in Practice and Theory, 2015, 45(6): 165-171. (in Chinese) |
| [7] |
Wang H W, Jiang Y D, Xue S, et al. Influence of fault slip on mining-induced pressure and optimization of roadway support design in fault-influenced zone[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(5): 660-671. DOI:10.1016/j.jrmge.2016.03.005 |
| [8] |
Cao R H, Cao P, Lin H. Support technology of deep roadway under high stress and its application[J]. International Journal of Mining Science and Technology, 2016, 26(5): 787-793. DOI:10.1016/j.ijmst.2016.05.046 |
| [9] |
李必红, 周健, 史秀志. 深基坑支护结构选型决策的Fisher判别分析模型[J]. 重庆大学学报, 2011, 34(9): 109-116. LI Bihong, ZHOU Jian, SHI Xiuzhi. Fisher discriminant analysis model for selecting the retaining structure type of deep foundation pit[J]. Journal of Chongqing University, 2011, 34(9): 109-116. (in Chinese) |
| [10] |
贺永俊, 李超. 基于主成分分析与BP神经网络的深基坑支护方案优选[J]. 四川建筑科学研究, 2015, 41(4): 32-35, 39. HE Yongjun, LI Chao. Optimization of supporting plan for deep foundation pit based on principal component analysis and BP neural network[J]. Sichuan Building Science, 2015, 41(4): 32-35, 39. (in Chinese) DOI:10.3969/j.issn.1008-1933.2015.04.008 |
| [11] |
王宏伟, 武旭, 陈瀚, 等. 神经网络在支护优选及变形预测中的应用[J]. 矿业研究与开发, 2016, 36(6): 25-29. WANG Hongwei, WU Xu, CHEN Han, et al. Application of neural network in optimal selection of support patterns and deformation prediction[J]. Mining Research and Development, 2016, 36(6): 25-29. (in Chinese) |
| [12] |
陈建宏, 郑海力, 刘振肖, 等. 基于优势关系的粗糙集的巷道支护方案评价体系[J]. 中南大学学报(自然科学版), 2011, 42(6): 1698-1703. CHEN Jianhong, ZHENG Haili, LIU Zhenxiao, et al. Rough sets of laneway supporting schemes evaluation system based on dominance relation[J]. Journal of Central South University(Science and Technology), 2011, 42(6): 1698-1703. (in Chinese) |
| [13] |
唐诗卉. 基于未确知理论的巷道支护方案评价体系及应用[J]. 科技导报, 2014, 32(17): 29-34. TANG Shihui. An unascertained theory based evaluation system for roadway support schemes and its application[J]. Science & Technology Review, 2014, 32(17): 29-34. (in Chinese) DOI:10.3981/j.issn.1000-7857.2014.17.004 |
| [14] |
周伟, 肖莉明, 黄广全, 等. 粗糙集指标简约的装配设计方案模糊评价[J]. 重庆大学学报, 2018, 41(6): 24-34. ZHOU Wei, XIAO Liming, HUANG Guangquan, et al. Fuzzy evaluation of assembly design scheme based on attribute value reduction of rough sets[J]. Journal of Chongqing University, 2018, 41(6): 24-34. (in Chinese) |
| [15] |
张钦礼, 程健, 王新民, 等. 基于灰色关联和加权TOPSIS法的采矿方法优选[J]. 科技导报, 2013, 31(31): 38-42. ZHANG Qinli, CHENG Jian, WANG Xinmin, et al. Mining method optimization based on GRA and weighted TOPSIS method[J]. Science & Technology Review, 2013, 31(31): 38-42. (in Chinese) DOI:10.3981/j.issn.1000-7857.2013.31.005 |
| [16] |
薛希龙, 王新民, 张钦礼, 等. 充填管道磨损风险评估的组合权重与可变模糊耦合模型[J]. 中南大学学报(自然科学版), 2016, 47(11): 3752-3758. XUE Xilong, WANG Xinmin, ZHANG Qinli, et al. An integrated model of combination weights and variable fuzzy on evaluating backfill pipeline wear risk[J]. Journal of Central South University(Science and Technology), 2016, 47(11): 3752-3758. (in Chinese) |
| [17] |
朱雪龙. 应用信息论基础[M]. 北京: 清华大学出版社, 2001: 257-258. ZHU Xuelong. Application of information theory[M]. Beijing: Tsinghua University Press, 2001: 257-258. (in Chinese) |
| [18] |
向洁, 邱泽晶. 基于TOPSIS法和灰色关联度的节能技术优选决策[J]. 节能技术, 2017, 35(2): 142-146, 176. XIANG Jie, QIU Zejing. Optimal decision of energy-saving technologies based on TOPSIS method and grey relational degree[J]. Energy Conservation Technology, 2017, 35(2): 142-146, 176. (in Chinese) |
| [19] |
王新民, 王石, 鄢德波, 等. 基于未确知测度理论的充填管道堵塞风险性评价[J]. 中国安全科学学报, 2012, 22(4): 151-156. WANG Xinmin, WANG Shi, YAN Debo, et al. Risk assessment on blocking of filling pipeline based on uncertainty measurement theory[J]. China Safety Science Journal, 2012, 22(4): 151-156. (in Chinese) DOI:10.3969/j.issn.1003-3033.2012.04.026 |
| [20] |
张钦礼, 肖崇春, 陈秋松, 等. 某矿山最佳充填站站址方案选择[J]. 科技导报, 2013, 31(19): 39-43. ZHANG Qinli, XIAO Chongchun, CHEN Qiusong, et al. Best selective scheme for the filling station location of a certain mine[J]. Science & Technology Review, 2013, 31(19): 39-43. (in Chinese) DOI:10.3981/j.issn.1000-7857.2013.19.005 |
 2019, Vol. 42
2019, Vol. 42


