1b. 辽宁工程技术大学 矿业学院, 辽宁 阜新 123000;
2. 辽宁工程技术大学 中华人民共和国应急管理部信息研究院, 北京 100029
1b. School of Mining, Liaoning Technical University, Fuxin 123000, Liaoning, P. R. China;
2. Information Research Institute of the Ministry of Emergency Management of the People's Republic of China, Beijing 100029, P. R. China
露天矿行车事故预测是实现露天矿山安全、科学、合理有效决策的基础,对于矿山隐患排查、事故预防和降低事故损失均具有重要意义[1]。
目前,典型的事故预测算法主要可以归类为如下几种方法:情景分析法、回归预测法、时间预测法、灰色理论方法、马尔可夫理论方法以及非线性系统分析方法[2],这些方法均在一定程度上增强了安全决策的科学性,对于指导工程和隐患预防均起到了一定积极作用。如李明洋等[3]采用最小二乘法拟合灰色模型中微分方程,并将一种改进的GM(1, 1)模型应用于对非煤矿山死亡率的预测中,并取得了理想的预测效果;顾晓叶等[4]提出构建最佳事故预测模型的基本思路和步骤,并结合实际探讨了国内事故死亡人数随经济发展的趋势;孙轶轩等[5]将自回归滑动平均模型和支持向量回归机模型相结合,构建时间序列组合预测模型,最终实现对道路交通事故相关指标的趋势预测。赵玲等[6]针对各种单一灰色预测模型存在的局限性,提出一种最优加权的灰色组合预测模型来实现交通事故死亡人数的预测;彭小玲[7]将支持向量机技术应用于海上船舶交通事故预测分析中;周荣义等[2]将主成分分析方法和人工神经网络方法相结合,对煤矿百万吨死亡率指标进行了合理预测;宋传平等[8]将GM(1, 1)灰色预测模型应用于军用车辆交通事故频数和死亡人数的短期预测中,验证了此方法对于预测问题的适用性;朱志洁等[9]将主成分分析方法与BP神经网络相结合,对煤与瓦斯突出问题进行了有效预测;李建刚等[10]针对于露天矿运输系统行车事故发生频次数据少的缺点,采用了灰色系统理论其进行了灰色预测;付华等[11]提出带有整定因子的扩展卡尔曼滤波器来优化加权最小二乘模型参数,并应用该算法提出一种瓦斯浓度动态预测的新方法。
综合上述文献可知,这些算法各有特定的适应领域,并对各自问题所应用的具体场景均起到了积极的作用,但这些算法也存在一定的局限性,主要体现在:对于现实工程中小样本数据的处理能力、在广泛存在离群点的情况下的算法抗噪容差能力等几方面,并且这些局限性因素也是造成预测精度损失的最根本原因。为此,在前人的研究成果基础上,针对现实工程中采样数据具有小样本特性、且离群点规模不定,易导致预测模型精度损失等问题展开研究,提出一种带有二次惩罚修正的加权最小二乘支持向量回归机预测模型。模型设计的基本思想是利用统计学习方法对于小样本数据的学习能力,来提高算法对小样本数据处理的拟合精度;对于离群点过滤问题,模型在加权最小二乘过滤的基础上,引入二次惩罚修正项,通过计算每一个点的损失代价,来剔除异常点,进一步提高模型精度。最终,经仿真对比实验验证,论证了所述算法的在求解事故预测问题、提高预测精度等方面的有效性。
1 WLS-SVR回归模型支持向量回归机技术[12-13](support vector regression, SVR)是20世纪末由AT&T贝尔实验室的Vapnic提出,此模型是对SVM模型(support vector machine)在回归问题中的一个推广应用。由于该算法解的稀疏性、对传统神经网络模型的局部极值和过拟合问题的独特处理能力,被广泛应用于非线性预测、拟合函数参数估计等场景[13]。加权最小二乘支持向量机(weighted least square support vector regression, WLSSVR)是在SVR及LS-SVR(least square support vector regression)两模型的基础上发展起来的,该算法保留了LS-SVR算法模型中的平方误差损失以及等式约束等特性,在有效降低传统SVR模型的计算成本的同时,消除了模型异方差性,具有更好的学习能力、泛化能力,预测准确率更高[13]。
对于给定样本集合{(xk, yk)|k=1, 2, …, N},其中xk∈Rp为p维的参数样本,yk∈R为样本输出集,基于WLSSVR的函数拟合问题的可表述为如下的凸二次优化模型:
| $ \left\{\begin{array}{l}{\min J(\boldsymbol{\omega}, \boldsymbol{\delta})=\frac{1}{2} \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}+\frac{1}{2} C \sum\limits_{i=1}^{\mathrm{N}} \lambda_{i} \delta_{i}^{2}} \\ {\text { s.t. } \delta_{i}=\boldsymbol{\omega}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b-y_{i}, i=1, 2, \cdots N}\end{array}\right., $ | (1) |
式中:ω为权系数向量;φ(xi)为输入参数到希尔伯特空间的映射;C为惩罚因子;b为模型偏差;λi为误差权值。
根据式(1)中优化模型采用拉格朗日算子法进行求解,建立二次凸优化对偶模型,对偶模型的拉格朗日方程可表示为:
| $ L(\boldsymbol{\omega}, b, \boldsymbol{\delta}, a)=J(\boldsymbol{\omega}, \boldsymbol{\delta})-\sum\limits_{i=1}^{N} a_{i}\left[\boldsymbol{\omega}^{\mathrm{T}} \cdot \varphi\left(\boldsymbol{x}_{i}\right)+b+\delta_{i}-y_{i}\right]。$ | (2) |
对式(2)采用函数极值求解方法进行求解,其偏导数方程组如式(3)。
| $ \left\{ \begin{array}{l} \frac{\partial L(\boldsymbol{\omega}, b, \boldsymbol{\delta}, \boldsymbol{a})}{\partial \boldsymbol{\omega}}=0 \Rightarrow \omega-\sum\limits_{i=1}^{N} a_{i} \varphi\left(\boldsymbol{x}_{i}\right), \\ \frac{\partial L(\boldsymbol{\omega}, b, \boldsymbol{\delta}, \boldsymbol{a})}{\partial b}=0 \Rightarrow \sum\limits_{i=1}^{N} a_{i}=0, \\ \frac{\partial L(\boldsymbol{\omega}, b, \boldsymbol{\delta}, \boldsymbol{a})}{\partial \delta_{i}}=0 \Rightarrow C \lambda_{i} \delta_{i}-a_{i}=0, \\ \frac{\partial L(\boldsymbol{\omega}, b, \boldsymbol{\delta}, \boldsymbol{a})}{\partial a_{i}}=0 \Rightarrow \boldsymbol{\omega}^{\mathrm{T}} \cdot \varphi\left(\boldsymbol{x}_{i}\right)+b+\delta_{i}-y_{i}=0。\end{array} \right. $ | (3) |
化简为线性方程组式(3),消除方程组中的无关变量ω和δi,其等价问题即为求解线性方程组中的未知变量a和b,整理方程组后可将其表述为矩阵形式如式(4)。
| $ \left[\begin{array}{cccc}{0} & {\boldsymbol{I}_{\lambda}^{\mathrm{T}}} \\ {\boldsymbol{I}_{\lambda}} & {{\mathit{\boldsymbol{\varOmega}}}+\frac{1}{\gamma} \operatorname{diag}\left(\frac{1}{\lambda_{1}}, \frac{1}{\lambda_{2}}, \cdots \frac{1}{\lambda_{N}}\right)}\end{array}\right]\left[\begin{array}{c}{b^{*}} \\ {{\boldsymbol{a}}^{*}}\end{array}\right]=\left[\begin{array}{l}{0} \\ {\boldsymbol{y}}\end{array}\right], $ | (4) |
式中:
其中标准的WLSSVR模型中给出误差权向量λ的定义形式如式(5)。
| $ \lambda_{i}=\left\{\begin{array}{cc}{1} & {\left|\delta_{i} / \hat{s}\right| \leqslant c_{1}} , \\ {\frac{c_{2}-\left|\delta_{i}\right|}{c_{2}-c_{1}}} & {c_{1} \leqslant\left|\delta_{i} / \hat{s}\right| \leqslant c_{2}}, \\ {10^{-4}} & {\text { otherwise }}, \end{array}\right. $ | (5) |
式中:
根据优化条件引入核函数
| $ y\left(\boldsymbol{x}_{i}\right)=\sum_{k=1}^{N} \alpha_{j}^{*} K\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)+b^{*} $ | (6) |
采用WLSSVR技术进行回归学习是有效解决复杂系统输出值预测问题的重要手段之一。但随着工程上的广泛应用,这类统计学习方法也暴露出自身的缺点,如预测模型精度质量受限于正则化参数c和核参数σ的选择、训练样本中离群点的过滤能力差、预测模型精度受限于离群点规模等几方面问题。为此,在结合行车事故预测问题的工程实际的基础上,将改进的二次惩罚修正策略(penalized trimmed squares, PTS)引入到WLSSVR算法模型中,实现对传统模型离群点的控制,并将改进的粒子群算法引入PTS-WLSSVR模型参数寻优问题中,从而提高整个预测模型的鲁棒特性。
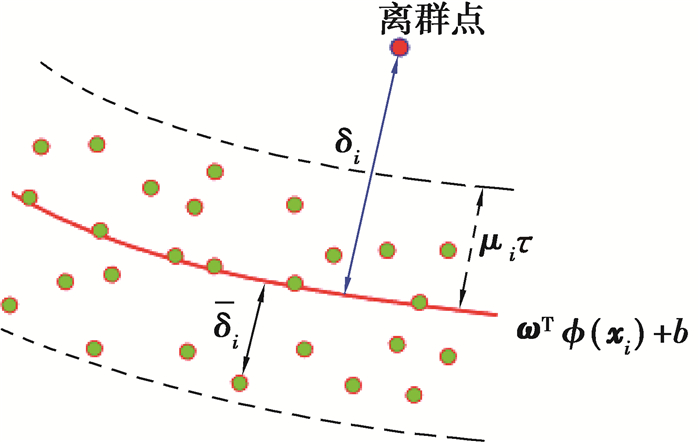
2.1 引入PTS改进WLSSVR算法模型对WLSSVR模型引入惩罚项的作用在于过滤掉回归模型中的离群点,以增强算法的抗噪能力。目前,在应用统计学领域,对于这类离群点的处理也提出了很多种改进方法[14-17],较为有效的如M估计、GM估计以及最小二次修正(LTS)估计等。这类修正方法的特点是在处理带有小规模的离群点回归问题时,能有效提高算法的稳健性,但精度易受离群点规模限制。然而,对于文中这样一个预测问题,在训练前期是无法判定离群点的具体规模的。因此,此种规模限制对于文中的预测结果将具有显著影响。为从本质上改进这种限制,增进算法的稳健性,作者在文献[15-16]提出的PTS修正策略的启发下,对WLSSVR目标函数进行了修正,其修正的基本思路是对每一个样本进行惩罚,并不断的计算每个样本被作为异常点清理后的惩罚代价,其原理如图 1所示。
|
图 1 离群点的过滤原理 Fig. 1 Filtering principle of outliers |
基于此种基本思路,首先采用最小二乘建立离群点识别模型,其目标函数如下:
| $ \min \left[\boldsymbol{y}-\left(\boldsymbol{\omega}^{\mathrm{T}} \cdot \varphi\left(\boldsymbol{x}_{i}\right)+b\right)\right]^{2}=\sum_{i=1}^{n} \max \left[e_{i}^{2}, \rho_{i}\left(c_{i} \sigma\right)^{2}\right]_{0}。$ | (7) |
通过式(7)识别后,将识别结果采用0-1决策变量εi的形式嵌入到回归模型中,故其目标函数模型可被改写为:
| $ \min J(\boldsymbol{\omega}, \boldsymbol{\delta})=\frac{1}{2} \boldsymbol{\omega}^{\mathrm{T}} \boldsymbol{\omega}+\frac{1}{2} C \sum_{i=1}^{N}\left(\lambda_{i} \overline{\delta}_{i}^{2}+{\varepsilon}_{i}\left(\mu_{i} \boldsymbol{\tau}\right)^{2}\right), $ | (8) |
| $ \begin{array}{l}{\text { s.t. } \quad {\boldsymbol{\omega}}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)+b-y_{i} \leqslant \overline{\delta}_{i}+\varepsilon_{i} Q-{\boldsymbol{\omega}}^{\mathrm{T}} \varphi\left(\boldsymbol{x}_{i}\right)-b+y_{i} \leqslant \overline{\delta}_{i}+\varepsilon_{i} Q}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon_{i} \in\{0, 1\}} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\overline{\delta}_{i} \geqslant 0 \quad i=1, 2, \cdots, N}, \end{array} $ | (9) |
式中:Q是一个常数,表示残差δi的上限;εi为是否删除离散点的决策变量;μi
| $ \mu_{i}=\mu \sqrt{1-h_{i}^{*}}。$ | (10) |
式中:hi*为Hessian阵的第i个元素,Hessian矩阵元素值的计算见式(11);μ为一个常数,根据文中模型训练场景中发现建议取值范围为μ∈[2.7, 3.0]。
| $ h_{i}^{*}=\left\{\begin{array}{ll}{\boldsymbol{x}_{i}^{\mathrm{T}}\left(\boldsymbol{X}_{k+1}^{\mathrm{T}} \boldsymbol{X}_{k+1}\right)^{-1} \boldsymbol{x}_{i}, } & {i=k+1, \cdots, N}, \\ {\boldsymbol{x}_{i}^{\mathrm{T}}\left(\boldsymbol{X}_{k}^{\mathrm{T}} \boldsymbol{X}_{k}\right)^{-1} \boldsymbol{x}_{i}, } & {i=1, 2, \cdots, K。}\end{array}\right. $ | (11) |
式中:Xk+1表示xi的最小协方差行列式矩阵。
模型中主要控制的一个参数即为
| $ \overline{\delta}_{i}=\left\{\begin{array}{ll}{\delta_{i}, } & {\left|\delta_{i}\right| \leqslant \mu_{i} {\boldsymbol{\tau}}} , \\ {\mu_{i} {\boldsymbol{\tau}}, } & {\text { otherwise }}。\end{array}\right. $ | (12) |
为提高非线性预测模型的拟合精度及收敛速度,笔者采用改进的粒子群算法(MPSO)对正则化参数和核参数进行优化。具体做法是将参数c, σ为平面粒子位置坐标,建立优化模型如式(13),将式(14)作为优化粒子群算法的适应值函数。
| $ \left\{\begin{array}{l}{\min _{c, \sigma} f(c, \sigma)=\frac{\sum_{k=1}^{N} \lambda_{k} \varepsilon_{k}}{\sum_{k=1}^{N} \lambda_{k}} \ll \frac{\sum_{k=1}^{N} \varepsilon_{k}}{n}}, \\ {\varepsilon_{k}=y_{k}-y_{k}^{*}}, \end{array}\right. $ | (13) |
| $ F(c, \sigma)=M / \frac{\sum_{k=1}^{N} \lambda_{k} \varepsilon_{k}}{\sum_{k=1}^{N} \lambda_{k}}=\frac{\sum_{k=1}^{N} \lambda_{k}}{\sum_{k=1}^{N} \lambda_{k} \varepsilon_{k}}。$ | (14) |
式中M表示全局目标的镇定系数,
考虑模型易受训练数据规模局限性以及其他多种综合因素限制,且上述影响对粒子群算法极为敏感,严重制约粒子群算法种群的搜索范围,导致随着迭代进行会促进种群丧失多样性,极易造成迭代初期算法便出现早熟现象。为使算法在迭代初期具有较强的空间搜索能力,在迭代后期具有较强的寻优能力,对粒子群状态转移模型中的惯性因子(w)、学习因子(c1、c2)进行了如式(15)的修正。此种修正的作用在于能有效的保证算法在迭代初期以较大的范围搜索最优解,保持种群多样性;在迭代后期能实现更精细的局部搜索,以提高整体优化建模精度。
| $ \left\{\begin{array}{l}{w=\left[\left(1-\left(\frac{k}{G}\right)^{\frac{1}{3}}\right) w_{\mathrm{s}}+\left(\frac{k}{G}\right)^{\frac{1}{3}} w_{\mathrm{e}}\right] / 2, } \\ {c_{1}=c_{1 \mathrm{s}}-\left(c_{1 \mathrm{s}}-c_{1 \mathrm{e}}\right)\left(\frac{k}{G}\right)^{\frac{1}{3}}} , \\ {c_{2}=c_{2 \mathrm{s}}+\left(c_{2 \mathrm{e}}+c_{2 \mathrm{s}}\right)\left(\frac{k}{G}\right)}, \end{array}\right. $ | (15) |
式中:ws和we分别表示惯性因子w的初始值和上一期迭代结果值;c1s和c1e分别表示学习因子c1的初始值和上一期迭代结果值;k表示迭代次数;G表示总的迭代次数。
为进一步扩大粒子搜索空间,减少个体寻优过程中易陷入局部最优状态的可能,在每次迭代产生的搜索空间内,算法会采用轮盘赌法随机调整部分粒子位置,来加大搜索空间内寻优策略的随机性,其轮盘赌事件概率如式(16)所示。
| $ P\left(\boldsymbol{p}_{s}\right)=\frac{\sum_{i}^{p} F_{i}(c, \sigma)}{\sum_{k}^{N} F_{k}(c, \sigma)}\;\;{s} \in \left[ {0, 最大粒子数} \right]。$ | (16) |
位置更新模型如式(17)所示。
| $ p_{i}=p_{i}+\left[\left(p_{\max }-p_{i}\right) \frac{p_{i}}{\left(p_{\max }-p_{\min }\right)}+\left(p_{i}-p_{\min }\right) \frac{\left(p_{\max }-p_{\min }\right)-p_{i}}{\left(p_{\max }-p_{\min }\right)}\right] \frac{k \gamma}{G}, $ | (17) |
式中:γ为[-1, 1]区间上的随机数, k为粒子种群更新的次数;pmax, pmin为粒子位置的区间边界;其他参数同上。
综合上述修正策略,基于PSO算法的核参数优化流程如算法1所示。
算法1:基于MPSO的核参数优化算法

|
图 2 基于MPSO的核参数优化算法 Fig. 2 Kernel parameter optimization algorithm based on MPSO |
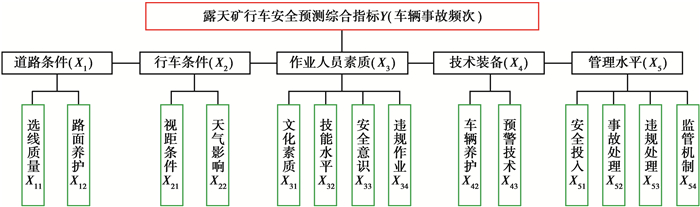
车辆事故频次是评价露天矿行车安全性的重要指标,也是露天矿行车事故预测的一个重要指标。为论证文中模型的可行性及求解预测问题的有效性,采用笔者提出的算法模型对某露天矿山车辆事故频次进行预测。依据该露天矿历年矿山行车事故的因素分析,构建该矿行车安全预测影响指标体系结构[18-21],如图 3所示。并依据行车安全影响指标体系中所列安全因素,收集该矿安全指标数据,数据主要采集自该矿2000—2017年运营的数据。考虑统计指标为该矿全年综合安全指标的评价,为此,统计数据Xij为指标分项打分的平均值,此项打分来自于10位现场专家对该矿全年指标体系分项状态的综合评价,其中打分标准为10分制,分数越高因素体系分项的综合质量越好;另外,事故频次(Y)采用历年的事故频次的统计数据。对于模型训练,将这18年的统计数据分为2组,其中2000-2009年采样数据作为模型的训练样本,2010-2017年采样数据作为模型的测试样本。
|
图 3 露天矿行车安全影响指标体系 Fig. 3 Impact indicator system of traffic safety in open-pit mine |
露天矿车辆事故频次是衡量露天矿行车安全的一项综合性指标,因露天矿运输系统庞杂、影响因素复杂、关联性指标众多,并且各指标间存在相互的耦合关系。鉴于此特点,文中采用主成分分析法[22-23]对原始影响指标进行预处理,分析出其主成分以降低原始指标数据维度,从而消除多种关联因素间的相互影响。
应用Matlab科学计算软件系统对行车安全影响因素数据进行主成分分析,并按照如下步骤进行主成分提取:
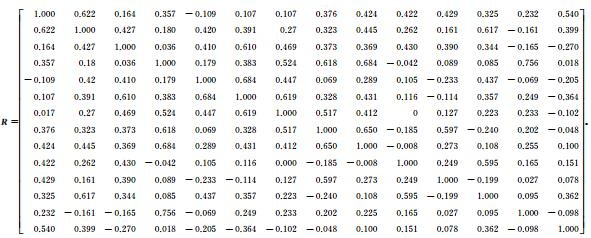
1) 相关系数矩阵R计算:由于指标数据均源于打分系统,因为其评分标准一致。因此,在PCA处理过程中无需进行标准化处理,为此,文中直接采用公式
|
(18) |
2) 计算矩阵R的特征值、特征向量及贡献率:采用Matlab中内置的函数计算矩阵R的特征值和特征向量。按照特征值的大小对各成分进行排序,并按照特征值所占特征值总体的比例来计算贡献率,计算结果如表 1所示。
| 表 1 载荷及贡献率 Table 1 Burden and contribution rates |
3) 主成分因子的得分矩阵确定:由表 1可知,第5个主成分的累计贡献率为86.59%。考虑保证系统数据的不确定性和真实性,采用累计贡献率大于85%的选择原则,选择前5成分为主成分。并根据这5组主成分的特征向量,整理出主成分因子的得分矩阵形式如式(19)所示。
| $ \begin{array}{l} \mathit{\boldsymbol{P}} = \left[ \begin{array}{l} \begin{array}{*{20}{r}} {0.0476}&{0.0179}&{0.2767}&{ - 0.3701}&{ - 0.0179}&{}\\ { - 0.0727}&{ - 0.340}&{0.1501}&{ - 0.2895}&{ - 0.1059}&{}\\ { - 0.4276}&{0.2337}&{ - 0.0041}&{0.0712}&{0.3902}&{}\\ {0.3759}&{0.0074}&{ - 0.0023}&{0.1330}&{ - 0.0355}&{}\\ {0.0466}&{ - 0.1936}&{0.1139}&{0.2731}&{ - 0.7013}&{} \end{array}\\ \begin{array}{*{20}{r}} {0.0458}&{0.0398}&{0.1890}&{ - 0.3928}&{0.1428}\\ {0.0028}&{ - 0.0508}&{ - 0.7451}&{ - 0.0865}&{0.0848}\\ { - 0.2513}&{ - 0.1299}&{ - 0.0464}&{ - 0.1511}&{ - 0.1043}\\ {0.0095}&{ - 0.2076}&{0.3242}&{0.6233}&{0.3371}\\ {0.0129}&{0.5894}&{ - 0.0109}&{0.2457}&{ - 0.0816} \end{array}\\ \begin{array}{*{20}{r}} { - 0.4789}&{0.2690}&{ - 0.1498}&{0.0883}&{ - 0.3952}\\ {0.2644}&{0.0515}&{ - 0.1673}&{0.0411}&{0.1218}\\ {0.5191}&{0.4226}&{0.0181}&{ - 0.1181}&{ - 0.1098}\\ {0.1785}&{ - 0.3560}&{ - 0.3727}&{0.1582}&{0.0360} \end{array} \end{array} \right]\\ \end{array}。$ | (19) |
4) 将所有的原始采样数据按照公式(20)进行PCA数据转换,经转换后的主成分载荷数据,即数据预处理结果如表 2所示。
| $ \hat{\boldsymbol{X}}_{i}=\boldsymbol{P}^{\mathrm{T}} X_{i j}, i=1, 2, \cdots, 5。$ | (20) |
| 表 2 PCA计算后的数据样本 Table 2 Data sample calculated by PCA |
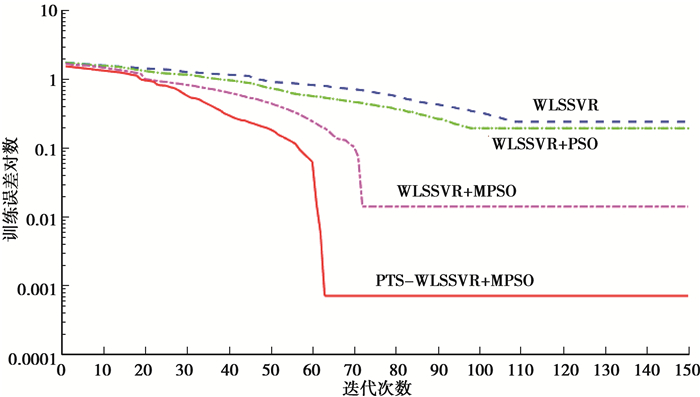
为论证算法的有效性,并进一步说明应用PTS方法修正预测模型的优越性,笔者将上述分解出5种主成分作为输入参数,并采用训练数据分别训练PTS-WLSSVR+MPSO、WLSSVR+MPSO、WLSSVR以及WLSSVR+PSO这4组模型。为消除平台及参数差异,4组算法模型均在一台I5 2.9GHz 8G内存的win7主机上编译和运行,4组模型中组合算法的初始化参数如下:c0=3.5, σ0=0.5;粒子群算法种群规模N=50,最大迭代次数G=150,c1=2.5, c2=3, ω=1。4组模型逐代的平均误差对数和训练的收敛效果如图 4所示,其中为满足各组模型间在同一坐标系下对比分析,图 4中误差曲线为逐代平均误差的对数曲线。
|
图 4 训练误差对比图 Fig. 4 Error contrast diagram |
由图 4中训练结果可以看出,WLSSVR模型训练效果最差,不但精度受限而且收敛速度也相对较慢;应用PSO对支持向量回归模型的参数进行优化后,其收敛速度有明显的提升,且文中给出的自适应参数调节机制,更能体现出收敛速度的提升效果;对比WLSSVR+MPSO算法可发现,引入改进的PTS修正策略后,能明显降低模型迭代过程中的训练误差,并能有效改善算法的迭代速度。综合上述分析,文中改进的算法模型较之传统算法,在此优化场景下适应性更强,能极好的满足当前的预测需求。
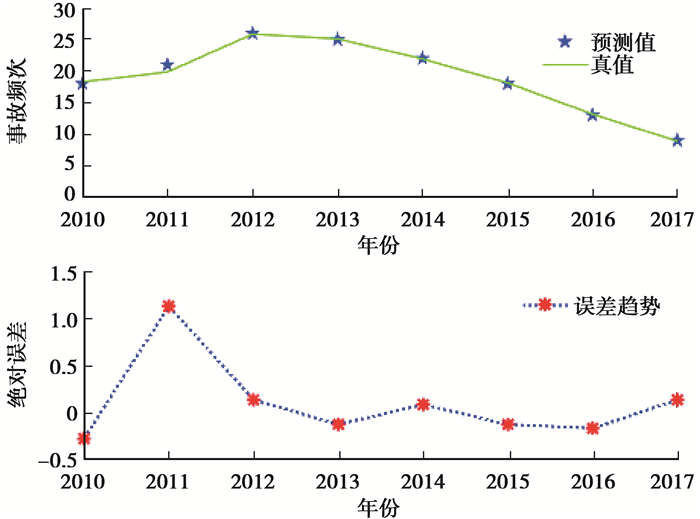
3.3 试验结果分析应用测试集数据对文中提出的PTS-WLSSVR模型进行仿真,测试集所得出的8组仿真结果,如图 5所示。
|
图 5 PTS-WLSSVR模型预测结果 Fig. 5 PTS-WLSSVR model prediction results |
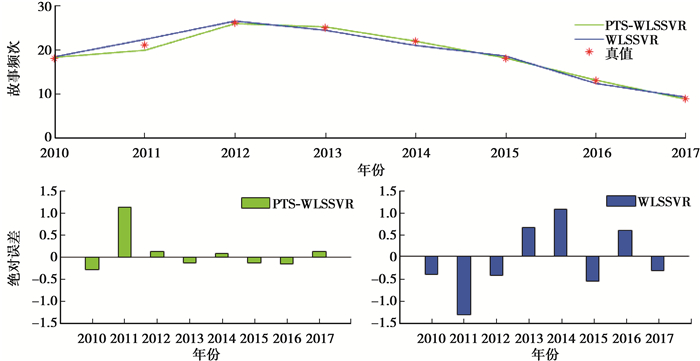
为进一步说明PTS引入后的平差效果,笔者应用测试数据对未引入文中PTS策略的模型进行仿真对比,两组模型绝对误差对比结果如图 6所示。
|
图 6 模型优化效果对比 Fig. 6 Comparison of model optimization results |
通过图 6中的对比曲线可以看出,经过一层的PTS过滤能有效控制误差的全局传播,对于控制模型的误差水平具有极为明显的效果。
4 结论1) 在传统WLSSVR模型中引入二次惩罚修正增强了算法模型的鲁棒性,提高了算法抗造能力,经过改进粒子群算法优化核参数后,有效提高了文中预测算法的效率和预测准确率。经多组算法模型的实例验证,论证了文中改进算法的有效性;
2) 采用PCA分析方法对原始样本数据进行了预处理,消除了多因素间的耦合联系,提高了主观性影响因素分析的精度。通过实例验证,论证了PCA方法在此类预测问题中应用的适用性和有效性;
3) 文中所建立的影响指标体系是根据特定实例建立,后续工作有必要进一步完善此体系结构以保证可适用于更多的行车事故指标参数的预测场景。
| [1] |
骆中洲, 吴亚平, 温思龙. 露天矿事故分析与预测及安全信息管理[J]. 化工矿山技术, 1992(5): 4-8. LUO Zhongzhou, WU Yaping, WEN Silong. Accident analysis and prediction and information system of safety management in surface mine[J]. Chemical Mining Technology, 1992(5): 4-8. (in Chinese) |
| [2] |
周荣义, 钟岸, 任竞舟, 等. 基于主成分分析和神经网络的事故预测方法及应用[J]. 中国安全科学学报, 2013, 23(7): 55-60. ZHOU Rongyi, ZHONG An, REN Jingzhou, et al. An accident forecasting method of ANN based on PCA and its application[J]. China Safety Science Journal, 2013, 23(7): 55-60. (in Chinese) |
| [3] |
李明洋, 姜福川. 基于最小二乘法的灰色GM(1, 1)改进模型在非煤矿山事故预测中的应用[J]. 中国安全生产科学技术, 2013, 9(11): 83-90. LI Mingyang, JIANG Fuchuan. Improved gray GM(1, 1) model in the non-coal mine accident prediction based on the methed of least square[J]. Journal of Safety Science and Technology, 2013, 9(11): 83-90. (in Chinese) |
| [4] |
顾晓叶, 于殿宝, 朱玉生, 等. 事故预测数学模型的研究与实践[J]. 中国安全科学学报, 2009, 19(12): 23-27, 204. GU Xiaoye, YU Dianbao, ZHU Yusheng, et al. Research and practice of accident prediction mathematicalmodels[J]. China Safety Science Journal, 2009, 19(12): 23-27, 204. (in Chinese) DOI:10.3969/j.issn.1003-3033.2009.12.003 |
| [5] |
孙轶轩, 邵春福, 计寻, 等. 基于ARIMA与信息粒化SVR组合模型的交通事故时序预测[J]. 清华大学学报(自然科学版), 2014, 54(3): 348-353, 359. SUN Yixuan, SHAO Chunfu, JI Xun, et al. Urban traffic accident time series prediction model based on combination of ARIMA and information granulation SVR[J]. Journal of Tsinghua University(ScienceandTechnology), 2014, 54(3): 348-353, 359. (in Chinese) |
| [6] |
赵玲, 许宏科, 程鸿亮. 基于最优加权组合模型的道路交通事故预测[J]. 计算机工程与应用, 2013, 49(24): 11-15. ZHAO Ling, XU Hongke, CHENG Hongliang. Road traffic accidents prediction based on optimal weighted combinedmodel[J]. Computer Engineering and Applications, 2013, 49(24): 11-15. (in Chinese) DOI:10.3778/j.issn.1002-8331.1305-0324 |
| [7] |
彭小玲. 支持向量机技术在海上船舶交通事故预测中的应用[J]. 舰船科学技术, 2018, 40(2): 55-57. PENG Xiaoling. Research on ship traffic accident prediction using state vector machine[J]. Ship Science and Technology, 2018, 40(2): 55-57. (in Chinese) |
| [8] |
宋传平, 王鹏飞, 李涛. 基于GM(1, 1)模型的军用车辆交通事故预测研究[J]. 中国安全科学学报, 2010, 20(11): 52-55. SONG Chuanping, WANG Pengfei, LI Tao. Forecast of military vehicle traffic accidents based on GM(1, 1)model[J]. China Safety Science Journal, 2010, 20(11): 52-55. (in Chinese) DOI:10.3969/j.issn.1003-3033.2010.11.009 |
| [9] |
朱志洁, 张宏伟, 韩军, 等. 基于PCA-BP神经网络的煤与瓦斯突出预测研究[J]. 中国安全科学学报, 2013, 23(4): 45-50. ZHU Zhijie, ZHANG Hongwei, HAN Jun, et al. Prediction of coal and gas outburst based on PCA-BP neural network[J]. China Safety Science Journal, 2013, 23(4): 45-50. (in Chinese) |
| [10] |
李建刚, 白润才, 刘光伟, 等. 露天矿行车事故频次的灰色预测[J]. 辽宁工程技术大学学报(自然科学版), 2005, 24(z1): 6-8. LI Jiangang, BAI Runcai, LIU Guangwei, et al. Grey forecast of travel accident frequency in open-pit mine[J]. Journal of Liaoning Technical University(Natural Science Edition), 2005, 24(z1): 6-8. (in Chinese) DOI:10.3969/j.issn.1008-0562.2005.z1.003 |
| [11] |
付华, 訾海, 孟祥云, 等. 一种EKF-WLS-SVR与混沌时间序列分析的瓦斯动态预测新方法[J]. 传感技术学报, 2015, 28(1): 126-131. FU Hua, ZI Hai, MENG Xiangyun, et al. A new method of mine gas dynamic prediction based on EKF-WLS-SVR and chaotic time series analysis[J]. Chinese Journal of Sensors and Actuators, 2015, 28(1): 126-131. (in Chinese) DOI:10.3969/j.issn.1004-1699.2015.01.022 |
| [12] |
Schuldt C, Laptev I, Caputo B. Recognizing human actions: alocal SVM approach[C]//Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004, 26-26 Aug 2004. Cambridge, UK, 2004: 32-36.
|
| [13] |
Cherkassky V, Ma Y Q. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004, 17(1): 113-126. DOI:10.1016/S0893-6080(03)00169-2 |
| [14] |
Zioutas G, Avramidis A. Deleting outliers in robust regression with mixed integer programming[J]. Acta Mathematicae Applicatae Sinica, English Series, 2005, 21(2): 323-334. DOI:10.1007/s10255-005-0240-0 |
| [15] |
Zioutas G, Avramidis A, Pitsoulis L. Penalized trimmed squares and a modification of support vectors for unmasking outliers in linear regression[J]. REVSTAT, 2007, 5(1): 115-136. |
| [16] |
Zioutas G, Pitsoulis L, Avramidis A. Quadratic mixed integer programming and support vectors for deleting outliers in robust regression[J]. Annals of Operations Research, 2009, 166(1): 339-353. DOI:10.1007/s10479-008-0412-4 |
| [17] |
Avramidis A, Zioutas G. Locally and globally robust penalized trimmed squares regression[J]. Simulation Modelling Practice and Theory, 2011, 19(1): 148-160. DOI:10.1016/j.simpat.2010.06.001 |
| [18] |
王少群, 张晓明. 高速公路交通事故概率预测方法研究[J]. 价值工程, 2014, 33(13): 67-68. WANG Shaoqun, ZHANG Xiaoming. Probability forecast method for freeway traffic accidents[J]. Value Engineering, 2014, 33(13): 67-68. (in Chinese) |
| [19] |
Tsuang M T, Boor M, Fleming J A. Psychiatric aspects of traffic accidents[J]. AmericanJournal of Psychiatry, 1985, 142(5): 538-546. |
| [20] |
张军, 杨维平, 杨立功, 等. 模糊综合评判在露天矿安全评价中的应用[J]. 安全与环境学报, 2011, 11(6): 259-263. ZHANG Jun, YANG Weiping, YANG Ligong, et al. Comprehensive fuzzy evaluation method and its application to the open-air mine safety forecasting[J]. Journal of Safety and Environment, 2011, 11(6): 259-263. (in Chinese) DOI:10.3969/j.issn.1009-6094.2011.06.060 |
| [21] |
贾水库. 大型露天矿运输安全控制与预警系统[J]. 北京科技大学学报, 2009, 31(5): 542-546. JIA Shuiku. Pre-warning and control system of transport safety in alarge-scale surface mine[J]. Journal of University of Science and Technology Beijing, 2009, 31(5): 542-546. (in Chinese) DOI:10.3321/j.issn:1001-053X.2009.05.003 |
| [22] |
Brown S D. Book reviews:introduction to multivariate statistical analysis inchemometrics[J]. Applied Spectroscopy, 2010, 64(4): 112A. DOI:10.1366/000370210791114185 |
| [23] |
Egeren L F. Multivariate statistical analysis[J]. Psychophysiology, 1973, 10(5): 517-532. DOI:10.1111/psyp.1973.10.issue-5 |
 2019, Vol. 42
2019, Vol. 42


