b. 重庆大学 机械传动国家重点实验室, 重庆 400044
b. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, P. R. China
20世纪90年代以来,节能与环保已成为人类社会可持续发展的两大主题。寻找一种高效、节能的汽车驱动方式,成为汽车工业刻不容缓的课题。混合动力汽车集传统内燃机汽车与电动汽车的优点,兼具高续航里程、低排放、低污染的特点,成为世界范围内各大汽车公司研究的热点[1]。其中,一种以行星排作为动力耦合机构的混合动力耦合系统(EVT, electric variable transmission)由于结构紧凑,工作效率高,并且搭载这款混合动力耦合系统的汽车自诞生至今的二十多年里已累计销售千万台,因此,这种混合动力EVT构型的研究成为当今混合动力汽车发展的重要方向之一[2]。
在混合动力EVT构型中,电机1(EM1, Electric Motor 1)通过行星齿轮机构无级调节发动机的转速,使其与车轮转速相互独立;电机2(EM2, electric motor 2)通过助力或再生制动使发动机转矩与负载转矩解耦;这样通过两电机实现发动机转速和转矩与外负载解耦,使得发动机运行在高效区。通过在构型中添加离合器/制动器,增加工作模式,还可以进一步提高整车燃油经济性[3-4]。
在混合动力EVT构型中,发动机、电机、车轮可以连接不同的行星构件,而行星构件和动力输入输出构件又可以通过离合器/制动器的启闭实现不同传动模式的切换,因此,包含双电机、双行星排的混合动力EVT系统构型布置方案就超过上千万种,给研发人员进行混合动力EVT构型设计带来了巨大的困难。为解决这一难题,国内外的很多高校和研究机构的诸多学者不断探索着各种设计优化方法,并且已有部分研究成果,这其中包括:杠杆法[3-4]、逆惯量矩阵法[5]、键合图法[6]、图论法等。
文中的学术贡献包括:采用图论分析法,参考混合动力EVT系统图论分层图画模型,提出混合动力EVT系统图论构型矩阵模型,并对混合动力EVT系统进行动力学建模;利用神经网络算法作为评价方式,通过建立构型矩阵模型与动态规划算法仿真所得的油耗值之间的关系,提出一种混合动力EVT耦合系统神经网络油耗模型,通过该油耗模型可以对构型油耗进行快速准确计算。
1 EVT系统构型图论建模在混合动力EVT系统中,包含的主要信息有:行星齿轮机构、输入/输出构件、齿轮机构运动副及构件间的连接关系,这些信息可以用图论分层图画进行完整地表示。借助图论理论中的邻接矩阵、关联矩阵可以将构型分层图画模型转化为数学模型。
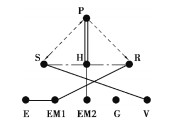
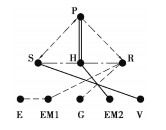
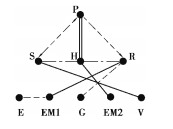
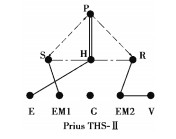
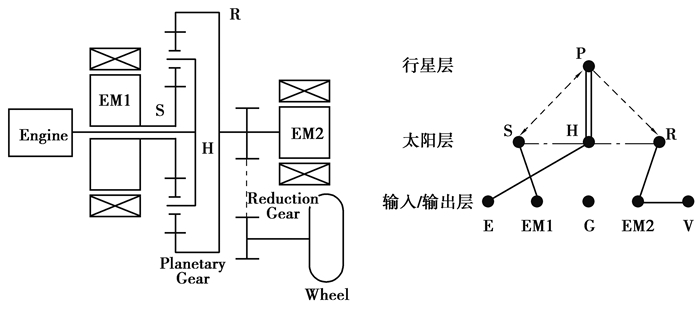
1.1 EVT构型图论分层图画模型根据米娇等[7]提出的混合动力EVT系统图论分层图画模型,丰田Prius THS-Ⅱ构型简图及图论分层图画模型如图 1所示。
|
图 1 THS-Ⅱ构型简图及图论分层图画模型 Fig. 1 Simplified graph and hirarchical graph model of Prius THS-Ⅱ |
为了利用数学模型描述混合动力EVT系统各个构件之间连接关系,笔者基于图论理论中的邻接矩阵[8],提出混合动力EVT构型的图论矩阵模型。
混合动力EVT构型中的连接关系主要有:固定连接(包括传动比为1与传动比不为1的连接)和离合器/制动器连接。对于这2种连接方式在矩阵模型中的表达形式,文中进行如下定义:1为固定连接;CL为离合器/制动器连接。
根据丰田Prius THS-Ⅱ混合动力耦合系统分层图画模型,可得其构型矩阵模型,如图 2所示。

|
图 2 丰田Prius THS-Ⅱ耦合系统矩阵模型 Fig. 2 Hybrid EVT matrix model of Prius THS-Ⅱ |
构型矩阵模型将混合动力EVT构型图论分层图画模型转化为数学模型,将混合动力EVT构型的图形表示转化为计算机可识别的数学语言,为利用计算机进行混合动力EVT构型建模计算奠定了基础。
1.3 混合动力EVT构型图论建模实例Prius THS-Ⅱ原有构型由于不含离合器/制动器,因此,只有一种固定连接模式,根据密歇根大学Zhang Xiaowu和重庆大学裴换鑫等[9-10]的研究,在不考虑2个电机位置互换的前提下,可以根据Prius THS-Ⅱ构型衍生出12种单行星排混合动力EVT基础构型,包括6种输入分配型构型和6种输出分配型构型。
为了进一步探索提高这些构型的燃油经济性,在既有混合动力EVT构型基础上通过增加离合器/制动器的方式,为生成神经网络训练测试所需的多样本奠定基础,文中采用在12种基础构型中添加离合器/制动器的方式,最终生成36种不同的构型方案,这36种构型方案中的部分方案的分层图画模型及构型矩阵如表 1所示。因为神经网络在建立构型与其对应油耗值之间的关系模型时,不仅要能够对优秀构型的油耗做出准确的判断,而且对运动学或动力学不满足要求的不可行构型要予以识别,以便于及时剔除,因此,对于36种方案不进行可行性的初步筛选,以保证训练样本的全面性。
| 表 1 混合动力EVT构型方案图论分层图画及构型矩阵 Table 1 Hirarchical graph and configuration matrices of hybrid EVT configurations |
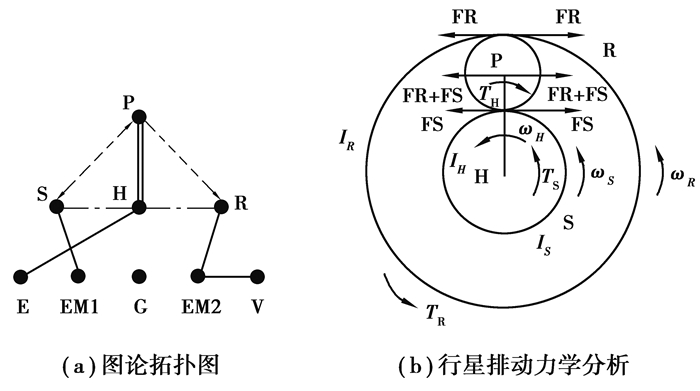
混合动力EVT构型的运动和动力学特性建模是系统燃油经济性仿真的基础。以Prius-Ⅱ耦合系统为例,其图论分层图画模型和行星排动力学分析模型如图 3所示。
|
图 3 Prius-Ⅱ耦合系统图论动力学分析模型 Fig. 3 Hybrid EVT dynamic analysis model of Prius-Ⅱ |
根据BenFord等[11]的研究及图 3中的转速分析,行星齿轮齿圈R,行星架H和太阳轮S之间的转速关系为
| $ \dot{\omega}_{\mathrm{EMl}} S+\dot{\omega}_{\mathrm{out}} R=\dot{\omega}_{\mathrm{e}}(R+S), $ | (1) |
式中:R,S分别为齿圈和太阳轮的齿数。
根据Zhang等[12-13]的研究,分别对太阳层和输入/输出层对应连接构件进行分析:
以电机EM1、太阳轮S为研究对象,为
| $ \left(I_{\mathrm{EM} 1}+I_{S}\right) \dot{\omega}_{\mathrm{EM} 1}=F S+T_{\mathrm{EM}1}, $ | (2) |
以发动机E、行星架H为研究对象,为
| $ \left(I_{e}+I_{H}\right) \dot{\omega}_{e}=T_{e}-F S-F R, $ | (3) |
以动力输出端V、电机EM2、齿圈R为研究对象,为
| $ \left(I_{v}+I_{\mathrm{EM} 2}+I_{R}\right) \dot{\omega}_{\mathrm{out}}=T_{\mathrm{EM} 2}+F R-T_{v}。$ | (4) |
将式(1)~式(4)写成矩阵形式,就可以得到Prius THS-Ⅱ的动力学矩阵,为
| $ \left[ {\begin{array}{*{20}{c}} {{I_R} + {I_v} + {I_{{\rm{EM}}2}}}&0&0&{ - R}\\ 0&{{I_H} + {I_e}}&0&{R + S}\\ 0&0&{{I_S} + {I_{{\rm{EM}}1}}}&{ - S}\\ { - R}&{R + S}&{ - S}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \omega }_{{\rm{cut}}}}}\\ {{{\dot \omega }_e}}\\ {{{\dot \omega }_{{\rm{EM}}1}}}\\ F \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{T_{{\rm{EM}}2}} - {T_v}}\\ {{T_e}}\\ {{T_{{\rm{EM}}1}}}\\ 0 \end{array}} \right], $ | (5) |
式中:
由于Prius THS-Ⅱ只有一种固定连接模式,该构型只对应一个动力学矩阵。在36种方案中,由于在构型中添加了离合器/制动器,因此,每一个构型方案在不同离合器/制动器的启闭状态切换下都可以在2个及以上的不同模式间切换,每个模式均对应一个动力学矩阵。文中按照上述过程对36种构型方案的全部模式进行了动力学建模。
3 神经网络油耗模型研究 3.1 混合动力EVT构型样本燃油经济性分析动态规划DP算法(dynamic programming)作为一种基于全局最优的能量管理策略,是分析混合动力EVT构型在特定工况下最佳燃油经济性的理想工具[14]。为了获取神经网络模型训练集中混合动力EVT构型在最优工作条件下的油耗值,笔者采用DP算法对36种混合动力EVT构型方案在NEDC工况下的油耗值进行仿真。仿真车型及参数采用丰田Prius THS-Ⅱ搭载的混合动力汽车系统及其相关参数[15-16]。
在DP算法中将NEDC工况划分为N个阶段,通过多阶段决策,计算整个工况下的混合动力EVT构型油耗。在此过程中,取发动机转速ωe、电池SOC及构型工作模式Mode作为仿真的状态变量,取电机EM1转矩TEM1及构型工作模式Mode作为控制变量[17]。DP算法满足的约束条件如式(6)所示。
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\omega _{{e_ - }\min }} \le {\omega _e}(k) \le {\omega _{{e_ - }\max }}, }\\ {{\omega _{{\rm{EM}}{1_ - }\min }} \le {\omega _{{\rm{EM}}1}}(k) \le {\omega _{{\rm{EM}}{1_ - }\max }}, }\\ {{T_{{\rm{EM}}{1_ - }\min }} \le {T_{{\rm{EM}}1}}(k) \le {T_{{\rm{EM}}{1_ - }\max }}, }\\ {{\omega _{{\rm{EM}}{2_ - }\min }} \le {\omega _{{\rm{EM}}2}}(k) \le {\omega _{{\rm{EM}}{2_ - }\max }}, } \end{array}\\ {T_{{\rm{EM}}2\_\min }} \le {T_{{\rm{EM}}2}}(k) \le {T_{{\rm{EM}}{2_ - }\max }}, \\ {\rm{SO}}{{\rm{C}}_{\min }} \le {\rm{SOC}}(k) \le {\rm{SO}}{{\rm{C}}_{{\rm{max}}}}, \\ {P_{{\rm{ batt\_charge }}}} \le {P_{{\rm{ batt }}}}(k) \le {P_{{\rm{ batt\_discharge }}}}, \end{array} \right. $ | (6) |
式中:下标min和max分别表示对应变量最小和最大值;Pbatt_charge,Pbatt,Pbatt_discharge分别为电池充电功率、实际功率和放电功率。
其目标函数由3部分组成:发动机油耗函数、SOC惩罚函数及模式切换惩罚函数,为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {J = q + {f_{{p_ - }{\rm{soc}}}} + {f_{p\_{\rm{mole}}}}, }\\ {q = \sum\limits_{k = 0}^{N - 1} {{{\dot m}_f}} \left[ {{\omega _e}(k), {T_e}(k)} \right], } \end{array}\\ {f_{{p_ - }{\rm{soc}}}} = \sum\limits_{k = 0}^{N - 1} \alpha \left[ {{\rm{SOC}}(k) - {\rm{SO}}{{\rm{C}}_{{\rm{des}}}}} \right], \\ {f_{p\_{\rm{mole}}}} = \sum\limits_{k = 0}^{N - 1} \beta |{\mathop{\rm Mode}\nolimits} (k + 1) - {\mathop{\rm Mode}\nolimits} (k)|, \end{array} \right. $ | (7) |
式中:J为构型在NEDC工况下的仿真油耗值;q为发动机油耗值,根据发动机转速ωe和转矩Te从发动机油耗模型
利用36个构型动力学模型分别对相应构型方案进行DP仿真,得到其油耗值(油耗单位:L/100 km),部分构型的油耗值如表 2所示。
| 表 2 部分样本油耗值 Table 2 Fuel consumption of some configurations |
在仿真时,部分构型的油耗值为NaN,即构型不满足要求,没有油耗值输出。通过对构型方案和仿真算法设计的分析,出现这种结果的原因主要有以下2种:
1) 构型能够实现的模式与电池参数不匹配,导致SOC无法维持在要求的范围内,且车辆因不具备充电模式,满足不了驾驶工况要求。
2) 构型参数与2电机、发动机型号的不匹配。在一些特定时段,发动机或者电机无法提供满足驾驶循环工况所需要的转速或转矩,即工况对于发动机或电机的需求转速或者转矩大于该状态下它能够达到的最大转速或转矩,导致DP算法在对应状态下无法获得可行决策。
3.2 神经网络油耗模型广义回归神经网络(GRNN, general regression neural network)最早是由Specht博士于1991年提出,属于径向基神经网络RBF(radial basis function)的一个分支,是一种基于非线性回归理论的前馈式网络模型,具有良好的非线性逼近性能[18]。
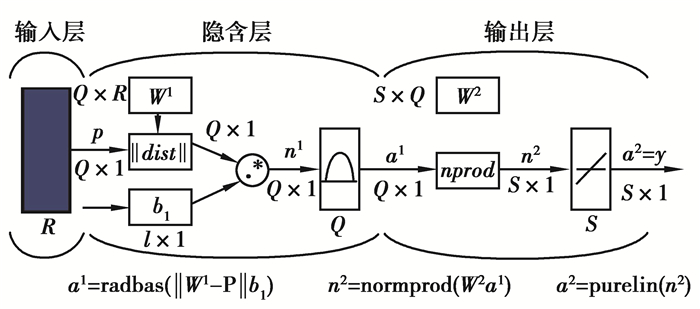
3.2.1 GRNN神经网络结构GRNN神经网络一般由输入层、隐含层和输出层组成,如图 4所示。其中,输入层仅接受样本的输入,不参与运算;隐含层的神经元个数等于训练集样本个数,该层的权值函数为欧式距离函数,用||dist||表示,其作用为计算网络输入与权值W1之间的距离,b1为隐含层的阀值,隐含层的传递函数为径向基函数,通常采用高斯函数;输出层为线性输出,其函数为规范化点积权函数,用nprod表示。计算网络的向量为n2,它的每个元素就是向量a1与权值矩阵W2中每行元素的点积再除以向量a1的各个元素之和得到;最终将结果n2提供给线性传递函数a2=purelin(n2)即可计算得到网络输出[19]。
|
图 4 GRNN神经网络结构 Fig. 4 GRNN structure |
搭建GRNN神经网络模型,需要确定神经网络的输入量和输出量。由于构型矩阵与混合动力EVT构型为一一对应关系,故将构型矩阵作为神经网络的输入,而对应混合动力EVT构型DP仿真油耗值作为神经网络的输出。
在GRNN神经网络中,Spread参数对于网络性能有重要影响。目前,Spread的选择较为常用且效果较好的为留一法,它是交叉验证法的特殊形式,适用于样本数量较小的神经网络参数调整,文中采用留一法调整Spread。
为了评价神经网络油耗模型准确性,文中引入2个指标:相对误差Ek和决定系数R2。
相对误差Ek表示神经网络的输出油耗值与构型DP仿真油耗值之间的差异程度,为
| $ E_{k}=\frac{\left|z_{k}-y_{k}\right|}{y_{k}} $ | (8) |
式中:zk为第k样本的神经网络计算值;yk为第k样本的DP仿真输出值。由于yk作为分母,其值不能为NaN,因此,为了增强神经网络的泛化能力,可以对每个构型进行油耗计算,文中做如下设定:对于仿真结果NaN的构型,取10 L/100 km作为其油耗值,选取10 L/100 km是由于与其他构型油耗值数量级相同,同时又存在明显的差别,对应此油耗值的构型效果明显很差,在筛选过程中可以直接剔除。通过这种数值变动可以增强神经网络对不可行构型方案的学习泛化能力,避免相对误差的计算因分母NaN而出现错误。
决定系数R2表征的是计算结果和仿真结果的一种相关关系,它的范围为[0, 1],愈接近于1,表明模型性能愈好;反之,愈接近于0,表明模型性能愈差[20],其计算公式为
| $ {R^2} = \frac{{{{\left( {l\sum\limits_{k = 1}^l {{z_k}} {y_k} - \sum\limits_{k = 1}^l {{z_k}} \sum\limits_{k = 1}^l {{y_k}} } \right)}^2}}}{{\left( {l\sum\limits_{k = 1}^l {z_k^2} - {{\left( {\sum\limits_{k = 1}^l {{z_k}} } \right)}^2}} \right)\left( {l\sum\limits_{k = 1}^l {y_k^2} - {{\left( {\sum\limits_{k = 1}^l {{y_k}} } \right)}^2}} \right)}}, $ | (9) |
式中, l为测试样本数量。
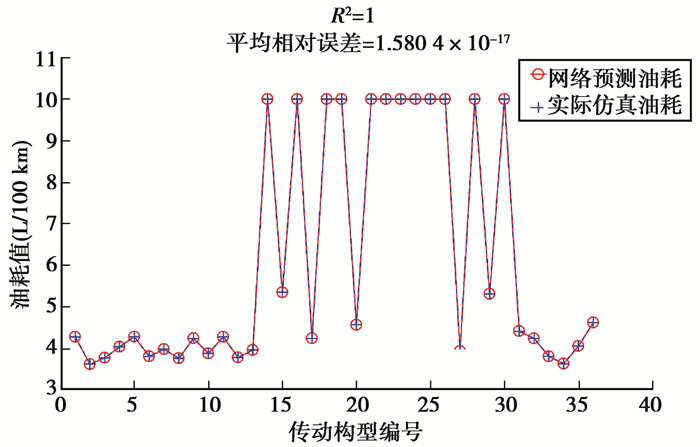
用调整好Spread的GRNN神经网络对36个构型学习结果如图 5所示。
|
图 5 GRNN网络学习结果比较 Fig. 5 Comparison of GRNN learning results |
从学习结果来看,GRNN神经网络有很好地学习能力,能够对36个学习样本方案进行很好地学习。结果显示,神经网络对于样本的学习决定系数等于1,平均相对误差接近0。
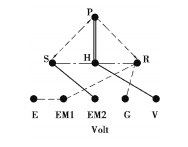
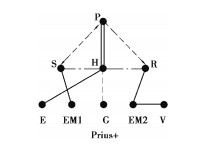
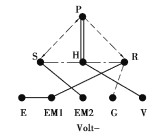
为了测试训练好的神经网络的泛化能力,文中选取4个待判别的典型EVT构型,其中包括丰田Prius THS-Ⅱ和通用Volt无离合器/制动器构型,同时还包括密歇根大学Zhang等[21]优化之后的Prius+与Volt-2个含离合器/制动器构型,这4个构型的图论分层图画及其构型矩阵如表 3所示。
| 表 3 待判别的构型分层图画及构型矩阵 Table 3 Hirarchical graph and configuration matrices to be discriminated |
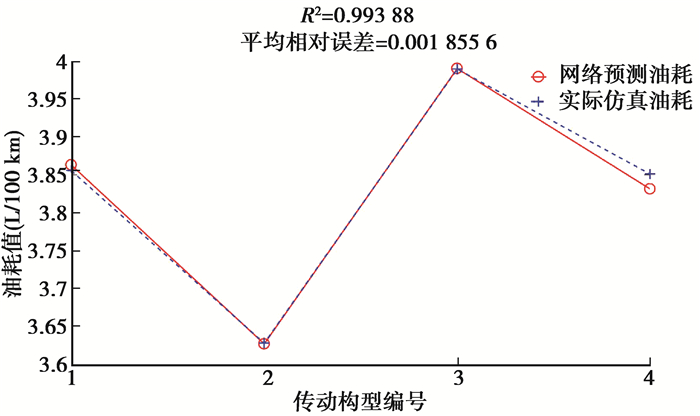
用训练好的GRNN神经网络对以上4个构型进行油耗值的计算,同时通过DP算法,得到以上4个构型在NEDC工况下的DP仿真油耗值,将神经网络计算结果与DP仿真结果进行对比,结果如图 6所示。
|
图 6 GRNN网络计算结果比较 Fig. 6 Comparison of GRNN calculation results |
预测结果与实际油耗的具体数值对比及误差分析如表 4所示。
| 表 4 混合动力EVT构型油耗结果及误差分析 Table 4 Fuel consumption results and error analysis of hybrid EVT configurations |
从图 6和表 4的结果分析可知,基于GRNN神经网络建立的混合动力EVT系统油耗模型具有很好的计算和泛化性能。对比神经网络对4个典型混合动力EVT构型油耗的计算结果,平均相对误差0.001 8,相关系数为0.994,准确率可以达到99.81%。
4 结论1) 在混合动力EVT系统分层图论模型的基础上提出混合动力EVT系统构型矩阵模型,为神经网络油耗模型的建立奠定基础;
2) 基于GRNN神经网络算法,提出一种快速判别混合动力EVT系统油耗模型。通过该GRNN神经网络油耗模型对4个典型混合动力EVT耦合系统方案进行油耗计算,并将结果与DP仿真结果进行比较,其准确率达到99.81%,验证了该方法的有效性。
| [1] |
杨亚联, 蒲斌, 胡晓松, 等. ISG型速度耦合混合动力系统全局最优控制方法[J]. 重庆大学学报, 2013, 36(9): 71-77. YANG Yalian, PU Bin, HU Xiaosong, et al. Study on global optimization control strategy of ISG velocity coupling hybrid electric vehicle[J]. Journal of Chongqing University(Natural Science Edition), 2013, 36(9): 71-77. (in Chinese) |
| [2] |
Sabri M F M, Danapalasingam K A, Rahmat M F. A review on hybrid electric vehicles architecture and energy management strategies[J]. Renewable and Sustainable Energy Reviews, 2016, 53: 1433-1442. DOI:10.1016/j.rser.2015.09.036 |
| [3] |
Liao Y G, Chen M Y. Analysis of multi-speed transmission and electrically continuous variable transmission using lever analogy method for speed ratio determination[J]. Advances in Mechanical Engineering, 2017, 9(8): 1687814017712948. |
| [4] |
Zhang Y, Ma X R, Yin C L, et al. Development and simulation of a type of four-shaft ECVT for a hybrid electric vehicle[J]. Energies, 2016, 9(3): 141. DOI:10.3390/en9030141 |
| [5] |
Zhuang W, Zhang X, Zhao D, et al. Optimal design of three-planetary-gear power-split hybrid powertrains[J]. International Journal of Automotive Technology, 2016, 17(2): 299-309. DOI:10.1007/s12239-016-0030-0 |
| [6] |
Zhuang W C, Zhang X W, Ding Y, et al. Comparison of multi-mode hybrid powertrains with multiple planetary gears[J]. Applied Energy, 2016, 178: 624-632. DOI:10.1016/j.apenergy.2016.06.111 |
| [7] |
刘振涛. EVT混合动力传动系统的图论建模与构型综合设计理论研究[D].重庆: 重庆大学, 2016. LIU Zhentao. Research on graph modeling and configuration synthesis and design of EVT hybrid electric powertrains[D]. Chongqing: Chongqing University, 2016.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1016730828.htm |
| [8] |
林建德, 李润方. 一种齿轮系的图画表示法及其在齿轮系运动分析上的应用[J]. 机械科学与技术, 2004, 23(1): 60-62, 76. LIN Jiande, LI Runfang. An application of a graph representation to the analysis of the kinematics of general gear trains[J]. Mechanical Science and Technology, 2004, 23(1): 60-62, 76. (in Chinese) |
| [9] |
Zhang X W, Peng H, Sun J. A near-optimal power management strategy for rapid component sizing of multimode power split hybrid vehicles[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 609-618. DOI:10.1109/TCST.2014.2335060 |
| [10] |
Pei H X, Hu X S, Yang Y L, et al. Configuration optimization for improving fuel efficiency of power split hybrid powertrains with a single planetary gear[J]. Applied Energy, 2018, 214: 103-116. DOI:10.1016/j.apenergy.2018.01.070 |
| [11] |
Benford H L, Leising M B. The lever analogy:A new tool in transmission analysis[J]. SAE Transactions, 1981, 429-437. |
| [12] |
Zhang X W, Li S E, Peng H, et al. Design of multimode power-split hybrid vehicles:a case study on the voltec powertrain system[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4790-4801. DOI:10.1109/TVT.2016.2531740 |
| [13] |
Yang Y L, Pei H X, Hu X S, et al. Fuel economy optimization of power split hybrid vehicles:A rapid dynamic programming approach[J]. Energy, 2019, 166: 929-938. DOI:10.1016/j.energy.2018.10.149 |
| [14] |
苏岭, 曾育平, 秦大同, 等. 插电式混合动力汽车能量管理策略研究现状和发展趋势[J]. 东华理工大学学报(自然科学版), 2017, 40(2): 10-15. SU Ling, ZENG Yuping, QIN Datong, et al. Current situation and development trend of plug-in hybrid electric vehicle's energy management strategies[J]. Journal of Chongqing University, 2017, 40(2): 10-15. (in Chinese) |
| [15] |
Staunton R H, Ayers C W, Burress B A, et al. Evaluation of 2004 toyota prius hybrid electric drive system[R]. Office of Scientific and Technical Information (OSTI), 2006. DOI: 10.2172/890029.
|
| [16] |
Zhuang W C, Zhang X W, Ding Y, et al. Comparison of multi-mode hybrid powertrains with multiple planetary gears[J]. Applied Energy, 2016, 178: 624-632. DOI:10.1016/j.apenergy.2016.06.111 |
| [17] |
Yang Y L, Hu X S, Pei H X, et al. Comparison of power-split and parallel hybrid powertrain architectures with a single electric machine:Dynamic programming approach[J]. Applied Energy, 2016, 168: 683-690. DOI:10.1016/j.apenergy.2016.02.023 |
| [18] |
王小川, 史峰, 郁磊. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013. WANG Xiaochuan, SHI Feng, YU Lei. Analysis of 43 neural network cases based on MATLAB[M]. Beijing: Beijing University Press, 2013. (in Chinese) |
| [19] |
张强劲, 陈忠华. 基于GRNN算法的潜在产出与产出缺口估算模型[J]. 重庆大学学报(自然科学版), 2016, 39(6): 148-154. ZHANG Qiangjin, CHEN Zhonghua. Potential output and output gap model based on GRNN algorithm[J]. Journal of Chongqing University(Natural Science Edition), 2016, 39(6): 148-154. (in Chinese) |
| [20] |
徐中明, 吕伟东, 夏小均, 等. 面向行人安全的保险杠结构改进优化[J]. 重庆大学学报(自然科学版), 2017, 40(4): 1-8. XU Zhongming, LYU Weidong, XIA Xiaojun, et al. Bumper structure optimization for pedestrian leg protection[J]. Journal of Chongqing University(Natural Science Edition), 2017, 40(4): 1-8. (in Chinese) |
| [21] |
Zhang X, Li C T, Kum D, et al. Prius(+) and Volt(-):configuration analysis of power-split hybrid vehicles with a single planetary gear[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3544-3552. DOI:10.1109/TVT.2012.2208210 |
 2019, Vol. 42
2019, Vol. 42