作业车间调度问题多年来一直是学术界的研究热点。现有研究对工作日历的处理主要有3种方式:不考虑工作日历、调度后考虑工作日历、调度中考虑工作日历。大部分研究属于第一种情况[1-3]。虽然计算量最小,但调度方案未与工作日历挂钩,显然会与实践脱节。部分研究属于第二种情况。调度时先不考虑工作日历,在设备连续可用的时间轴上安排工序,将调度方案根据工作日历,通过“整体平移”映射到具体的日历时间点上[4]。第二种方式计算量较小,仅适用于设备具有相同工作日历的场合。极少部分研究属于第三种情况。调度过程中根据各设备的工作日历安排工序的起止时刻。虽然计算量较大,但能保证调度方案与实践相吻合,适用于设备具有混合工作日历的场合。考虑到设备自动化程度、运行可靠性、固定成本、生产任务量及人性化管理等的需要,中国机械加工企业或车间内设备往往采用不尽相同的工作日历,即混合工作日历现象还较普遍。另外,柔性作业车间调度问题是作业车间调度问题的扩展,在生产实践中应用更为广泛;随着市场环境的变迁,出于竞争的需要,调度目标并不单一,往往要综合考虑生产周期、生产成本等多个目标。因此,研究混合工作日历下柔性作业车间多目标调度具有重要意义。
混合工作日历下柔性作业车间多目标调度问题属于高度复杂的组合优化问题。从考虑的要素看,由于考虑设备的混合工作日历,无疑增加了工序安排的难度。设备工作日历是工作制和工作班次(工作时段)的合称,调度中必须二者兼顾,同时又要考虑到可操作性和计算量。现有关于混合工作日历的作业车间调度尚存在一些不足。武志军等[5]提出了动态工作日历的实现策略和关键算法,但未考虑工作班次。黄瑜岳等[6]在调度中考虑了工作班次,但未考虑工作制。万春辉等[7]在调度中虽然既考虑了工作制又考虑了工作班次,但存在可操作性不强、计算量大的不足。从优化的对象看,不仅要确定工序的加工顺序,还要确定工序的加工设备,其组合数随工序数和设备数的增加而呈指数级增加。从优化的目标看,需要在多个目标之间进行协调。对多目标优化的处理方法有间接法和直接法两种。间接法又称“化多为少法”,该方法通过一些技术手段将多目标转化为单目标,然后在单目标空间中寻优[8-9],只能求得一部分最优解,不能得到完整的Pareto解集。直接法是直接在多目标空间中寻优的方法,主要包括线性加权和变系数法[10]和基于Pareto寻优的方法[11-12]。线性加权和变系数法要求随机权重足够均匀,很难找到比较完整的Pareto解集。基于Pareto寻优的方法是相对更理想的多目标优化方法,其中,非支配排序遗传算法(NSGA,non-doing sorting genetic algorithm)是一种比较成熟和理想的Pareto寻优算法[13-14]。2002年,Deb等[15]在NSGA的基础上提出了带精英策略的非支配排序遗传算法(NSGA Ⅱ, non-doing sorting genetic algorithm with elite strategy),使其性能又得以进一步提升。
基于此,针对一类混合工作日历下柔性作业车间调度问题(设备具有不尽相同的工作制或工作时段,一旦某设备的工作制和工作时段被设定,则该设备在同一个调度周期内每个工作日均按相同且固定不变的工作时段运行),提出基于设备工作日历的时间推算机制和函数用于调度中进行工序安排,调度过程中将工序的加工顺序和设备选择2个优化对象统一进行编码处理,选择生产周期、生产成本为优化目标,研究提出一种基于NSGA Ⅱ的多目标优化方法。
1 问题描述车间需在c台设备(编号依次为1~c)上安排m个工件(编号依次为1~m)的加工任务。假设:①设备按指定的工作日历运行。工作日历是工作制和工作时段的合称,一旦某设备的工作制和工作时段被设定,则该设备在同一个调度周期内每个工作日均按相同且固定不变的工作时段运行;②每个工件有多道工序,每道工序可选设备可能有多个;③工件的工艺流程已知,工序在可选设备上的调整时间和加工时间已知;④当一个工件正在加工时,不能停下来加工其他工件;⑤当设备按工作日历停工时,设备停止调整、工件停止加工,待设备重新开工时继续未完成的工作;⑥调度从指定的调度起始时刻往后进行;⑦初始状态下设备自调度起始时刻往后的时间轴连续。要求:在以上假设条件下进行合理调度,使生产周期最短、生产成本最低。
2 NSGA Ⅱ算法设计以Excel VBA为平台设计了一种带精英策略的非支配排序遗传算法(NSGA Ⅱ)。
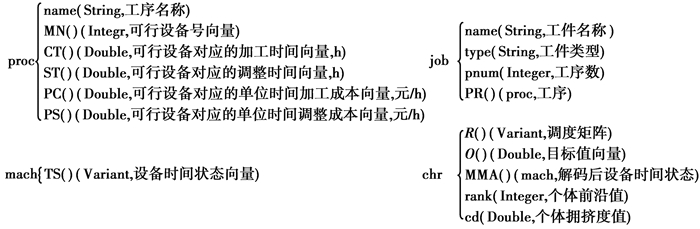
2.1 类型、变量及数组定义根据算法需要,定义了图 1所示的类型proc、job、mach、chr和表 1所示的变量及数组。其中,chr.R为tpnum×12的数组,1~12列分别存储任务序号、工件号、工序号、设备号、调整时间、加工时间、调整开始时刻、调整结束时刻、加工开始时刻、加工结束时刻、调整成本、加工成本。MA为mnum×22的数组(根据需要可扩展),用于存储各设备的参数。JB为jnum个元素的数组,其元素类型为job,用于存储各工件的参数。MMB为mnum个元素的数组,其元素类型为mach,用于存储解码前设备的时间状态。
|
图 1 自定义类型 Fig. 1 Custom type |
| 表 1 变量及数组定义 Table 1 Definition of variables and arrays |
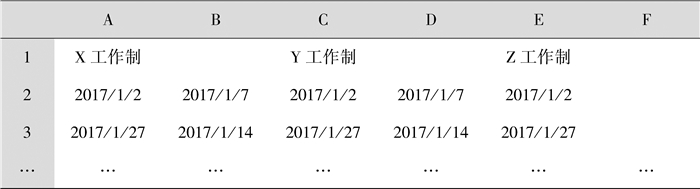
首先,按照假设条件①,根据需要,用Excel设计“工作制”工作表,用于设置工作制。图 2中,从左到右每两列对应一个工作制,第1行奇数列单元格为工作制名称,其他行奇数列存放该工作制非周末休息日期、偶数列存放该工作制周末上班日期。
|
图 2 “工作制”工作表 Fig. 2 'Working system' sheet |
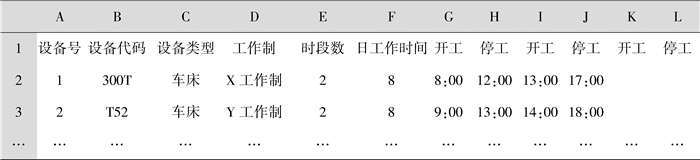
然后,设计了“设备”工作表,用于为设备指定工作制和设置工作时段。图 3中,D列用于为设备指定工作制,从G列开始的各列用于为设备设置工作时段。工作时段须成对输入,范围从0:00~24:00,且须保证停工时刻大于开工时刻,各工作时段之间不能有交叉。以设备300T为例,当前被指定的工作制为“X工作制”,每天的工作时段有2个,即8:00~12:00和13:00~17:00,日工作时间为8 h。
|
图 3 “设备”工作表 Fig. 3 'Machines' sheet |
最后,利用Excel VBA编写时间推算函数实现基于设备工作日历的时间推算,分别是Isworkday、Nextworkday、Getsd、Forwardwd、Backwd、Getat。
1) Isworkday函数
该函数有2个参数,md(Date型)和wds(String型),其作用是根据设备工作制wds判断日期md是否为其工作日,若是工作日则返回1,否则返回0。
2) Nextworkday函数
该函数有3个参数,md(Date型)、x(Integer型)和wds(String型),其作用是获得根据设备工作制wds从日期md推算x天后的工作日,x>0时为正向推算,x < 0时为反向推算。
3) Getsd函数
该函数有2个参数,t(Double型)、mn(Integer型),其作用是根据设备mn的工作时段获得时间t所在的位置,其返回值为数组A。该数组有2个元素,A(2)是标志元素,其值为0表示时间t属于设备mn第A(1)个非工作时段,其值为1则表示时间t属于设备mn第A(1)个工作时段。在图 4中,该设备的工作日有2个工作时段,8:00~12:00(编号为1)和13:00~17:00(编号为2),把时间0:00~24:00划分成5个时间段,另外3个时间段为非工作时段,0:00~8:00(编号为0)、12:00~13:00(编号为1)、17:00~24:00(编号为2)。

|
图 4 某设备工作时段与非工作时段 Fig. 4 Work time and non-work time periods of a machine |
4) Forwardwd函数
该函数有3个参数,mdt(Date型)、tt(Double型)和mn(Integer型),其作用是根据设备mn的工作日历获得从某个工作时刻mdt正向推算tth后的工作时刻。
5) Backwd函数
该函数有3个参数,mdt(Date型)、tt(Double型)和mn(Integer型),其作用是根据设备mn的工作日历获得从某个工作时刻mdt反向推算tth后的工作时刻。
6) Getat函数
该函数有2个参数,mdt(Date型)和mn(Integer型),其作用是根据设备mn的工作日历获得从某个时刻mdt正向推算得到的最早工作时刻。
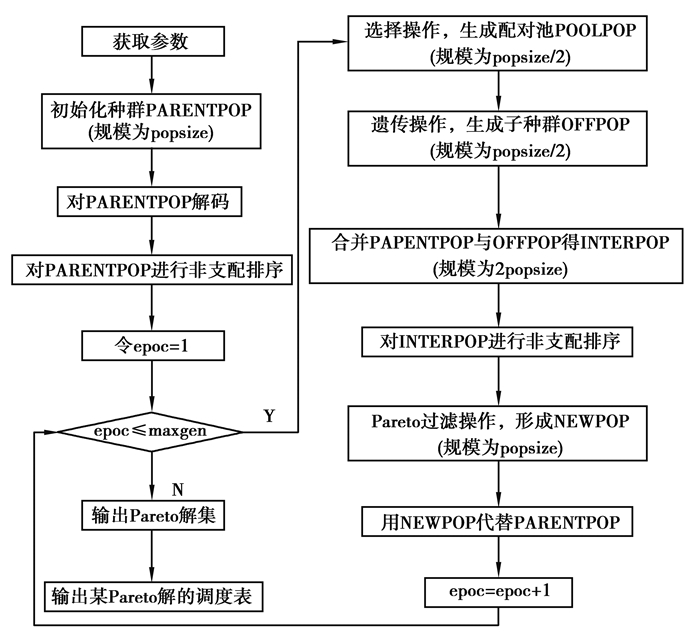
2.3 算法流程取popsize为偶数,设计的算法流程如图 5所示。
|
图 5 算法流程 Fig. 5 Flow of the algorithm |
根据算法需要,设计了“工件”“调度工件”“工艺流程”“其他参数”工作表,用于调度人员进行参数设置。算法从工作表“其他参数”读取参数赋给表 1中的变量。从工作表“设备”读取第2行及以后的数据赋给数组MA。采用for循环对数组MMB进行赋初值:对设备i,令MMB(i).TS(1)=bt,MMB(i).TS(2)=tln。采用for循环对JB的每一个元素赋值:对于工件i,首先从工作表“工件”中读取第i个工件的工件名称、型号、工序数分别赋给JB(i).name、JB(i).type、JB(i).pnum,然后用Redim JB(i).PR(JB(i).pnum)重新定义JB(i).PR的维数,再用for循环从工作表“工艺流程”的中读取该工件对应工序参数分别赋给JB(i).PR(1)~JB(i).PR(JB(i).pnum)。
2.5 编码方式采用“分段”方式分别对工序和加工设备进行编码。设种群为POP,如式(1)所示,POP(i).R为tpnum×12的数组,第2列和第4列为编码所用,其他各列为辅助或解码所用。其中,第2列基因值为1~jnum的自然数,代表工件号,各自然数出现的次数等于对应工件的工序数;第4列为各工序的可行加工设备号。
| $ {\mathop{\rm POP}\nolimits} (i) \cdot \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&2&1&3& \cdots &{510}\\ 2&1&1&4& \cdots &{618}\\ 3&1&2&2& \cdots &{380}\\ 4&2&2&2& \cdots &{760}\\ \vdots & \vdots & \vdots & \vdots &{}& \vdots \\ {{\mathop{\rm tpnum}\nolimits} }&5&6&9& \cdots &{360} \end{array}} \right) $ | (1) |
按照图 6所示的流程依次产生popsize个随机个体,存入种群PARENTPOP,完成种群初始化。其中,给R第4列赋可行设备号的流程如图 7所示。从图 6和图 7可见,产生的随机个体为可行个体。
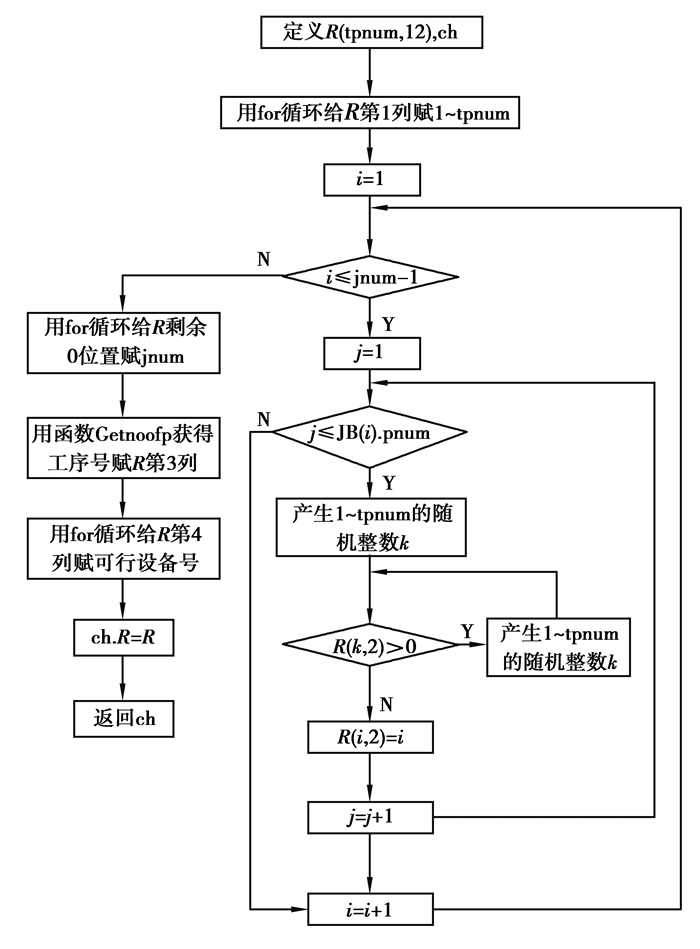
|
图 6 产生随机个体 Fig. 6 Generation of random individuals |
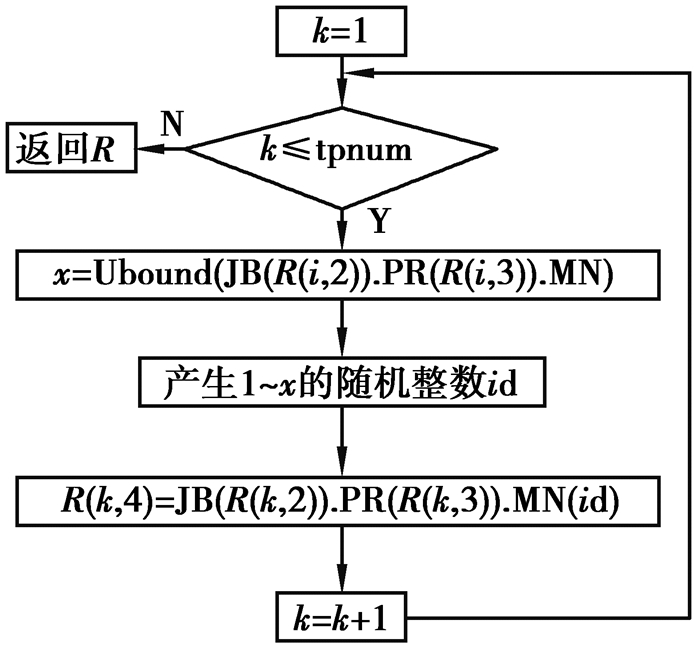
|
图 7 给R第4列赋设备号 Fig. 7 Assigning feasible machine number to column 4 of R |
通过“联赛机制”从父代种群PARENTPOP中选择“优秀”个体形成规模为popsize/2的配对池POOLPOP。设联赛规模为tour-size,用for循环每次从父代种群PARENTPOP中随机选出tour-size个个体,从tour-size个个体中根据个体前沿值rank和拥挤度cd选出一个“优秀”个体加入配对池,直到for循环结束,返回POOLPOP。
2.8 遗传操作由配对池POOLPOP通过交叉、变异操作产生规模为popsize的子代种群OFFPOP,流程如图 8所示。
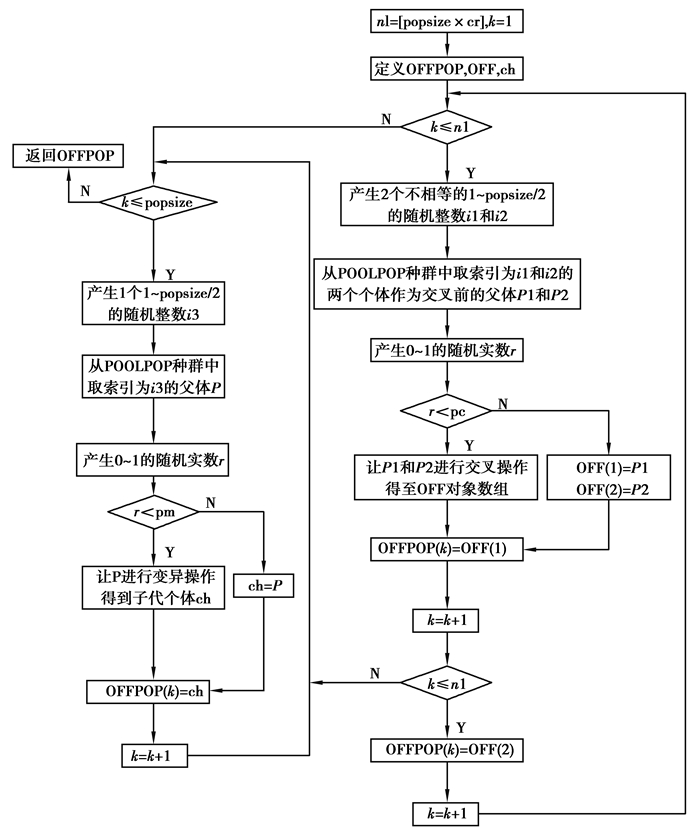
|
图 8 遗传操作 Fig. 8 Genetic operation |
采用“分段”方式分别对工序和加工设备进行交叉。
1) 工序交叉
基于“遗传算子改进策略”,采用“基于工序顺序的交叉”方式来保证子代个体可行性[16]:同一工件的工序之间具有先后顺序,为保证交叉操作不破坏这种先后顺序,固定某父体的某个工件号所在行(工件号、工序号和设备号)不变,从上到下依次用另一父体中除该工件号所在行之外的其他行取代本父体剩余行,如式(2)中,若P1.R中固定工件1,P2.R中固定工件3不动,则P1.R与P2.R交叉后的结果如式(3)所示。
| $ P1.\mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&3&1&4\\ 2&1&1&1\\ 3&2&1&3\\ 4&3&2&2\\ 5&1&2&4\\ 6&2&2&3\\ 7&4&1&2\\ 8&4&2&4 \end{array}} \right), P2.\mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&2&1&5\\ 2&3&1&2\\ 3&1&1&3\\ 4&1&2&1\\ 5&4&1&4\\ 6&2&2&2\\ 7&4&2&5\\ 8&3&2&3 \end{array}} \right), $ | (2) |
| $ P{1^\prime }.\mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&2&1&5\\ 2&1&1&1\\ 3&3&1&2\\ 4&4&1&4\\ 5&1&2&4\\ 6&2&2&2\\ 7&4&2&5\\ 8&3&2&3 \end{array}} \right), P{2^\prime } \cdot \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&1&1&1\\ 2&3&1&2\\ 3&2&1&3\\ 4&1&2&4\\ 5&2&2&3\\ 6&4&1&2\\ 7&4&2&4\\ 8&3&2&3 \end{array}} \right)。$ | (3) |
2) 加工设备交叉
采用“两点交叉”方式进行设备交叉:产生2个1~tpnum的随机整数mp1、mp2,保证mp1 < mp2,对于父体P1′,根据P1′.R的第k行(k从mp1~mp2变化)工件号P1′.R(k, 2)、工序号P1′.R(k, 3),在父体P2′.R中找到对应的工件号、工序号所在行号h,令P1′.R(k, 4)=P2′.R(h, 4);对于父体P2′按类似方法进行处理。例如,若mp1=3,mp2=5,式(3)的P1′、P2′设备交叉后的结果如式(4)所示。显然,通过这种交叉操作能保证交叉后的设备号为对应工序的可行设备号,从而保证交叉后的子代个体可行。
| $ {\mathop{\rm OFF}\nolimits} (1).\mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&2&1&5\\ 2&1&1&1\\ 3&3&1&2\\ 4&4&1&2\\ 5&1&2&4\\ 6&2&2&2\\ 7&4&2&5\\ 8&3&2&3 \end{array}} \right), {\mathop{\rm OFF}\nolimits} (2) \cdot \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&1&1&1\\ 2&3&1&2\\ 3&2&1&5\\ 4&1&2&4\\ 5&2&2&2\\ 6&4&1&2\\ 7&4&2&4\\ 8&3&2&3 \end{array}} \right)。$ | (4) |
交叉后需对新个体进行重新解码,分别赋给OFF(1)和OFF(2)。
2.10 变异操作采用“分段”方式分别对工序和加工设备进行变异。
1) 工序变异
基于“遗传算子改进策略”,采用“滑动变异”方式来保证子代个体可行性[16]:对于父体P,产生一个1~tpnum之间的随机整数mp作为变异点,以此点为基准向上向下分别寻找与该点工件号相同的最近位置s1和s2,若向上未找到则令s1=0,向下未找到则令s2=tpnum+1;取k1=s1+1、k2=s2-1,产生k1~k2的随机整数k,将该工件号、工序号及设备号滑移至k位置。例如,式(5)中,若mp=3,可求得k1=2、k2=8,若产生的随机整数k=6,变异后的结果如式(6)所示。
| $ P.\mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&3&1&1\\ 2&1&1&1\\ 3&3&2&3\\ 4&2&1&4\\ 5&1&2&3\\ 6&2&2&5\\ 7&1&3&2\\ 8&2&3&3 \end{array}} \right), $ | (5) |
| $ {P^\prime } \cdot \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} 1&3&1&1\\ 2&1&1&1\\ 3&2&1&4\\ 4&1&2&4\\ 5&2&2&5\\ 6&3&2&3\\ 7&1&3&2\\ 8&2&3&3 \end{array}} \right)。$ | (6) |
2) 加工设备变异
采用“单点变异”方式进行设备变异:产生1个1~tpnum的随机整数mp作为变异点,令k=Ubound(JB(P′.R(mp, 2)).PR(P′.R(mp, 3)).MN),产生1~k的随机整数id作为新的加工设备号的索引,再令P′.R(mp, 4)=JB(P′.R(mp, 2)).PR(P′.R(mp, 3)).MN (id)。
变异后需对新个体进行重新解码赋给ch。
2.11 解码操作为尽可能缩短生产周期,在解码操作中采用2种技术:①将工序时间细分为设备调整时间和加工时间,使得下道工序的设备调整工作有条件提前进行,从而使上道工序加工完毕后能尽早开始加工[16-17]。②采用正向可插入式挤压调度方法在设备的时间轴上安排工序,以尽可能减少设备的空闲时间。解码操作流程如图 9所示。
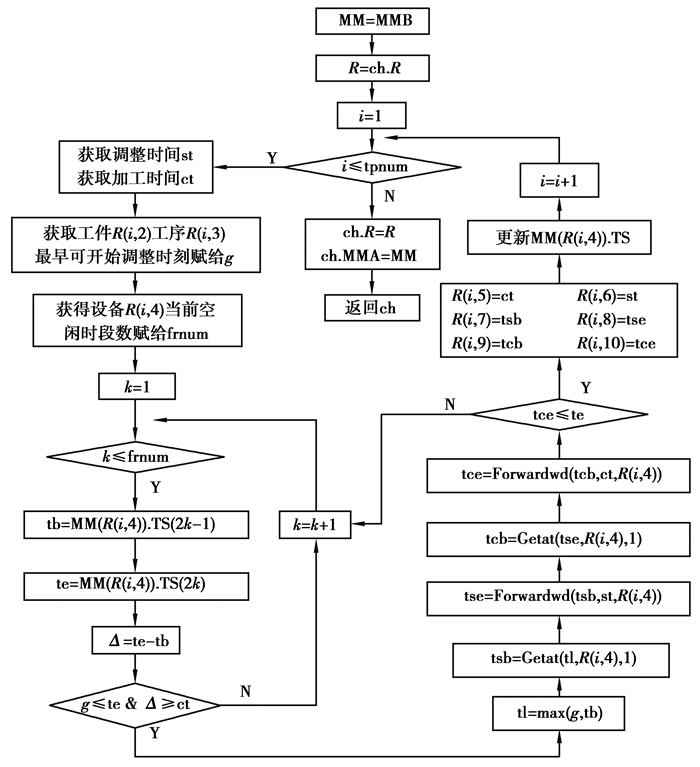
|
图 9 解码操作流程 Fig. 9 Flow of decoding operation |
解码操作分三步。第一步:将解码前设备对象数组MMB赋给MM,将ch.R赋给R。第二步:令i=1~tpnum,依次安排各工序,确定R的第5~12列值。第三步:当把1~tpnum个工序全部安排完毕后,将得到的调度数组R及MM赋给ch的属性R、MMA,即令ch.R=R、ch.MMA=MM,解码结束。其中,需要说明以下三点。
1) 获取设备调整时间st和加工时间ct的方法:由设备号R(i, 4)求得其在JB(R(i, 2)).PR(R(i, 3)).MN中的索引号id,取st=JB(R(i, 2)).PR(R(i, 3)).st(id),ct=JB(R(i, 2)).PR(R(i, 3)).ct(id)。
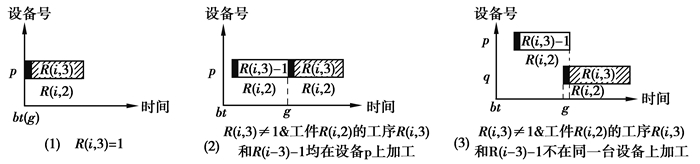
2) 获取工件R(i, 2)的工序R(i, 3)的设备最早可开始调整时刻g的方法:如图 10所示,分3种情况处理。①R(i, 3)=1时,即待安排工序是工件R(i, 2)的第1道工序,则取g=bt。②R(i, 3)≠1且工件R(i, 2)的工序R(i, 3)与R(i, 3)-1均在同一台设备p上加工,在这种情况下,工件R(i, 2)的工序R(i, 3)必须等到工序R(i, 3)-1完工后才能开始设备调整,故取g为工件R(i, 2)的工序R(i, 3)-1的加工结束时刻。设工件R(i, 2)的工序R(i, 3)-1在R中的行号为h,则取g=R(h, 10)。③R(i, 3)≠1且工件R(i, 2)的工序R(i, 3)与R(i, 3)-1不在同一台设备上加工,此时工件R(i, 2)的工序R(i, 3)可从R(i, 3)-1的加工结束时刻提前sth开始设备调整,待设备调整完毕,工序R(i, 3)-1正好完成加工,使工序R(i, 3)可立即开始加工。设工件R(i, 2)的工序R(i, 3)-1在R中的行号为h,则首先采用Getat函数根据设备R(i, 4)的工作日历正向推算得到工作时刻t(工序R(i, 3)-1的加工结束时刻未必在设备R(i, 4)的工作时间段内,其最早可能开始加工时刻为正向推算得到的工作时刻t),再利用Backwd函数从时刻t反向推算sth得到设备最早可开始调整时刻g。先令t=Getat(R(h, 10), R(i, 4);再令g=Backwd(t, st, R(i, 4))。
|
图 10 获取工件R(i, 2)的工序R(i, 3)的设备最早可开始调整时刻g Fig. 10 Obtaining the machines' earliest start time g in the process R(i, 3) of job R(i, 2) |
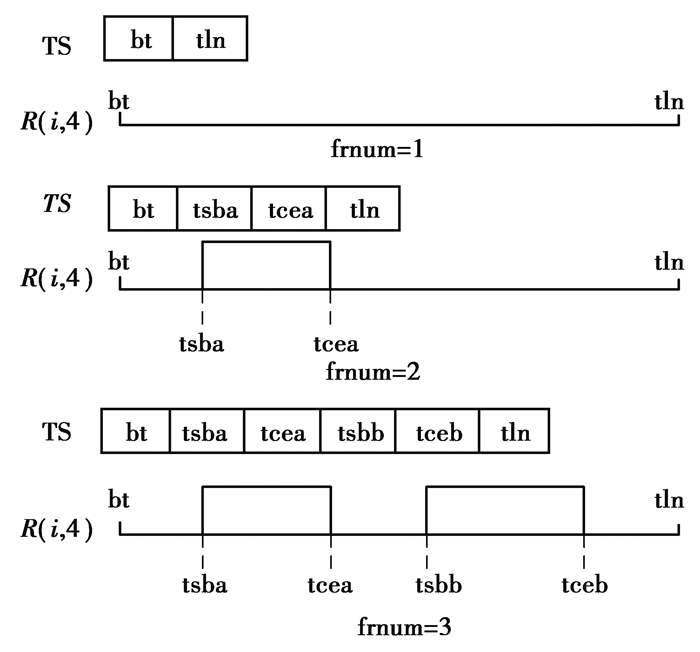
3) 更新MM(R(i, 4)).TS的方法:如图 11所示,MM(R(i, 4)).TS的初始长度为2,仅包含两个元素,第1个为调度起始时刻bt,第2个是时间大值tln。此时空闲时间段数frnum=1。当为设备R(i, 4)安排某工序a后,需在bt~tln之间插入2个值,分别是tsba(调整开始时刻)和tcea(加工结束时刻)。此时bt~tln被分割成2个空闲时间段,分别是bt~tsba和tcea~tln,此时空闲时间段数frnum=2。当再为R(i, 4)安排某工序b后(假设工序b安排在工序a加工结束时刻之后),空闲时间段分别为bt~tsba、tcea~tsbb、tceb~tln,此时空闲时间段数frnum=3。依次类推,随着工序的不断安排,MM(R(i, 4)).TS的长度动态变化、元素动态更新。需说明的是:若tcea=tsbb则MM(R(i, 4)).TS数据结构仍旧不变,空闲时间段数和空闲时间段保持不变。只是第2个空闲时间段的时间差为0,在后续的工序安排中,由解码流程可以看出不会在tcea~tsbb之间插入工序。设插入时段为设备R(i, 4)的第k个空闲时段,则更新MM(R(i, 4)).TS的步骤如下:首先,将MM(R(i, 4)).TS的长度增加2位;然后,从k空闲时段对应的第2个数据起,将后面的数据后移2位,从而腾出2个空位;最后,在2个空位处分别填入待插入工序的设备调整开始时刻和加工结束时刻。
|
图 11 更新MM(R(i, 4)).TS Fig. 11 Updating MM(R(i, 4)).TS |
用for循环找出ch.R第7列的最小值赋给smin、第10列的最大值赋给smax、第11列和12列的和赋给s,再令ch.O(1)=smax-smin,ch.O(2)=s。
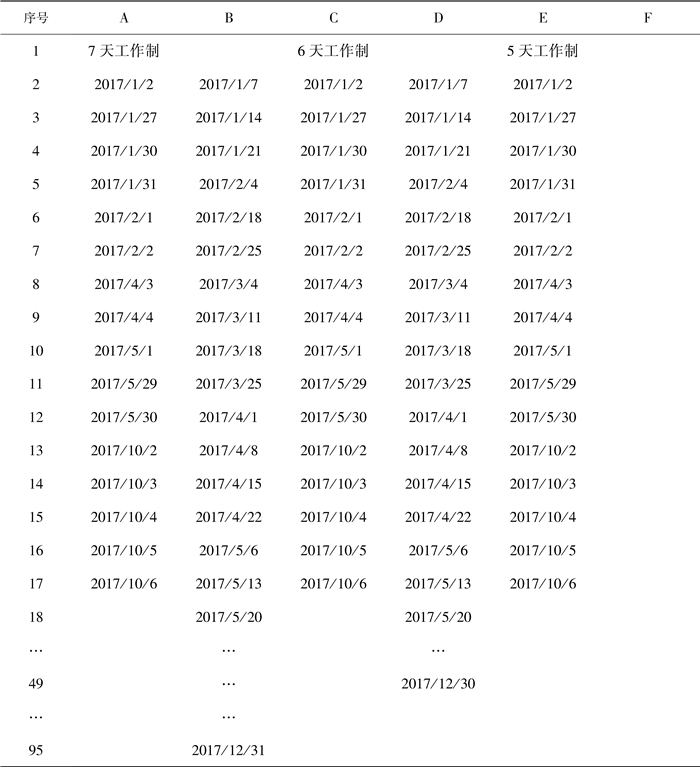
3 案例分析某机加车间要在10台设备上安排7个工件的加工任务,各工件信息如表 2所示、工艺流程如表 3所示,设备信息如表 4所示,其他参数如表 5所示。本例中设备所用工作制共有3个,即5天工作制、6天工作制和7天工作制。“工作制”工作表的设置内容如图 12所示。
| 表 2 工件 Table 2 Jobs |
| 表 3 工艺流程 Table 3 Process flow |
| 表 4 设备 Table 4 Machines |
| 表 5 其他参数 Table 5 Other parameters |
|
图 12 “工作制”工作表设置内容 Fig. 12 Content of 'working system' sheet |
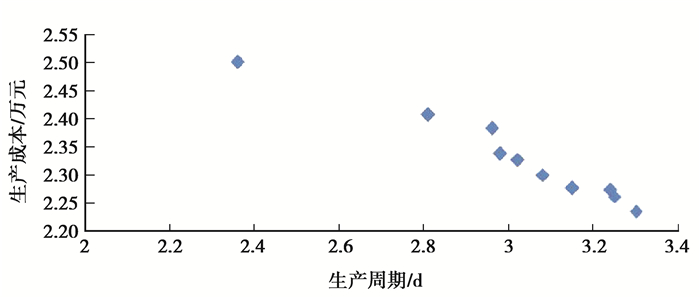
在上述设置之下,利用算法独立运行多次,均能得到基本相同且均匀的Pareto解集,表明收敛效果较好。图 13是某次进化计算得到的Pareto解集,调度人员可从中进行选择。表 6是某方案(生产周期为2.81 d,生产成本为24 078元)对应的调度表,图 14和图 15是该方案对应的工件甘特图和设备甘特图。
|
图 13 Pareto解集 Fig. 13 Pareto solution set |
| 表 6 某方案的调度表 Table 6 Scheduling table of a solution |
|
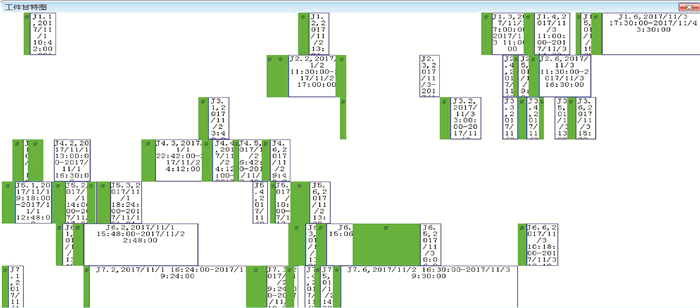
图 14 工件甘特图 Fig. 14 Gantt chart of the jobs |
|
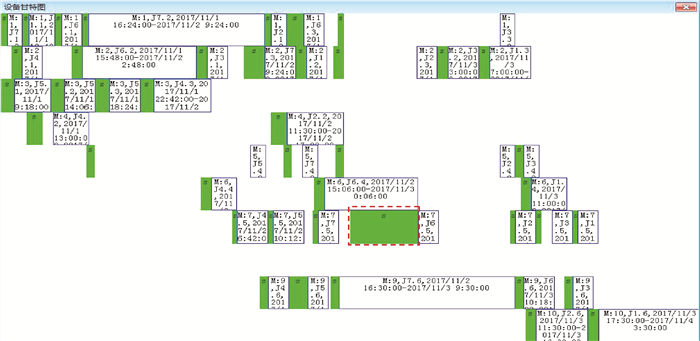
图 15 设备甘特图 Fig. 15 Gantt chart of the machines |
图 14和图 15中,带s标识符的方框表示设备调整起止时段,带J或M标识符的方框表示工序的加工起止时刻。例如,图 15中虚线方框是工件6第5道工序的设备调整起止时段,紧随其后的方框表示工件6第5道工序在设备号7上加工的起止时段。从表 6第33行可以看出,该工序的设备调整起始时刻为2017/11/2 17:36、调整结束时刻为2017/11/3 0:06,其加工起始时刻为2017/11/3 0:06、加工结束时刻为2017/11/3 2:06。根据设备7(代码为3U5)的工作日历进行验算,2017/11/2 17:36~2017/11/3 0:06的日历时间为6.5h,但工作时间却为0.5 h;2017/11/3 0:06~2017/11/3 2:06之间的日历时间和工作时间相等,均为2 h,0.5 h和2 h正好与表 3中该工序的设备调整时间st和加工时间ct相吻合,表明计算结果正确。
从表 6的18行和32行可见,工件1的工序3和4为相邻工序,由于分别在不同的设备上加工,因此可以提前进行设备调整,当上道工序(工序3)完成加工时,可立即开始下道工序(工序4)的加工,采用这种安排方式能在一定程度上缩短生产周期。
从表 6可以看出,按序号升序排列,设备2(代码为200T)上安排的工序依次为J7.3、J6.2、J4.1、J2.3、J3.1、J1.2、J3.2、J1.3,而从图 15可以看出,设备2上从左到右安排的工序依次为J4.1、J6.2、J3.1、J7.3、J1.2、J2.3、J3.2、J1.3,二者并不完全一致。产生这种现象的原因在于解码过程中采用了正向可插入式挤压调度方法。采用这种方法可以尽可能地减少设备空闲时间从而缩短生产周期。
4 结论为解决混合工作日历下柔性作业车间多目标调度的困难,提出了一种基于NSGA Ⅱ的多目标优化方法。论文的研究结论如下:
1) 在工序调度过程中,通过时间推算函数准确推算设备调整起止时刻和工序加工起止时刻,能保证调度方案的可行性。
2) 算法在解码过程中采用2项技术能在一定程度上缩短生产周期:将工序时间细分为设备调整时间和加工时间,能使下道工序的设备可提前开始设备调整;采用正向可插入式挤压调度方法安排工序。
3) 文中提出的方法突破了传统柔性作业车间调度的局限,能在可接受的计算时间内得到有效的混合工作日历下柔性作业车间多目标调度方案集(Pareto解集)供调度人员决策。
| [1] |
Gao L, Pan Q K. A shuffled multi-swarm micro-migrating birds optimizer for a multi-resource-constrained flexible job shop scheduling problem[J]. Information Sciences, 2016, 372: 655-676. DOI:10.1016/j.ins.2016.08.046 |
| [2] |
Amirghasemi M, Zamani R. An effective asexual genetic algorithm for solving the job shop scheduling problem[J]. Computers & Industrial Engineering, 2015, 83: 123-138. |
| [3] |
Kundakcı N, Kulak O. Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem[J]. Computers & Industrial Engineering, 2016, 96: 31-51. |
| [4] |
熊唯, 李宗斌, 郝建波. 解决动态作业车间调度关键问题的方法研究[J]. 组合机床与自动化加工技术, 2008(7): 105-108, 112. XIONG Wei, LI Zongbin, HAO Jianbo. Research on solving the key problem of dynamic job shop scheduling[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2008(7): 105-108, 112. (in Chinese) DOI:10.3969/j.issn.1001-2265.2008.07.031 |
| [5] |
武志军, 宁汝新, 万春辉. 车间调度中的动态工作日制研究与实现[J]. 制造业自动化, 2006, 28(4): 46-48, 75. WU Zhijun, NIN Ruxin, WAN Chunhui. Research and realization of dynamic shop calendar in shop scheduling[J]. Manufacturing Automation, 2006, 28(4): 46-48, 75. (in Chinese) DOI:10.3969/j.issn.1009-0134.2006.04.014 |
| [6] |
黄瑜岳, 李克清, 郑晓峰. 考虑班次约束的Job Shop等量分批调度算法[J]. 科学技术与工程, 2013, 13(1): 1-7, 16. HUANG Yuyue, LI Keqing, ZHENG Xiaofeng. A scheduling algorithm to equal amount of batches for job shop considering the constraint of work-shifts[J]. Science Technology and Engineering, 2013, 13(1): 1-7, 16. (in Chinese) DOI:10.3969/j.issn.1671-1815.2013.01.001 |
| [7] |
万春辉, 闫艳, 武志军, 等. 面向车间生产动态调度的动态工作日制研究[J]. 组合机床与自动化加工技术, 2006(3): 102-104. WAN Chunhui, YAN Yan, WU Zhijun, et al. Research and realization of dynamic shop calendar orienting dynamic scheduling[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2006(3): 102-104. (in Chinese) DOI:10.3969/j.issn.1001-2265.2006.03.033 |
| [8] |
Ponnambalam S G, Ramkumar V, Jawahar N. A multiobjective genetic algorithm for job shop scheduling[J]. Production Planning & Control, 2001, 12(8): 764-774. |
| [9] |
张师博华, 车阿大, 宋强磊. 基于Pareto排序和混沌加权的多目标项目调度[J]. 计算机集成制造系统, 2012, 18(6): 1215-1222. ZHANG Shibohua, CHE Ada, SONG Qianglei. Multi-objective project scheduling based on Pareto sorting and chaos weighting[J]. Computer Integrated Manufacturing Systems, 2012, 18(6): 1215-1222. (in Chinese) |
| [10] |
Zhu Z Q. Construction of Integrated Objective Function/Adaptive Function for Multiobjective/Multidisciplinary Optimization[C]//China Aerodynamics Society. 2003 Advances in Aerodynamic Frontier Research. China Aerodynamics Society, 2003: 6.
|
| [11] |
刘晓霞, 谢里阳, 陶泽, 等. 柔性作业车间多目标调度优化研究[J]. 东北大学学报(自然科学版), 2008, 29(3): 362-365, 382. LIU Xiaoxia, XIE Liyang, TAO Ze, et al. Research on multi-objective scheduling optimization for flexible job shop[J]. Journal of Northeastern University(Natural Science), 2008, 29(3): 362-365, 382. (in Chinese) DOI:10.3321/j.issn:1005-3026.2008.03.016 |
| [12] |
彭建刚, 刘明周, 张玺, 等. 基于Pareto优化的离散自由搜索算法求解多目标柔性作业车间调度问题[J]. 中国机械工程, 2015, 26(5): 620-626. PENG Jiangang, LIU Mingzhou, ZHANG Xi, et al. Discrete free search based on pareto-optimality for multi-objective flexible job-shop scheduling problem[J]. China Mechanical Engineering, 2015, 26(5): 620-626. (in Chinese) DOI:10.3969/j.issn.1004-132X.2015.05.009 |
| [13] |
El-Abbasy M S, Elazouni A, Zayed T. MOSCOPEA:Multi-objective construction scheduling optimization using elitist non-dominated sorting genetic algorithm[J]. Automation in Construction, 2016, 71: 153-170. DOI:10.1016/j.autcon.2016.08.038 |
| [14] |
Zitzler E, Thiele L, Laumanns M, et al. Performance assessment of multiobjective optimizers:an analysis and review[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 117-132. DOI:10.1109/TEVC.2003.810758 |
| [15] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [16] |
陈华平, 谷峰, 卢冰原, 等. 自适应多目标遗传算法在柔性工作车间调度中的应用[J]. 系统仿真学报, 2006, 18(8): 2271-2274, 2288. CHEN Huaping, GU Feng, LU Bingyuan, et al. Application of self-adaptive multi-objective genetic algorithm in flexible job shop scheduling[J]. Journal of System Simulation, 2006, 18(8): 2271-2274, 2288. (in Chinese) DOI:10.3969/j.issn.1004-731X.2006.08.054 |
| [17] |
周亚勤, 李蓓智, 杨建国. 考虑批量和辅助时间等生产工况的智能调度方法[J]. 机械工程学报, 2006, 42(1): 52-56. ZHOU Yaqin, LI Beizhi, YANG Jianguo. Intelligent scheduling algorithm for problems with batch and non cutting time[J]. Chinese Journal of Mechanical Engineering, 2006, 42(1): 52-56. (in Chinese) DOI:10.3321/j.issn:0577-6686.2006.01.010 |
| [18] |
潘全科, 朱剑英. 多工艺路线多资源多目标的作业调度优化[J]. 中国机械工程, 2005, 16(20): 1821-1826. PAN Quanke, ZHU Jianying. An opimization method for a multi-objective job-shop scheduling problem under multi-resource constraints[J]. China Mechanical Engineering, 2005, 16(20): 1821-1826. (in Chinese) DOI:10.3321/j.issn:1004-132X.2005.20.010 |
 2019, Vol. 42
2019, Vol. 42

