b. 重庆大学 低品位能源利用技术及系统教育部重点实验室, 重庆 400044
b. Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Ministry of Education, Chongqing University, Chongqing 400044, P. R. China
人体心血管系统是一种复杂周期性受迫的流体网络动力系统。为仿真研究血液循环系统的动力学特征,主要采用流体网络模型[1-2]和电网络模型[3-4]两大类。流体网络模型在Navier-Stokes方程的基础上,通过建立流体网络模型和方程组,数值仿真求解模型,主要用于分析动脉段流阻对血流场或压力场的影响;但无法考虑血管壁弹性力等因素的影响,因而,仿真得到的不同动脉段脉搏波波形与输入波形相似。电网络模型能考虑血管壁弹性力等因素的影响,依据血液循环的流体动力学方程和电网络传输线方程类比相似的特征,将血压、血流量、血流阻力、血管顺应性和血流惯性类比为电压、电流、电阻、电容和电感,具有明确的物理意义和清晰的生理意义等特点,已成为研究心血管系统仿真的热点。
自1959年MacDonald等[5]首次利用人体动脉传输线模型来仿真人体脉搏波以来,各种模型被不断提出和完善。肖汉光等[6]利用55段传输线模型来仿真个体差异性中动脉参数对脉搏波的影响。刘莹等[7]在典型的双弹性模型的基础上,建立了人体心血管系统电网络模型,仿真研究外周阻力和血管顺应性变化对动脉血压和血流的影响规律。Xiao等[8]基于传输线模型建立了人体动脉树脉搏波仿真模型,用于模拟心率、身高、动脉半径、外周阻力、动脉粘弹性力和顺应性等参数对脉搏波的影响。Butlin等[9]基于传输线模型来评估影响心率、左心室射血时间和反射波参数对人体动脉硬化脉搏波传播的应用研究。Xiao等[10]基于55段动脉树传输线模型来仿真研究动脉狭窄对人动脉树整体血流动力学特征的影响;模拟不同的动脉狭窄部位、程度和长度,探讨对血压和血流量波形的影响。脉象是由生理病理变化引起脉搏波不同所致,因而,人体病变可通过不同的脉象来诊断,《脉经》提出了以桡动脉为基点的寸口诊脉法[11]。王唯工[12-13]将桡动脉周期性波动视为由各种不同频率的谐波振荡所组成,且各器官对应一个特殊的谐波共振频率;在实际测量中发现感冒病人脉搏波的第四(肺)和第七(膀胱)谐波幅值变大,第三(脾)、第六(胆)和第九(小肠)谐波幅值变小。
脉搏波谐波与人体的生理病理变化密切相关,尽管目前对人体心血管系统脉搏波的研究较多,但对脉搏波频域分析的研究较少。为了分析不同器官生理病理变化对脉搏波的影响规律,将器官病变等效为外周阻力的变化,外周阻力主要是指血液在小动脉和毛细血管中的流动阻力;采用标准的55段人体动脉树的简化模型来模拟人体血液循环心血管动力系统,分析人体各器官外周阻力变化对血压、血流量等血流动力学参数和脉搏波谐波的影响。
1 方法 1.1 方法概述人体主要动脉段组成的人体动脉树模型是研究脉搏波传播等血液动力学现象的有效模型。首先,建立人体血液循环的传输线电网络模型,如图 1所示,选用Liang等[14]实际测量的55段人体心血管系统的基本参数,通过传输线理论计算出各动脉段的输入阻抗;其次,采用Milnor[15]测得的升主动脉处的体积流率波作为模型的输入信号;最后,通过改变各器官分支的外周阻力,利用传输线模型脉搏波的传播过程求解。

|
图 1 55段人体动脉树模型 Fig. 1 The 55-segment model of human arterial tree |
在求解过程中,假设心脏输出体积流率波不变,忽略血管跨膜压力的影响,同时将人体器官病变等效为模型中外周阻力的变化。通过仿真计算得到不同器官外周阻力变化对血压、血流量等血流动力学参数和脉搏波谐波的影响。
1.2 模型的建立1) 特征阻抗和传播常数。在传输线模型中,将动脉段看成具有惯性和粘弹性的薄壁圆柱形管道的基本计算单元。通过Navier-Stokes方程求解得到血压和血流量的传播特征。
根据Womersley的推导[16-17],单段动脉的传播常数和特征阻抗可表示为
| $ \gamma_{0}=\frac{j w}{c_{0}}\left(1-\sigma^{2}\right)^{1 / 2}\left(1-F_{10}\right)^{-1 / 2}, $ | (1) |
| $ Z_{0}=\frac{\rho c_{0}}{\pi r^{2}}\left(1-\sigma^{2}\right)^{-1 / 2}\left(1-F_{10}\right)^{-1 / 2}, $ | (2) |
式中:根据Womerley的命名法,
| $ c_{0}=\sqrt{E h / \rho D}, $ | (3) |
式中:h为动脉壁的厚度;ρ为血液密度;当血液温度为37 ℃时,ρ为1.056 g/cm3;E为动脉的静态弹性模量;D为动脉内直径。
动脉壁被看成具有粘性的材料,运动可以产生应力和位移相位差Φ。在考虑了动脉壁的粘性后,其波速由原来的c0变成c0ejΦ/2。根据Tatylor[18]的推导,Φ的角频率函数可以表示为
| $ \mathit{\Phi} = {\mathit{\Phi} _0}\left( {1 - {{\rm{e}}^{ - kw}}} \right), $ | (4) |
其中, Φ0和k的一般取值为15°和2,Φ0为Φ的渐进值。Φ和h/2r之间的关系[19]:
| $ \mathit{\Phi} =\mathit{\Phi} (10 h /(2 r)), $ | (5) |
式中,Φ是指特定的参数, 如:5°、10°和15°。
把考虑动脉壁为粘性材料时的波速值带入,求得修正后的传播常数和特征阻抗为
| $ \gamma_{0}=\frac{j w}{c_{0}}\left(1-\sigma^{2}\right)^{1 / 2}\left(1-F_{10}\right)^{-1 / 2} \mathrm{e}^{-j \mathit{\Phi} / 2}, $ | (6) |
| $ Z_{0}=\frac{\rho c_{0}}{\pi r^{2}}\left(1-\sigma^{2}\right)^{-1 / 2}\left(1-F_{10}\right)^{-1 / 2} \mathrm{e}^{j \mathit{\Phi} / 2}。$ | (7) |
2) 输入阻抗和反射系数。以某段动脉为例,通过公式计算出其传播常数γ0和特征阻抗Z0,并已知该段动脉的入口体积流率和负载阻抗ZL,则该段动脉的输入阻抗为
| $ Z_{\mathrm{input}}=Z_{0}\left[\frac{\left(Z_{L}-Z_{0}\right) \mathrm{e}^{-\gamma_{0} l}+\left(Z_{L}+Z_{0}\right) \mathrm{e}^{+\gamma_{0} l}}{\left(Z_{0}-Z_{L}\right) \mathrm{e}^{-\gamma_{0} l}+\left(Z_{L}+Z_{0}\right) \mathrm{e}^{+\gamma_{0} l}}\right], $ | (8) |
定义反射系数:
| $ \mathit{\Gamma}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}。$ | (9) |
则输入阻抗可改写为
| $ Z_{\mathrm{input}}=Z_{0}\left[\frac{1+\mathit{\Gamma} \mathrm{e}^{-2 \gamma_{0} l}}{1-\mathit{\Gamma} \mathrm{e}^{-2 \gamma_{0} l}}\right]。$ | (10) |
3) 脉搏波的传播。根据传输线理论, 从动脉段的入口端到出口端,血压和血流量的脉动可以通过传播常数γ0和反射系数Γ计算。长度为l的动脉段入口处(近心段)的血压为Pproximal,则出口处(远心段)Pdistal的血压为
| $ P_{\text { distal }}=P_{\text { proximal }}(1+\mathit{\Gamma} ) /\left(\mathrm{e}^{\gamma l}+\mathit{\Gamma} \mathrm{e}^{-\gamma l}\right)。$ | (11) |
输入阻抗是从动脉系统中某一点观察动脉系统的后负荷。在频域范围内,输入阻抗表示为血压和血流量波经傅里叶变换后各对应频率的比值;动脉树中任意一点的血压和血流量可通过输入阻抗相互转换,即:
| $ P(w)=Z_{\text { input }}(w) \cdot Q(w)_{0}。$ | (12) |
左心室射血进入升主动脉,为体循环提供血液和动力,因此,将左心室看作典型的血流源,模型的输入信号如图 2所示。在1个周期中,其收缩期占30%左右,舒张期为70%左右,1个周期的血流量约为80 mL。

|
图 2 升主动脉的体积流率波形 Fig. 2 Volume flow rate waveform of ascending aorta |
输入阻抗的计算参考了肖汉光的递归计算法[20]。通过脉搏波的传播计算出动脉树中各点血压和血流量的频域特征,利用反傅里叶变换得到血压和血流量的时域波形。图 3和图 4分别表示从升主动脉到股动脉的血压和血流量波形的分布图,从图中可以清楚地看到,人体动脉树中各点脉搏波的波形和其传播过程;随着脉搏波的传播,血压波的波峰逐渐升高,血流量波峰逐渐减小,可以清晰地观察到脉搏波传播延迟现象。例如,从升主动脉到股动脉脉搏波的波足延迟时间约为0.2 s,距离超过120 cm,即脉搏波速度为600 cm/s。
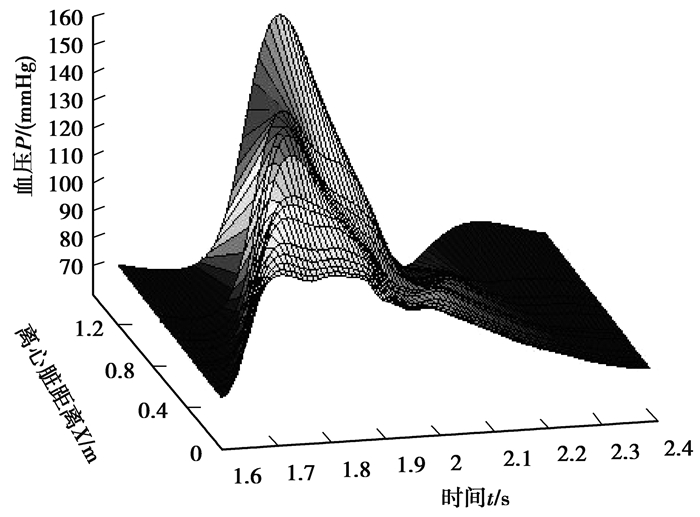
|
图 3 升主动脉到股动脉的血压波 Fig. 3 Blood pressure waves from the ascending aorta to the femoral artery |
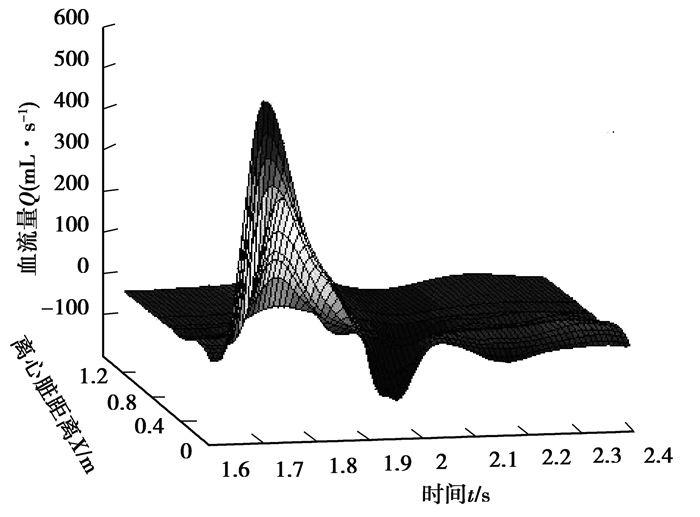
|
图 4 升主动脉到股动脉的血流量波 Fig. 4 Blood flow waves from the ascending aorta to the femoral artery |
定义阻力比η=R′/R,其中,R′表示生理发生病变后的外周阻力,R表示正常外周阻力值,则η为无量纲比值,可以反映器官病变时外周阻力的变化情况。在计算过程中,η分别取值为0.5、1、2、3、4进行对比分析。
2.1 时域分析在心脏输出体积流率波一定的条件下,研究得到了不同器官分支外周阻力变化对主动脉和桡动脉血压的影响规律。图 5表示脾分支阻力变化对主动脉和桡动脉血压的影响曲线。可以看出,主动脉和桡动脉血压波波峰随脾分支阻力比的增加而升高,但升高的趋势逐渐减小。计算得出,随着肝分支阻力比的增大,主动脉和桡动脉血压也有一定的增加,但肝分支阻力变化对主动脉和桡动脉压力影响小于脾分支。
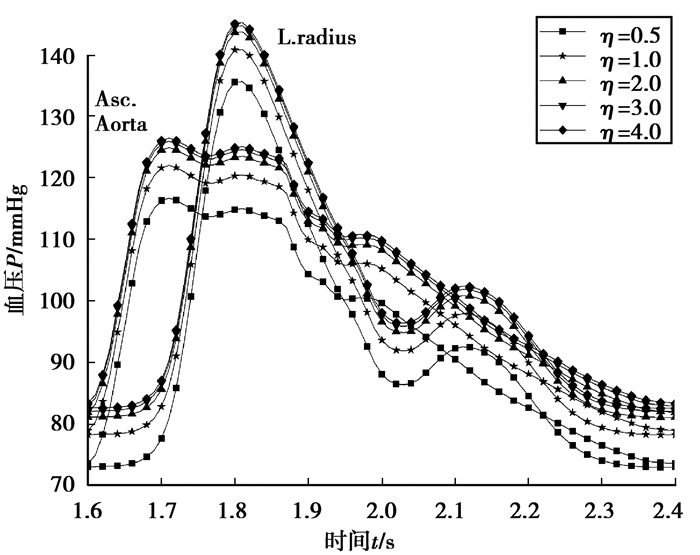
|
图 5 主动脉和桡动脉血压随脾分支阻力变化 Fig. 5 Change of the aortic and radial artery pressure with the spleen branch resistance |
图 6是胃分支阻力变化对主动脉和桡动脉血压影响曲线。可以看出,随着胃分支阻力比的增加主动脉血压增加,但增加的趋势较小,阻力比变化对桡动脉血压的影响也较小;胃和下肠膜阻力比变化对主动脉和桡动脉的影响基本相似。
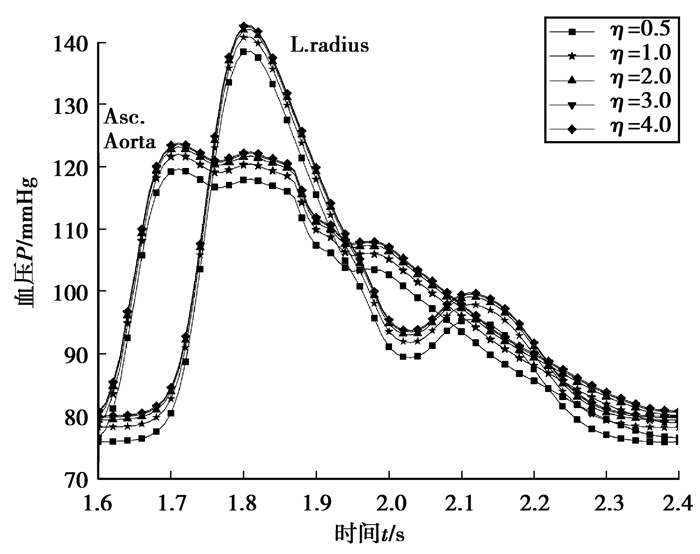
|
图 6 主动脉和桡动脉血压随胃分支阻力变化 Fig. 6 Change of the aortic and radial artery pressure with the gastric branch resistance |
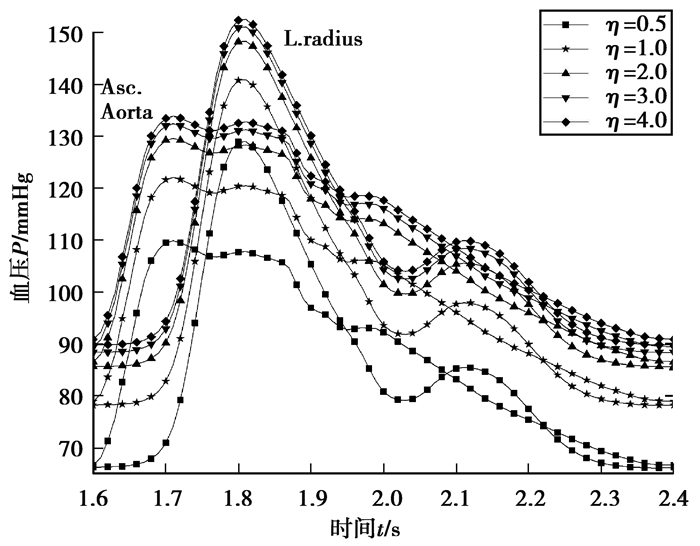
图 7是上肠膜分支阻力变化对主动脉和桡动脉血压影响曲线。可以看出,主动脉和桡动脉血压随上肠膜分支阻力比的增加而增加,相对于其它器官分支,上肠膜分支阻力变化对主动脉和桡动脉血压的影响更大。
|
图 7 主动脉和桡动脉血压随上肠膜分支阻力变化 Fig. 7 Change of the aortic and radial artery pressure with the superior mesenteric branch resistance |
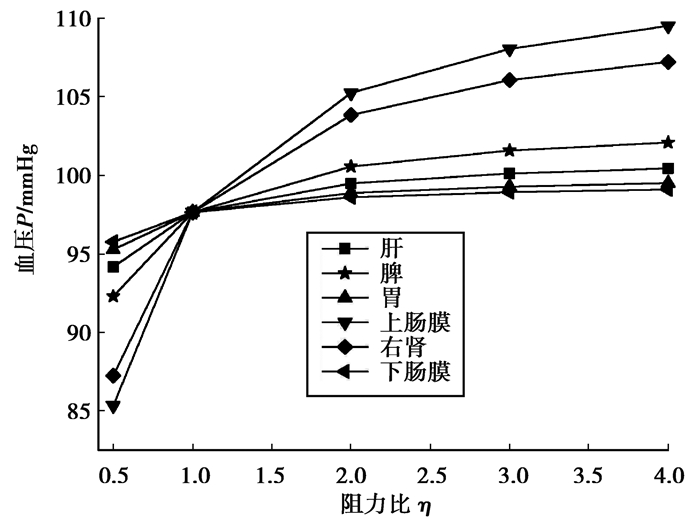
不同器官阻力比变化对桡动脉平均血压的影响曲线如图 8所示。可以看出,人体桡动脉的平均血压约为97.6 mmHg,在心输出体积流率波一定的情况下,随着不同器官阻力比的增加,桡动脉的平均血压升高。当阻力比η=4时,肝、脾、胃、上肠膜、右肾、下肠膜分支桡动脉平均血压较正常值分别增加2.86%、4.55%、1.90%、12.15%、9.81%、1.49%。
|
图 8 桡动脉平均血压随阻力比变化的影响 Fig. 8 Change of the radial artery mean pressure with the resistance ratio |
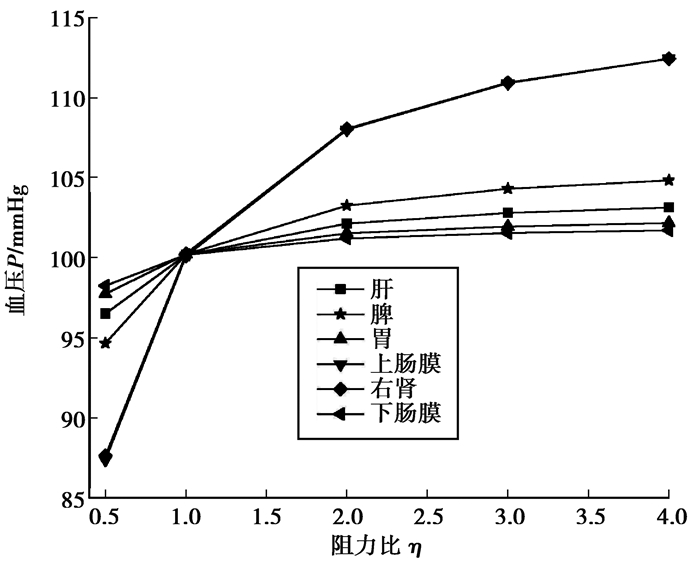
图 9表示自身平均血压随阻力比变化的影响,可以看出,随着阻力比的增加自身的平均血压升高,其中,上肠膜和右肾的增加趋势比较显著,其它器官分支小幅度升高。当阻力比η=4时,肝、脾、胃、上肠膜、右肾、下肠膜分支平均血压较正常分别增加2.94%、4.61%、1.95%、12.30%、12.17%、1.51%。
|
图 9 自身平均血压随阻力比变化的影响 Fig. 9 Change of the one's own mean blood pressure with the flow resistance ratio |
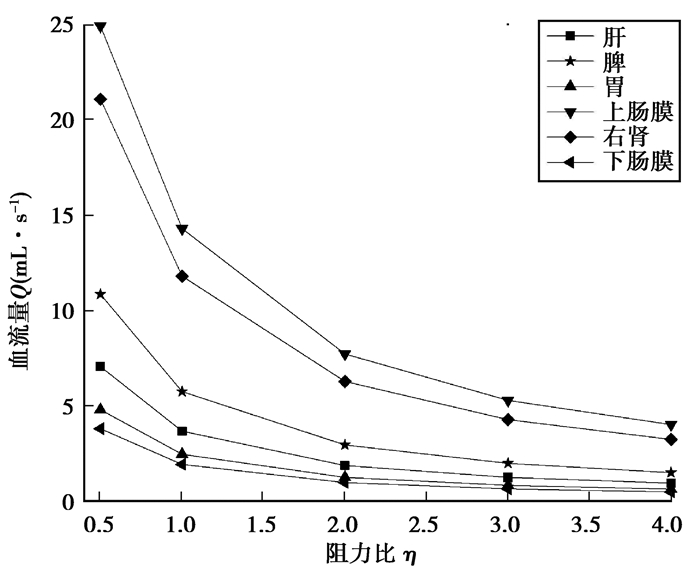
图 10表示自身平均血流量随阻力比变化的影响,可以看出,随着阻力比η的增加自身的血流量迅速下降。当阻力比η=4时,肝、脾、胃、上肠膜、右肾、下肠膜分支平均血流量较正常分别下降74.2%、73.8%、74.5%、71.9%、72.5%、74.6%。
|
图 10 自身平均血流量随阻力比变化的影响 Fig. 10 Change of the one's own mean blood flow with the flow resistance ratio |
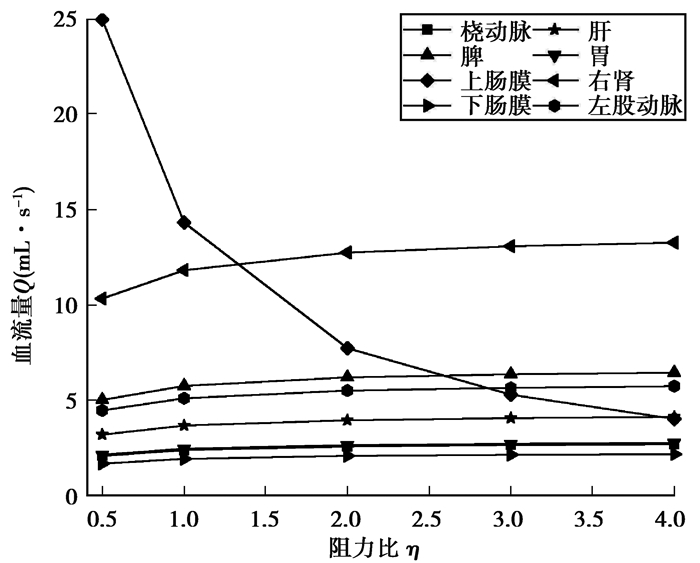
图 11表示上肠膜阻力变化对其他分支平均血流量的影响,由图 11可知,随着上肠膜分支流阻比的增大其自身的平均血流量迅速下降,且下降的趋势逐渐减小,当η=4时,相对于正常值下降了71.9%。随着上肠膜阻力比的增大,各分支的平均血流量均有小幅度增大,它是对各分支平均血流量影响最大的器官;当阻力比η=4时,右肾分支的平均血流量较正常值增加12.1%。
|
图 11 上肠膜阻力变化对其他分支平均流量的影响 Fig. 11 The effect of the intestinal membrane branch resistance change on other branches' average blood flow |
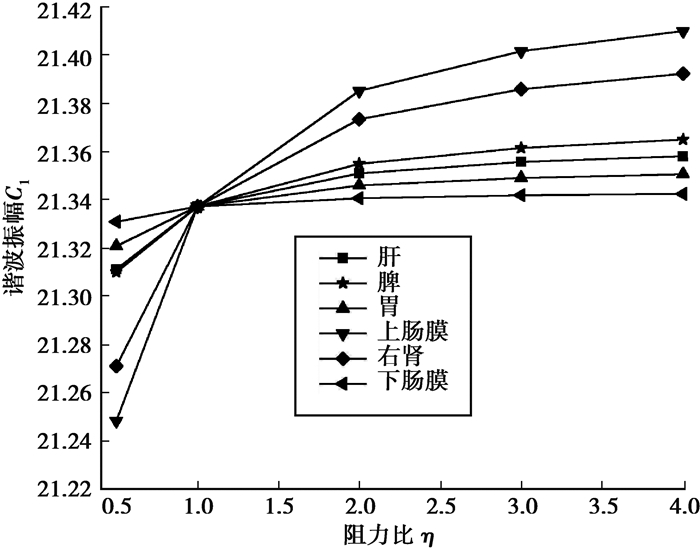
图 12为桡动脉血压波谐波振幅C1随各器官阻力比变化的影响情况。由图可知,不同器官阻力比变化对桡动脉谐波幅值C1的影响较小,当阻力比η=4时,肝、脾、胃、上肠膜、右肾、下肠膜桡动脉血压谐波振幅C1较正常值分别增加0.1%、0.13%、0.06%、0.34%、0.26%、0.03%;不同器官阻力比变化对桡动脉血压波其它谐波振幅的影响与C1基本相似。
|
图 12 桡动脉血压谐波振幅随阻力比变化影响 Fig. 12 Change of the harmonic amplitude of the radial artery pressure with the resistance ratio |
通过对不同器官分支外周阻力变化对脉搏波的影响进行数值仿真,发现不同器官阻力变化对主动脉和桡动脉脉搏波均有一定的影响,随阻力变化的程度不同而不同。研究表明,在心脏输出体积流率波一定的情况下,不同器官分支的血流量随自身的阻力增大而减小,血压随自身阻力增加而增加;桡动脉平均血压随不同器官阻力增加而增加,但增加的趋势逐渐减小;其中,上肠膜阻力变化对主动脉血压影响最大;其次,是肾和脾,其它分支的影响相对较小。中医脉诊是根据人体桡动脉脉搏波信号来诊断疾病的,研究表明,桡动脉脉搏波会随不同器官阻力变化而变化,这为中医脉诊提供了一定科学支撑。
与文中研究内容相关的临床试验有:Lu等[21]对肝胆疾病患者进行的脉搏波诊断,采用了5种相关性很高的检查脉搏波肝异常的标准,诊断准确率高达到90%以上;王唯工等[13]通过测量进一步指出,胃病患者脉搏波谐波的第三谐波(脾)幅值明显下降,第五谐波(胃)幅值增加,这说明脉搏波谐波与各器官阻力变化之间存在联系。笔者也尝试讨论各器官外周阻力变化对脉搏波谐波的影响关系,研究表明,胃阻力比变化对桡动脉血压波谐波幅值的影响很小,不同器官阻力变化对桡动脉谐波幅值的影响也较小;仿真未发现王唯工[12]实验得到的各器官对应特殊的共振谐波,这是因为文中假设升主动脉体积流率波不变,考虑了人体心血管系统各分支之间的相互影响,但未考虑各器官病变对升主动脉体积流率波变化的影响,导致仿真分析中器官阻力变化对脉搏波谐波振幅的影响较小,因此,需要考虑心脏自身的调节作用才能更真实有效地仿真心血管动力系统的运行。
| [1] |
隋金雪, 杨莉. 复杂流体网络分析与控制[M]. 北京: 电子工业出版社, 2013: 69-109. SUI Jinxue, YANG Li. Analysis and control of complex fluid networks[M]. Beijing: Publishing House of Electronics Industry, 2013: 69-109. (in Chinese) |
| [2] |
徐克, 赵良举, 李明阳. 基于流体网络的人体血液体循环分析[J]. 中国生物医学工程学报, 2017, 36(5): 580-588. XU Ke, ZHAO Liangju, LI Mingyang. The analysis of the systemic circulation of human blood based on fluid network[J]. Chinese Journal of Biomedical Engineering, 2017, 36(5): 580-588. (in Chinese) DOI:10.3969/j.issn.0258-8021.2017.05.010 |
| [3] |
Hassania K, Navidbakhsh M, Rostami M. Simulation of the cardiovascular system using equivalent electronic system[J]. Biomedical Papers, 2006, 150(1): 105-112. DOI:10.5507/bp.2006.015 |
| [4] |
Tsabs A, Goulermas J Y, Vartela V, et al. The Windkessel model revisited:a qualitative analysis of the circulatory system[J]. Medical Engineering & Physics, 2009, 31(5): 581-588. |
| [5] |
Mcdonald D A, Taylor M G. The hydrodynamics of the arterial circulation[J]. Progress in Biophysics and Biophysics Chemistry, 1959(9): 105-173. |
| [6] |
肖汉光, 何为, 李松浓, 等. 基于传输线模型的脉搏波传播数值仿真及参数分析[J]. 医用生物力学, 2012, 27(5): 527-533. XIAO Hanguang, HE Wei, LI Songnong, et al. Numerical simulation of pulse wave propagation and parameter analysis based on transmission line model[J]. Journal of Medical Biomechanics, 2012, 27(5): 527-533. (in Chinese) |
| [7] |
刘莹, 殷艳飞, 章德发. 心血管系统电网络模型的脉动信号仿真分析[J]. 生物医学工程学杂志, 2015, 32(6): 1207-1211. LIU Ying, YIN Yanfei, ZHANG Defa, et al. Simulation analysis of pulsating signals of electrical network model of cardiovascular system[J]. Journal of biomedical engineering, 2015, 32(6): 1207-1211. (in Chinese) |
| [8] |
Xiao H G, Butlin M, Tan I, el al. PWPSim: A new simulation tool of pulse wave propagation in the human arterial tree[C]//39th Annual. International Conference of the IEEE Engineering in Medicine & Biologly Society, 2017(6): 3672-3675.
|
| [9] |
Butlin M, Xiao H, Tan I. Effects of cardiac timing and peripheral resistance on measurement of pulse wave velocity for assessment of arterial stiffness[J]. Scientific Reports, 2017(7): 5990. |
| [10] |
Xiao H G, Avolio A P, Zhao M F, et al. Hemodynamic simulation of human arterial stenosis via transmission line model[J]. Journal of Mechanics in Medicine and Biology, 2016, 16(5): 1650067. DOI:10.1142/S0219519416500676 |
| [11] |
严石林, 李正华. 脉经[M]. 成都: 四川科学技术出版社, 2008. YAN Shilin, LI Zhenghua. The Pulse Classic[M]. Chengdu: sichuan science and technology press, 2008. (in Chinese) |
| [12] |
张修诚, 王唯工, 陈荣洲, 等. 脉搏谐波频谱分析——中医脉诊研究新方法[J]. 中国中西医结合杂志, 1995, 15(12): 743-745. ZHANG Xiucheng, WANG Weigong, CHEN Rongzhou, et al. New method of TCM pulse diagnosis-analysis of pulse harmonic spectrum[J]. Chinese Journal of Integrated Traditional and Western Medicine, 1995, 15(12): 743-745. (in Chinese) DOI:10.3321/j.issn:1003-5370.1995.12.016 |
| [13] |
王唯工. 看懂经气脉络:霍普金斯大学生物物理博士眼里的中医[M]. 海口: 海南出版社, 2015. WANG Weigong. Understand the meridian:The view of Chinese medicine Dr. Biophysics of Hopkins university[M]. Haikou: Hainan publishing house, 2015. (in Chinese) |
| [14] |
Liang F Y, Takagi S, Himeno R, et al. Multi-scale modeling of the human cardiovascular system with applications to aortic valvular and arterial stenoses[J]. Medical & Biological Engineering & Computing, 2009, 47(7): 743. |
| [15] |
Milnor W R. Hemodynamics[M]. Baltimore: Williams & Wilkinson, 1989.
|
| [16] |
Womersley R. Oscillatory flow in arteries:the constrained elastic tube as a model of arterial flow and pulse transmission[J]. Physics in Medicine and Biology, 1957, 2(2): 178-187. DOI:10.1088/0031-9155/2/2/305 |
| [17] |
Zhang H J, Li J K. A novel wave reflection model of the human arterial system[J]. Cardiovascular Engineering, 2009, 9(2): 39-48. DOI:10.1007/s10558-009-9074-3 |
| [18] |
Taylor M C. An approach to an analysis of the arterial pulse wave Ⅰ. oscillations in an attenuating line[J]. Physics in Medicine and Biology, 1957, 1(3): 258-269. DOI:10.1088/0031-9155/1/3/304 |
| [19] |
Avolio A P. Multi-branched model of the human arterial system[J]. Medical & Biological Engineering & Computing, 1980, 18(6): 709-718. |
| [20] |
肖汉光, 何为, 刘兴华, 等. 基于电网络模型的动脉树输入阻抗递归计算及参数分析[J]. 医用生物力学, 2011, 1(26): 18-23. XIAO Hanguang, HE Wei, LIU Xinghua, et al. Numerical simulation of pulse wave propagation and parameter analysis based on transmission line model[J]. Journal of Medical Biomechanics, 2011, 1(26): 18-23. (in Chinese) |
| [21] |
Lu W A, Cheng C H, Wang Y Y. Pulse spectrum analysis of hospital patients with possible liver problems[J]. American Journal of Chinese Medicine, 1996, 24(3/4): 315. |
 2019, Vol. 42
2019, Vol. 42



