2. 浙江财经大学 公共管理学院, 杭州 310018;
3. 浙江省空间结构重点实验室, 杭州 310058;
4. 宁波大学 建筑工程与环境学院, 浙江 宁波 315211
2. College of Public Administration, Zhejiang University of Finance & Economics, Hangzhou 310018, P. R. China;
3. Zhejiang Provincial Key Laboratory of Space Structures, Hangzhou 310058, P. R. China;
4. Faculty of Architectural, Civil Engineering and Environment, Ningbo University, Ningbo 315211, Zhejiang, P. R. China
随着计算机辅助设计技术的发展,自由曲面的建筑形式因其强大的视觉效果得到了人们的青睐。然而,对复杂的自由曲面进行建筑网格划分十分困难,是目前空间结构领域研究的一个热点与难点。对自由曲面建筑网格划分的研究很多,但针对复杂边界的报道较少。近年来,也有一些学者对包含孔洞或裁剪边界的曲面网格划分问题进行了深入研究,并提出了一些解决方案。丁慧[1]在参数域对边界进行分类讨论。潘炜[2]、Gao[3]等借助曲面展开,在平面上对边界进行分类处理。这些方法最终结果都不是特别理想。
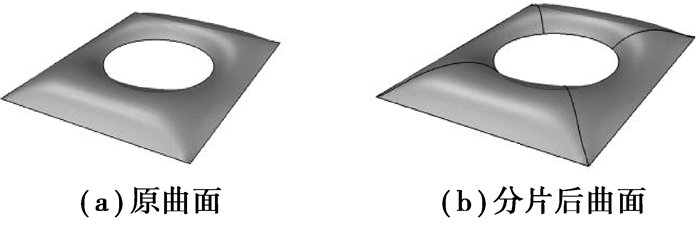
对于比较复杂的曲面,通过曲面分片重构,可以消除孔洞、裁剪边界等不利影响,有效地提高建筑网格划分的质量。例如,对于带孔洞的曲面,典型算例如大英博物馆大中庭屋顶[4]。如图 1所示,原曲面中央有1个孔洞,将给部分对曲面边界质量要求较高的网格划分算法带来不便。而对曲面进行分片形成4个曲面后,孔洞的影响将不复存在,4个子曲面都是由4段边界围成的不含孔洞的曲面,性质较好,将有效提升网格划分效果。另外,曲面被分成了无关联的多个曲面后,可以应用并行计算技术进一步加速网格划分,提升用户交互体验。
|
图 1 大英博物馆大中庭屋顶曲面分片 Fig. 1 Surface slicing of atrium roof of British Museum |
基于曲面分片与重构,提出针对复杂曲面的网格划分算法框架。经过复杂自由曲面算例的验证,表明该网格划分算法框架的有效性、可靠性。
1 算法概览本算法框架的基本流程如下:
步骤1:绘制分片曲面边界;
步骤2:区域识别;
步骤3:子曲面重构;
步骤4:各子曲面分别形成子网格;
步骤5:子网格合并,并在原曲面进行松弛。
其中,分片边界的绘制需要操作者根据经验人工绘制,分片质量会影响重构过程。
算法框架中关键算法分述如下:
1.1 区域识别算法对于曲面分片,需要解决区域识别问题,可采用多边形构造算法。
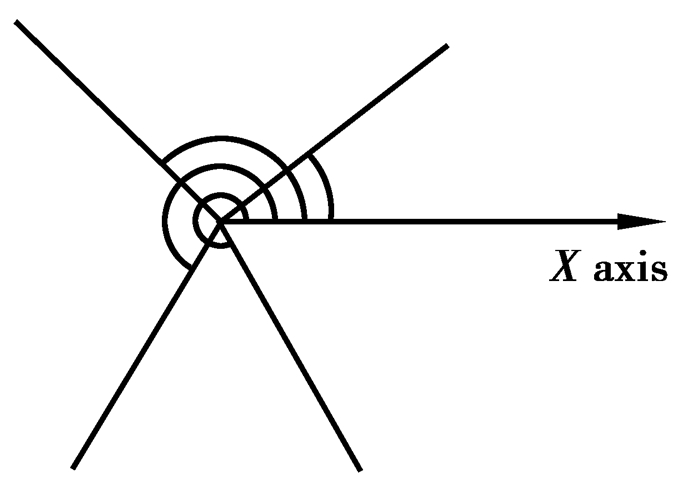
1.1.1 经典多边形构造算法该算法的输入为“顶点-边”关系,输出是“顶点-边-面”关系。首先,进行预处理,顶点所连的边按方向角进行排序。其中,方向角的定义为从X轴正向绕逆时针角度旋转到该边经过的角度,如图 2所示。预处理后,对于从一个顶点引出的边,可以方便地找到它左侧的下一条边。
|
图 2 方向角 Fig. 2 Direction angle |
经典多边形构造算法步骤如下[5]:
步骤1:选取一个未被访问的点作为起始点vstart,若点都被访问,跳转步骤6;
步骤2:选取vstart所连接的边中未访问的边作为起始边estart,若边都被访问,则将该顶点标记为已访问,跳转步骤1;
步骤3:找到该边的另一个顶点,作为下一个点vnext,如果vnext=vstart,则说明面已被找到,跳转步骤5;
步骤4:选取当前边对于vnext的下一条边,跳转步骤3;
步骤5:记录该面,标记estart为已访问,跳转步骤1;
步骤6:结束。
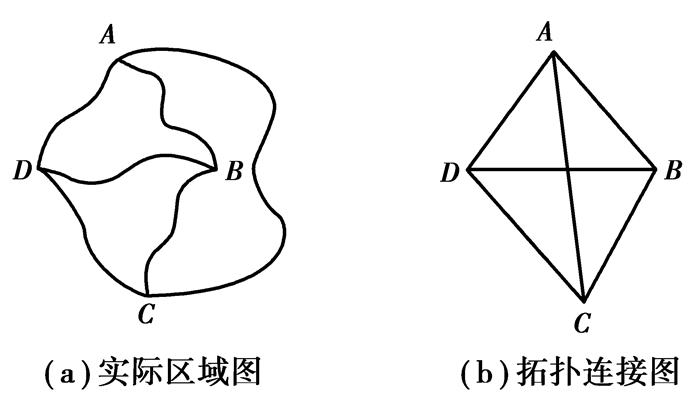
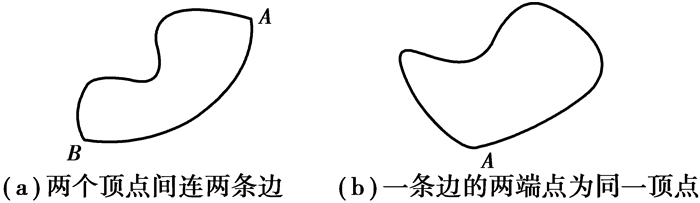
1.1.2 对经典多边形构造算法的改进在本文场景中,应用以上算法时,遇到了一些问题。一是如何将曲面上的曲线转换为边。对于NURBS[6]方法表示的曲线,若直接使用拓扑连接作为边,可能产生错误,如图 3所示。图 3(a)中的拓扑由面ADB、ABC和BDC组成,而图 3(b)中的拓扑则是由ADB、BDC、ADC(新产生的面)和ACB(边顺序不一致)。将曲线离散过于粗糙会出现如图 3所示的问题,离散过于精细又会产生过多冗余的顶点和边。文中采用在预处理阶段求曲线在其端点的切线的方式来计算方向角,解决了该问题。另一个问题是,对于一些极端情况,如图 4所示,2条边的端点是相同的点,或形成自环。在朴素算法中,这些情形将被考虑为孤边,没有面会被构造。在本文的算法中,对边进行区分,允许2条边或1条边构成1个面。
|
图 3 拓扑连接直接转为边的错误结果 Fig. 3 Wrong result of converting topological connections to edges |
|
图 4 面构造中的极端情况 Fig. 4 Extreme condition during face construction |
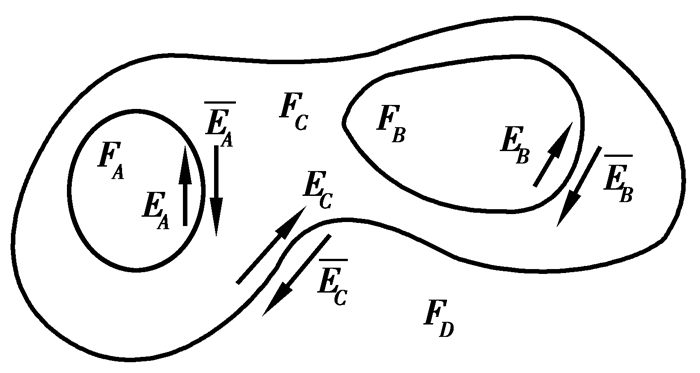
最后,需要处理“岛”的问题,如图 5所示,即1个面中包含其他面,或包含内部边界,这在建筑曲面中是一个常见现象。文中1个面的边界被考虑为2条方向相反的边。边的左侧是其参与构成的面,边的右侧是外部。在图 5中,从几何上讲,EA和
|
图 5 复杂面 Fig. 5 Complex faces |
至此,曲面可以被顺利地进行分片,实践中遇到的各种特殊情况也都得到了可靠的处理。
1.2 曲面重构算法区域识别得到的子曲面,其实质是原曲面的几何信息加裁剪边界表达的,并没有改变曲面的几何。对于基于映射的划分方法,这种程度的分片,并不会带来帮助。此时,需要曲面重构,在保持子曲面形状不变的情况下,改变其几何表示,得到独立于原曲面的参数域,使应用算法的范围更广。
很多学者尝试用NURBS曲面实现曲面重建,该问题在机械行业的逆向工程中有十分重要的应用。然而,该问题在数学上十分复杂,至今没有令人满意的算法。
一种思路是先将原曲面离散为大量的散乱点,再由散乱点拟合NURBS曲面[7-8]。然而,这类方法针对机械专业逆向工程的需求,关注光滑性、拟合精度等需求,带来一个副作用是将整个曲面用大量细碎的曲面表示,而多曲面表示方法将给网格划分带来很大的麻烦,不适合文中需求。
另一种思路是,将原曲面离散为规整的n×m形式的采样点,再进行曲面构造,构造算法简单[6],但是规整采样点的获取是一个难点。潘炜[9]采用手工在点云中选取n×m形式的规则采样点阵的方法实现了单NURBS曲面重构,但效率低、易出错,对操作要求高。
根据实际应用场景,采用第2种思路,提出了能解决具体需求的合适方法。建筑曲面的复杂程度要远低于机械逆向工程中的曲面,一般很少使用尖点、尖锐转角等,而少量的尖锐转角可以通过曲面分片处理成2个子曲面。建筑曲面相比于机械逆向工程对精度的要求并不苛刻,一般认为只需要维持几何形状基本不变,保证视觉效果,一定的误差是可以接受的。
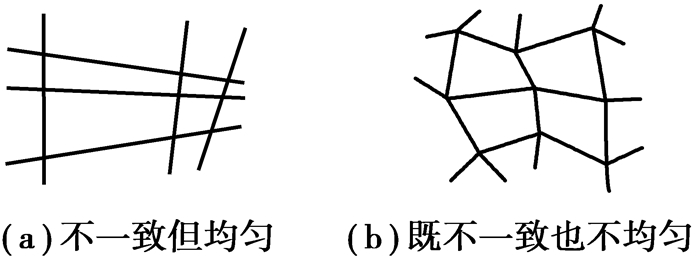
NURBS曲面构造算法[6],仅接受n×m形式的规则点阵作为插值点,生成双向的张量积曲面。这对采样结果提出了一定的要求,同一方向上,前后两排采样点间距可以不一致,但是要均匀。如图 6(a)所示的采样点分布虽不一致但是变化均匀,是可以接受的;而图 6(b)所示的采样点分布变化既不一致也不均匀,将会影响曲面插值效果。
|
图 6 曲面重构采样点分布形式 Fig. 6 Distribution of sampling points for surface reconstruction |
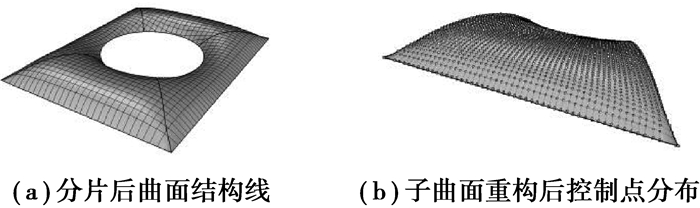
大英博物馆大中庭屋顶曲面分片所产生的4个子曲面,如图 7所示。需要进行曲面重构,难点在于如何获取n×m的插值点矩阵。核心的思想是采样点尽量均匀,且保持n×m点阵拓扑关系不变。
|
图 7 大英博物馆大中庭屋顶曲面分片子曲面重构 Fig. 7 Subsurface reconstruction of atrium roof of British Museum |
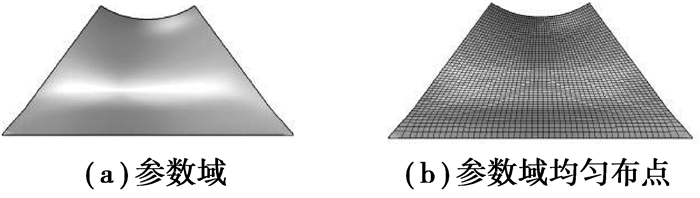
以图 8中的子曲面为例,可以在二维参数域中采样,最后再映射回曲面。首先,指定u, v方向,将u向的2条边界分别平均分成n份,得到2(n+1)个点{Q′k, 0}, {Q′k, m}, k=0, 1, ..., n,将v向的2条边界平均分成m份,得到2(m+1)个点{Q′0, l}, {Q′n, l}, l=0, 1, …, m。Q′k, l的坐标u分量由Q′0, l, Q′n, l的u分量插值生成,v分量由点Q′k, 0, Q′k, m的v分量插值生成。
| $ \left\{\begin{array}{l}{Q_{k, l}^{\prime u}=Q_{0, l}^{\prime u}+\frac{k}{n}\left(Q_{n, l}^{\prime u}-Q_{0, l}^{\prime u}\right)} \\ {Q_{k, l}^{\prime v}=Q_{k, 0}^{\prime v}+\frac{l}{m}\left(Q_{k, m}^{\prime v}-Q_{k, 0}^{\prime v}\right)}\end{array}\right. $ |
|
图 8 大英博物馆大中庭屋顶曲面分片子曲面采样 Fig. 8 Subsurface sampling of atrium roof of British Museum |
即得到(n+1)×(m+1)个采样点。
除了在二维参数域中采样之外,若曲面较为平坦,亦可以将曲面投影到某一特定平面再进行采样;对于类环面,可以先将其投影到某一圆柱上。计算这些平面采样点的空间曲面坐标,即是插值点{Qk, l}。
对于较为复杂的情形,以上步骤得到的插值点不够均匀。可应用弹簧质点动力松弛算法[10]优化,得到更均匀的插值点分布。之后采用NURBS曲面构造算法[6],即可拟合出一个满足条件的曲面。对于本例,最终重构得到的曲面及求得的控制点{Pi, j},如图 7(b)所示。
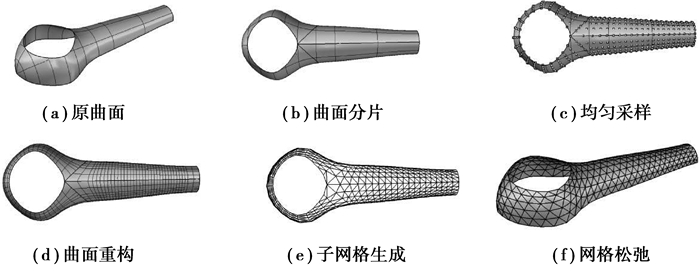
2 算例分析 2.1 算例1创建了1个一端为半圆柱,一端为扁球的曲面,其中扁球一端中央开孔,如图 9所示,该曲面映射变形较大,且扁球一端存在退化边,这些特性都对基于映射关系的网格划分方法带来不利。
|
图 9 算例1曲面分片重构及网格划分结果 Fig. 9 The reconstruction of surface and meshing result of case 1 |
根据曲面特征将曲面分为3片,在3个子曲面分别进行均匀采样得到采样点和独立的子曲面。重构后的子曲面性质良好,可以应用映射法进行网格划分。
2.2 算例2——大英博物馆选用大英博物馆大中庭屋顶[4]作为算例,如图 10所示。中央有1个孔洞,该曲面的原始完整曲面中央存在一个剧烈的下降,基于原曲面映射关系的划分方法难以应用。采用文中方法,可将其分片并重构形成4个子曲面。采用引导线推进法[11]分别进行网格划分,得到四边形网格和三角形网格。网格在各分片子曲面范围中均匀、流畅、规整。将子网格合并,并在原始曲面上进行松弛,得到整体均匀、流畅、规整的网格。尽管网格建筑效果难以评价,但毫无疑问,曲面分片重构算法提高了网格划分算法的适应性。

|
图 10 大英博物馆大中庭屋顶曲面分片网格划分结果 Fig. 10 The meshing result of atrium roof of British Museum |
采用考虑边界的改进引导线推进法[3]得到结果,如图 10(h)所示,亦均匀流畅,但中央孔洞边界附近的网格流畅性不够理想。
曲面分片不仅能使网格划分的过程得到简化,结合并行计算技术,还能减少计算时间,提高用户的交互体验。在本例中,子曲面重构后互相独立,可为每一个子曲面分配一个线程,进行并行计算。笔者对图 10(d)的网格,在4核心4线程的Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz上进行了验证,运行时间如表 1所示。采用并行技术后,运算速度得到大幅提升,交互体验得到了明显的提升。
| 表 1 算例2三角形网格生成运行时间 Table 1 Runtime of the triangular grids generation of case 2 |
提出了曲面分片重构方法,将原始曲面分片并重构形成多个子曲面,再分别应用合适的网格划分算法,最后在原曲面上进行松弛,得到均匀流畅的网格。介绍并补充了区域识别算法,提出了适合文中应用场景的自动化点阵采样算法。结合具体算例,阐明曲面分片重构算法的具体应用方法及效果。
结果表明,文中方法可以用于预处理一些性质不佳的初始曲面,如裁剪边界、内部孔洞等,有效提高网格划分效率与质量。缺点在于分片过程需要人工干预,对设计人员的经验要求较高,需要进一步提高设计方法的自动化程度。
| [1] |
丁慧, 罗尧治. 自由形态网壳结构网格生成的等参线分割法[J]. 浙江大学学报(工学版), 2014, 48(10): 1795-1801. DING Hui, LUO Yaozhi. Isoparametric line dividing grid generation method for free-form lattice shells[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(10): 1795-1801. (in Chinese) |
| [2] |
潘炜, 吴慧, 李铁瑞, 等. 基于曲面展开的自由曲面网格划分[J]. 浙江大学学报(工学版), 2016, 50(10): 1973-1979. PAN Wei, WU Hui, LI Tierui, et al. Grid generation on free-form surface based on surface flattening[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(10): 1973-1979. (in Chinese) DOI:10.3785/j.issn.1008-973X.2016.10.018 |
| [3] |
Gao B, Hao C, Li T, et al. Grid generation on free-form surface using guide line advancing and surface flattening method[J]. Advances in Engineering Software, 2017, 110(C): 98-109. |
| [4] |
Williams C. The analytic and numerical definition of the geometry of the British Museum Great Court Roof[J]. Mathematics & design, 2001, 434-440. |
| [5] |
Fazal S. GIS Basics[M]. New Age International Publishers, 2008.
|
| [6] |
Piegl L, Tiller W. The NURBS book[M]. 2nd ed. Berlin Heidelberg: Springer Berlin Heidelberg, 1997.
|
| [7] |
Crivellaro A, Perotto S, Zonca S. Reconstruction of 3D scattered data via radial basis functions by efficient and robust techniques[J]. Applied Numerical Mathematics, 2017, 113: 93-108. DOI:10.1016/j.apnum.2016.11.003 |
| [8] |
Ne-Thi-thu N, Nguyen-Tan K, Nguyen-Thanh T. Reconstruction of low degree B-spline surfaces with arbitrary topology using inverse subdivision scheme[J]. Journal of Science and Technology:Issue on Information and Communications Technology, 2017, 3(1): 82-88. DOI:10.31130/jst.2017.41 |
| [9] |
潘炜.自由曲面网格结构的网格划分方法研究与实现[D].杭州: 浙江大学, 2016. PAN Wei. Research and Implementation of Grid Meshing Method for Free-form Grid Structures[D]. Hangzhou: Zhejiang University, 2016. (in Chinese) |
| [10] |
Li J T, Zhang D L, Lu G D, et al. Flattening triangulated surfaces using a mass-spring model[J]. The International Journal of Advanced Manufacturing Technology, 2005, 25(1/2): 108-117. |
| [11] |
Gao B Q, Li T R, Ma T, et al. A practical grid generation procedure for the design of free-form structures[J]. Computers & Structures, 2018, 196(2): 292-310. |
 2019, Vol. 42
2019, Vol. 42


