2. 中国海洋大学 环境科学与工程学院, 山东 青岛 266100;
3. 青岛理工大学 土木工程学院, 山东 青岛 266033;
4. 中化岩土集团股份有限公司, 北京 102600
2. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, Shandong, P. R. China;
3. School of Civil Engineering, Qingdao University of Technology, Qingdao 266033, P. R. China;
4. China Zhonghua Geotechnical Group Co. Ltd., Beijing 102600, P. R. China
随着经济快速发展,大量人口不断涌入城市,造成交通堵塞、人均住房面积不足等社会问题,亟待拓展城市空间,对于西部山区城市,充分利用城市周边的沟壑、荒地,实现城市空间的横向拓展,是实现空间拓展的重要措施[1]。山区城市空间拓展中将形成大量的高填方场地,一般填土的压缩模量小,即使场地经强夯处理后,填土层的沉降量仍可能大于桩身沉降量,导致负摩阻力的产生。负摩阻力作为下拉荷载作用于桩身,会降低桩基承载力,若设计考虑不当,容易引发工程事故[2-3]。因而,深入研究高填方夯实地基桩侧负摩阻力计算方法具有重要的工程意义。
目前,不少学者从多个角度对桩侧负摩阻力的计算方法进行了研究,并取得了一些有益的结论。Johanessen等[4]建议采用有效应力计算桩侧负摩阻力, 该方法仅考虑了负摩阻力的极限值,计算结果较实际值偏大。Yao等[5]基于位移平衡方程推导出反映超长桩负摩阻力变化的三线性计算模型。Cao等[6]基于桩土界面剪切试验提出一种双曲线模型荷载传递函数用于计算桩侧负摩阻力,该方法考虑了桩-土界面剪切强度的变化。Lee[7]提出采用多个简化的荷载传递函数求解群桩的负摩阻力, 简化方法虽使用简便,但没有考虑负摩阻力衍变的时间效应。Kong等[8]、Lee等[9]、Hanna等[10]采用有限元数值模拟方法获得了桩侧负摩阻力随深度和固结时间的变化规律。赵明华等[11-13]推导出了考虑桩土相互作用及土层非线性分布的桩侧负摩阻力分段解析解, 该方法考虑了土体沿深度方向刚度的差异及桩土剪切界面受力性状。从桩侧土体发生沉降时,桩-土能量平衡的角度求解负摩阻力,但计算桩侧土沉降时采用Boussinesq弹性解与实际情况有差异。在考虑地基土非线性固结的基础上,推导了产生负摩阻力时桩周土沉降的理论计算公式, 该方法考虑了负摩阻力的衍变过程及土体沿深度方向刚度的差异性,对强夯实土层及未夯实土层的负摩阻力计算有借鉴意义。孙军杰等[14]从能量平衡的角度推导出计算桩侧负摩阻力的理论模型, 该模型从理论上说明了桩侧负摩阻力产生的实质,如在计算负摩阻力时考虑到其本质成因,可将该理论模型应用于不同桩型、不同土质时的负摩阻力估算。孔纲强等[15]将推导出的桩侧下拉荷载计算值与实测值进行比较,结果吻合较好。肖俊华等[16]拟合得到桩侧负摩阻力随固结时间变化的计算公式, 说明了由桩侧负摩阻力引起的下拉荷载的衍变存在时间效应。马露等[17]从负摩阻力衍生机理和有效应力原理的角度推导了桩侧负摩阻力分段理论计算公式, 该负摩阻力分段计算公式能较好地考虑土体的分层性及负摩阻力的衍变过程,对高填方夯实地基的桩侧负摩阻力计算有一定的借鉴意义。
针对桩侧负摩阻力的计算方法,已有研究分别在桩土界面作用、土体分层特性以及时间效应等角度得到一些有益结论。但对于高填方夯实地基桩侧负摩阻计算方法的研究尚待补充,文中依托在高填方夯实地基上进行的桩侧负摩阻力现场试验,根据负摩阻力测试结果,提出考虑固结效应的桩侧负摩阻力计算方法。
1 桩侧负摩阻力测试现场试验 1.1 试验场地工程地质条件桩基负摩阻力测试场地位于四川南充市,场地原为地貌起伏较大的沟壑,试验前已采用全风化泥质粉砂岩回填整平,回填料密度约为1.54 g/cm3,不均匀系数Cu≈6,曲率系数Cc≈1.5,塑限Ip约为7.15%,液限IL约为13.25%。场地平均回填厚度约15 m,最大回填厚度约30 m。
负摩阻力测试区选择在回填土层较厚且上部为拟建输送管廊的区域。试验区土层情况分布,如表 1所示。
| 表 1 试验区土层情况分布表 Table 1 Properties of soils |
经全风化泥质粉砂岩回填形成场地后,采用3 000 kN·m能级强夯预处理并整平场地,之后在试验区打设4根钻孔灌注桩,桩基呈矩形布置,横向间距为9 m,纵向间距为3 m,桩基参数如表 2所示。在桩身钢筋笼主筋上安装钢筋应力计,测试正常使用期间桩身轴力值,从而得到桩基侧摩阻力变化规律。
| 表 2 桩基参数表 Table 2 Properties of piles |
强夯前后在试验场地进行了2组重型动力触探试验,动力触探深度约为15 m,通过对比夯前、夯后锤击数随深度变化曲线,得到强夯的有效加固深度约为6 m。通过定期记录桩身钢筋应力计频率,计算得到强夯未处理填土层桩侧摩阻力的变化曲线如图 1所示。其中,测试时4#桩不显示应力计的变化频率,无法得到侧摩阻力变化数据。

|
图 1 桩侧摩阻力变化曲线 Fig. 1 Curves of negative skin friction with different depths |
由图 1可知,3根测试桩桩侧摩阻力沿深度方向均呈现“负-正”的变化规律,强夯未处理填土层均出现负摩阻力,在7~11 m深度范围内,桩侧负摩阻力值较为稳定,说明该深度范围内桩土相对位移基本不变。对于3#桩,15~19 m深度范围填土层,在固结时间为30 ~170 d时,桩侧呈现正摩阻力,当固结时间为260 d时,桩侧呈现负摩阻力,说明随着固结时间的增加,桩周土固结沉降会大于桩身沉降,强夯未处理填土层会由固结初期提供的正摩阻力衍变为负摩阻力,故应考虑填土深度范围内由于桩周土固结效应导致的负摩阻力衍生。
2 桩侧负摩阻力计算方法 2.1 计算公式的提出采用考虑桩土相互作用的荷载传递法基本公式,提出考虑固结效应的桩侧负摩阻力计算方法。该方法利用由界面剪切试验得到的函数
| $ \frac{\mathrm{d}^{2} s_{\mathrm{p}}}{\mathrm{d} z^{2}}=\frac{U}{A_{\mathrm{p}} E_{\mathrm{p}}} \tau(z), $ | (1) |
式(1)的求解结果决定于桩土荷载传递函数
| $ {q_{\rm{s}}}(z) = \left\{ {\begin{array}{*{20}{l}} {q_{\rm{s}}^\prime \left( {{\tau _1}\left( {z, {s_{\rm{p}}} - s(z, t)} \right)} \right), }&{0 \le {s_{\rm{p}}} - s(z, t) \le {u_{{\rm{pl}}}};}\\ {\lambda \sigma _i^\prime , }&{{s_{\rm{p}}} - s(z, t) \ge {u_{{\rm{pl}}}};}\\ {q_{\rm{s}}^{\prime \prime }\left( {{\tau _2}\left( {z, s(z, t) - {s_{\rm{p}}}} \right)} \right), }&{0 \le s(z, t) - {s_{\rm{p}}} \le {u_{{\rm{nl}}}};}\\ {\beta \sigma _i^\prime , }&{s(z, t) - {s_{\rm{p}}} \ge {u_{{\rm{nl}}}}。} \end{array}} \right. $ | (2) |
式中:
假定桩土产生相对塑性滑移后,桩侧摩阻力与桩土界面抗剪强度相等,且λ的取值与规范[22]中β的取值一致。为确定
1) 桩侧土沉降量s(z, t)
当土层承受大面积超载q作用时,在深度z处、t时刻、厚度为dz的土层沉降量为
| $ {\rm{d}}s(z, t) = \frac{{\Delta {u^\prime }}}{{{E_{{\rm{s}}i}}}}{\rm{d}}z = \frac{{q - u(z, t)}}{{{E_{{\rm{s}}i}}}}{\rm{d}}z, $ | (3) |
式中:Esi为第i土层压缩模量;u(z, t)为t时刻、z深度处的孔隙水压力;
式(3)中的孔隙水压力u(z, t)可采用太沙基固结理论的解答[23]:
| $ u(z, t)=\frac{4}{\pi} q \sum\limits_{m=1}^{\infty} \frac{1}{m} \sin \frac{m \pi z}{2 H} \cdot \mathrm{e}^{-\frac{m 2 \pi 2}{4}} T_{\mathrm{v}} $ | (4) |
式中,Tv为时间因数,
则在深度z处、t时刻沉降量为
| $ \begin{array}{*{20}{c}} {s(z, t) = \int_0^z {\rm{d}} s(z, t){\rm{d}}z = \int_0^z {\frac{{q - u(z, t)}}{{{E_{{\rm{si}}}}}}} {\rm{d}}z = }\\ {\frac{1}{{{E_{{\rm{s}}i}}}}\int_0^z {\left( {q - \frac{4}{{\rm{ \mathsf{ π} }}}q\sum\limits_{m = 1}^\infty {\frac{1}{m}} \sin \frac{{m\pi z}}{{2H}} \cdot {{\rm{e}}^{ - \frac{{m2{\rm{ \mathsf{ π} }}2}}{4}{T_{\rm{v}}}}}} \right)} {\rm{d}}z = }\\ {\frac{q}{{{E_{{\rm{s}}i}}}}\left[ {z - \sum\limits_{m = 1}^\infty {\frac{{8H}}{{{m^2}{{\rm{ \mathsf{ π} }}^2}}}} \left( {1 - \cos \frac{{m\pi z}}{{2H}}} \right){{\rm{e}}^{ - \frac{{m2{\rm{ \mathsf{ π} }}2}}{4}{T_{\rm{v}}}}}} \right]} \end{array} $ | (5) |
在工程实用中,常取第1项值(m=1)得:
| $ s(z, t) = \frac{q}{{{E_{{\rm{s}}i}}}}\left[ {z - \frac{{8H}}{{{{\rm{ \mathsf{ π} }}^2}}}\left( {1 - \cos \frac{{{\rm{ \mathsf{ π} }}z}}{{2H}}} \right){{\rm{e}}^{ - \frac{{{\rm{ \mathsf{ π} }}2}}{4}{T_v}}}} \right]。$ | (6) |
2) 桩身沉降量sp计算
① 桩身弹性压缩量ss
由于混凝土灌注桩桩身弹性模量大,竖向荷载作用下变形小,一般处于弹性状态,可采用式(7)计算dl段的桩身压缩量:
| $ \mathrm{d} s_{\mathrm{s}}=\frac{Q(z) \mathrm{d} l}{A_{\mathrm{p}} E_{\mathrm{p}}},$ | (7) |
式中:Q(z)为桩身深度z处的轴力值,kN;
桩身在深度z处至z+dz处的轴力值Q(z)为
| $ Q(z)=\int z+\mathrm{d} z_{z} 2 \pi r \cdot \tau(z) \mathrm{d} z。$ | (8) |
将dl段的桩身压缩量沿桩长全长积分,得到桩身弹性压缩量ss:
| $ s_{\mathrm{s}}=\int_{0}^{l} \mathrm{d} s_{\mathrm{s}}=\int_{0}^{l} \frac{Q(z)}{A_{\mathrm{p}} E_{\mathrm{p}}} \mathrm{d} l。$ | (9) |
3) 桩端沉降量sb
根据文献[24],计算桩端沉降量sb时,可将桩端假设为刚性墩体,采用下式计算:
| $ s_{\mathrm{b}}=\frac{P_{\mathrm{b}}\left(1-v_{\mathrm{s}}\right)}{4 r G_{\mathrm{s}}} \eta, $ | (10) |
式中:υs为桩端土体泊松比;Pb为作用于桩端土体处的集中力,kN;η为桩基入土深度影响因素,可取0.85~1.0;r为桩身半径,m;Gs为桩端土体剪切模量,MPa;
剪切模量Gs与压缩模量Es之间有如下关系式[25]:
| $ G_{\mathrm{s}}=\frac{E}{2(1+v)}=\frac{E_{s}}{2(1+v)}\left(1-\frac{2 v^{2}}{1-v}\right), $ | (11) |
将式(11)代入式(10)得:
| $ s_{\mathrm{b}}=\frac{P_{\mathrm{b}}\left(1-v_{\mathrm{s}}\right)^{2}}{2 r E_{\mathrm{s}}\left(1-2 v_{\mathrm{s}}\right)} \eta, $ | (12) |
由式(9)、式(12)得到桩身沉降sp:
| $ s_{\mathrm{p}}=s_{\mathrm{s}}+s_{\mathrm{b}}=\int_{0}^{l} \frac{Q(z)}{A_{\mathrm{p}} E_{\mathrm{p}}} \mathrm{d} l+\frac{P_{\mathrm{b}}\left(1-v_{\mathrm{s}}\right)^{2}}{2 r E_{\mathrm{s}}\left(1-2 v_{\mathrm{s}}\right)} \eta。$ | (13) |
由式(6)、式(13)得到桩土相对位移s:
| $ \begin{array}{*{20}{c}} {s = {s_{\rm{p}}} - s(z, t) = }\\ {\int_0^l {\frac{{Q(z)}}{{{A_{\rm{p}}}{E_{\rm{p}}}}}} {\rm{d}}l + \frac{{{P_{\rm{b}}}{{\left( {1 - {v_{\rm{s}}}} \right)}^2}}}{{2r{E_{\rm{s}}}\left( {1 - 2{v_{\rm{s}}}} \right)}}\eta - \frac{q}{{{E_{{\rm{s}}i}}}}\left[ {z - \frac{{8H}}{{{{\rm{ \mathsf{ π} }}^2}}}\left( {1 - \cos \frac{{{\rm{ \mathsf{ π} }}z}}{{2H}}} \right){{\rm{e}}^{ - \frac{{{{\rm{ \mathsf{ π} }}^2}}}{4}{T_{\rm{v}}}}}} \right]} \end{array} $ | (14) |
当桩周土沉降大于桩身沉降时,桩侧产生负摩阻力,引起桩土界面间剪切应力的传递[26-29]。为得到
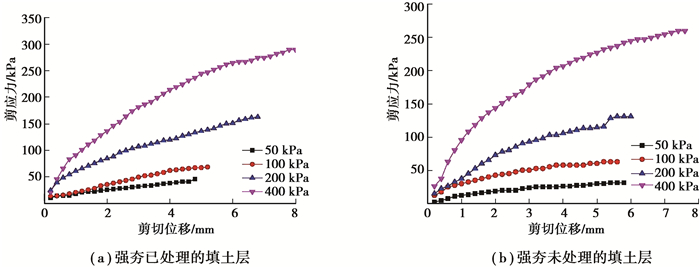
试验采用应变控制式直剪仪,剪切盒内径约6.18 cm,上盒放土样,下盒放置粗糙度与桩侧接近的自制圆形混凝土块[30]。试验得到的界面剪切应力与位移的关系,如图 2所示。
|
图 2 界面剪切应力与位移的关系曲线 Fig. 2 Relationship between shear stress and shear deformation |
可以看出,剪切应力
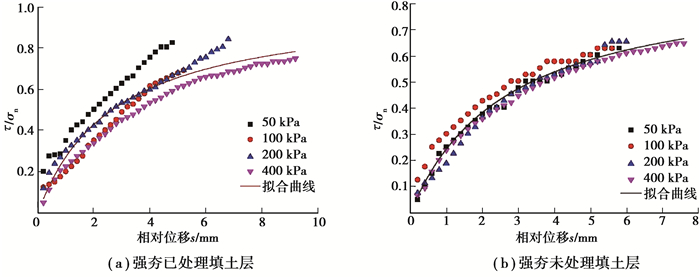
通过
|
图 3 归一化处理后 |
可以看出,归一化处理后的
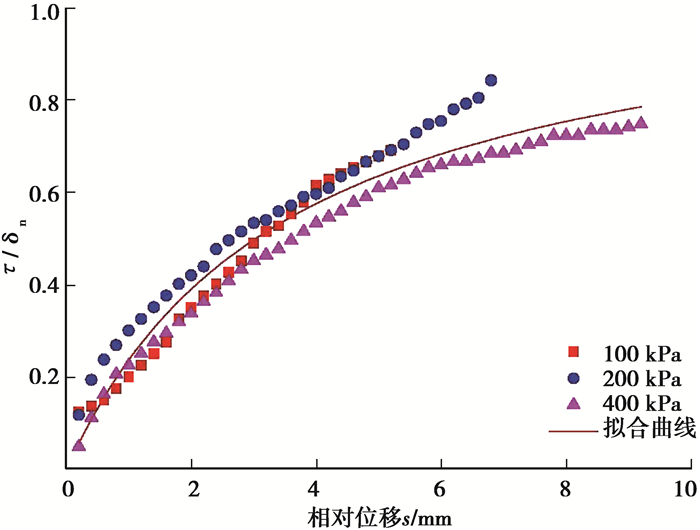
|
图 4 归一化处理后 |
可以看出,当σn为100、200、400 kPa时,
土与混凝土界面剪切时,法向应力σn相当于土体作用于桩身的静止水平土压力σh,即σn=σh,根据朗肯土压力理论,σh可按下式计算:
| $ \sigma_{\mathrm{h}}=\left(q+\gamma_{z}\right) K_{0}, $ | (15) |
式中:q为作用于地表的超载,kPa;γ为土体重度,kN/m3;K0为静止土压力系数。
将式(15)代入
| $ \tau (z) = \frac{s}{{a + {b_{\rm{s}}}}}{\sigma _{\rm{n}}} = \frac{{s{K_0}}}{{a + {b_{\rm{s}}}}}(q + \gamma z)。$ | (16) |
经曲线拟合得到的桩土荷载传递函数及系数取值如表 2所示。
| 表 2 桩土荷载传递函数和系数表 Table 2 Fitting formula and coefficient of load transfer function |
由图 3、图 4可以得到,不同法向应力σn作用下,土体达到抗剪强度

|
图 5 界限位移值ul与法向应力σn的拟合关系曲线 Fig. 5 Fitting curve of the relationship between limiting deformation ul and vertical stress σn |
由图 5可以看出,土体达抗剪强度
| 表 3 界限位移拟合函数和系数表 Table 3 Fitting formula and coefficient of limiting deformation |
将式(15)代入拟合后的方程得:
| $ u_{1}=c \sigma_{\mathrm{n}}+d=c K_{0}(q+\gamma z)+d。$ | (17) |
由于计算方程式(1)、式(2)难以获得准确的解析解,文中采用有限差分法求解二次微分方程。
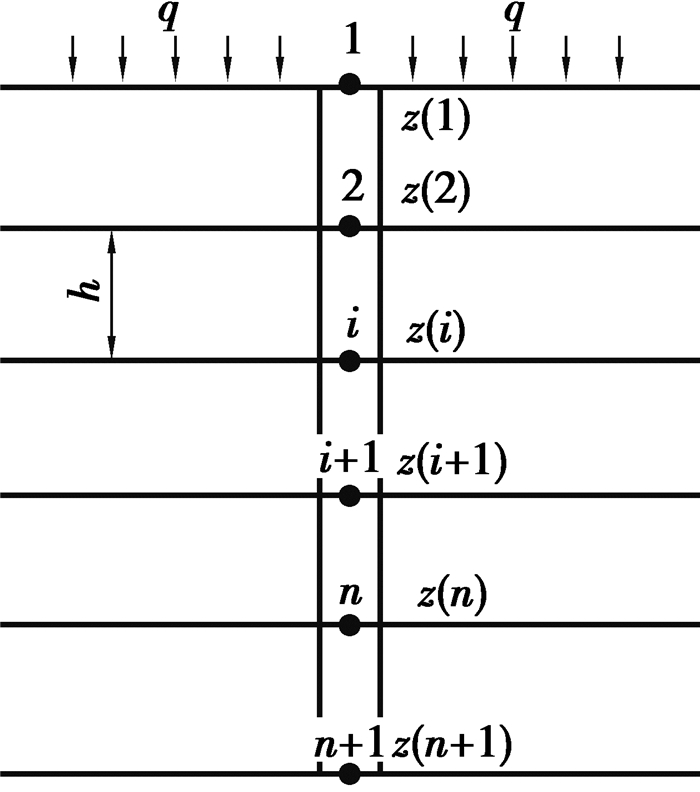
如图 6所示,将桩身及桩周土划分成离散的n个单元,假设每个单元的长度为h,并对每个单元节点进行编号。
|
图 6 桩身及桩周土离散示意图 Fig. 6 Divided element of pile and adjacent soils |
设桩身第i单元节点处的位移为spi,则spi的一阶、二阶导数分别为
| $ \left. \begin{array}{l} s_{{\rm{p}}i}^\prime = \left( {{s_{{{\rm{p}}_{i + 1}}}} - {s_{{{\rm{p}}_i}}}} \right)/h\\ s_{{\rm{p}}i}^{\prime \prime } = \left( {{s_{{\rm{p}}i + 1}} - 2{s_{{\rm{p}}i}} + {s_{{\rm{p}}i - 1}}} \right)/{h^2} \end{array} \right\}。$ | (18) |
假定桩身中单元节点的位移仅与该点的桩侧摩阻力有关,则桩身第i节点位移spi与桩身弹性压缩量ssi相等,其与桩身轴力Qi的关系式为
| $ \frac{{{\rm{d}}{s_{{\rm{s}}i}}}}{{{\rm{d}}z}} = - \frac{{{Q_i}}}{{{A_{\rm{p}}}{E_{\rm{p}}}}}。$ | (19) |
将式(18)代入式(19)可得到离散后各单元节点的方程:
| $ {Q_i} = \frac{{\left( {{s_{{\rm{s}}i}} - {s_{{\rm{s}}i + 1}}} \right)}}{h}{A_{\rm{p}}}{E_{\rm{p}}}。$ | (20) |
式(10)中作用于桩端土体处的集中力Pb为作用于桩身最后一个单元节点的轴力值:
| $ {P_{\rm{b}}} = {Q_{n + 1}} = \frac{{{s_{{\rm{s}}n + 1}}}}{h}{A_{\rm{p}}}{E_{\rm{p}}} \approx \frac{{{s_{{\rm{s}}n}}}}{h}{A_{\rm{p}}}{E_{\rm{p}}}。$ | (21) |
将式(18)代入式(1)得到离散后的代数方程:
| $ {s_{{\rm{s}}i + 1}} = \frac{{U{h^2}}}{{{A_{\rm{p}}}{E_{\rm{p}}}}}\tau (i) + 2{s_{{\rm{s}}i}} - {s_{{\rm{s}}i - 1}}。$ | (22) |
第i单元的桩土相对位移s为
| $ {s_i}{\rm{ = }}{s_{{\rm{s}}i}}{\rm{ + }}{s_b}{\rm{ - }}s(z, {\rm{ }}t)。$ | (23) |
桩身第一个单元节点的桩身轴力为
| $ Q_{1}=\frac{\left(s_{\mathrm{s1}}-s_{\mathrm{s} 2}\right)}{h} A_{\mathrm{p}} E_{\mathrm{p}}, $ | (24) |
式中,Q1为作用在桩身第一个单元的竖向荷载,kPa;
同理,桩身第i单元节点的桩身轴力为
| $ Q_{i}=\frac{\left(s_{\mathrm{s} i}-s_{\mathrm{s} i+1}\right)}{h} A_{\mathrm{p}} E_{\mathrm{p}}, $ | (25) |
则第i单元节点的桩侧摩阻力为
| $ {q_{{\rm{s}}i}} = \frac{{{Q_i} - {Q_{i + 1}}}}{{u{l_i}}} = \frac{{{Q_i} - {Q_{i + 1}}}}{{{\rm{ \mathsf{ π} }}D{l_i}}}, $ | (26) |
式中:qsi为深度i处的桩侧摩阻力,kPa;D为桩身直径,mm;li为第i截面和第i+1截面间距离,m。
经上文推导,提出的考虑固结效应的高填方夯实地基桩侧负摩阻力计算方法如下:
① 根据要求的计算精度、桩身长度和直径将桩分成n个单元,假设桩端沉降量取一值,即sb=s′b,根据强夯预处理有效加固深度及式(16)选择相应的桩土荷载传递函数,根据式(22)、式(24)求得桩身各节点弹性压缩量ss1、ss2;
② 将求得的ss1、ss2根据①中的方法迭代计算桩身各单元节点的弹性压缩量ssi,由式(6)、式(23)求得桩身各单元节点的桩土相对位移si;根据式(12)、式(21)计算桩端沉降s″b;
③ 若
该方法是通过太沙基固结理论分层求解桩侧土的沉降,假设桩端为刚性墩求解桩身沉降,进而得到桩土相对位移理论解,基于荷载传递法推导得到桩身轴力理论解,利用界面直剪试验分别得到强夯已处理土层、未处理土层桩土荷载传递函数,利用有限差分法将理论解离散后得到桩土相对位移及桩身轴力序列,最后分段求得考虑固结效应的负摩阻力值。
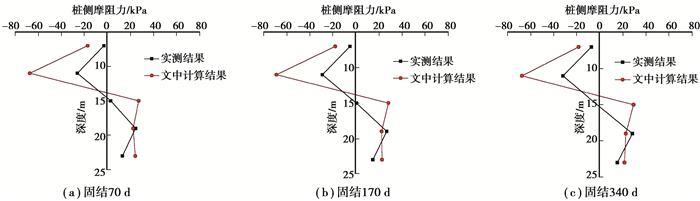
2.6 计算公式验证采用式(2)中,负摩阻力现场试验的案例进行计算,计算结果与现场试验结果(取平均值)的对比,如图 7所示。
|
图 7 文中公式计算值与实测结果的对比图 Fig. 7 Comparison of skin frictions by the calculation with those by field test results |
可以看出,公式(2)的计算值与现场实测桩侧摩阻力沿深度的变化趋势基本一致,当固结时间t=170 d时,试验测试的中性点深度为15 m,理论计算的中性点深度为13.9 m,两者相差约7.3 %,基本满足工程使用要求。但现场实测负摩阻力值约是计算值的1/2,相差较大,这是由于推导公式时用到的假设与真实情况有差距而导致的误差,这需要更多的现场试验进行实测验证,实际应用时可将文中方法计算的桩侧负摩阻力值乘以0.5的折减系数。
3 结论根据高填方夯实地基桩侧负摩阻力现场试验结果,提出考虑固结效应的桩侧负摩阻力计算方法,给出计算公式的数值计算解法,并将计算结果与现场试验结果对比分析。
1) 高填方夯实地基未处理土层桩侧摩阻力随深度变化呈现由负摩阻力向正摩阻力衍变的规律,虽然经过300 kN·m能级强夯预处理,未经强夯加固范围的填土层仍然存在负摩阻力。
2) 根据高填方夯实地基桩侧摩阻力随深度的衍变规律,提出桩侧摩阻力的分段计算方法。利用土-混凝土界面剪切试验获得的函数
3) 采用文中计算方法得到的桩侧摩阻力沿深度的变化趋势与现场试验结果一致,计算的中性点深度与实测结果相差约7.3 %,基本满足工程使用要求。
4) 现场实测负摩阻力值约为计算值的1/2,需要更多的现场试验进行实测验证,实际应用时可将文中方法计算的桩侧负摩阻力值乘以0.5的折减系数。
| [1] |
水伟厚, 董炳寅, 梁富华.湿陷性黄土地区高填方夯实场地20000 kN.m超高能级强夯处理试验研究[C].第十四届全国地基处理学术会议论文集.南昌: 江西科学技术出版社, 2016: 247-253. SHUI Weihou, DONG Bingyin, LIANG Fuhua. Experiment research of 20000 kN.m ultra-high dynamic compaction about the collapsible loess area high fill foundation after compaction[C]. The Paper Collection of Fourteenth National Conference on Foundation Treatment. Nanchang: Jiangxi Science and Technology Press, 2016: 247-253. (in Chinese) |
| [2] |
刘明维, 周世良, 梁越. 桩基工程[M]. 北京: 中国水利水电出版社, 2015. LIU Mingwei, ZHOU Shiliang, LIANG Yue. Piles Engineering[M]. Beijing: China Water Power Press, 2015. (in Chinese) |
| [3] |
胡瑞庚.高填方夯实地基桩侧负摩阻力计算方法研究[D].青岛: 青岛理工大学, 2018. HU Ruigeng. Study of calculation method of negative skin friction for a single pile in high filled compaction embankment[D]. Qingdao: Qingdao Tehcnology University, 2018.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10429-1018072030.htm |
| [4] |
Johanessen, Bjerrum. Measurements of a Steel pile to Rock due to Settlements of the Surrounding Clay[J]. Proc 6th ICOSMFE Canada, 1965, 2: 261-264. |
| [5] |
Yao W J, Liu Y M, Chen J. Characteristics of negative skin friction for superlong piles under surcharge loading[J]. International Journal of Geomechanics, 2012, 12(2): 90-97. DOI:10.1061/(ASCE)GM.1943-5622.0000167 |
| [6] |
Cao W P, Chen Y M, Wolfe W E. New Load Transfer Hyperbolic Model for Pile-Soil Interface and Negative Skin Friction on Single Piles Embedded in Soft Soils[J]. Int. J. Geomech, 2014, 14(1): 92-100. DOI:10.1061/(ASCE)GM.1943-5622.0000289 |
| [7] |
Lee C Y. Pile groups under negative skin friction[J]. Journal of Geotechnical Engineering, 1993, 119(10): 1587-1600. DOI:10.1061/(ASCE)0733-9410(1993)119:10(1587) |
| [8] |
Kong G, Yang Q, Luan M. Study of loading rate effects on characteristics of negative skin friction for pile groups[J]. Electronic Journal of Geotechnical Engineering, 2008(13): 1-12. |
| [9] |
Lee C J, Lee J H, Jeong S. The influence of soil slip on negative skin friction in pile groups connected to a cap[J]. Géotechnique, 2006, 56(1): 53-56. DOI:10.1680/geot.2006.56.1.53 |
| [10] |
Hanna A, Hoque M A. Coupled consolidation model for negative skin friction on piles in clay layers[J]. Geomechanics and Geoengineering, 2009, 4(2): 141-149. DOI:10.1080/17486020902855654 |
| [11] |
赵明华, 贺炜, 曹文贵. 基桩负摩阻力计算方法初探[J]. 岩土力学, 2004, 25(9): 1442-1446. ZHAO Minghua, HE Wei, CAO Wengui. Study on calculation of negative skin friction resistance on piles[J]. Rock and Soil Mechanics, 2004, 25(9): 1442-1446. (in Chinese) DOI:10.3969/j.issn.1000-7598.2004.09.019 |
| [12] |
赵明华, 刘思思, 杨明辉. 基于能量法的软土地基中基桩负摩阻力计算方法[J]. 水利学报, 2010, 41(5): 581-587. ZHAO Minghua, LIU Sisi, YANG Minghui. Calculation of negative skin friction on single pile in soft soil foundation based on energy method[J]. Journal of Hydraulic Engineering, 2010, 41(5): 581-587. (in Chinese) |
| [13] |
赵明华, 胡倩, 杨超炜, 等. 考虑地基土非线性固结的桩侧负摩阻力计算方法研究[J]. 岩土工程学报, 2016, 38(8): 1417-1424. ZHAO Minghua, HU Qian, YANG Chaowei, et al. Negative skin friction of piles considering nonlinear consolidation of soil[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1417-1424. (in Chinese) |
| [14] |
孙军杰, 王兰民. 桩侧负摩阻力研究中几个基本理论问题的探讨[J]. 岩石力学与工程学报, 2006(1): 211-216. SUN Junjie, WANG Lanmin. Discussion on some important theoretic problems of investigation for negative skin friction of pile foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2006(1): 211-216. (in Chinese) DOI:10.3321/j.issn:1000-6915.2006.01.035 |
| [15] |
孔纲强, 周杨, 彭怀风, 等. 负摩阻力作用下桩基中性点位置、下拽力及下拽位移与时间的关系[J]. 中南大学学报(自然科学版), 2016, 47(11): 3884-3889. KONG Gangqiang, ZHOU Yang, PENG Huaifeng, et al. Relationship of neutral point position, dragload or downdrag of pile versus time under negative skin friction[J]. Journal of Central South University(Science and Technology), 2016, 47(11): 3884-3889. (in Chinese) |
| [16] |
肖俊华, 袁聚云, 赵锡宏, 等. 桩基负摩擦力的下拉荷载与时间关系研究[J]. 岩土力学, 2009, 30(9): 2779-2782. XIAO Junhua, YUAN Juyun, ZHAO Xihong, et al. Studies of relation between drag load and time of negative skin friction of pile foundation[J]. Rock and Soil Mechanics, 2009, 30(9): 2779-2782. (in Chinese) DOI:10.3969/j.issn.1000-7598.2009.09.041 |
| [17] |
马露, 王钰轲, 于敏, 等. 基于有效应力法的单桩负摩阻力计算[J]. 水文地质工程地质, 2017, 44(1): 71-77. MA Lu, WANG Yuke, YU Min, et al. Calculation of negative skin friction of pile based on effective stress method[J]. Hydrogeology & Engineering Geology, 2017, 44(1): 71-77. (in Chinese) |
| [18] |
薛玉.强夯后黄土地基中桩的承载特性研究[D].西安: 西安建筑科技大学, 2009. XUE Yu. Researches on load-bearing characteristics of pile in loess foundation after dynamic consolidation[D]. Xi'an: Xi'an University of Architecture and Technology, 2009. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10703-2009135934.htm |
| [19] |
刘明.新近深厚填土桩基负摩阻力计算及特性研究[D].湘潭: 湖南科技大学, 2014. LIU Ming. Research on the calculation and characteristic of negative friction of pile foundation in newly thick fill[D]. Xiangtan: Hunan University of Science and Technology, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10534-1015015224.htm |
| [20] |
侯书利, 蒋世林, 李文明, 等. 开山石厚填土滨海场地桩基设计[J]. 建筑结构, 2016, 46(24): 61-65. HOU Shuli, JIANG Shilin, LI Wenming, et al. Pile foundation design of coastal site with thick hillstone backfill[J]. Building Structure, 2016, 46(24): 61-65. (in Chinese) |
| [21] |
Chen R P, Zhou W H, Chen Y M. Influences of soil consolidation and pile load on the development of negative skin friction of a pile[J]. Computers and Geotechnics, 2009, 36(8): 1265-1271. DOI:10.1016/j.compgeo.2009.05.011 |
| [22] |
中华人民共和国住房和城乡建设部.建筑桩基技术规范: JGJ 94-2008[S].北京: 中国建筑工业出版社, 2008. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical Code for Piles of Buildings: JGJ94-2008[S]. Beijing: China Architecture & Building Press, 2008. (in Chinese) |
| [23] |
童小东, 黎冰. 土力学[M]. 武汉: 武汉大学出版社, 2014. TONG Xiaodong, LI Bing. Soil Mechanics[M]. Wuhan: Wuhan University Press, 2014. (in Chinese) |
| [24] |
张雁, 刘金波. 桩基手册[M]. 北京: 中国建筑工业出版社, 2009. ZHANG Yan, LIU Jinbo. Pile foundation manual[M]. Beijing: China Architecture &Building Press, 2009. (in Chinese) |
| [25] |
屠毓敏. 承受超载作用的桩基性状研究[J]. 土木工程学报, 2002, 35(1): 79-82. TU Yumin. Study on the behavior of pile foundation under overload[J]. China Civil Engineering Journal, 2002, 35(1): 79-82. (in Chinese) DOI:10.3321/j.issn:1000-131X.2002.01.016 |
| [26] |
Desai C S, Drumm E C, Zaman M M. Cyclic testing and modeling of interfaces[J]. Journal of Geotechnical Engineering, 1985, 111(6): 793-815. DOI:10.1061/(ASCE)0733-9410(1985)111:6(793) |
| [27] |
Uesugi M, Kishida H, Tsubakihara Y. Friction between sand and steel under repeated loading[J]. Soils and Foundations, 1989, 29(3): 127-137. DOI:10.3208/sandf1972.29.3_127 |
| [28] |
Rajapakse R. Negative Skin Friction and Bitumen-Coated Pile Design[M]//Rajapakse R. eds. Pile Design and Construction Rules of Thumb. Elsevier, 2008: 263-278.
|
| [29] |
Huang T, Zheng J H, Gong W M. The group effect on negative skin friction on piles[J]. Procedia Engineering, 2015, 116: 802-808. DOI:10.1016/j.proeng.2015.08.367 |
| [30] |
肖俊华, 袁聚云, 赵锡宏. 桩基负摩擦力的试验模拟和计算应用[M]. 北京: 科学出版社, 2009. XIAO Junhua, YUAN Juyun, ZHAO Xihong. The experimental simulation and calculation of negative skin friction on piles[M]. Beijing: Science Press, 2009. (in Chinese) |
| [31] |
Liu J Y, Gao H M, Liu H L. Finite element analyses of negative skin friction on a single pile[J]. Acta Geotechnica, 2012, 7(3): 239-252. DOI:10.1007/s11440-012-0163-x |
| [32] |
Rajapakse R.Negative skin friction (downdrag)[M]. Pile Design and Construction Rules of Thumb (Second Edition), Rajapakse R, Butterworth-Heinemann, 2016, 213-223.
|
| [33] |
Chen R P, Zhou W H, Chen Y M. Influences of soil consolidation and pile load on the development of negative skin friction of a pile[J]. Computers and Geotechnics, 2009, 36(8): 1265-1271. DOI:10.1016/j.compgeo.2009.05.011 |
 2019, Vol. 42
2019, Vol. 42


